2. 信息工程大学地理空间信息学院, 郑州 450001;
3. 西安测绘研究所, 西安 710054;
4. 61365部队, 天津 300000
2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. 61365 Troops, Tianjin 300000, China
传统基于等角地理网格的地球重力场描述面临着许多无法克服的局限性,包括网格面积不等、重力场平滑因子复杂、观测数据冗余、积分离散化误差大等,而六边形的“离散球面网格系统”(Discrete Global Grid System, DGGS)因其良好的特性,在遥感、气象、水文等领域取得了广泛应用(Sahr et al., 2003). 作为地理网格的延伸,美国著名学者富勒(Fuller)最早进行了球面离散化的相关研究并且发明了“网格球顶”(Geodesic Dome)结构,之后许多学者关于球面网格系统的研究都直接或间接地受到了他的影响(张永生等, 2007). 近年来,随着DGGS网格系统不断完善,其已经在诸如矢量数据结构(Dutton,1999)、空间数据索引(Dutton, 1996a)、制图综合(Dutton, 1996b)、全球动态数据结构(Goodchild and Shiren, 1992)、全球土地监测(Suess et al., 2004)、全球海洋分析(Kidd et al., 2003)、全球气候模型(Randall et al., 2002)、海洋路径规划、城市交通规划(Brodsky, 2018)等方面得到了应用.
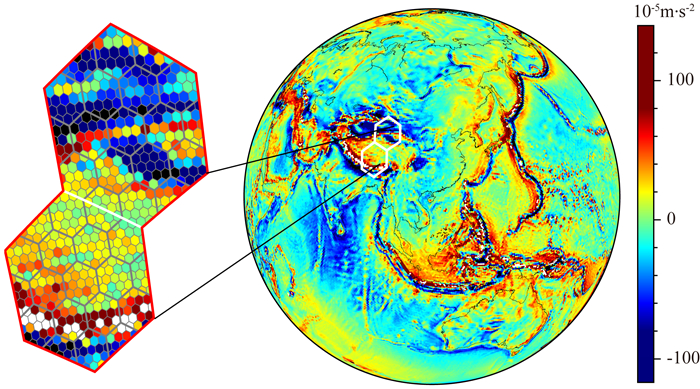
基于六边形的DGGS网格本应在重、磁场这一类具有各向同性特征的物理场中发挥更大作用,但是目前相关研究很少. 类六边形网格结构在重磁场应用方面,Vestine等(1963a, 1963b)较早研究了基于球面均匀分布点的地磁场的Poisson积分应用,Eicker(2008)将多种点位均匀分布方式引入到径向基函数中进而求解卫星重力场取得了较好结果,Slobbe等(2012)将Fibonacci均匀分布引入球形斯列普基函数求解平均海水面和海面地形,Ran等(2018)将Fibonacci格网用于Mascon方法来反演冰盖质量变化,以上均是在数值积分求解方面引入均匀分布结构,而鲜有在球谐分析与综合中开展研究,其中最主要的原因在于,基于六边形网格系统的点位并不像地理网格那样是等纬度分布的,如图 1所示,从而需要大量缔合Legendre函数(associated Legendre functions, ALFs)的求解,这对计算能力提出了更高要求(Pavlis, 1988; 李新星等, 2014; 田家磊等, 2018).
|
图 1 基于全球六边形网格的360阶全球重力异常分布图 Fig. 1 360-degree gravity anomaly values based on global hexagonal grids |
同时, 观测资料的精度与数量的增多使得对应球谐展开的阶次也不断升高, 对计算能力同样提出了挑战. 例如目前有720阶次的NGDC-720地壳磁异常模型(Maus, 2010), 有经典的2160阶次地球重力场模型EGM2008(Pavlis et al., 2012), 还有10800阶次的地形、布格异常、均衡异常模型(Balmino et al., 2012; Hirt and Rexer, 2015). 受限于球谐展开所需庞大的计算量, 现有网格数据的分辨率已经远远走在现有模型阶次对应分辨率的前列. 例如地磁场的磁异常网格数据EMAG2v3分辨率达到2′, 根据Nyquest采样定律, 因磁场为偶极子场, 其对应10800阶次的球谐展开; sandwell和DTU15版本的海洋卫星测高重力异常分辨率达到1′(Sandwell and Smith, 2008; Andersen and Knudsen, 2016), 因重力场为标量场, 所以其对应10800阶次; GEBCO2014和GEBCO2019海底地形网格数据的分辨率分别达到了30″和15″, 对应21600和43200阶次; SRTM3、ARTER和ALOS全球DEM数据分辨率分别达到90 m、30 m和12 m, 对应的球谐展开阶次更高, 因此, 球谐展开中的严重耗时问题也是急需解决的.
针对ALFs及其相应积分、导数等函数的计算问题, 许多学者从递推方法、计算精度、计算效率和溢出问题等方面做了大量的工作. 对于ALFs的递推方法, 主要包括行推法、列推法、Belikov和跨阶次递推等四种方法, 其中Belikov方法的计算效率最佳(李新星, 2013). 为了解决递推过程中的溢出问题, Fukushima (2012)提出了X数法实现了任意阶次ALFs的递推计算, 代价是损失了一定的计算效率; Xing等(2020)改进了Belikov方法, 解决了Belikov原递推公式在高阶次出现溢出的情况, 例如纬度为75°的ALFs当阶次达到4800时,ALFs的计算出现溢出; 张传定等(2004)首次提出ALFs的跨阶次递推方法, 并经验证在20000阶次以内其计算准确且不会发生溢出(于锦海等, 2015).
关于ALFs递推计算效率的进一步提升, 目前还没有较为显著的方法. 学者大多绕过ALFs的计算, 通过尽量减小ALFs的计算量来寻求提升球谐综合(Spherical Harmonic Synthesis, SHS)和球谐分析(Spherical Harmonic Analysis, SHA)计算效率的方法, 例如在SHS和SHA中要求相应的计算点等纬度网格分布, 从而计算同一纬圈上所有点的模型值只需要计算一次该纬度的ALFs. Clenshaw(1957)提出Clenshaw求和方法避免大部分Legendre函数值的求解来提高SHS的计算效率, 同时快速傅里叶变换(Fast Fourier Transform, FFT)技术的使用大大加速了球谐分析与综合的计算, 例如Colombo(1981)在球谐分析中使用了一维FFT, Sneeuw和Bun (1996)利用球面到轮胎面映射实现了二维FFT的球谐分析与综合. 尽管FFT技术加快了SHS的计算速度, 但其仅限于在计算规则网格分布下具有相同高度的点集, 针对非等纬度、不同高度分布点的SHS和SHA, 有学者采用了泰勒级数展开或等间隔内插的思想来提升效率(Kunis and Potts, 2003; Moazezi et al., 2016; Seif et al., 2018).
实际应用中, 更多是针对局部重力场或磁场数据的处理, 为了解决因球谐方法计算量庞大而不便于局部使用的问题, 学者们避开球谐模型, 使用局部拟合、等效源、矩谐分析、球冠谐分析等方法来进行局部物理场的建模(徐文耀和朱岗昆, 1984; 高金田等, 2005; Younis, 2013), 而上述方法存在的边界效应、基函数不正交、非整阶Legendre递推等问题还需要深入研究, 如果球谐模型变得更加高效, 也必然能够在局部重磁场模型构建中发挥重要作用.
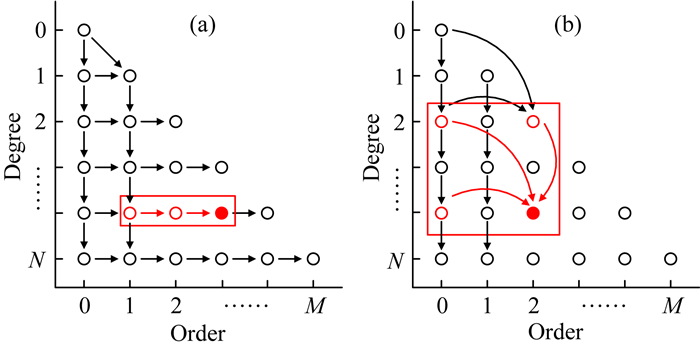
本文从ALFs求解方面入手, 寻求提升其计算效率的方法. Jekeli等(2007)总结了不同纬度下ALFs函数值的量级随阶次升高的衰减关系, 通过利用图 2a所示的逆向行推方法, 求解ALFs值的有效部分, 对于绝对值较小(例如<10-15)的值默认为0而不进行计算, 从而节约了递推过程中的计算量, 在全球SHS过程中, 该方法理论上能够节约36%的计算量, 但是由于其逆向行推方法计算效率偏低, 并没有给出最终的计算耗时比较.
|
图 2 ALFs的逆向行推法(a)和跨阶次递推(b)方法 Fig. 2 The increasing order (a) and cross-degree-order (b) recursion formula for ALFs |
本文利用该思想, 结合跨阶次递推方法, 提出了非全次Legendre(Non-full-order Legendre, NFOL)计算方法, 实现了高纬度区域任意点的快速球谐综合. NFOL方法是在利用跨阶次递推方法计算ALFs时, 当递推到达ALFs有效值(例如>10-15)边界即可停止递推, 从而减小计算量, 提升效率, 由于有效值分布在全部“阶”中“次”偏小的区域, 所以该递推只需要递推全部阶的部分“次”.
对于中低纬度的ALFs计算, 由于ALFs有效值区域几乎遍布整个阶次, 所以NFOL方法在低纬度区域并不适用, 针对该问题, 本文引入球谐旋转变量变换(Spherical Harmonic Rotation, SHR)方法, 该方法实现了坐标系旋转下, 对球谐展开系数的变换. 利用该方法将低纬度待求解区域的中心通过坐标系旋转移至北极点, 从而使得旋转后的点位均位于“高纬度”, 使得与之对应的ALFs有效值区域集中于低“次”部分, 从而可采用NFOL方法提升SHS效率.
SHR方法在多领域具有重要作用. 地磁场模型中, 该方法对于不同坐标系下磁场模型球谐系数间的比较、日变磁场Sq的内/外源场分离等具有重要作用(De Santis et al., 1996). 该方法求解过程中, Wigner D矩阵起到了重要的作用, 许多学者研究了D矩阵及其递推求解方法(Aubert, 2013; Fukushima, 2017).国内, 许厚泽和蒋福珍(1964)较早研究了SHR原理并推导了公式, 其在飞行器轨道扰动引力快速赋值中得到应用(任萱, 1985; 郑伟等, 2011; 王建强等, 2013), 但是这些应用中采用的球谐系数阶次较低, 且其变换精度均没有经过严格的精度评估. Fukushima (2017)利用X数法实现了2160阶次球谐系数的90°旋转.
本研究基于NFOL和SHR方法, 分别实现了高纬度南极地区低分辨率的六边形网格点重力异常、低纬度加里曼丹岛地区的高分辨率六边形网格点重力异常的构建, 通过比较分析, 验证了方法的精度与效率, 得到了有益结果, 成果值得推广.
1 非全次Legendre函数的递推 1.1 球谐展开基本公式对于球面上的平方可积函数, 通过SHA能够得到对应的球谐展开系数, 这里以重力场中重力异常的球谐展开为例, 其与重力场位系数之间的关系如下:
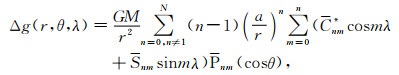
|
(1) |
其中, Δg是球坐标为(r, θ, λ)的点的空间(或自由)重力异常, θ表示地心余纬, λ表示地心经度, r表示点至地心的距离, GM为地心引力常数, a是参考半径, (GM, a)由位模型所采用的地球参考椭球决定(EGM2008模型使用的a为6378137 m), N为模型截断阶次, (Cnm*, Snm)表示扰动位系数, 利用引力位系数(Cnm, Snm)和正常位偶阶带谐项系数C′nm计算得到, 正常位偶阶带谐项系数只需要考虑(C′20、(C′40、(C′60、(C′80这4个即可满足精度要求.
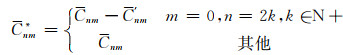
|
(2) |
Pnm(cosθ)是完全正常化(或归一化、标准化)缔合勒让德函数, 其与非正常缔合勒让德多项式Pnm(cosθ)之间满足以下关系式:
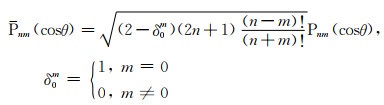
|
(3) |
需要注意的是, 在地磁场中常用施密特(Schmidt)半正常化缔合勒让德函数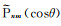
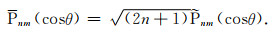
|
(4) |
考虑到跨阶次递推方法稳定,不会发生溢出导致计算错误, 且计算效率相对较高, 本文Pnm(cosθ)的计算采用跨阶次递推方法. 当m<2时, 采用列推公式(5)求解m=0和m=1时的Pnm(cosθ)(Colombo, 1981).
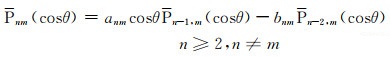
|
(5) |
其中
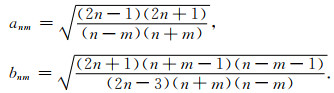
|
(6) |
递推初始值为
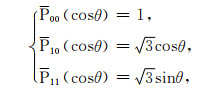
|
(7) |
当m≥2时, 采用以下递推公式(于锦海等, 2015):
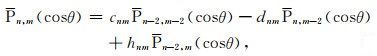
|
(8) |
其中
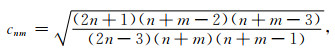
|
(9) |
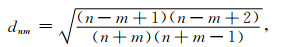
|
(10) |
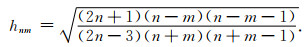
|
(11) |
当m>2时, 递推系数cnm, dnm, hnm的值均小于1, 因此跨阶次递推是稳定可靠的, 递推过程如图 2b所示.
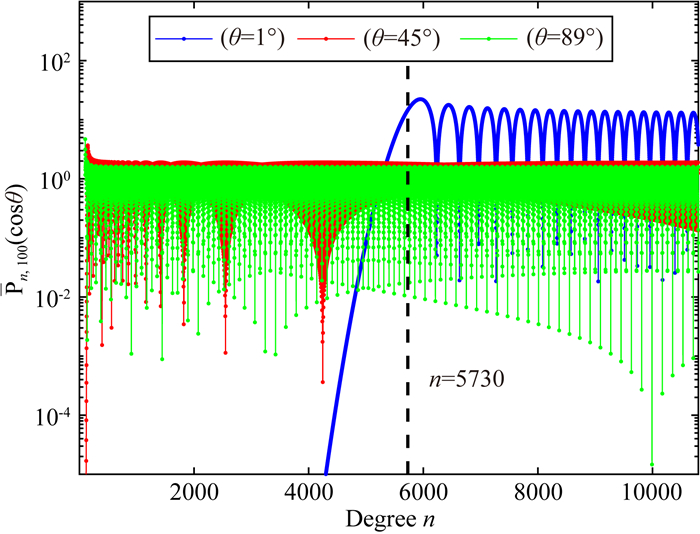
1.2 非全次Legendre方法为了说明ALFs函数值的特点, 这里利用跨阶次递推方法精确计算了余纬为1°、45°和89°且m=100的Pnm(cosθ)值, 见图 3, 由此可以看出, 同一纬度m相等的Pnm(cosθ)值, 其较大的值在同一水平, 且这些较大值是影响递推精度的主要部分.
|
图 3 m=100时, θ=1°、45°和89°的ALFs的大小 Fig. 3 The value of ALFs with θ=1°, 45° and 89° when m=100 |
基于ALFs值的以上特点, 当m固定时, 令余纬θ处的Pnm(cosθ)值近似为一个平均值, 令其为常数C, 即Pnm(cosθ)≈Pn-1, m(cosθ)≈Pn-2, m(cosθ)=C, 那么当n足够大时, 可近似认为2n+1≈2n-1≈2n, n-1≈n, 根据公式(5)、(6)可以得到
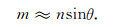
|
(12) |
当θ=1°, m=100时, 求解得到n≈5730, 这正是Pnm(cosθ)值发生突变的位置, 见图 3黑线部分, 也就是说n>m/sinθ是保证Pnm(cosθ)的值与C为同量级的条件, 一旦越过该范围, Pnm(cosθ)值会迅速衰减为0.
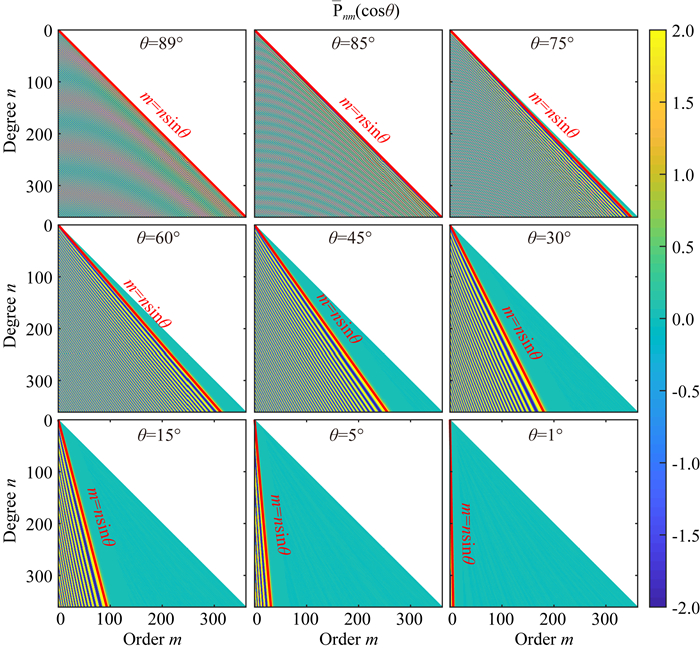
上述阶n和次m之间的这种简单线性关系, 很好地将整个ALFs值域中的正常振荡区域和快速衰减区域划分开来. 为了更加清晰地展示这一特殊直线的意义, 我们计算了不同纬度处360阶次的Pnm(cosθ)值, 其值大小及绝对值的量级分别如图 4、图 5所示.
|
图 4 ALFs值中稳定振荡区与快速衰减区的分界线, 图中绿色区域值较小, 近似为0 Fig. 4 The boundary between the stable oscillation zone and the fast decay zone of the value of ALFs, the green area in the figure illustrates that the value is extremely small, approximately 0 |
|
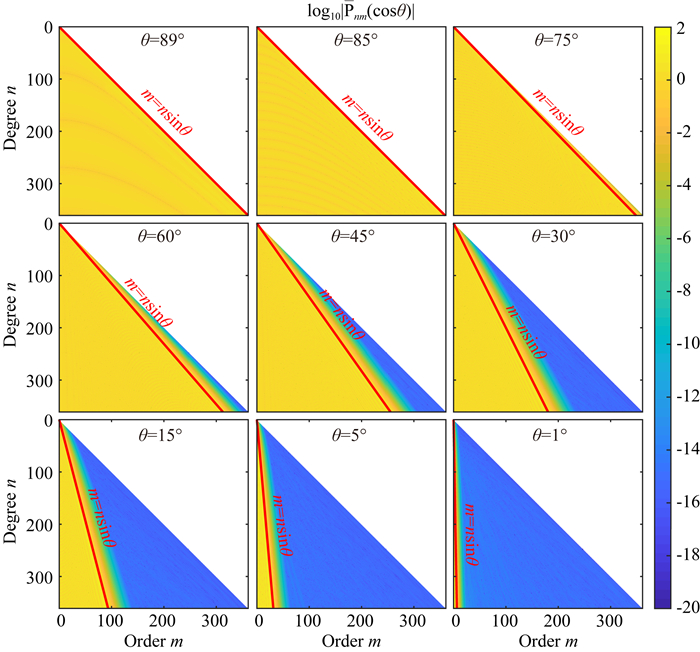
图 5 分界线周边ALFs值的衰减过程, 图中蓝色区域值小于10-20, 可近似为0 Fig. 5 The decay process of the values of ALFs near the boundary, the blue area in the figure represents that the values are less than 10-20, approximately 0 |
因此, 在高纬度区域的ALFs递推计算中, 分界线右侧值近似为0的Pnm(cosθ), 在不参与后续阶次递推的情况下, 可不再计算, 因此理论上可节约原来(1-sinθ)×100%的计算量或计算时间, 当计算θ=30°的Pnm(cosθ)时, 理论耗时是原来的一半.
由于ALFs的值在该分界线周边有一个衰减过程, 如图 5所示, 因此想要保证整个ALFs的计算精度, 不能直接以式(12)所给出的直线作为分界线, 而应该适当地向m增大和n减小的方向移动该直线, 得到新的分界线
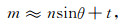
|
(13) |
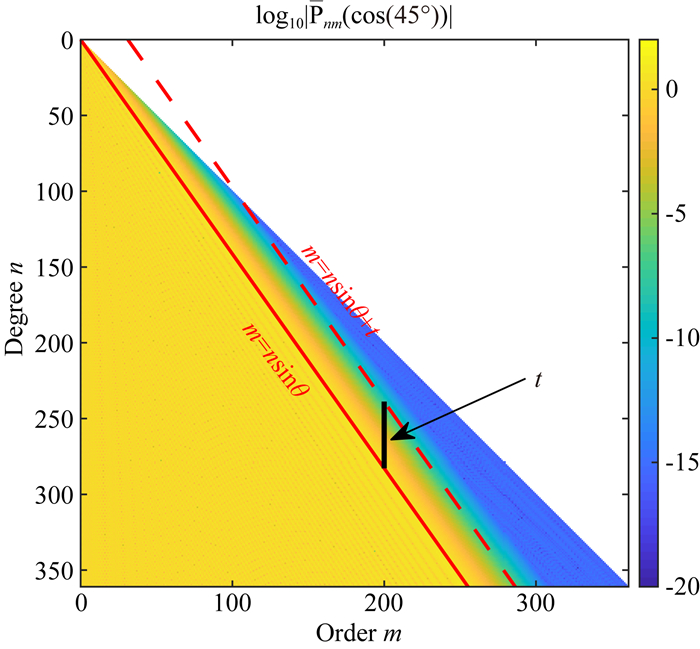
其中参数t的大小决定了ALFs递推值的精度和计算效率, t越大, 精度越有保证, 但ALFs需要递推的区域会变大(见图 6), 相应计算效率会降低, 关于参数t的确定, 会在后续实验部分给出.
|
图 6 参数t的含义 Fig. 6 The meaning of parameter t |
因此, 上述方法确定了ALFs的递推范围, 我们开创性地避开Jekeli等(2007)所采用的逆向行推方法, 采用跨阶次递推方法计算了非全次递推范围内的ALFs值, 解决了逆向行推不稳定且计算效率低下的问题.由图 5可知, 对于非高纬度位置处的ALFs, 显然上述方法并不能有效提升计算效率, 因此引入球谐系数的旋转变量变换, 通过换极将计算区域移至“高纬”区域, 从而提升计算效率.
2 球谐旋转变量变换(SHR) 2.1 沿z轴的旋转变换已知球面上一点Q(r, θ, λ), 当坐标系O-xyz沿着z轴旋转α角, 记为Rz(α), 得到新的坐标系O-x′y′z, 则Q点在新坐标系下的球坐标为(r, θ, λ1), 其中λ1=λ-α, 即λ=λ1+α,如图 7所示.

|
图 7 沿z轴的坐标系旋转 Fig. 7 Rotation of the coordinate system along axis z |
因此Q点的重力异常在新的球坐标系O-x′y′z下可展开为新的球谐系数
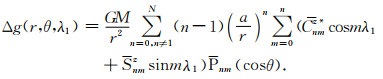
|
(14) |
根据λ与λ1的以下三角关系式:
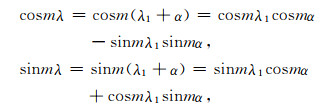
|
(15) |
代入式(1)并与式(14)进行比较, 可得两个坐标系下球谐系数之间的关系
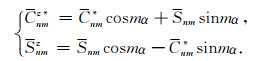
|
(16) |
式(16)即为坐标系沿z轴旋转α角时, 对应的球谐系数的变换公式.
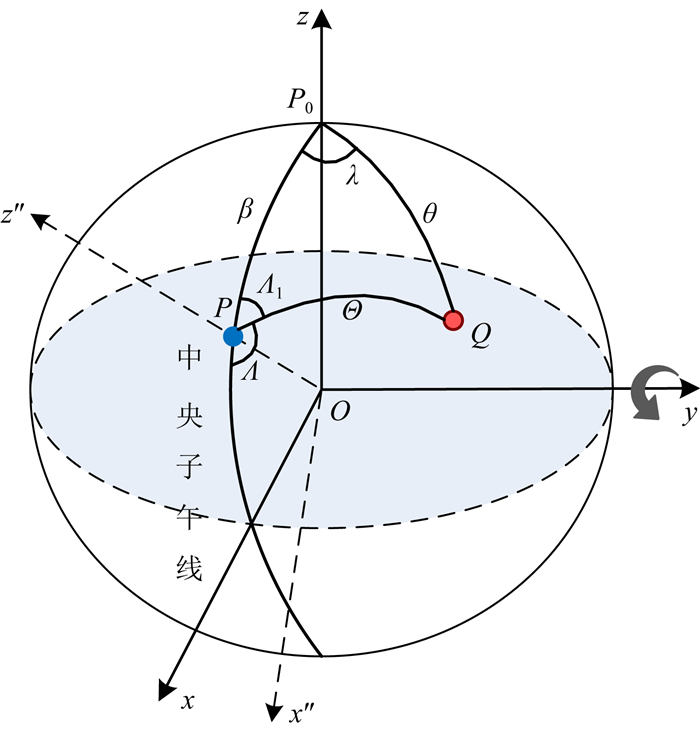
2.2 沿y轴的旋转变换已知球面上一点Q(r, θ, λ), 当坐标系O-xyz沿着y轴旋转β角, 记为Ry(β), 得到新的坐标系O-x″yz″.
如图 8, Q点在新坐标系下的球坐标为(r, Θ, Λ), 其中Θ为新坐标系下的球心余纬, Λ为新坐标系下的球心经度, Λ1与Λ互补, Q点的重力异常在新的球坐标系O-x″yz″下可展开为新的球谐系数, 表达式与式(1)类似,
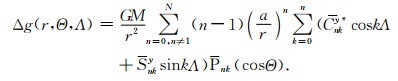
|
(17) |
|
图 8 沿y轴的坐标系旋转 Fig. 8 Rotation of the coordinate system along axis y |
为寻找(Cnmy*, Snmy)与(Cnm*, Snm)之间的变换关系, 借助球面三角形P0PQ中(θ, λ)与(Θ, Λ1)之间的球面三角公式, 许厚泽和蒋福珍(1964)通过确定Pnm(cosΘ)cosmΛ1、Pnm(cosΘ)sinmΛ1与Pnm(cosθ)cosmλ、Pnm(cosθ)sinmλ之间的关系, 从而确定系数之间的如下转换:
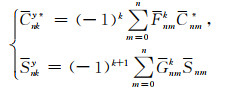
|
(18) |
基于许厚泽和蒋福珍(1964)给出的方法推导了转换参数(Fnmk, Gnmk)的初始值及递推表达式
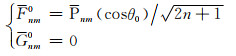
|
(19) |
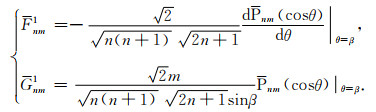
|
(20) |
当n=m时(图 9b所示), Fnmk, Gnmk的递推公式为

|
(21) |

|
(22) |
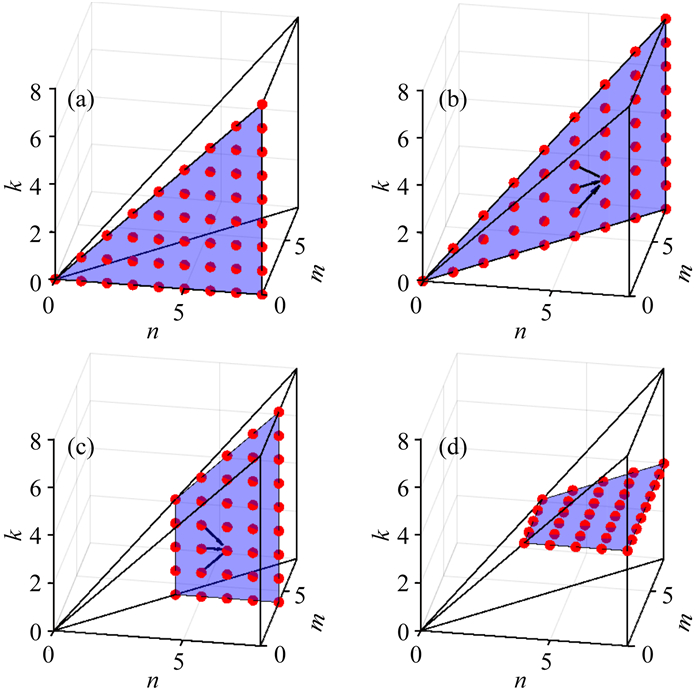
|
图 9 转换参数(Fnmk, Gnmk) 的递推关系示意图 (a) 公式(19), m=0; (b) 公式(21), m=n; (c) 公式(24), m=4; (d) 公式(26), k=4 Fig. 9 Schematic diagram of the recursion relationships of the transformation parameters (Fnmk, Gnmk) (a) Eq.(19), m=0; (b) Eq.(21), m=n; (c) Eq.(24), m=4; (d) Eq.(26), k=4. |
其中
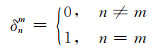
|
(23) |
当m固定的时候(图 9c所示), (Fnmk, Gnmk)满足如下递推公式:
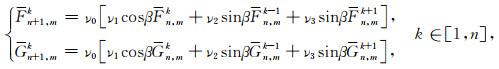
|
(24) |

|
(25) |
该公式纠正了任萱(1985)中给出的ν2=κ2这一错误, 该错误在之后多篇文献中普遍使用.图 9a—c展示了上述递推关系, 这里我们还总结归纳了(Fnmk, Gnmk)以下的对称结构
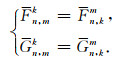
|
(26) |
(26) 式可利用D函数的对称性及其与该两组变量之间的对应关系得证, 具体见Aubert(2013), 即图 9d中k=4与图 9c中m=4对应的元素值相等.
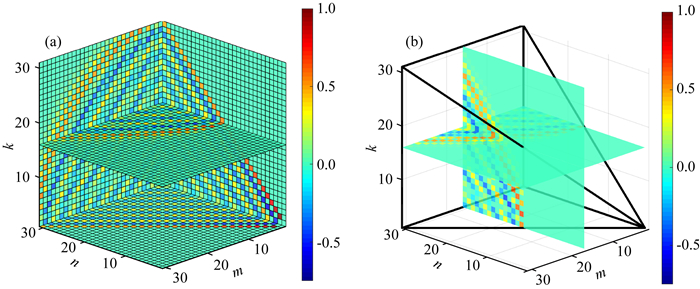
图 10a展示了β=90°的30阶Fnmk值的切片图, 为了说明式(26)的对称结构, 图 10b分别列出了m=15和k=15的切片, 由该图可知, 两切片值是对应相等的.
|
图 10 β=90°的30阶Fnmk值的切片图 (a) 30阶球谐转换矩阵Fnmk的值; (b) Fn, 15k与Fn, m15比较说明式(29)对称结构. Fig. 10 Slice graph of the value of Fnmk with β=90° and the n up to 30 (a) Values of transformation matrix of Fnmk up to 30 degrees; (b) Symmetrical structure of Fn, 15k and Fn, m15 in Eq.(29). |
然而, 实践证明, 基于上述公式的(Fnmk, Gnmk)递推并不稳定, 当n大于200后, (Fnmk, Gnmk)的值会发生量级上的变化, 导致最终球谐系数变换的失败. 为了解决该问题, 本文引入Fukushima(2017)的X-数法进行球谐系数沿y轴90°旋转的变换, 并对其进行改进实现了沿y轴任意角度的旋转变换. 这里补充一点, Aubert (2013)给出了一种改进的“稳定”的(Fnmk, Gnmk)递推方法, 经实验验证, 该递推虽然能够保证(Fnmk, Gnmk)有效值的稳定递推, 但是该递推在(Fnmk, Gnmk)的理论值趋近于0过程中会发散, 后续递推结果失真从而污染有效值, 如何有效解决发散问题还有待研究, 这一点需要注意.
2.3 沿y轴90°的旋转变换当β=90°时, Fnmk与Gnmk的值是“棋盘分布”的, 即0值是间隔分布的(如图 10所示, 其中绿色表示值为0), 且对于不同的n、m、k, 当Fnmk=0时, Gnmk≠0, 反之亦然, 根据Aubert(2013)总结的(Fnmk, Gnmk)与Wigner-D函数之间的关系, 有

|
(27) |
其中
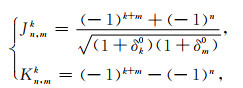
|
(28) |
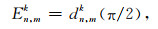
|
(29) |
式中dn, mk(θ)是转角为θ的Wigner-D函数, 其定义见Edmonds(1957), 该函数可通过超几何函数、递推等多种方法求解.Kostelec和Rockmore(2008)给出了D函数的稳定递推方法, 由Fukushima (2017)总结如下:
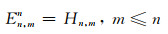
|
(30) |
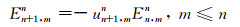
|
(31) |
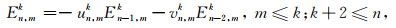
|
(32) |
其中
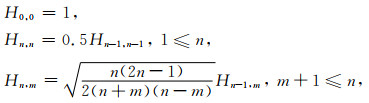
|
(33) |
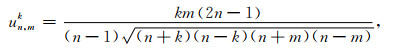
|
(34) |
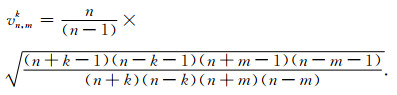
|
(35) |
上述递推方法的计算过程中, Hn, m随着n的增大快速减小, 当其绝对值小于2.225×10-308的时候, 数值发生溢出而强制为0, 会影响后续递推工作, 因此在该递推过程中应使用X-数法进行求解.
X-数法的基本思想是, 为Hn, m和En, mk变量附加一个整数类型的变量hn, m和en, mk, 该整数的初始值为0, 当Hn, m、En, mk大于2480(≈3.12×10144)时, 令Hn, m、En, mk乘以2-480(≈3.20×10-145), 使其值回归到有效范围内, 同时对应的变量hn, m和en, mk加1, 用来记录Hn, m、En, mk的指数部分, 同理, 当Hn, m、En, mk小于2-480时, 令Hn, m、En, mk乘以2480, 使其值回归到有效范围内, 同时对应的变量hn, m和en, mk减1, 最终的值即为Hn, m×2480hn, m、En, mk×2480en, mk, 详细参数及步骤参见Fukushima(2012, 2017).
2.4 将(θ, λ)视为北极点的旋转变换对笛卡尔坐标系进行旋转, 使得地面上一点Q(r, θ, λ)落在新坐标系的z轴上, 即北极点位置, 由图 7和图 8可知, 只需要先沿z轴旋转λ, 再沿y轴旋转θ即可, 即Ry(θ)Rz(λ).然而, 如前面2.1和2.2节所述, 沿z轴的系数变换简单高效, 而沿y轴旋转计算复杂, 且任意角的球谐系数变换中的转换参数(Fnmk, Gnmk)递推不稳定, 但是沿y轴旋转90°的球谐系数变换则可利用X-数法得到, 因此可对Ry(θ)Rz(λ)进行调整, 实现快速稳定的变换.
Zotter (2009)文中指出, Ry(θ)可分解为以下旋转的组合:
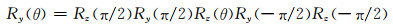
|
(36) |
还可以写为

|
(37) |
因此, 只需要计算沿y轴旋转90°的球谐系数变换以及简单的z轴变换, 就可以实现任意角度的旋转变换, 即
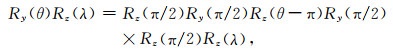
|
(38) |
其中系数的变换采用公式(16)和(18).
3 数值实验及分析为了验证NFOL和SHR方法在局部六边形网格重力场快速球谐综合方面的应用, 共进行三个实验, 计算环境如下:2.30GHz主频的Intel Core i5-6200U CPU和8 GB主内存的PC机, 64位Windows XP OS操作系统下VS2017编译环境.
3.1 参数t的确定第1节中指出, 使用NFOL方法进行球谐综合, 需要确定公式(13)中的参数t, t取值越大, 计算精度越高而对应效率越低, 反之亦然. 因此, 需要在满足精度要求的情况下, 合理的选择t的大小来提高球谐综合的计算效率.
利用2160阶2159次的EGM2008模型位系数, 计算地球表面点的模型重力异常值, 利用不同纬度、不同t取值的NFOL方法计算重力异常, 并与常规全阶次方法计算的结果作为真值进行比较, 结果统计见表 1.
|
|
表 1 不同纬度、不同t的2160阶NFOL方法的球谐综合结果统计 Table 1 Statistics of spherical harmonic synthesis results of 2160-degree non-full order Legendre methods with different t at different latitudes |
通过以上试验, 采用2160阶次模型进行计算时, 如果t取0, 计算结果是错误的, 说明t参数不能省略, 取t=110可保证地面任意点位10-19m·s-2量级的计算精度, 因此后续实验采用t=110. 同时发现, 当纬度低于45°的时候, 利用NFOL方法并没有明显的优势, 纬度为60°~70°时利用NFOL方法效率提升近1倍.
3.2 南极地区(高纬度)六边形网格重力场计算本文基于张永生等(2007)所采用的基于二十面体的Synder等积投影(Synder, 1992)及相应剖分方法生成ISEA4H(Icosahedral Snyder Equal Area aperture 4 Hexagon)网格系统, 其中南极区域内包含17732个非等纬度分布的六边形网格点, 单个网格平均实地面积780 km2, 网格平均间距约15.76 km. 这里利用2160阶次EGM2008模型, 采用全次和NFOL两种方法计算网格点处的重力异常值, 验证NFOL方法在高纬度区域球谐综合中的计算效能和精度, 其计算结果和精度统计见表 2和图 11、图 12.
|
|
表 2 NFOL方法求解南极地区17732个点重力异常的性能统计(单位:10-5m·s-2) Table 2 Performance of the non-full order Legendre method for calculating 17732 point gravity anomalies in Antarctica (Unit: 10-5m·s-2) |
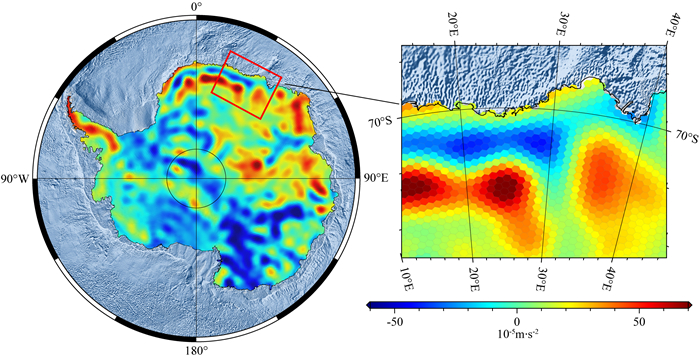
|
图 11 南极地区17732个六边形网格点重力异常分布 Fig. 11 Distribution of gravity anomalies at 17732 hexagonal grid points in Antarctica |

|
图 12 南极地区六边形网格点重力异常NFOL解的精度 Fig. 12 Accuracy of gravity anomalies calculated by the non-full order Legendre method on hexagonal grids in Antarctica |
由以上图表可见, NFOL方法能够保证平均10-19m·s-2量级精度水平的重力异常球谐综合, 计算耗时不到常规全阶次求解耗时的一半, 具有明显的性能提升. 需要注意的是, 当利用NFOL方法计算纬度小于45°的区域重力异常时, 将失去其计算优势. 为了将NFOL方法应用于中低纬度区域, 我们结合SHR方法, 构建位于赤道附近的加里曼丹岛区域的六边形高分辨率网格重力场.
3.3 加里曼丹岛区域(低纬度)六边形网格重力场计算利用高分辨率的ISEA4H网格结构剖分加里曼丹主岛区域, 生成15125个非等纬度分布的六边形网格点, 单个网格平均实地面积48.75 km2, 网格平均间距约3.94 km.
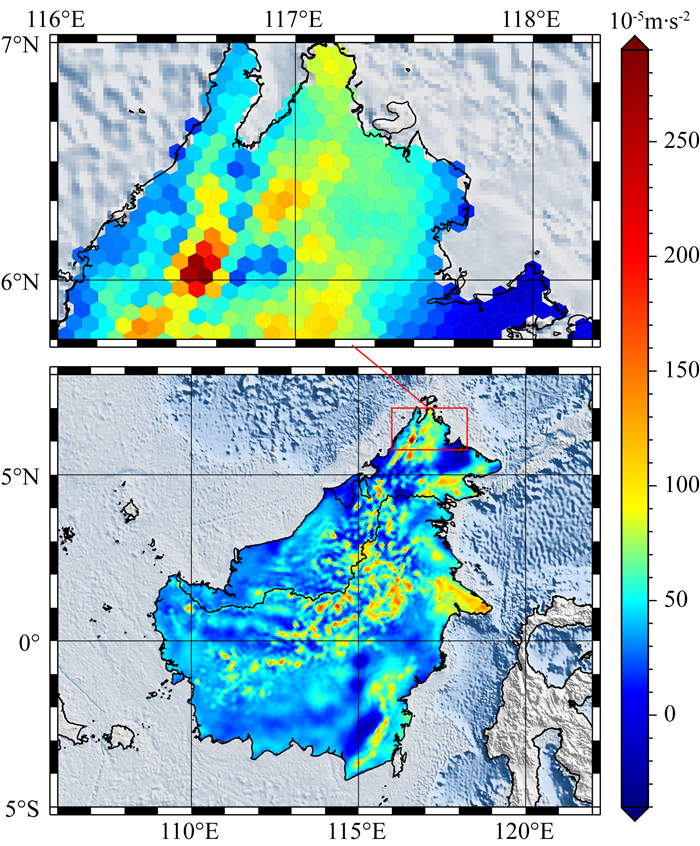
首先确定加里曼丹岛区域中心的地心坐标(θ=89.141°, λ=114.2°), 然后根据2.4节所述方法, 将北极点旋转至该中心点, 利用2160阶次EGM2008模型位系数, 通过(38)式的旋转变换, 得到新的球谐系数EGM2008R, 该转换过程总耗时不足500 s, 通常可根据计算区域的位置提前计算.在旋转变换后的坐标系中, 加里曼丹岛的六边形网格点均位于新北极点附近, 故均属于“高纬”, 因此使用NFOL方法, 以EGM2008R系数和旋转后的坐标作为输入, 计算15125个点的重力异常值, 并与利用EGM2008模型和旋转前的坐标、基于常规全阶次方法的计算结果进行比较, 结果见表 3以及图 13和图 14.
|
|
表 3 SHR+NFOL方法求解加里曼丹岛地区15125个点重力异常的性能统计(单位:10-5m·s-2) Table 3 Performance of the NFOL combined with SHR for calculating 15125 point gravity anomalies in the Kalimantan area (Unit: 10-5m·s-2) |
|
图 13 加里曼丹岛地区15125个六边形网格点基于SHR+NFOL方法计算的重力异常结果 Fig. 13 The results of gravity anomalies calculated by the non-full order Legendre method combined with SHR at 15125 hexagonal grid points in Kalimantan Island area |

|
图 14 加里曼丹岛地区15125个六边形网格点基于SHR+NFOL方法计算重力异常的精度情况 Fig. 14 The accuracy of gravity anomalies calculated by the non-full order Legendre method combined with SHR at 15125 hexagonal grid points in Kalimantan Island area |
本次计算的重力异常的精度水平为10-16m·s-2, 比3.2节中直接使用NFOL方法求解精度水平10-19m·s-2低, 说明SHR由于采用坐标变换和球谐系数的变换, 引入了计算误差, 该误差导致重力异常的计算误差约10-16m·s-2; 同时可以发现, 此次实验中,NFOL方法计算效率是全阶次解的近5倍, 加速效果更加明显, 这说明, 相比3.2节中的大区域、低分辨率六边形网格点重力异常的球谐综合, NFOL方法在小区域、高分辨率离散点的球谐综合中更具优势.
4 结论为实现局部六边形网格重力场元模型值的快速计算, 以南极洲和加里曼丹岛区域的六边形网格点重力异常计算为例, 研究了NFOL和SHR方法在球谐综合快速计算中的应用.
首先, 对ALFs递推过程及其数值特征进行了详细分析, 给出了其值从稳定振荡区到快速衰减区的分界线的理论表达式, 利用分界线表达式对“次”进行有效截断, 联合跨阶次递推, 提出了基于NFOL方法的高纬度点快速球谐综合. 在低纬度区域六边形网格重力异常计算方面, 首次将SHR与NFOL方法结合, 通过坐标系旋转, 将低纬度区域的点变换到“高纬度”区域, 从而利用NFOL方法实现低纬度区域的快速球谐综合. 通过变量变换理论推导, 借助X-数法, 实现了2160阶次球谐系数的任意角度旋转下的变换.
通过数值实验及分析, 我们得到以下结论:对于2160阶次的Legendre递推, 若保证全球任意点处计算重力异常的精度满足10-19m·s-2, ALFs从稳定振荡区到快速衰减区的分界线理论表达式中t的最佳取值为110; 在高纬度区域(≥60°), NFOL方法能够平均提升ALFs求解和球谐综合的效率近1倍, 纬度越高, 效率提升越明显, 最高可提速近10倍, 且在双精度数值运算中, 能够保证重力异常10-19m·s-2的平均精度水平, 基于此构建了南极洲地区的六边形网格重力异常; 在中低纬度区域(<60°), NFOL方法借助SHR, 同样能够实现加速效果, 其重力异常计算精度在10-16m·s-2水平, 精度足够满足应用需求,且本文提出的SHR+NFOL方法在进行小区域高分辨率大量离散点的球谐综合应用中具有明显优势.
需要强调说明, NFOL方法是对ALFs计算效率的提升, 而对于非等纬度点球谐综合的计算效率提升方法还有很多, 例如采用Seif等(2018)提出的Legendre内插方法, 能够更快地实现六边形网格重力异常的计算, 而本文提出的NFOL方法与其他提升球谐综合效率的方法并不冲突(FFT方法除外, 因为其不需要计算ALFs), 加速效果可叠加.
致谢 感谢战略支援部队信息工程大学李姗姗教授对文章提出的指导性修改意见, 贲进、童晓冲教授在生成六边形网格方面给予的帮助和指导.
Andersen O B, Knudsen P. 2016. Deriving the DTU15 Global high resolution marine gravity field from satellite altimetry. Abstract from ESA Living Planet Symposium 2016, Prague, Czech Republic. http://lps16.esa.int/page_session189.php#1558p
|
Aubert G. 2013. An alternative to Wigner d-matrices for rotating real spherical harmonics. AIP Advances, 3(6): 062121. DOI:10.1063/1.4811853 |
Balmino G, Vales N, Bonvalot S, et al. 2012. Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies. Journal of Geodesy, 86(7): 499-520. DOI:10.1007/s00190-011-0533-4 |
Brodsky I. 2018. H3: Uber's Hexagonal Hierarchical Spatial Index. https://eng.uber.com/h3/.
|
Clenshaw C W. 1957. The numerical solution of linear differential equations in Chebyshev series. Mathematical Proceedings of the Cambridge Philosophical Society, 53(1): 134-149. DOI:10.1017/S0305004100032072 |
Colombo O L. 1981. Numerical Methods for Harmonic Analysis on the Sphere. The Ohio State University Department of Geodetic Science and Surveying. Report No. 310.
|
DeSantis A, Torta J M, Falcone C. 1996. A simple approach to the transformation of spherical harmonic models under coordinate system rotation. Geophysical Journal International, 126(1): 263-270. DOI:10.1111/j.1365-246X.1996.tb05284.x |
Dutton G. 1996a. Encoding and handling geospatial data with hierarchical triangular meshes. //Proceedings of the 7th Symposium on Spatial Data Handling. Delft, Netherlands, 505-518.
|
Dutton G. 1996b. Improving locational specificity of map data-a multi-resolution, metadata-driven approach and notation. International Journal of Geographical Information Systems, 10(3): 253-268. DOI:10.1080/02693799608902078 |
Dutton G. 1999. A Hierarchical Coordinate System for Geoprocessing and Cartography. Berlin: Springer-Verlag.
|
Edmonds A R. 1957. Angular Momentum in Quantum Mechanics. Princeton: Princeton University Press.
|
Eicker A. 2008. Gravity field refinement by radial basis functions from in-situ satellite data[Ph. D. thesis]. Bonn: University of Bonn, Institute of Theoretical Geodesy.
|
Fukushima T. 2012. Numerical computation of spherical harmonics of arbitrary degree and order by extending exponent of floating point numbers. Journal of Geodesy, 86(4): 271-285. DOI:10.1007/s00190-011-0519-2 |
Fukushima T. 2017. Rectangular rotation of spherical harmonic expansion of arbitrary high degree and order. Journal of Geodesy, 91(8): 995-1011. DOI:10.1007/s00190-017-1004-3 |
Gao J T, An Z C, Gu Z W, et al. 2005. Selections of the geomagnetic normal field and calculations of the geomagnetic anomalous field. Chinese Journal of Geophysics (in Chinese), 48(1): 56-62. |
Goodchild M F, Shiren Y. 1992. A hierarchical spatial data structure for global geographic information systems. CVGIP: Graphical Models and Image Processing, 54(1): 31-44. DOI:10.1016/1049-9652(92)90032-S |
Hirt C, Rexer M. 2015. Earth2014:1 arc-min shape, topography, bedrock and ice-sheet models-Available as gridded data and degree-10, 800 spherical harmonics. International Journal of Applied Earth Observation and Geoinformation, 39: 103-112. DOI:10.1016/j.jag.2015.03.001 |
Jekeli C, Lee J K, Kwon J H. 2007. On the computation and approximation of ultra-high-degree spherical harmonic series. Journal of Geodesy, 81(9): 603-615. DOI:10.1007/s00190-006-0123-z |
Kidd R A, Trommler M, Wagner W. 2003. The development of a processing environment for time-series analysis of SeaWinds scatterometer data. //2003 IEEE International Geoscience and Remote Sensing Symposium. Toulouse, France: IEEE, 4110-4112.
|
Kostelec P J, Rockmore D N. 2008. FFTs on the rotation group. Journal of Fourier Analysis and Applications, 14(2): 145-179. DOI:10.1007/s00041-008-9013-5 |
Kunis S, Potts D. 2003. Fast spherical Fourier algorithms. Journal of Computational and Applied Mathematics, 161(1): 75-98. DOI:10.1016/S0377-0427(03)00546-6 |
Li X X. 2013. Building of an ultra-high-degree geopotential model[Master's thesis] (in Chinese). Zhengzhou: PLA Information Engineering University.
|
Li X X, Wu X P, Li S S, et al. 2014. The application of block-diagonal least-squares methods in geopotential model determination. Acta Geodaetica et Cartographica Sinica (in Chinese), 43(8): 778-785. DOI:10.13485/j.cnki.11-2089.2014.0110 |
Maus S. 2010. An ellipsoidal harmonic representation of Earth's lithospheric magnetic field to degree and order 720. Geochemistry, Geophysics, Geosystems, 11(6): Q06015. DOI:10.1029/2010GC003026 |
Moazezi S, Zomorrodian H, Siahkoohi H R, et al. 2016. Fast ultrahigh-degree global spherical harmonic synthesis on nonequispaced grid points at irregular surfaces. Journal of Geodesy, 90(9): 853-870. DOI:10.1007/s00190-016-0915-8 |
Pavlis N K. 1988. Modeling and estimation of a low degree geopotential model from terrestrial gravity data. The Ohio State University Department of Geodetic Science and Surveying. Report No. 386.
|
Pavlis N K, Holmes S A, Kenyon S C, et al. 2012. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). Journal of Geophysical Research: Solid Earth, 117: B04406. DOI:10.1029/2011jb008916 |
Ran J, Ditmar P, Klees R, et al. 2018. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. Journal of Geodesy, 92(3): 299-319. DOI:10.1007/s00190-017-1063-5 |
Randall D A, Ringler T D, Heikes R P, et al. 2002. Climate modeling with spherical geodesic grids. Computing in Science and Engineering, 4(5): 32-41. DOI:10.1109/mcise.2002.1032427 |
Ren X. 1985. A new method of calculation for the free flight trajectory when vehicle is effected by the disturbing gravity. Journal of National University of Defense Technology (in Chinese), (2): 41-52. |
Sahr K, White D, Kimerling A J. 2003. Geodesic discrete global grid systems. Cartography and Geographic Information Science, 30(2): 121-134. DOI:10.1559/152304003100011090 |
Sandwell D T, Smith W H. 2008. Global marine gravity and bathymetry at 1-minute resolution. //AGU Fall Meeting Abstracts.
|
Seif M R, Sharifi M A, Eshagh M. 2018. Polynomial approximation for fast generation of associated Legendre functions. Acta Geodaetica et Geophysica, 53(2): 275-293. DOI:10.1007/s40328-018-0216-1 |
Slobbe D C, Simons F J, Klees R. 2012. The spherical Slepian basis as a means to obtain spectral consistency between mean sea level and the geoid. Journal of Geodesy, 86(8): 609-628. DOI:10.1007/s00190-012-0543-x |
Sneeuw N, Bun R. 1996. Global spherical harmonic computation by two-dimensional Fourier methods. Journal of Geodesy, 70(4): 224-232. DOI:10.1007/BF00873703 |
Snyder J P. 1992. An equal-area map projection for polyhedral globes. Cartographica: The International Journal for Geographic Information and Geovisualization, 29(1): 10-21. DOI:10.3138/27h7-8k88-4882-1752 |
Suess M, Matos P, Gutierrez A, et al. 2004. Processing of SMOS level 1c data onto a Discrete Global Grid. //2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage, AK, USA: IEEE, 1914-1917.
|
Tian J L, Li X X, Wu X P, et al. 2018. Fast realization of ultra-high-degree geopotential model by improved leastsquares method. Acta Geodaetica et Cartographica Sinica (in Chinese), 47(11): 1437-1445. DOI:10.11947/j.AGCS.2018.20170659 |
Vestine E H, Sibley W L, Kern J W, et al. 1963a. Integral and spherical-harmonic analyses of the geomagnetic field for 1955.0, Part 1. Journal of Geomagnetism and Geoelectricity, 15(2): 47-72. DOI:10.5636/jgg.15.47 |
Vestine E H, Sibley W L, Kern J W, et al. 1963b. Integral and spherical-harmonic analyses of the geomagnetic field for 1955.0, Part 2. Journal of Geomagnetism and Geoelectricity, 15(2): 73-89. DOI:10.5636/jgg.15.73 |
Wang J Q, Li J C, Wang Z T, et al. 2013. Pole transform of spherical harmonic function to quickly calculate gravity the disturbance on earth-orbiting satellites. Geomatics and Information Science of Wuhan University (in Chinese), 38(9): 1039-1043. DOI:10.13203/j.whugis2013.09.003 |
Xing Z B, Li S S, Tian M, et al. 2020. Numerical experiments on column-wise recurrence formula to compute fully normalized associated Legendre functions of ultra-high degree and order. Journal of Geodesy, 94(1): 2. DOI:10.1007/s00190-019-01331-0 |
Xu H Z, Jiang F Z. 1964. A discussion on the transformation of the development of spherical harmonics of gravity anomaly. Acta Geodaetica et Cartographica Sinica (in Chinese), 7(4): 252-260. |
Xu W Y, Tschu K K. 1984. A study of the RHA for the geomagnetic field of China and neighbouring region. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 27(6): 511-522. |
Younis G. 2013. Regional Gravity Field Modeling with Adjusted Spherical Cap Harmonics in an Integrated Approach. Schriftenreihe Fachrichtung Geodäsie der Technischen Universität Darmstadt.
|
Yu J H, Zeng Y Y, Zhu Y C, et al. 2015. A recursion arithmetic formula for Legendre functions of ultra-high degree and order on every other degree. Chinese Journal of Geophysics (in Chinese), 58(3): 748-755. DOI:10.6038/cjg20150305 |
Zhang C D, Xu H Z, Wu X. 2004. Torus problem of the harmonic analysis in the Earth's gravity field. //Proceedings of Geodesy and Geodynamics Development (in Chinese). Wuhan: Science and Technology Press.
|
Zhang Y S, Ben J, Tong X C. 2007. Theory, Algorithm and Application of the Geoinformatic Discrete Global Grid System (in Chinese). Beijing: Science Press.
|
Zheng W, Xie Y, Tang G J. 2011. Pole transformation of spherical harmonic method in gravity anomaly calculation for unpowered phase trajectory. Journal of Astronautics (in Chinese), 32(10): 2103-2108. |
Zotter F. 2009. Analysis and synthesis of sound-radiation with spherical arrays[Ph. D. thesis]. Austria: University of Music and Performing Arts.
|
高金田, 安振昌, 顾左文, 等. 2005. 地磁正常场的选取与地磁异常场的计算. 地球物理学报, 48(1): 56-62. |
李新星. 2013. 超高阶地球重力场模型的构建[硕士论文]. 郑州: 解放军信息工程大学.
|
李新星, 吴晓平, 李姗姗, 等. 2014. 块对角最小二乘方法在确定全球重力场模型中的应用. 测绘学报, 43(8): 778-785. DOI:10.13485/j.cnki.11-2089.2014.0110 |
任萱. 1985. 扰动引力作用时自由飞行弹道计算的新方法. 国防科技大学学报, (2): 41-52. |
田家磊, 李新星, 吴晓平, 等. 2018. 超高阶重力场模型最小二乘快速实现. 测绘学报, 47(11): 1437-1445. DOI:10.11947/j.AGCS.2018.20170659 |
王建强, 李建成, 王正涛, 等. 2013. 球谐函数变换快速计算扰动引力. 武汉大学学报·信息科学版, 38(9): 1039-1043. DOI:10.13203/j.whugis2013.09.003 |
许厚泽, 蒋福珍. 1964. 关于重力异常球函数展式的变换. 测绘学报, 7(4): 252-260. DOI:10.3321/j.issn:1001-1595.1964.04.002 |
徐文耀, 朱岗昆. 1984. 我国及邻近地区地磁场的矩谐分析. 地球物理学报, 27(6): 511-522. DOI:10.3321/j.issn:0001-5733.1984.06.002 |
于锦海, 曾艳艳, 朱永超, 等. 2015. 超高阶次Legendre函数的跨阶数递推算法. 地球物理学报, 58(3): 748-755. DOI:10.6038/cjg20150305 |
张传定, 许厚泽, 吴星. 2004. 地球重力场调和分析中的"轮胎"问题. 大地测量与地球动力学进展. 武汉: 科学技术出版社.
|
张永生, 贲进, 童晓冲. 2007. 地球空间信息球面离散网格——理论、算法及应用. 北京: 科学出版社.
|
郑伟, 谢愈, 汤国建. 2011. 自由段弹道扰动引力计算的球谐函数极点变换. 宇航学报, 32(10): 2103-2108. DOI:10.3873/j.issn.1000-1328.2011.10.002 |
 2021, Vol. 64
2021, Vol. 64


