近场波动数值模拟是地震工程、地球物理、电磁学等学科共同关注的重要研究方向,其涉及内域数值算法和人工边界条件,其中人工边界用来截断外部无限域,并模拟外行波无反射地穿过边界.迄今常用的内域算法有差分法、有限元法(Finite Element Method, FEM)和谱元法(Liu et al., 2019)等,而人工边界主要有黏性及黏弹性边界(Liu and Li, 2005; Zhao et al., 2011),Higdon边界及其辅助变量实现(Higdon, 1987; Hagstrom et al., 2008),透射边界(廖振鹏等, 2002),物理阻尼层(Semblat et al., 2011),加权混合人工边界(Liu and Sen, 2012)和完美匹配层(Bérenger, 2007)等.由内域和边界算法的两者组合将形成诸多近场波动数值模拟方案,其稳定性是获得可靠模拟结果的前提.
透射边界亦称多次透射公式(Multi-Transmitting Formula, MTF),是一类典型的具有高阶精度、低计算量、易于实现等特点的人工边界条件,其已应用于诸多波动模拟领域,如电磁学(Taflove and Hagness, 2005)、地震工程(陈厚群, 2006)、流体力学(Xu et al., 2016)等.然而在波动模拟中MTF存在数值失稳现象.下面结合稳定性分析方法加以概述已有失稳机理的研究结果.
从大量失稳的数值实验中可以发现,失稳的肇始具有局域性,即由边界开始向内域扩散,可见失稳仅是边界与相邻的运动方程不当耦合所致,而与远处的运动方程和边界无关.基于正则模态分析建立的GKS(Gustafsson, Kreiss, Sundström)定理及其群速度解释(Trefethen, 1983)是分析局域失稳的重要理论.周正华和廖振鹏(2001)基于GKS定理分析了MTF引发的飘移失稳,指出数值解中的零频零波数谐波从边界进入内域引发失稳.景立平等(2002)基于群速度解释分析了SH波动有限元模拟中MTF引发的高频失稳,指出失稳是由MTF与内域格式组成的半无限模型支持群速度向内而相速度向外的高频平面谐波所致.Duru等(2015)基于正则模态分析了不同截断边界的PML稳定性,指出采用自由边界截断的PML存在随时间增长的模态.然而,正则模态分析亦有其局限性,除局域引发的失稳外,远处边界和运动方程亦可能导致全局性失稳.基于人工边界反射系数可揭示MTF引发的反射放大失稳,其失稳机理为在有限区域内MTF对外行波的反复反射放大(Liao and Liu, 1992; 章旭斌等, 2019).
基于对失稳现象和机理的认识,MTF引发的数值失稳可归纳为局域(Locality)耦合失稳和全局(Globality)反射放大失稳,前者依据失稳形态可区分为高频失稳和飘移失稳.对于上述失稳问题,研究人员已提出多种稳定措施.针对反射放大失稳,选择合理的数值模拟参数可避免这类失稳;针对飘移失稳,通过小量修正MTF或内域格式,可有效抑制飘移失稳(周正华和廖振鹏, 2001; 李小军和杨宇, 2012).针对高频失稳,曾采用阻尼滤波来消除(廖振鹏等, 2002),但会影响数值模拟的精度;对于波导模型,可以设置合理的长方形单元长宽比来避免高频失稳(谢志南和廖振鹏, 2012),但该措施并不适用全空间模型和实际场地采用的半空间模型.
P-SV弹性矢量波动方程是地震波动模拟常用的计算模型,在地形效应、盆地效应以及全球地震动模拟(Li et al., 2014)都存在应用.MTF在矢量波动模拟中相比标量波动更易引发失稳,而针对标量波动模拟中得到的MTF稳定条件(章旭斌等, 2015)并不能用于更为复杂的矢量波动模拟.另外,GKS定理的群速度解释虽然是针对一维和标量波动,但其失稳模态能自然地推广到P-SV波动中的P波和SV波.本文将在以往研究基础上,将GKS定理及其群速度解释应用到P-SV波动模拟中MTF的稳定性分析,揭示MTF引发的失稳机理,并采用修改的数值积分方法(Yue and Guddati, 2005)修改有限元刚度来调整内域格式的频散,消除引发MTF失稳的波动成分,从而稳定实现MTF.同时利用长持时数值实验加以验证.
1 数值格式均匀、各向同性P-SV弹性波动方程
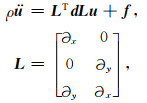
|
(1) |
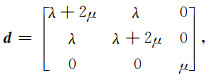
|
其中位移u=[ux uy]T,荷载f=[fx fy]T,ρ为密度,μ为弹性模量,λ为拉梅常数,偏导∂x=∂/∂x,∂y=∂/∂y.(1)式对应的弱形式为
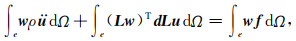
|
(2) |
其中w为试函数,Ω为单元e上的积分变量.(2)式引入等参变换
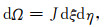
|
(3) |
其中J为雅克比行列式.位移场和试函数采用线性形函数插值
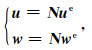
|
(4) |
其中N为形函数矩阵,ue和we分别为单元节点位移向量和试函数向量.由此可得单元节点格式

|
(5) |

|
(6) |
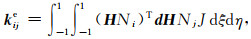
|
(7) |

|
(8) |
其中算子矩阵H由矩阵L作链式法则得到,即
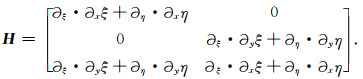
|
由于一致质量的空间耦联特征将极大地增加数值模拟的计算量,通常将一致质量作行和集中,从而得到空间解耦的集中质量(廖振鹏, 2002)
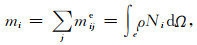
|
(9) |
由此(5)式可以写成
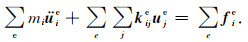
|
(10) |
刚度阵(7)式通常采用Gauss数值积分计算,而本文将采用修改的数值积分方法(Yue and Guddati, 2005)
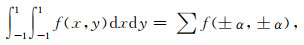
|
(11) |
其中待定积分点α∈[0, 1].当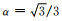
边界区域通常采用规则的长方形单元,采用数值积分方法(11)式分别计算(6)和(7)式可以得到长方形单元节点质量

|
(12) |
以及单元刚度阵
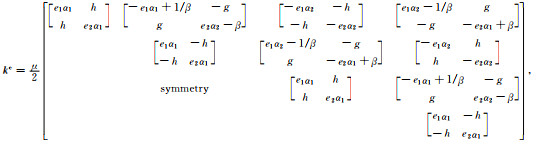
|
(13) |
其中α1=1+α2,α2=1-α2,e1=(ε2β2+1)/2β,e2=(ε2+β2)/2β,g=(3-ε2)/2,h=(ε2-1)/2.进而对(10)式采用时间中心差分离散,可得长方形单元的局部节点系格式

|
(14) |
其中Δτ=csΔt/Δx,β=Δy/Δx,ε=cp/cs,cp=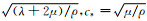
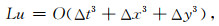
|
(15) |
|
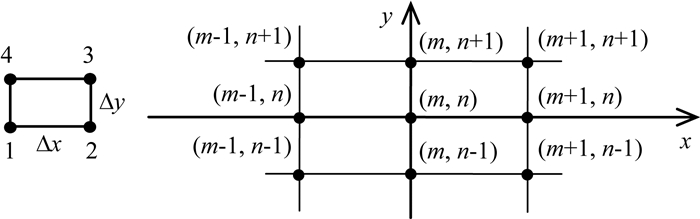
图 1 长方形单元和局部节点系 Fig. 1 Rectangle element and local grid system |
可知无论α取何值,该格式都具有二阶精度.
人工边界采用MTF,在垂直x方向的人工边界上的节点格式为
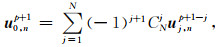
|
(16) |
在垂直y方向的人工边界上的节点格式为
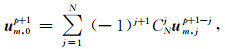
|
(17) |
其中uj, np和um, jp分别为距人工边界jΔx和jΔy处的节点在pΔt时刻的位移,CNj为二项式系数.当MTF计算点与离散节点不一致时,其计算点位移由离散节点位移作空间插值得到.
2 失稳机理及稳定实现根据对数值失稳现象的观察,失稳扰动从一个或若干个节点开始出现,然后随时间增长并向周围扩散.也就是说失稳的肇始具有局域性,即仅与邻近的节点运动方程之间的耦合相关,而与远处的节点运动方程和边界条件无关.因此,对于内域数值格式的稳定性,可以在无限模型中采用傅里叶模态来分析局域失稳,要求内域格式不支持随时间步数无限增长的傅里叶模态,即von Neumann稳定条件(Strikwerda, 2004).
边界引发的失稳是从边界节点开始,然后逐步向内域扩散.可见,失稳是边界节点与内域邻近节点的相互作用所致,其同样具有局域性.因此,边界稳定性分析是针对由边界和内域组成的半无限模型,并采用更为一般的正则模态
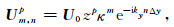
|
(18) |
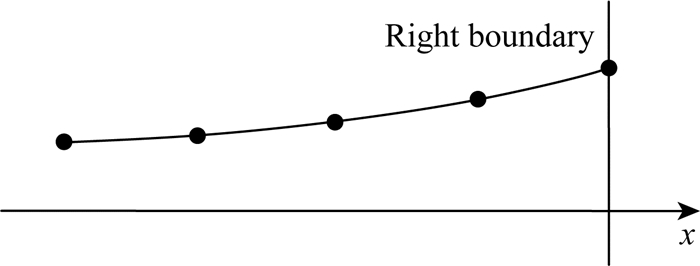
当z=eiωΔt,κ=e-ikxΔx时,正则模态退化为傅里叶模态.数值稳定也就是要求半无限模型不支持随时间步数无限增长的正则模态(|z|>1, |κ|>1),即Godunov-Ryabenkii稳定条件(Gustafsson et al., 1972).其中|κ|>1的含义为:在内域稳定条件下,数值格式已不再支持|z|>1,|κ|=1的模态,并考虑到正则模态在无穷远处应为有限值,因此对右边界而言,|κ|>1.图 2给出了正则模态示意图.
|
图 2 正则模态示意图 Fig. 2 Sketch of normal model |
Gustafsson等(1972)指出Godunov-Ryabenkii稳定条件未考虑|z|=1,|κ|=1时的失稳谐波模态,即z由|z|>1趋近于|z|=1,相应的κ由|κ|>1趋近于|κ|=1的极限状态,因此要求半无限模型不支持这一失稳谐波模态,并证明了Godunov-Ryabenkii稳定条件加上这一补充条件为稳定的充要条件,这个结果称为GKS定理.Trefethen(1983)基于扰动分析,对这一失稳模态给出了具有物理直观的群速度解释.由于
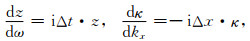
|
从而可得群速度
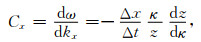
|
(19) |
如果Cx<0,意味着z受到扰动向单位圆外移动变为|z|>1时,κ也将向单位圆外移动变为|κ|>1.因此,GKS定理补充条件的物理含义为:半无限模型不支持群速度指向内域的谐波模态.由于群速度是描述波动能量的行进速度,如果半无限模型支持群速度指向内域的谐波模态,波动能量将不断地从边界进入内域,从而导致失稳.
GKS定理的群速度解释物理概念清晰,易于操作.边界和内域频散曲线的交点就是两者共同支持的谐波模态,其交点切线斜率就是谐波的群速度.对于右边界而言,如果群速度为负,则表示向内行进,边界将会引发失稳.值得说明的是,GKS定理的群速度解释虽是针对一维和SH波动的,但其失稳模态能自然地推广到P-SV波动中的P波和SV波.考虑到P波和SV波的频散是完全独立的,因此分别针对P波和SV波,验证边界和内域格式是否支持群速度指向内域的失稳谐波模态.
频散分析所采用的平面谐波形式为

|
(20) |
其时空离散形式为
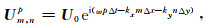
|
(21) |
其中ω为圆频率,k为波数,θ为谐波入射方向与x轴正向的夹角,沿x和y轴正向的视波数分别为kx=kcosθ和ky=ksinθ.
将(20)式代入(1)式,并忽略荷载项,可得连续模型的频散关系
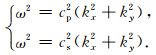
|
(22) |
将(21)式代入(14)式,可得有限元的频散关系
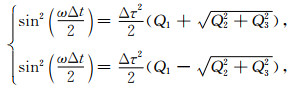
|
(23) |

|
其中s1=sin(kxΔx/2),c1=cos(kxΔx/2),s2=sin(kyΔy/2),c2=cos(kyΔy/2).当Δx→0, Δy→0,Δt→0时,(23)式可化简成(22)式,可知(23)式的两个式子分别是P波和SV波的频散.
将(21)式分别代入(16)和(17)式,可得MTF的频散关系

|
(24) |
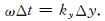
|
(25) |
由于频散关系的对称性及混淆效应(廖振鹏, 2002),可仅考虑第一象限的频散,即ωΔt∈[0, π], kxΔx∈[0, π], kyΔy∈[0, π].
图 3为连续模型和传统有限元的频散曲线.其中连续模型的频散改写为
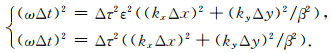
|
(26) |
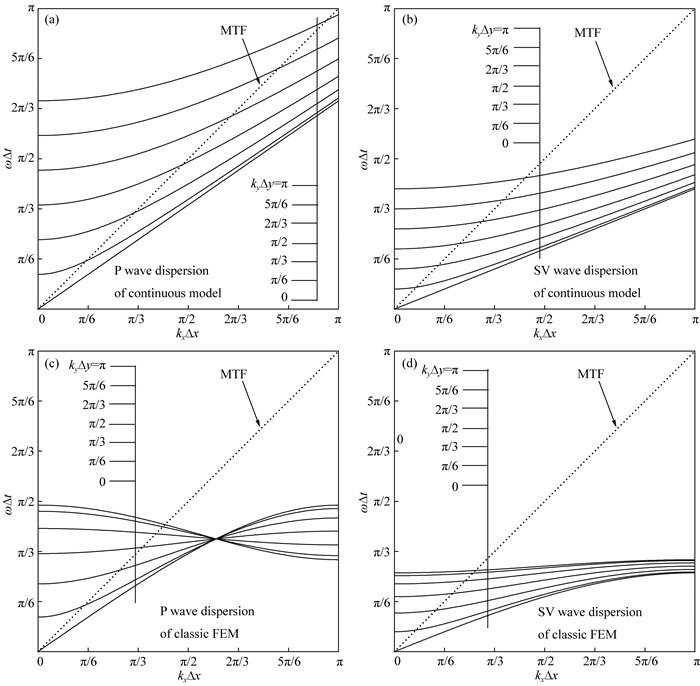
|
图 3
连续模型和传统有限元的频散曲线,及在垂直x方向人工边界上的MTF频散曲线,其中参数ε=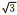 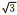 |
首先,从图 3c可以看出传统有限元P波频散存在单调递减的曲线,其与MTF频散曲线在高频段(ωΔt>1)存在负切线斜率的交点.由于频散曲线上一点的切线斜率表示该点对应的平面谐波群速度,对于右边界而言,群速度为负表明谐波向内域行进.由此可知,MTF和传统有限元共同支持了群速度指向内域的平面谐波.依据GKS定理的群速度解释,MTF会引发数值失稳.另外,从图 3a可以看出连续模型P波频散曲线始终单调递增,切线斜率始终为正,因此并不存在群速度向內的谐波.这意味着传统有限元离散引入了在连续模型中并不存在的群速度向内的谐波,这正是引发MTF高频失稳的谐波成分.
基于对失稳机理的认识,若有限元频散曲线单调递增,则可消除P-SV波动模拟中MTF引发的高频失稳.由于有限元频散由其质量阵和刚度阵决定,(12)和(13)式表明数值积分方法并不会改变长方形单元的集中质量大小,但会改变刚度阵,可见数值积分方法可以改变有限元频散.因此,在垂直x方向人工边界上的MTF稳定实现条件,即为有限元P波和SV频散曲线在x方向上单调递增
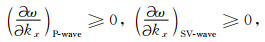
|
(27) |
同理,在垂直y方向人工边界上的MTF稳定实现的条件为
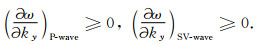
|
(28) |
这里直接给出(27)式的充要条件
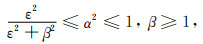
|
(29) |
以及(28)式的充要条件
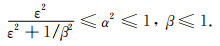
|
(30) |
上式表明积分点选取与介质波速比和单元长宽比有关.具体推导过程见附录.
对于正方形单元(β=1)而言,MTF稳定实现条件由(29)和(30)式可简化为
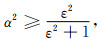
|
(31) |
由于ε>1,可知Guass数值积分点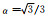
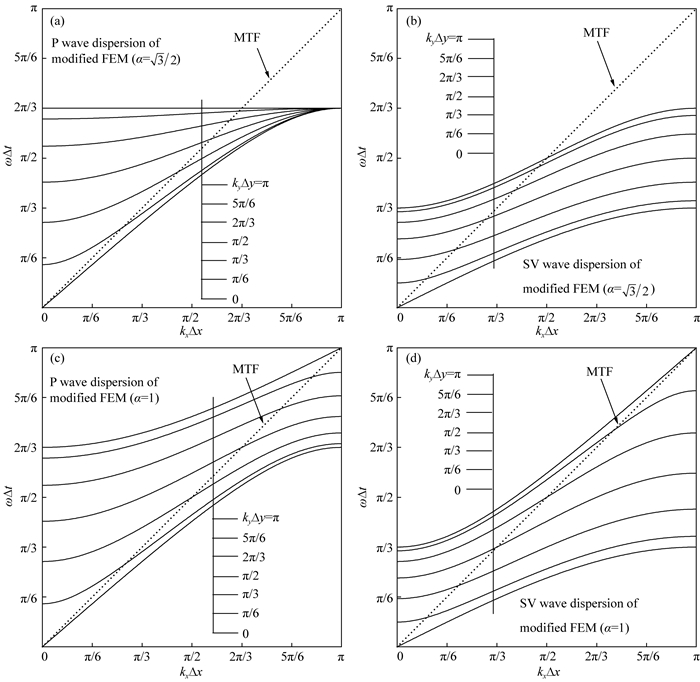
图 4为修正有限元的频散曲线,可以看出修正有限元(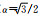
|
图 4
修正有限元和在垂直x方向人工边界上的MTF频散曲线,其中参数ε=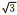 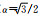 )的P波和SV波频散;(c)(d) 分别为修正有限元(α=1)的P波和SV波频散.
Fig. 4
The dispersion curves of modified FEM and MTF scheme when artificial boundary is perpendicular to x-axis with these parameters, ε= )的P波和SV波频散;(c)(d) 分别为修正有限元(α=1)的P波和SV波频散.
Fig. 4
The dispersion curves of modified FEM and MTF scheme when artificial boundary is perpendicular to x-axis with these parameters, ε=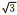 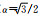 ); (c) and (d) The dispersion curves of P wave and SV wave in modified FEM (α=1). ); (c) and (d) The dispersion curves of P wave and SV wave in modified FEM (α=1).
|
内域格式的稳定条件由Von-Neumann稳定性分析方法可以得到.在(29)式条件下,容易得到修正有限元的稳定条件为
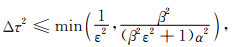
|
(32) |
同理,在(30)式条件下,修正有限元稳定条件为
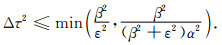
|
(33) |
考虑基岩均匀半空间模型,介质密度ρ=2.7 g·cm-3,cp=5.5 km·s-1,cs=3.2 km·s-1.计算模型如图 5所示,Xb=2Yb=10 km.在自由地表(2 km, 5 km)处作用竖直方向的瑞克子波荷载
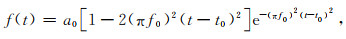
|
(34) |

|
图 5 基岩半空间模型 Fig. 5 Rock half-space model |
其中卓越频率f0=5 Hz,延迟时间t0=0 s,幅值系数a0=5×1010.接收点取在自由地表(0 km, 5 km)处.除自由地表外,其余三边均采用人工边界截断并设置MTF.离散单元尺寸Δx=Δy=10 m,时间步距Δt=0.001 s,积分点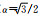
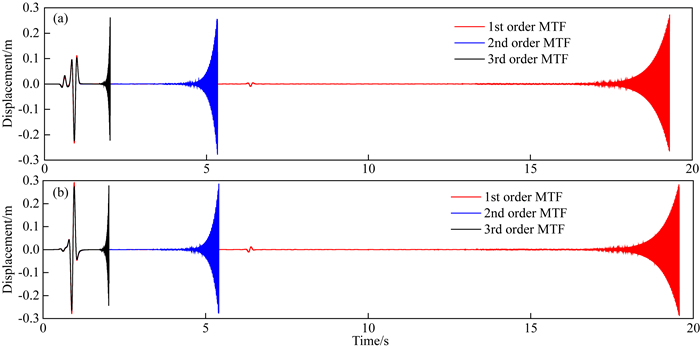
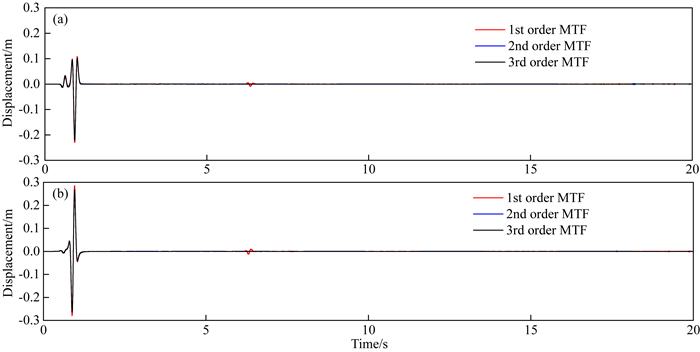
从图 6可以看出传统有限元结合MTF引发数值失稳现象,MTF阶数越高,失稳增长越剧烈,失稳出现时间越早.图 7显示修正有限元结合MTF可以稳定实现,各阶MTF均未引发高频失稳,其中三阶MTF存在飘移失稳,已通过小量修正MTF加以消除(周正华和廖振鹏, 2001),小量取为0.005.图 8a为计算模型参数条件下,传统有限元和MTF的频散曲线,图中红线为一条水平频散曲线,因此传统有限元和MTF的负切线斜率交点将落在红色方框内,从而可以得到引发MTF失稳的谐波频率范围,即为图中红色方框内的频带ωΔt∈[0.91, 1.07],换算为频率f∈[144.8 Hz, 170.3 Hz].图 8b为截取的接收点失稳增长数值解,其表现为节点位移高频振荡,通过快速傅里叶变换可以得到其失稳主频为147.3 Hz,处在理论失稳频率范围内.
|
图 6 传统有限元结合MTF计算的接收点位移时程 (a) x方向;(b) y方向. Fig. 6 The displacement time history of the receiver computed by classic FEM with MTF (a) x direction; (b) y direction. |
|
图 7 修正有限元结合MTF计算的接收点位移时程 (a) x方向;(b) y方向. Fig. 7 The displacement time history of the receiver computed by modified FEM with MTF (a) x direction; (b) y direction. |

|
图 8 (a) 计算模型参数条件下,传统有限元和MTF的频散曲线,红线为一条水平频散曲线,红色方框为引发MTF失稳的谐波频率范围;(b) 截取的接收点失稳增长数值解;(c) 失稳增长数值解的频谱 Fig. 8 (a) The dispersion curves of classic FEM and MTF at the given parameters of computational model, the red line is horizontal dispersion curve, and the red box indicates the harmonic frequency range that causes MTF instability; (b) Truncated numerical instability solution of receiver; (c) Spectrum of numerical instability solution |
本文得到的MTF稳定性条件是针对规则的长方形单元,然而实际场地存在地形起伏、介质分界面等复杂情形,划分的有限元网格必然存在非规则单元.由于局域高频失稳是边界与邻近内域节点的相互作用所致,因此只需保证边界区域为规则的长方形单元且满足稳定条件,远处的离散形式并不会影响MTF的稳定性.
在上述基岩半空间上设置深度0.5 km,长度6 km的盆地(如图 9),介质密度ρ=2.6 g·cm-3,cp=4.5 km·s-1,cs=2.6 km·s-1,其他参数不变,接收点设置在盆地地表距离右边界1 km处.该模型可用于研究盆地对面波的放大效应(Bowden and Tsai, 2017).本文用于验证内域存在介质非均匀和网格单元非规则时MTF的稳定性.

|
图 9 盆地-基岩半空间模型 Fig. 9 Basin-rock half-space model |
图 10为修正有限元分别结合MTF和黏弹性边界计算的接收点位移时程,MTF未出现失稳.与远置边界数值解相比,二阶和三阶MTF的吸收效果较好,一阶MTF和黏弹性边界存在较大的反射波.由于MTF人工波速取为S波波速,提高了对面波的吸收效果,因此显示一阶MTF的精度略高于黏弹性边界.

|
图 10 修正有限元结合MTF和黏弹性边界以及远置边界时计算的接收点位移时程 (a) x方向;(b) y方向. Fig. 10 The displacement time history of the receiver computed by modified FEM with MTF, viscous-spring boundary and extend boundary (a) x direction; (b) y direction. |
P-SV弹性波动有限元模拟中MTF引发的高频失稳机理可用GKS定理群速度解释加以阐明,即有限元离散引入了在连续方程中并不存在的群速度指向内域的高频P波或SV波,并得到了MTF的支持,从而导致数值失稳.可见数值模拟中由于引入人工边界所导致的失稳并非仅是边界的问题.本文进而采用修改的数值积分方法修改有限元刚度来调整内域格式的频散,消除了引发边界失稳的波动成分,稳定实现了MTF,从而构建了稳定的近场P-SV波动模拟方案.对于实际复杂问题,通过保证边界区域为规则的长方形单元且满足稳定条件,数值实验显示MTF同样能够稳定实现.本文研究思路可进一步推广到三维弹性波动数值模拟,对于其他类型数值格式中人工边界的稳定问题亦具有参考价值.
附录 证明(27)式的充要条件为(29)式对(23)式求偏导可得
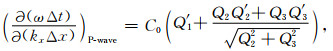
|
(A1) |

|
(A2) |

|
其中C0=Δτ2/(4sin(ωΔt)),Q′i=∂Qi/∂(kxΔx),i=1, 2, 3.由(A1)和(A2)式可得(27)式的等价形式

|
(A3) |
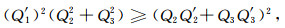
|
(A4) |
因此,要证明(27)式的充要条件为(29)式,即证明(A3)和(A4)式的充要条件为(29)式.
下面先证明(A3)和(A4)式的必要条件为(29)式.取值kyΔy=π,此时s2=1,c2=0,Q3=0,分别代入(A3)和(A4)式得到
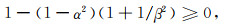
|
(A5) |

|
(A6) |
由于ε>1且α∈[0, 1],由(A5)和(A6)整理可得
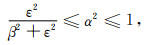
|
(A7) |
(A7) 式即为(29)式的前半部分,对于β≥1这一必要条件,可采用反证法证明.如果β<1,取值s22=


|
(A8) |
由s1→1可知,c1→0,(Q′1)2→0,(Q′3)2→ 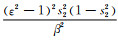

|
(A9) |
(A7) 和(A9)式的组合即(29)式,因此(A3)和(A4)式的必要条件为(29)式.
下面证明(A3)和(A4)式的充分条件亦为(29)式.由(29)式可以推导得到
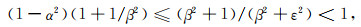
|
(A10) |
由于s1, s2, c1, c2∈[0, 1],因此可得(A3)式成立.
为了证明由(29)式可以得到(A4)式,可以通过证明由(A4)式分解得到的如下两个不等式成立
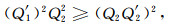
|
(A11) |

|
(A12) |
将Qi, Q′i代入(A11)式,经整理可知,要证明(A11)式仅需证明不等式
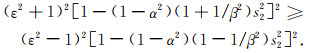
|
(A13) |
对(A13)式进一步整理可得
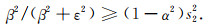
|
(A14) |
由(29)式容易得到(A14)式成立.将Qi, Q′i代入(A12)式, 并利用(A13)式,经整理可得
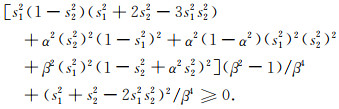
|
(A15) |
由(29)式容易得到(A15)式成立,因此(A3)和(A4)式的充分条件亦为(29)式.综上可知,(27)式的充要条件为(29)式.同理可以证明(28)式的充要条件为(30)式.
致谢 感谢审稿专家对本文提出的宝贵意见.
Bérenger J P. 2007. Perfectly Matched Layer (PML) for Computational Electromagnetics. Arcueil: Morgan & Claypool. |
Bowden D C, Tsai V C. 2017. Earthquake ground motion amplification for surface waves. Geophysical Research Letters, 44(1): 121-127. DOI:10.1002/2016GL071885 |
Chen H Q. 2006. Discussion on seismic input mechanism at dam site. Journal of Hydraulic Engineering (in Chinese), 37(12): 1417-1423. |
Duru K, Kozdon J E, Kreiss G. 2015. Boundary conditions and stability of a perfectly matched layer for the elastic wave equation in first order form. Journal of Computational Physics, 303: 372-395. DOI:10.1016/j.jcp.2015.09.048 |
Gustafsson B, Kreiss H O, Sundström A. 1972. Stability theory of difference approximations for mixed initial boundary value problems.Ⅱ. Mathematics of Computation, 26(119): 649-686. DOI:10.1090/S0025-5718-1972-0341888-3 |
Hagstrom T, Mar-Or A, Givoli D. 2008. High-order local absorbing conditions for the wave equation: Extensions and improvements. Journal of Computational Physics, 227(6): 3322-3357. DOI:10.1016/j.jcp.2007.11.040 |
Higdon R L. 1987. Numerical absorbing boundary conditions for the wave equation. Mathematics of Computation, 49(179): 65-90. DOI:10.1090/S0025-5718-1987-0890254-1 |
Jing L P, Liao Z P, Zou J X. 2002. A high-frequency instability mechanism in numerical realization of multi-transmitting formula. Earthquake Engineering and Engineering Vibration (in Chinese), 22(1): 7-13. |
Li D Z, Helmberger D, Clayton R W, et al. 2014. Global synthetic seismograms using a 2-D finite-difference method. Geophysical Journal International, 197(2): 1166-1183. DOI:10.1093/gji/ggu050 |
Li X J, Yang Y. 2012. Measures for stability control of transmitting boundary. Chinese Journal of Geotechnical Engineering (in Chinese), 34(4): 641-645. |
Liao Z P, Liu J B. 1992. Numerical instabilities of a local transmitting boundary. Earthquake Engineering and Structural Dynamics, 21(1): 65-77. DOI:10.1002/eqe.4290210105 |
Liao Z P. 2002. Introduction to Wave Motion Theories in Engineering (in Chinese). 2nd ed. Beijing: Science Press.
|
Liao Z P, Zhou Z H, Zhang Y H. 2002. Stable implementation of transmitting boundary in numerical simulation of wave motion. Chinese Journal of Geophysics (in Chinese), 45(4): 533-545. DOI:10.3321/j.issn:0001-5733.2002.04.011 |
Liu Y S, Xu T, Wang Y H, et al. 2019. An efficient source wavefield reconstruction scheme using single boundary layer values for the spectral element Method. Earth and Planetary Physics, 3(4): 342-357. DOI:10.26464/epp2019035 |
Liu J B, Li B. 2005. A unified viscous-spring artificial boundary for 3-D static and dynamic applications. Science in China Series E Engineering & Materials Science, 48(5): 570-584. |
Liu Y, Sen M K. 2012. A hybrid absorbing boundary condition for elastic staggered-grid modelling. Geophysical Prospecting, 60(6): 1114-1132. DOI:10.1111/j.1365-2478.2011.01051.x |
Semblat J F, Lenti L, Gandomzadeh A. 2011. A simple multi-directional absorbing layer method to simulate elastic wave propagation in unbounded domains. International Journal for Numerical Methods in Engineering, 85(12): 1543-1563. DOI:10.1002/nme.3035 |
Strikwerda J C. 2004. Finite Difference Schemes and Partial Differential Equations. 2nd ed. Philadelphia: SIAM.
|
Taflove A, Hagness S C. 2005. Computational Electrodynamics: The Finite-Difference Time-Domain Method. 3rd ed. Norwood, MA: Artech House, Inc.
|
Trefethen L N. 1983. Group velocity interpretation of the stability theory of Gustafsson, Kreiss, and Sundström. Journal of Computational Physics, 49(2): 199-217. DOI:10.1016/0021-9991(83)90123-7 |
Xie Z N, Liao Z P. 2012. Mechanism of high frequency instability caused by transmitting boundary and method of its elimination——SH wave. Chinese Journal of Theoretical and Applied Mechanics (in Chinese), 44(4): 745-752. |
Xu G, Hamouda A M S, Khoo B C. 2016. Time-domain simulation of second-order irregular wave diffraction based on a hybrid water wave radiation condition. Applied Mathematical Modelling, 40(7-8): 4451-4467. DOI:10.1016/j.apm.2015.11.034 |
Yue B, Guddati M N. 2005. Dispersion-reducing finite elements for transient acoustics. The Journal of the Acoustical Society of America, 118(4): 2132-2141. DOI:10.1121/1.2011149 |
Zhang X B, Liao Z P, Xie Z N. 2015. Mechanism of high frequency coupling instability and stable implementation for transmitting boundary-SH wave motion. Chinese Journal of Geophysics (in Chinese), 58(10): 197-206. DOI:10.6038/cjg20151017 |
Zhang X B, Xie Z N, Liao Z P. 2019. Reflection amplification instability of the transmitting boundary in SH wave simulation. Journal of Harbin Engineering University (in Chinese), 40(6): 1031-1035. |
Zhao M, Du X L, Liu J B, et al. 2011. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide. International Journal for Numerical Methods in Engineering, 87(11): 1074-1104. DOI:10.1002/nme.3147 |
Zhou Z H, Liao Z P. 2001. A measure for eliminating drift instability of the multi-transmitting formula. Acta Mechanica Sinica (in Chinese), 33(4): 550-554. |
陈厚群. 2006. 坝址地震动输入机制探讨. 水利学报, 37(12): 1417-1423. DOI:10.3321/j.issn:0559-9350.2006.12.004 |
景立平, 廖振鹏, 邹经湘. 2002. 多次透射公式的一种高频失稳机制. 地震工程与工程振动, 22(1): 7-13. DOI:10.3969/j.issn.1000-1301.2002.01.002 |
李小军, 杨宇. 2012. 透射边界稳定性控制措施探讨. 岩土工程学报, 34(4): 641-645. |
廖振鹏. 2002. 工程波动理论导论. 2版. 北京: 科学出版社.
|
廖振鹏, 周正华, 张艳红. 2002. 波动数值模拟中透射边界的稳定实现. 地球物理学报, 45(4): 533-545. DOI:10.3321/j.issn:0001-5733.2002.04.011 |
谢志南, 廖振鹏. 2012. 透射边界高频失稳机理及其消除方法——SH波动. 力学学报, 44(4): 745-752. DOI:10.6052/0459-1879-11-312 |
章旭斌, 廖振鹏, 谢志南. 2015. 透射边界高频耦合失稳机理及稳定实现——SH波动. 地球物理学报, 58(10): 197-206. DOI:10.6038/cjg20151017 |
章旭斌, 谢志南, 廖振鹏. 2019. SH波动模拟中透射边界反射放大失稳研究. 哈尔滨工程大学学报, 40(6): 1031-1035. |
周正华, 廖振鹏. 2001. 消除多次透射公式飘移失稳的措施. 力学学报, 33(4): 550-554. DOI:10.3321/j.issn:0459-1879.2001.04.015 |
 2021, Vol. 64
2021, Vol. 64

