2. 福州大学, 福州 350108;
3. 中国地震局厦门海洋地震研究所, 厦门 361021
2. Fuzhou University, Fuzhou 350108, China;
3. Xiamen Institute of Marine Seismology, China Earthquake Administration, Xiamen 361021, China
地震预警震级的快速测定是地震学家面临的挑战性难题,其难度在于所利用的台站既少又离震中较近,而且只能利用P波触发后几秒钟的信息,而此时P波的发育还不充分,难以准确测定震级,尤其是大震震级(金星等,2012;李山有,2018).为此,地震学家进行了艰辛的探索,提出了许多预警震级的测定方法,其中最有代表性的就是利用周期和位移峰值测定震级的方法.与周期相关的算法,如利用τc参数测定地震预警震级(Wu et al., 2007;马强,2008;Peng et al., 2017)和τPmax参数(Kanamori, 2005;Chen et al., 2017).Wu和Kanamori(2005)和Yamada和Mori(2009)研究得出,τPmax方法测定地震震级时,地震仪器采样频率、数据预处理、时间窗的长度、滤波等因素均会对特征周期产生影响,从而导致震级测定效果的准确性和稳定性较为一般.宋晋东和李山有(2012)研究表明,单台提取的τPmax参数离散度较大,但经过多台平均后可以取得较稳定的震级测定效果.Ziv(2014)研究认为τlog与震级的相关性要优于τc和τPmax周期,但还存在稳定性和准确性不足的问题.与地震动幅值相关的算法,如利用位移峰值Pd参数(Wu and Zhao, 2006;Zollo et al., 2010;彭朝勇等,2013;冯继威,2019).Chen等(2012)利用峰值位移Pd参数来测定地震震级研究表明Pd参数测定震级比τc参数测定震级结果来得稳定、可靠,同时单台提取的Pd参数测定震级的离散度也较低,但容易出现震级饱和问题.为了消除震级饱和现象的影响,张红才(2013)对Pd进行连续追踪测定,从而实现了震级连续测定,随着时间窗长度的增加,位移振幅Pd与震级间相关性明显增强,震级饱和现象越来越不明显,震级估计的方差也随之逐渐减小.当时间窗的长度达到10 s时,震级估计方差可以减少为0.37个震级单位.
总结上述方法,主要思路都是从地震初期少量地震波形记录中提取与地震震级相关的频率、振幅信息,并从历史地震数据中通过统计方法获得相关统计公式用于地震震级测定中.但是,地震震级测定是一个十分复杂的过程,需要综合考虑震源过程、传播介质、场地条件、仪器响应等多个方面因素的影响,单一的幅值或周期参数在一定程度上能够较好映射出地震的规模,但较难反映出地震的全部特征,从而导致地震震级测定的精度不足.
近年来,随着地震数据资料不断积累,以及深度学习算法的出现,使得人工智能技术在地震学领域中的应用进入新的阶段.Perol等(2018)应用CNN网络实现地震检测和定位,可检测出比常规地震目录多17倍的地震,且检测效率也比模板匹配快了好几个数量级.Zhu和Beroza(2019)利用U-net神经网络将震相拾取问题看成分割问题,提高了P波和S波的拾取精度.赵明等(2019b)应用卷积神经网络对汶川地震余震波形进行自动分类与识别,其训练和检测准确率均达到95%以上.Lomax等(2019)设计了单台50 s波形输入的ConvNetQuake_INGV网络来检测地方震和远震,根据震中距、方位角、震源深度和震级等特征获得地震的概率估计,模型展示了即使地震事件在空间位置和震级上的广度,也能获得较高的识别效果(准确率达87%).Mousavi和Beroza(2020)设计了单台30 s的卷积神经网络和递归神经网络联合的震级预测模型,震级预测标准差约为0.2,网络可有效提高地方性震级和持时震级测量精度.胡安冬和张海明(2020)设计了NN模型和CNN模型对地震紧急预警震级进行预估,目前已实现以NN网络为基础的模型,与已有单台震级预估算法相比有着更好的效果,但因数据量不足的原因暂时还未实现CNN模型对震级的预估.以上研究进一步证明了CNN在地震检测及在地震预警方面的应用存在较好的潜力.为此,本文设计了以地震三分量波形数据作为输入,震级类别作为输出,训练出3 s样本的CNN震级预测模型.该方法充分利用首台前3 s全波形信息,通过多层卷积核自动提取波形综合、深层次的特征,相比于传统单一特征提取方法更加全面、可靠,提高了震级测定精度和可靠度,有望解决地震预警震级测定这一世界性难题.
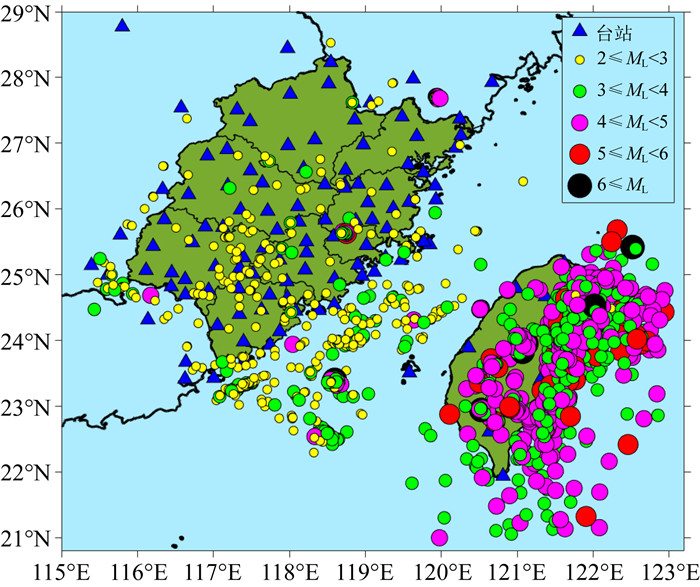
1 数据与处理福建测震台网由88个测震台站、16个台湾台及12个周边邻省台站共116台组成.本文选取了2012—2019年福建台网记录到的福建地区、台湾海峡及台湾地区ML>2.0共1928个地震作为研究资料,其中2≤ML<3的地震共721个,3≤ML<4的地震共607个,4≤ML<5的地震共474个,5≤ML<6的地震共99个,ML≥6的地震共27个,地震分布图如图 1所示.所有台站记录均包含E、N、Z三分量,采样率为100 Hz,均为扣除台站仪器响应后获得实际地动速度记录(单位um·s-1).
|
图 1 福建台网记录2012—2019年份的地震分布图 Fig. 1 Seismic distribution map from 2012 to 2019 were recorded by Fujian Station Network |
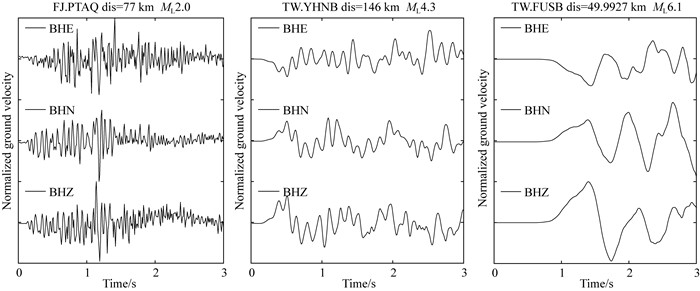
样本数据是根据P波到时信息从原始波形截取每个台站的样本,本文主要训练了3 s样本长度模型.截取规则如下,截取P波到时前0.2 s至P波到时后2.8 s的数据段(带有振幅信息).图 2展示了不同震级的3 s样本波形存在较大差异,如ML2.0样本波形含有较为丰富的高频信息,ML6.1样本波形的长周期成分较强,即随着震级增加,波形的优势周期增大,为深度神经网络的学习奠定重要基础.
|
图 2 3 s长度的样本波形记录 Fig. 2 The sample waveform record of three-seconds length |
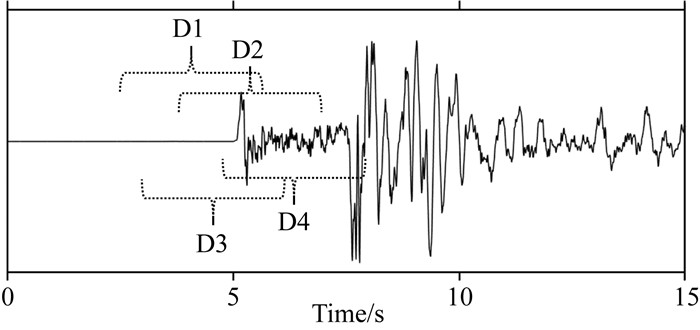
福建台网的大震样本较为稀缺,故收集川滇地区2017—2019年记录的21次ML>5的地震震例进行补充,同时使用随机截取地震事件对大震样本进行增强处理.具体处理方法是,利用滑动窗在P波到时附近滑动,随机截取出若干条记录作为样本.如图 3为随机截取地震样本记录示意图,一条地震记录可截取出D1、D2、D3、D4等4条3 s长度的数据段作为增强样本.
|
图 3 随机截取地震记录实现数据增强 Fig. 3 Random interception of seismic records for data enhancement |
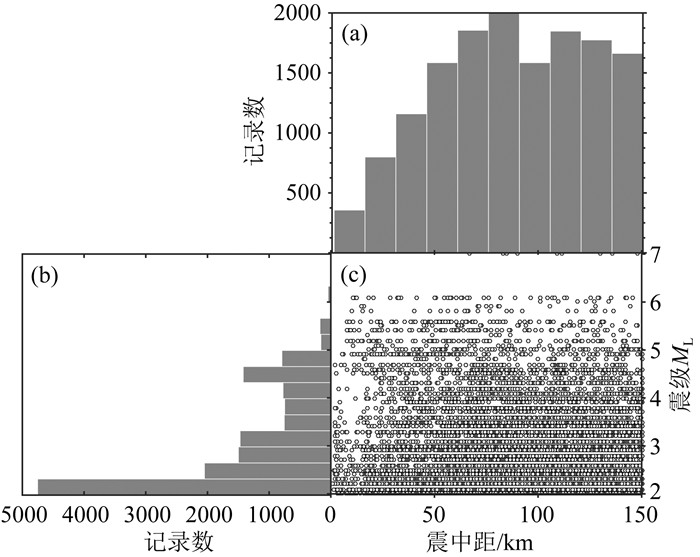
当地震触发后,为更快地估算地震震级,通常选用前几台的地震记录信息进行判别,因此本文只截取出1949个历史地震事件中150 km内的台站记录作为研究资料,经过重复小震记录的剔除、大震样本增强处理、记录质量筛选后共得到14644条三分向地震记录,所有记录相对于震级和震中距的分布情况,如图 4所示,样本震中距分布在0~150 km,震级主要分布在ML2.0~6.5之间,样本所覆盖的震中距范围和震级范围都较广,而非针对某个特定区域的研究,使得训练好的模型具有更好的实际应用价值.
|
图 4 地震记录相对震中距和震级的分布情况 (a) 地震记录相对于震中距的分布直方图;(b) 地震记录相对于震级的分布直方图;(c) 所用记录(散点)的震中距-震级分布情况. Fig. 4 The distribution of epicentral distance and magnitude relative to seismic records (a) The distribution diagram of seismic records relative to epicentral distance; (b) The distribution diagram of magnitude relative to seismic records; (c) The distribution (scatter plot) of epicentral distance and magnitude. |
将其中2012—2018年震例资料共11807条记录作为训练集样本,供卷积神经网络模型学习训练;将2019年震例资料共2837条记录作为测试集样本,检验模型对震级的预测效果.
1.4 震级标签生成由于卷积神经网络具有强大的分类功能,且地震震级通常可允许的误差在±0.3(南芳芳等,2019),故本文将震级测定看成是分类问题,对震级大小进行等级分类,具体分类情况如表 1所示,将ML2.0~2.2分为第1类,ML2.3~2.5为第2类,…,ML>7.6为第20类,共将ML>2.0的震级分成20个不同等级类别.
|
|
表 1 震级分类及标签 Table 1 Magnitude classification and labels |
当模型在实际检测中,若识别出该地震为第10个等级类别,按表 1可得震级范围在ML4.7~4.9,本文规定模型最终预测震级值取中间值,故为ML4.8,这样有可能造成模型预测的震级值与实际震级值之间存在±0.1的系统误差,但该误差是在可接受的范围内.
1.5 振幅信息对震级测定的重要性卷积神经网络具有自动提取特征和长输入数据的缩放能力,与地震信号处理的需求相契合.然而,卷积神经网络对未归一化输入数据较为敏感,使其在震级估算中遇到较大的挑战.地方性震级ML规定(中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会,2017),即
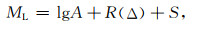
|
(1) |
式中,A为水平向的峰值振幅;R(Δ)为仪器的量规函数,随震中距变化的函数,其物理意义是补偿地震波随距离的衰减;S为台站场地校正项.为了测定震级,需要获取平均衰减模型和场地函数.神经网络可以从训练数据中学习到这些关系,我们只需确保向网络提供学习这些关系所需要的信息.
从式(1)可知振幅信息对震级测定非常关键,但是数据归一化处理可使典型卷积神经网络获得较好的性能.为此,Lomax等(2019)通过提取振幅信息作为额外数值输入到网络中来克服这个问题.而Mousavi和Beroza(2020)设计了一个主要由卷积层和循环层构成的网络,其中卷积层没有任何激活函数,仅用于降维和特征提取.但是以上两种方法网络较为复杂也不是很高效,因此本文设计了针对带振幅信息输入的卷积神经网络,将震级输出划分为20个不同震级类别,降低了震级输出的离散性,提高了每组类型判别的样本数量.另外,通过在卷积层中增加RELU激发函数以及采用ADAM优化算法使模型参数值更加稳定,解决了输入未归一化数据容易引起梯度变化过大的问题,提高模型的识别效果.
2 卷积神经网络模型构建针对地震震级测定问题,将单台三通道的3 s波形作为输入,震级类别作为输出,进行卷积神经网络的训练与识别.卷积神经网络通过卷积核提取波形的内在特征,设置多层卷积层,提取更多的特征,综合以上特征信息,最后采用类似投票的方式输出该事物所属震级类型的概率(图 5).

|
图 5 卷积神经网络模型的输入与输出 Fig. 5 The input and output of convolution neural network model |
卷积神经网络(Convolutional Neural Network,简称CNN)的核心部分是卷积,卷积层是通过将上一层的每个通道特征图和卷积核(如1×3)进行卷积、叠加、增加偏置项、外加一个非线性的激活函数获得(如公式(2)):
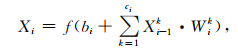
|
(2) |
式中,f为非线性RELU激活函数;Xi为第i个卷积层输出;bi是第i层的偏置;Ci为第i层的通道数量;Xi-1k为第i-1层第k个通道的输出;Wik是第i层第k个通道的卷积核权值.
经过多层卷积、池化,全连接层处理,最后一层的输出设为Z=(z1, z2, …, zj, …, zm),共分为m个类别.经过分类函数(softmax)处理后,得出模型的输出概率,其表达式如下:
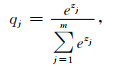
|
(3) |
式中,zj为最后一层输出Z的第j个元素值,qj为属于第j种类别的概率值(通常在0~1之间,概率值越大表示属于该类别的可能性越大).
本文的损失函数H是采用实际的标签pj和预测概率分布qj之间的交叉熵,表达式如下:
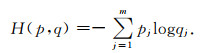
|
(4) |
从交叉熵的公式来看,交叉熵刻画的是pj和qj两个概率分布之间的距离,可以理解为交叉熵值越小,实际与预测的概率分布越接近.预测概率分布p为二值化编码形式的标签,如[0, 0, 1, 0, 0],可判断是属于第三种类别.
2.2 调参试验搭建一个好的卷积神经网络模型需要对卷积核大小、卷积通道数、激活函数类型、卷积层数、全连接层数、训练批次数等参数进行设计.本研究采用Tensorflow框架进行模型搭建和训练.参数选取的原则,一方面总结前人的研究经验(Krizhevsky et al., 2012; Ma et al., 2015; Perol et al., 2018; 赵明等,2019a),针对地震波三通道检测,采用卷积核1×3,每层卷积通道数为64道,选用128批次和RELU激活函数.另一方面根据实测数据的调参试验获得最优模型参数.
表 2列出不同模型参数,训练集与测试集的准确率和耗时情况,以测试集的准确率来评判模型的优劣.通过试验S01、S02、S03,可知7层卷积层的模型识别效果较优;通过试验S02、S04、S05,可知2层连接层的模型识别效果较优.由于本试验采用GPU配置的工作站进行训练,因此在耗时上相差无几.
|
|
表 2 卷积层数和全连接层数的调参试验 Table 2 Parameter adjustment experiment of convolution layer and full connection layer |
综上所述,设计出3s样本输入的震级测定模型架构,如图 6所示,以台站三通道的地震波形数据作为输入,采用1×3卷积核进行卷积,用0填充对边缘处理,2×2最大值池化.本例输入波形层(也就是第0层)用3个通道,从第1到第7个卷积层都采用64个通道数.经过7层卷积池化后,特征图由原来的64@300缩小为64@3,该过程可看成从原始地震数据中提取和压缩有用信息到特征图,使得最后一层特征图具有深层、概括性强的特征表征能力.将这些特征图展开为一维向量,共得到192个特征点,最后采用2层全连接模式输出20个震级等级中概率最大的类别.

|
图 6 震级预测的卷积神经网络模型架构 Fig. 6 Magnitude prediction of convolution neural network model structure |
本模型训练在Windows10、64位系统运行,设备安装Tensorflow深度学习框架的相关环境,采用Tensorflow-gpu版本进行训练,大大提高训练效率.模型训练所配备的硬件和软件配置如表 3所示.
|
|
表 3 模型训练所配备的硬件和软件环境 Table 3 The hardware and software environment for model training |
训练过程采用小批次随机梯度下降法(SGD)算法、增加L2正则化防止过拟合、以及ADAM优化算法,学习率取0.001,训练的目标误差为0.08,迭代10000次进行学习训练.通常耗时都集中在训练上,对于普通的CPU配置机子,迭代10000次耗时大约需要300 min,不过采用GPU计算耗时只需3~5 min左右,提高了上百倍的模型训练效率.
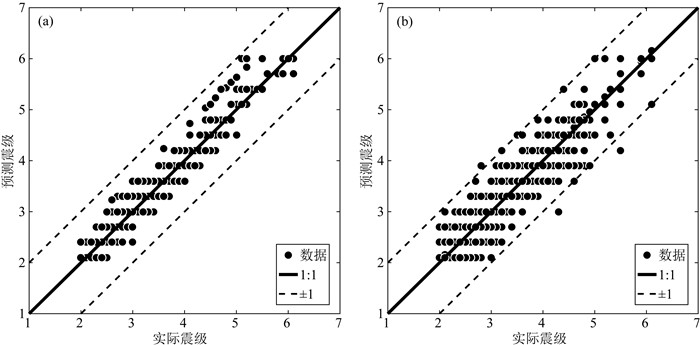
3 结果分析通过训练集数据训练出震级预测网络模型MagNet,将训练集数据通过MagNet仿真预测,得到训练集的预测震级与实际震级的关系(图 7a);将测试集数据通过MagNet仿真预测,得到测试集的预测震级与实际震级的关系(图 7b).可以看出训练集的离散度较小,几乎都集中1:1的对角线上,震级偏差的标准差为0.106;而测试集的离散度较大些,震级偏差的标准差为0.231.
|
图 7 MagNet模型预测震级与实际震级的关系 (a) 训练集;(b) 测试集. Fig. 7 Relationship between the magnitude prediction by MagNet and the actual magnitude (a) Training set; (b) Testing set. |
将MagNet模型预测的震级值与实际震级值进行对比,逐一计算震级偏差,公式如下:
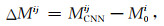
|
(5) |
式中,ΔMij为第i个地震第j个台站的震级偏差,MCNN为卷积神经网络模型预测震级值,M0为该地震最终的编目震级.根据省级测震台网地震速报评比标准,通常震级误差的允许范围为±0.3.
由于测试样本对模型来说属于新鲜样本,因此可统计测试集的震级偏差来评判模型的优劣.将测试集MagNet模型的预测结果MCNN,并与实际震级值M0之间求偏差进行分析,结果如图 8所示,测试结果的震级偏差整体呈正态分布,平均震级偏差为0.028,标准差为0.231,最大震级偏差为-1.3.其中MCNN与M0震级偏差控制在±0.3以内的占85.6%,MCNN与M0震级偏差控制在±0.5以内高达95.7%.

|
图 8 MagNet模型的测试结果 (a) MCNN与M0的震级偏差分布散点图;(b) MCNN与M0震级偏差分布直方图. Fig. 8 Test results of the MagNet model (a) Scatterplot of MCNN and M0 magnitude deviation distribution; (b) Distribution histogram of magnitude deviation of MCNN and M0. |
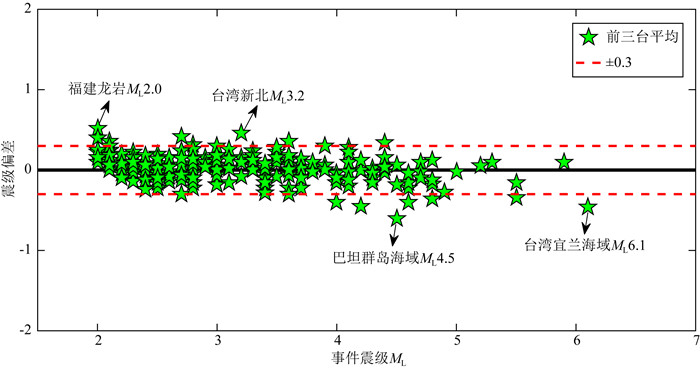
为了提高MagNet模型预测的可靠性,针对同一个地震事件中多台的预测结果进行综合平均.将测试集2837条地震记录,以地震事件进行归类,共有278个地震事件.统计测试集278个事件的前三台预测震级的平均偏差,如图 9所示,得出91.8%的地震事件震级偏差控制在±0.3级以内,相比较单台预测而言,最大震级偏差由-1.3减小为-0.6,标准差由0.231降至0.160,离散度减小,预测效果更优更可靠.其中2019年1月30日23时14分台湾花莲海域5.1级震例的前三台平均震级偏差为0.033,MagNet震级预测效果好,预测效果基本和实际一致,这是由于该地震区域存在较多历史震例,使得MagNet模型充分学习到该区域地震波形特征与震级之间的映射关系,从而做出可靠的预测.
|
图 9 前三台平均的震级偏差统计图 Fig. 9 Statistical figure of the average magnitude deviation of the first three stations |
从测试集278个地震事件中挑出前三台平均震级偏差大于或等于0.45的事件共有4个,具体结果见表 4.对较大震级偏差的事件进行分析如下:福建龙岩ML2.1的震级偏差主要由于该区域周围无历史震例样本,导致MagNet模型无法学习到该区域属地化波形特征,例如龙岩台观测仪器布设在半山腰,台站记录受场地放大效应的影响,使得模型预测的震级值偏大;台湾新北ML3.2的震级偏差主要由于该地震震源深度为102 km,福建ML测定是未考虑震源深度的影响,故而测得的ML偏小.然而MagNet模型通过深度学习历史震例,训练出一套不同于传统方法的震级预测模式,该模式可能有考虑震源深度的影响,故而预测出的震级值比实际ML偏大;巴坦群岛海域ML4.5、台湾宜兰海域ML6.1这两个事件具有共同的分布特征是:一是该事件周围历史样本较稀疏,导致CNN模型训练时样本数量不够,使得模型预测效果较差;二则这些事件属于网外地震,离最近台站较远,可能对事件本身震级测定精度造成一定的影响.同时这两个事件都为台湾岛东部海域地震,该地区的地下构造受太平洋板块和亚欧板块的俯冲作用影响,使得其发震机理较为复杂,体现的波形特征具有多样性,再加上样本数有限,最终导致模型预测偏差较大.
|
|
表 4 事件震级偏差大于0.4的地震统计表 Table 4 Statistical table of earthquake with magnitude deviation greater than 0.40 |
利用文中CNN模型所使用的样本数据,筛选出震源距小于60 km的台站记录作为研究资料,分别采用τc和Pd两种方法拟合出特征参数与地震震级间的关系,统计得出预估震级与实际震级偏差的标准差,并与上述获得的CNN震级测定方法进行比较.
3.4.1 τc方法根据周期特征类τc方法(Kanamori,2005;张红才等,2017)提取出每条台站记录P波段的周期特征参数,再采用M=a+blg(τc)形式拟合,得到τc特征参数与地震震级间的关系:

|
(6) |
式中,τc为P波触发后3s数据的台站垂直向获得的特征周期,单位为s;M为事件震级ML.图 10a为每条台站记录的周期τc值与震级M的统计关系,震级与周期τc呈正相关.图 10b为采用τc方法预测的震级值与实际震级值之间的关系,并获得两者震级偏差的标准差为0.79个震级单位.

|
图 10 利用τc方法预测震级 (a) τc与震级;圆点表示每条台站记录的τc值,实线表示线性拟合曲线,虚线表示一倍标准差;(b) 采用τc方法预测震级与实际震级间的关系;实线表示预测震级值等于实际震级值,虚线表示一个震级单位的震级偏差. Fig. 10 Earthquake magnitude prediction of τc method (a) τc vs. magnitude; circles represent the τc value of each record. The solid lines are the best fit curves evaluated through a linear regression. The dashed lines are one standard deviation; (b) The τc method of relationship between prediction magnitude and actual magnitude; the solid lines are the prediction magnitude value is equal to the actual magnitude value. The dashed lines are a unit of magnitude of magnitude deviation. |
根据幅值特征类Pd方法(Zollo et al., 2006)提取出经过高通滤波器(低频截至频率为0.075 Hz)滤波的位移幅值特征参数,再采用M=a+blg(R)+clg(Pd)形式拟合,得到Pd特征参数与地震震级间的关系:
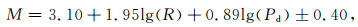
|
(7) |
式中,Pd为利用P波触发后3 s数据的台站三分量记录合成获得的峰值位移,R为震源距,M为事件震级ML.图 11a中纵轴Pd10 km表示将不同震源距处的位移幅值Pd统一校正到“参考”震源距10 km的位移幅值,这样处理主要是为了画图方便.图 11b为采用Pd方法预测的震级值与实际震级值之间的关系,并获得两者震级偏差的标准差为0.40.

|
图 11 利用Pd方法预测震级 (a) Pd与震级,圆点表示每台记录校正到“参考”震源距10 km的Pd值,实线表示线性拟合曲线,虚线表示一倍标准方差;(b) 采用Pd方法预测震级与实际震级间的关系,实线表示预测震级值等于实际震级值,虚线表示一个震级单位的震级偏差. Fig. 11 Earthquake magnitude prediction of Pd method (a) Pd vs. magnitude; circles represent the Pd value of each record normalized to a common reference distance of 10 km. The solid lines are the best fit curves evaluated through a linear regression. The dashed lines are one standard deviation; (b) The Pd method of relationship between prediction magnitude and actual magnitude; the solid lines are the prediction magnitude value is equal to the actual magnitude value. The dashed lines are a unit of magnitude of magnitude deviation. |
对以上周期特征类τc方法和幅值特征类Pd方法分析表明,统计得出预估震级与实际震级偏差的标准差分别为0.79和0.40,均大于CNN模型测定震级的标准差(无论是训练集还是测试集).另外,CNN模型所使用的资料是对震中距150 km范围内的台站记录(包括浅源和深源地震)共14644条样本做统计,而特征参数方法只筛选出震源距60 km的台站记录(浅源地震)共2310条样本进行统计拟合,相比而言,CNN模型统计的数据更加全面、多样性,更加接近真实地震可能存在的情况.综上所述,验证了本文提出CNN的震级测定方法优于传统的特征统计方法.
3.5 典型震例的预测效果分析为了进一步验证CNN模型对地震震级的测定效果,本文选取样本资料充足区域的台湾花莲ML5.9震例和样本资料稀疏区域的巴坦群岛海域ML4.5震例进行分析.
利用CNN模型、τc、Pd三种方法对典型震例的震级进行预测,结果如表 5所示.对于台湾花莲ML5.9地震,CNN模型、τc、Pd方法的预测震级与实际震级偏差分别为0.04、-0.88、-0.16,CNN模型预测效果最优,其次Pd方法,τc方法最差,这是由于该地震区域存在较多历史震例,使得神经网络训练时对该区域震例的特征学习更加充分,CNN模型相比传统特征方法具有更强的非线性、多因素的拟合能力,所以CNN模型预测效果优于传统特征方法.对于巴坦群岛海域ML4.5地震,CNN模型、τc、Pd方法的预测震级与实际震级偏差分别为-0.50、0.12、-0.64,τc方法最优,CNN模型次之,Pd方法最差,这是由于该地震历史样本较少,训练时神经网络未能充分学习到该区域的历史震例特征,神经网络会发挥一部分泛化能力对未知区域进行预测,但是传统特征方法简单的线性预测,有可能效果会优于CNN模型.综上,可以看出τc方法和Pd方法还不够稳定,既有好的预测效果,也有差的预测效果.CNN模型在样本充足的情况下可以做出高可靠的预测,因此在实际应用中有必要将多种方法联合分析,更大程度的发挥新技术带来的优势.
|
|
表 5 典型震例的预测效果对比分析 Table 5 Comparative analysis of prediction effect of typical earthquake cases |
本文充分利用卷积神经网络具有较强的分类功能,把震级测定问题看成分类问题来处理,将震级ML>2.0的地震共分成20个震级类型进行识别,提供了一种震级测定的新思路.应用卷积神经网络建立了单台三通道3 s样本波形与震级大小的映射模型,并用2012—2018年历史震例资料训练出适用于震级预测的MagNet模型,模型能够又快又准地测定出地震震级,相较于传统方法,模型测定的震级值更加稳定可靠,为解决地震预警震级测定这一挑战性难题提供了新的技术手段.
通常地震样本数据会存在空间分布和震级分布的不均匀性,可通过剔除地震频发地带较小的相似地震,并对较大地震数据进行样本增强处理,使得样本分布更加均匀,可提高模型的识别效果.在模型构建过程中,针对3 s地震波形的输入,采用1×3的小卷积核效果较佳.通过调参试验可知,6层卷积层未能充分提取到全局特征,8层卷积层过度压缩,使得部分局部特征被掩盖,因此得到7层卷积层效果较优.而1层全连接层可能对事物特征表达力不够,但3层全连接层可能会造成过拟合现象,因而得2层全连接层较优.典型卷积神经网络的输入数据通常需要做归一化处理,如震相识别、地震定位等处理.但是针对地震震级测定问题,由于振幅信息的重要性,因此构建了带振幅信息输入的卷积神经网络,一方面将震级输出划分为20个不同震级类别,减小震级输出的分类类别,增加每类样本数量;另一方面通过在卷积层中增加RELU激发函数以及采用ADAM优化算法来解决未归一化的问题,进而使得模型的识别效果更佳.
用2019年新震例对模型进行测试分析,得出单台的震级偏差有85.6%可以控制在±0.3以内,前三台平均的震级偏差有91.8%可以控制在±0.3以内,可见多台平均的震级预测效果比单台更加稳定可靠.分析震级偏差较大的事件,得出对于缺乏历史震例的地震样本的识别效果较差,同时对于台湾岛东部海域远岸的地震由于发震机制复杂多样,导致波形特征多样性,在历史样本不足且台站距离较远的情况下,容易导致模型预测出现较大偏差.虽然深度神经网络的新方法总体上优于传统特征方法,但这并不代表在实际应用中可以完全取代传统震级测定方法.换言之,可以将两者结合起来,发挥各自的优点,比如对于历史多震区域的地震,则以深度神经网络预测的震级结果为主;而对于历史少震或无震区域的地震,则需要传统特征方法联合辅助判断,使得结果更加可靠.预警工程是一个十分复杂的工程,除了考虑震级偏差外,还需考虑误报率.不同地区的预警报警等级不同,例如对于福建地区的地震,通常震级大于3.5级或者近台烈度超过一定限值,即发出预警警报;对于台湾地区的地震,通常5级或5.5级以上地震,便向福建全省发出预警警报.而一旦将小地震发布成大地震,所带来的社会和经济影响将会很大,因此还需要进一步防止误报现象.
地震震级测定是一个非常难的问题,其受地震震源深度、区域衰减、台站场地等多种因素的影响.根据地震震源深度的不同,震级度量方法也不同.对于浅源地震,通常选用里氏震级ML和面波震级MS;对于深源地震,通常采用体波震级mb.考虑区域衰减的影响,主要体现在量规函数项,即补偿量随震中距的变化函数,不同地区的量规函数会存在一定的差异但不会太大.台站场地也会对震级造成一定影响,主要体现在台站校正值,如台站受场地放大效应的影响,常导致单台震级测量偏大.针对单台震级测量偏差问题,深度神经网络通过自学习波形特征,训练出单台波形与最终台网平均震级之间的映射关系,即可消除不同台站场地造成的震级偏差影响.文中震级预测模型采用ML震级进行训练,但由于ML震级本身的局限性,当测定的震级大于6.5级时将趋于饱和,对于7.0级以上大震显然难以从ML测定中得到较科学的震级,因此可选用其它震级标度(如MS、mb或MW)作为最终震级值进行训练.同时对于深源地震,可选用mb震级作为最终震级值进行训练.
另外,还需考虑噪声、异常波形的影响,文中所用的训练数据都是不同震级的地震波形,这会导致训练出来的网络偏向对地震波形感兴趣,而实际应用中必不可少会存在地震噪声或异常波形,可能导致网络出现一定的偏差,因此后续需要增加一个专门区分地震、噪声和异常波形的网络先将地震数据分离出来,再做CNN震级测定.
文中的训练数据虽然有增加部分川滇地区ML>5.0的地震记录,并进行了大震样本增强处理,但是大震样本数量还是比较有限,今后可收集全国各地域的大震记录加入模型训练,并探究模型在不同地区的适用能力.随着地震数据量不断积累,网络模型不断加深和优化,在3 s样本的基础上再训练出5 s、8 s、10 s、20 s等样本的震级预测模型,以满足地震预警震级连续测定的要求,可进一步提高预警震级的精度和可靠度.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!
Chen D Y, Lin T L, Wu Y M, et al. 2012. Testing a P-wave earthquake early warning system by simulating the 1999 Chi-Chi, Taiwan, MW7.6 Earthquake. Seismological Research Letters, 83(1): 103-108. DOI:10.1785/gssrl.83.1.103 |
Chen D Y, Wu Y M, Chin T L. 2017. An empirical evolutionary magnitude estimation for early warning of earthquakes. Journal of Asian Earth Sciences, 135: 190-197. DOI:10.1016/j.jseaes.2016.12.028 |
Feng J W. 2019. Real-time estimation of the ground motion field of large earthquakes[Ph. D. thesis] (in Chinese). Harbin: Institute of Engineering Mechanics, China Earthquake Administration.
|
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. 2017. GB 17740-2017 General ruler for earthquake magnitude (in Chinese). Beijing: Standards Press of China: 5-13.
|
Hu A D, Zhang H M. 2020. Application of machine learning to magnitude estimation in earthquake emergency prediction system. Chinese Journal of Geophysics (in Chinese), 63(7): 2617-2626. DOI:10.6038/cjg2020N0070 |
Jin X, Zhang H C, Li J, et al. 2012. Research on earthquake early warning magnitude estimate. Acta Seismologica Sinica (in Chinese), 34(5): 593-610. |
Kanamori H. 2005. Real-time seismology and earthquake damage mitigation. Annual Review of Earth and Planetary Sciences, 33(1): 195-214. DOI:10.1146/annurev.earth.33.092203.122626 |
Krizhevsky A, Sutskever I, Hinton G E. 2012. ImageNet classification with deep convolutional neural networks. //Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 1097-1105.
|
Li S Y. 2018. Approaching the earthquake early warning. Overview of Disaster Prevention (in Chinese), (2): 14-23. |
Lomax A, Michelini A, Jozinović D. 2019. An investigation of rapid earthquake characterization using single-station waveforms and a convolutional neural network. Seismological Research Letters, 90(2A): 517-529. DOI:10.1785/0220180311 |
Ma J S, Sheridan R P, Liaw A, et al. 2015. Deep neural nets as a method for quantitative structure-activity relationships. Journal of Chemical Information and Modeling, 55(2): 263-274. DOI:10.1021/ci500747n |
Ma Q. 2008. Study and application on earthquake early warning[Ph. D. thesis] (in Chinese). Harbin: Institute of Engineering Mechanics, China Earthquake Administration.
|
Mousavi S M, Beroza G C. 2020. A machine-learning approach for earthquake magnitude estimation. Geophysical Research Letters, 47(1): e2019GL085976. DOI:10.1029/2019GL085976 |
Nan FF, Zhang F, Gong G B, et al. 2019. Preliminary analysis of magnitude degree in automatic rapid report of earthquakes in Xinjiang region. Seismological and Geomagnetic Observation and Research (in Chinese), 40(4): 45-52. |
Peng C Y, Yang J S, Xue B, et al. 2013. Research on correlation between early-warning parameters and magnitude for the Wenchuan Earthquake and its aftershocks. Chinese Journal of Geophysics (in Chinese), 56(10): 3404-3415. DOI:10.6038/cjg20131016 |
Peng C Y, Yang J S, Zheng Y, et al. 2017. New τc regression relationship derived from all P wave time windows for rapid magnitude estimation. Geophysical Research Letters, 44(4): 1724-1731. DOI:10.1002/2016GL071672 |
Perol T, Gharbi M, Denolle M. 2018. Convolutional neural network for earthquake detection and location. Science Advances, 4(2): e1700578. DOI:10.1126/sciadv.1700578 |
Song J D, Li S Y. 2012. A comparison between two magnitude estimating methods using predominant period in earthquake early warning. Journal of Earthquake Engineering and Engineering Vibration (in Chinese), 32(6): 174-181. |
Wu Y M, Kanamori H. 2005. Experiment on an onsite early warning method for the Taiwan early warning system. Bulletin of the Seismological Society of America, 95(1): 347-353. DOI:10.1785/0120040097 |
Wu Y M, Zhao L. 2006. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning. Geophysical Research Letters, 33(16): L16312. DOI:10.1029/2006GL026871 |
Wu Y M, Kanamori H, Allen R M, et al. 2007. Determination of earthquake early warning parameters, τc and Pd, for southern California. Geophysical Journal International, 170(2): 711-717. DOI:10.1111/j.1365-246X.2007.03430.x |
Yamada M, Mori J. 2009. Using τc to estimate magnitude for earthquake early warning and effects of near-field terms. Journal of Geophysical Research, 114(B5): B05301. DOI:10.1029/2008JB006080 |
Zhang H C. 2013. Study of key technologies in earthquake early warning system[Ph. D. thesis] (in Chinese). Harbin: Institute of Engineering Mechanics, China Earthquake Administration.
|
Zhang H C, Jin X, Li J, et al. 2017. Application of Pd-τc compatibilitycriterion to distinguishing triggered events. Acta Seismologica Sinica (in Chinese), 39(1): 102-110. DOI:10.11939/jass.2017.01.009 |
Zhao M, Chen S, Fang L H, et al. 2019a. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network. Chinese Journal of Geophysics (in Chinese), 62(8): 3034-3042. DOI:10.6038/cjg2019M0495 |
Zhao M, Chen S, Yuen D. 2019b. Waveform classification and seismic recognition by convolution neural network. Chinese Journal of Geophysics (in Chinese), 62(1): 374-382. DOI:10.6038/cjg2019M0151 |
Zhu W Q, Beroza G C. 2019. PhaseNet: A deep-neural-network-based seismic arrival time picking method. Geophysical Journal International, 216(1): 261-273. |
Ziv A. 2014. New frequency-based real-time magnitude proxy for earthquake early warning. Geophysical Research Letters, 41(20): 7035-7040. DOI:10.1002/2014GL061564 |
Zollo A, Lancieri M, Nielsen S. 2006. Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records. Geophysical Research Letters, 33(23): L23312. DOI:10.1029/2006GL027795 |
Zollo A, Amoroso O, Lancieri M, et al. 2010. A threshold-based earthquake early warning using dense accelerometer networks. Geophysical Journal International, 183(2): 963-974. DOI:10.1111/j.1365-246X.2010.04765.x |
冯继威. 2019. 大震地震动场的实时估计[博士论文]. 哈尔滨: 中国地震局工程力学研究所.
|
胡安冬, 张海明. 2020. 机器学习在地震紧急预警系统震级预估中的应用. 地球物理学报, 63(7): 2617-2626. DOI:10.6038/cjg2020N0070 |
金星, 张红才, 李军, 等. 2012. 地震预警震级确定方法研究. 地震学报, 34(5): 593-610. DOI:10.3969/j.issn.0253-3782.2012.05.002 |
李山有. 2018. 走近地震预警. 防灾博览, (2): 14-23. |
马强. 2008. 地震预警技术研究及应用[博士论文]. 哈尔滨: 中国地震局工程力学研究所.
|
南芳芳, 张锋, 龚固斌, 等. 2019. 新疆地区自动地震速报震级偏差分析. 地震地磁观测与研究, 40(4): 45-52. DOI:10.3969/j.issn.1003-3246.2019.04.007 |
彭朝勇, 杨建思, 薛兵, 等. 2013. 基于汶川主震及余震的预警参数与震级相关性研究. 地球物理学报, 56(10): 3404-3415. DOI:10.6038/cjg20131016 |
宋晋东, 李山有. 2012. 地震预警中两种利用卓越周期估算震级方法的比较. 地震工程与工程振动, 32(6): 174-181. |
张红才. 2013. 地震预警系统关键技术研究[博士论文]. 哈尔滨: 中国地震局工程力学研究所.
|
张红才, 金星, 李军, 等. 2017. Pd-τc相容性检验方法在触发事件判别分析中的应用. 地震学报, 39(1): 102-110. DOI:10.11939/jass.2017.01.009 |
赵明, 陈石, 房立华, 等. 2019a. 基于U形卷积神经网络的震相识别与到时拾取方法研究. 地球物理学报, 62(8): 3034-3042. DOI:10.6038/cjg2019M0495 |
赵明, 陈石, Yuen D. 2019b. 基于深度学习卷积神经网络的地震波形自动分类与识别. 地球物理学报, 62(1): 374-382. DOI:10.6038/cjg2019M0151 |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 2017. GB 17740-2017地震震级的规定. 北京: 中国标准出版社: 5-13.
|
 2021, Vol. 64
2021, Vol. 64


