俯冲带是海洋板块向大陆板块或另一个海洋板块下面俯冲的板块边界.两个板块之间的接触边界是俯冲带大断层.本文讨论有关这个大断层的强度的一些问题.本文的定位比较特殊.它不是关于本学科的前沿综述,而是简述作者对于这个领域一系列科学问题的系统认识,内容主要基于作者自己团队发表过的研究成果.多数图件采自这些文献并经过加工修改.读者对象不光是研究俯冲带的学者,也包括其他对俯冲带研究感兴趣的、有地质和地球物理背景的研究生和科研人员,所以主要定性地讲原理,简化定量分析,尽量避免数学公式.由于俯冲带研究近十几年发展很快,本文的一些内容与传统的认识相悖.许多问题还没有完全理解或存有争议.对这些问题的讨论也从很大程度上代表了未来的研究方向.
断层的强度是指造成它滑动所需的剪应力.俯冲带大断层的强度是岩石圈板块动力学的一个重要问题.板片俯冲时在这里遇到多大阻力,大断层给上覆板块构造应力场提供什么样的边界条件,都取决于大断层的强度.文中涉及的许多概念对理解任何其他断层也是重要的,因而有普遍的地球动力学意义.研究俯冲带大断层的强度也有社会意义.大断层的突然错动会产生大地震,往往还伴随着海啸.2004年9.2级苏门答腊大地震破裂面沿海沟走向长达1300 km,引发的海啸在北印度洋周边造成24万人死亡.2011年9.0级日本海沟大地震断层错距最大处达60余米(Sun et al., 2017),带来的海啸致死近2万人.迄今大于8.5级的地震基本都发生在俯冲带大断层上.了解大断层的强度有助于揭示这些地震的物理机制,并对减灾实践有指导意义.
俯冲带大断层是一个复杂的剪切带(Wang, 2010; Rowe et al., 2013; Agard et al., 2018; Raimbourg et al., 2019).洋底遍布地垒-地堑、海山、海岭、断裂带等不同尺度的高低起伏,俯冲后造成断层不规则的几何形态.俯冲板片在俯冲前和俯冲后的弯曲变形又引起新的正断层活动,加剧了几何不规则性.修整和磨平这些不规则形态的过程会引起小断层活动、岩块旋转、岩石破碎、断层泥发育、变形的局域化等,在断层带内外造成一系列复杂构造.洋底的沉积层在有些情况下整体俯冲下去,增加了大断层的平滑度,有些情况下仅部分俯冲,余下的形成增生楔,而有些俯冲洋底本来就没有多少沉积物.断层带里的材料不仅有从海沟带下去的沉积物,也裹挟了来自俯冲洋壳顶部的玄武岩块屑和从上覆板块底部剥蚀下来的其他岩石.随着温度压力向深处的增高,断层带内的物质发生变质,同时也形成一些新的矿物.俯冲板片里的一些矿物由于温压增高也发生脱水,给断层带加入了新的流体和溶于其中的矿物.丰富的含矿流体不但引起断层材料组分的变化,还引起一些重要的物理过程,如提高孔隙液压、改变渗透率、促进压溶流变作用等等.从许多出露地表的古俯冲断层来看,断层带里的材料往往是经过不同程度变质的混杂岩体,夹有一些局域化的剪切带,其中包括极薄的滑动层.这些滑动层有时含有被公认为是古地震直接证据的假玄武玻璃.
本文讨论的断层强度是对上述复杂系统的一个最基本的力学性质的宏观描述.地球动力学中,几乎所有参数描述的都是某种时间、空间和物理过程的平均效应,只不过平均尺度多种多样.其他常见的大尺度平均参数还有地壳密度、岩石圈有效弹性厚度、地幔黏性系数、岩层渗透率等.了解实际地质系统的复杂性,对理解这种宏观描述的合理性、必要性和局限性十分关键.不了解现实的复杂性而盲目简化,往往会丢掉本质问题.仅关注复杂细节而不知如何简化,往往就事论事,看不到普适性的本质问题.
1 俯冲带大断层的温度环境和岩石学环境虽然本文主要讨论大断层的强度,但是十分必要先简单介绍一下俯冲带的温度和岩石学环境,以提供一个大的构造物理背景.为了叙述方便,以下忽略现实中各种具体的复杂情况,仅假设一个上覆板块为大陆的“典型”理想俯冲带.俯冲带最重要的一个特征是弧前地区温度低,而火山弧与弧后地区温度高(图 1)(Wada and Wang, 2009).全球陆地的热流平均值是65 mW·m-2左右,而弧前地区的热流值一般可以低至30~40 mW·m-2.弧后地区热流普遍较高,往往为80 mW·m-2左右(Currie and Hyndman, 2006).习惯上常将“弧与弧后”作为一个单元来讨论.

|
图 1 热俯冲带和冷俯冲带的典型代表(自Wada和Wang (2009)原图修改而成) (a) 卡斯卡迪亚,俯冲板片年轻而温度高; (b) 日本海沟,俯冲板片年老而温度低.两图中所示温度场的模型计算细节和剖面位置见Wada和Wang(2009).红点是实测地表热流,蓝线是模型计算值.两平行虚线之间是俯冲洋壳,其中蓝色部分是玄武质岩石,白色部分是榴辉岩.俯冲洋壳脱水高峰伴随玄武岩向榴辉岩的转变.俯冲地幔和上覆地幔的紫色部分圈出叶蛇纹石(antigorite)可以稳定存在的温压条件;实际上叶蛇纹石存在与否以及富集度还取决于是否有足够的H2O.上覆地幔的这个紫色部分也大体代表了地幔冷楔.剖面中的箭头显示模型中地幔热楔物质流动方向.黑三角代表火山弧位置. Fig. 1 End-member representatives of warm and cold subduction zones (Modified from original figures in Wada and Wang (2009)) (a) Cascadia, where the subducting plate is young and warm; (b) Japan Trench, where the subducting plate is old and cold. For details of the temperature modelling and locations of the model profiles, see Wada and Wang (2009). Red dots and the blue curve represent observed and model-predicted heat flow values, respectively. The two parallel dashed lines encompass the subducting crust, in which the blue part is meta-basalt and the white part is eclogite. Peak dehydration of the subducting crust accompanies the basalt-eclogite transformation. Purple areas in the slab mantle and mantle wedge indicate P/T conditions for the stability of antigorite; the actual presence and abundance of antigorite depend on whether adequate H2O is available. Nevertheless, the purple area of the mantle wedge basically represents the cold nose. Arrows in the hot part of the mantle wedge show model-predicted direction of wedge flow. The black triangle marks the location of the volcanic arc. |
弧前温度低的原因是俯冲板片把浅层较冷的岩石带到深处,给上覆岩层“降温”.弧与弧后温度高的原因是地幔楔物质的流动把深部较热的岩石带到浅处,给上覆岩层“升温”.在图 1以外、离俯冲带较远的弧后地区,地幔流动方式一般认为是热浮力引起的小尺度自然对流(Currie et al., 2004; Currie and Hyndman, 2006).而图 1以内的弧与弧后地区的地幔流动方式是被俯冲板片拖拽驱动的“角落流”.弧前——弧与弧后的温度反差反映了俯冲板片对地幔楔的拖拽从70~80 km深度开始(Wada and Wang, 2009; Syracuse et al., 2010).在此以深,地幔楔底部与俯冲板片完全耦合,即同速运动.由此造成的角落流从深部和弧后带来大量的热,在地幔楔里造成产生岩浆的高温条件.在此以浅,两者完全解耦,以致这一部分地幔楔处于停滞状态,不参与角落流,成为上板块岩石圈的一部分(Wada and Wang, 2009; Uchida et al., 2020).不流动的这部分地幔楔不断被俯冲板片降温,称为“冷楔”(图 1).冷楔是弧前力学体系的一个重要部分(Luo and Wang, 2021),这一点的重要性在第3.1节还会涉及.我们不妨把参与角落流部分的地幔楔称为“热楔”.至于从解耦到耦合的转变普遍发生于70~80 km处的原因,还没有很好的理论解释.Peacock和Wang(2021)最近从岩石学角度在这方面做了一些探索,认为滑石稳定性在这一深度的改变起了重要作用.
在海洋岩石圈逐渐冷却和老化的过程中,大量的海水通过水热循环和水热变质进入岩石形成含水矿物.越老的板片含水越多.显然,水主要储存在地壳里(一般6、7 km厚).如果断层可以把水带到地幔,而且地幔浅部已经充分冷却,含水矿物亦可以在地幔部分沿断层和裂隙形成(Miller et al., 2021).当海洋板片向深处俯冲时,裂隙闭合使岩石里的自由水在很浅的地方就被挤出.随着温度和压力的增高,洋壳岩石发生一系列变质作用,最终玄武质洋壳变质为密度更高的榴辉岩.洋壳里的各种含水矿物在变质过程中分解、脱水,而脱水高峰出现于玄武质岩石向榴辉岩的转化过程(Peacock and Wang, 1999).年轻而热的板片,变质脱水在比较浅的地方达到高峰.年老而冷的板片,变质脱水要到100~150 km深处才达到高峰.图 1以卡斯卡迪亚和日本海沟为例,对比年轻和年老板片不同的脱水高峰深度.俯冲板片的地幔部分主要是橄榄岩.它的变质要到地幔转换带(约410~660 km)才发生,但是它带下去的含水矿物可以在比较浅的地方就分解和脱水.
俯冲带一个重要的岩石学过程是冷楔充水.地幔楔橄榄岩充水形成的含水矿物包括蛇纹石、绿泥石、滑石、水镁石等.少数几个最年轻的俯冲洋壳如卡斯卡迪亚脱水高峰很浅(图 1),可以给冷楔提供大量的水源,以致于其尖端区域可以完全充水,出现蛇纹石饱和,影响了其附近大断层的力学性质(Gao and Wang, 2017).老一些的洋壳如日本海沟脱水高峰较深(图 1),给冷楔提供的水十分有限,所以多数俯冲带的冷楔充水程度不高(Abers et al., 2017).但是,因为冷楔的充水是自下而上,即使少量的水也会在冷楔最底部靠近大断层的地方形成富集含水矿物.再往陆地方向,洋壳脱水则是给热楔充水,降低岩石熔点,产生岩浆.这是公认的俯冲带火山弧形成的主要机制,在此不加详述.
2 大断层强度的参数化 2.1 从摩擦滑动到黏性剪切引言提到,俯冲带大断层是一个构造丰富、材料多样的剪切带.如何简化一个复杂系统取决于研究焦点是哪个主要物理过程和该过程的时空尺度.在地震学理论和大尺度地球动力学模拟中,俯冲带大断层在温度比较低的浅部,即岩石呈脆性的地方,常常简化为一个没有厚度的摩擦接触面.因此脆性区也称为摩擦区.而在温度比较高的深部,即岩石呈韧性的地方,常常简化为一个黏性层.因此韧性区也称为黏性区.和温压有关的岩石流变性质控制了从脆性到韧性的转换(图 2).

|
图 2 俯冲带大断层脆性摩擦和黏性剪切分布示意图虽然是手画示意图,但是各曲线基本特征均参照Gao和Wang(2014)计算结果.各线摩擦部分略微向上弯曲是因为断层倾角沿深度逐渐增高.摩擦到黏性的转换仅在一条曲线上标出,但也适用于其他两曲线.若摩擦强度高或俯冲板片年轻,转换在比较浅的位置发生.“低μ′、年轻板片”和“低μ′、老板片”分别适用于卡斯卡迪亚(图 1a)和日本海沟(图 1b). Fig. 2 Schematic illustration of frictional and viscous parts of the megathrust This is a hand-drown schematic illustration, but the main characteristics of the various curves are based on the model results of Gao and Wang (2014). The slight concave upward shape of the frictional part of each curve is due to the increase in fault dip with depth. The frictional-viscous transition is marked only on one curve but applies also to the other two curves. For a greater fault strength or a younger slab, the transition occurs at a shallower depth. The "low μ′, young plate" and "low μ′, old plate" scenarios apply to the Cascadia (Fig. 1a) and Japan Trench (Fig. 1b) subduction zones, respectively. |
在脆性区,断层的强度τs,即造成断层滑动的剪应力,由库仑摩擦系数μ表征:

|
(1) |
其中σn是断层上的正应力,pf是孔隙液压,而σn=σn-pf是有效正应力.一般来说σn与静岩压力pL=ρgz差别不大,其中ρ是岩石平均密度,g是重力加速度,z是深度.式(1)是用真实摩擦系数和有效正应力表示断层强度.如果定义λ=pf/σn≈pf/pL,则断层强度也可以反过来用有效摩擦系数μ′=μ(1-λ)和真实正应力来表示:

|
(2) |
以上两式用一个参数μ或μ′代表了一个庞大系统.它强调了摩擦过程的最基本特征——剪切强度随正应力(即随围压、深度)增高而增大,而平均掉了小尺度时空变化和其他物理过程的贡献.地球动力学研究常用的Byerlee′s law(Byerlee, 1978)是上述库仑摩擦准则的特殊形式,μ值为0.7左右.如果假设σn≈pL而pf是静水压力(把静岩压力中的岩石密度换成水的密度),则λ≈0.4,μ′≈0.4.当我们说一个断层强或弱,对比的就是这个“参照值”.
需要强调,大断层的滑动是沿一个厚度从几毫米到数百米不等的剪切带发生的(见引言),而μ或μ′刻画的实际上是在厚度方向积分起来的效应.一个“蠕滑”型断层的脆性区域可能是整个剪切带以碎屑流方式蠕动,可以用库仑塑性连续介质描述(Wang, 2021),也可能是其中一个或多个软弱层在慢慢滑动.无论如何,断层厚度方向积分起来的总体强度可以用(1)(2)两式表征.这种情况下,因为断层滑动的平均阻力就是τs,断层强度的意义比较简单.而所谓“锁-滑”(stick-slip)型断层,一般不滑动,呈闭锁态(锁),但间歇性发生大地震(滑),断层强度概念略有不同.地震滑动带是很薄的剪切层,厚度一般几毫米或数厘米,在这个方面比许多蠕滑断层简单一点.但是由于强度在地震过程中发生变化,它的参数化稍为复杂一点.这一点在2.2节再进一步解释.另外,stick-slip一词以前翻译成“黏-滑”.因为“黏-滑”与“黏性滑动”意思相反但用字类似,容易引起误解,所以此处译为意思更明确的“锁-滑”.
沿断层再往深处去,温度增高,断层性质从脆性摩擦滑动转为韧性剪切蠕变.这个蠕变的区域一般用一层非线性黏性流体来代表,其主要参数是有效黏滞系数(Gao and Wang, 2014).什么样的流体最适合代表这个黏性层并不清楚,也可能因地而异.因为俯冲断层带介质中含有许多石英,而石英在温度较高的情况下韧性“强度”很小从而主导介质的总体流变行为,我们在模拟中一般用石英含量较高的岩石如花岗岩、花岗闪长岩等的流变学性质来描述这层黏性流体.因为信息不足,无论用什么方法对黏性区进行参数化,都有一定的任意性.但是在研究断层强度和地震过程时,摩擦区是主角而黏性区是配角,这种任意性带来的误差一般不影响主要结论.前面提到,脆性区摩擦过程的最基本特征是摩擦强度随围压增高而增大.相比之下,韧性区黏性蠕变的一个基本特征则是对温度的敏感性.随温度升高,黏性层对剪切变形的阻力迅速降低.当我们讨论断层强度时,主要聚焦于μ或μ′,但是也隐含了黏性区域的贡献.在实际俯冲带中(不一定在模型里)黏性剪切层可以认为是俯冲带大断层逐渐丧失其独立性而与地幔热楔合为一体的过渡区.作者猜测,由浅至深,剪切层厚度应逐渐增大,流变越来越不局域化,其黏性剪切变形与地幔热楔黏性流动的区别越加模糊.到70~80 km以深,热楔底界与俯冲板片同速运动,即第1节所说的完全耦合,造成热楔的剪切流动.这时,大断层仅仅是一个不同岩石的物质分界面,而不再是一个变形的间断面.
从摩擦到黏性的转变不是突变,而是要经过一个不大的转换带(Shimamoto and Noda, 2014);在转换带里断层上的剪应力达到峰值(图 2).在图 1的两个俯冲带中,这个转换发生于温度为400℃左右的地方.显然,如果俯冲板片年轻(如图 1中的卡斯卡迪亚),大断层温度高,这个转换会在很浅的地方发生.这个由温度控制的脆-韧(即摩擦-黏性)转换深度是俯冲带大断层的一个重要参数.例如,即使图 1中两个大断层μ′值相同,冷的那个(日本海沟)由于脆-韧转换深度大、摩擦区域延伸的深、断层剪应力的峰值也高,其对上覆板块总体的横向挤压力比热的那个(卡斯卡迪亚)要大得多,亦如图 2所示.所以,大断层强度对上板块应力场的控制和这个转换有关.这一点在第3.1节还会涉及.还有几点,虽然超出本文讨论范围,但是也值得提一下.第一,如果温度很高,韧性区无法积累弹性应变能,不能孕育大地震,所以脆-韧转换对大断层发震带的截止深度有一阶控制.第二,如果俯冲板片非常年轻(如卡斯卡迪亚),脆-韧转换浅于上覆板块莫霍面的深度,也就是说达不到地幔冷楔的深度,而冷楔尖端又出现蛇纹石饱和(见第1节末),大断层在这一带会表现出特殊的幕式滑移行为(Gao and Wang, 2017).第三,许多俯冲带的脆-韧转换深于上覆板块莫霍面.冷楔底部的含水矿物,特别是蛇纹石和滑石,可能被裹挟进断层带.这些矿物的力学性质很特殊,可以影响断层脆性区深部的摩擦和发震行为(Wang et al., 2020).
2.2 “锁-滑”断层的强度2.1节描述的摩擦区强度仅仅是静摩擦强度.对于锁-滑型断层来说,摩擦系数μ除了一个刻画静摩擦强度的常数项以外,还有一些和其他因素有关的高阶项.断层发生地震或慢滑移事件时,μ会随滑动距离或滑动速率变化,而如何变化由这些高阶项决定.有关理论,包括依赖速率和状态的摩擦理论、动态(或高速率)弱化理论等,还往往与pf的变化和摩擦热引起的材料性质变化有关.这些高阶效应是地震动力学的主题,在此略去不讨论.但是,为了解释锁-滑断层的强度,必需先对地震破裂的起始和传播过程做一个简单的介绍,同时引入断层真实强度τp和视强度τo的概念.对于永不闭锁的蠕滑断层,τs=τp,比较简单.以下解释,锁-滑断层应该有τs=τo.
地震是断层间歇性的失稳行为.断层闭锁时,周围岩石受构造力驱动发生弹性变形、积累应变能,而断层上的剪应力逐渐增加.断层上各点的应力和强度其实高低不等.当某一点的应力τo达到了真实强度τp,这一点便开始滑动.如果滑动引起断层的弱化(即μ减小,在摩擦理论中由上面提到的高阶项描述),进而引起更快的滑动和进一步的弱化,断层便局部失稳.这就是一个地震的起始(震源).图 3a简单示意震源部位滑动时的断层剪应力变化过程.震源开始滑动时,闭锁断层其他部位的应力τo还低于τp.但是在局部失稳的滑动带(称破裂带)的前沿,应力突然增高达到τp,使相邻区域也出现屈服和失稳.新的破裂又同样引起相邻区域新的失稳,这样破裂就沿断层传播开来.图 3b简单示意破裂带中非震源处失稳滑动前后的应力演化过程.注意,此处说的震间闭锁跟第1节说的70~80 km以深的耦合是两回事:如果很多次地震的错距可以完全补上闭锁期间积累的“滑移欠缺”,断层发震带在长时间尺度上是完全解耦的.

|
图 3 平滑断层不同位置在同一个地震滑动中的应力变化示意图(图(b)部分修改自Brown等(2015)) (a) 震源位置.震前一刻应力τo达到断层真实强度τp,断层随即滑动并弱化; (b) 破裂前沿.震前应力τo低于τp,但是应力瞬间增到τp,继之断层强烈弱化.破裂得以传播; (c) 卷入地震过程的断层强化部位.应力随滑动增高(但不像(b)那样瞬间突增).强化程度很高时,可以停止破裂传播.不太高时,则可以被周围弱化部位驱动而“被动”参与滑动,但其应力增(即负应力降)会减缓破裂传播速率; (d) 强化转弱化的部位.强化阶段与(c)类似,但是当被动滑动的速率太高时,断层在其他机制作用下强烈弱化,变成类似如(b)所示的主动滑动.另外,在任何部位,应力在滑动停止以后还会受相邻部位的影响而继续变化,本图略去. Fig. 3 Cartoon showing how stress changes in different parts of a smooth fault during the same seismic rupture (Panel (b) is modified from Brown et al. (2015)) (a) Hypocentral area. When the pre-earthquake stress τo reaches fault strength τp, fault begins to slip and weaken. (b) Rupture front. The pre-earthquake stress is lower than fault strength, but the stress instantaneously increases to τp, followed by intense weakening. The rupture is then able to propagate. (c) Patches of the fault that are involved in the rupture process but exhibit strengthening. The stress increases with slip (but unlike the sudden rise in the beginning of (b)). A high degree of coseismic strengthening can stop rupture propagation. Moderate strengthening may result in the patch being "passively" driven to participate in the slip, but the accompanying stress increase (i.e., negative stress drop) serves to retard rupture velocity. (d) Patches that turns from strengthening to weakening. The initial strengthening phase is similar to that in (c). When its slip rate is adequately high, other mechanisms cause intense weakening, and the patch actively participates in the rupture as in (b). Stress may continue to change after the slip stops because of influence from neighbouring parts of the fault, but it is not shown here. |
如图 3b所示,在闭锁期间和地震发生的时刻,断层上的剪应力τo普遍低于真实强度τp,而只有在破裂传播前沿,应力才瞬间达到τp.在动态过程中,破裂前沿的应力峰值可以极为短暂的超过τp;但是为了简化讨论,此处假设峰值就是τp.我们一般既无法知道也并不关心τp.我们关心的是τo,因为它是断层在地震发生前所能承受的最高剪应力,所以称为断层的视强度.当公式(1)和(2)应用于锁-滑型断层时,τs应理解为视强度τo,相应的μ或μ′也应理解为“视摩擦系数”和“视有效摩擦系数”.至于锁-滑断层的视强度比真实强度低多少,没有统一认识.此处不详细讨论;感兴趣的读者可以查找有关动力学地震破裂和传播模型的文献(如, Lambert et al., 2021).本文作者的看法是,在一个俯冲带大断层这样的构造和材料都很复杂的断层里,作为平均参数,两者的差别相较于断层强度本身应该不大.在地震破裂带某些局部位置,两者有可能差别较大.因为本文讨论的是大断层的整体平均强度,所以除有必要,以下将不再特别强调真实强度和视强度的区别.另外,除了真实强度和视强度以外,断层滑动时还有动摩擦强度.这在第3.2节讨论摩擦生热时还会提到.
地震时发震带每一点的滑动速率在m·s-1量级,而破裂前沿的传播速率(称破裂速度)一般在km·s-1量级.俯冲带断层大地震沿走向的破裂速度常在2 km·s-1上下.破裂传播的越远,发震带越大,地震也就越大.所以,控制破裂传播能力的因素如断层的粗糙度、不均一性、断层泥性质等主导了地震的大小.断层上有些部位,包括一部分的滑动带,不是像图 3b那样失稳滑动.相反地,这些部位可能由于滑动而强化,呈稳定滑动(图 3c),从而减慢甚至阻止破裂传播.有时可能先强化而阻碍地震,待滑动速率高到一定程度时又突然弱化而推进地震(图 3d)(Noda and Lapusta, 2013).显然,当我们说一个断层是锁-滑型,并不是说断层上每一点都像图 3b那样,只是说像图 3c和图 3d那样的部位比例比较小,不足以主宰断层的整体滑动行为.尽管图 3b显示的是断层某一点的行为,但是在本文主题的尺度上,视强度τo和真实强度τp用来描述整个滑动带的平均行为,一般不再单独强调图 3c或图 3d那种部位的贡献.俯冲带大断层可以产生9级大地震,是因为它可以提供适于破裂传播的地质条件.在任何构造环境中,小地震远远多于大地震(其规律由Gutenberg-Richter法则中的b值代表),就是因为绝大多数的地震破裂都不能传播扩展成大的破裂带.
既然只有断层弱化才能导致地震,断层的应力降是地震的基本参数.地震破裂带上某一点的静力学应力降Δτ就是这一点的τo与这一点震后剪应力的差值(图 3b).一般说的地震应力降指的就是这个静力学应力降,但是常常是一定面积内(如整个破裂带)的平均应力降.破裂带里往往包括一些应力降为负值的、图 3c代表的那种部位.这些负应力降的存在大大影响了平均应力降的大小.这个问题被普遍忽略,在第4.1节还会提及.地震学观测的一个至关重要的结论是:大地震的平均应力降一般都很小,在几兆帕的量级(Ye et al., 2016).这个结论现在已经是常识,在此不再解释.在第3节介绍俯冲带大断层强度的估算方法和结果时,这个结论的重要性会充分体现出来.
3 大断层强度的宏观估算估算大断层的强度不是一个简单问题.我们可以假设断层泥组分、断层形态和粗糙度、孔隙液压等,进而理论推算断层强度,但是因为对几公里到几十公里深处断层实际情况知之甚少,推算结果往往会有数量级的误差,没有实用价值.不论是地震波还是同震地壳变形的观测,都不包含静摩擦强度信息(即上面提到的μ里面的常数项),因为地震位错只反映了断层强度的瞬时变化(即上面提到的μ里面的高阶项)和应力降(扰动值).至今,对俯冲带大断层强度的宏观估计只有两个比较有效的方法.一个是以地壳应力观测为约束,通过力平衡推算弧前地区的边界条件——大断层上的应力.在这个方法里,因为垂向应力值可以从岩石密度和重力加速度简单得出,提供了应力的一个绝对标定值,而非扰动值.另一个方法是以弧前大地热流测量为约束,通过热场模拟推算大断层产生的摩擦热.在这个方法里,摩擦生热反映的是绝对应力,而非扰动值.以下简单介绍这两个方法以及它们的主要结果.
3.1 弧前应力场和大断层强度弧前地壳应力可以用上板块内许多小地震的震源机制来约束.活动断层的滑动方向、钻孔应力方向测量、甚至在一定条件下剪切波各向异性观测,也可以提供有用的应力信息.为了估算俯冲带大断层的强度,我们仅关注弧前垂向应力和垂直于俯冲带的横向挤压应力(图 4a),探索一个平面应变问题.为讨论原理,我们仅考虑平均效应,而且暂不考虑大陆边缘陆高海深的地形对主应力倾角的影响.垂向应力主要取决于上覆岩柱的重量.给定温度场,也就是说给定了脆-韧转化的深度(见2.1节和图 2),横向挤压力主要取决于俯冲带大断层的强度.若大断层强,弧前上板块受到的横向挤压大,横向应力则可能大于垂向应力.若大断层弱,则反之.根据这个思路,我们可以建立简单的二维模型,用观测到的垂、横向应力相对大小和陆缘地形(即海陆之间的高差)来约束大断层的有效摩擦系数μ′.

|
图 4 Wang等(2019)日本海沟2011年弧前应力变化模型(自Wang等(2019)原图修改而成.为与图 1对应,俯冲方向改为从左向右) (a) 原理示意.弧前垂向应力由重力控制(ρ是岩石平均密度,g是重力加速度),横向应力由大断层强度控制(式(2)); (b) 模型结构示意.E是杨氏模量.为简化模型,俯冲板片基本设为刚性,地幔热楔几乎没有刚度; (c) Wang等(2019)文中用到的库仑楔模型,示意除了断层剪力和重力,介质几何形态也控制应力方向.本文对此未加讨论. Fig. 4 Model used by Wang et al. (2019) to study stress change in Japan Trench forearc in 2011 (Modified from an original figure of Wang et al. (2019). For compatibility with Fig. 1, the direction of subduction is shown to be from left to right) (a) Conceptual illustration. The vertical stress in the forearc is controlled by gravity (here ρ is average rock density and g is gravitational acceleration), but the horizontal stress is controlled by the strength of the megathrust (Equation (2)). (b) Model geometry. E is Young′s modulus. For model simplification, the slab is assumed to be nearly rigid, and the hot mantle wedge has almost zero stiffness. (c) The Coulomb wedge model that was also used by Wang et al. (2019), illustrating the control of stress orientation by system geometry as well as fault stress and gravity. The Coulomb wedge model is not discussed in this paper. |
俯冲带不是造山带.这一点在地学界存在广泛的误解,原因是人们在板块理论发展的早期误以为毗邻秘鲁—智利俯冲带的安第斯山脉是俯冲带构造的典型代表.其实安第斯山脉恰恰是全球俯冲带唯一的例外,而且该山也不是近期“正常”俯冲时造的(Oncken et al., 2006).这里只是澄清一下作者的观点,不去深入讨论这个争议极大的问题.在碰撞带挤压造山过程中,横向挤压力大大超过岩层自重.而俯冲带不一样,最常见的是横向力与垂向力不相上下,或横向力略小(Wang and He, 1999; Seno, 2009),也就是说,大断层提供的横向挤压力基本上仅能保证上板块在大陆边缘不因自重而垮塌.勉强支撑而已,何提造山.假设火山弧处垂、横向应力大小相等(中性),与陆缘地形相匹配的大断层μ′值一般在0.03左右(Lamb, 2006; Dielforder et al., 2020),比2.1节提到的断层强度参照值0.4小一个量级.个别俯冲带稍高一点.此处讨论的是弧前地区整体平均应力状态.另外还有一些研究用图 4c所示库仑楔模型讨论海沟附近的楔形岩体的应力问题(Dahlen, 1984; Wang and Hu, 2006; Wang et al., 2019),本文不予详述.
2011年以前的各种观测显示,日本海沟弧前地区横向挤压明显大于垂向,与多数其他俯冲带不一样.可是先前无法知道大出多少.如果真是大很多,那么这里的大断层可能比较强.但是Wang和Suyehiro(1999)指出,因为这里的俯冲板片老、温度低,使脆-韧转换的深度大(见第2.1节和图 1b、图 2),从而即使大断层很弱,总的横向挤压还是可以超过岩层自重的效应.他们的计算结果显示,即使假设大断层弱到μ′≈0.03,横向力还是可以略超出垂向力.日本海沟可能有如此低的μ′值,在当时只是一个假说.2011年9级大地震,造成了弧前海域地区地壳应力状态反转,从震前的横向挤压变到震后的横向拉伸.这一变化验证了Wang和Suyehiro的假说.详见Wang等(2019),以下只是解释一下基本原理.
与其他俯冲带大地震一样,日本海沟大地震破裂带的平均应力降不大(Brown et al., 2015).因此它给弧前应力场造成的扰动很小.这么小的扰动可以使弧前应力状态反转,可见这里震前应力状态接近中性,即横向压力仅仅略大于垂向压力.图 4b显示Wang等(2019)用于进行定量计算的二维有限元模型的几何结构;模型剖面穿过大地震滑动面的中心.这个模型与Wang和Suyehiro(1999)用的模型相似,但是更好地反映了日本海沟俯冲带的温度环境(见图 1b):(1)由于弧前低温,大断层的摩擦区域深达五、六十公里,(2)温度极低的地幔冷楔在流变学上变成了上覆弹性板块的一部分,(3)弧与弧后的高温环境使得上覆弹性板块在这里厚度较小.图 5给出用这个模型计算的结果.大断层2011年地震时沿剖面的应力降分布可以从许多文献提供的同震断层错距分布近似得出(Wang et al., 2018).图 5b显示的是这个应力降对弧前应力场造成的扰动.震前应力场(图 5a)加上这个扰动场就变成了震后应力场(图 5c).欲使弧前海域地壳应力在震前以横向挤压为主而在震后以横向拉伸为主,必须令大断层的μ′≈0.032.太大,则震后不会出现拉伸;太小,则震前不会出现挤压.另外,日本海沟并非特例.2010年智利8.8级俯冲带大地震也引起弧前有些地方应力状态反转(Aron et al., 2013).

|
图 5 Wang等(2019)日本海沟2011年弧前应力变化计算结果(自Wang等(2019)原图修改而成.为与图 1对应,俯冲方向改为从左向右) (a)2011年9级大地震前的差应力(各向同性部分已经减掉); (b) 9级地震大断层应力降引起的差应力扰动场; (c) 大地震后的差应力,即(a)+(b).图中差应力用相互垂直的两双箭头表示.红色表示横向压力大于垂向,蓝色反之,蓝棕色表示两者接近.大的红色双箭头标注断层上最大主压应力方向. Fig. 5 Model results of Wang et al. (2019) for the stress change in Japan Trench forearc in 2011 (Modified from an original figure of Wang et al. (2019). For compatibility with Fig. 1, the direction of subduction is shown to be from left to right) (a) Deviatoric stresses before the M=9 great earthquake in 2011 (the isotropic component has been removed). (b) Perturbation to the deviatoric stress caused by megathrust stress drop during the M=9 earthquake. (c) Deviatoric stresses after the great earthquake, i.e., (a)+(b). In all the panels, two mutually perpendicular pairs of arrows represent deviatoric stress. Red indicates horizontal compression is greater, and blue indicates vertical compression is greater. Blueish brown indicates the two are similar. Large red arrow pairs show the direction of maximum principal compressive stress on the fault. |
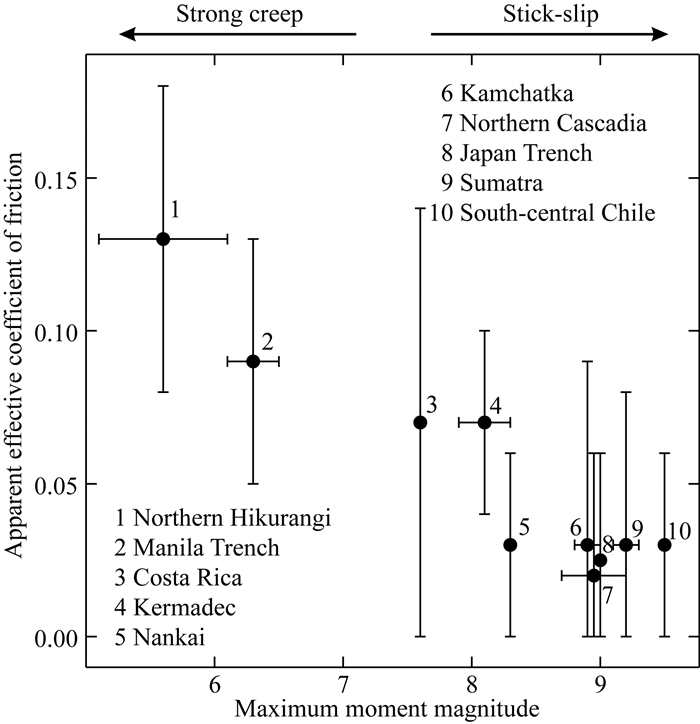
断层滑动一段距离d产生的摩擦热,就是它克服摩擦阻力τ做的功τd.所以,如果v是俯冲速率,俯冲带大断层的摩擦生热率就是τv.先考虑τ=τs,直接由(1)或(2)式给出.如本文第1节所述,我们对俯冲带温度场,尤其是弧前地区,已经有比较成熟的认识.除断层有效摩擦系数μ′以及由它控制的摩擦生热率外,其他参数值和误差都比较容易确定.这样,如果有比较好的热流测量,我们就可以把观测和计算的热流值相比较从而估算摩擦生热率,得出τs,进而估算μ′值.图 6是Gao和Wang(2014)用本方法估算的一些俯冲带大断层强度的总结.所用模拟方法与图 1所示结果所用的方法类似,但在摩擦生热部分有较大改进,在此不细讲,详见Gao和Wang(2014). 世界上其他俯冲带热流观测太少,尚不能应用这个方法.从图 6的结果可以推论,俯冲带大断层普遍很弱,而那些产生大地震的锁-滑型断层尤其弱,其μ′为0.03左右.从摩擦生热估算出来的断层强度与从弧前力平衡推算出来的强度极为吻合.两种互不相关的方法给出类似的结果,大大增强我们对这些结果的信心.当然,由于热模拟中各种参数的误差,用摩擦生热估算的μ′值有很大的不确定性.但是如图 6所示,即使在误差范围内选取使摩擦生热偏大的参数值,μ′在多数情况下也不会大于0.1.例如,England(2018)用一种简易方法进行温度计算,引入了更大的误差,而且对有些俯冲带在参数处理上也与Gao和Wang(2014)多有不同.他得出的μ′值多在0.06左右,还是比Byerlee′s law参照值小一个量级.此外,Gao和Wang(2014)一文强调的另一个问题是所谓“强蠕滑”,将在下面第4.3节讨论.
|
图 6 Gao和Wang(2014)用摩擦生热估算的大断层视有效摩擦系数(自Gao和Wang(2014)原图修改而成) 横轴是各俯冲带迄今观测到的大断层上的地震的最大地震距震级(详见Gao和Wang (2014)).20世纪40年代,图中第一个俯冲带在海沟附近有过7级以上地震.如果的确发生在大断层上,也必定是在极浅处,不代表大断层整体性质,因此略去.图中前三个俯冲带不同程度的蠕滑行为都有现代测地学证据(Wang and Bilek, 2014). Fig. 6 Apparent effective coefficient of friction of megathrusts estimated by Gao and Wang (2014) by modelling frictional heating (Modified from an original figure of Gao and Wang (2014)) The horizontal axis is the moment magnitude of the largest megathrust earthquake in these subduction zones ever observed (for details see Gao and Wang (2014)). At the first subduction zone in the figure, earthquakes greater than magnitude 7 occurred near the trench in the 1940s. If these events indeed occurred on the megathrust, they must have been extremely shallow and thus are not representative of the main part of the megathrust and hence are left out. There are modern geodetic observations to confirm various degrees of creep behaviour of the first three subduction zones in the figure (Wang and Bilek, 2014). |
对于蠕滑断层,τ=τs=τp.对于锁-滑断层,图 6所示μ′值所代表的强度还有一个要注意的问题.断层闭锁时是不生热的,滑动时才生热.如果摩擦阻力一样,断层以1 m·s-1的地震速率和以5 cm·a-1的板片俯冲速率滑动同样距离产生的摩擦热是一样的.弧前热场的时间尺度是几百万年量级,在计算时可以忽略地震周期,直接用板片俯冲速率v.但是,地震滑动时的摩擦阻力τ既不是断层真实强度τp,也不是视强度τo,而是地震时的动摩擦强度.由于断层在地震时的弱化和应力降,动摩擦强度比τo低(图 3b).所以,用摩擦生热估算出来的锁-滑断层的强度比视强度还要小一些.要知道小多少,需要把地震的应力降Δτ和断层的视强度τo作一个比较.
由于不同构造体系中断层性质的差别,同震滑动所受阻力和震后断层上的剪应力可能会有较大差别.图 3b所示两者近似的情况适用于俯冲带大断层(Lambert et al., 2021).所以我们在此可以合理假设滑动时的动摩擦强度接近τo-Δτ=τo(1-Δτ/τo),也就是说是视强度的(1-Δτ/τo)倍.多年来大量的地震研究告诉我们,俯冲带断层大地震滑动带的平均应力降一般在1~5 MPa范围.让我们做一个简单估算.假设σn≈pL=ρgz(见2.1节),ρ=3333 kg·m-3,g=10 m·s-2,μ′=0.03,由式(2)可知τo随断层深度的增长率是1 MPa·km-1.在z=20 km处,τo=20 MPa.若Δτ=4 MPa,则Δτ/τo=20%.如果假设Δτ/τo在10%~30% 之间,那么用摩擦生热估算出来的μ′=0.03加上10% 或30% 便代表了视有效摩擦系数0.033或0.039.区别远在误差之内,所以图 6忽略这一区别.有些其他断层的动摩擦强度可能会比τo-Δτ小很多(未在图 3显示),上述简单比较就未必适用了.
4 弱断层的动力学意义 4.1 极小应力降还是完全应力降?一个大地震释放了断层周围介质内弹性应变能的多大部分?这是一个争论了上百年的基本问题,至今还是众说纷纭.问题可以近似表述成断层应力降Δτ相当于断层视强度τo的多大部分?如果Δτ仅是τo的1%,所耗能量可谓微乎其微.如果Δτ是τo的100%,即所谓完全应力降,那么所有的能量一下都用完了.争论不清的原因就是因为τo很难约束.现在我们既然大体知道了俯冲带断层的强度,这个问题在俯冲带就清楚了.第3.2节提到,如果μ′=0.03,在20 km处Δτ/τo约20%.20 km是俯冲带大地震比较有代表性的深度.合理地变化一下深度和μ′值,都不会改变这一基本认识:大地震的应力降是断层强度可观的一小部分,既不是微乎其微也不是百分之百.也就是说,岩石中原来积累的弹性应变能中可观的一小部分被大地震释放掉.被释放掉的应变能中很小的一部分提供了破裂传播需要的能量,还有一小部分由地震波传开和用于同震变形(同震垂向位移时重力做功也贡献能量);一般来说被释放掉的最大部分转变为摩擦热(动摩擦阻力τo-Δτ做功耗散的热能).
20世纪80年代以前,比较流行的观点是断层强度很高(因而Δτ/τo极小),认为Byerlee′s law的参数如μ≈0.7, μ′≈0.4(甚至μ′≈0.7)可以直接用.80年代板块边界大断层强度的争议较大.90年代末开始,大断层很弱的认识开始逐渐占上风.今天,学界普遍接受俯冲带μ′一般小于0.1,很少有人再对μ′=0.03或0.04这样小的值感到吃惊了.在2011年日本海沟大地震之后,又广泛出现了完全应力降的说法(即Δτ/τo接近100%).这个说法显然是站不住脚的,完全没有考虑到,即便断层弱到μ′=0.03,在二三十公里或更深处τo也比Δτ大很多.出现这种说法,原因主要是混淆了局部应力降和地震滑动带平均应力降.如引言中提到,俯冲带大断层是一个几何、构造、材料都很复杂的系统.大地震滑动分布和应力降分布的一个基本特点是高度不均一.有些部位出现弱化,推动地震;而有些部位出现强化,阻碍地震(见第2.2节的讨论).有些错距很大的局部地带,尤其是在σn(从而τo)很低的靠近海沟的最浅处,Δτ/τo有可能接近100%.最近十几年许多岩石摩擦实验确实显示摩擦界面在滑动速率接近约1 m·s-1时会剧烈弱化,可能导致很大的应力降(Di Toro et al., 2011).但是,真实大断层的滑动带内有些部位会出现强化,应力降是负值,即应力升(图 3c).这些部位在附近弱化部分的推动下“被动”滑动,在运动学上是地震的参与者,但是从动力学上它们是地震的阻碍者.由于滑动带内应力降正负相间,整个滑动带的平均应力降不会很大.Brown等(2015)以2011年日本大地震为例详细解释了这个问题.
4.2 造成弱断层的地质原因我们估算μ′而不是μ和pf(以及σn),在计算中躲避了极难约束的pf.但是,要理解像μ′=0.03或0.04这样的值在地质上代表了什么,必须分别面对μ和pf.是什么因素使得大断层如此的弱呢?普遍估计pf应该很高,但是高到什么程度没有可靠答案.通过分析地震波有时可以得出P波速度和S波速度之比(Vp/Vs),然后推论pf.但是在实际断层带里Vp/Vs与pf的关系十分复杂,结果有很大的不确定性.如果假设Byerlee′s law的μ≈0.7,那么μ′=0.03意味着λ=0.96,即pf几乎是静岩压力(见式(2)).有些人认为有些大断层某些局部位置pf可能更高,如地幔冷楔尖端附近(Gao and Wang, 2017).虽然尚无有力的观测证据,一般猜测大断层整体来说pf可能大大高于静水压力,但是离静岩压力还尚有距离(Saffer and Tobin, 2011).超高的pf需要极低的岩层渗透率.如引言所述,俯冲带大断层是一个活跃的剪切带,不断有小断层和裂隙活动.虽然俯冲下去的海底沉积物和俯冲板片可提供大量水源,但在大区域保持极低渗透率想来比较困难.另外,也没有必要把Byerlee′s law直接用于大断层.归纳出Byerlee′s law的摩擦实验多数是岩石界面直接接触,其中少数有断层泥的实验给出不同的结果,取决于断层泥的性质(Byerlee, 1978).引言提到,俯冲带大断层里面混杂了各种材料.有些含水矿物如滑石、绿泥石和低温蛇纹石一旦混于断层泥内,可以大大降低断层强度.比如,如果μ=0.2,那么μ′=0.03只需要λ=0.85.
4.3 强度与滑动模式的关系从来没有任何证据显示强断层易于锁-滑(即产生大地震),而弱断层易于蠕滑.从逻辑上讲也完全没有必要,因为大地震的应力降都很小.但这却是学界的传统观点.常有文献说高应力引起大地震,也是指需要强断层.第3节总结的研究结果显示,产生最大地震的俯冲带大断层是极弱的断层.特别是,图 6显示的趋势与传统观点正相反.该图所用的每一俯冲断层迄今最高震级在很大程度上反映了该地断层滑动模式(发震带极浅的异常地震除外).某些以蠕滑为主的大断层最高震级小,但是μ′却高.
图 6趋势最好的解释是,断层的强弱和发震能力首先取决于断层的成熟度.地质上讲的断层成熟度主要是平滑度和剪切运动局域化程度.不成熟断层不平整,断层带内岩块岩粒较大,剪切运动常分散于多个分支或呈碎屑流.因为俯冲板片不断带来不规则形态的洋底(见引言),使许多俯冲带大断层处于粗糙、不太成熟的状态,以局域化程度较低的剪切滑动为主,中、小震频繁(Wang and Bilek, 2014).这种粗糙断层的应力和构造极不均匀,很难大规模闭锁.这一判断最近被关于俯冲板片粗糙度与俯冲带大地震全球统计关系的研究不断确认(Wang and Bilek, 2014; Scholl et al., 2015; Brizzi et al., 2018; Lallemand et al., 2018; Van Rijsingen et al., 2018).看来,粗糙断层对剪切运动的阻力比较大,即μ′偏高.Gao和Wang(2014)称这种阻力较大的蠕滑为“强蠕滑”(图 6).相反,成熟断层的剪切运动高度局域化,主要集中于颗粒细、形态平滑的薄剪切层(常常薄到可以当作一个摩擦面),给地震破裂传播提供了良好的几何条件,但是总体上对剪切运动的阻力比较小,即μ′偏低.许多俯冲带,因为俯冲洋底比较平整或者俯冲下去很多沉积物,大断层比较成熟和平滑(Scholl et al., 2015).在这种情况下,能否孕育大地震就取决于断层泥是否易于产生锁-滑行为,也即2.2节讲的不稳定滑动.如果某平滑断层的断层泥很弱并且引起蠕滑,这种蠕滑可以称为“弱蠕滑”,以别于上述粗糙断层的强蠕滑.
为什么传统观点认为大地震需要强断层呢?其基本原因是忽视了几何形态和断层构造对断层成熟度的一阶控制.地震学把发震带近似为一个平滑面本来是合理的.但是因为忽视了真实地质背景,便接着假设控制发震行为的只是这个平滑面的摩擦性质,即滑动时是否弱化(见2.2节).“凹凸体”无论尺度大小,一律当成摩擦性质,完全丧失几何原意.甚至连俯冲海山也用摩擦性质或局部应力异常来代表.用地质语言讲,就是误以为没有几何上不成熟的断层,只有断层泥性质的区别.只要断层不闭锁,便误以为是弱蠕滑.这种看法,用于解释同一个平滑而薄的成熟剪切层的不同部位是可以的.有些部位,如果断层泥含有许多片状结构的层状硅酸盐,比如一些黏土矿物和滑石、低温蛇纹石等,断层不但强度低而且稳定滑动(Ikari et al., 2011).其他强度高一些的部位则孕育地震.但是把这种见解推广到成熟度互有不同的断层就不合理了(Wang and Bilek, 2011, 2014).
5 总结21世纪以来,科学界对俯冲带大断层的结构、滑动行为和孕震机制积累了许多新的认识,对其最基本的力学参数——断层强度,也有了全新的了解.本文介绍作者对大断层强度问题的系统看法,但是内容基本上反映了这个领域的研究现状.文章要点总结如下.
(1) 大断层在温度较低的浅部主要表现为摩擦滑动,包括蠕滑和锁-滑.在温度较高的深部呈黏性剪切.摩擦-黏性的转换受温度控制.断层摩擦强度高或俯冲板片年轻的俯冲带温度高,转换在较浅处发生.
(2) 大断层的强度可以用大尺度平均有效摩擦系数μ′表征.μ′描述一个摩擦面,但实际上代表了断层带厚度方向积分的效应.它在蠕滑断层代表真实强度,而在锁-滑断层代表视强度(即断层在地震前能承受的最大剪应力),故而称视有效摩擦系数.
(3) 大断层强度可以从弧前横向应力与垂向应力的比较来估算.横、垂向应力一般差别不大,反映出μ′值一般仅在0.03左右.有些地方可能略大.日本海沟2011年9级地震引起的弧前应力反转再次证实横、垂向应力差别不大,断层很弱.
(4) 大断层强度也可以从用地表热流约束的摩擦生热来估算.这种方法给出的多数俯冲带的μ′值一般也是在0.03左右,有的略大于0.1.
(5) 最弱的大断层是那些产生大地震的锁-滑断层.大地震不需要强断层和高应力,而需要有助于破裂传播的地质条件.较为平滑的断层易于提供这种条件.
(6) 大地震的断层应力降是断层强度可观的一部分,例如20%.发震面有的部位应力降可能很大,但是也有的部位出现应力增,限制了平均应力降的大小.
(7) 导致俯冲带大断层极弱的地质过程有待进一步研究.一般认为孔隙液压一定很高,但是断层泥中的软弱材料也会起很大作用.
致谢 谨以此文纪念北大地质系王仁教授诞辰100周年.本文受益于作者的许多学生和合作者过去20年的研究贡献,如何江衡(Jiangheng HE)、Ikuko WADA(和田育子)、Clare Currie、胡岩(Yan HU)、高翔(Xiang GAO)、Lonn Brown、孙田昊哲(Tianhaozhe SUN)、Susan Bilek、Simon Peacock、罗海鹏(Haipeng LUO)等人,在此一并致谢.南方科技大学徐世庆、加拿大地调局太平洋地学中心孙田昊哲、中国科学院青岛海洋研究所高翔、以及两位匿名审稿人为本文提供了宝贵意见.波士顿大学Rachel Abercrombie和京都大学Hiroyuki NODA(野田博之)为图 3的绘制提供了宝贵建议.本文的加拿大自然资源部文献编号是20210181.
Abers G A, Van Keken P E, Hacker B R. 2017. The cold and relatively dry nature of mantle forearcs in subduction zones. Nature Geosci., 10(5): 333-337. DOI:10.1038/ngeo2922 |
Agard P, Plunder A, Angiboust S, et al. 2018. The subduction plate interface: Rock record and mechanical coupling (from long to short timescales). Lithos, 320-321: 537-566. DOI:10.1016/j.lithos.2018.09.029 |
Aron F, Allmendinger R W, Cembrano J, et al. 2013. Permanent fore-arc extension and seismic segmentation: Insights from the 2010 Maule earthquake, Chile. J. Geophys. Res., 118(2): 724-739. DOI:10.1029/2012JB009339 |
Brizzi S, Sandri L, Funiciello F, et al. 2018. Multivariate statistical analysis to investigate the subduction zone parameters favoring the occurrence of giant megathrust earthquakes. Tectonophysics, 728-729: 92-103. DOI:10.1016/j.tecto.2018.01.027 |
Brown L, Wang K L, Sun T H Z. 2015. Static stress drop in the MW9 Tohoku-Oki earthquake: Heterogeneous distribution and low average value. Geophys. Res. Lett.,, 42(24): 10595-10600. DOI:10.1002/2015GL066361 |
Byerlee J. 1978. Friction of rocks. Pure Appl. Geophys., 116(4-5): 615-626. DOI:10.1007/BF00876528 |
Currie C A, Wang K, Hyndman R D, et al. 2004. The thermal effects of steady-state slab-driven mantle flow above a subducting plate: The Cascadia subduction zone and backarc. Earth Planet. Sci. Lett., 223(1-2): 35-48. DOI:10.1016/j.epsl.2004.04.020 |
Currie C A, Hyndman R D. 2006. The thermal structure of subduction zone back arcs. J. Geophys. Res., 111(BB): B08404. DOI:10.1029/2005JB004024 |
Dahlen F A. 1984. Noncohesive critical Coulomb wedges: An exact solution. J. Geophys. Res., 89(B12): 10125-10133. DOI:10.1029/JB089iB12p10125 |
Di Toro G, Han R, Hirose T, et al. 2011. Fault lubrication during earthquakes. Nature, 471(7339): 494-498. DOI:10.1038/nature09838 |
Dielforder A, Hetzel R, Oncken O. 2020. Megathrust shear force controls mountain height at convergent plate margins. Nature, 582(7811): 225-229. DOI:10.1038/s41586-020-2340-7 |
England P. 2018. On shear stresses, temperatures, and the maximum magnitudes of earthquakes at convergent plate boundaries. J. Geophys. Res., 123(8): 7165-7202. DOI:10.1029/2018JB015907 |
Gao X, Wang K L. 2014. Strength of stick-slip and creeping subduction megathrusts from heat flow observations. Science, 345(6200): 1038-1041. DOI:10.1126/science.1255487 |
Gao X, Wang K L. 2017. Rheological separation of the megathrust seismogenic zone and episodic tremor and slip. Nature, 543(7645): 416-419. DOI:10.1038/nature21389 |
Ikari MJ, Marone C, Saffer D M. 2011. On the relation between fault strength and frictional Stability. Geology, 39(1): 83-86. DOI:10.1130/G31416.1 |
Lallemand S, Peyret M, Van Rijsingen E, et al. 2018. Roughness characteristics of oceanic seafloor prior to subduction in relation to the seismogenic potential of subduction zones. Geochem. Geophys. Geosyst., 19(7): 2121-2146. DOI:10.1029/2018GC007434 |
Lamb S. 2006. Shear stresses on megathrusts: Implications for mountain building behind subduction zones. J. Geophys. Res., 111(B7): B07401. DOI:10.1029/2005JB003916 |
Lambert V, Lapusta N, Perry S. 2021. Propagation of large earthquakes as self-healing pulses or mild cracks. Nature, 591(7849): 252-258. DOI:10.1038/s41586-021-03248-1 |
Luo H P, Wang K L. 2021. Postseismic geodetic signature of cold forearc mantle in subduction zones. Nat. Geosci., 14(2): 104-109. DOI:10.1038/s41561-020-00679-9 |
Miller N C, Lizarralde D, Collins J A, et al. 2021. Limited mantle hydration by bending faults at the Middle America Trench. J. Geophys. Res., 126(1): e2020JB020982. DOI:10.1029/2020JB020982 |
Noda H, Lapusta N. 2013. Stable creeping fault segments can become destructive as a result of dynamic weakening. Nature, 493(7433): 518-521. DOI:10.1038/nature11703 |
Oncken O, Hindle D, Kley J, et al. 2006. Deformation of the Central Andean upper plate system-facts, fiction, and constraints for plateau models. //Oncken O, Chong G, Franz G, et al eds. The Andes. Berlin: Springer, 3-27.
|
Peacock S M, Wang K L. 1999. Seismic consequences of warm versus cool subduction metamorphism: Examples from southwest and northeast Japan. Science, 286(5441): 937-939. DOI:10.1126/science.286.5441.937 |
Peacock S M, Wang K L. 2021. On the stability of talc in subduction zones: a possible control on the maximum depth of decoupling between the subducting plate and mantle wedge. Geophys. Res. Lett., 48(17). DOI:10.1029/2021GL094889 |
Raimbourg H, Famin V, Palazzin G, et al. 2019. Distributed deformation along the subduction plate interface: The role of tectonic mélanges. Lithos, 334-335: 69-87. DOI:10.1016/j.lithos.2019.01.033 |
Rowe C D, Moore J C, Remitti F, et al. 2013. The thickness of subduction plate boundary faults from the seafloor into the seismogenic zone. Geology, 41(9): 991-994. DOI:10.1130/G34556.1 |
Saffer D M, Tobin H J. 2011. Hydrogeology and mechanics of subduction zone forearcs: fluid flow and pore pressure. Annu. Rev. Earth Planet. Sci., 39: 157-186. DOI:10.1146/annurev-earth-040610-133408 |
Scholl D W, Kirby S H, Von Huene R, et al. 2015. Great (≥ MW80) megathrust earthquakes and the subduction of excess sediment and bathymetrically smooth seafloor.. Geosphere, 11(2): 236-265. DOI:10.1130/GES01079.1 |
Seno T. 2009. Determination of the pore fluid pressure ratio at seismogenic megathrusts in subduction zones: Implications for strength of asperities and Andean-type mountain building. J. Geophys. Res., 114(B5). DOI:10.1029/2008JB005889 |
Shimamoto T, Noda H. 2014. A friction to flow constitutive law and its application to a 2-D modeling of earthquakes. J. Geophys. Res., 119(11): 8089-8106. DOI:10.1002/2014JB011170 |
Sun T H Z, Wang K L, Fujiwara T, et al. 2017. Large fault slip peaking at trench in the 2011 Tohoku-Oki earthquake. Nature Commun, 8: 14044. DOI:10.1038/ncomms14044 |
Syracuse E M, Van Keken P E, Abers G A. 2010. The global range of subduction zone thermal models. Phys. Earth Planet. Inter., 183(1-2): 73-90. DOI:10.1016/j.pepi.2010.02.004 |
Uchida N, Nakajima J, Wang K L, et al. 2020. Stagnant forearc mantle wedge inferred from mapping of shear-wave anisotropy using S-net seafloor seismometers. Nature Comm., 11(1): 5676. DOI:10.1038/s41467-020-19541-y |
VanRijsingen E, Lallemand S, Peyret M, et al. 2018. How subduction interface roughness influences the occurrence of large interplate earthquakes. Geochem. Geophys. Geosyst., 19(8): 2342-2370. DOI:10.1029/2018GC007618 |
Wada I, Wang K L. 2009. Common depth of slab-mantle decoupling: Reconciling diversity and uniformity of subduction zones. Geochem. Geophys. Geosyst., 10(10): Q10009. DOI:10.1029/2009GC002570 |
Wang K L, He J H. 1999. Mechanics of low-stress forearcs: Nankai and Cascadia. J. Geophys. Res., 104(B7): 15191-15205. DOI:10.1029/1999JB900103 |
Wang K L, Suyehiro K. 1999. How does plate coupling affect crustal stresses in northeast and southwest Japan?. Geophys. Res. Lett., 26(15): 2307-2310. DOI:10.1029/1999GL900528 |
Wang K L, Hu Y. 2006. Accretionary prisms in subduction earthquakecycles: The theory of dynamic Coulomb wedge. J. Geophys. Res., 111(B6): B06410. DOI:10.1029/2005JB004094 |
Wang K L. 2010. Finding fault in fault zones. Science, 329(5988): 152-153. DOI:10.1126/science.1192223 |
Wang K L, Bilek S L. 2011. Do subducting seamounts generate or stop large earthquakes?. Geology, 39(9): 819-822. DOI:10.1130/G31856.1 |
Wang K L, Bilek S L. 2014. Fault creep caused by subduction of rough seafloor relief. Tectonophysics, 610: 1-24. DOI:10.1016/j.tecto.2013.11.024 |
Wang K L, Sun T H Z, Brown L, et al. 2018. Learning from crustal deformation associated with the M=9 2011 Tohoku-Oki earthquake. Geosphere, 14(2): 552-571. DOI:10.1130/GES01531.1 |
Wang K L, Brown L, Hu Y, et al. 2019. Stable forearc stressed by a weak megathrust: Mechanical and geodynamic implications of stress changes caused by the M=9 Tohoku-Oki earthquake. J. Geophys. Res., 124(6): 6179-6194. DOI:10.1029/2018JB017043 |
Wang K L, Huang T Z, Tilmann F, et al. 2020. Role of Serpentinized mantle wedge in affecting Megathrust Seismogenic behavior in the area of the 2010 M=8. 8 Maule earthquake.. Geophys. Res. Lett., 47(22): e2020GL090482. DOI:10.1029/2020GL090482 |
Wang K L. 2021. If not brittle: ductile, plastic, or viscous?. Seismol. Res. Lett., 92(2A): 1181-1184. DOI:10.1785/0220200242 |
Ye L L, Lay T, Kanamori H, et al. 2016. Rupture characteristics of major and great (MW ≥ 7. 0) megathrust earthquakes from 1990 to 2015:2. Depth dependence. J. Geophys. Res. Solid Earth, 121(2): 845-863. DOI:10.1002/2015JB012427 |
 2021, Vol. 64
2021, Vol. 64

