2. 中国地质调查局发展研究中心, 北京 100037;
3. 桂林理工大学地球科学学院, 桂林 541006
2. Development and Research Center, China Geological Survey, Beijing 100037, China;
3. College of Earth Sciences, Guilin University of Technology, Guilin 541006, China
大地电磁(MT)方法广泛用于石油、天然气、地热资源勘探以及地球深部电性结构研究(Sheard et al., 2005;Bedrosian, 2007;赵国泽等, 2007).过去几十年中, 大地电磁正反演算法发展迅速, 经历了从20世纪80年代发展的一维反演(Constable et al., 1987), 到十几年前的二维反演(de Groot-Hedlin and Constable, 2004;Mehanee and Zhdanov, 2002), 以及现在主流的三维反演(邓琰等, 2019;阮帅等, 2020).然而目前主流的三维大地电磁反演代码主要是基于L2范数的光滑约束实现的(Rodi and Mackie, 2001;Newman and Alumbaugh, 2002;Siripunvaraporn et al., 2005;Egbert et al., 2014), 其优势是可保证反演稳定收敛, 但其主要缺点是过度光滑会严重损失边界的分辨率.为了克服这一缺点, 一系列提高边界刻画能力的正则化反演方法被提出, de Groot-Hedlin和Constable(2004)提出了一种基于Occam反演方法的尖锐边界反演(sharp boundary inversion), 提高了边界的分辨率, 但是反演效果严重依赖于初始模型.Mehanee和Zhdanov(2002)提出了二维聚焦反演方法, 并将其与非线性共轭梯度(NLCG)和快速松弛反演(RRI)方法进行比较, 验证聚焦反演可以得到更为清晰的边界.Farquharson(2008)提出了基于L1范数的最小结构二维反演, 该反演不仅考虑了水平和垂直方向的模型粗糙度, 还考虑倾斜方向的模型粗糙度, 由此可以恢复异常体的倾斜边界.张罗磊等(2010)将最小梯度支撑泛函用于二维大地电磁正则化反演, 得到了具有尖锐边界的反演结果.Jahandari和Farquharson(2017)采用非结构有限元法实现最小结构反演, 并将其成功应用于三维大地电磁数据反演中.虽然上述基于L1范数的正则化反演在刻画异常体边界上具有一定的优势, 但是其具体参数选取以及收敛稳定性仍需进一步研究.
近年来, 地球物理学家采用一种新的系数正则化项替代传统的模型粗糙度, 以获得更可靠的反演结果.Abubakar等(2012)使用离散傅里叶变换和离散小波变换压缩模型空间, 并将该方法应用于挪威TrollWest Gas Province地区的可控源电磁(CSEM)数据反演.Nittinger和Becken(2016)提出基于复小波变换的二维大地电磁反演, 获得了与L2范数相似的反演结果.苏扬等(2018)将哈尔(Haar)小波变换应用于一维航空电磁数据反演, 并提出广义模型约束反演算法, 提高对地层界面位置的刻画.Liu等(2018)引入小波变换建立三维航空电磁稀疏正则化反演方法, 并对挪威Bynest地区的实测数据进行测试, 结果表明基于小波变换的稀疏正则化反演可以很好地提高模型分辨率.然而小波变换的固有缺陷是缺少方向性, 不能最佳地表示高维数据.与小波变换相比, Candès等(2006)提出的第2代曲波变换不仅具有多尺度性, 还具有多方向特征, 可以很好地提取目标体的边缘特征.曲波变换最初主要应用于图像压缩和去噪(Starck et al., 2002).Herrmann和Verschuur(2004)首先采用曲波变换进行地震数据处理.Shan等(2009)提出了小波和曲波的组合方案, 通过求解L1范数优化问题对地震数据进行去噪, 取得了良好的效果.此外, Herrmann等(2008)还将曲波变换应用于一次波和多次波分离, Wang等(2008)将贝叶斯概率分析与曲波变换相结合, 建立一种稀疏正则化反演方法进行一次波和多次波分离, Herrmann和Hennenfent(2008)将曲波变换用于地震数据恢复.
截止目前, 曲波变换还没有像小波变换那样被广泛应用于电磁数据反演中.在本文中, 我们从传统的空间域正则化反演出发, 利用曲波变换将空间域中的电阻率模型转换为曲波域中的稀疏系数来构建新的正则化项, 构建迭代加权最小二乘(IRLS)算法, 并通过共轭梯度(CG)方法求解高斯-牛顿(GN)方程.首先介绍大地电磁的反演策略, 然后分析曲波变换的多尺度和多方向特征并介绍实施步骤, 进而通过设计理论合成算例, 分析不同尺度系数和不同正则化项对反演结果的影响, 验证基于曲波变换的正则化反演比传统L1和L2范数反演方法的优越性.最后, 通过对南非SAMTEX项目中的二维大地电磁实测数据反演进一步验证本文反演算法的有效性.
1 方法原理 1.1 反演策略我们先给出空间域中基于Lp范数正则化反演的目标函数:
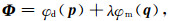
|
(1) |
其中, φd(p)是数据拟合项, φm(q)是模型约束项, λ是正则化因子.p和q的具体形式为
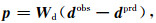
|
(2) |
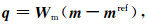
|
(3) |
式中, Wd是一个对角矩阵, 其元素为观测电磁响应中噪声的倒数, dobs为数据向量, dprd为反演模型m经正演计算得到的响应数据, Wm是平滑算子矩阵, mref是包含地质信息的参考模型.公式(2)中dprd可以表示为

|
(4) |
其中, F是正演算子.
公式(1)中φd和φm的一般形式为
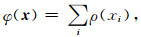
|
(5) |
其中, x表示公式(2)和(3)中的p或者q, i表示向量x中元素的索引.ρ(xi)可有多种选择, 具体选择在下文中给出.我们对数据拟合项采用L2范数约束, 而对正则化项采用L1范数约束, 给出迭代过程中公式(2)和(3)的形式

|
(6) |
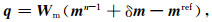
|
(7) |
其中, dn-1是上次迭代的模型mn-1经正演计算得到的响应数据, δm=mn-mn-1, J是空间域模型参数的灵敏度矩阵, 可以通过伴随正演技术计算得到(Liu and Yin, 2016).将公式(5)对模型更新量δm求导可得(Farquharson, 2008)
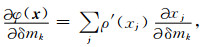
|
(8) |
(8) 式可表示为
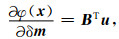
|
(9) |
式中, 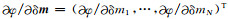

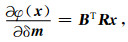
|
(10) |
其中, R为一个对角矩阵, R=diag{ρ′(x1)/x1, …, ρ′(xN)/xN}.对于数据拟合项, B=-WdJ, 对于模型约束项, B=Wm.
对于公式(5)中的ρ(xi), 我们使用Ekblom(1987)提出Lp范数的形式:

|
(11) |
式中, ε是一个很小的正实数, 用于确保导数在x=0处存在.由此, 对角矩阵R的非零元素表示为
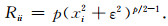
|
(12) |
由于我们对数据拟合项使用L2范数约束, 因此根据公式(12), 矩阵Rd的对角元素为2;对模型约束项使用L1范数约束, 广义约束矩阵用Rm表示.
对目标函数求导并令其为零, 利用Gauss-Newton法求解最优化问题, 可以得到反演迭代中求解的线性方程组为

|
(13) |
本文中我们目的是开发基于曲波变换的稀疏正则化反演算法, 根据前文空间域中的Lp范数正则化反演策略, 我们改变上述反演中的模型约束项, 利用曲波变换将空间域中的电阻率模型转换为稀疏域中的曲波系数进行求解, 曲波系数向量
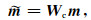
|
(14) |
其中, Wc表示曲波正变换算子.我们首先利用二维快速离散曲波变换(Candès et al., 2006)将电阻率模型m转变为曲波域中的系数矩阵, 并将这些矩阵重新排列组成一维向量.根据链式法则, 曲波域中的灵敏度矩阵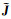
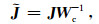
|
(15) |
其中, Wc-1表示曲波逆变换算子.曲波正算子与曲波逆变换算子的表示在下文给出.根据公式(13)推导曲波域中的反演迭代线性方程组为
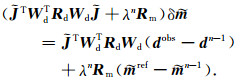
|
(16) |
同时, 根据曲波基函数的正交性, 将(16)式改写为

|
(17) |
这里不再需要给出正则化项的平滑算子矩阵Wm, 因为我们将模型转换为曲波系数本身就是对模型的一种整体约束.同样的我们对系数正则化项采用L1范数约束, Donoho(2006), Loris等(2007)和Simons等(2011)证明了反演中对稀疏域系数采用L1范数约束更倾向于得到稀疏解.(17)式中对角矩阵R以及灵敏度矩阵J都取决于模型, 它们在每次迭代时更新, 这种方法被称为迭代加权最小二乘(IRLS)算法.对于每次迭代, 我们用共轭梯度方法求解上述方程.在利用方程(17)求解出曲波系数改正量后, 空间域中的模型更新可表示为
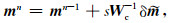
|
(18) |
其中s是通过线性搜索确定的比例因子(Haber, 2014).
1.2 曲波变换作为多尺度分析方法, 曲波变换目前已广泛应用于图像处理、医学成像和地震勘探等诸多领域.曲波变换克服了传统的多尺度分析方法(比如小波变换)缺乏方向性的弱点.为了更好地理解基于曲波变换的稀疏正则化反演的优越性, 我们在对频率域和空间域中曲波进行数学描述的基础上, 重点介绍如何实现曲波变换并分析曲波变换的稀疏性特征.
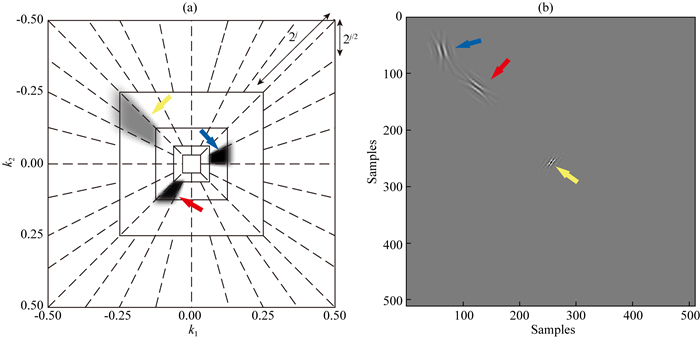
1.2.1 频率域中的曲波根据Herrmann和Hennenfent(2008), 二维曲波窗函数U是由径向窗函数W和角度窗函数V共同定义的多尺度和多方向的楔形基(见图 1a).这里我们仅给出笛卡尔坐标系中二维离散曲波的定义形式.为此, 首先引入径向窗函数(Candès et al., 2006)
|
图 1 (a) 频率域中的楔形曲波基对应于空间域中的曲波;(b)通过曲波逆变换可从图(a)中的三个楔形基获得空间域中的三个不同曲波.两个域中曲波之间的方向正交性是由傅里叶变换旋转90°引起的(参考Herrmann et al., 2007) Fig. 1 (a) Curvelets in frequency domain with each wedge corresponding to the frequency support of a curvelet in the space domain; (b) Three different curvelets in the space domain are obtained from 3 polar wedges in (a) by inverse curvelet transform. The directional orthogonality between the curvelets in two domains is resulted from 90° rotation of Fourier transform (after Herrmann et al., 2007) |

|
(19) |
其中, ω=(ω1, ω2)是频率变量, Φ是两个一维低通窗函数φ的乘积, 即
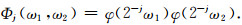
|
(20) |
同样, 我们引入角度窗函数
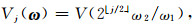
|
(21) |
其中, 

|
(22) |
进而, 我们引入一组等间距的斜率tanθl:=l·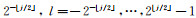
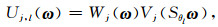
|
(23) |
其中, Sθ是剪切矩阵, 具体形式为
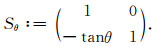
|
(24) |
图 1a给出频率域(又称曲波域)中的楔形曲波基与空间域中曲波之间的对应关系.其中, 实线表示径向窗函数W划分的同心正方格, 而虚线表示角度窗函数V又将同心正方格划分为多个曲波基.k1和k2为频率域参数, 曲波基是长度为2j, 宽度为2j/2的各向异性楔形基.其中, 最内侧的第1尺度曲波基是无方向的, 第1尺度的系数是粗尺度系数, 而其他尺度的系数为细节系数.随着尺度增加, 楔形基的方向数也随之增加(Herrmann and Hennenfent, 2008).
1.2.2 空间域中的曲波
在空间域中定义离散曲波与连续曲波遵循相似的规则(Ying et al., 2005).尺度为2-j, 方向为θl=
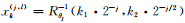

|
(25) |
其中, x=(x1, x2)是空间域参数, 0≤θl<2π, k=(k1, k2)∈Z2是旋转参数, 而Rθl是弧度θl的旋转矩阵, 即
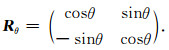
|
(26) |
曲波系数可以通过信号f∈L2(R2)与曲波φj, l, k(x)进行内积得到, 即
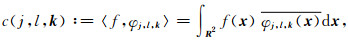
|
(27) |
其中, 上划线表示复共轭.空间域中的曲波如图 1b所示.蓝色和红色箭头指示第3尺度上不同方向和位置的曲波, 黄色箭头指示第4尺度的曲波.空间域中曲波的形状是狭长的, 其包络的有效长度为2-j/2, 有效宽度为2-j, 满足各向异性尺度关系.此外, 曲波沿脊方向平滑衰减, 而在垂直脊方向上振荡衰减(Ying et al., 2005).随着尺度的增加, 曲波变得越来越细小, 对图像中弯曲边缘的敏感性更高.从公式(27)可以看出曲波系数是图像和曲波在空间域中的内积, 如果曲波的方向与目标体的边界方向一致, 则曲波系数很大;否则, 曲波系数接近于0.由此, 目标体边缘在每个精细尺度下都对应于大的系数.换句话说, 通过对各尺度下较大的系数进行反演可以实现对目标体边界的精细刻画.
1.2.3 曲波变换的实现Candès等(2006)提出了两种用于实现快速离散曲波变换(FDCT)的算法, 分别是Unequispaced FFTs (USFFT)和Wrapping算法.本文中我们采用Curvelab工具箱(www.curvelet.org)提供的Wrapping算法开发我们的反演方法.该方法比USFFT算法更易于实现且运行速度快.利用Wrapping算法的快速离散曲波变换包括以下步骤(Ying et al., 2005;Candès et al., 2006):
(1) 将二维快速傅里叶变换(FFT)用于模型参数, 获得如下傅里叶样本集:

|
其中, [n1, n2]是二维离散函数的数组索引, n是数组的维数.
(2) 将傅里叶样本与每个尺度j和角度l的Uj, l相乘, 形成如下乘积:
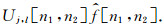
|
(3) 对乘积进行周期性重复, 并以直角坐标系原点为中心进行数据提取, 得到
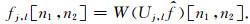
|
(28) |
(4) 对每个fj, l使用二维逆FFT, 获得离散曲波系数.
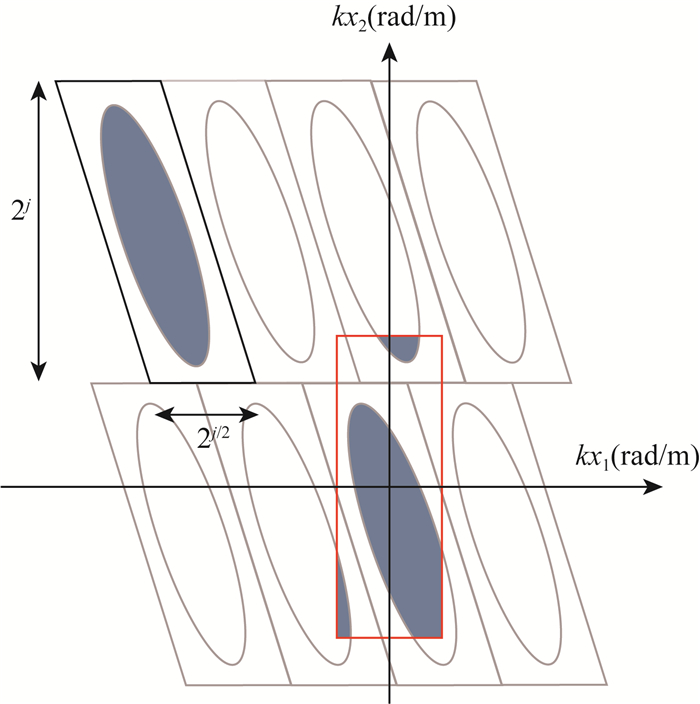
该算法的关键是将楔形基环绕在直角坐标系原点周围, 以形成可用于二维逆FFT的标准矩形.楔形基数据包含在大小为2j×2j/2的平行四边形中(图 2中的黑色框).我们对平行四边形内的数据进行分块, 然后将其Wrapping到围绕坐标系原点的标准矩形区域内, 这样就可将原始平行四边形包含的数据集中到大小为2j×2j/2的标准矩形中并完成数据提取.
|
图 2 用于楔形基数据提取的Wrapping技术 黑色平行四边形包含楔形基数据, 而灰色平行四边形是周期性平滑移动产生的复制结果.楔形基数据通过平滑移动复制到环绕原点的红色平行四边形中(参照Candès et al., 2006). Fig. 2 Wrapping wedge data The black parallelogram contains the polar wedge data, whereas the gray parallelograms are the replicas resulting from periodization. The parallelogram data are wrapped around the origin and contained in the red rectangle (after Candès et al., 2006). |
在本文中, 为方便读者理解, 我们定义曲波正变换算子为Wc(张华等, 2017),
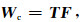
|
(29) |
其中, F表示二维快速傅里叶变换, T表示曲波拼接算子, 即将频率域转换到曲波系数的过程.与小波变换类似, 曲波基函数也满足正交性, 因此可以定义曲波逆变换算子为

|
(30) |
其中, F-1表示二维快速傅里叶逆变换, T-1表示曲波逆拼接算子, 即将曲波系数转换到频率域的过程.
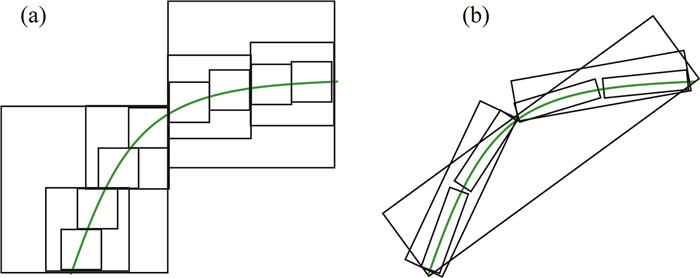
1.2.4 目标体边缘的最佳稀疏表示参见图 3, 由于曲波的多方向性和遵循抛物线比例关系(各向异性尺度关系), 因此与小波相比, 我们利用数量较少的曲波就可以拟合目标体边缘.这意味着曲波变换的一个突出优点是可以对目标体的边缘进行最佳稀疏表示.
|
图 3 (a) 小波拟合弯曲边缘;(b)曲波拟合弯曲边缘 (参看Alzubi et al., 2011) Fig. 3 Comparison of wavelets (a) and curvelets (b) for curved edges (after Alzubi et al., 2011) |
本文中我们提出的新方法是使用曲波变换将电阻率模型转换为曲波系数进行求解的, 这与基于相邻单元之间电阻率差异的模型约束反演不同, 基于曲波变换的反演是对频域中曲波系数的整体约束.第1尺度的系数恢复了电阻率模型的整体结构, 而其余尺度中的较大系数恢复了目标体的边缘细节.因此, 以曲波系数为正则化项的反演算法是一种多尺度、多分辨率反演方法.
2.1 二维大地电磁理论算例在下面的反演算例中, 我们均采用如下规则的矩形网格对模型进行剖分:垂直方向上共有64层.第1层的厚度为500 m, 随后各层的厚度为前一层的1.07倍, 模型总体深度范围约240 km.水平方向上共有128个网格单元, 计算区域的宽度为5000 m, 扩边区域的网格宽度为前一个网格宽度的1.2倍, 总体延伸约400 km.我们在计算区域内设计31个均匀分布的测点, 间距为15316 m.进而, 利用ModEM软件(Kelbert et al., 2014)计算了0.001~110 Hz范围内10个频率的TE和TM阻抗, 并对所有数据添加阻抗模长的3%高斯噪声后进行反演.对于基于曲波变换的稀疏正则化反演, 我们使用具有4个尺度的曲波变换, 其中第2尺度有16个方向, 第3和第4尺度有32个方向, 这样选择可以在有限的系数下就很好地表达模型特征.反演中首先给定初始的正则化因子, 在每步迭代中正则化因子以一个固定的衰减率下降, 通过对比不同初始正则化因子的反演结果, 发现采用这种方法反演结果相差不大, 我们选择迭代次数最少的初始正则化因子.对于实测数据, 为提高曲波系数稀疏正则化项的权重, 反演初始阶段我们选择一个较大的正则化因子, 随着反演进程逐渐趋近于收敛, 正则化因子逐渐减小.
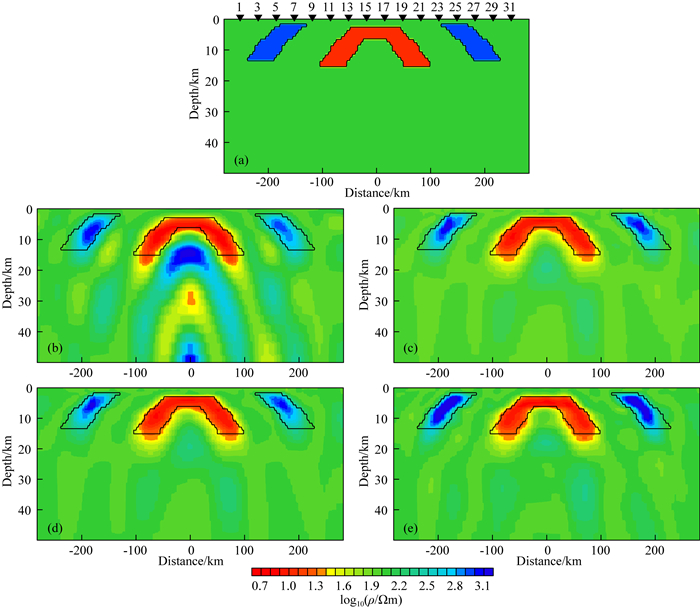
2.1.1 算例1:不同尺度系数反演结果对比本文的第1个算例是比较不同尺度系数的反演结果.参见图 4a, 背景电阻率为100 Ωm.中间红色区域的电阻率为10 Ωm, 两侧蓝色区域的电阻率为1000 Ωm.设定初始模型为100 Ωm的均匀半空间, 设定正则化因子为10, 并且每次迭代减小十分之九.
|
图 4 不同尺度系数的反演结果 (a)理论模型;(b)第1尺度系数反演结果;(c)第1和第2尺度系数反演结果;(d)第1、第2和第3尺度系数反演结果;(e)所有4个尺度系数的反演结果. Fig. 4 Inversion results of different scale coefficients (a) Original theoretical model; (b) Inversion result of 1st scale coefficients; (c) Inversion result of 1st and 2nd scale coefficients; (d) Inversion result of 1st, 2nd and 3rd scale coefficients; (e) Inversion result of all 4 scales coefficients. |
图 4b—e给出不同尺度曲波系数的反演结果.从图 4b可以看出, 第1尺度系数的反演结果很粗糙, 存在较多的假异常.随着我们在反演中逐渐增加更多尺度的系数, 反演结果越来越接近真实模型(参见图 4c—e).从图 4e中可以看出, 当所有尺度的系数参与反演时, 反演结果越可靠.由于本文算法中曲波变换具有多尺度特征, 不同尺度的系数包含了模型的不同信息, 粗尺度系数表征模型轮廓的低频信息;而细尺度系数则表征模型精细特征(比如模型边界)的高频信息.因此, 如果仅将粗尺度系数用于反演, 结果将是粗糙的并且存在假异常, 只有将所有的曲波系数都用于反演, 才能获得最可靠的反演结果.
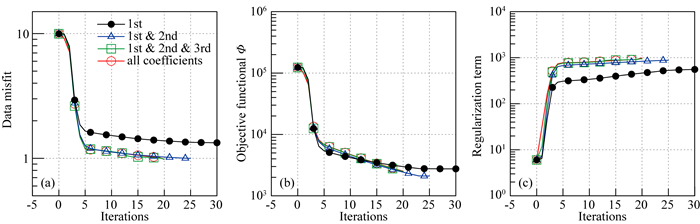
图 5给出数据拟合差、目标函数和正则化项数值.从图 5a中可以看出, 所有的反演都具有相似的收敛速度, 但仅使用第1尺度系数的反演没有很好地收敛.相比之下, 其他3套组合系数反演的数据拟合差经过20次迭代后均降至1, 说明在恢复了模型的主要特征后, 对模型的细节特征进行刻画不会改变反演的收敛性.
|
图 5 (a) 数据拟合差;(b)目标函数Φ;(c)正则化项 Fig. 5 (a) Data misfit; (b) Objective functional Φ; (c) Regularization term |
本文的第2个算例是比较L1和L2范数, 以及基于小波变换和曲波变换的稀疏正则化反演方法对反演结果的影响.参见图 6a, 背景半空间的电阻率为100 Ωm, 蓝色起伏层的电阻率为1000 Ωm, 而红色侵入层的电阻率为5 Ωm.所有4种反演算法的正则化因子均设定为10, 并且每次迭代将其降低十分之九.初始模型设定为100 Ωm的均匀半空间.图 6b—e分别给出L1范数, L2范数, 基于小波变换和基于曲波变换的稀疏正则化反演结果.从图中可以看出, L1范数反演的结果是块状的, 无法恢复异常体的真实结构;L2范数反演结果过于光滑, 目标体的边界没有被清楚地恢复.对于基于小波变换的稀疏正则化反演, 我们选择db20小波, 这是因为通过使用较大消失矩的小波可以更好地表征模型(Liu et al., 2018).由图 3可以看出小波基函数是块状, 而曲波基函数是楔形, 因此与小波变换相比, 用较少的曲波基函数就可以拟合曲线边界, 所以曲波变换的系数比小波变换的系数更加稀疏.对于稀疏正则化反演, 正则化项采用L1范数约束, 系数越稀疏, 越容易在反演过程中恢复出关键系数.同时, 由于小波变换的振荡特性, 反演结果会出现一些冗余构造.从图 6d给出的结果可以看出, 基于小波变换的稀疏正则化反演结果存在许多假异常, 目标体的边界也没有准确地恢复.然而, 从图 6e给出的曲波系数正则化反演可以看出, 反演结果较好地恢复了异常体的边界.实际上, 当我们将模型参数转换为曲波系数时, 精细尺度中较大系数对应于异常体的边界, 对这些大系数进行反演可恢复模型的边界特征.因此, 较之于其他算法, 基于曲波变换的稀疏正则化反演可以更好地刻画地下结构的边界特征.

|
图 6 (a) 真实模型;(b) L1范数反演模型;(c) L2范数反演模型;(d)基于小波变换的稀疏正则化反演模型;(e)基于曲波变换的稀疏正则化反演模型 Fig. 6 (a) True model; (b) Model for L1-norm inversion; (c) Model for L2-norm inversion; (d) Model for sparse inversion based on wavelet transform; (e) Model for sparse inversion based on curvelet transform |
图 7展示了所有4种算法的数据拟合差, 目标函数和正则化项数值.由图可以看出, 所有算法都具有良好的收敛性(图 7a), 反演迭代20次后数据拟合差都降至1.在后期迭代中, 正则化项接近一个恒定值(图 7c).另外, 所有反演中基于L2范数的反演收敛最快, 基于曲波变换的稀疏正则化反演收敛最慢, 而L1范数和基于小波变换的稀疏正则化反演居于其中.这种现象很容易进行解释.事实上, L2范数反演的模型粗糙度项是凸函数, 易于收敛;相比之下, 基于曲波变换的稀疏正则化反演方法在反演出模型的总体特征(轮廓)后, 还需要搜索精细的边界信息, 导致反演速度较慢.

|
图 7 (a) 数据拟合差;(b)目标函数Φ;(c)正则化项 Fig. 7 (a) Data misfit; (b) Objective functional Φ; (c) Regularization term |
从计算成本的角度来看, 我们得出相同的结论.对于图 6中的模型, L1范数反演需要70 min, L2范数反演需要60 min, 基于小波变换的稀疏正则化反演需要90 min, 而基于曲波变换的稀疏正则化反演需要76 min.这说明基于曲波的反演虽然对地下电阻率结构具有更好的分辨率, 但要获得模型的细节特征, 需花费的时间要比L1范数和L2范数反演长.需要说明的是, 由于小波变换不具有方向性, 为刻画目标体的边界等细节特征, 基于小波变换的反演需要花费更长的时间用于搜索模型空间.
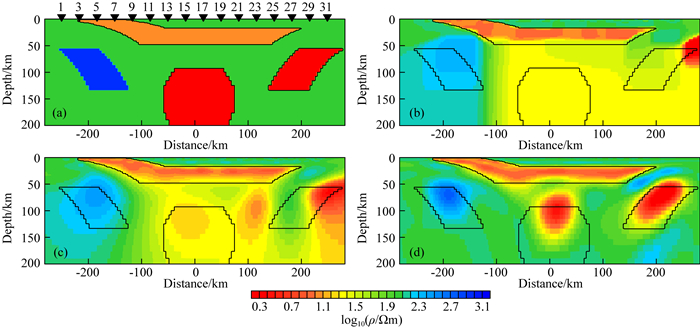
2.1.3 算例3:深部目标体的分辨能力为了研究本文曲波变换稀疏正则化反演对深层目标体的探测能力, 我们设计了一个如图 8a所示的模型:背景电阻率为100 Ωm, 浅层异常体的电阻率为10 Ωm, 深蓝色异常体的电阻率为1000 Ωm, 红色异常体的电阻率为2 Ωm.我们分别采用L2范数, L1范数和基于曲波变换的稀疏正则化反演对理论数据进行反演.反演中初始正则化因子均设为100, 每次迭代将其降低十分之九, 初始模型均设定为100 Ωm的均匀半空间.
|
图 8 (a) 真实模型;(b) L1范数反演模型;(c) L2范数反演模型;(d)基于曲波变换的稀疏正则化反演模型 Fig. 8 (a) True model; (b) Model for L1-norm inversion; (c) Model for L2-norm inversion; (d) Model for sparse inversion based on curvelet transform |
图 8给出L1范数, L2范数和基于曲波变换的稀疏正则化反演的对比结果.从图 8b和8c可以看出, L1和L2范数反演都恢复了浅层地下模型, 异常体的浅层边界较为清晰.然而, 对于50 km以下的三个异常体, L1范数和L2范数反演都无法准确地恢复其电阻率和边界位置.从图 8d中可以看出, 除了对浅部异常体具有较高的分辨率外, 基于曲波变换的稀疏正则化反演对深部异常体的分辨也较L1和L2范数反演效果好.
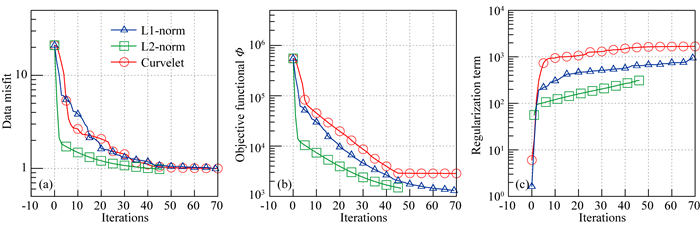
图 9展示了所有三种算法的数据拟合差, 目标函数和正则化项数值.由图可以看出, 所有算法都具有良好的收敛性(图 9a), 反演迭代50次后数据拟合差都降至1.
|
图 9 (a) 数据拟合差;(b)目标函数Φ;(c)正则化项 Fig. 9 (a) Data misfit; (b) Objective functional Φ; (c) Regularization term |
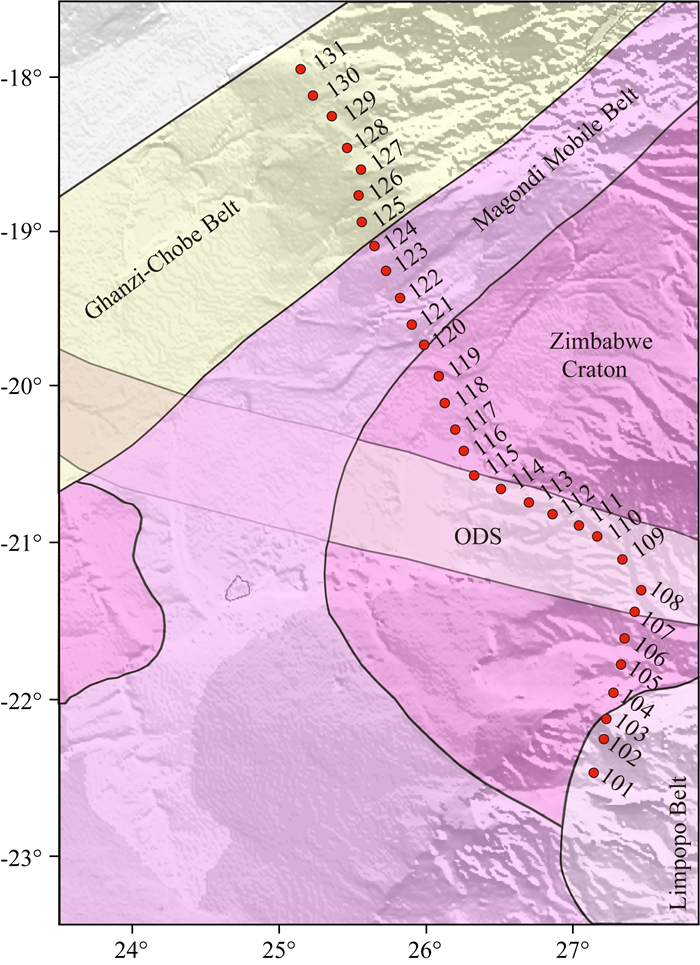
为了进一步测试基于曲波变换的稀疏正则化反演的有效性, 我们对来自非洲南部大地电磁实验项目SAMTEX的ZIM数据进行反演(Miensopust et al., 2011).参见图 10, 二维剖面跨越津巴布韦(ZIM)克拉通, Magondi带和Ghanzi-Chobe带, 全长约500 km, 共计31个测点(图中红点标识).大地电磁观测周期为0.008986~856.091 s.本文着重于分析不同反演方法的差异以及噪声估计对反演结果的影响, 相关的详细地质解释参见Miensopust等(2011).
|
图 10 非洲南部SAMTEX项目的ZIM数据集对应的测点位置(根据Miensopust et al., 2011修改) Fig. 10 Locations of ZIM subset data from SAMTEX survey in Southern Africa (modified from Miensopust et al., 2011) |
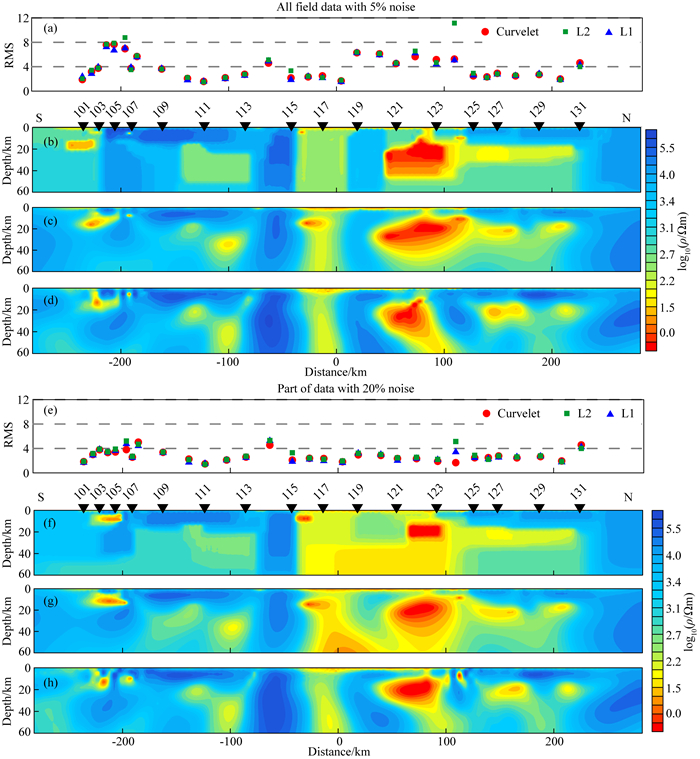
我们建立了一个128×64的电阻率网格模型.计算区域中沿水平方向的网格单元大小为5000 m, 而垂直方向上顶部网格单元厚度为500 m, 下部网格单元厚度以1.07的比率增加.背景半空间初始电阻率设置为1000 Ωm.对于L2范数、L1范数及曲波变换稀疏正则化三种反演算法, 初始正则化因子均设定为1000, 每次迭代将其降低至先前值的十分之九, 直到降为1时保持不变.我们首先假设所有测点的噪声水平为5%.图 11b—d展示了L1范数, L2范数和基于曲波变换的稀疏正则化的反演结果对比.由图可以看出, 三种方法给出了相似的反演结果, 地下主要电性结构特征得到刻画.在断面南部107~115测点下有一个近地表的高电阻率层, 即Okavango Dike Swarm(ODS), 同时在横向范围内有若干个中低阻异常体(de Beer et al., 1975), 在剖面北部位于125~131测点处的高电阻率结构对应于Ghanzi-Chobe带(GCB).然而, 从图 11a可以看到, 104~108测点和119~124测点的数据拟合差明显大于其他测点.为此, 我们将这些数据拟合差较高测点的噪声水平从5%更改为20%, 并重新进行反演.图 11e给出基于新噪声估计的反演结果.由图可以看出, 这些测点的数据拟合差显著降低.对比图 11b—d和10f—h中的结果, 我们发现当这些测点噪声水平被改变后, L2范数和L1范数反演结果发生很大变化.相比之下, 基于曲波变换的稀疏正则化反演结果几乎没有发生变化.这意味着与L2范数和L1范数反演相比, 基于曲波变换的稀疏正则化反演对噪声估计不太敏感.
|
图 11 非洲南部SAMTEX项目的ZIM数据集反演结果 (a) L1 / L2范数反演和基于曲波变换的稀疏正则化反演的数据拟合差;(b) L1范数反演结果;(c) L2范数反演结果;(d)基于曲波变换的稀疏正则化反演结果;(e) L1 / L2范数反演和基于曲波变换的稀疏正则化反演的数据拟合差;(f) L1范数反演结果;(g) L2范数反演结果;(h)基于曲波变换的稀疏正则化反演结果.对于(a)—(d), 所有测点的噪声设定为5%, 而对于(e)—(h), 在测点104~108和119~124的噪声设定为20%, 其他测点的噪声仍为5%.图中仅展示奇数测点. Fig. 11 Inversion results of ZIM subset data from SAMTEX survey in Southern Africa (a) RMS for L1-/L2-norm and the curvelet-based inversions; (b) Model for L1-norm inversion; (c) Model for L2-norm inversion; (d) Model for curvelet-based inversion; (e) RMS for L1-/L2-norm and the curvelet-based inversions; (f) Model for L1-norm inversion; (g) Model for L2-norm inversion; (h) Model for curvelet-based inversion. For (a)—(d), the noise is assumed to be 5% at all survey sites, while for (e)—(h), the noise is assumed to be 20% at survey sites 104~108 and 119~124 and 5% at other sites. For simplicity, we only show the odd stations. |
图 12展示了所有三种算法在两种噪声水平类型下的数据拟合差, 目标函数和正则化项, 可以看出所有算法都正常收敛.

|
图 12 (a, d)数据拟合差;(b, e)目标函数Φ;(c, f)正则化项 对于(a)—(c), 所有测点的噪声水平设定为5%, 而对于(d)—(f), 在测点104~108和119~124的噪声水平设定为20%, 其他测点的噪声水平仍为5%. Fig. 12 (a, d) Data misfit; (b, e) Objective functional Φ; (c, f) Regularization term For (a)—(c), the noise is assumed to be 5% at all survey sites, while for (d)—(f), the noise is assumed to be 20% at survey sites 104~108 and 119~124 and 5% at other sites. |
L1和L2范数反演的模型约束是空间域中相邻单元之间的电阻率差异.对于L1范数反演, 允许相邻单元之间存在较大差异, 并且模型差分沿水平和垂直方向.从图 6b和图 8b可以看出, 异常体的反演结果在水平和垂直方向均是块状的;对于L2范数反演, 模型要求相邻单元之间的差异不大.因此, 从图 6c和图 8c给出的反演结果中未观察到异常体之间的明显边界, 电阻率在水平和垂直方向上均呈现光滑过度的特征.从图 6e和图 8d可以看出, 基于曲波变换的稀疏正则化反演的结果更接近真实模型(既没有出现块状又没有出现过度光滑的反演结果).基于曲波变换的稀疏正则化反演的这种优点可以得到很好的解释.事实上, 与传统的空间域反演不同, 我们将空间域模型转换为曲波域中的稀疏系数, 并对曲波系数实施L1范数正则化来保证系数的稀疏性.曲波系数包含大量的模型信息.根据曲波变换的多尺度和多方向性, 第1尺度的系数相对较大, 包含模型的整体概貌, 细尺度中较大系数对应于模型的细节信息(比如异常体边界).通过对稀疏系数应用L1范数正则化, 我们可以求解出第1尺度的系数和细尺度的关键系数.这些反演获得的稀疏系数既包含了模型的整体概貌, 又包含与边界相关的细节信息.因此, 基于曲波变换的稀疏正则化反演更有利于恢复地下复杂的电性结构.
4 结论本文将曲波变换引入到电磁数据反演中, 成功实现了二维大地电磁稀疏正则化反演.与传统的将模型粗糙度作为正则化约束项不同, 我们的反演结合了曲波系数的L1范数约束和数据拟合项的L2范数约束以获得最佳解, 保证反演结果具有良好的分辨率.理论模型反演结果表明, 当所有尺度的曲波系数参与反演时, 基于曲波变换的稀疏正则化反演能获得最佳分辨率.另外, 对比L1范数和L2范数反演及基于小波变换的稀疏正则化反演结果, 我们进一步证实基于曲波变换的稀疏正则化反演可以更好地恢复地下异常电阻率边界特征的结论.对非洲南部SAMTEX项目实测大地电磁数据的反演表明, 基于曲波变换的稀疏正则化反演不仅可以获得较理想的反演结果, 反演结果受数据噪声估计的影响也较小.
致谢 我们衷心感谢Curvelab的作者提供曲波变换开源代码, 感谢Mod2DMT代码的开发人员Gary Egbert教授和Anna Kelbert教授, 同时也感谢SAMTEX联盟提供的大地电磁实测数据.
Abubakar A, Habashy T M, Lin Y, et al. 2012. A model-compression scheme for nonlinear electromagnetic inversions. Geophysics, 77(5): E379-E389. |
Alzubi S, Islam N, Abbod M. 2011. Multiresolution analysis using wavelet, ridgelet, and curvelet transforms for medical image segmentation. International Journal of Biomedical Imaging, 2011: 136034. DOI:10.1155/2011/136034 |
Bedrosian P A. 2007. MT+, integrating magnetotellurics to determine earth structure, physical state, and processes. Surveys in Geophysics, 28(2-3): 121-167. |
Candès E, Demanet L, Donoho D, et al. 2006. Fast discrete curvelet transforms. Multiscale Modeling & Simulation, 5(3): 861-899. |
Constable S C, Parker R L, Constable C G. 1987. Occam's inversion:a practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics, 52(3): 289-300. |
de Beer J H, Gough D I, Van Zijl J S V. 1975. An electrical conductivity anomaly and rifting in southern Africa. Nature, 255(5511): 678-680. |
de Groot-Hedlin C, Constable S. 2004. Inversion of magnetotelluric data for 2D structure with sharp resistivity contrasts. Geophysics, 69(1): 78-86. |
Deng Y, Tang J, Ruan S. 2019. Adaptive regularized three-dimensional magnetotelluric inversion based on the LBFGS quasi-Newton method. Chinese Journal of Geophysics (in Chinese), 62(9): 3601-3614. DOI:10.6038/cjg2019M0045 |
Donoho D L. 2006. For most large underdetermined systems of linear equations the minimal $\ell$1-norm solution is also the sparsest solution. Comm. Pure Appl. Math., 59(6): 797-829. |
Ekblom H. 1987. The L1-estimate as limiting case of an Lp-or Huber-estimate.//Dodge Y ed. Statistical Data Analysis Based on the L1-Norm and Related Methods. Amsterdam: Elsevier Science Publ. Co., Inc., 109-116.
|
Farquharson C G. 2008. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics, 73(1): K1-K9. |
Haber E. 2014. Computational Methods in Geophysical Electromagnetics. Philadelphia: SIAM.
|
Herrmann F J, Verschuur E. 2004. Curvelet-domain multiple elimination with sparseness constraints.//74th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1333.
|
Herrmann F J, Böniger U, Verschuur D J. 2007. Non-linear primary-multiple separation with directional curvelet frames. Geophys. J. Int., 170(2): 781-799. |
Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames. Geophys. J. Int., 173(1): 233-248. |
Herrmann F J, Wang D L, Verschuur D J. 2008. Adaptive curvelet-domain primary-multiple separation. Geophysics, 73(3): A17-A21. |
Jahandari H, Farquharson C G. 2017. 3-D minimum-structure inversion of magnetotelluric data using the finite-element method and tetrahedral grids. Geophys. J. Int., 211(2): 1189-1205. |
Kelbert A, Meqbel N, Egbert G D, et al. 2014. ModEM:a modular system for inversion of electromagnetic geophysical data. Computers & Geosciences, 66: 40-53. |
Liu Y H, Yin C C. 2016. 3D inversion for multipulse airborne transient electromagnetic data. Geophysics, 81(6): E401-E408. |
Liu Y H, Farquharson C G, Yin C C, et al. 2018. Wavelet-based 3-D inversion for frequency-domain airborne EM data. Geophys. J. Int., 213(1): 1-15. |
Loris I, Nolet G, Daubechies I, et al. 2007. Tomographic inversion using $\ell$1-norm regularization of wavelet coefficients. Geophys. J. Int., 170(1): 359-370. |
Mehanee S, Zhdanov M. 2002. Two-dimensional magnetotelluric inversion of blocky geoelectrical structures. J. Geophys. Res., 107(B4): 2065. DOI:10.1029/2001JB000191 |
Miensopust M P, Jones A G, Muller M R, et al. 2011. Lithospheric structures and Precambrian terrane boundaries in northeastern Botswana revealed through magnetotelluric profiling as part of the Southern African Magnetotelluric Experiment. J. Geophys. Res., 116(B2): B02401. DOI:10.1029/2010JB007740 |
Newman G A, Alumbaugh D L. 2002. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophys. J. Int., 140(2): 410-424. |
Nittinger C G, Becken M. 2016. Inversion of magnetotelluric data in a sparse model domain. Geophys. J. Int., 206(2): 1398-1409. |
Rodi W L, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics, 66(1): 174-187. |
Ruan S, Tang J, Chen X B, et al. 2020. Three-dimensional magnetotelluric inversion based on adaptive L1-norm regularization. Chinese Journal of Geophysics (in Chinese), 63(10): 3896-3911. DOI:10.6038/cjg2020N0453 |
Shan H, Ma J W, Yang H Z. 2009. Comparisons of wavelets, contourlets and curvelets in seismic denoising. J. Appl. Geophys., 69(2): 103-115. |
Sheard S N, Ritchie T J, Christopherson K R, et al. 2005. Mining, environmental, petroleum, and engineering industry applications of electromagnetic techniques in geophysics. Surveys in Geophysics, 26(5): 653-669. |
Simons F J, Loris I, Nolet G, et al. 2011. Solving or resolving global tomographic models with spherical wavelets, and the scale and sparsity of seismic heterogeneity. Geophys. J. Int., 187(2): 969-988. |
Siripunvaraporn W, Egbert G, Lenbury Y, et al. 2005. Three-dimensional magnetotelluric inversion:data-space method. Physics of the Earth and Planetary Interiors, 150(1-3): 3-14. |
Starck J L, Candès E J, Donoho D L. 2002. The curvelet transform for image denoising. IEEE Transactions on Image Processing, 11(6): 670-684. |
Su Y, Yin C C, Liu Y H, et al. 2019. Inversions of time-domain airborne EM based on generalized model constraints. Chinese Journal of Geophysics (in Chinese), 62(2): 743-751. DOI:10.6038/cjg2019M0217 |
Wang D L, Saab R, Özgür Y, et al. 2008. Bayesian wavefield separation by transform-domain sparsity promotion. Geophysics, 73(5): A33-A38. |
Ying L X, Demanet L, Candès E. 2005. 3D discrete curvelet transform.//Proceedings of SPIE 5914, Wavelets XI. San Diego, CA: SPIE, 351-361.
|
Zhang H, Wang D N, Li H X, et al. 2017. High accurate seismic data reconstruction based on non-uniform curvelet transform. Chinese Journal of Geophysics (in Chinese), 60(11): 4480-4490. DOI:10.6038/cjg20171132 |
Zhang L L, Yu P, Wang J L, et al. 2010. A study on 2D magnetotelluric sharp boundary inversion. Chinese Journal of Geophysics (in Chinese), 53(3): 631-637. DOI:10.3969/j.issn.0001-5733.2010.03.017 |
Zhao G Z, Chen X B, Tang J. 2007. Advanced geo-electromagnetic methods in China. Progress in Geophysics (in Chinese), 22(4): 1171-1180. |
邓琰, 汤吉, 阮帅. 2019. 三维大地电磁自适应正则化有限内存拟牛顿反演. 地球物理学报, 62(9): 3601-3614. DOI:10.6038/cjg2019M0045 |
阮帅, 汤吉, 陈小斌, 等. 2020. 三维大地电磁自适应L1范数正则化反演. 地球物理学报, 63(10): 3896-3911. DOI:10.6038/cjg2020N0453 |
苏扬, 殷长春, 刘云鹤, 等. 2019. 基于广义模型约束的时间域航空电磁反演研究. 地球物理学报, 62(2): 743-751. DOI:10.6038/cjg2019M0217 |
张华, 王冬年, 李红星, 等. 2017. 基于非均匀曲波变换的高精度地震数据重建. 地球物理学报, 60(11): 4480-4490. DOI:10.6038/cjg20171132 |
张罗磊, 于鹏, 王家林, 等. 2010. 二维大地电磁尖锐边界反演研究. 地球物理学报, 53(3): 631-637. DOI:10.3969/j.issn.0001-5733.2010.03.017 |
赵国泽, 陈小斌, 汤吉. 2007. 中国地球电磁法新进展和发展趋势. 地球物理学进展, 22(4): 1171-1180. |
 2021, Vol. 64
2021, Vol. 64


