2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95060, USA;
3. 吉林大学, 地球探测科学与技术学院, 长春 130026;
4. 常州工学院, 土木建筑工程学院, 常州 213000
2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95060, USA;
3. College of Geo-Exploration science and Technology, Jilin University, Changchun 130026, China;
4. School of Civil Engineering and Architecture, Changzhou Institude of Technology, Changzhou 213000, China
随着油气勘探技术的不断发展,同时对地下构造探测精度要求也逐渐提高,如今正从构造勘探阶段逐步转向岩性勘探阶段,其中地震数据偏移成像方法在油气勘探领域占有重要的地位.近年来Kirchhoff偏移、高斯束偏移、单程波偏移和逆时偏移等地震成像方法得到了快速发展(秦宁等,2015;You et al., 2019;豆辉和徐逸鹤,2019;Sun et al., 2020).在复杂介质中,逆时偏移(RTM)方法具有成像精度高的优点,能够适用于横向速度变化剧烈的区域,获取地下构造高精度反射系数(Sun and Zhang, 2009;马方正等,2016;You et al., 2017).但是逆时偏移的伴随算子是正演算子的共轭转置,而并非其逆算子(Claerbout,1991),因此无法获得真振幅成像结果.
为了进一步提高逆时偏移的成像精度,发展了最小二乘逆时偏移方法(LSRTM),其在反演的理论框架下,利用反偏移数据来不断地与观测数据相匹配,并通过优化算法进行迭代,最终获取地下构造的高精度成像结果.关于LSRTM的发展,首先由Nemeth等(1999)在最小二乘目标函数的框架下实现了Kirchhoff偏移.随后,Dai等(2012)、Dai和Schuster(2013)利用多源地震数据进行测试,很大程度上提高了LSRTM的计算效率.任浩然等(2013)将Hessian算子应用于LSRTM中,获得了相对保真的成像结果,改善了地震偏移的成像精度.Tan和Huang(2014)在原始LSRTM的基础上,提出了波场分离成像条件,并通过更新震源波场实现陡倾角断层成像.此外,为了克服LSRTM对偏移模型的依赖问题,刘玉金和李振春(2015)提出扩展成像条件下的LSRTM方法,测试结果表明该方法可以获得更准确的振幅属性信息.Huang等(2015)、周东红等(2020)提出了带地形的LSRTM方法,进一步考虑地表起伏对波动方程成像结果的影响,指出无需对地震数据进行校正便可以获得起伏地表高精度的成像结果.地震数据中的多次波同样携带地下构造信息,刘学建和刘伊克(2016)建立了基于多次波的LSRTM方法,并指出该方法能提供比反射波偏移成像更大的照明角度.陈生昌和周华敏(2018)在反射波成像的基础上,研究了入射波与反射波在传播算子上的差异,提出了新的反射波LSRTM方法.方修政等(2018)指出基于常规互相关成像条件的LSRTM梯度含有很强的低频噪声,为此提出了基于逆散射成像条件的LSRTM方法.田坤等(2018)、巩向博等(2019)利用多源地震数据,在稀疏约束的理论框架下展开研究.Liu等(2020)在LSRTM中加入了Gabor反褶积滤波来提高盐下构造的成像精度.Li等(2020)通过引入权重因子来衰减地震数据中较强的反射波信息,进而增强弱散射信号,实现改善深部构造成像精度的目标.经过多年的研究,LSRTM技术得到了快速地发展,逐渐成为当前的研究热点问题.但是地震波传播是一个较为复杂的过程,使得LSRTM成像结果仍然受地震数据振幅信息影响较为严重.为了减弱振幅信息的影响,在互相关LSRTM目标函数的基础上提出了很多的改进的方法(Zhang et al., 2015;Liu et al., 2016, 2017;李庆洋等,2016;Yi et al., 2019).但是如何在LSRTM方法基础上,实现透过上覆强散射地质体来获得深部精细构造的高精度成像目标,仍有待进一步研究.
为此,本文在前人的研究基础上,提出时频域振幅相位联合的最小二乘逆时偏移方法(PA-LSRTM),来实现对地下深部精细构造的高精度成像.本文首先介绍PA-LSRTM目标函数的构建方法;其次,为了减弱地震数据振幅信息对成像结果的影响,在目标函数中引入振幅权重因子,提高弱地震信号的可成像精度;然后,详细推导了PA-LSRTM目标函数对模型参数的梯度算子,并给出扰动模型迭代表达式.最后,利用Marmousi模型和盐丘模型进行数值测试,并对RTM、LSRTM和PA-LSRTM的成像结果进行对比分析.
1 方法原理 1.1 线性化Born正演在常密度介质中,声波方程可以表示为
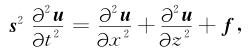
|
(1) |
其中s为慢度场,即速度的倒数;u为声压波场;f为震源子波.式(1)中可以将慢度场的平方分解为背景慢度场平方与扰动慢度场平方的和(李庆洋等,2016):

|
(2) |
其中s2为总慢度场的平方;s02为背景慢度场的平方;Δs2扰动慢度场的平方.在此基础上,同样可以将地震波的总场分解为背景波场和扰动波场的叠加,即:
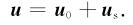
|
(3) |
根据式(3),背景波场和扰动波场满足以下关系:

|
(4) |
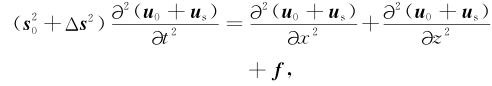
|
(5) |
当扰动场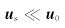

|
(6) |
欲求解扰动波场us,只需要在偏移模型上将背景波场u0代入公式(6)中,再做一次波动方程正演模拟即可.
1.2 最小二乘逆时偏移原理LSRTM是利用模拟数据来不断地与观测数据相匹配,通过最小化目标函数来获取扰动模型的高精度成像结果.因此,LSRTM的目标函数可以定义为
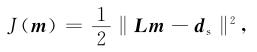
|
(7) |
其中‖·‖2表示L2范数,L表示线性Born正演模拟算子,模型参数m=Δs2=s2-s02,us=Lm表示扰动波场.则目标函数可以用扰动波场的形式来表示:
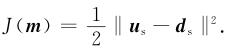
|
(8) |
目标函数对模型参数的梯度可以表示为
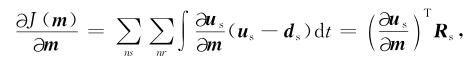
|
(9) |
其中T表示矩阵转置;ns、nr分别表示震源数目和检波器数目;Rs=(us-ds)表示伴随震源.因此,目标函数对模型参数的梯度可以表示为反传波场与正传波场的零延迟互相关:

|
(10) |
LSRTM梯度推导过程,详见附录B.其中反传波场ures=[(AsT)-1Rs]满足:
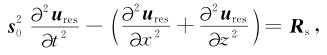
|
(11) |
本文设定初始模型参数为m0=0,对应的模拟数据us=0,此时Rs=-ds.因此,LSRTM第一次的梯度等价于常规逆时偏移成像结果.随着模型参数不断地被更新,模拟数据us逐渐趋近于观测数据ds,同时对应的LSRTM的目标函数也逐渐减小,最终获得地下构造高精度偏移成像结果.
1.3 时频域振幅相位联合的最小二乘逆时偏移时频域振幅相位联合的最小二乘逆时偏移(PA-LSRTM)是利用模拟数据的时频域振幅相位信息来不断地与观测数据的时频域振幅相位信息相匹配,通过最小化目标函数来获取扰动模型的高精度成像结果.与常规LSRTM相似,PA-LSRTM的目标函数定义为:
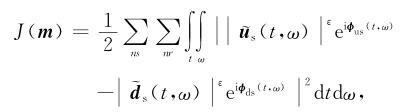
|
(12) |
其中;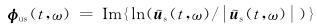
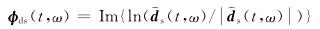

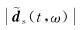
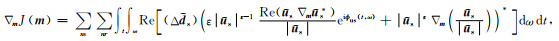
|
(13) |
其中
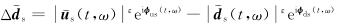

|
(14) |
式(14)可以简化为(详见附录C):
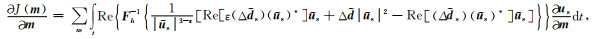
|
(15) |
根据式(15),伴随震源可以定义为
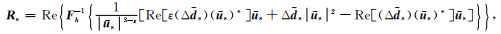
|
(16) |
式(16)为了避免分母为0,可在分母处加一个微小的常数.其中,PA-LSRTM的梯度计算过程与常规LSRTM梯度计算相似,只需要将伴随震源Rs反传至模型空间并与正传波场做零延迟互相关.
图 1给出了伴随震源某一道数据对应的时频域分析结果.从图 1a中可以看出,地震信号的振幅谱在浅部能量较强,但随着传播时间增大能量快速衰减.深部反射的弱振幅地震信号在目标函数中占有很小的权重,因此增加了深部精细构造的成像难度.当ε=0.6时,伴随震源的深部信号得到了明显地增强(图 1b),同时也均衡了浅部强能量,有助于提高深部弱反射信号在目标函数中的权重.当进一步减小振幅权重因子ε=0.3,相应的相位谱信息在PA-LSRTM目标函数中得到了进一步地增强(图 1c).当ε=0时,从浅部到深部的振幅谱基本具有相同的权重,即使在5 s时,深部弱反射地震信号依然清晰可辨.但是,此时PA-LSRTM目标函数中完全忽略了振幅信息,则此时目标函数易受到噪声相位的影响.因此,本文PA-LSRTM方法首先选用振幅权重因子ε=0.6来更新模型参数;然后,逐渐减小振幅权重因子,提高深部区域扰动模型的成像精度,直至振幅权重因子为ε=0.3.这样既能减弱振幅信息对深部区域成像不足的影响,同时也避免纯相位目标函数产生的噪声干扰,实现最大化提高深部弱反射信号成像精度的目标.
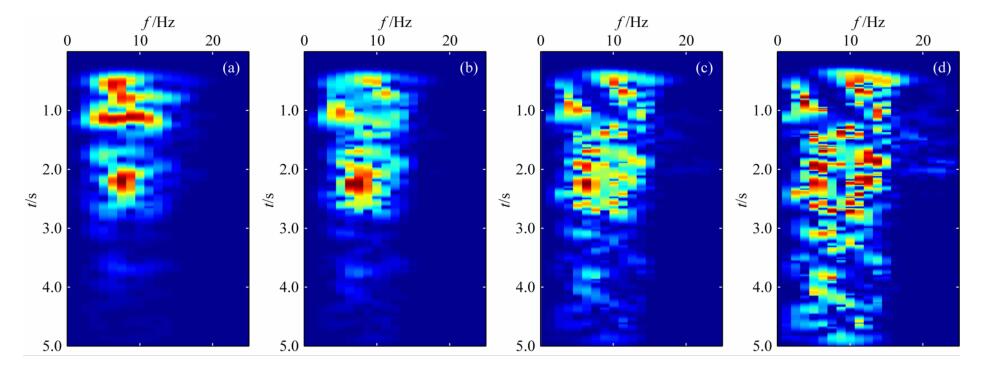
|
图 1 PA-LSRTM伴随震源单道时频域振幅谱(不同振幅权重因子) (a) ε=1;(b) ε=0.6;(c) ε=0.3;(d) ε=0. Fig. 1 Time-frequency domain amplitude information of the single trace PA-LSRTM adjoint source with different amplitude weight factors |
地震波在地下传播过程较为复杂,常受到强散射介质的屏蔽作用,致使深部构造对应的地震波场响应较弱,难以获得高精度成像结果.为了解决深部精细构造成像问题,PA-LSRTM方法通过增强时频域相位谱的权重,同时减弱振幅信息的影响,提高深部弱地震信号的可成像精度,进而实现深部区域和强散射地质体下部构造的高精度成像.PA-LSRTM算法的具体实施流程如图 2所示:首先,将观测数据和模拟数据变换至时频域,通过振幅权重因子在目标函数中调整振幅相位占比,增强相位信息在成像过程中所占权重;然后,利用Gabor逆变换将时频域伴随震源变换至时间域,再利用伴随算子把伴随震源反传至模型空间,获得反传波场;最后,计算正传波场与反传波场的零延迟互相关,即为模型参数的更新梯度,并结合局部优化算法对成像结果不断地迭代.

|
图 2 时频域振幅相位联合的最小二乘逆时偏移(PA-LSRTM)流程图 Fig. 2 Flow chart of joint least square reverse time migration of phase and amplitude in the time-frequency domain (PA-LSRTM) |
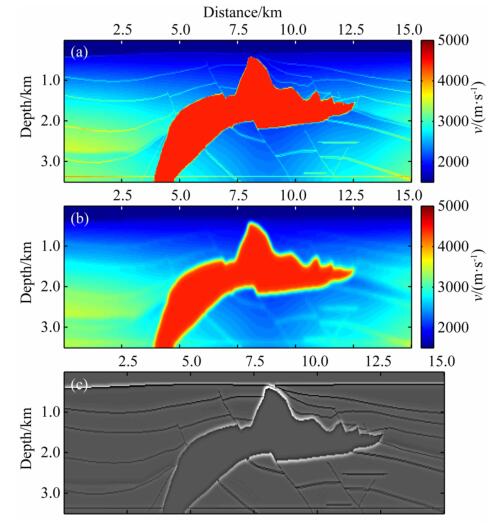
本文首先利用Marmousi速度模型来测试RTM、LSRTM和PA-LSRTM的成像效果.Marmousi速度模型如图 3a所示,经过平滑以后的速度模型如图 3b所示,真实扰动模型如图 3c所示.Marmousi速度模型构造复杂,同时在深部区域含有强散射构造,增加了深部精细构造的成像难度.Marmousi速度模型的横向距离为15 km,纵向深度为3.5 km,网格间距为25 m.在地表以300 m间隔均匀分布50炮,每炮对应600个检波器全接收.雷克子波震源主频为8 Hz,地震数据观测最大时长为5 s,时间采样间隔为2 ms.

|
图 3 (a) Marmousi速度模型;(b)偏移速度模型;(c)真实扰动模型 Fig. 3 (a) Marmousi velocity model; (b) Migration velocity model; (c) True model perturbations |
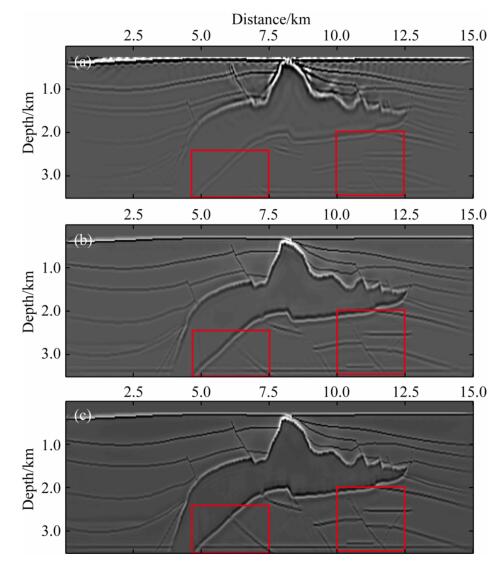
图 4为Marmousi模型成像结果,与图 3c所示的真实扰动模型对比可以看出,RTM成像结果基本能恢复Marmousi模型的构造信息,但是在深部区域存在明显的成像不足问题,同时在振幅上与真实扰动模型相差较大.将图 4a、b对比发现,LSRTM成像结果很好地恢复了Marmousi速度模型的深部构造信息,使得深浅区域成像振幅更加均衡,分辨率也得到了很大的改善.将图 4a、b、c对比发现,PA-LSRTM成像结果在薄细层位成像精度上有了明显地提高,同时成像振幅也更加接近真实扰动模型.此外,在Marmousi模型的强散射构造下部区域(左下侧红色线框)和储层构造区域(右下侧红色线框)的成像分辨率与LSRTM成像结果相比较,有了较大改善.

|
图 4 Marmousi模型成像结果 (a) RTM成像结果;(b) LSRTM成像结果;(c) PA-LSRTM成像结果. Fig. 4 Imaging results of the Marmousi model (a) RTM result; (b) LSRTM result; (c) PA-LSRTM result. |
为了清晰地看出PA-LSRTM方法在深部精细构造成像优势,提取图 4所示成像结果的局部放大图来进行对比分析,如图 5所示.可以看出PA-LSRTM成像结果相比于LSRTM成像结果在不整合面上的成像有了明显地改善(左下侧红色线框),同时强散射介质底部的倾斜构造也得到了清晰地成像.提取了图 4中Marmousi模型右侧含油气储层构造区域的成像结果进行对比分析(右下侧红色线框),如图 6所示.可以看出PA-LSRTM成像结果在储层位置处的成像分辨率上相比于RTM和LSRTM成像结果有了明显的提高.根据Marmousi模型成像结果的局部放大图可以看出,PA-LSRTM方法相比于RTM和LSRTM方法在深部区域的成像方面有着一定的优势.

|
图 5 Marmousi模型成像结果局部放大图(图 4左下侧红色线框) (a)真实扰动模型;(b) RTM成像结果;(c) LSRTM成像结果;(d) PA-LSRTM成像结果. Fig. 5 Magnified view of Marmousi model imaging results (red rectangular at lower left side in Fig. 4) (a) True perturbation model; (b) RTM result; (c) LSRTM result; (d) PA-LSRTM result. |

|
图 6 Marmousi模型成像结果局部放大图(图 4右下侧红色线框) (a)真实扰动模型;(b) RTM成像结果;(c) LSRTM成像结果;(d) PA-LSRTM成像结果. Fig. 6 Magnified view of Marmousi model imaging results (red rectangular at lower right side in Fig. 4) (a) True perturbation model; (b) RTM result; (c) LSRTM result; (d) PA-LSRTM result. |
进一步分析RTM、LSRTM和PA-LSRTM的成像结果的可靠性,利用图 4所示成像结果进行Born正演模拟,震源位置设置在横向距离7.5 km处,并将产生的地震数据与真实扰动数据进行对比(图 7).将图 7a、b对比可以发现,RTM的成像结果对应的模拟数据与真实扰动波场相差较大,不仅在深部区域地震扰动波场存在明显的差异,在浅部区域RTM成像结果对应的扰动波场同相轴也存在着明显的噪声干扰问题.将图 7a、c、d对比可以发现,LSRTM和PA-LSRTM成像结果对应的模拟数据更接近真实的扰动波场.但是在LSRTM成像结果对应的模拟数据中缺失一些弱同相轴信息,这主要是因为LSRTM的深部成像结果与真实扰动模型仍存在一定的差距.将图 7a、d对比可以发现,即使观测数据中的一些微弱同相轴信息,在基于PA-LSRTM成像结果进行Born正演的模拟数据中也有与之对应的同相轴信息.同时提取图 4的单道成像剖面进行对比分析,如图 8所示,可以看出RTM成像振幅与真实扰动模型振幅相差较大,LSRTM成像振幅有了明显的改善.在图 8深部区域,可以明显看到PA-LSRTM的振幅更加接近真实扰动模型振幅,也进一步证明了PA-LSRTM方法在弱地震信号成像方面具有一定的优势.

|
图 7 地震扰动波场数据 (a)真实扰动模型;(b) RTM成像结果;(c) LSRTM成像结果;(d) PA-LSRTM成像结果. Fig. 7 Seismic perturbation data True perturbation model; (b) RTM result; (c) LSRTM result; (d) PA-LSRTM result. |
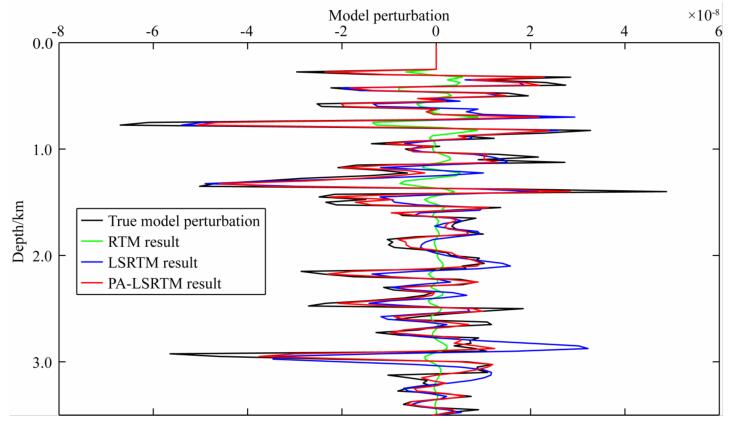
|
图 8 单道成像剖面图(Marmousi模型11 km处) Fig. 8 Single trace imaging profile (Marmousi model at 11 km) |
利用盐丘模型对RTM、LSRTM和PA-LSRTM方法进行数值测试,旨在分析盐丘底界面及其盐下构造的成像精度.真实盐丘速度模型如图 9a所示,经过平滑以后的偏移速度模型如图 9b所示,真实盐丘扰动模型如图 9c所示.盐丘模型横向距离为15 km,纵向深度为3.5 km,网格间距为25 m.在地表以300 m间隔均匀分布50炮,每炮对应600个检波器全接收.在测试过程中,采用震源主频为8 Hz的雷克子波,地震数据的最大记录时间为5 s,采样时间间隔为2 ms.图 9所示模型中存在强散射盐丘构造,致使大部分地震波能量很难透过盐丘体,携带盐下构造信息返回地表.此外,盐下构造的反射波至少需要往返两次穿过盐体,致使检波器接收到盐下构造的地震波响应信号较弱,使得盐丘底界面及其盐下精细构造成像精度不足.
|
图 9 盐丘模型 (a)真实盐丘速度模型;(b)偏移速度模型;(c)真实扰动模型. Fig. 9 Salt model (a) True salt velocity model; (b) Migration velocity model; (c) True perturbations model. |
图 10分别展示了RTM、LSRTM和PA-LSRTM的盐丘模型成像结果.从图 10a中可以看出,RTM成像结果浅部能量较强.这主要是因为基于波动方程的互相关成像条件受到震源的影响较为严重.与此同时,RTM成像结果在深部区域存在明显的成像不足等问题,这主要是因为地震波能量在传播过程中快速衰减,深部反射的地震信号较弱,很难获得高质量的成像结果.将图 10a、b对比发现,LSRTM成像结果很好地呈现出了盐丘速度模型的深部构造信息,使得整个盐丘模型从浅部到深部成像振幅更加均衡,盐丘构造的成像分辨率得到了较大的改善.将图 10a、b、c对比发现,PA-LSRTM方法在盐丘下部区域精细构造成像分辨率上有了较大提高.此外,PA-LSRTM方法通过增强相位权重法,减弱振幅影响,有效缓解了震源处的强能量对浅部区域成像的干扰,使得PA-LSRTM成像结果从浅层到深层振幅更加均衡.
|
图 10 盐丘模型成像结果 (a) RTM成像结果;(b) LSRTM成像结果;(c) PA-LSRTM成像结果. Fig. 10 Imaging results of the salt model (a) RTM result; (b) LSRTM result; (c) PA-LSRTM result. |
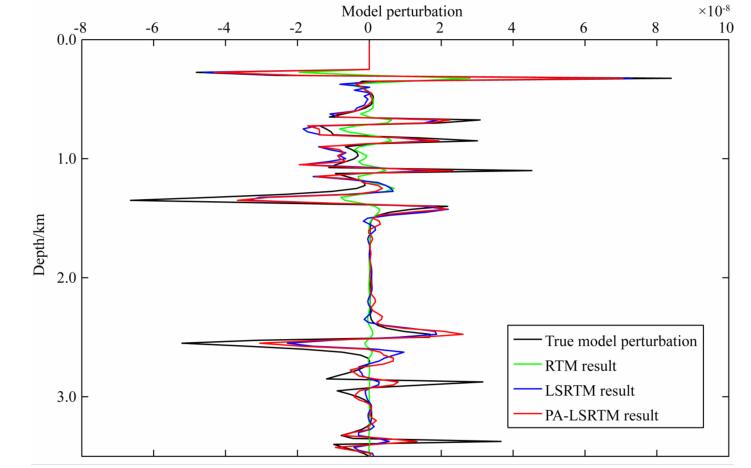
接着提取盐丘模型成像结果的局部放大图进行分析,如图 11和图 12所示.图 11是盐下构造成像结果左下侧的局部放大对比图,该区域主要是分析盐下精细构造的成像精度.根据图 11的对比结果可以看出,PA-LSRTM成像结果相比于RTM和LSRTM成像结果在盐丘的下界面及其盐下构造成像更接近真实扰动模型.图 12是盐丘模型右下侧的局部放大对比图,相比于RTM和LSRTM成像结果,可以看出PA-LSRTM成像结果在深部区域精细构造成像分辨率上有了很大的提高.图 13是单道成像剖面图,可以看出RTM成像振幅与真实扰动模型振幅相差较大,尤其是在深部区域,RTM几乎无法获得盐下深部构造信息.与RTM成像结果相比,LSRTM成像振幅有了较大的提高,但是在深部区域的成像振幅仍然与真实扰动模型有一定的差距.在深度为3 km处(图 13),PA-LSRTM成像振幅最接近真实扰动模型振幅.综合盐丘模型成像结果、局部放大对比图及其单道成像剖面对比图可以看出,PA-LSRTM方法在透过上覆强散射地质体(盐丘)对盐下构造成像方面具有一定优势.

|
图 11 盐丘模型成像结果局部放大图(图 10左下侧红色线框) (a)真实扰动模型;(b) RTM成像结果;(c) LSRTM成像结果;(d) PA-LSRTM成像结果. Fig. 11 Magnified view of salt model imaging results (red rectangular at lower left side in Fig. 10) (a) True perturbation model; (b) RTM result; (c) LSRTM result; (d) PA-LSRTM result. |

|
图 12 盐丘模型成像结果局部放大图(图 10右下侧红色线框) (a)真实扰动模型;(b) RTM成像结果;(c) LSRTM成像结果;(d) PA-LSRTM成像结果. Fig. 12 Magnified view of salt model imaging results (red rectangular at lower right side in Fig. 10) (a) True perturbation model; (b) RTM result; (c) LSRTM result; (d) PA-LSRTM result. |
|
图 13 单道成像剖面图(盐丘模型6.25 km处) Fig. 13 Single trace imaging profile (salt model at 6.25 km) |
地震数据中相位信息相比于振幅信息具有与地下介质更好的线性对应关系(Fichtner et al., 2008;Djebbi and Alkhalifah, 2014;胡勇等,2018),但是纯相位目标函数容易受到噪声的干扰,为此本文提出振幅相位联合的最小二乘逆时偏移成像方法(PA-LSRTM).为了测试该方法的抗噪性,在地震数据中加入了较强高斯噪声,含噪单炮记录如图 14所示,其中深部区域的弱散射信号几乎被噪声掩盖,这给深部区域成像带来了一定的困难.在负信噪比的情况下(SNR=-3.59),盐丘模型的PA-LSRTM成像结果如图 15所示.将图 15与图 10c对比可以发现,盐丘内部区域成像结果受到噪声影响较为严重,但依然能够很好地对盐丘边界及其盐下精细构造进行成像.这主要是因为振幅权重因子开始设定为ε=0.6,然后逐渐减小至ε=0.3,目标函数中的这一部分振幅信息很好地缓解了噪声相位对成像结果的干扰.因此,在PA-LSRTM目标函数中重新分配振幅和相位的占比,既能很好的利用相位信息对深部构造进行成像,同时还能在一定程度上缓解噪声相位对成像结果的干扰.从含强高斯噪声的测试结果中可以看出,PA-LSRTM适合针对深部区域、强散射构造、及其盐下构造进行精细成像,同时该方法还具有一定的抗噪性.

|
图 14 含噪扰动波场(信噪比SNR=-3.59) Fig. 14 Perturbation wavefield with Gaussian noise (SNR=-3.59) |

|
图 15 含噪PA-LSRTM成像结果 Fig. 15 PA-LSRTM result with Gaussian noise |
针对常规最小二乘逆时偏移盐下精细构造成像困难的问题,本文提出时频域振幅相位联合的最小二乘逆时偏移方法,结合理论分析和模型测试得出以下几点结论与认识:
(1) LSRTM方法很好地解决了RTM成像振幅不均衡的问题,同时大大提高了成像分辨率.但是由于LSRTM方法受振幅影响较为严重,因此很难获得盐下构造等深部区域的高精度成像结果.
(2) 时频域目标函数能够很好地分离了地震信号的振幅和相位信息,通过引入振幅权重因子,调节振幅和相位信息在目标函数中的权重,弱化振幅对成像结果的影响.在此基础上,PA-LSRTM方法很好地实现了深部弱地震信号的高精度成像.
(3) 纯相位目标函数容易受到噪声的干扰,本文通过在时频域目标函数中联合使用振幅和相位信息,在提高地下深部区域精细构造的成像质量的情况下,同时也保证了PA-LSRTM算法的抗噪性和稳定性.
最后,Marmousi模型和盐丘模型的数值测试结果表明,PA-LSRTM方法能够很好地利用弱地震信号的时频域振幅相位信息,实现透过上覆强散射地层获得深部构造高精度成像的目标.
附录A时频域目标函数对应的振幅谱和相位谱,可以通过Gabor时频变换获得,其中观测数据和模拟数据的Gabor变换为
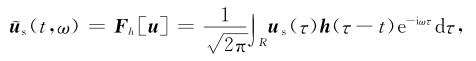
|
(A1) |
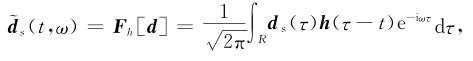
|
(A2) |
其中h(τ-t)表示高斯窗函数;t表示高斯窗函数对应的时间移动量;ω为角频率,us(t)和ds(t)分别表示模拟数据和观测数据;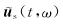
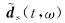

|
(A3) |
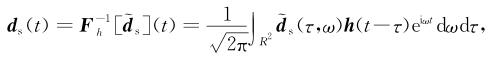
|
(A4) |
其中Fh-1[·]表示Gabor时频逆变换算子.
附录B根据波动方程的表达式,在计算扰动波场的过程中,Born正演模拟也可以用矩阵的形式来表示:
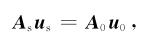
|
(B1) |
其中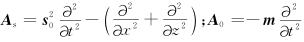
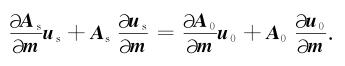
|
(B2) |
由于As和u0与模型参数无关,则式(B2)变为
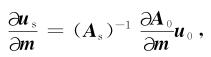
|
(B3) |
因此,LSRTM的目标函数相对于模型参数的偏导数可以表示为

|
(B4) |
其中Rs=us-ds表示伴随震源;ures=[(AsT)-1Rs]表示反传波场.伴随震源和反传波场满足关系:
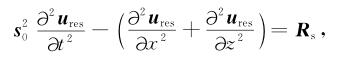
|
(B5) |
因此,LSRTM和PA-LSRTM目标函数对模型参数的梯度可以表示为正传波场与反传波场的零延迟互相关.
附录CPA-LSRTM目标函数是利用模拟数据的时频域振幅相位信息来不断地与观测数据的时频域振幅相位信息相匹配,则PA-LSRTM的目标函数可以定义为
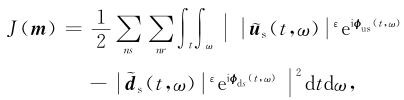
|
(C1) |
其中ω为角频率;
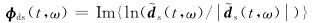
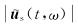
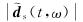
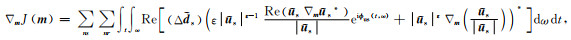
|
(C2) |
其中

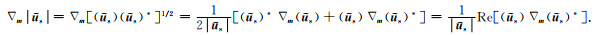
|
(C3) |
将式(C3)代入式(C2)中,则目标函数对模型参数的偏导数可以表示为

|
(C4) |
由于

|
(C5) |
将式(C5)代入式(C4)中,则目标函数对模型参数的梯度算子可以表示为
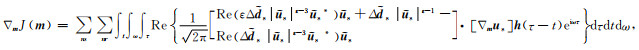
|
(C6) |
由于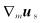

|
(C7) |
将式(A3)代入式(C7)中,目标函数对模型参数的梯度可以简化为

|
(C8) |
则伴随震源可以定义为
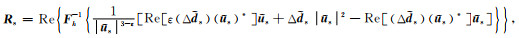
|
(C9) |
因此,PA-LSRTM目标函数对模型参数的梯度与LSRTM梯度计算方法相同,只需将伴随震源反传至模型空间获得的反传波场,并与正传波场做零延迟互相关.
附录D利用L-BFGS优化算法计算模型参数的更新方向,其迭代公式为

|
(D1) |
其中mk为第k步模型参数;αk为步长;Δm为模型参数的更新方向.关于LSRTM优化过程,实际上就是寻找目标函数最小值的过程.假设目标函数的起始点与最小值点在一个微小的邻域内,则LSRTM目标函数的最小值点存在如下关系:

|
(D2) |
舍去式(D2)中的高阶项:

|
(D3) |
当模型扰动量较小的情况下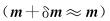
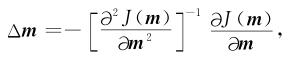
|
(D4) |
其中

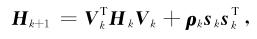
|
(D5) |

|
(D6) |

|
(D7) |
其中Hk+1是根据向量对{sk, yk}和Hk计算得到;Hkgk的乘积可以通过梯度gk与向量对{sk, yk}之间一系列向量的内积与向量的和来获得的.其中的近似Hessian矩阵的逆Hk需满足以下更新公式:
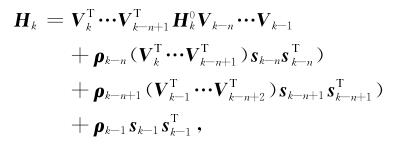
|
(D8) |
因此,在L-BFGS优化算法中只需要保存少数的向量对,即可获得Hessian矩阵逆的近似,大大提高了计算效率,同时很大程度上节约了计算机的内存.
Chen S C, Zhou H M. 2018. Least squares migration of seismic data with reflection wave equation. Chinese Journal of Geophysics (in Chinese), 61(4): 1413-1420. DOI:10.6038/cjg2018L0025 |
Claerbout J F. 1991. Earth Soundings Analysis:Processing Versus Inversion. Stanford: Stanford University.
|
Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration. Geophysical Prospecting, 60(4): 681-695. |
Dai W, Schuster G T. 2013. Plane-wave least-squares reverse-time migration. Geophysics, 78(4). |
Djebbi R, Alkhalifah T. 2014. Traveltime sensitivity kernels for wave equation tomography using the unwrapped phase. Geophysical Journal International, 197(2): 975-986. |
Dou H, Xu Y H. 2019. Progress in the Q-compensated reverse time migration imaging. Progress in Geophysics (in Chinese), 34(5): 1866-1877. DOI:10.6038/pg2019CC0279 |
Fang X Z, Niu F L, Wu D. 2018. Least-squares reverse-time migration enhanced with the inverse scattering imaging condition. Chinese Journal of Geophysics (in Chinese), 61(9): 3770-3782. DOI:10.6038/cjg2018L0721 |
Fichtner A, Kennett B L N, Igel H, et al. 2008. Theoretical background for continental-and global-scale full-waveform inversion in the time-frequency domain. Geophysical Journal International, 175(2): 665-685. |
Gong X B, Wang S C, Han L G. 2019. Sparse least-squares reverse time migration of small scatters in seismic exploration. Chinese Journal of Geophysics (in Chinese), 62(10): 4028-4038. DOI:10.6038/cjg2019M0420 |
Hu Y, Han L G, Yu J L, et al. 2018. Time-frequency domain multi-scale full waveform inversion based on adaptive non-stationary phase correction. Chinese Journal of Geophysics (in Chinese), 61(7): 2969-2988. DOI:10.6038/cjg2018L0421 |
Huang J P, Li C, Wang R R, et al. 2015. Plane-wave least-squares reverse time migration for rugged topography. Journal of Earth Science, 26(4): 471-480. |
Li C, Gao J H, Wang R R, et al. 2020. Enhancing subsurface scatters using reflection-damped plane-wave least-squares reverse time migration. IEEE Geoscience and Remote Sensing Letters, 17(4): 706-710. |
Li Q Y, Huang J P, Li Z C, et al. 2016. Mean-residual normalized cross-correlation least-squares reverse time migration and its application. Chinese Journal of Geophysics (in Chinese), 59(8): 3006-3015. DOI:10.6038/cjg20160823 |
Liu Q C, L u, Y M, Hui S, et al. 2020. Single-step data-domain least-squares reverse-time migration using Gabor deconvolution for subsalt imaging. IEEE Geoscience and Remote Sensing Letters, 17(1): 13-16. |
Liu X J, Liu Y K. 2016. Least-squares reverse-time migration of surface-related multiples. Chinese Journal of Geophysics (in Chinese), 59(9): 3354-3365. DOI:10.6038/cjg20160919 |
Liu X J, Liu Y K, Lu H Y, et al. 2017. Prestack correlative least-squares reverse time migration. Geophysics, 82(2): S159-S172. |
Liu Y J, Li Z C. 2015. Least-squares reverse-time migration with extended imaging condition. Chinese Journal of Geophysics (in Chinese), 58(10): 3771-3782. DOI:10.6038/cjg20151027 |
Liu Y S, Teng J W, Xu T, et al. 2016. An efficient step-length formula for correlative least-squares reverse time migration. Geophysics, 81(4): S221-S238. |
Ma F Z, Guo S J, Wang J. 2016. Least squares migration imaging method and its application. Progress in Geophysics (in Chinese), 31(2): 741-747. DOI:10.6038/pg20160232 |
Nemeth T, Wu C, Schuster G T. 1999. Least-squares migration of incomplete reflection data. Geophysics, 64(1): 208-221. |
Qin N, Wang Y G, Yang X D, et al. 2015. Gaussian beam reverse time migration and application. Progress in Geophysics (in Chinese), 30(2): 658-663. DOI:10.6038/pg20150224 |
Ren H R, Huang G H, Wang H Z, et al. 2013. A research on the Hessian operator in seismic inversion imaging. Chinese Journal of Geophysics (in Chinese), 56(7): 2429-2436. DOI:10.6038/cjg20130728 |
Sun H, Gao C, Zhang Z, et al. 2020. High-resolution anisotropic prestack Kirchhoff dynamic focused beam migration. IEEE Sensors Journal, 20(20): 11753-11760. DOI:10.1109/JSEN.2019.2933200 |
Sun J, Zhang Y. 2009. Practical issues of reverse time migration:True-amplitude gathers, noise removal and harmonic-source encoding. ASEG Extended Abstracts, (1): 1-5. |
Tan S R, Huang L J. 2014. Least-squares reverse-time migration with a wavefield-separation imaging condition and updated source wavefields. Geophysics, 79(5): S195-S205. |
Tian K, Yu H C, Zhang X T, et al. 2018. Sparse constrained multi-source least-squares reverse-time migration using Seislet transform. Progress in Geophysics (in Chinese), 33(3): 1142-1148. DOI:10.6038/pg2018BB0192 |
Yi J, Liu Y K, Yang Z Q, et al. 2019. A least-squares correlation-based full traveltime inversion for shallow subsurface velocity reconstruction. Geophysics, 84(4): R613-R624. |
You J, Liu X, Wu R S. 2017. First-Order Acoustic Wave Equation Reverse Time Migration Based on the Dual-Sensor Seismic Acquisition System. Pure and Applied Geophysics, 174(3): 1345-1360. DOI:10.1007/s00024-017-1468-3 |
You J, Liu Z, Liu J, et al. 2019. One-way propagators based on matrix multiplication in arbitrarily lateral varying media with GPU implementation. Computers & Geosciences, 130(SEP.): 32-42. DOI:10.1016/j.cageo.2019.05.010 |
Zhang Y, Duan L, Xie Y. 2015. A stable and practical implementation of least-squares reverse time migration. Geophysics, 80(1): V23-V31. |
Zhou D H, Qu Y M, Li Z C, et al. 2020. Multisource least-squares reverse time migration for irregular surface. Progress in Geophysics (in Chinese), 35(4): 1528-1538. DOI:10.6038/pg2020DD0217 |
陈生昌, 周华敏. 2018. 地震数据的反射波动方程最小二乘偏移. 地球物理学报, 61(4): 1413-1420. DOI:10.6038/cjg2018L0025 |
豆辉, 徐逸鹤. 2019. 黏性逆时偏移成像研究进展. 地球物理学进展, 34(5): 1866-1877. DOI:10.6038/pg2019CC0279 |
方修政, 钮凤林, 吴迪. 2018. 基于逆散射成像条件的最小二乘逆时偏移. 地球物理学报, 61(9): 3770-3782. DOI:10.6038/cjg2018L0721 |
巩向博, 王升超, 韩立国. 2019. 小尺度散射体稀疏最小二乘逆时偏移方法研究. 地球物理学报, 62(10): 4028-4038. DOI:10.6038/cjg2019M0420 |
胡勇, 韩立国, 于江龙, 等. 2018. 基于自适应非稳态相位校正的时频域多尺度全波形反演. 地球物理学报, 61(7): 2969-2988. DOI:10.6038/cjg2018L0421 |
李庆洋, 黄建平, 李振春, 等. 2016. 去均值归一化互相关最小二乘逆时偏移及其应用. 地球物理学报, 59(8): 3006-3015. DOI:10.6038/cjg20160823 |
刘学建, 刘伊克. 2016. 表面多次波最小二乘逆时偏移成像. 地球物理学报, 59(9): 3354-3365. DOI:10.6038/cjg20160919 |
刘玉金, 李振春. 2015. 扩展成像条件下的最小二乘逆时偏移. 地球物理学报, 58(10): 3771-3782. DOI:10.6038/cjg20151027 |
马方正, 郭书娟, 王杰. 2016. 最小二乘偏移成像方法及应用. 地球物理学进展, 31(2): 741-747. DOI:10.6038/pg20160232 |
秦宁, 王延光, 杨晓东, 等. 2015. 高斯束逆时偏移方法及应用. 地球物理学进展, 30(2): 658-663. DOI:10.6038/pg20150224 |
任浩然, 黄光辉, 王华忠, 等. 2013. 地震反演成像中的Hessian算子研究. 地球物理学报, 56(7): 2429-2436. DOI:10.6038/cjg20130728 |
田坤, 于海铖, 张学涛, 等. 2018. 基于Seislet变换的稀疏约束多震源最小二乘逆时偏移. 地球物理学进展, 33(3): 1142-1148. DOI:10.6038/pg2018BB0192 |
周东红, 曲英铭, 李振春, 等. 2020. 起伏地表条件下的混叠数据最小二乘逆时偏移. 地球物理学进展, 35(4): 1528-1538. DOI:10.6038/pg2020DD0217 |
 2021, Vol. 64
2021, Vol. 64


