0 引言

陆上地震数据采集时，受野外工区勘探环境(某些难以逾越的障碍物如道路、桥梁、建筑等)、复杂地表条件(如河湖、山谷等)以及禁采区会导致检波器的布置是不规则分布且有缺失的；此外，有的检波器与地表耦合情况不佳或者检波器不工作时会出现废道，导致地震数据的随机缺失；海上地震数据采集时，洋流的作用使拖缆出现羽状漂移，使检波器偏离原本设计的规则网格位置.不规则且缺失的地震数据，会影响后续多道处理技术的效果：对叠加技术而言，每个面元内数据进行叠加时会改变某些道的振幅和相位，同时不规则采样会导致共中心点覆盖次数不均, 最终影响CMP叠加效果；对波动方程偏移技术而言，空间不规则缺失采样会引起空间假频, 影响波动方程偏移成像的精度；对时移地震技术而言，先后采集的地震数据观测系统很难保持完全一致，为了使不同时期的地震资料具有可比性, 需要对数据进行规则化处理保证反射面元的一致性.因此, 不规则地震数据重建技术成为数据处理流程中的重要一环.

自20世纪80年代以来，国内外地球物理界的学者们针对该问题提出了多种地震数据重建方法，概括起来主要分为四大类.第一类是利用数学变换将时空域地震数据变换到其他稀疏域，或者是将数学变换与稀疏反演相结合的重建方法，如Fourier变换(Duijndam and Schonewille, 1999; 刘喜武等, 2004；Gao et al., 2011; Naghizadeh and Innanen, 2011)、Curvelet变换(Naghizadeh and Sacchi, 2010; 刘国昌等, 2011; Zhang et al., 2015; 王本锋等, 2015；吴蔚等，2016)和Radon变换(Landa et al., 1987; Sacchi and Ulrych, 1995; Kabir and Marfurt, 1999; 黄新武等, 2003; 王维红等，2007; 石颖等，2014；薛亚茹等, 2014; 王亮亮等, 2017)，这些基于数学变换理论的重建方法，对地震数据的要求较少，不需要准确的地质速度及构造信息.这类方法的缺点是对于含假频数据重建效果不佳，且对3D不规则地震数据，其重建效率较低.第二类是基于矩阵降秩的重建方法(Cadzow, 1988; Oropeza and Sacchi, 2011; Gao et al., 2011, 2013; Jia et al., 2016)，这种重建方法是假设缺道数据会增加矩阵或者张量的秩，将缺失地震数据构建为Hankel矩阵，通过对Hankel矩阵降秩来实现数据重建，这类方法的不足之处是一方面需要构建大型Hankel矩阵，运算量大，二是在矩阵分解过程中截断误差不容易预测.第三类是基于波动方程的重建方法(Ronen, 1987; Fomel, 2003; Malcolm et al., 2005)，它充分利用地下介质的速度信息，能够对缺失数据进行准确的振幅和相位重建.但是实际上地下介质的速度信息是不精确的，会严重影响其重建精度，同时，基于波动方程重建方法的计算量巨大，难以满足工业生产的需求.第四类是近年来发展起来的基于机器学习的重建理论(Jia and Ma, 2017; Mikhailiuk and Faul, 2018)，该理论完全基于数据驱动，自动挖掘数据内部特征和相关性，不依赖于各种近似以及地下介质信息的特征.由于受到训练样本多样性及计算效率的限制，目前还没有在工业上得到广泛应用.因此，快速而稳定的3D不规则地震数据保幅重建方法是石油工业生产中急需解决的问题.

在3D不规则采样中，地震数据规则化和插值, 都可以称为地震数据重建，前者解决的是数据的道数不变但位置进行了规则化问题；后者解决的是对空缺道进行插值，数据的道数增加且位置也进行规则化问题，后者是本文的研究目标.自Hampson首次提出使用抛物Radon变换对部分NMO后数据进行积分变换后，由于Radon变换简单易实现的特征，近三十多年Radon变换在地震数据重建应用中得到不断的改进和发展，Kabir等提出基于迭代抛物Radon变换的重建方法(Kabir and Verschuur, 1995)，该方法对近偏移距缺失数据能够进行有效重建；Sacchi等提出频率域高分辨率抛物Radon变换地震道重建方法(Sacchi and Ulrych, 1995)，该方法可以得到比传统Radon变换更高的重建精度；刘喜武等(2004)将最小二乘反演方法引入到Radon变换的研究中，使计算效率得到进一步提高；王维红等(2007)提出加权抛物线Radon变换重构方法，提高了重建数据的分辨率和精度；Zhang等(2013)提出了一个新的高分辨率3D tau-p变换，将线性Radon变换从二维推广到了三维；高阶抛物Radon变换(HOPRT)理论(薛亚茹等, 2008, 2014; 唐欢欢和毛伟建, 2014; 王亮亮等，2017；唐欢欢等，2018)，是在传统抛物Radon变换基础上引入了正交多项式变换，增加了振幅随偏移距变化的相关参数，在地震数据重建时具有更强的保幅能力.这些基于Radon变换的重建方法分别在重建精度及效率方面得到了改进和提高，但都是针对规则的2D数据和3D数据，不适用于不规则采样且缺失的地震数据重建.

因此，本文将基于保幅特性的非均匀高阶抛物Radon变换(NHOPRT)理论，利用Delaunay三角网格剖分计算不规则采样点的权值，通过最小二乘反演出不规则数据的高阶Radon域系数，对得到的高阶Radon域系数进行规则高阶Radon反变换即可得到重建后的规则数据.同时，利用频率域3D高阶抛物Radon变换算子为指数函数，具有线性可分解特性，将二维空间的变换算子分解为两个独立的一维空间变换算子，减小变换算子的矩阵大小，从而提高计算效率.该方法解决了基于抛物Radon变换理论的3D不规则地震数据重建问题，具有良好的保幅性，规则化后数据同相轴更连续，分辨率更高，且计算效率能够满足工业生产需求.

1 方法原理 1.1 基于高阶抛物Radon变换2D不规则地震数据重建原理

二维规则高阶抛物Radon正变换的离散公式为

(1)

公式中m表示高阶抛物Radon域系数，d是时空域2D地震数据，q_x为曲率参数，P_j为第j阶正交多项式，本文中正交多项式最高阶数为2，N为检波点个数，Δx为采样间隔.

在不规则采样条件下，公式(1)可表示为

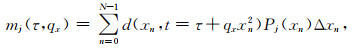
(2)

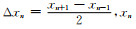
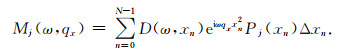
其中，为不规则采样点位置，我们将公式(2)定义为不规则离散高阶抛物Radon正变换，对该公式时间方向做FFT变换，得到频率不规则离散高阶抛物Radon正变换为

(3)

由于Radon变换的正反变换算子不具备互逆性，在求解Radon域系数时一般从Radon反变换公式出发，通过反演的方法求取.由正变换公式可以定义频率域不规则离散高阶抛物Radon反变换为

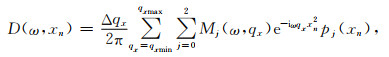
(4)

其中的Δq_x的值在选取时应足够小以避免产生假频，为表述简介，公式(4)可以写成向量形式：

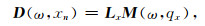
(5)

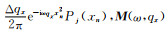
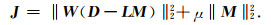
其中，D(ω, x_n)为频率域不规则地震数据，L_x= 为高阶抛物Radon域系数.公式(5)中D和L是已知量，M为待求的模型向量，显然，这是一个经典的线性反演问题，本文通过建立目标函数来求取M：

(6)

在由不完整数据D恢复出完整数据的高阶抛物Radon系数M时，这是个不适定问题, 需要引入规则化系数.在2D数据重建中，本文引入一种基于采样点之间距离的加权函数W使不规则缺失数据在高阶抛物Radon域的能量更为集中，W为对角矩阵，对应的元素值为W_ii=Δx_i，本文采用最小二乘法对公式(6)进行求解，M的最小二乘解为

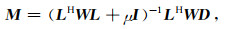
(7)

其中，μ为阻尼因子，取值一般为对角线元素的1%.公式(7)中矩阵的求逆运算，本文通过SVD分解来求取，可以得到快速且稳定的解.

得到完整数据的高阶抛物Radon系数M后，再通过规则高阶抛物Radon反变换算子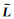来计算重建后规则数据，公式为

(8)

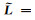
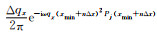
其中，规则的高阶抛物Radon反变换算子，这里Δx为数据重建后规则化的道间距，一般在设计观测系统时已确定；n的取值为(x_max－x_min)/Δx，x_min、x_max分别为最小偏移距和最大偏移距.

1.2 基于高阶抛物Radon变换3D不规则地震数据重建原理

在2D不规则高阶抛物Radon正变换公式的基础上，推导出3D不规则高阶抛物Radon正变换的公式为

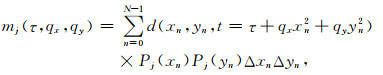
(9)

公式中m表示高阶抛物Radon域系数；d是时空域3D地震数据；q_x和q_y为曲率参数，P_j为第j阶正交多项式，分为x、y两个方向，本文中正交多项式最高阶数为2；N为3D数据的检波点个数；Δx和Δy分别为inline方向和crossline方向的采样间隔，由于3D不规则采样，Δx和Δy不易计算，本文将其记为Δs_n=Δx_nΔy_n，ΔS_n是采样点(x_n, y_n)分配的面积，该参数的计算将在下文详细讨论.

同样地，不规则3D高阶抛物Radon变换域系数的求取，也从Radon反变换公式出发，3D频率域不规则离散高阶抛物Radon反变换为

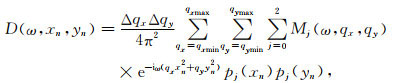
(10)

为表述简洁，将公式(10)写成向量形式：

(11)

其中，D(ω, x_n, y_n)为频率域3D不规则地震数据，L_{x, y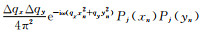}= 为3D不规则高阶抛物Radon反变换算子，M(ω, q_x, q_y)为高阶抛物Radon域系数.

比较公式(5)和(11)可以看出，2D和3D不规则高阶抛物Radon反变换的向量形式一致，但3D变换的计算量明显增大：除了输入数据量成倍增加外，变换算子L_{x, y}的规模不仅与输入数据的道数N相关，还与曲率参数q_x、q_y的采样个数n_qx、n_qy以及正交多项式的阶数相关，在正交多项式阶数为2的情况下，L_{x, y}的大小为[N, 9n_qx·n_qy]，在用最小二乘反演求解M(ω, q_x, q_y)时，关于L_{x, y}的求逆运算将会十分耗时.因此，本文利用L_{x, y}变换算子中的指数函数e^{－iω(q_xx_n2+q_yy_n2)}线性可分解性，将其分解为e^{－iωq_xx_n2}·e^{－iωq_yy_n2}，算子L_{x, y}可改写为

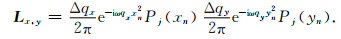
(12)

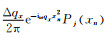
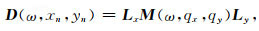
我们将公式(12)中的记为L_x，其大小为[N, 3n_qx]；记为L_y，其大小为[3n_qy, N]，将L_x和L_y代入公式(11)可得到：

(13)

公式(13)中M的最小二乘解为

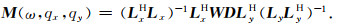
(14)

通过公式(14)可知，未分解前L_{x, y}直接参与运算，待求逆矩阵的大小为[9n_qx·n_qy, 9n_qx·n_qy]，当n_qx、n_qy的取值超过一百时，该矩阵规模将十分庞大，不仅会导致求逆运算不稳定而且非常耗时；分解为L_x和L_y后，待求逆矩阵的大小分别为[3n_qx, 3n_qx]和[3n_qy, 3n_qy]，与[9n_qx·n_qy, 9n_qx·n_qy]相比，其规模成百倍减小，求解的稳定性和效率都得到极大提高.

公式(14)中的权重W是对角矩阵，其对角线上的元素与采样点周围分配的各个三角形面积相关：

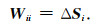
(15)

本文通过Delaunay三角形剖分(刘锋涛和凡友华, 2008; 刘国峰等, 2005)来计算ΔS_i，Delaunay三角形网格剖分是目前最常用的全自动网格生成方法，可以将二维空间中随机分布的采样点划分为最佳的三角形网格且给出每个三角形的相邻信息.每个采样点的权重ΔS_i计算方法为：根据Delaunay三角形网格剖分给出的每个三角形的相邻信息，找出以该采样点为顶点的所有三角形(假设有k个)，则权重ΔS_i的计算公式为

(16)

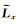
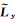
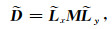
将各参数代入公式(14)计算得到高阶抛物Radon系数M后，再通过规则高阶抛物Radon反变换算子和得到重建后规则数据，公式为

(17)

其中，规则高阶抛物Radon反变换算子

这里Δx和Δy为数据重建后规则化的道间距，一般在设计观测系统时已确定；n_x的取值为(x_max－x_min)/Δx，x_min、x_max分别为x方向最小偏移距和最大偏移距；n_y的取值为(y_max－y_min)/Δy，y_min、y_max分别为y方向最小偏移距和最大偏移距.

根据3D不规则高阶抛物Radon变换原理以及相关参数计算方法，3D不规则地震数据的重建流程如下：

(1) 将t－x－y域的3D不规则地震数据作时间方向的傅里叶变换到f－x－y；

(2) 计算每个频率成分x方向和y方向的不规则高阶抛物Radon变换算子L_x和L_y；

(3) 利用Delaunay三角剖分方法对不规则观测系统进行三角剖分，利用公式计算每个采样点的加权系数w；

(4) 利用公式M(ω, q_x, q_y)=(L_x^HL_x)^－1L_x^HWDL_y^H(L_yL_y^H)^－1反演出高阶抛物Radon域系数M；

(5) 计算每个频率成分x和y方向的规则高阶抛物Radon反变换算子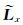和；

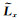
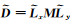
(6) 将步骤(4)中求解的高阶Radon域系数M，步骤(5)计算的和代入公式中，得到重建后频率域规则地震数据；

(7) 将步骤(6)中结果作傅里叶反变换，得到t－x－y域重建的3D规则地震数据.

不规则采样点的间距最大值为Δx_nmax，步骤(4)中矩阵L_x^HL_x的条件数与Δx_nmax存在关系为(Feichtinger et al., 1995)：

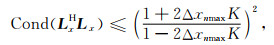
(18)

其中K为空间波数采样个数，由(18)式可知，Δx_nmax越大，矩阵L_x^HL_x的病态程度越大，难以得到适定解，对间隔太大的地震道重建时不能有效恢复，使重建效果变差.定义空间奈奎斯特采样间隔为Δx，根据Duijndam研究结果(Duijndam and Schonewille, 1999)，当Δx_nmax≥3Δx时矩阵L_x^HL_x无法保证求逆准确，该规则同样适用于y方向.因此，本文方法重建数据的有效空间间隔不大于max(3Δx, 3Δy).

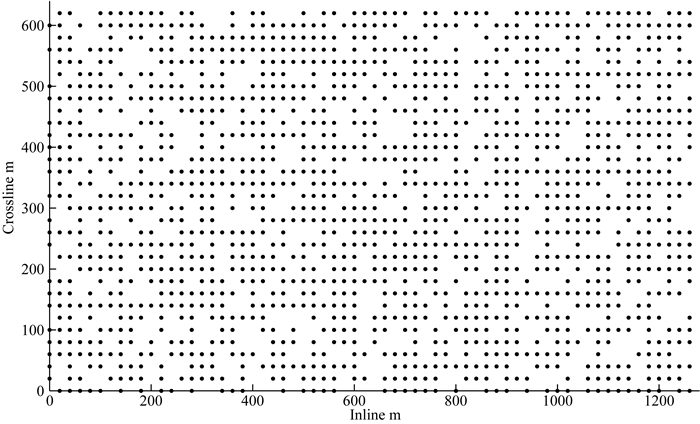
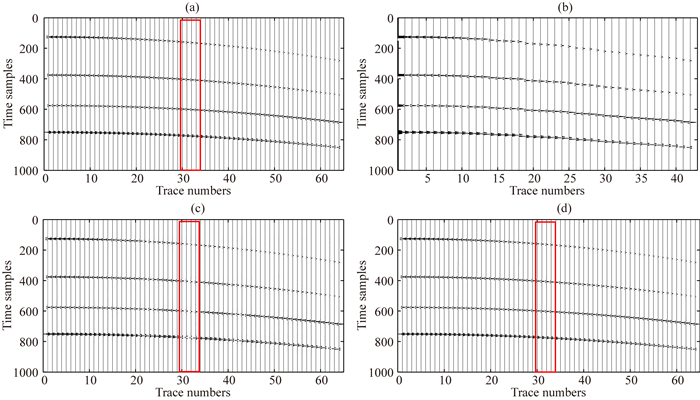
2 理论模型测试

为验证本文方法的有效性，正演了一个3D模型数据，共有32条测线，每条测线64道，线间距和道间距都为20 m，时间方向共有1000个采样点，时间间隔为4 ms.为了有效对比数据重建前后效果，将模型设计成规则采样后不规则缺失形式.如图 1所示，该图为3D不规则缺失数据的观测系统；图 2是规则重建方法和不规则重建方法效果对比图，其中图 2a为第一条测线原始数据；图 2b为第一条测线不规则缺失后数据(其中第[1, 7, 9, 11, 14, 16, 17, 21, 22, 23, 25, 30, 31, 32, 33, 40, 42, 43, 47, 49, 53, 62]道缺失，共22道)，不规则缺失后同相轴有明显的不连续性及抖动现象，图 2c为第一条测线用规则高阶Radon变换方法重建后的数据，图 2d为用本文3D NHOPRT方法重建后的数据，比较图 2c、d中红色方框标记位置可以看出，用规则重建方法，缺失数据的振幅不能够被完全恢复.

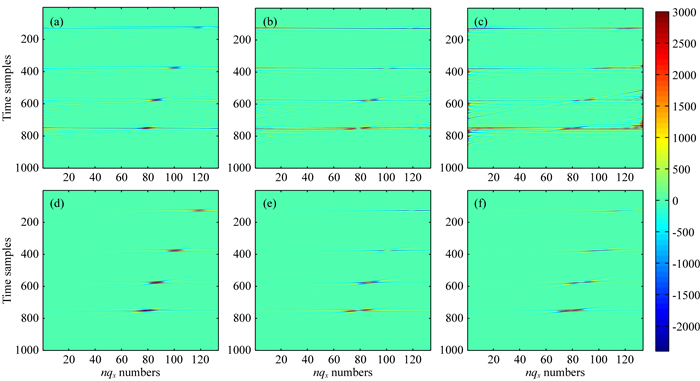
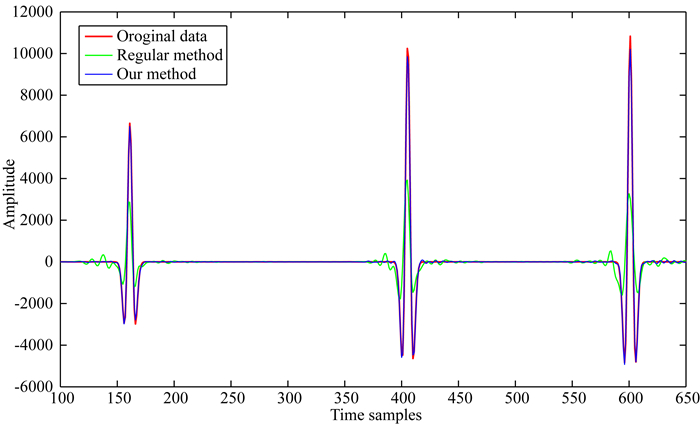
用规则高阶Radon变换方法重建时，在数据缺失位置补零形成空道使道集变为规则，计算高阶Radon域系数时由于空道的参与使Radon域系数扩散，能量不集中，如图 3a、b、c所示分别为0阶、1阶、2阶Radon系数；图 3d、e、f为不规则高阶Radon变换方法反演求取的0阶、1阶、2阶Radon系数.图中q_x和q_y的取值范围[0.05×10^－7, 2× 10^－7]，单位是s²·m^－2.从图 3可以看出，和规则方法相比，NHOPRT方法反演得到的Radon域能量明显集中，因此重建数据的振幅与原始数据更为接近，如图 4所示，红色曲线是第一条测线第31道原始数据，绿色是规则高阶Radon变换方法重建的第31道数据，蓝色是NHOPRT方法的重建结果，很明显，不规则方法重建数据的振幅和相位都与原始数据更为接近.本文用误差公式Err=Σ(d_i－来计算重建数据的误差，其中d_i为原始数据，为重建后数据，无噪模型数据缺失重建相对误差为2.28%，达到重建精度要求.

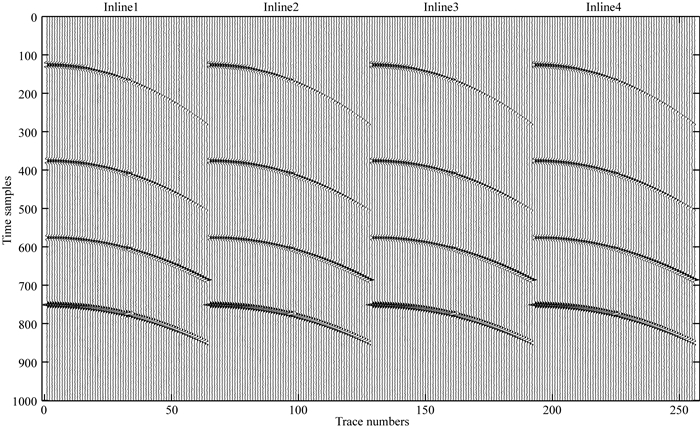
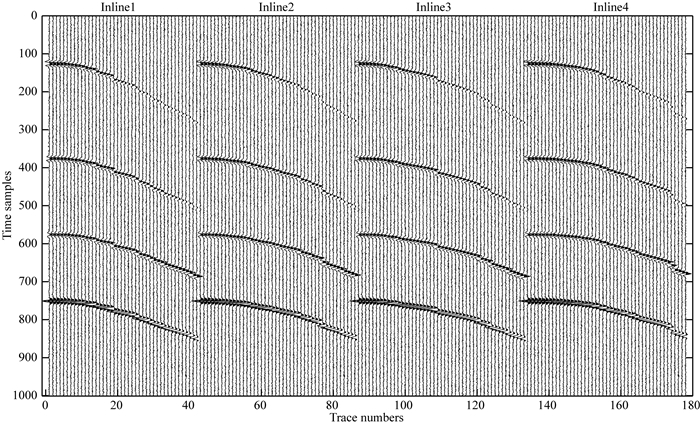
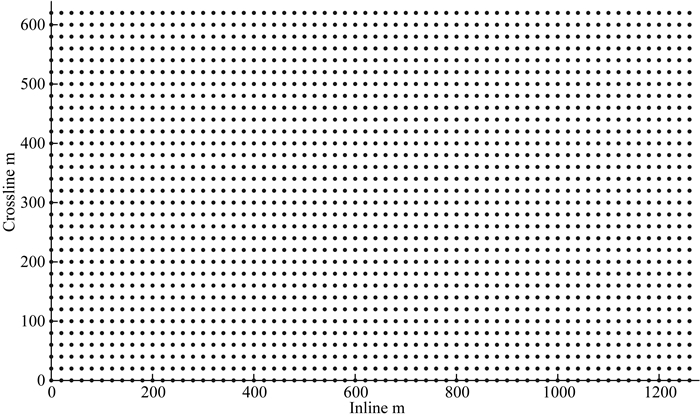
为验证本文方法的抗噪能力，在原始数据中加入了SNR=5的随机噪声，如图 5所示为inline1至inline4，4条测线不规则缺失后的含噪数据，同相轴不连续，有明显的抖动现象，图 6为用本文方法重建后inline1-inline4数据，重建后数据同相轴更为光滑，振幅连续性良好，随机噪声也有所减弱，含噪数据重建相对误差为3.84%，该方法同样适用于含噪数据的缺失重建；重建后数据的观测系统如图 7所示.通过本文NHOPRT方法对不规则采样且有缺失的数据重建后，缺失位置数据能够得到有效恢复且观测系统规则，有利于后续多道处理技术的进行.

在重建效率方面，该3D模型数据不规则缺失后大小为[1433, 1000]，其中1433为检波点个数，1000为每道地震数据的时间采样点个数，重建过程中两个方向的曲率采样个数为nq_x=nq_y=133，在Linux系统64G内存单个节点的计算环境下，用本文提出的将变换算子分解为L_x和L_y方法耗时276 s，而用未分解的变换算子L_{x, y}直接参与运算，耗时4826 s.很明显，将二维空间的高阶抛物Radon变换算子分解为两个独立的一维空间变换算子方法的计算效率得到了极大提高.

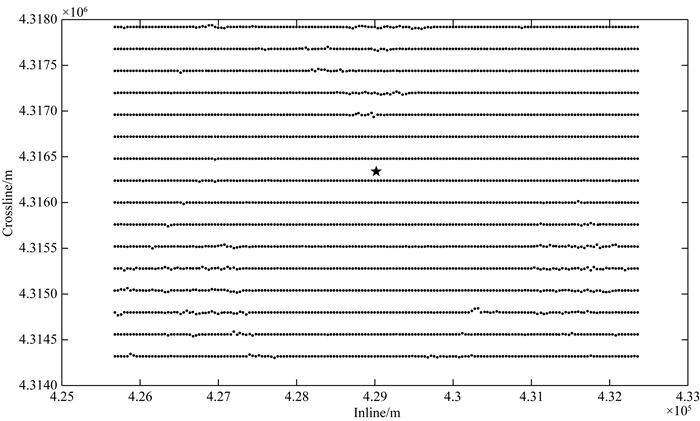
3 3D不规则实际地震数据重建试算

模型数据验证了本文方法的有效性，将该方法应用到某石油勘探区域的叠前3D不规则数据中，该工区采集前设计的观测系统是规则的，有16条测线，线间距为240 m，每条测线168道，道间距为40 m，时间方向采样间隔为2 ms, 共3001个时间采样点.在实际采集时，由于各种不可避免的原因，检波点是不完全规则分布的，特别是西南角检波点不规则排列很明显，如图 8所示，五角星位置是炮点，黑色点为检波点位置.

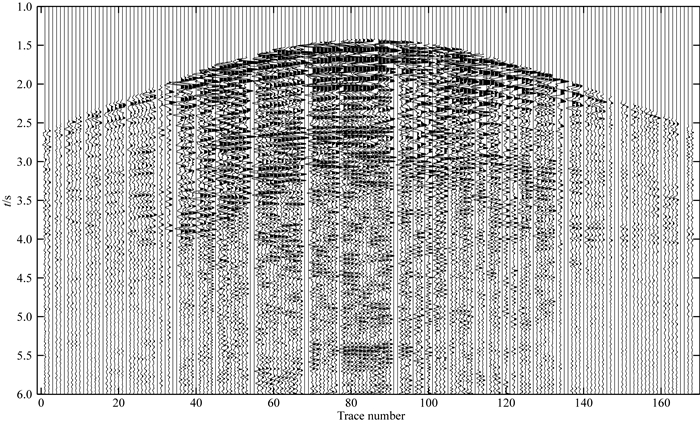
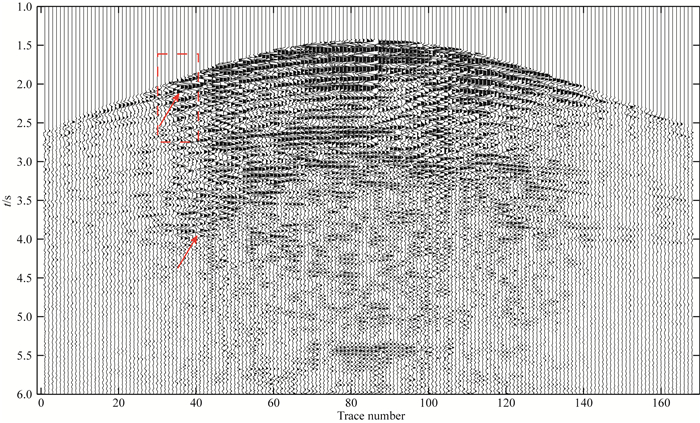
我们将该数据随机缺失20%，缺失后的观测系统如图 9所示，缺失后每条测线上检波点数量不同；图 10为第一条测线的缺失后的地震剖面，图 11为第一条测线用本文方法重建后的地震剖面，图 12为第一条测线无缺失原始数据，从图 11可以看出，缺失位置的数据得到恢复，与相邻位置同相轴的走向一致，振幅连续.

比较图 11和图 12中红色箭头标记位置的数据(对应观测系统中西南角检波点不规则排列部分)，可以看出重建且坐标规则化后的数据同相轴连续性更好，分辨率也有所提高；为更清晰地看出重建效果，将图 11和图 12中红色方框区域放大，如图 13所示，图 13a为原始数据，由于观测系统不规则的原因，同相轴的走向不清晰；图 13b为用本文NHOPRT方法规则化重建后结果，规则化后同相轴的连续性得到明显提高.

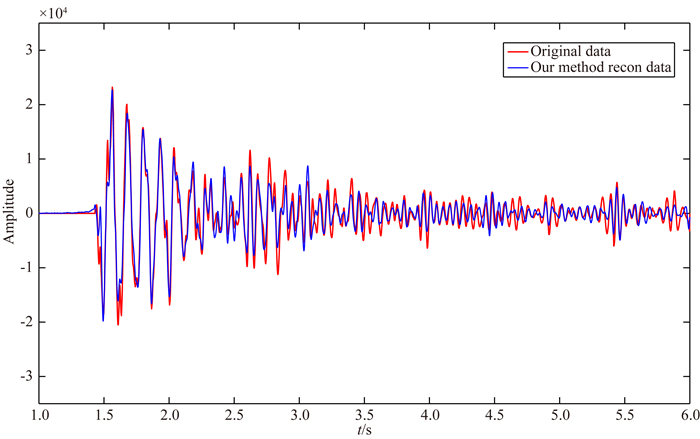
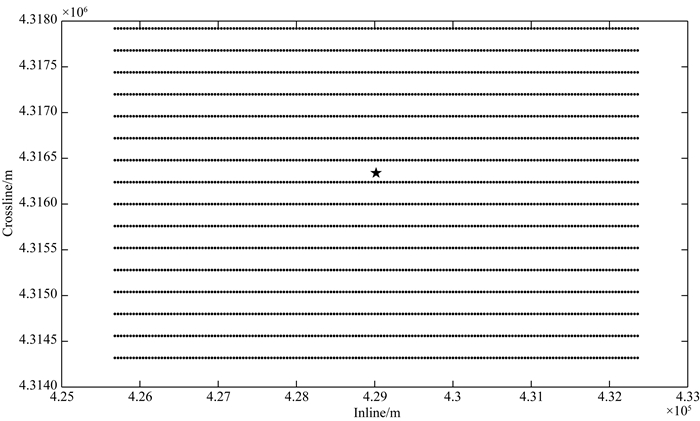
在检波点规则排列位置(对应于观测系统中间部分)，缺失数据的重建效果细节(振幅及相位信息)，如图 14所示，红色曲线为第一条测线中部的第77道原始数据，蓝色是本文方法重建数据，可以看出重建数据的振幅和相位都与原始数据高度一致，实际数据重建相对误差为4.97%.规则化的观测系统如图 15所示，与前期设计的规则观测系统一致.该单炮数据在Linux系统64G内存8个节点的环境下重建耗时419 s，在重建效果及效率上都能够满足工业生产的需求.

4 结论

本文研究了基于NHOPRT的3D不规则地震数据的规则化重建问题，将二维空间不规则高阶抛物Radon变换理论和Delaunay三角网格剖分相结合，通过最小二乘反演实现对3D不规则地震数据的保幅重建，同时利用高阶抛物Radon变换算子在频率域为指数函数，具有线性可分解特性，将二维空间的高阶抛物Radon变换算子分解为两个独立的一维变换算子，减小了变换矩阵的大小，从而提高了计算效率.理论模型和实际资料的重建结果验证了本文方法的正确性和有效性.不足之处是对于存在严重空间假频的地震数据, 本文重建方法需要进一步改进，从而实现抗假频重建；另外，采集到的实际3D数据不规则程度可能比本文测试数据的不规则程度更高，我们将在后续工作中进一步测试本文方法的应用效果.