2. 成都理工大学地球物理学院, 成都 610059
2. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
频率域电磁法是实际中使用最为广泛的一类电磁勘探方法之一,包括大地电磁法、可控源音频大地电磁法、海洋可控源电磁法和航空电磁法等,在地球深部结构探测、矿产油气资源勘探和工程探勘等领域中应用非常广泛.三维反演是定量解释的最终手段,提高反演的计算速度可有效提高方法的应用效果.在反演过程中,正演占用了大多数的计算时间,因此最终的落脚点在于如何提高正演的计算速度.在频率域电磁法的三维正演领域,近年来国内外的研究热点是矢量有限元法(Da Silva et al., 2012; Ren et al., 2013; Schwarzbach and Haber, 2013; 杨军等, 2015; Kordy et al., 2016; Yin et al., 2016; 刘颖等, 2017; 李勇等, 2017; 殷长春等, 2017).有限元法中使用的非结构化网格(四面体或形变六面体)具有很强的适应性,能够模拟复杂的异常体和地形,同时相对于有限差分法,有限元方法的精度也更高.
在三维正演中,主要的计算量集中在求解由偏微分方程离散得到的线性方程组上,其求解速度直接关系着三维正演的计算速度.目前常用的线性方程组求解算法分为两类,其中一类是直接解法.直接解法将原矩阵分解为下三角矩阵和上三角矩阵的乘积,通过两次回带即可获得线性方程组的解.直接解法具有非常高的的稳定性,对于一个线性方程组,如果其解存在,直接解法总能在有限的时间内获得其精确解.经过多年发展,直接解法的效率已得到大幅提升.基于已有的开源直接解法程序库,如MUMPS、PARDISO和SuperLU等,在程序实现中可以很方便的实现方程组的求解过程,同时直接解法的结果还可以作为参考解来验证迭代解法的求解精度.很多学者在频率域电磁法三维正演研究中使用了直接解法来求解线性方程组(Da Silva et al., 2012; Ren et al., 2013; Schwarzbach and Haber, 2013; Kordy et al., 2016; Yin et al., 2016; 刘颖等, 2017; 殷长春等, 2017).但是,直接解法需要存储原矩阵分解得到的上、下三角矩阵,分解过程计算量非常大,且存储分解结果需要大量存储空间.
迭代解法是求解线性方程组的另一类算法,它通过迭代过程中的不断修正来获得线性方程组的近似解.迭代解法仅需计算矩阵与向量的乘积或矩阵的转置与向量的乘积,其内存需求远小于直接解法.若使用了合适的迭代算法,则其计算量也要小于直接解法.在迭代算法中,预条件的使用对于提高迭代算法的收敛速度有至关重要的作用.由于由Maxwell方程组得到的线性方程组的条件数非常大,特别是在低频情况下,通用的预条件算法不能起到很好的加速效果,迭代算法在大多数的情况下不收敛或收敛不到需要的精度.国内外学者做了大量的工作来改进线性方程组迭代算法的效率,Um在三维电磁模拟中的使用了改进的ILU分解预条件(Um et al., 2013),Puzyrev等分别研究了基于代数多重网格预条件的并行有限元算法(Puzyrev et al., 2013)以及分块Krylov子空间迭代算法在多源问题中的应用(Puzyrev and Cela, 2015),这些工作取得了良好的效果,将原来需要数千次迭代才能收敛甚至不收敛的迭代算法优化至需要数百次至数十次即可收敛.但是,还存在一些待改进的地方.首先,基于ILU或代数多重网格的预条件的扩展性不强,其迭代次数会随着矩阵阶数的增大而快速增大.其次,频率较低时矩阵的条件数较大,迭代算法仍有可能不收敛.最后,在电磁场模拟过程中,为满足边界条件或提高计算精度,我们会使用不均匀网格或者局部加密的网格,这也会对迭代算法的性能产生很大影响.
针对上述问题,Hiptmair等提出了辅助空间预条件算法(Auxiliary space Maxwell Solver, AMS)(Hiptmair and Xu, 2007),该方法基于赫姆霍兹分解和代数多重网格方法,可大大加快使用有限方法求解Maxwell方程组时迭代算法的收敛速度.Chen等在求解时谐Maxwell方程组时将复系数线性方程组分解为实对称形式,构造了分块对角预条件,并结合辅助空间预条件取得了很好的效果(Chen et al., 2010).在地球电磁领域,Grayver等在基于六面体单元的三维大地电磁法有限元正演中也使用了上述方法(Grayver and Bürg, 2014; Grayver and Kolev, 2015).
基于上述学者的工作,本文研究了频率域电磁法三维正演中线性方程组的迭代求解算法.我们将由Maxwell方程组离散得到的复系数线性方程组转化为其实对称形式,使用迭代算法求解实对称形式,并通过构造分块对角预条件加快其收敛速度.在应用预条件时,需要求解两个较小的实数方程,通过共轭梯度解法和辅助空间预条件技术求解.通过一系列的数值算例对迭代算法的时间和空间效率进行了分析.与前人工作的不同之处在于,我们验证了分块对角预条件和辅助空间预条件算法在有源问题中的有效性,并同时针对四面体单元和六面体单元进行了试验,对其他学者的后续研究工作具有一定的借鉴意义.
1 三维矢量有限元正演算法 1.1 控制方程取时谐因子为eiωt,频率域电磁场应满足的方程为
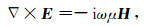
|
(1) |
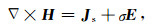
|
(2) |
其中ω是角频率,μ是真空中的磁导率,其值为4π×10-7,σ是地下介质的电导率,Js表示场源项.在常规频率域电磁法的实际应用中,我们通常只观测频率小于10000 Hz的响应,因此可以忽略位移电流.对(1)式两边求旋度,并将(2)式代入可得介质中电场所满足的二阶矢量亥姆霍兹方程:
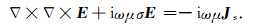
|
(3) |
有两种方法可以用来处理场源Js,一种是总场法,一种是二次场法(秦策等, 2017).在可控源电磁法的模拟中,一般使用二次场法来减弱由场源所带来的奇异性.但是在模型比较复杂,特别是存在地形时,二次场法中的背景模型很难选取,此时总场法的适应性更强.经综合考虑,本文使用总场法.实际上,由总场法和二次场法的区别仅在于所得线性方程组的右端项不同,在实现上并没有太大差异.
对于大地电磁法,可以令场源项为0,并在边界上施加第一类边界条件,即

|
(4) |
其中n是边界网格的外法向向量,E0是边界上一维介质的电场响应,可以通过解析法求得.
对于可控源电磁法,位于(x0, y0, z0)处的电偶极子场源可表示为
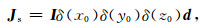
|
(5) |
其中I为电流,δ为狄拉克函数,d是场源的方向.若计算区域足够大,我们可以认为电磁场已充分衰减,则边界条件为
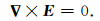
|
(6) |
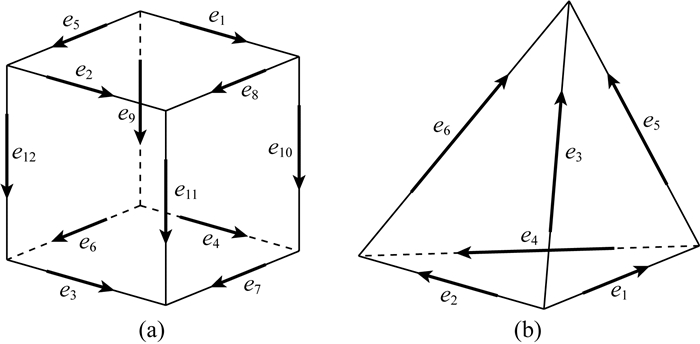
使用非结构化六面体网格或四面体网格对求解区域进行离散化.为满足电场的连续性条件,将形函数定义在网格的棱边上(Nédélec, 1986),如图 1所示,这就是所谓的矢量单元.在(3)式两边同时点乘矢量形函数V,并对全区域积分:
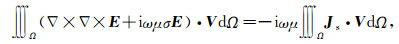
|
(7) |
|
图 1 矢量形函数定义 (a)六面体单元;(b)四面体单元. Fig. 1 Definition of vector shape function (a) Hexahedron element; (b) Tetrahedron element. |
其中V∈H(curl; Ω),H(curl; Ω)是希尔伯特空间上的旋度平方可积函数空间,其定义为
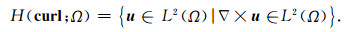
|
(8) |
根据矢量恒等式和分部积分原理,式(7)可转换为
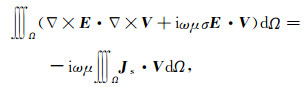
|
(9) |
式(9)即为与式(3)所等价的泛函形式.将式(9)在区域中的每个单元进行计算并求和,可得
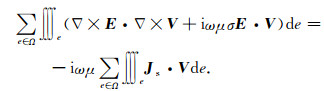
|
(10) |
各单元上的积分可以由解析方法或数值积分进行计算,最终可得如下线性方程组

|
(11) |
其中,K是系数矩阵,s是场源项,e是形函数的插值系数.
对于由式(5)表示的场源,右端项s仅在包含场源的单元内不为0,因为狄拉克函数的积分为1,s可表示为
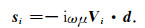
|
(12) |
求解式(11)可得每个棱边上的插值系数,则任意点处的电场值可由公式
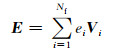
|
(13) |
计算,其中Nf是单元上形函数的个数,对于六面体单元和四面体单元,Nf分别是12和6.根据法拉第定律,任意点处的磁场可表示为
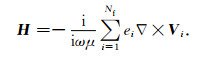
|
(14) |
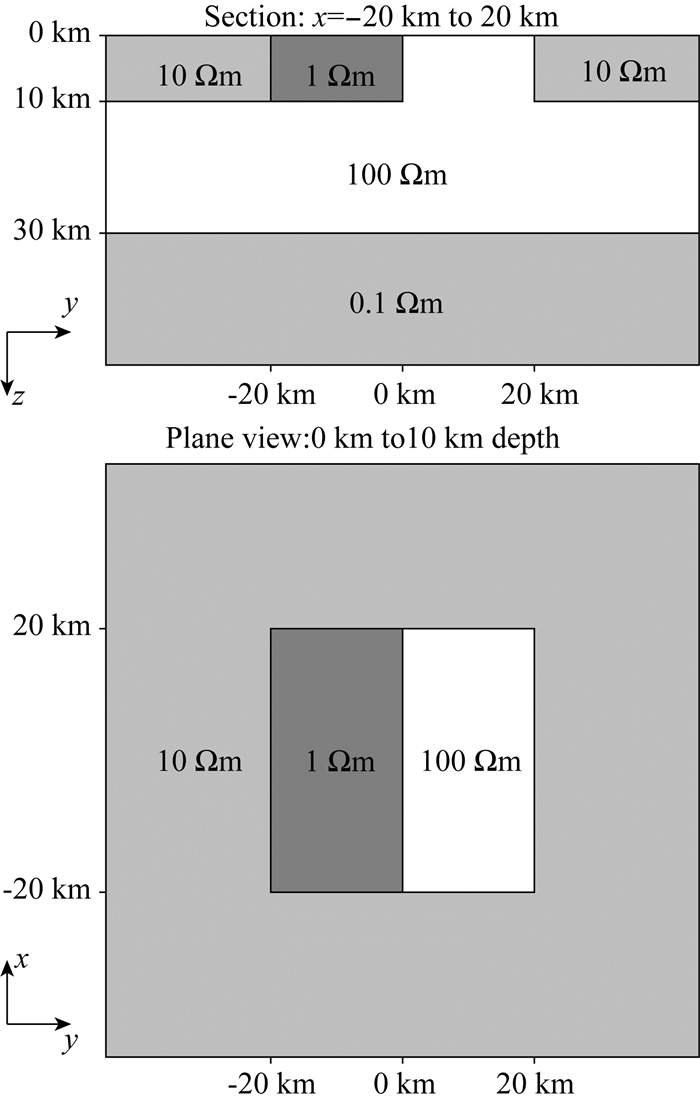
式(11)中的矩阵K是复系数稀疏矩阵,在三维问题中,K的阶数通常可达数百万至上千万.如前文所述,直接解法的计算量和内存需求很高,因此本文主要考虑迭代解法.在频率域电磁法的正演中,影响迭代算法性能的因素主要有两个:频率和网格的规模,接下来我们通过对COMMEMI 3D-2模型(Zhdanov et al., 1997)进行模拟分析这两个因素对迭代算法性能的影响.图 2是COMMEMI 3D-2模型示意图,有多个学者计算了该模型的响应(Ren et al., 2013; Grayver and Bürg, 2014).同时,该模型比较复杂,电阻率差异巨大,非常适合用来检验算法的精度和适应性.我们使用的计算平台配备了Intel Xeon E5 2680 V4 CPU,包含14个处理器核心,主频为2.4 GHz,内存为128 GB.
|
图 2 COMMEMI3D-2模型示意图 Fig. 2 Sketch of COMMEMI3D-2 model |
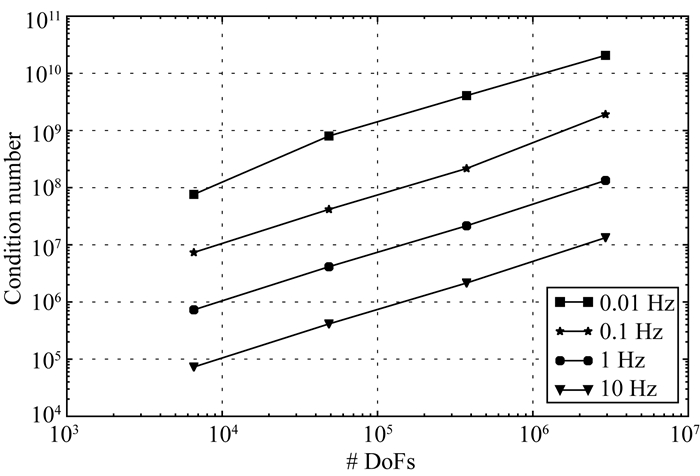
矩阵的条件数可以衡量线性方程组求解的难易程度,一般来说,条件数越低,方程组越容易求解,反之,条件数越高,方程组求解起来越困难.首先分析矩阵条件数随矩阵阶数和频率的变化规律.初始网格为12×12×13,矩阵阶数为6565,随后对网格进行3次全局加密.进行全局加密时,将每个单元在三个方向上都一分为二,因此每加密一次矩阵阶数约增大8倍.每次加密之后的矩阵阶数分别为48650、374164和2934056.使用了4个频率,分别是0.01、0.1、1.0 Hz和10.0 Hz.图 3展示了复系数线性方程组式(11)中矩阵K的条件数随着频率和矩阵阶数的变化规律.因为低频时方程的定解条件变弱,在图中表现为频率越低,矩阵的条件数越大.同时矩阵的阶数越大,矩阵的条件数越大.这意味着频率越低、矩阵阶数越大,使用迭代算法求解复系数线性方程组时迭代算法越难收敛.
|
图 3 复数矩阵条件数随频率和矩阵阶数变化趋势 Fig. 3 The trend of condition number of complex matrix with frequency and matrix order |
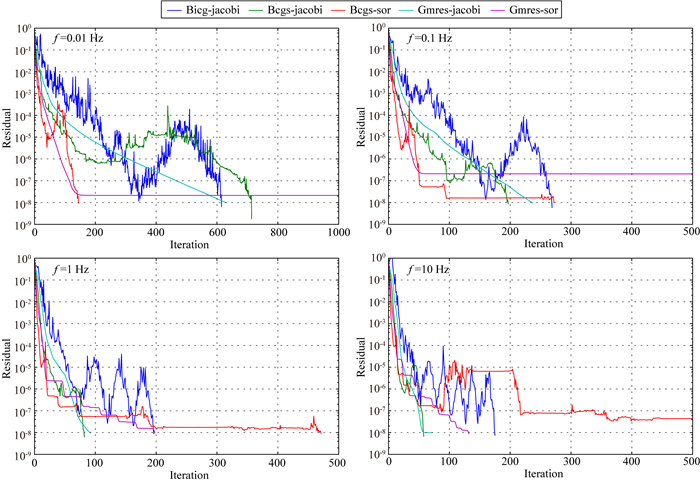
为验证这一结论,试验了常用的迭代算法和通用的预条件在求解复系数线性方程组时的性能.迭代算法包括BICG、BICGStab和GMRES,预条件包括SOR、Jacobi.图 4和图 5是迭代算法求解复系数线性方程组时的收敛过程.从图中可以看出,频率越低、矩阵阶数越大需要的迭代次数越多,结合前面对矩阵条件数的分析,这与对矩阵条件数进行分析所得出的结论是一致的.
|
图 4 常用迭代算法求解复系数线性方程组时收敛过程(矩阵阶数为6565) Fig. 4 Convergence process of commonly used iterative algorithms for solving complex coefficient linear equations (the matrix order is 6565) |
|
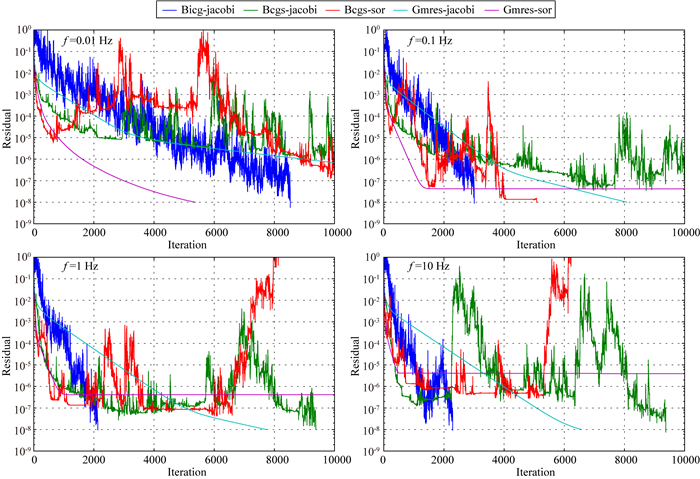
图 5 常用迭代算法求解复系数线性方程组时收敛过程(矩阵阶数为2934056) Fig. 5 Convergence process of commonly used iterative algorithms for solving complex coefficient linear equations (the matrix order is 2934056) |
需要指出的是,上述的几种迭代算法的收敛速度很不稳定.例如,在矩阵阶数为2934056时,GMRES几何SOR预条件在频率为0.01 Hz时可以收敛到10-8,而在频率为0.1、1 Hz和10 Hz时却无法收敛.总的来说,GMRES的迭代曲线比较平滑,但是所有算法均无法保证在任何情况下都能收敛.另外,随着矩阵阶数的增大,收敛到给定精度所需要的迭代次数也快速增大.
2.2 实对称形式和分块对角预条件通过前文的分析知道,常用的迭代算法和通用的预条件在求解复系数线性方程组时效率很低,不适用于大规模的三维问题.为解决这一问题,将式(11)分解为实数形式:
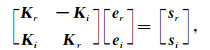
|
(15) |
同时为了保证其对称性,将上式中的第二行同时乘以-1,可得
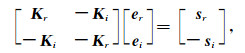
|
(16) |
式(16)中矩阵阶数为式(11)中矩阵阶数的2倍,与式(11)完全等价,它们的解相同.为方便起见,将式(16)中的矩阵记为A.对于式(16),可以构造分块对角矩阵:
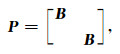
|
(17) |
其中B=Kr+Ki.因为Kr与Ki是对称正定矩阵,所以B是对称正定且可逆的.令κ表示矩阵P-1A的条件数,可以证明对于任意的频率、模型电阻率和矩阵阶数,满足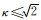
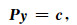
|
(18) |
其中c是任意向量.因为P是分块对角的,上式可以转换为求解两次如下方程:
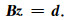
|
(19) |
与求解复系数线性方程组一样,也可以使用直接解法求解式(19),将矩阵B分解为上三角和下三角矩阵的乘积.对于同一个线性方程组,仅对B进行一次分解,应用预条件的过程中只需计算量小很多的后向和前向回带.因为复数占用的内存是实数的2倍,同时其运算也要慢于实数,因此和分解复数矩阵K相比,对实数矩阵B的分解要节约一半的内存空间,计算过程也要快得多.
如前文所述,在大规模三维正演模拟中,矩阵的阶数可能达到千万级别,直接解法的伸缩性(Scalability)仍然不足,即其计算时间和内存需求会随着矩阵阶数的增大而快速增大,需进一步研究伸缩性好的解法.矩阵B可以由

|
计算获得,其包含的零空间使得通用的预条件很难获得较好的收敛速度.我们使用辅助空间预条件解法来求解此线性方程组.辅助空间预条件基于离散赫姆霍兹分解的基本原理,即任何向量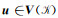
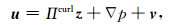
|
(20) |
其中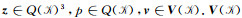
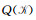
式(20)将向量u分解为无散度和无旋度的向量以及残差向量v之和.它表明,我们可以由多层次施瓦茨方法(Zhang, 1992; Smith et al., 2004)和辅助空间理论(Xu, 1996)来为矩阵B构造预条件.假设存在k个辅助空间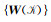
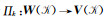

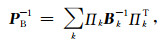
|
(21) |
其中, Bk=ΠkTBΠk.取Π1=R, Π2=G, Π3=I,上式可重写为
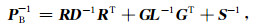
|
(22) |
其中, D=RTBR,L=GTBG.矩阵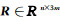
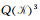
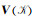
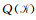
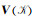
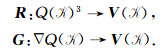
|
S是对称正定矩阵,它的作用是去除高频误差.
式(22)中包含了三个矩阵D、L和S的逆运算,计算量仍然很大.在应用预条件过程中,我们不需要计算矩阵PB的逆矩阵PB-1,只需计算PB-1与任意向量的乘积,可转化为计算D-1、L-1和S-1与向量的乘积.同时计算结果也不需要非常精确,因此可以使用近似方法来计算.其中,D-1、L-1和向量的乘积可由代数多重网格方法来快速完成.另外,矩阵S表示矩阵B的光滑算子,我们可以使用高斯-赛德尔迭代快速消除残差向量v中的离散误差和局部扰动分量,在实际计算中,通常可以在数次迭代内完成S-1与向量的乘积.综上,应用预条件PB-1的过程被简化为求三个矩阵的逆矩阵与向量的乘积,这些操作可以通过代数多重网格方法或高斯-赛德尔迭代快速完成.
实现辅助空间预条件算法是非常困难的,幸运的是,目前已经有开源程序库HYPRE(Falgout and Yang, 2002; Kolev and Vassilevski, 2009)提供了辅助空间预条件算法.HYPRE是由美国能源部下属的Lawrence Livermore实验室开发的开源程序库,实现了各类线性方程组求解算法和预条件.在程序中调用HYPRE所实现的辅助空间预条件函数,HYPRE提供的接口非常简洁,对于一阶棱边单元,只需提供矩阵B、G以及网格中每个结点的坐标,更多细节请参考HYPRE的文档(https://computing.llnl.gov/sites/default/files/public/hypre-2.11.2_usr_manual.pdf, P46).使用共轭梯度法来求解式(19),通过使用辅助空间预条件,CG法可以在很少的迭代内收敛.
2.3 算法效率分析本节仍使用COMMEMI 3D-2模型作为例子分析本文所使用算法的效率.使用相对误差
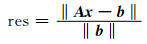
|
控制算法的运行过程,迭代解法的终止条件是相对误差小于给定tol.求解式(16)时,取tol为10-8.不需要式(19)的精确解,因此在求解式(19)时取tol为10-2.表 1展示了计算过程中求解线性方程组时迭代算法的迭代次数,其中Niter是求解式(16)时FGMRES的迭代次数,NiterCG是求解式(19)时CG方法的平均迭代次数.为测试算法的适应性,也针对不同频率和矩阵阶数进行了试验.可以看到,对于所有频率和不同的矩阵阶数,FGMRES都可以在20次迭代内收敛,且迭代次数基本不随频率减小和矩阵阶数的增大而增大,这是由于所使用的分块对角预条件具有良好的性质,且该性质与频率和矩阵阶数无关.CG法收敛到10-2一般需要3~5次迭代,在频率较低和矩阵阶数较大时迭代次数有所增大,这是因为此时矩阵B的条件数变大,求解起来更加困难(秦策, 2018).
|
|
表 1 使用辅助空间预条件时迭代算法迭代次数 Table 1 Iterations of iterative solvers when using Auxiliary Space Maxwell solvers |
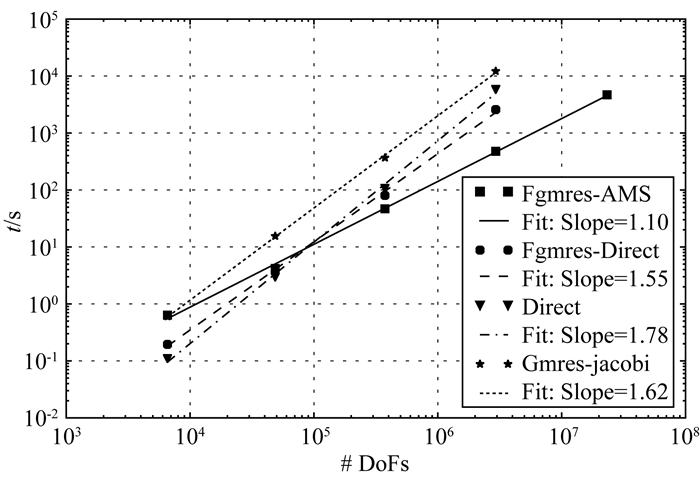
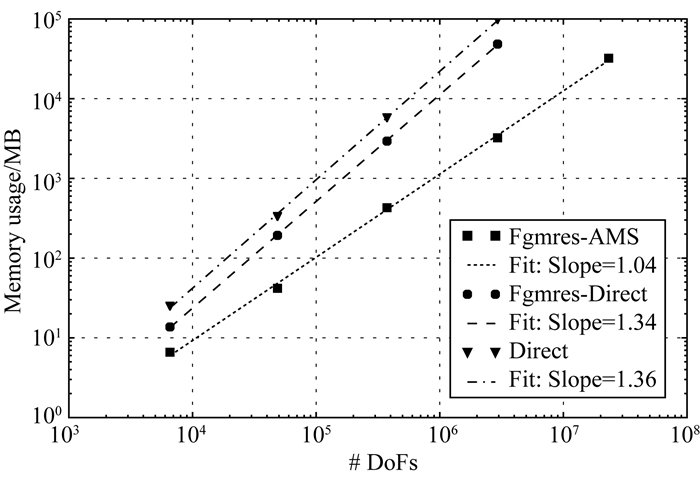
统计不同算法的计算时间和内存需求,如图 6和图 7所示.可以看到,在问题规模增大到一定程度之后(矩阵阶数大于105),本文使用的FGMRES迭代算法结合AMS预条件的计算时间要小于其他方法,同时计算时间随问题规模的增长速度最慢,也即问题规模越大其优势越大.内存需求远小于直接解法,与直接解法相比,用相同甚至更少的内存可以解决规模大10倍的问题.
|
图 6 不同计算方法的计算时间对比 Fig. 6 Comparison of computational time for different methods |
|
图 7 不同计算方法的内存需求对比 Fig. 7 Comparison of memory requirements for different methods |
总的来说,与传统的方法相比,本文使用的算法在收敛速度、计算时间和内存需求等方面具有很强的优势.
3 数值算例需要指出的是,对于不同的场源,并不会改变式(11)中的矩阵K,只会改变右端项,因此本文的方法适用于各种频率域电磁方法,包括大地电磁法和可控源电磁法.同时分块对角预条件的性质也和网格无关,也适用于四面体和六面体网格.我们通过两个算例来说明算法的应用.
3.1 大地电磁法DTM3.0(https://www.dias.ie/mt3dinv3/3D_forward_model_dtm301.html)模型是在2018年召开的第三届三维大地电磁反演研讨会上提出的标准正演模型.模型背景是1000 Ωm的均匀半空间,包含两个块状异常体,分别是区域低阻体和局部低阻体,如图 8所示.表 2中给出了两个块状异常体的范围和电阻率.

|
图 8 DTM3.0模型示意图 Fig. 8 Sketch of DTM3.0 model |
|
|
表 2 DTM3.0模型两个块状异常体范围及电阻率 Table 2 Dimensions and resistivity values of the two blocks in the DTM3.0 model |
计算区域覆盖了大约1000 km×1000 km×1000 km的范围.在该算例的网格剖分中,使用结构化的六面体网格,网格为96×201×78,最终的棱边总数为4687469.计算了10-4~100 Hz共21个频率的响应,总的计算时间约为17.5 h.同时,为验证我们所实现正演算法的正确性,还与ModEM(Kelbert et al., 2014)所计算的结果进行了对比,两者使用相同的网格.图 9是两个测点的视电阻率和相位响应,测点位于图 8中XY截面的五角星处.可以看到,除了低频部分的个别频率,我们的计算结果和ModEM的结果基本吻合,这从一定程度上证明了我们算法的正确性.需要指出的是,该模型没有解析解,因此无法判断哪种方法的精确度更高.另外,两个测点的阻抗相位响应出现了异常,主要表现为YX模式的阻抗相位超越了第三象限.相位超象限现象在实际观测中非常常见,该模型的结果对解释实际观测中相位超象限现象具有一定指导意义.

|
图 9 DTM3.0模型响应 Fig. 9 Response of DTM3.0 model |
计算过程中迭代算法FGMRES都在20次以内收敛到残差小于10-8,其中频率为10-4Hz时迭代次数为10,频率为100 Hz时迭代次数为20,与前文COMMEMI3D-2模型的结论是一致的.
3.2 海洋可控源电磁法第二个算例是海洋储层模型.海水深度为1 km,电阻率为0.3 Ωm.海水下方是电阻率为1 Ωm的沉积层.沉积层中包含了一个高阻的储层,范围是-1 km≤x≤1 km,-1.5 km≤y≤1.5 km,2 km≤z≤2.1 km,电阻率为100 Ωm.一个Y方向的电偶极场源放置于(0 km, -4 km, 0.9 km),测点放置于海底,范围为-6~6 km,共121个.
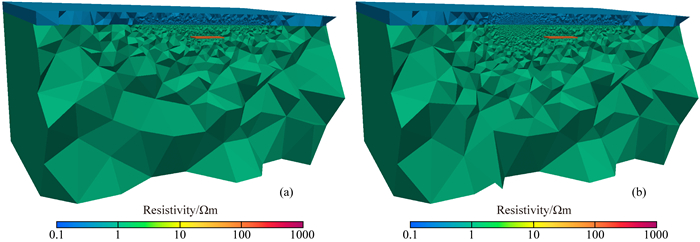
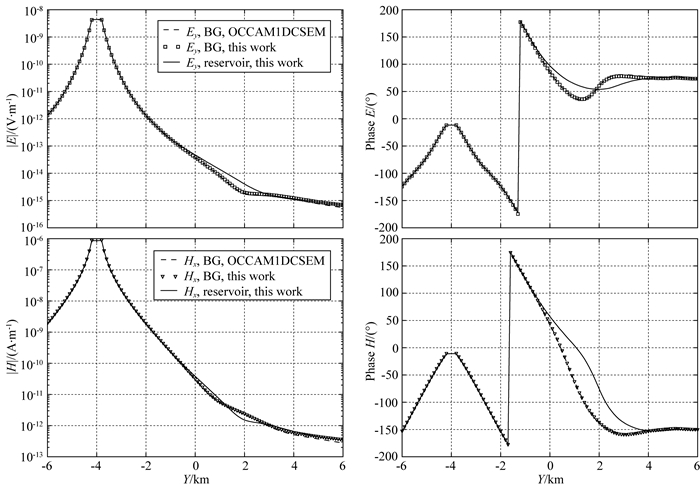
使用四面体网格对计算区域进行网格剖分,初始网格包含了442551个四面体单元,棱边数为414404.另外,我们对网格进行了自适应加密,经过5次自适应加密后最终网格中的单元数为2059902,棱边数为2384000,计算时间约为9 min.图 10是初始网格和最终网格的剖分示意图,可以看到场源和异常体附近的网格得到了加密,保证了计算结果的精确性.我们还和无储层时的响应进行了对比,无储层时该模型为一维介质,我们同时使用了Kerry Key开发的OCCAM1DCSEM程序(Key, 2009)和我们所实现的正演程序对其进行计算.图 11是频率为0.5 Hz时的Ey和Hx响应.可以看到,无储层时我们的计算结果和OCCAM1DCSEM的计算结果吻合得非常好,这证明了我们算法的正确性和计算精度.另外,在靠近场源的位置有储层和无储层的响应基本是重合的,在距离场源4~8 km的位置曲线出现了分离,说明对于该深度范围的储层,只有中间收发距的响应才对储层有所反应.
|
图 10 海洋储层模型网格剖分 (a)初始网格; (b)最终网格. Fig. 10 Sketch of mesh for Marine reservoir model (a) Initial mesh; (b) Final mesh. |
|
图 11 海洋储层模型的Ey和Hx响应(频率为0.5 Hz) Fig. 11 Ey and Hx response for Marine reservoir model(the frequency is 0.5 Hz) |
网格的局部加密对矩阵B的性质影响很大,使得求解式(19)的效率出现了下降.具体表现为,在初始网格中求解式(19)的CG平均迭代次数为5,而在最终网格中求解式(19)的CG平均迭代次数为21.尽管如此,本文所使用的方法总的计算时间和内存需求仍远小于直接解法.另外,由于分块对角预条件的性质,求解式(16)时的FGMRES的迭代次数没有受影响,两者均为18.
4 结论本文研究了频率域电磁法三维有限元正演中线性方程组的迭代求解算法.将复系数矩阵分解为实对称形式并构造分块对角预条件,并使用共轭梯度法结合辅助空间预条件技术求解两个小的实数方程.与使用迭代算法求解复系数线性方程组相比,收敛速度得到明显提升.与直接解法相比,时间效率和空间效率也大大提高.本文的算法适用于各种频率域方法和不同的网格剖分,同时算法的效率基本不受频率和问题规模的影响,为实现快速、高精度的三维正演打下了基础.
附录A本节证明矩阵P-1A条件数的上界(Chen et al., 2010).定义
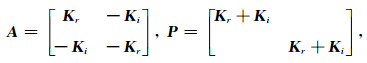
|
(A1) |
根据条件数的定义,
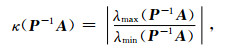
|
(A2) |
其中λmax(P-1A)和λmin(P-1A)分别是P-1A的极大和极小特征值.
令γ(P-1A)是P-1A的特征值集合,λ∈γ(P-1A)且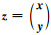
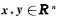
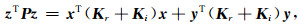
|
(A3) |
根据柯西-施瓦茨不等式可得
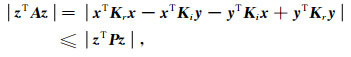
|
(A4) |
又(P-1A)z=λz,可得Az=λPz,所以
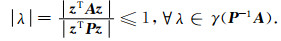
|
(A5) |
至此,我们已得到|λ|的上界,为得到|λ|的下界,令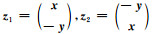
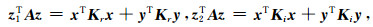
|
(A6) |
因此(z1+z2)TAz=zTPz.更进一步,我们得到
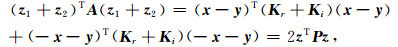
|
(A7) |
再次利用Az=λPz可得

|
(A8) |
联立式(A5)和式(A8),可得
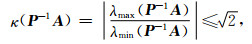
|
(A9) |
得证.
致谢 在本文的修改过程中,两位审稿专家提出了宝贵的修改意见,同时本文的研究工作中还使用了河南理工大学高性能计算中心的计算资源,在此一并表示感谢.
Chen J Q, Chen Z M, Cui T, et al. 2010. An adaptive finite element method for the eddy current model with circuit/field couplings. SIAM Journal on Scientific Computing, 32(2): 1020-1042. |
Da Silva N V, Morgan J V, MacGregor L, et al. 2012. A finite element multifrontal method for 3D CSEM modeling in the frequency domain. Geophysics, 77(2): E101-E115. |
Falgout R D, Yang U M. 2002. hypre: a library of high performance preconditioners.//Sloot P M A, Hoekstra A G, Tan C J K, et al eds. Computational Science-ICCS 2002. Berlin, Heidelberg: Springer, 632-641.
|
Grayver A V, Bürg M. 2014. Robust and scalable 3-D geo-electromagnetic modelling approach using the finite element method. Geophysical Journal International, 198(1): 110-125. DOI:10.1093/gji/ggu119 |
Grayver A V, Kolev T V. 2015. Large-scale 3D geoelectromagnetic modeling using parallel adaptive high-order finite element method. Geophysics, 80(6): E277-E291. |
Hiptmair R, Xu J C. 2007. Nodal auxiliary space preconditioning in H (curl) and H (div) spaces. SIAM Journal on Numerical Analysis, 45(6): 2483-2509. DOI:10.1137/060660588 |
Kelbert A, Meqbel N, Egbert G D, et al. 2014. ModEM:A modular system for inversion of electromagnetic geophysical data. Computers & Geosciences, 66: 40-53. |
Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics, 74(2): F9-F20. |
Kolev T V, Vassilevski P S. 2009. Parallel auxiliary space AMG For H(Curl) problems. Journal of Computational Mathematics, 27(5): 604-623. DOI:10.4208/jcm.2009.27.5.013 |
Kordy M, Wannamaker P, Maris V, et al. 2016. 3-D magnetotelluric inversion including topography using deformed hexahedral edge finite elements and direct solvers parallelized on SMP computers-Part I:forward problem and parameter Jacobians. Geophysical Journal International, 204(1): 74-93. DOI:10.1093/gji/ggv410 |
Li Y, Wu X P, Lin P R, et al. 2017. Three-dimensional modeling of marine controlled-source electromagnetism using the vector finite element method for arbitrary anisotropic media. Chinese Journal of Geophysics (in Chinese), 60(5): 1955-1978. DOI:10.6038/cjg20170528 |
Liu Y, Li Y G, Han B. 2017. Adaptive edge finite element modeling of the 3D CSEM field on unstructured grids. Chinese Journal of Geophysics (in Chinese), 60(12): 4874-4886. DOI:10.6038/cjg20171227 |
Nédélec J C. 1986. A new family of mixed finite elements in R3. Numerische Mathematik, 50(1): 57-81. DOI:10.1007/BF01389668 |
Puzyrev V, Cela J M. 2015. A review of block Krylov subspace methods for multisource electromagnetic modelling. Geophysical Journal International, 202(2): 1241-1252. DOI:10.1093/gji/ggv216 |
Puzyrev V, Koldan J, De La Puente J, et al. 2013. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling. Geophysical Journal International, 193(2): 678-693. DOI:10.1093/gji/ggt027 |
Qin C, Wang X B, Zhao N. 2017. Parallel three-dimensional forward modeling and inversion of magnetotelluric based on a secondary field approach. Chinese Journal of Geophysics (in Chinese), 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
Qin C. 2018. Three-dimensional magnetotelluric forward modeling and inversion based on adaptive vector finite element method[Ph. D. thesis] (in Chinese). Chengdu: Chengdu University of Technology.
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Saad Y. 1993. A flexible inner-outer preconditioned GMRES algorithm. SIAM Journal on Scientific Computing, 14(2): 461-469. |
Schwarzbach C, Haber E. 2013. Finite element based inversion for time-harmonic electromagnetic problems. Geophysical Journal International, 193(2): 615-634. DOI:10.1093/gji/ggt006 |
Smith B, Bjørstad P, Gropp W. 2004. Domain Decomposition:Parallel Multilevel Methods for Elliptic Partial Differential Equations. Cambridge: Cambridge University Press.
|
Um E S, Commer M, Newman G A. 2013. Efficient pre-conditioned iterative solution strategies for the electromagnetic diffusion in the Earth:finite-element frequency-domain approach. Geophysical Journal International, 193(3): 1460-1473. DOI:10.1093/gji/ggt071 |
Xu J. 1996. The auxiliary space method and optimal multigrid preconditioning techniques for unstructured grids. Computing, 56(3): 215-235. |
Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids. Chinese Journal of Geophysics (in Chinese), 58(8): 2827-2838. DOI:10.6038/cjg20150817 |
Yin C C, Zhang B, Liu Y H, et al. 2016. A goal-oriented adaptive finite-element method for 3D scattered airborne electromagnetic method modeling. Geophysics, 81(5): E337-E346. |
Yin C C, Zhang B, Liu Y H, et al. 2017. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling. Chinese Journal of Geophysics (in Chinese), 60(1): 327-336. DOI:10.6038/cjg20170127 |
Zhang X J. 1992. Multilevel Schwarz methods. Numerische Mathematik, 63(1): 521-539. DOI:10.1007/BF01385873 |
Zhdanov M S, Varentsov I M, Weaver J T, et al. 1997. Methods for modelling electromagnetic fields Results from COMMEMI-the international project on the comparison of modelling methods for electromagnetic induction. Journal of Applied Geophysics, 37(3-4): 133-271. DOI:10.1016/S0926-9851(97)00013-X |
李勇, 吴小平, 林品荣, 等. 2017. 电导率任意各向异性海洋可控源电磁三维矢量有限元数值模拟. 地球物理学报, 60(5): 1955-1978. DOI:10.6038/cjg20170528 |
刘颖, 李予国, 韩波. 2017. 可控源电磁场三维自适应矢量有限元正演模拟. 地球物理学报, 60(12): 4874-4886. DOI:10.6038/cjg20171227 |
秦策, 王绪本, 赵宁. 2017. 基于二次场方法的并行三维大地电磁正反演研究. 地球物理学报, 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
秦策. 2018.基于自适应矢量有限元法的三维大地电磁正反演研究[博士论文].成都: 成都理工大学.
|
杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827-2838. DOI:10.6038/cjg20150817 |
殷长春, 张博, 刘云鹤, 等. 2017. 面向目标自适应三维大地电磁正演模拟. 地球物理学报, 60(1): 327-336. DOI:10.6038/cjg20170127 |
 2020, Vol. 63
2020, Vol. 63


