2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院油气资源研究院重点实验室, 北京 100029;
4. 中国科学院大学, 北京 100049
2. Institute of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
非均匀介质中波传播的数值模拟是逆时偏移(RTM)成像方法(Loewenthal et al., 1991; Soubaras andZhang,2008; Zhang and Zhang, 2009)和全波形反演(FWI)(Tarantola,1984)的重要组成部分.在地震波模拟的各种数值方法中,时域有限差分(TDFD)方法被广泛应用于求解波动方程;因为相比其他方法,例如有限元法(Marfurt,1984)和谱元法(Komatitsch and Vilotte, 1998;李孝波等, 2014),它更容易实现、计算成本更低(Hu et al., 2017).在使用TDFD方法时,数值频散现象不可避免,这是由网格离散化引起的(Alford et al., 1974; Kelly et al., 1976).通过时间和空间网格细化,我们可以提高数值模拟的精度,但计算成本和内存需求也大大增加.
为了压制空间频散误差,地球物理学家通常采用高阶FD(Dablain,1986)、交错网格(Madariaga,1976; Virieux,1986; Graves,1996)和旋转交错网格策略(Saenger et al., 2000)更好地近似空间导数.为了减轻时间频散和提高数值稳定性,在付出额外的内存代价下,高阶TDFD或隐式法(Liu and Sen, 2009a)是一种选择.为了获得更高的精度,基于空间频散关系(Zhang and Yao, 2013; Liu,2014)或时空域频散关系(Liu and Sen, 2009b; Tan and Huang, 2014; Hu et al., 2016)的优化FD方法也是另外一种选择.
伪谱(PS)方法(Fornberg,1975; Gazdag,1981; Kosloff and Baysal, 1982)已被证明是空间高阶FD的极限(Chu and Stoffa, 2012)并且具有无限阶精度,因为空间导数是通过傅里叶变换计算的.利用在奈奎斯特采样极限下允许的最大空间步长的优势,PS是一种可用于大模型中准确模拟波传播的技术(Fornberg, 1987, 1990).然而,由于时间离散是采用的中心二阶FD,传统PS仍然需要非常精细的时间步长以减少时间频散误差并避免不稳定情况.此外,诸如Lax-Wendroff方法,分裂方法和Nyström方法(Chen,2007)的高阶时间离散化需要较大的内存开销、计算复杂性高,这降低了PS方法的实用性.通过将FFT计算的空间导数与基于Chebyshev的快速扩展方法(REM)计算的时间导数相结合,当使用大时间步长时,可以正确地模拟所有时间和空间频率的波场(Tal-Ezer et al., 1987; Kosloff et al., 1989); Stoffa and Pestana, 2009).这些方法是基于波动方程的形式积分解,因此被归类为递归积分时间延拓类方法(RITE)(Fowler et al., 2010; Du et al., 2013),其具有两步和一步法.一步延拓法(OSE)的指数算子可以通过优化的可分表示来求解(Zhang and Zhang, 2009),并允许用任意大的时间步长.但OSE需要引入复值波场,并且在RTM中由于需要保存许多中间波场快照时,其优势会降低.两步外推的余弦算子也可以通过优化扩展(Soubaras and Zhang, 2008)而不是泰勒展开来解决,而后者导出了传统的Lax-Wendroff方法.因此,两步显式推进算法(Soubaras and Zhang, 2008)允许在时间上采用奈奎斯特采样步长,并且不受数值稳定性或频散问题的影响.然而,RITE方法需要结合空间导数精确的数值计算方法,如高阶FD或PS算子,在时间和空间离散化方面都没有近似,且编程实现略显复杂,因此如我们知道的一样,它们在石油工业中应用较少.
相比之下,另一种名为k-space方法的谱方法为蛙跳PS方法引入了时间校正项,为基于奈奎斯特的时间和空间步长采样的均匀介质提供了精确解.Mast等(2001)提出了一种求解二阶声波方程的k-space方法,可以为弱散射介质提供高精度的波场模拟结果.Tabei等(2002)提出了一种k-space方法,适用于求解一阶声波方程,其中还采用交错网格和平滑技术来提高强散射介质的波场模拟精度.然而,原始的k-space算子(Mast et al., 2001; Tabei et al., 2002)不适用于非均匀介质中的波场模拟,因为补偿速度是恒定的.此外,拟解析(PA)方法也可以解决均匀介质波场模拟问题(Etgen and Brandsberg-Dahl, 2009).为了适应变速度介质,PA方法采用由几个原始二阶k-space算子外推的参考波场之间的插值,以获得拟解析的解.k-space方法在弹性波波场模拟中的应用更具挑战性,它通常基于各向同性解耦的二阶和一阶弹性方程分别补偿P波和S波(Liu,1995; Firouzi et al., 2012).然而,在非均匀介质中,除非剪切模量和密度恒定,否则使用解耦弹性波方程不能完全分离P波和S波(Du et al., 2017).Chu和Stoffa(2011)在变密度介质中扩展了声波和弹性波传播的PA方法,但是仍用恒定的补偿速度也即原始的k-sapce算子.此外,该方法是基于耦合的二阶位移-应力弹性波方程而不是解耦的弹性波方程,因此更准确并且因为涉及更少的方程而节省了大量的计算成本.尽管通过FFT可以有效地求解由恒定补偿速度构造的k-space算子,但是上述方法不适用于需要大时间步长的非均匀介质中的波场模拟.
为了使k-space方法适应具有强烈速度和密度变化的介质,在本文中,我们用非均匀真实速度代替原始k-space算子中的恒定补偿速度.因此,k-space算子成为一个空间波数混合域算子,它依赖于波数和随空间变化的速度,因而直接计算的成本很高.为了降低计算成本并确保准确性,我们引入了低秩分解(LR)以近似混合域算子,它仅涉及少量FFT(Fomel et al., 2013; Fang et al., 2014).基于混合域象征的低秩分解,Sun等(2017)扩展了OSE,用于非均匀各向异性介质中的弹性波传播.k-space伪谱方法也被推广用于非均匀各向异性弹性波情形(Firouzi and Khuri-Yakub, 2017).进一步,前人已经提出低秩有限差分(LFD)以完全避免FFT并提高计算效率(Song et al., 2013; Fang et al., 2014; Han et al., 2016; Yuan et al., 2017;袁雨欣等,2018),但在时间和空间上都失去了一定的准确性.在k-space算子的基础上,最近又发展了其他的优化FD方法(Chen et al., 2016, 2017; Gong et al., 2017).显然,这是精度和效率之间的平衡,我们选择LR,因为它在空间方向上具有较高的模拟精度和可接受的计算成本.在我们的工作中,我们考虑耦合的二阶位移弹性波方程,因为与一阶波动方程相比可以节省相当大的内存.
本文的结构如下.我们首先给出了基于二阶波动方程的非均匀介质中各向同性弹性波传播的控制方程.然后,我们为之构造了新的k-space方法,并引入了低秩近似(Fomel et al., 2013)以降低求解新k-space的计算成本.并且,基于二阶波动方程的新的k-space方法在数学上被证明等效于基于一阶波动方程的原始k-sapce方法和交错网格低秩近似(SGL)方法(Fang et al., 2014).此外,我们讨论了不同类型的源项和内存计算成本,以及新k-space方法对于大时间步长模拟的准确性.最后,我们使用复杂的非均匀二维模型来证明所提方法与传统PS,交错网格PS(SGPS)用于弹性波模拟相比的优势.
1 方法理论 1.1 控制方程谱方法因其空间导数通过傅里叶变换计算而具有很高的精度,如伪谱(PS)方法(Kosloff and Baysal, 1982).对于弹性波传播,二阶控制方程则具有形式为
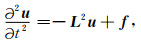
|
(1) |
其中,t表示时间,u是波场,f是源项,并且-L2是空间线性算子.在本文的研究中,我们关注的是各向同性非均匀介质中的弹性波传播,u分别包括x、y和z方向的位移分量,f包含x、y和z方向的体波应力.为简单起见,我们提出了运算符-L2的二维公式,它可以用2×2的矩阵表达,由式(2)给出:
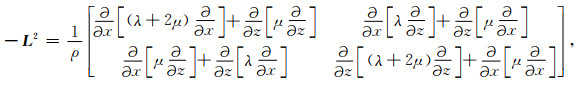
|
(2) |
其中ρ=ρ(x)是密度方程,并且x代表了矢量坐标(x, y, z),λ=λ(x)和μ=μ(x)是基于纵波速度α=α(x)=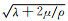

将k-space方法扩展到弹性波情况相比声波更具挑战性,因为包含了更多的波模式和它们之间更复杂的相互作用. Chu和Stoffa(2011)提出了包含时间校正的外推矩阵的因式分解,然后在可变密度介质中推导了用于3D弹性波传播的PA公式(附录B),但使用了常数P波和S波补偿速度.采用与经典SGPS方法相同的交错网格配置:正应力分量在主要网格节点上定义,剪切应力在其中心节点上定义,而粒子速度分量在中间网格节点上定义.因此,PA方法可以分别有效地补偿具有可变密度但具有恒定P波和S波速度的介质中P波和S波时间步递推误差.
这些PA公式也即是原始的弹性波k-space算子.同样,通过用相应的真实速度替换PA方案中的恒定P波和S波速度,可以得出交错网格下弹性波的新的k-space算子,公式为
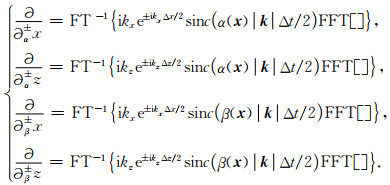
|
(3) |
由P波速度和S波速度定义的两个算子为
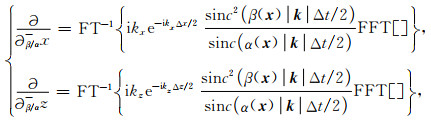
|
(4) |
其中,下标α、β、β/α用于区分依赖于P波或S波速度或两者的算子.此外,消除方程(B1)、(B2)中的应力项,只考虑离散方程的位移项,可得:
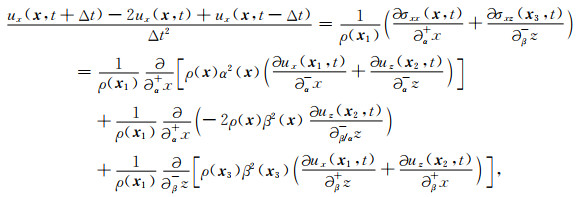
|
(5) |
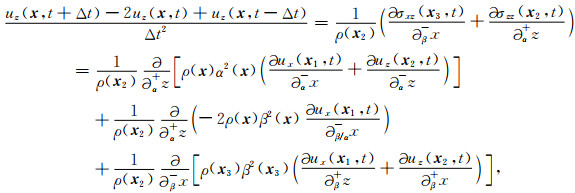
|
(6) |
其中,x1≡(x+Δx/2, z),x2≡(x, z+Δz/2)以及x3≡(x+Δx/2, z+Δz/2).
这是一种新的弹性波情况下的k-space方法,它可以有效地同时补偿具有强速度或密度差异的非均匀介质中的P波和S波.不幸的是,根据方程(4)-(6),弹性波外推的空间算子不能分为两组:一组与P波速度相关,另一组与S波速度相关.因此,我们的方法间接证明了非均匀介质中,P波和S波不能完全分离(Du et al., 2017).
在均匀弹性介质中,我们提出的方法退化为
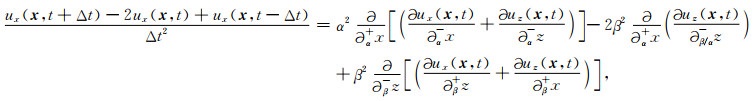
|
(7) |
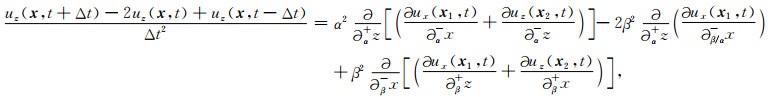
|
(8) |
退化的形式不仅可以模拟耦合的P波和S波模式的传播,而且可以模拟均匀介质中大时间步长的解耦的P波和S波传播.
1.3 低秩分解近似新的k-space算子从方程(3)、(4),我们应该注意到,所有新的k-space算子是波数、速度和时间步长的函数,所以称为混合域空间-波数域算子.当补偿速度为0时,新k-space算子自然地退化为相应的伪谱算子.在非均匀介质情况,直接计算新的k-space算子,复杂度为O(Nxz2),其中Nxz是模型的总网格点数.为了降低计算成本,我们将这些算子用低秩分解近似,这在附录中详细的描述了.通过低秩表示,Fang等(2014)也提出了交错网格低秩近似(SGL)方案来求解精确的k-space算子,而SGL是基于耦合的一阶声波方程,而不是二阶方程.最终的SGL方法离散式是由公式(A3)-(A5)给出的.因此,新的k-space方法实际上提供了在数值上等同于SGL方法的解.
这里,在非均匀密度介质中,我们在数学上证明了新的k-space方法和SGL之间的等价性.根据方程(A5),我们可以得到在t-=t-Δt/2中压力波场的时间导数,即:
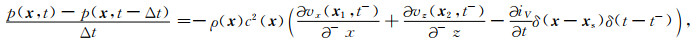
|
(9) |
随后,通过等式(B5)减去等式(9),得到:
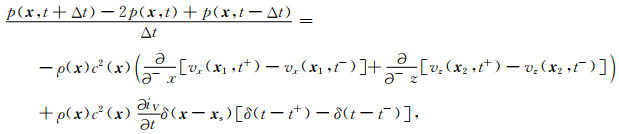
|
(10) |
最后,将等式(A3)、(A4)代入等式(10),得到结果:
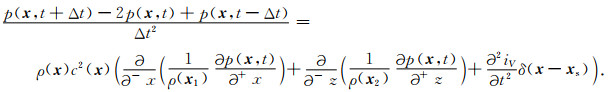
|
(11) |
忽略源项,公式(11)就是变密度声波方程用新k-space方法求解的离散化公式.此外,将低秩分解引入近似混合域算子,不会破坏它们的等价性.关于震源项,本文中我们仅考虑质量源项.通过比较SGL中的源项(方程(A5))与新的k-space方法(方程(11))的源项,质量加载参数iV的一阶时间导数和该参数二阶时间导数的半步长时移应当分别用于这两种方法,以达到完全等价.在这项工作中,加载参数iV由负高斯函数给出.因此,当新方案使用Ricker子波时(图 1a),应该在SGL中使用高斯一阶导数子波(图 1b)以产生完全等效的结果.此外,新的k-space方法也拥有SGL对于非均匀介质的高精度和稳定性.

|
图 1 (a) 高斯一阶导数子波-∂tiV;(b)雷克子波-∂t2iV Fig. 1 (a) The Gaussian first-order derivative wavelet -∂tiV; (b) The Ricker wavelet -∂t2iV |
此外,新的k-space方法仅涉及压力波场的外推.除了压力波场之外,矢量速度场的存储也优于SGL方法.在2D情况,SGL需要存储三个外推波场,一个速度场和一个密度场.在3D情况下,SGL需要的存储空间是新的k-space方法的两倍.与SGL方案相比,新方法提供了非均匀介质中声波传播省内存的优化方法.
对于弹性波传播,可以直接得到基于一阶速度-应力耦合方程的精确的k-space方法,用同样的方法也可证明该方法与新k-space方法的等价性.在只有外力的情况下,该方法的源项与我们的方法相同.但是,该方法在二维情况下有5个波场,三维情况下有9个波场需要同时存储.而基于二阶弹性波方程的新的k-space方法,二维只需要存储2个波场,三维仅有3个波场.从这一点来说,利用二阶耦合位移弹性波方程,无论波场的性质如何,我们都可以得到了高精度且节省内存的k-space方法.在效率方面,新方法的计算成本与SGL法的相当,因为它们有相同数量的空间运算符,这占用了大部分的时间.在弹性情况下也是如此.利用GPU加速技术,用CUDAFFTs代替FFTs,可以进一步提高新方案的效率,从而在三维测试中实现有价值的加速.
另外,通过将实际补偿速度修改为所提供的恒定速度,可以从新方案中很容易地得到原始k-space方法的模拟结果.并且,通过将实际补偿速度修改为零,我们可以使用新方法的代码直接实现SGPS.关于PS方法,我们可以通过去除SGPS算法中的移位因子来实现.
2 数值实验在本节中,我们首先在2D均匀模型上测试新k-space方法用大时间步长模拟的准确性.然后进行数值实验,测试新的k-space在复杂非均匀中弹性波传播的适用性.在所有实验中,我们使用Ricker小波,最大频率为50 Hz,幅度A=1.为简单起见,海绵吸收边界条件(ABC)(Cerjan et al., 1985)在我们的例子中被用来抑制来自边界的反射.其他ABCs,如完美匹配层(Komatitsch and Tromp, 2003)也可以扩展到我们新的k-space方法.
2.1 均匀模型为了验证新k-space方法的求解精度,我们对2D均匀声波模型进行了测试.声波解析解由式(12)给出(Alford et al., 1974):

|
(12) |
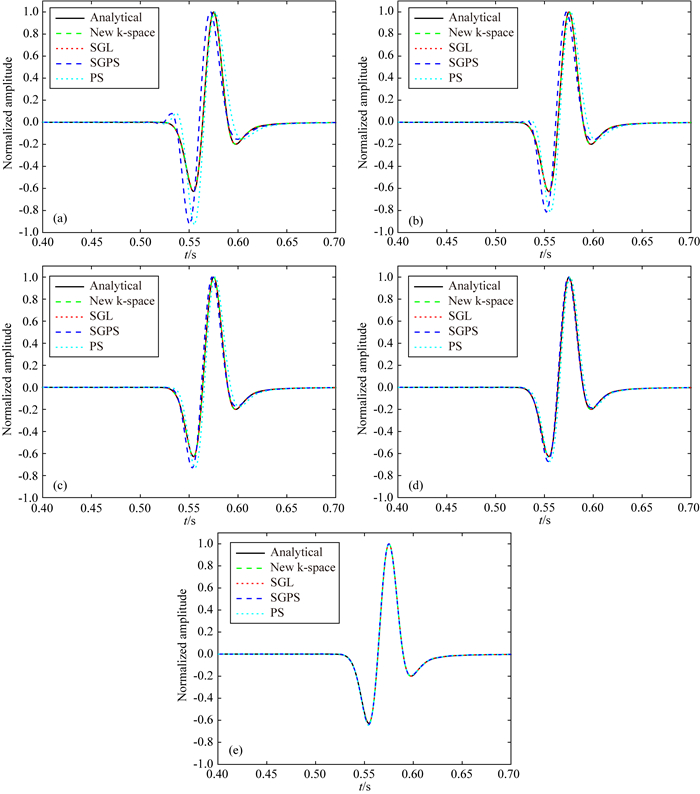
均匀模型中,速度为2000 m·s-1,密度为1 g·cm-3.当我们使用方程(12)来获得解析解时,将主频为20 Hz的Ricker小波作为源项,并且我们应用PS和新的k-space方法来获得数值解.同时,相同主频的高斯一阶导数子波被用于SGL和SGPS方法.四种数值方法中我们采用Δx=Δz=20 m.图 2显示了在距震源1 km的点的解的对比图,这些图是由之前提到的五种方法,分别采用了时间间隔Δt=2.5, 2.0, 1.5, 1.0,0.5 ms产生的.
|
图 2 解析解和不同方法的数值解之间的对比 时间间隔分别为(a)2.5 ms; (b) 2 ms; (c) 1.5 ms; (d) 1 ms; (e) 0.5 ms. Fig. 2 Comparisons between the analytical solution and numerical solutions calculated by different methods The temporal intervals are (a) 2.5 ms; (b) 2 ms; (c) 1.5 ms; (d) 1 ms; (e) 0.5 ms. |
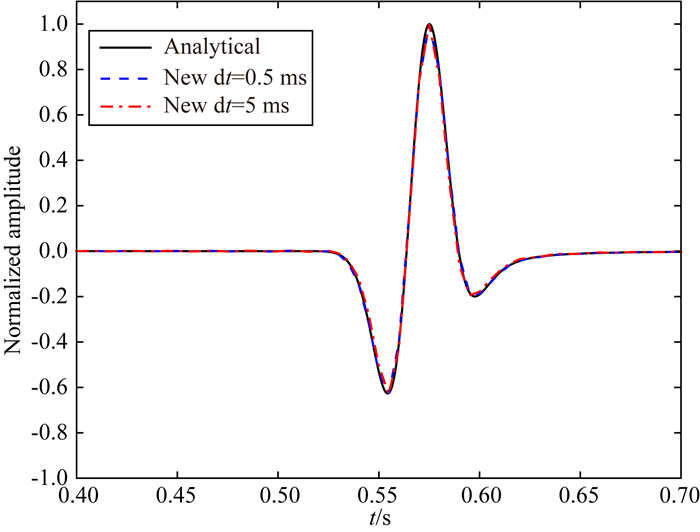
对于图 2a,Δt=2.5 ms,我们可以看到通过新k-space方法获得的归一化解与解析解和SGL方法的解析解可以很好地匹配.即使利用低秩近似,新的k-space仍然可以保证均匀介质的精确解.然而,PS和SGPS方法会引起波形的严重失真和不正确的相位信息,这是时间频散误差.通过降低Δt,PS和SGPS的频散误差也逐渐减小.如图 2e所示,当Δt=0.5 ms时这四种方法的数值解具有很好的一致性,并且很好地匹配了解析解.然而,当将时间步长增加到5 ms时,PS和SGPS方法变得不稳定.由于精确的时间步进补偿,我们提出的方法可以在时间步长为0.5 ms和5 ms下产生相同的结果,如图 3所示.
|
图 3 新k-space方法在Δt=2.5 ms和Δt=0.5 ms下与解析解的对比(三种解十分匹配) Fig. 3 Comparisons between the analytical solution and solutions obtained by the new k-space scheme using Δt=2.5 ms and Δt=0.5 ms (three solutions are in good agreement with each other) |
对于均匀介质,混合域矩阵的秩为1,因此类似于PS算子的一个精确k-space算子的计算仅涉及一个逆FFT.因此为了与新的k-space方法具有相同的精度,SGPS和PS方法需要较小的时间步长.
2.2 Marmousi2模型在这个例子中,我们利用Marmousi2模型来验证新k-space方法在具有复杂地质结构的非均匀介质中弹性波传播的优势. P波和S波速度模型和密度模型分别如图 4a-c所示.在x方向和z方向上以20 m的空间步长离散.震源位于水层(2, 0.02)km,并在x和z方向上作为点力注入.接收器位于海底,深度为0.46 km.

|
图 4 Marmousi2模型 (a) P波速度;(b) S波速度;(c)密度. Fig. 4 Marmousi2 model (a) The P-wave velocity; (b) The S-wave velocity; (c) The density. |
在这里,我们采取时间步长1.6 s,稳定性因子CFL数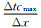

|
图 5 新k-space方法下时间步长为1.6 ms,在1.6 s时的波场快照 (a) z分量;(b) x分量. Fig. 5 Snapshots calculated by the new k-space scheme at 1.6 s with the time step of 1.6ms (a) z-component; (b) x-component. |
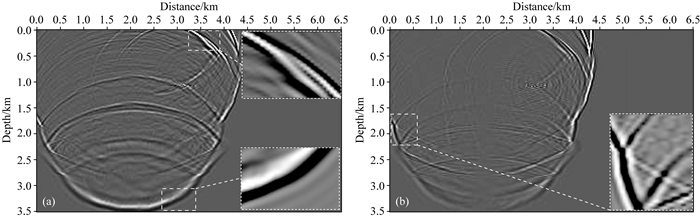
|
图 6 SGPS方法下时间步长为1.6 ms,在1.6 s时的波场快照 (a) z分量;(b) x分量. Fig. 6 Snapshots calculated by the SGPS scheme at 1.6 s with the time step of 1.6 ms (a) z-component; (b) x-component. |
|
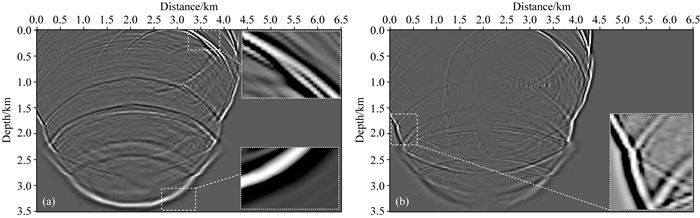
图 7 PA方法下时间步长为1.6 ms,在1.6 s时的波场快照 (a) z分量;(b) x分量. Fig. 7 Snapshots calculated by the PA scheme at 1.6 s for with the time step of 1.6 ms (a) z-component; (b) x-component. |
此外,我们从每个地震图中提取8 km偏移距的单道地震记录,以比较三种方法的准确性.在时间步长为1.6 s时,由SGPS方法产生的z和x分量都具有如图 8所示的大振幅变化.通过将时间步长增加到2 ms,SGPS变得不稳定,其中CFL数为0.47.
|
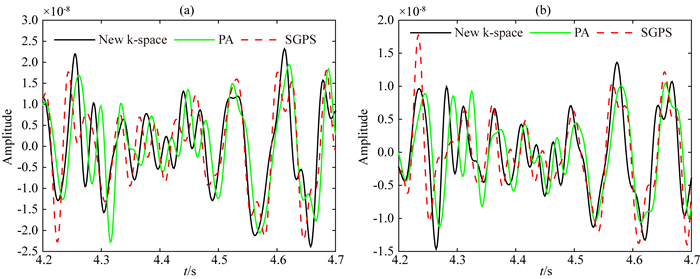
图 8 与8 km偏移距对应的单道比较,时间步长为1.6 ms (a) z分量;(b) x分量. Fig. 8 Single trace comparisons corresponding to 8 km offset with the time step of 1.6 ms (a) z-component; (b) x-component. |
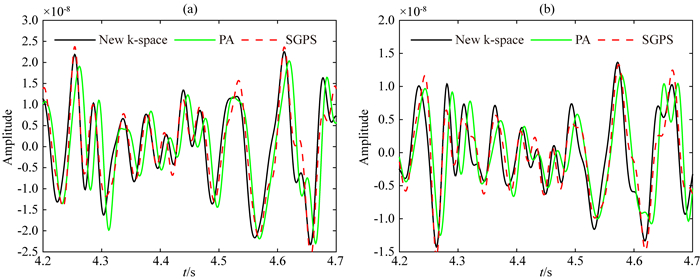
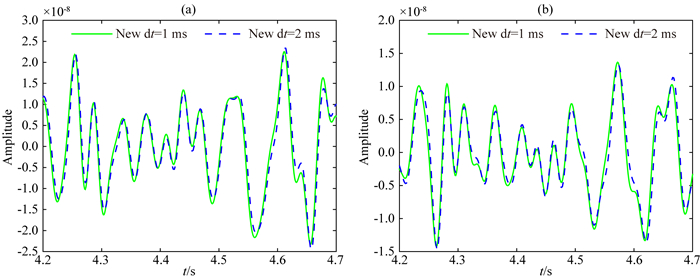
从图 8和图 9可以看出,与新的k-space方法相比,PA方法不仅具有幅度差异,而且具有较大的相位变化.通过将时间步长减少到1 ms,SGPS和PA方法产生更准确的结果,这与新方法计算得到的图 10更好地一致.然而,我们提出的方法可以获得大时间步长的相对准确的结果,这与图 2所示的具有小时间步长的那些几乎相同.如图 11所示,时间步长从1 ms增加到2 ms,新方法的变化幅度很小,计算结果也比较稳定.尽管在2 ms的时间步长中秩为3,但是所提出的方法可以在非均匀介质中对弹性波进行高精度模拟.

|
图 9 大时间步长2 ms下对应的8 km偏移距的单道对比,其中SGPS方法变得不稳定 (a) z分量;(b) x分量. Fig. 9 Single trace comparisons corresponding to 8 km offset with the large time step of 2ms, where SGPS becomes unstable (a) z-component; (b) x-component. |
|
图 10 小时间步长为1 ms对应的8 km偏移距单道比较 (a) z分量;(b) x分量. Fig. 10 Single trace comparisons corresponding to 8 km offset with the small time step of 1 ms (a) z-component; (b) x-component. |
|
图 11 新k-space方法,8 km偏移距下的单道对比,时间步长分别为1 ms和2 ms (a) z分量;(b) x分量. Fig. 11 Single trace comparisons corresponding to 8 km offset for the new k-space scheme with the time steps of 1 ms and 2 ms (a) z-component; (b) x-component. |
我们在交错网格上连续应用k-space算子,基于二阶非均匀耦合弹性波方程发展了准确模拟弹性波的k-space算子.在具有较高速度和密度差异的介质中,通过用实际速度替换原始k-space算子中的恒定补偿速度,我们获得了一系列新的k-space算子.低秩近似被用于求解新的k-space算子,这在保证精度的同时还大大降低了新方法的计算成本.
通过数学推导和数值例子,我们验证了所提出的方法在声波情况下与基于一阶声波方程的SGL等效,并且具有以下几点创新.首先,所提出的方法2D(3D)情况下对比于SGL方法更加节省内存;其次,在大时间步长情况下,传统的PS、SGPS和k-space方法变得不稳定时,我们的方法仍然具有很高的数值精度;最后,本文所提出的方法可以拓展到3D耦合弹性波正演模拟,从而进一步可应用于逆时偏移成像.
附录A 一阶声波方程以及交错网格低秩近似方法(SGL)理想流体介质中的一阶声波方程可以从流体动力学和压力与密度之间的绝热关系中推导出来,公式为
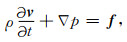
|
(A1) |
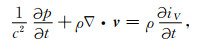
|
(A2) |
其中,v是声波粒子速度标量; f是外力密度,比如重力;m代表质量源项(Bartolo et al., 2012),iV代表m的注入参数.
假定外力密度f=0, 用以解方程(A1)、(A2)的SGL方法中的离散方程为
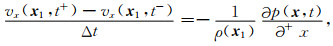
|
(A3) |

|
(A4) |

|
(A5) |
其中,t+=t+Δt/2, t-=t-Δt/2, δ是delta函数,且xs指示源的位置.
附录B 三维弹性波方程的伪解析公式三维位移应力方程的交错网格伪解析公式表示为(Chu and Stoffa, 2011):

|
(B1) |

|
(B2) |
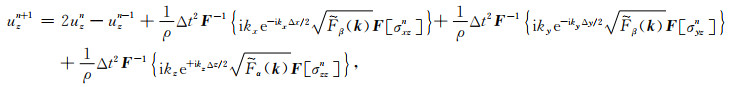
|
(B3) |

|
(B4) |
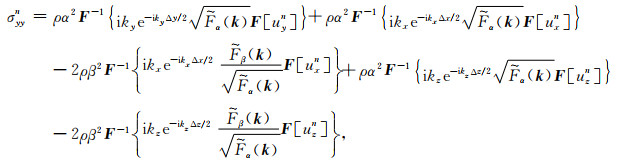
|
(B5) |
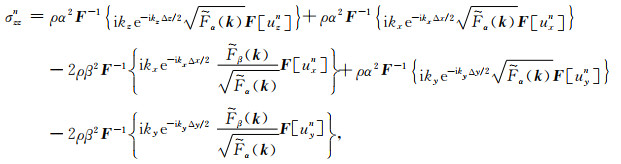
|
(B6) |
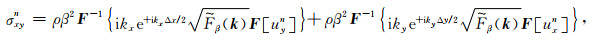
|
(B7) |
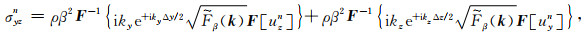
|
(B8) |
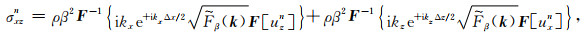
|
(B9) |
其中:
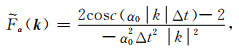
|
(B10) |
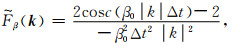
|
(B11) |
其中, α0和β0分别是P波和S波的背景速度.
附录C 低秩近似分解在所提出的方法中,所有涉及到声波情况的精确k-space算子都包含一个相同的混合域矩阵,即:
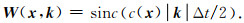
|
(C1) |
在弹性波情况下,需要构造三个混合域矩阵;其中两个矩阵如方程(7):一个取决于P波速度,另一个取决于S波速度;另一个矩阵很复杂且同时取决于P波和S波速度.
通过低秩分解(Fomel et al., 2013),我们可以获得它的可分离表达式为
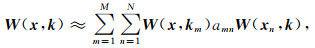
|
(C2) |
其中,W(x, km)是由W(xn, k)与{km}相关联的选定列组成的子矩阵,而W(xn, k)是由与{xn)相关联的选定行组成的另一个子矩阵,并且amn表示中间矩阵系数.方程式(C2)中分离表示的数值实现参考Engquist和Ying(2009)的方法.
由于混合域矩阵的低秩分解,我们可以将
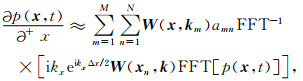
|
(C3) |
因此,在一个精确的k-space算子的实现中,只需要几个FFT.在每个时间步长中,我们只需要对每个算子做一个正向的FFT和N个反向的FFT.其中,N与相应的混合域矩阵的秩有关,与模型的大小Nxz相比,它通常很小.计算复杂度大约为o(NNxzlgNxz).声波和弹性波情况下其余的新k-space算子同样可以用该方法有效地求解.
致谢 感谢审稿人的宝贵意见.
Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. |
Cerjan C, Kosloff D, Kosloff R, et al. 1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 50(4): 705-708. |
Chen H M, Zhou H, Zhang Q C, et al. 2016. A k-space operator-based least-squares staggered-grid finite-difference method for modeling scalar wave propagation. Geophysics, 81(2): T45-T61. |
Chen H M, Zhou H, Zhang Q C, et al. 2017. Modeling elastic wave propagation using K-space operator-based temporal high-order staggered-grid finite-difference method. IEEE Transactions on Geoscience and Remote Sensing, 55(2): 801-815. DOI:10.1109/TGRS.2016.2615330 |
Chen J B. 2007. High-order time discretizations in seismic modeling. Geophysics, 72(5): SM115-SM122. |
Chu C L, Stoffa P L. 2011. Application of normalized pseudo-Laplacian to elastic wave modeling on staggered grids. Geophysics, 76(5): T113-T121. |
Chu C L, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics, 77(3): W17-W26. |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. |
Du Q Z, Guo C F, Zhao Q, et al. 2017. Vector-based elastic reverse time migration based on scalar imaging condition. Geophysics, 82(2): S111-S127. |
Du X, Fowler P J, Fletcher R. 2013. Recursive integral time-extrapolation methods for waves:A comparative review. Geophysics, 79(1): T9-T26. |
Etgen J T, Brandsberg-Dahl S. 2009. The pseudo-analytical method: application of pseudo-Laplacians to acoustic and acoustic anisotropic wave propagation.//79th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2552-2556.
|
Fang G, Fomel S, Du Q Z, et al. 2014. Lowrank seismic-wave extrapolation on a staggered grid. Geophysics, 79(3): T157-T168. |
Firouzi K, Cox BT, Treeby BE, et al. 2012. A first-order k-space model for elastic wave propagation in heterogeneous media. The Journal of the Acoustical Society of America, 132(3): 1271-1283. DOI:10.1121/1.4730897 |
Firouzi K, Khuri-Yakub B T. 2017. A k-space pseudospectral method for elastic wave propagation in heterogeneous anisotropic media. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 64(4): 749-760. DOI:10.1109/TUFFC.2017.2653063 |
Fomel S, Ying L X, Song X L. 2013. Seismic wave extrapolation using lowrank symbol approximation. Geophysical Prospecting, 61(3): 526-536. DOI:10.1111/j.1365-2478.2012.01064.x |
Fornberg B. 1975. On a fourier method for the integration of hyperbolic equations. Siam Journal on Numerical Analysis, 12(4): 509-528. |
Fornberg B. 1987. The pseudospectral method:Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501. |
Fornberg B. 1990. High-order finite differences and the pseudospectral method on staggered grids. Siam Journal on Numerical Analysis, 27(4): 904-918. |
Fowler P J, Du X, Fletcher R. 2010. Recursive integral time extrapolation methods for scalar waves.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 3210-3215.
|
Gazdag J. 1981. Modeling of the acoustic wave equation with transform methods. Geophysics, 46(6): 854-859. |
Gong X F, Du Q Z, Zhao Q, et al. 2017. Pseudo-analytical finite-difference elastic wave extrapolation based on k-space method. Geophysics, 83(1): 1-71. |
Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bulletin of the Seismological Society of America, 86(4): 1091-1106. |
Han D, Du Q Z, Fang G. 2016. Elastic wave propagation on a staggered-grid using lowrank finite-difference method.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 3900-3904.
|
Hu T, Liu H, Feng H X, et al. 2017. Comparison of two staggered-grid finite-difference schemes for elastic wave propagation in anisotropic media on GPU devices.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Hu W, Hu C S, Liu Y N. 2016. A new time-space domain dispersion-relation-based implicit staggered-grid finite-difference scheme for scalar wave-equation modeling.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms; a finite-difference approach. Geophysics, 41(1): 2-27. |
Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
Komatitsch D, Vilotte J P. 1998. The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88(2): 368-392. |
Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
Kosloff D D, Filho A Q, Tessmer E, et al. 1989. Numerical solution of the acoustic and elastic wave equations by a new rapid expansion method. Geophysical Prospecting, 37(4): 383-394. DOI:10.1111/j.1365-2478.1989.tb02212.x |
Li X B, Bo J S, Qi W H, et al. 2014. Spectral element method in seismic ground motion simulation. Progress in Geophysics (in Chinese), 29(5): 2029-2039. DOI:10.6038/pg20140506 |
Liu Q H. 1995. Generalization of the k-space formulation to elastodynamic scattering problems. Journal of the Acoustical Society of America, 97(3): 1373-1379. |
Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
Liu Y, Sen M K. 2009a. An implicit staggered-grid finite-difference method for seismic modelling. Geophysical Journal International, 179(1): 459-474. DOI:10.1111/j.1365-246X.2009.04305.x |
Liu Y, Sen M K. 2009b. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806. DOI:10.1016/j.jcp.2009.08.027 |
Loewenthal D, Wang C J, Johnson O G, et al. 1991. High order finite difference modeling and reverse time migration. Exploration Geophysics, 22(3): 533-545. |
Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. |
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. |
Mast T D, Souriau L P, Liu D L D, et al. 2001. A k-space method for large-scale models of wave propagation in tissue. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 48(2): 341-354. DOI:10.1109/58.911717 |
Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
Song X L, Fomel S, Ying L X. 2013. Lowrank finite-differences and lowrank fourier finite-differences for seismic wave extrapolation in the acoustic approximation. Geophysical Journal International, 193(2): 960-969. DOI:10.1093/gji/ggt017 |
Soubaras R, Zhang Y. 2008. Two-step explicit marching method for reverse time migration.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2272-2276.
|
Stoffa P L, Pestana R C. 2009. Numerical solution of the acoustic wave equation by the rapid expansion method (REM) - A one step time evolution algorithm.//79th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2672-2676.
|
Sun J Z, Fomel S, Sripanich Y, et al. 2017. Recursive integral time extrapolation of elastic waves using low-rank symbol approximation. Geophysical Journal International, 211(3): 1478-1493. DOI:10.1093/gji/ggx386 |
Tabei M, Mast T D, Waag R C. 2002. A k-space method for coupled first-order acoustic propagation equations. The Journal of the Acoustical Society of America, 111(1): 53-63. |
Tal-Ezer H, Kosloff D, Koren Z. 1987. An accurate scheme for seismic forward modelling. Geophysical Prospecting, 35(5): 479-490. DOI:10.1111/j.1365-2478.1987.tb00830.x |
Tan S R, Huang L J. 2014. A staggered-grid finite-difference schemeoptimized in the time-space domain for modeling scalar-wave propagation in geophysical problems. Journal of Computational Physics, 276: 613-634. DOI:10.1016/j.jcp.2014.07.044 |
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Virieux J. 1986. P-SV wave propagation in heterogeneous media; Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. |
Yuan Y X, Hu T, Wang Z Y, et al. 2018. Solving second-order decoupled elastic wave equation using low-rank decomposition and low-rank finite differences. Chinese Journal of Geophysics (in Chinese), 61(8): 3324-3333. DOI:10.6038/cjg2018L0257 |
Yuan Y X, Liu H, Hu T, et al. 2017. A new staggered-grid scheme for decoupled elastic-wave modeling based on low-rank finite-difference method. 87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4164-4168.
|
Zhang J H, Yao Z X. 2013. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. Journal of Computational Physics, 250: 511-526. DOI:10.1016/j.jcp.2013.04.029 |
Zhang Y, Zhang G Q. 2009. One-step extrapolation method for reverse time migration. Geophysics, 74(4): A29-A33. |
李孝波, 薄景山, 齐文浩, 等. 2014. 地震动模拟中的谱元法. 地球物理学进展, 29(5): 2029-2039. DOI:10.6038/pg20140506 |
袁雨欣, 胡婷, 王之洋, 等. 2018. 求解二阶解耦弹性波方程的低秩分解法和低秩有限差分法. 地球物理学报, 61(8): 3324-3333. DOI:10.6038/cjg2018L0257 |
 2020, Vol. 63
2020, Vol. 63


