地电场是重要的地球物理场,根据场源的不同可以分为自然电场和大地电场.其中,自然电场是地球介质受到局部的各种物理化学作用而产生的局部稳定电场.大地电场是地球外部各种电流体系地球内部感应产生的全球性或区域性的变化电场.对地电场时间序列信号的研究可以为地震监测等提供参考依据(席继楼,2019).
在国内外地电场观测台网中,许多台站都观测到了地电场的静日变化,这些变化通常都具有比较规律的形态.黄清华和刘涛(2006)在对日本伊豆群岛新岛台地电场信号中的潮汐响应定量提取和分析后发现,潮汐响应包含周期为24 h的全日分潮、12 h的半日分潮等不同周期的频率成分,并且不同成分的潮汐响应也呈现出半月变、半年变等周期活动规律.谭大诚等(2010, 2011)在讨论地电场周期性变化的产生机理和变化特征时同样发现地电场信号包含24 h、12 h、8 h和6 h等谐波信号,靠近海洋和大型湖泊的台站的日变现象更加明显,呈现出类似固体潮的变化形态.叶青等(2007)指出地电场日变幅度呈现出明显的季节性变化.以上研究表明,在没有地电场异常和干扰较小的情况下,地电场信号可以通过不同频率谐波来拟合.
随着城市化、现代化进程加快,大型工业电器设备向郊区转移,大型城市兴建轨道交通系统,电磁环境干扰因素越来越多.由此产生的高压输电电流、工业游散电流、轨道泄漏电流等,都对地电场的观测造成了严重的影响(席继楼,2019).这导致地电场观测数据中有用的信息不能被充分挖掘和利用.如何从观测到的数据中准确迅速去除干扰的影响,成为了亟待解决的问题.
Koganeyama等(2003)考虑列车噪声的统计分析情况利用独立成分分析方法(Independent Component Analysis, ICA),从实际观测地电场信号中把电车噪声和地震电信号分离开来,且分离出的电车噪声波动特点不同.Ishikawa等(2005)也将独立成分分析方法应用至地电场数据,从位于长野县松代台站的数据中分离出可能的地震电信号,并分析了提取出的地震电信号与新潟中越地震的关系.Telesca等(2004)利用主成分分析方法(Principal Component Analysis, PCA)分析了意大利南部朱利亚诺台站地电场数据,发现地震前主成分呈现出变大的特征.
安张辉等(2011)将希尔伯特-黄变换(HHT)方法应用于北京市通州区西集镇地电场台站的实际观测数据处理,在一定程度上抑制了轨道交通产生的噪声.李伟等(2013)利用小波变换方法来分解地电场实际观测数据,去除了日常的背景噪声干扰,重构后的信号保留了原始信号中的主要特征.朱肖雄等(2015)在对加入不同大小噪声的自然电场数据进行反演时,设计了一种粒子群优化算法,能够有效去除噪声的影响,使反演收敛快、精度高.崔益安等(2017)在对加入噪声的自然电场模拟数据进行卡尔曼滤波递归处理后,仍能进行时序反演,重构动态地电模型,表明了卡尔曼滤波法在时序反演算法中可以去除噪声的影响.冯红武等(2019)利用基于经验模态分解(Empirical Mode Decomposition, EMD)的小波阈值去噪方法滤除地电场中的地铁干扰.陈全(2019)利用扩张因果卷积网络对地电场模拟信号进行预测及提取地电场实际观测数据中的特征,但网络模型构建和参数设计仍需优化,陈全同时也利用奇异谱方法去除地铁、高压直流输电线、空间电磁环境中的高频干扰.但此类方法多基于地电场信号和噪声信号的频率特征不同,通常对频率较高的噪声信号进行滤除,因而去除噪声后的信号高频部分损失严重,容易丢失相关频段的信息.在处理一些非线性问题时,这些方法也存在一定的局限性.
神经元网络方法是目前最流行的机器学习方法之一,在时间序列数据处理上取得了显著的成绩.它不依赖数据的频谱特征,具有处理非线性数据的能力,若能将它应用到地电场数据处理中,对地电场观测台网的数据去噪具有重要意义.因此,有必要开展相关研究.本文通过日本新岛台实际数据进行谐波拟合并添加不同种类干扰(高斯随机噪声、泊松噪声及特定频率噪声)生成合成数据集,将其中的训练集对特定结构长短时记忆(Long Short-Term Memory, LSTM)神经网络进行训练,并将训练所得网络对测试集数据进行测试,测试结果显示LSTM网络通过不断更新网络参数学习到了训练集数据特征,能够有效去除测试集中输入数据添加的高斯噪声、泊松噪声和特定频率噪声.与其他神经元网络相比,长短时记忆神经网络能够对时间序列数据建立长短期记忆体系.
为进一步验证该方法的实用性和有效性,本文将训练所得网络对日本伊豆群岛新岛台地电场实际观测数据进行处理,并从处理后得到的地电场数据中提取不同成分的潮汐响应.与黄清华和刘涛(2006)利用频谱分析和BAYTAP-G(Bayesian Tidal Analysis Program-Grouping Model)方法(Ishiguro et al., 1984)对同时期数据分析得到的地电场潮汐响应日变、半日变、半月变、半年变等特征对比,验证了长短时记忆神经网络在地电位信号处理中的有效性.训练好的网络在处理实际数据时,处理时间短,不需人工干预,而且网络可用新的合成数据补充训练以识别新的特征,对不同类型噪声去除具有良好的适应性,为去除地电场数据各类干扰提供了新的方法.
1 数据 1.1 数据来源,数据频谱特征日本物理化学研究所于1997年底在伊豆群岛的新岛建立了地电场连续观测台站,共布设了16条长短方向不一的测线,默认采样周期为10 s.该台站通过电话向数据中心传输数据.在遇到地震等紧急事件时可以通过数据中心向台站发送指令,将采样周期更改为1 s模式.本文使用的地电场数据为日本伊豆群岛新岛台1998—2000年的观测数据.
由于地电场数据常常受到不同噪声的干扰,实际观测难以获得理想的无噪声数据.为便于对比数据处理效果,有必要利用合成数据来开展研究.本文基于1998—1999年日本伊豆群岛的新岛台的实测数据来建立合成数据,合成数据包含理想无噪声数据以及添加噪声数据.
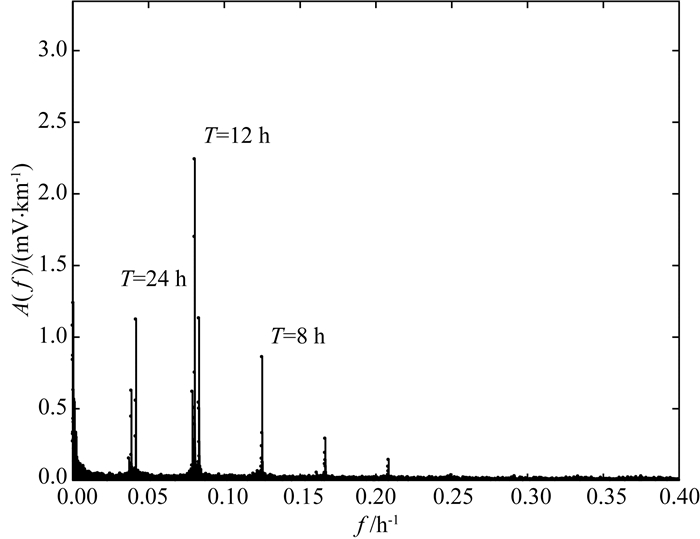
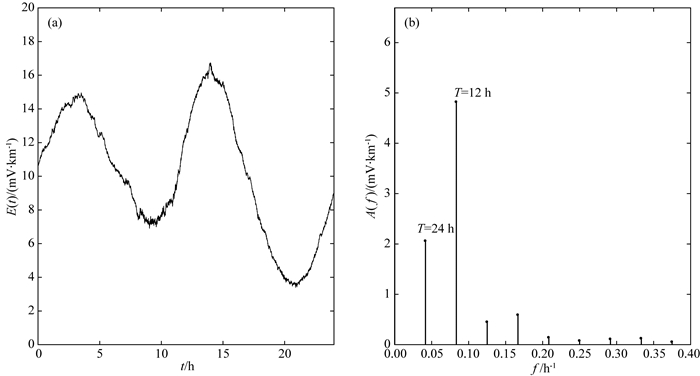
图 1给出了新岛台第一条测线1998—1999两年实际观测数据的频谱分析结果,从图中可以明显发现在周期为24 h、12 h、8 h均具有很大的幅值,对应不同周期的潮汐成分.作为例子,图 2给出了1999年12月21日的地电场时间序列和它的频谱分析图.可以看出,一天的数据也具有明显的频谱特征.
|
图 1 新岛台1998—1999两年实测数据频谱分析 Fig. 1 Spectrum of geoelectric potential data at Niijima station during 1998—1999 |
|
图 2 (a) 1999-12-21信号时间序列, (b)图(a)信号频谱分析 Fig. 2 (a) Time series of geoelectric potential data at Niijima station on 21 December 1999, (b) Spectrum of figure (a) |
因此,本文将实际观测数据进行谐波拟合,拟合所得的数据作为理想无噪声数据,在此数据基础上添加泊松噪声、高斯噪声以及特定频率噪声,得到添加噪声数据.
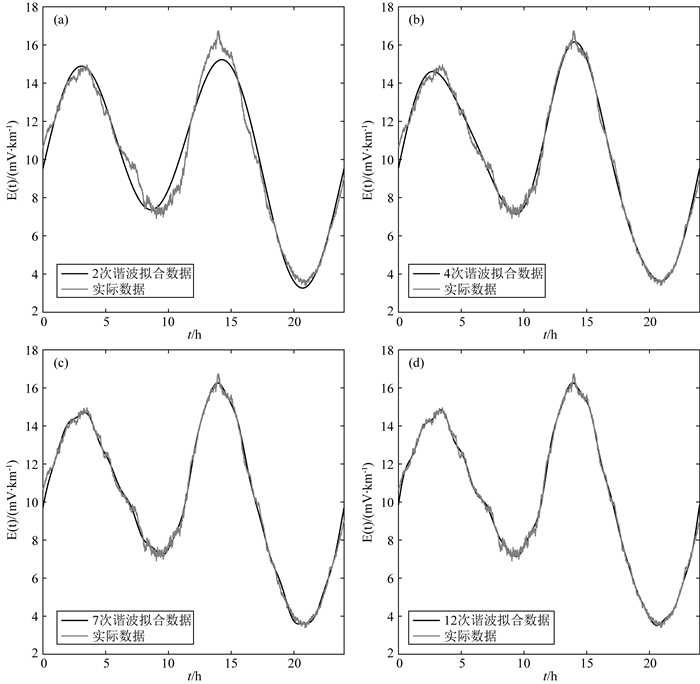
1.2 合成数据作为一个例子,图 3给出了1999年12月21日的不同次谐波拟合情况.显然,随着谐波次数的增加,谐波合成的数据和实际观测数据越吻合.在保留实际观测数据特征的前提下又希望尽可能去除噪声的影响.本文选择将7次谐波拟合得到的数据作为理想无噪声数据.
|
图 3 (a) 2次谐波拟合实际数据, (b)4次谐波拟合实际数据, (c)7次谐波拟合实际数据, (d)12次谐波拟合实际数据 Fig. 3 Data fitting based on harmonic analysis with different order, n: (a) n=2, (b) n=4, (c) n=7, and (d) n=12 |
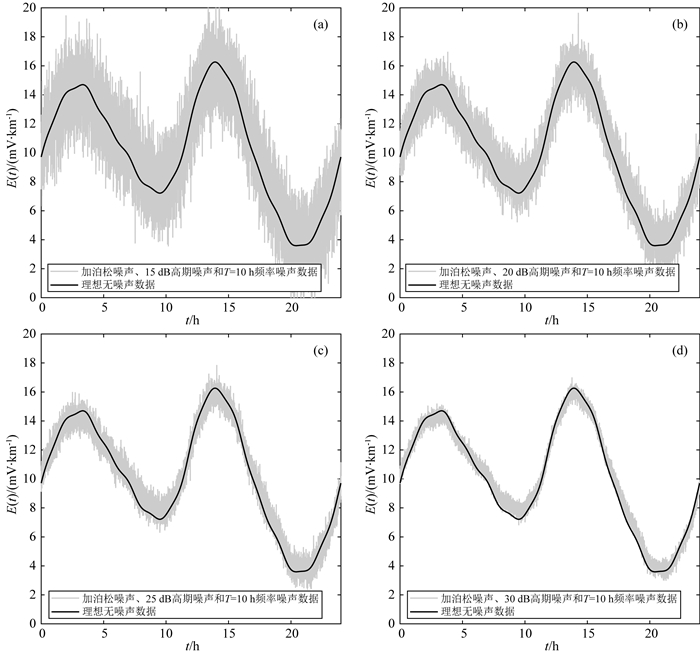
在得到理想无噪声数据的基础上,本文选择添加泊松噪声、高斯噪声和特定频率噪声作为添加噪声数据,图 4给出了分别添加泊松噪声、15 dB,20 dB,25 dB与30 dB高斯噪声以及周期T=10 h噪声前后的数据.
|
图 4 理想无噪声数据和添加泊松噪声和T=10 h频率噪声后数据: (a) 15 dB高斯噪声, (b) 20 dB高斯噪声, (c) 25 dB高斯噪声, (d) 30 dB高斯噪声 Fig. 4 Ideal noise-free data and data with Poisson noise, and T=10 h frequency noise data: (a) 15 dB Gaussian noise, (b) 20 dB Gaussian noise, (c) 25 dB Gaussian noise, (d) 30 dB Gaussian noise |
以一天的数据为一个单位,将合成的理想无噪声数据和添加噪声数据分别作为长短时记忆神经网络的一个输出和输入,这样,1998—1999两年的数据共730组输出和输入.为扩大训练网络的样本,本文在输入数据中随机添加15~30 dB高斯噪声、泊松噪声以及幅度相位在一定范围内随机取值的固定频率噪声,重复添加28次,共得到20440组数据作为网络的输出和输入.
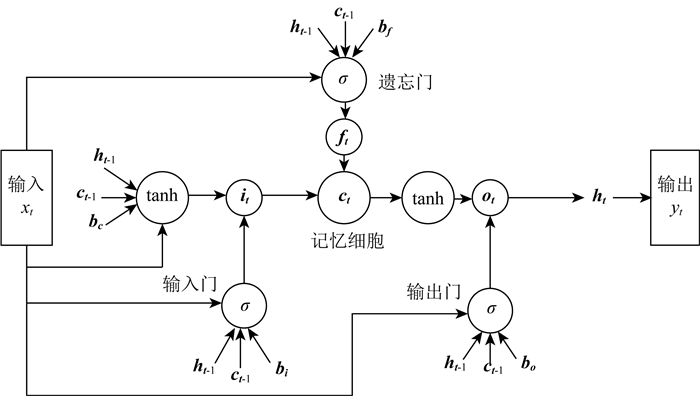
2 方法长短时记忆神经网络(LSTM)是一种特殊的循环神经网络,最早由Hochreiter和Schmidhuber(1997)提出,用于解决循环神经网络梯度爆炸、梯度消失等问题,能够处理长短期的时间序列问题,在之后使用的过程中被不断优化(Gers et al., 2000;Levy et al., 2018).LSTM网络最显著的特点是它具有一个记忆单元模块,包含三个门(输入门、输出门、遗忘门)和一个记忆细胞,具体结构如图 5所示.
|
图 5 LSTM记忆单元模块,包含输入门、输出门、遗忘门和一个记忆细胞 Fig. 5 A long short-term memory block, containing the input, output, forget gate and a memory cell |
三个门结构更新通过记忆细胞的信息流,控制记忆单元模块的行为,可以将其总结如下:
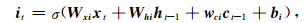
|
(1) |
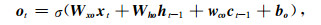
|
(2) |
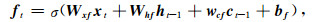
|
(3) |
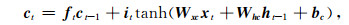
|
(4) |
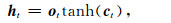
|
(5) |
其中it、ot、ft、ct为t时刻,输入门、输出门、遗忘门、记忆细胞的状态,Wxi 、Wxo 、Wxf 、Wxc 分别为输入与输入门、输出门、遗忘门和记忆细胞之间的传播权重矩阵,Whi 、Who 、Whf 、Whc 分别为隐藏单元与输入门、输出门、遗忘门和记忆细胞之间的传播权重矩阵.w ci 、wco 、wcf 是记忆细胞传播权重向量.bi、bo、bf、bc为偏置向量,σ为激活函数.
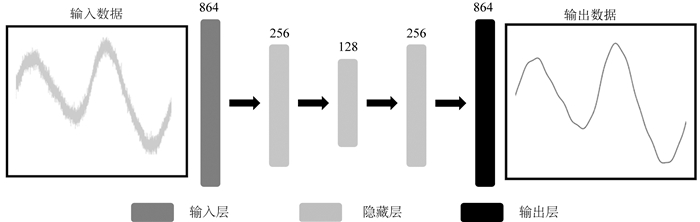
2.1 用训练集对LSTM网络进行训练如图 6所示,本文采用了一个五层的长短时记忆神经网络,包含一个输入层、一个输出层和三个隐藏层.由于计算机运算内存限制,在合成数据中每10个点提取出一个点作为训练数据,即每一天的输入和输出(添加噪声数据和理想无噪声数据)的向量长度由采样间隔为10 s的8640变为采样间隔为100 s的864.参考Vincent等(2010)提出的栈式自编码器中对称的编码和解码结构,经多种结构网络测试比较,本文长短时记忆神经网络选取的拓扑结构为864×256×128×256×864,权重矩阵W和偏置b在长短时记忆神经网络中初置为0~1之间的随机数.在神经元网络方法中,常见的做法是把测试集输入数据全部历遍一次作为一个训练循环周期.随着训练循环周期的增加,长短时记忆神经网络通过反向传播和梯度下降法,以缩小损失函数为目标来不断更新W和b,损失函数定义如(6)式所示.
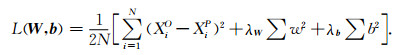
|
(6) |
|
图 6 长短时记忆神经网络结构,输入数据是添加噪声数据,输出数据是理想无噪声数据 Fig. 6 The structure of long short-term memory neural network. The input is the data with noise and the output is the ideal noise-free data |
在网络训练开始之前,合成数据会随机分成一个训练集和测试集,分别占合成数据的70%和30%.使用训练集训练上述设定的网络模型,随着循环周期的增加,损失函数的缩小不再变的明显时,认为网络已经学会处理此类数据的能力.
将训练所得的网络对测试集输入数据(添加噪声数据)进行处理得到的去噪数据和测试集原有输出数据(理想无噪声数据)进行对比,可初步判断训练所得网络的有效性.
2.3 训练所得网络对实际数据进行处理我们最终的目的是将训练完的网络应用至实际数据中,将实际数据中与我们训练集中特征类似的噪声去除.因此,本文将2.2节训练得到的网络对实际数据进行处理,提取去噪数据的信号特征,进一步判断训练所得网络的有效性.
值得注意的是,我们在训练网络过程中所使用的是采样间隔为100 s的数据.因此,在对实际数据进行测试之前,需要对实际数据进行同样的处理,即把数据的采样间隔从10 s抽稀为100 s,以匹配数据向量的长度.
3 结果和讨论 3.1 误差和准确性评价为评价训练所得网络的有效性,本文选取了三种计算误差的方式,分别为均方差(RMSE)、绝对平均误差(MAE)、1-余弦相似度(1-CS),计算公式如(7)—(9)式所示.

|
(7) |
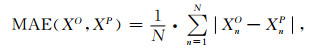
|
(8) |
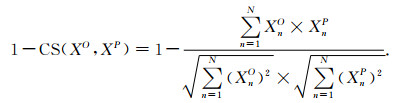
|
(9) |
在评价网络训练过程完成度时,XO为当前训练循环周期的网络输出数据,XP为对应的理想无噪声数据.在评价网络对测试集数据处理结果时,XO为测试集的网络输出数据,XP为测试集中对应的理想无噪声数据.
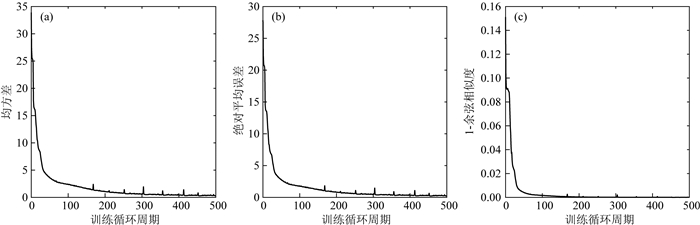
如图 7所示,在网络训练的过程中,随着训练循环周期的次数增加,训练集的三种误差不断缩小,然后随着循环周期的次数增加,三种误差趋于稳定.
|
图 7 (a) 均方差随循环周期变化,(b)绝对平均误差随循环周期变化,(c) 1-余弦相似度随循环周期变化 Fig. 7 (a) Variations of the error measurements RMSE of the testing sets with training epochs, (b) Variations of the error measurements MAE of the testing sets with training epochs, (c) Variations of the error measurements 1- CS of the testing sets with training epochs |
除了对输出数据进行三种误差计算,本文也计算了网络处理前后信号信噪比的大小,从另一个角度分析网络的有效性.
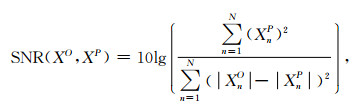
|
(10) |
其中XO为网络输出的数据,XP为理想无噪声数据.
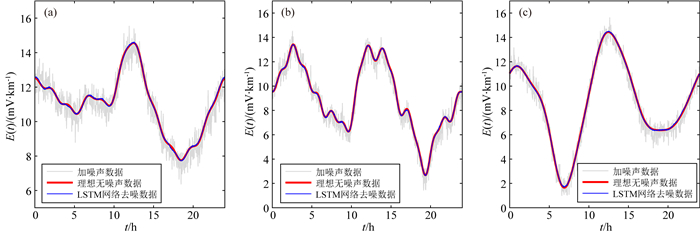
3.2 网络对合成数据处理评价经过一定次数的循环周期后,网络的损失函数和三种误差趋于稳定.此时的网络已经具有处理此类数据的能力,我们将训练得到的网络对占比30%的测试集数据进行测试,来评价网络的有效性.作为例子,图 8给出了网络去噪后的数据与测试集对应理想无噪声数据及添加噪声数据的对比.图中清晰的可以看到,经过网络去噪后的数据与测试集理想无噪声数据非常一致.换言之,经过网络处理的去噪数据,很好地完成了对输入数据中噪声的去除.信噪比由处理前的19.5 dB、24.62 dB、25.89 dB提升到39.9 dB、43.2 dB、45.1 dB,噪声得到了约20 dB的压制.
|
图 8 网络去噪数据与测试集理想无噪声数据及输入数据(添加噪声数据)对比的三个示例 Fig. 8 Three examples of the comparisons among the predicted data from LSTM neural network, the ideal noise-free data, and the data with noise |
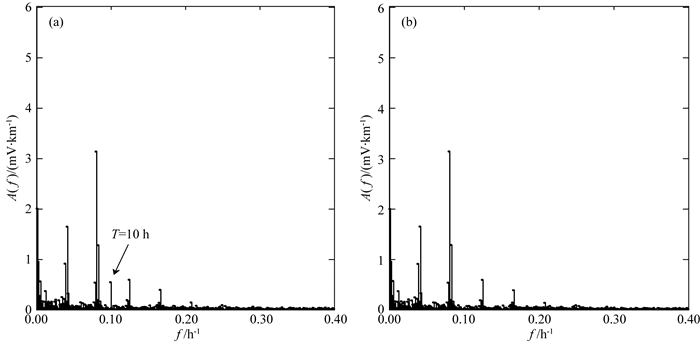
为进一步验证该网络的有效性,我们用训练好的网络处理连续三十天的合成数据(含泊松噪声、高斯噪声和特定频率噪声),并对处理前后的数据进行频谱分析,从图 9可以明显看出,作为噪声加入的T=10 h的周期成分被过滤,其他周期T=24 h、12 h、8 h等成分依然保留.
|
图 9 (a) 连续三十天合成数据频谱分析,(b)网络处理后数据频谱分析 Fig. 9 (a) Spectrum of synthetic data for 30 consecutive days, (b) Spectrum of predicted data from LSTM neural network |
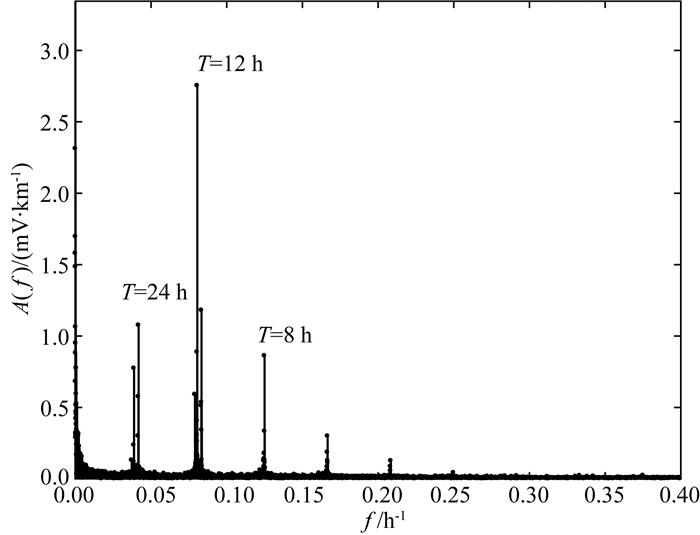
长短时记忆神经网络的去噪能力在地电场实际观测数据处理中具有重要的意义.在这里,我们将训练所得网络对新岛台第一条测线1998—2000三年的实际数据进行处理,得到实际数据的去噪结果,其中2000年7—8月数据因泥石流发生存在缺失.为评价网络训练的质量,我们将网络处理后的三年实际数据进行频谱分析,如图 10所示,所得数据具有明显24 h、12 h、8 h的潮汐成分.
|
图 10 训练所得网络对1998—2000三年实际观测数据处理后结果频谱分析 Fig. 10 Spectrum of the results by applying the network to the observed data during 1998—2000 |
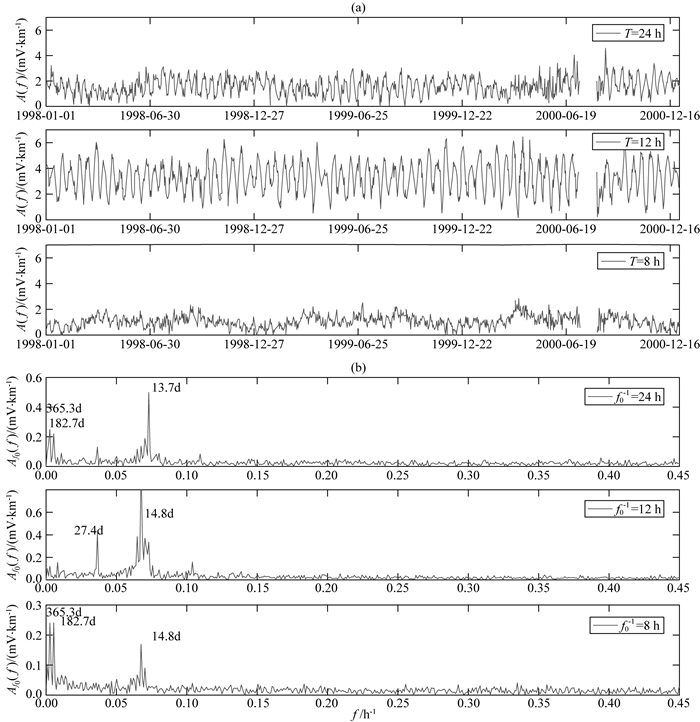
为进一步评价经过网络处理后的实际数据的质量,我们对不同成分潮汐响应进行定量分析,从频谱分析中分别提取出周期为24 h、12 h、8 h的潮汐成分,并对其幅度进行频谱分析.图 11给出了不同周期成分幅度随时间的变化和对不同潮汐成分幅度的频谱分析,可以明显看出不同潮汐成分具有半月变、月变、半年变、年变等活动规律,与黄清华和刘涛(2006)得到一致结论,验证了长短时记忆神经网络在地电场实际数据处理中的有效性.
|
图 11 (a)不同周期潮汐成分随时间变化, (b)图(a)中潮汐响应谱分析 Fig. 11 (a) Temporal variation of various tidal responses; (b) Frequency analysis of various tidal responses in figure (a) |
对于本文选取的长短时记忆神经网络拓扑结构和现有数据量,网络训练耗时5.4 h.将训练好的网络应用到1998—2000三年实际数据的处理,耗时仅6 s.可以看出,虽然网络训练的过程较为耗时,但经过训练的网络在实际数据处理时的效率很高.
4 结论本文通过基于新岛台观测到的地电场实际数据谐波拟合得到的数据对具有特定结构的长短时记忆神经网络进行训练,将训练得到的网络对合成数据中的测试集进行测试,能够很好地去除测试集中不同种类的噪声.将经过测试的网络应用至实际地电场数据,通过对处理后数据的频谱分析,可以观察出地电场数据中记录到的潮汐响应,其表现出明显的日变、半日变,以及半月变、月变、半年变、年变等特征,得到与黄清华和刘涛(2006)关于新岛台地电场的潮汐响应一致的结论.
神经元网络经过训练后可重复使用,还可以使用新的合成数据进行补充训练,处理数据不依赖相关背景知识,虽然训练比较耗时,但应用到实际数据处理的耗时非常短.由于实际地电场数据质量参差不齐,数据量大,神经元网络方法可以摆脱人工挑选特征的繁琐过程,为海量地电场数据的处理提供了便捷的新方法.
An Z H, Du X B, Yuan L H, et al. 2011. Application of Hilbert-Huang transform to geo-electric data disturbed by urban track traffic. Acta Seismologica Sinica (in Chinese), 33(2): 243-251. DOI:10.3969/j.issn.0253-3782.2011.02.011 |
Chen Q. 2019. Deep learning and its application in geoelectric field anomaly detection[Master's thesis] (in Chinese). Lanzhou: Lanzhou Institute of Seismology, China Earthquake Administration.
|
Cui Y A, Wei W S, Zhu X X, et al. 2017. Time-lapse inversion of self-potential data using Kalman filter. Chinese Journal of Geophysics (in Chinese), 60(8): 3246-3253. DOI:10.6038/cjg20170829 |
Feng H W, Yan W H, Wang J C, et al. 2019. Interference elimination generated by urban track traffic during the geoelectric field observation. Seismological and Geomagnetic Observation and Research (in Chinese), 40(3): 70-78. DOI:10.3969/j.issn.1003-3246.2019.03.010 |
Gers F A, Schmidhuber J, Cummins F, et al. 2000. Learning to Forget:Continual Prediction with LSTM. Neural Computation, 12(10): 2451-2471. DOI:10.1162/089976600300015015 |
Hochreiter S, Schmidhuber J. 1997. Long short-term memory. Neural Computation, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
Huang Q H, Liu T. 2006. Earthquakes and tide response of geoelectric potential field at the Niijima station. Chinese Journal of Geophysics (in Chinese), 49(6): 1745-1754. DOI:10.3321/j.issn:0001-5733.2006.06.022 |
Ishiguro M, Sato T, Tamura Y, et al. 1984. Tidal data analysis:an introduction to BAYTAP. Proc. Inst. Stat. Math., 32(1): 71-85. |
Ishikawa C, Watanabe C, Nagao T, et al. 2005. Extracting Seismic Electronic Signals from the Telluric Current Data for the Nigata Chuetsu Earthquake by ICA.//Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications. Las Vegas, Nevada, USA: DBLP, 2005.
|
Koganeyama M, Sawa S, Shouno H, et al. 2003. An effective evaluation function for ICA to separate train noise from telluric current data.//Proceedings of fourth International Symposium on Independent Component Analysis and Blind Signal Separation (ICA2003). Nana, Japan, 837-842.
|
Levy O, Lee K, FitzGerald N, et al. 2018. Long short-term memory as a dynamically computed element-wise weighted sum.//Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers). Melbourne, Australia: Association for Computational Linguistics, doi: 10.18653/v1/P18-2116.
|
Li W, Ma Z Q, Song Z P, et al. 2013. Application of wavelet transform to the analysis of geoelectric field data. Acta Seismologica Sinica (in Chinese), 35(1): 26-35. DOI:10.3969/j.issn.0253-3782.2013.01.004 |
Tan D C, Zhao J L, Xi J L, et al. 2010. A study on feature and mechanism of the tidal geoelectrical field. Chinese Journal of Geophysics (in Chinese), 53(3): 544-555. DOI:10.3969/j.issn.0001-5733.2010.03.008 |
Tan D C, Wang L W, Zhao J L, et al. 2011. Influence factors of harmonic waves and directional waveforms of tidal geoelectrical field. Chinese Journal of Geophysics (in Chinese), 54(7): 1842-1853. DOI:10.3969/j.issn.0001-5733.2011.07.018 |
Telesca L, Colangelo G, Hattori K, et al. 2004. Principal component analysis of geoelectrical signals measured in the seismically active area of Basilicata Region (southern Italy). Natural Hazards and Earth System Sciences, 4(5-6): 663-667. DOI:10.5194/nhess-4-663-2004 |
Vincent P, Larochelle H, Lajoie I, et al. 2010. Stacked denoising autoencoders:learning useful representations in a deep network with a local denoising criterion. Journal of Machine Learning Research, 11(12): 3371-3408. |
Xi J L. 2019. A review of geoelectric field observation methods and techniques. Seismological and Geomagnetic Observation and Research (in Chinese), 40(2): 1-20. DOI:10.3969/j.issn.1003-3246.2019.02.001 |
Ye Q, Du X B, Zhou K C, et al. 2007. Spectrum characteristics of geoelectric field variation. Acta Seismologica Sinica (in Chinese), 29(4): 382-390. DOI:10.3321/j.issn:0253-3782.2007.04.005 |
Zhu X X, Cui Y A, Li X Y, et al. 2015. Inversion of self-potentialanomalies based on particle swarm optimization. Journal of Central South University (Science and Technology) (in Chinese), 46(2): 579-585. DOI:10.11817/j.issn.1672-7207.2015.02.028 |
安张辉, 杜学彬, 元丽华, 等. 2011. HHT方法在受城市轨道交通干扰地电场观测数据中的应用. 地震学报, 33(2): 243-251. DOI:10.3969/j.issn.0253-3782.2011.02.011 |
陈全. 2019.深度学习及其在地电场异常检测中的应用研究[硕士论文].兰州: 中国地震局兰州地震研究所.
|
崔益安, 魏文胜, 朱肖雄, 等. 2017. 基于卡尔曼滤波的自然电场数据时序反演. 地球物理学报, 60(8): 3246-3253. DOI:10.6038/cjg20170829 |
冯红武, 颜文华, 王建昌, 等. 2019. 地电场观测中城市轨道交通干扰剔除. 地震地磁观测与研究, 40(3): 70-78. DOI:10.3969/j.issn.1003-3246.2019.03.010 |
黄清华, 刘涛. 2006. 新岛台地电场的潮汐响应与地震. 地球物理学报, 49(6): 1745-1754. DOI:10.3321/j.issn:0001-5733.2006.06.022 |
李伟, 马钦忠, 宋志平, 等. 2013. 小波变换在地电场数据分析中的应用. 地震学报, 35(1): 26-35. DOI:10.3969/j.issn.0253-3782.2013.01.004 |
谭大诚, 赵家骝, 席继楼, 等. 2010. 潮汐地电场特征及机理研究. 地球物理学报, 53(3): 544-555. DOI:10.3969/j.issn.0001-5733.2010.03.008 |
谭大诚, 王兰炜, 赵家骝, 等. 2011. 潮汐地电场谐波和各向波形的影响要素. 地球物理学报, 54(7): 1842-1853. DOI:10.3969/j.issn.0001-5733.2011.07.018 |
席继楼. 2019. 地电场观测方法与观测技术研究. 地震地磁观测与研究, 40(2): 1-20. DOI:10.3969/j.issn.1003-3246.2019.02.001 |
叶青, 杜学彬, 周克昌, 等. 2007. 大地电场变化的频谱特征. 地震学报, 29(4): 382-390. DOI:10.3321/j.issn:0253-3782.2007.04.005 |
朱肖雄, 崔益安, 李溪阳, 等. 2015. 基于粒子群优化的自然电场数据反演. 中南大学学报(自然科学版), 46(2): 579-585. DOI:10.11817/j.issn.1672-7207.2015.02.028 |
 2020, Vol. 63
2020, Vol. 63


