2. Istituto Nazionale di Oceanografia e di Geofisica Sperimentale (OGS), Borgo Grotta Gigante 42c, Sgonico, Trieste 34010, Italy
2. Istituto Nazionale di Oceanografia e di Geofisica Sperimentale(OGS), Borgo Grotta Gigante 42 c, Sgonico, Trieste 34010, Italy
随着人类社会对化石能源需求的不断增高,以及常规石油和天然气资源的日益紧缺,近年来,国内外的专家学者以及企业对有巨大潜力的非常规油气资源的勘探开发愈发重视.致密砂岩储层的天然气产量是全球非常规资源天然气产量的主要部分(Khlaifat et al., 2011).同时,致密砂岩油气是中国非常规油气资源的重要部分,且分布广泛.但含气致密砂岩储层一般具有强非均质性及低孔低渗的特征,其勘探开发相对常规天然气资源表现出了更大的难度(邹才能等,2011).在钻井完井、开发和增产等作业过程中,致密砂岩含气层的孔隙结构特征和裂缝尺寸会随有效应力的变化而变化,气层渗透率将受到影响(游利军等,2006).研究有效压力变化、储层孔隙结构变化条件下的地震波速度频散以及衰减特性,对在钻井完井和勘探开发过程中有效地保护、开采致密气层有重要指导意义.
为研究地震波通过复杂孔隙介质时的传播及响应特征,已有一系列岩石物理理论模型被提出(Müller et al., 2010;Ba, 2013).Biot-Gassmann理论(Biot, 1962;Gassmann, 1951)常被用于常规中、高孔隙度岩石在低频极限下的流体替换.然而,Gregory(1976)的研究揭示,流体对致密砂岩在低围压条件下的弹性波传播速度的影响,与基于Biot-Gassmann理论的估计不一致.这一认识后来也被Murphy(1984)证实,并且研究认为,弹性波通过流体饱和的多孔岩石引起的局部流体流动导致了波的频散和衰减.Mavko和Nur(1975)基于岩石内部单位孔隙的非均匀结构提出了喷射流理论模型.Dvorkin等(1994)同时考虑了含流体岩石内部的Biot流与喷射流,提出了BISQ理论模型.聂建新等(2010)考虑泥质含量的影响,推导了含泥质孔隙各向异性黏弹性介质的BISQ模型.Pride等(2004)首次采用双重孔隙介质波动理论方程成功描述了喷射流机制.巴晶等(Ba et al., 2011; 巴晶等,2012)考虑两类孔隙的流体界面上存在的压力梯度所导致的流体局部流动,推导了具有严格物理含义的双重孔隙介质波动方程,该模型可以确凿描述不同频率下岩石内部局域流导致的波的频散和衰减特征.
前人文献已进行了大量实验测量和系统分析研究,以研究不同类型的流体及围压变化对岩石内部弹性波响应特征的影响,特别是对于Berea砂岩和Fontainebleau砂岩等的影响(Chapman et al., 2016, 2017;Pimienta et al., 2015, 2016).实验观测表明,随着围压的增加,多孔砂岩中弹性波传播速度增加,同时衰减减小,而其速度、衰减对压力变化的响应程度,则是随微观结构和黏土含量的改变而改变(刘斌等,1998).Han等(1986)认为,黏土含量的增大是使孔隙度和纵波速度减小的主要原因.Smith等(2010)研究了超声波频率下围压和孔隙结构对致密气砂岩纵、横波速度的影响.Tutuncu等(1994)发现致密砂岩相邻颗粒间存在紧密接触,这种接触在颗粒边缘形成了大量的纵横比很小的微裂隙,导致致密砂岩纵、横波速度对压力变化比普通砂岩更为敏感.
岩石中裂隙的存在不仅影响岩石的弹性性质,同时控制孔、裂隙中的流体流动(Müller et al., 2010;Carcione, 2014).国内外众多学者通过采用等效介质理论与岩石物理实验(Song et al., 2016; Yin, 2017)研究裂隙对岩石弹性性质的影响.David和Zimmerman(2011)计算了包含随机分布的椭球状裂隙的岩石的弹性模量,虽然裂隙在岩石中所占含量较小,但对弹性性质的影响很显著.考虑到岩石中微裂隙的特征与压力变化紧紧相关,岩石的裂隙的分布特征(裂隙纵横比,裂隙密度,裂隙孔隙度,裂隙半径)可从与压力相关的弹性模量中进行提取(Cheng and Toksöz, 1979;Tran et al., 2008;David and Zimmerman, 2012).但是这些方法没有考虑孔隙、裂隙间的局部流体流动,无法描述岩石中的速度频散特征.因此,需要考虑地下岩石内部微观孔隙结构的复杂性与孔-裂隙间流体流动的特点,针对含裂隙致密砂岩的实验观测和波响应特征研究仍需进一步开展.
本文研究基于超声波实验观测,研究有效压力变化对致密砂岩孔隙结构和弹性波响应特征的影响.基于实验测量的纵横波速度反演随有效压力变化的裂隙参数,然后采用双重孔隙介质模型描述不同有效压力下饱水致密砂岩纵波速度频散和衰减随频率的变化规律,统计分析不同有效压力下模拟的致密砂岩裂隙参数随岩石孔隙度的变化规律.
1 实验观测结果本文进行超声波实验观测的13块样本取自四川盆地广安气田须家河组致密砂岩储层.将致密砂岩样本按孔隙度分为小于5%、5%~10%、大于10%的三组,其基础岩石物理性质如表 1所示.
|
|
表 1 广安致密气砂岩岩石物性参数 Table 1 Physical properties of Guang′an tight gas sandstones |
实验所选用的岩石样品采自广安地区上三叠统须家河组致密砂岩储层.上三叠统须家河组致密砂岩储层由于其独特的生储盖组合,是四川盆地最具勘探潜力的层系之一(谢继容等,2008).其储层具有低孔、低渗、含水饱和度高等特征,属于辫状河三角洲沉积体系,砂岩陆湖碎屑成分主要为石英、长石、岩屑以及云母、重矿等矿物.须家河组砂岩普遍见石英次生加大现象,尤其在石英含量高、分选好的砂岩中更为丰富.石英次生加大会减少原生粒间孔、堵塞喉道.本次研究所使用砂岩类型主要为岩屑石英砂岩,少量含硅质石英砂岩.所选致密砂岩样本中石英含量在50%以上,当石英含量超过75%左右时,硅质胶结物增加,硅质的胶结作用将颗粒之间的孔隙充填.这也是须家河组砂岩储层低孔、低渗的主控因素之一.
三块不同孔隙度范围内的典型岩样薄片如图 1所示.GAR11样本(图 1a)孔隙度最小,以石英为主,颗粒内见固态包裹体,填隙物以水云母杂基为主,少量硅、灰质胶结.GAR12样本(图 1b)孔隙度在三块岩样居中,颗粒以中粒石英为主,粗粒次之,少量长石,呈次棱角状,分选中等.GAR8样本(图 1c)孔隙度最大,颗粒分选好,粗粒为主,中粒次之.以石英为主,接触、孔隙型胶结,填隙物为水云母杂基及硅质胶结物.粒间溶孔、超大孔隙发育,连通性好.

|
图 1 三块不同孔隙度典型岩样GAR11 (a)、GAR12 (b)、GAR8 (c)薄片图,样本孔隙度分别为3.03%、8.97%和13.35% Fig. 1 Thin sections of the three typical rock samples GAR11 (a), GAR12 (b), GAR8 (c) with different porosities. The porosities are 3.03%, 8.97%, and 13.35%, respectively |
本文采用与Guo等(2009)相同的实验装置,通过超声波脉冲法测量岩石样本中的波传播速度.对于饱气实验观测,首先将样本烘干,用橡胶套将岩样密封并置入实验装置中,对各样本施加5 MPa、10 MPa、15 MPa、20 MPa、25 MPa、30 MPa、35 MPa的有效压力(围压减去孔隙压力),然后利用装置内的电热丝加热施加围压的流体,加热至80 ℃并维持半小时,进行超声波实验测量,记录通过岩石样本的超声波波形.对于饱水实验观测,用抽真空加压饱和的方法使致密砂岩样本饱水,然后依照饱气实验流程进行超声波实验测量,记录通过岩石样本的超声波波形.基于提取的纵横波波形的初至计算不同有效压力下致密砂岩在饱气和饱水条件下的纵、横波速度.
1.3 实验结果分析图 2所示为饱气及饱水条件下致密砂岩样本的纵、横波速度随着差压变化的实验测量结果.从不同孔隙度范围的三组致密砂岩样本中各选取两块致密砂岩,调查其纵、横波波传播速度随差压变化的规律.图 3、4、5分别为所选6块致密砂岩样本纵波速度、横波速度、纵横波速度比随差压的变化规律.图 3和图 4表明,饱气及饱水状态下致密砂岩的纵、横波速度随差压的增大而逐渐增大.这主要是因为随着有效应力的增大,致密砂岩中微裂隙逐渐闭合,其体积模量和剪切模量逐渐增大,导致纵、横波速度增大.从图 5中可以看出致密砂岩饱气状态下除样本GAR12外,纵横波速度比均随着差压的增大呈增大趋势,这与宋连腾等(2015)在干燥状态下测得的致密砂岩纵横波速度比随围压变化的规律趋势基本一致,样本GAR12纵横波速度比随差压的增大而减小.饱水状态下所选的6块致密砂岩样本的纵横波速度比均随着差压的增大逐渐减小.由于实验样本物理性质的不同以及实验条件的不同,实验结果规律可能存在一定差异.

|
图 2 饱气(a)、饱水(b)条件下6块致密砂岩样本纵、横波速度随差压变化交汇图 Fig. 2 Crossplots of Vp and Vs under different differential pressures in the six tight sandstone samples at full-gas saturation (a) and full-water saturation (b), respectively |

|
图 3 饱气(a)、饱水(b)条件下6块致密砂岩样本纵波波速随差压的变化规律 Fig. 3 Variations of Vp with differential pressure in the six tight sandstone samples under full-gas saturation (a) and full-water saturation (b), respectively |

|
图 4 饱气(a)、饱水(b)条件下6块致密砂岩样本横波波速随差压的变化规律 Fig. 4 Variations of Vs with differential pressure in the six tight sandstone samples under full-gas saturation (a) and full-water saturation (b), respectively |

|
图 5 饱气(a)、饱水(b)条件下6块致密砂岩样本纵横波速度比随差压的变化规律 Fig. 5 Variations of Vp/Vs ratio with differential pressure in the six tight sandstone samples under full-gas saturation (a) and full-water saturation (b), respectively |
进行岩石裂隙参数反演,首先需要获取致密砂岩样本随压力变化的超声波实验数据,然后建立符合孔、裂隙储层微观孔隙结构特征的等效介质理论,结合实验数据,求取致密砂岩内部的微观孔隙结构特征,具体步骤如下:
(1) 基于Mori-Tanaka理论(Mori and Tanaka, 1973)建立岩石弹性模量与微观孔隙结构的关系,则岩石介质的等效弹性模量可表达为:

|
(1) |

|
(2) |
其中Kstiff和Gstiff分别为仅含硬孔隙(粒间孔隙)岩石的等效体积与剪切模量,K0和G0分别为岩石颗粒的体积与剪切模量,ϕstiff为岩石中硬孔隙的孔隙度,P、Q为硬孔隙的形状因子,与椭球形孔隙的纵横比α以及岩石颗粒的泊松比ν有关,分别被定义为

|
(3) |

|
(4) |
其中,ν=(3K0-2G0)/(6K0+2G0),

|
以包含硬孔隙的介质为背景相,考虑裂隙对岩石弹性性质的影响,则岩石介质的等效弹性模量将表达为(Mori and Tanaka, 1973):

|
(5) |

|
(6) |
其中,Keff、Geff分别为岩石的等效体积与剪切模量,νstiff=(3Kstiff-2Gstiff)/(6Kstiff+2Gstiff)是仅含硬孔隙岩石的泊松比,Γ是裂隙密度(嵌入在单元体中的裂隙总数).
由于高有效压力下软孔隙(裂隙)近似完全关闭,岩石中仅有硬孔隙存在.因此,可通过实验室所测量的高有效压力下岩石的纵横波速度(Vphp,Vshp),估算岩石高压下的等效体积模量Khp与剪切模量Ghp,则有:

|
(7) |
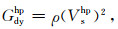
|
(8) |
其中上标“hp”为高有效压力,ρ为岩石的密度,即ρ=(1-ϕ)ρs+ϕρf,ρs和ρf分别为颗粒密度和流体密度.假设所有裂隙都在极高压条件下闭合,因此主相材料的有效弹性模量即为高压模量.因此,可以从测量的高压体积压缩率直接获得有效静态体积模量,即基于公式(1),通过高压静态体积模量的最小二乘回归来求取最吻合的硬孔隙的纵横比αstiffhp.
(2) 有效模量的压力依赖性与裂缝密度密切相关.当给出裂缝密度时,弹性模量可以用式(5)和(6)获得,反之亦然.因此,可基于各个有效压力下测得的弹性模量和式(5)和(6),利用最小二乘回归来拟合各个压力下的累积裂隙密度Γp(α).
(3) 基于所给出的各有效压力p下的裂隙密度,建立裂隙密度随有效压力变化的定量关系(Shapiro, 2003):

|
(9) |
其中,Γi是在有效压力为零时的初始裂隙密度,
(4) 用αi和α(p)分别表示有效压力为零和压力p下的裂纹纵横比.在压差增加时,裂隙闭合,Γi逐渐减小.在压力p下打开的所有裂隙都具有初始纵横比αpi的最小值,并且根据David和Zimmerman(2012):

|
(10) |
其中K(Γp)是由式(1)给出的压力p下的有效静态体积模量.
将式(9)代入式(10),得到
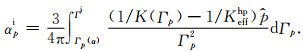
|
(11) |
在Γi和Γp(α)之间积分式(11)得到

|
(12) |
其中νhp=(3Keffhp-2Geffhp)/(6Keffhp+2Geffhp)是高压下的有效静态泊松比.
基于式(9)和式(12),建立初始状态的孔隙纵横比与有效压力之间的定量关系,可表达为

|
(13) |
其中,Eeffhp是高有效压力下的等效杨氏模量,定义为Eeffhp=3Keffhp[1-2νeffhp].考虑到有效压力p逐渐增大时,具有不同纵横特征的裂隙随压差增量dp的变化量是相同的.因此,当dp足够小时,裂隙密度的减少量可归因于纵横比小于αpi的裂隙闭合造成的.裂隙孔隙度与裂隙密度的关系为(David and Zimmerman, 2012):

|
(14) |
故可以基于实验室测量的纵横波速度获得岩石内部裂隙孔隙度与密度的分布特征(Zhang et al., 2019).
将测得的所选6块致密砂岩样本的纵横波速度分别代入上述岩石内部裂隙参数反演方法,估算实验差压下致密砂岩内部的裂隙孔隙度以及裂隙密度.从图 6-7中可以看出,致密砂岩样本裂隙孔隙度及密度均随着差压的增大而逐渐减小,当差压从5 MPa增加到35 MPa时,裂隙孔隙度一般从10-3减小到10-4.在不同样本中,随着孔隙度的增大,岩石内部裂隙的孔隙度以及密度也越大.

|
图 6 6块致密砂岩样本的裂隙孔隙度随差压的变化关系 Fig. 6 Variation of crack porosity with differential pressure in the six tight sandstone samples |

|
图 7 6块致密砂岩样本的裂隙密度随差压的变化关系 Fig. 7 Variation of crack density with differential pressure in the six tight sandstone samples |
致密砂岩的孔隙结构具有强非均匀性,即岩石内部的孔隙参数是不均一的,不同形状、不同压缩性与不同渗透率的孔隙被嵌入、分布于同一岩石骨架中,形成多重孔隙结构(Pettijohn et al., 1972).本文主要考虑致密砂岩的微观非均质性,即粒间孔与颗粒断裂(颗粒接触,即微裂隙)组成的微观双孔结构.在弹性波挤压双孔结构岩石过程中,两类孔隙内部的流体分别以不同的动力学特征与岩石骨架发生耦合振动.由于孔隙结构不同在两类孔隙之间产生了压力梯度,流体在这种压力梯度作用下,产生局部流动,导致了致密砂岩纵波速度的频散和衰减.基于超声波实验测得的数据,进行裂隙参数反演,并利用双重孔隙模型分析不同差压下致密砂岩速度频散和衰减特征,其流程如图 8所示.

|
图 8 不同差压下致密砂岩纵波速度频散和衰减特征分析流程图 Fig. 8 The flowchart of analysis on velocity dispersion and attenuation characteristics for P-waves in the tight sandstones under different differential pressures |
针对岩石的双重孔隙结构特征,Ba等(2011)提出了Biot-Rayleigh双重孔隙介质模型.该双重孔隙介质模型的波动控制方程是由Hamilton原理推导得出的,将不同孔隙区域间的局部流体流动相互作用引入应变能、动能,建立了相应的势能函数、动能函数和耗散函数,进而推导出相应的双孔介质波传播控制方程为(Ba et al., 2011):

|
(15a) |

|
(15b) |

|
(15c) |
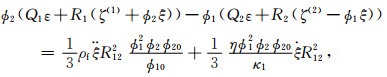
|
(15d) |
式中u, U(1), U(2)分别为固体骨架的平均颗粒位移,流体相1(主骨架中的流体)、流体相2(微裂隙中的流体)的位移;ε, ζ(1), ζ(2)是对应的3个位移散度场;ξ表示局域流过程中导致的流体应变增量,其物理意义是粒间孔隙与微裂隙交换的流体体积.岩石内部由于孔隙结构的非均匀性发育有两类不同孔隙,ϕ10和ϕ20是主体骨架和裂隙的局部孔隙度;R12为微裂隙的半径.ϕ1, ϕ2是两类孔隙的绝对孔隙度.b1, b2是Biot耗散系数.ρf, η, κl为水的密度、黏度与渗透率.ρ11, ρ12, ρ13, ρ22, ρ33为密度参数,A, Q1, Q2, R1, R2为弹性参数.
通过平面波分析法求解方程(9)(Ba et al., 2017),代入平面波解析解,可给出含流体岩石的波速及衰减的模型预测结果.
在分析前述含微观非均质性的致密砂岩模型的过程中,主体骨架即为低孔低渗的致密砂岩主骨架,裂隙骨架则为局部的微裂隙或颗粒接触形成的软骨架.基于岩石样本的实际岩石物理参数,采用双重孔隙介质模型来模拟饱和水条件下三块不同孔隙度范围的致密砂岩样本(GAR11、GAR12、GAR8)在不同有效压力下的频散和衰减,如图 9-11所示.其中可以利用Batzle-Wang公式(Batzle and Wang, 1992)计算得到实验条件下水的密度、体积模量、黏度.基于所测得饱气状态的纵、横波速度,利用Gassmann方程计算致密砂岩干骨架体积模量和剪切模量.
|
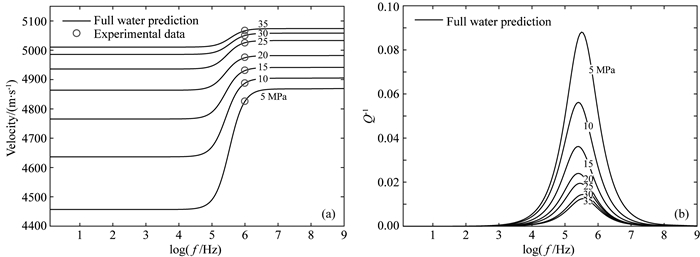
图 9 样本GAR11在5 MPa、10 MPa、15 MPa、20 MPa、25 MPa、30 MPa、35 MPa下纵波速度(a)与衰减(b)随频率的变化关系 圆圈给出了不同差压下的纵波速度实验数据. Fig. 9 Variations of Vp (a) and attenuation (b) with frequency in sample GAR11 at 5 MPa, 10 MPa, 15 MPa, 20 MPa, 25 MPa, 30 MPa, and 35 MPa differential pressure, respectively The circles give the experimental Vp data under different differential pressures. |

|
图 10 样本GAR12在5 MPa、10 MPa、15 MPa、20 MPa、25 MPa、30 MPa、35 MPa下纵波速度(a)与衰减(b)随频率变化关系 圆圈给出了不同差压下的纵波速度实验数据. Fig. 10 Variations of Vp (a) and attenuation (b) with frequency in sample GAR12 at 5 MPa, 10 MPa, 15 MPa, 20 MPa, 25 MPa, 30 MPa, and 35 MPa differential pressure, respectively The circles give the experimental Vp data under different differential pressures. |

|
图 11 样本GAR8在5 MPa、10 MPa、15 MPa、20 MPa、25 MPa、30 MPa、35 MPa下纵波速度(a)与衰减(b)随频率的变化关系 圆圈给出了不同差压下的纵波速度实验数据. Fig. 11 Variations of Vp (a) and attenuation (b) with frequency in sample GAR8 at 5 MPa, 10 MPa, 15 MPa, 20 MPa, 25 MPa, 30 MPa, and 35 MPa differential pressure, respectively The circles give the experimental Vp data under different differential pressures. |
由图 9-11可知,模型预测结果和超声波实验测得的纵波速度吻合良好,双重孔隙介质模型能够有效的描述致密砂岩纵波速度变化随差压的变化规律.对于每个致密砂岩样本,随着差压的增大,致密砂岩的纵波速度的频散现象有减小的趋势,而对应的纵波衰减减小.同时随着差压的增大,衰减减弱的幅度逐渐降低,并且衰减峰主频向高频端移动.对于所选三块不同孔隙度的致密砂岩,随着岩石孔隙度的增大,纵波速度频散程度整体呈增大趋势,其对应的衰减相应增大.并且随着孔隙度的增大,致密砂岩纵波衰减峰主频向高频端偏移.在相同的应力条件下,不同孔隙度的致密砂岩的频散和衰减特征是不同的,孔隙度较大的岩石纵波速度较低,速度频散更显著,衰减更强,衰减主频较高.
3.2 不同差压作用下的致密砂岩孔隙结构分析由图 12a可知,通过裂隙参数反演计算得到的裂隙孔隙度表现了与裂隙半径同样的变化趋势,即随着差压的增加而减小,且在差压增大到30 MPa左右趋于平缓.图 12b给出了差压变化对致密砂岩裂隙半径的影响,随着差压增加,岩石内部原始由颗粒破裂组成的裂隙被压密、趋于闭合,裂隙半径减小;而随着差压继续增大,当差压达到30 MPa左右时,裂隙半径减小的趋势趋于平缓.而对于不同孔隙度的致密砂岩,孔隙度越大,裂隙半径也越大,并且裂隙半径的减小幅度也越大.图 12c显示,致密砂岩裂隙体积模量随差压的增大逐渐增大,大部分样本在压力加载初期裂隙体积模量的变化较明显,当差压达到25 MPa时,裂隙体积模量变化较小.

|
图 12 裂隙孔隙度(a)、裂隙尺寸(b)以及裂隙体积模量(c)与差压的关系 Fig. 12 Variations of crack porosity (a), crack size (b) and crack bulk modulus (c) with different differential pressure |
由所选三块不同孔隙度致密砂岩岩样(GAR11、GAR12、GAR8)孔隙结构及弹性波响应特征随差压变化的直方图(图 13)可知,三块岩样在差压加载过程中,裂隙孔隙度、裂隙半径以及衰减逆品质因子存在明显的减小趋势,而裂隙体积模量随着差压的增大而增大,且差压越大,变化趋势越平缓.图 13也表明,孔隙度越大的岩样,上述变化趋势越明显.

|
图 13 GAR11 (a)、GAR12 (b)、GAR8 (c)三块致密砂岩裂隙孔隙度(ϕ2)、半径(R12)、体积模量(Kb2)及衰减(Q-1)随差压变化的直方图 Fig. 13 Crack porosity (ϕ2), radius (R12), bulk modulus (Kb2) and attenuation (Q-1) versus differential pressure in the three tight sandstone samples of GAR11 (a), GAR12 (b) and GAR8 (c), respectively |
图 14所示为不同孔隙度范围的三组致密砂岩裂隙参数及衰减随差压变化的直方图.随着差压的增加,裂隙孔隙度、裂隙半径及纵波衰减逐渐减小,裂隙的体积模量增大.致密砂岩在孔隙度小于10%范围内,裂隙半径均值一般小于20 μm,孔隙度大于10%范围内,裂隙半径均值迅速增大.在孔隙度小于5%的致密砂岩中,波衰减平均值较小,孔隙度大于5%范围内,纵波衰减明显增大.需要注意的是,致密砂岩裂隙体积模量平均值在不同孔隙度范围内变化不大.

|
图 14 低孔隙度范围(ϕ < 5%)(a)、中低孔隙度范围(5% < ϕ < 10%)(b)、中孔隙度范围(ϕ>10%)(c)三组致密砂岩裂隙孔隙度(ϕ2)、半径(R12)、体积模量(Kb2)及衰减(Q-1)均值随差压变化直方图 Fig. 14 The average values for crack porosity (ϕ2), radius (R12), bulk modulus (Kb2) and attenuation (Q-1) versus differential pressure in the three sets of tight sandstone samples in low-porosity range (ϕ < 5%) (a), moderate-low-porosity range (5% < ϕ < 10%) (b) and moderate-porosity range (ϕ>10%) (c), respectively |
图 15给出了不同压力下裂隙孔隙度变化量、裂隙半径变化量、裂隙体积模量变化量随孔隙度的变化规律.根据对模型模拟参数的统计分析,致密砂岩随着差压的增大,其内部裂隙孔隙度变化量和半径变化量随着孔隙度的增大呈减小趋势,而体积模量变化量与孔隙度的关系并不明显.岩石孔隙度越大,当差压增加时,微裂隙更容易被压缩,其微裂隙体积的变化也更大.

|
图 15 不同压力下(5 MPa与35 MPa)裂隙孔隙度变化量(a)、裂隙半径变化量(b)、裂隙体积模量变化量(c)随孔隙度变化关系 Fig. 15 Variations of the differences of crack porosity (a), crack radius (b), and crack bulk modulus (c) between different differential pressures (5 MPa and 35 MPa) with porosity |
利用双重孔隙介质模型,根据实际岩石的模拟参数,建立了致密砂岩裂隙孔隙度、裂隙半径和裂隙体积模量随岩石总孔隙度、差压变化的三维拟合结果,拟合平面与样本数据的对比结果如图 16所示.由图中可知,致密砂岩裂隙体积模量和裂隙孔隙度受差压的影响强于岩石自身孔隙度的影响,而裂隙半径受岩石孔隙度的影响强于差压变化的影响.建立相关的拟合关系,可以定量的描述所测量的致密砂岩裂隙参数与孔隙度、差压的联系,从而进一步可应用于分析、预测实际地层致密砂岩的结构特征.

|
图 16 裂隙孔隙度(a)、裂隙半径(b)、裂隙体积模量(c)随差压、孔隙度变化的关系 Fig. 16 Variations of crack porosity (a), crack radius (b) and crack bulk modulus (c) with differential pressure and porosity |
本文对低孔低渗致密砂岩进行了超声波实验测量.基于所建立的含微裂隙致密砂岩等效介质理论,结合实验数据,进行裂隙参数反演,利用双重孔隙介质模型研究了有效压力变化对纵波速度频散和衰减的影响,并对样本模拟参数进行分析,得到如下结论:
(1) 饱气、饱水条件下致密砂岩样本的纵、横波速度随着有效压力的增大而增大.饱气状态下,纵横波速度比随着有效压力的增大呈增大趋势;饱水状态下,纵横波速度比随着差压的增大逐渐减小.通过裂隙参数反演得到的裂隙孔隙度和裂隙密度均随着有效压力的增大逐渐减小.
(2) 模拟结果显示:模型预测的纵波速度频散和衰减幅度随着有效压力的增加而明显减弱,并且模型预测结果与实验测得的速度数据吻合良好.此外,随着有效压力的增加,纵波衰减峰值频率有向高频端移动的趋势.
(3) 通过对样本模拟参数的分析可知:当有效压力相同时,致密砂岩裂隙半径及裂隙孔隙度随着岩石样本孔隙度的增大呈增大趋势,而裂隙体积模量随着样本孔隙度的增大而减小;当有效压力不同时,致密砂岩裂隙半径和裂隙孔隙度随着有效压力的增大呈减小趋势,而裂隙体积模量随着有效压力的增大呈增大趋势.并且根据岩石的模拟裂隙参数建立了孔隙度、有效压力的三维拟合结果.
本文研究了实验室内测量的致密砂岩超声波速度随有效压力的变化特征,由于观测频率在超声波频段,因此主要波动现象反映的是岩石内部微观的裂隙随压力的分布特征.这些微观的孔隙-裂隙结构特征对于调查更大尺度的结构特征具有参考与指导意义,并且本文的模型反演方法,可类似推广应用于测井乃至地震尺度,进而估算、预测中观乃至宏观尺度的裂缝结构.
Ba J, Carcione J M, Nie J X. 2011. Biot-Rayleigh theory of wave propagation in double-porosity media. Journal of Geophysical Research: Solid Earth, 116(B6). DOI:10.1029/2010JB008185 |
Ba J, Carcione J M, Cao H, et al. 2012. Velocity dispersion and attenuation of P waves in partially-saturated rocks:Wave propagation equations in double-porosity medium. Chinese Journal of Geophysics (in Chinese), 55(1): 219-231. DOI:10.6038/j.issn.0001-5733.2012.01.021 |
Ba J. 2013. Progress and Review of Rock Physics (in Chinese). Beijing: Tsinghua University Press: 111-277.
|
Ba J, Xu W H, Fu L Y, et al. 2017. Rock anelasticity due to patchy saturation and fabric heterogeneity:A double double-porosity model of wave propagation. Journal of Geophysical Research: Solid Earth, 122(3): 1949-1976. |
Batzle M L, Wang Z J. 1992. Seismic properties of pore fluids. Geophysics, 57(11): 1396-1408. DOI:10.1190/1.1443207 |
Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33(4): 1482-1498. DOI:10.1063/1.1728759 |
Carcione J M. 2014. Wave Fields in Real Media: Theory and Numerical Simulation of Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media. 3rd ed. Amsterdam: Elsevier.
|
Chapman S, Tisato N, Quintal B, et al. 2016. Seismic attenuation in partially saturated Berea sandstone submitted to a range of confining pressures. Journal of Geophysical Research: Solid Earth, 121(3): 1664-1676. DOI:10.1002/2015JB012575 |
Chapman S, Quintal B, Tisato N, et al. 2017. Frequency scaling of seismic attenuation in rocks saturated with two fluid phases. Geophysical Journal International, 208(1): 221-225. DOI:10.1093/gji/ggw387 |
Cheng C H, Toksöz M N. 1979. Inversion of seismic velocities for the pore aspect ratio spectrum of a rock. Journal of Geophysical Research: Solid Earth, 84(B13): 7533-7543. DOI:10.1029/JB084iB13p07533 |
David E C, Zimmerman R W. 2011. Compressibility and shear compliance of spheroidal pores:exact derivation via the Eshelby tensor, and asymptotic expressions in limiting cases. International Journal of Solids and Structures, 48(5): 680-686. DOI:10.1016/j.ijsolstr.2010.11.001 |
David E C, Zimmerman R W. 2012. Pore structure model for elastic wave velocities in fluid-saturated sandstones. Journal of Geophysical Research: Solid Earth, 117(B7): B07210. DOI:10.1029/2012JB009195 |
Dvorkin J, Nolen-Hoeksema R, Nur A. 1994. The Squirt-flow mechanism:Macroscopic description. Geophysics, 59(3): 428-438. DOI:10.1190/1.1443605 |
Gassmann F. 1951. Uber Die Elastizität Poroser Medien. Vierteljahrsschrift der Naturforschenden Gesellschaft in Zurich, 96: 1-23. |
Gregory A R. 1976. Fluid saturation effects on dynamic elastic properties of sedimentary rocks. Geophysics, 41(5): 895-921. DOI:10.1190/1.1440671 |
Guo M Q, Fu L Y, Ba J. 2009. Comparison of stress-associated coda attenuation and intrinsic attenuation from ultrasonic measurements. Geophysical Journal International, 178(1): 447-456. DOI:10.1111/j.1365-246X.2009.04159.x |
Han D, Nur A, Morgan D. 1986. Effects of porosity and clay content on wave velocities in sandstones. Geophysics, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
Khlaifat A L, Qutob H, Barakat N. 2011. Tight gas sands development is critical to future world energy resources.//81st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1-12.
|
Liu B, Kern H, Popp T. 1998. Velocities and attenuation of P-and S-waves in dry and wet rocks with different porosities under different confining pressures. Chinese Journal of Geophysics (in Chinese), 41(4): 537-546. |
Müller T M, Gurevich B, Lebedev M. 2010. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics, 75(5): 147-174. |
Mavko G, Nur A. 1975. Melt squirt in the asthenosphere. Journal of Geophysical Research: Atmospheres, 80(11): 1444-1448. DOI:10.1029/JB080i011p01444 |
Mori T, Tanaka K. 1973. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica, 21(5): 571-574. DOI:10.1016/0001-6160(73)90064-3 |
Murphy III W F. 1984. Acoustic measures of partial gas saturation in tight sandstones. Journal of Geophysical Research:Solid Earth, 89(B13): 11549-11559. DOI:10.1029/JB089iB13p11549 |
Nie J X, Yang D H, Ba J. 2010. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Chinese Journal of Geophysics (in Chinese), 53(2): 385-392. DOI:10.3969/j.issn.0001-5733.2010.02.016 |
Pettijohn F J, Potter P E, Siever R. 1972. Sand and Sandstone. New York: Springer-Verlag.
|
Pimienta L, Fortin J, Guéguen Y. 2015. Experimental study of Young's modulus dispersion and attenuation in fully saturated sandstones. Geophysics, 80(5): L52-L72. |
Pimienta L, Fortin J, Guéguen Y. 2016. Effect of fluids and frequencies on Poisson's ratio of sandstone samples. Geophysics, 81(2): D183-D195. DOI:10.1190/geo2015-0310.1 |
Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow. Journal of Geophysical Research: Solid Earth, 109(B1): B01201. DOI:10.1029/2003JB002639 |
Shapiro S A. 2003. Elastic piezosensitivity of porous and fractured rocks. Geophysics, 68(2): 482-486. DOI:10.1190/1.1567215 |
Smith T, Sondergeld C, Tinni A O. 2010. Microstructural controls on electric and acoustic properties in tight gas sandstones; some empirical data and observations. The Leading Edge, 29(12): 1470-1474. DOI:10.1190/1.3525362 |
Song L T, Wang Y, Liu Z H, et al. 2015. Elastic anisotropy characteristics of tight sands under different confining pressures and fluid saturation states. Chinese Journal of Geophysics (in Chinese), 58(9): 3401-3411. DOI:10.6038/cjg20150932 |
Song Y J, Hu H S, Rudnicki J W, et al. 2016. Dynamic transverse shear modulus for a heterogeneous fluid-filled porous solid containing cylindrical inclusions. Geophysical Journal International, 206(3): 1677-1694. DOI:10.1093/gji/ggw245 |
Tran D T, Rai C S, Sondergeld C H. 2008. Changes in crack aspect-ratio concentration from heat treatment:A comparison between velocity inversion and experimental data. Geophysics, 73(4): E123-E132. DOI:10.1190/1.2928848 |
Tutuncu A N, Podio A L, Sharma M M. 1994. An experimental investigation of factors influencing compressional-and shear-wave velocities and attenuations in tight gas sandstones. Geophysics, 59(1): 77-86. |
Xie J R, Zhang J, Li G H, et al. 2008. Exploration prospect and gas reservoir characteristics of Xujiahe formation in Sichuan Basin. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 30(6): 40-44. |
Yin H J, Zhao J G, Tang G Y, et al. 2017. Pressure and fluid effect on frequency-dependent elastic moduli in fully saturated tight sandstone. Journal of Geophysical Research: Solid Earth, 122(11): 8928-8942. |
You L J, Kang Y L, Chen Y J, et al. 2006. Stress Sensitivity of fractured tight gas sands in consideration of fractures and water saturation. Journal of China University of Petroleum (in Chinese), 30(2): 59-63. |
Zhang L, Ba J, Fu L Y, et al. 2019. Estimation of pore microstructure by using the static and dynamic moduli. International Journal of Rock Mechanics and Mining Sciences, 113: 24-30. DOI:10.1016/j.ijrmms.2018.11.005 |
Zou C N, Tao S Z, Hou L H, et al. 2011. Unconventional Oil and Gas Geology (in Chinese). Beijing: Geological Publishing House.
|
巴晶, Cardione J M, 曹宏, 等. 2012. 非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程. 地球物理学报, 55(1): 219-231. DOI:10.6038/j.issn.0001-5733.2012.01.021 |
巴晶. 2013. 岩石物理学进展与评述. 北京: 清华大学出版社.
|
刘斌, Kern H, Popp T. 1998. 不同围压下孔隙度不同的干燥及水饱和岩样中的纵横波速度及衰减. 地球物理学报, 41(4): 537-546. DOI:10.3321/j.issn:0001-5733.1998.04.012 |
聂建新, 杨顶辉, 巴晶. 2010. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报, 53(2): 385-392. DOI:10.3969/j.issn.0001-5733.2010.02.016 |
宋连腾, 王赟, 刘忠华, 等. 2015. 不同围压和流体饱和状态下致密砂岩弹性各向异性特征. 地球物理学报, 58(9): 3401-3411. DOI:10.6038/cjg20150932 |
谢继容, 张健, 李国辉, 等. 2008. 四川盆地须家河组气藏成藏特点及勘探前景. 西南石油大学学报(自然科学版), 30(6): 40-44. DOI:10.3863/j.issn.1000-2634.2008.06.010 |
游利军, 康毅力, 陈一健, 等. 2006. 考虑裂缝和含水饱和度的致密砂岩应力敏感性. 中国石油大学学报(自然科学版), 30(2): 59-63. DOI:10.3321/j.issn:1000-5870.2006.02.013 |
邹才能, 陶士振, 侯连华, 等. 2011. 非常规油气地质. 北京: 地质出版社.
|
 2020, Vol. 63
2020, Vol. 63


