2. 山东科技大学山东省沉积成矿作用与沉积矿产重点实验室, 青岛 266590;
3. 中国石油大学(华东)理学院, 青岛 266580
2. Shandong Provincial Key Laboratory of Depositional Mineralization & Sedimentary Mineral, Shandong University of Science and Technology, Qingdao 266590, China;
3. College of Science of China University of Petroleum(East China)), Qingdao 266580, China
地震反演是一类利用从地表或井中收集的数据中恢复地下地质结构的数学或物理方法的总称.随着对地下结构精细描述的需求不断增加, 全波形反演(Full Waveform Inversion, 简称为FWI;Tarantola, 1984;Pratt, 1999)近年来变得很流行.FWI方法首先通过全波方程获得模拟数据, 然后根据合成数据和观测数据之间的差异计算模型参数的更新梯度, 然后使用迭代算法更新模型参数.但是, 在实际的工业生产中FWI仍然面临许多问题.为了获得高精度的反演结果, FWI方法需要长偏移数据和丰富的低频信息.同时, 由于反演的非线性和波形匹配原则, 经常会出现局部极值和周期跳跃问题(Beydoun and Tarantola, 1988; Virieux and Operto, 2009; Pratt et al., 2008; 董良国等, 2013;陈生昌和陈国新, 2016).
FWI本质上是一个偏微分方程(Partial Differential Equation, 简称为PDE)约束的优化问题.对于此类约束优化问题, 一般的解决方案是拉格朗日乘子法(Bertsekas, 1996).但是, 该方法需要对所有变量同时进行更新, 从而导致巨大的计算成本(Ben-Hadj-Ali et al., 2008; Sourbier et al., 2009).一种折衷方法是首先确定初始模型以计算拉格朗日乘子和其他变量, 然后使用梯度方法更新模型参数, 直到获得最优解为止(Tarantola, 1984;Plessix, 2006).不过, 该方法需假设所有变量都是可微的并可以用泰勒-拉格朗日近似(Plessix, 2006)进行表示.而且, 一般情况下很难准确给定反演的初始模型, 而当初始模型远离真实解时, 由于目标函数的非凸性, 反演极易陷于局部极值.为解决拉格朗日乘子法引起的计算量大问题, 同时保证PDE对反演的约束性, 许多学者(van Leeuwen and Herrmann, 2013; Li et al., 2017; 蔺玉瞾等, 2018)发展了波场重构反演方法, 该方法将PDE约束条件作为惩罚项加入到波形反演中, 循环更新波场和模型参数, 减弱了局部极值对反演的影响.
近年来, 许多学者针对初始模型的确定问题提出了很多理论和方法.Symes和Carazzone(1991)使用差分相似度优化(Differential Semblance Optimization, 简称DSO)方法获得准确的背景速度.但是, 此方法需要大量的计算生成扩展的成像集.Luo和Schuster(1991)提出了一种基于波动方程的走时的反演方法, 该方法利用走时信息作为背景模型的载体.然而, 准确确定复杂波传播的传播时间残差一直是该方法的难点.其他学者(Xu et al., 2012; De Hoop et al., 2006; Ma and Hale, 2013; AlTheyab and Schuster, 2015; Sun et al., 2016)还提出了相应反射波反演方法, 利用反射数据重建背景速度模型, 该方法同样面临着准确估计走时残差等一系列挑战.
由于上述低波数反演方法的复杂性和准确性, 一些学者提出了在高频反演中实现低波数补偿的方法.Bunks等(1995)提出了多尺度FWI方法, 该方法将观测数据分解为多个频率组, 然后从低频开始反演, 逐步移动到高频, 分别在各个尺度得到准确的反演结果, 最终得到具有准确的低波数和高波数成分的介质参数.Wu等(2014)将包络反演方法引入FWI, 通过计算观测数据的包络来提取极低频信息并用于重构小尺度低波数构造.Hu(2014)和Li等(2018)通过减去和乘以略微频移的不同波场来提取低频信息, 用于重构初始模型并减轻周期跳跃的影响.Choi和Alkhalifah(2011, 2015)则使用解缠绕相位来解决初始速度问题.该方法需要阻尼因子来降低反演的非线性度, 但只能恢复小规模模型分量, 而且计算成本较高.上面的所有方法都有一个共同的特征, 即将目标函数中采样后的波场进行替换, 并适当地修改目标函数的表示式.与传统函数相比, 修改后的目标函数虽然具有更强的凸性, 但对解决强非线性问题不是那么有效.为了解决这些问题, Zhang等(2018)提出使用直接包络Fréchet导数来解决强非线性问题.
本文结构如下:我们首先介绍基于伴随状态方法的FWI基本理论, 然后概述传统的减弱初始模型依赖性的优化反演方法, 并分析其缺点, 即针对采样后波场映射引入的伴随状态方程中的链式微分项使FWI依然在波场空间计算介质梯度.针对该问题, 我们提出了相位空间内的解缠绕相位反演方法.通过将模型空间映射到相位空间, 并采用基于振幅排列的多聚类解缠绕算法对相位进行解缠绕, 可以有效提高FWI处理强非线性问题的能力.最后, 将该新方法应用于Marmousi和部分BP模型, 证明了该方法的有效性.
1 基本理论 1.1 FWI理论FWI本质上是一个PDE约束的反演问题:

|
(1) |
其中, h表示目标函数的形式, 一般为L2范数.P是采样算子, 使波场u的坐标与观测数据d的坐标匹配, u表示满足波动方程F的波场, m表示介质参数.注意到波场u属于波场空间U, 其在频率域为一个复数空间.伴随状态法假设u(m)、h和F连续可微, 并且u(m)是唯一定义的(Plessix, 2006).
为了反演模型空间M中的模型参数m, 需要建立一个将U×U′×M映射到实数空间R的增广方程:
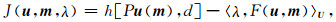
|
(2) |
其中λ表示波场对偶空间U′中的伴随状态, 而〈, 〉U表示波场空间中的标量积.目标函数的梯度可以通过拉格朗日公式获得, 该公式可以表示为

|
(3) |
上述方法要求同时计算所有变量.由于地震反演计算量大、声波方程的复杂性等原因, 拉格朗日法难以应用到FWI中.与之对应的折中方法是先给定初始模型介质参数, 然后根据给定的初始介质参数使用下述公式计算伴随状态:

|
(4) |
有了伴随状态之后, 可以进一步计算目标函数对介质参数的梯度:
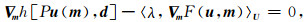
|
(5) |
然后通过迭代法逐步更新介质参数从而获得最佳的反演结果.然而, 对于不准确的初始介质模型, 观测数据和合成数据之间的走时超过半个周期, 反演会遇到周期跳跃问题, 从而收敛到错误的反演结果.或者从数学的角度来看, 由于目标函数的非凸性, 反演难以收敛到全局极值点.
为了减弱反演对初始介质参数的依赖性并克服周期跳跃问题, 许多学者提出了一些解决方法, 这些方法具有一些共同的特征, 即通过一个映射, 将目标函数中的采样后波场映射到新的变量, 以增强目标函数的凸性, 这些方法可以概括如下:
首先引入一个针对采样后波场的新映射:ϕ:Pu→
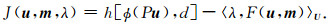
|
(6) |
由此可得新的伴随状态方程和模型梯度:
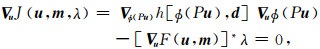
|
(7) |
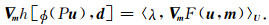
|
(8) |
比较方程(4)和(7)可以看到, 虽然引入新映射的目的是为了增强新目标函数的凸性, 但在计算伴随状态的过程中, 新的伴随状态方程引入了一个链式微分项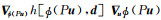
从上面的讨论中可以看出, 针对采样后波场的映射(而非针对波场的映射)引入了新反演中伴随状态方程中的链式微分项, 依然是FWI在波场空间计算介质梯度无法处理强非线性问题的主要原因.因此, 本文提出用解缠绕后的相位替换目标函数中采样前的波场, 同时将波场方程替换为频率域波动方程的相位形式, 由此将由模型空间到波场空间的映射转化为模型空间到相位空间的映射.该方法具有以下优点:①针对波场的映射可以避免伴随状态方程中的链式微分项;②解缠绕后的相位表现出对大尺度构造的强敏感性;③在相位空间中进行反演可以充分利用模型参数和解缠绕相位之间的弱非线性.
频率域波动方程的相位形式可以表示为

|
(9) |
其中ω表频率, x是空间坐标, S表示经傅里叶变换后地震子波, 而L是离散的拉普拉斯算子(van Leeuwen and Herrmann, 2013), θ(x, ω)=unwrap(arctan

|
(10) |
其中θ(mt)是观测到的真实相位, 而F(θ, m)=0表示波动方程的相位形式.新增广方程转化成一个将θ×θ′×M映射到实数空间R的新映射:

|
(11) |
由于新映射是将模型空间映射到相位空间, 可以得到相位空间内的伴随状态方程:

|
(12) |
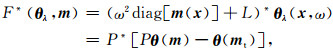
|
(13) |
其中θλ表示伴随状态或者伴随相位.
比较式(12)和式(7)可以看到, 由于新的映射是将波场空间替换为了相位空间, 避免了模型空间到波场空间再到其他空间的链式关系, 因此伴随状态方程是在相位空间内计算的, 式(7)的链式微分项也因此而消失.此外, 通过将模型空间直接映射到相位空间, 可以避免将波场作为中间变量, 从而直接利用模型参数和解缠绕相位的弱线性关系.其中相位空间的模型梯度可以表示为
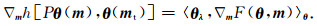
|
(14) |
上式的角标θ表明该方法是在相位空间中计算梯度, 表明我们可以充分利用解缠绕相位和模型参数之间的弱非线性关系.此外, 解缠绕相位包含模型的大尺度低波数信息(请参阅下一节), 这意味着相位空间的解缠绕相位反演方法可以处理强非线性问题.
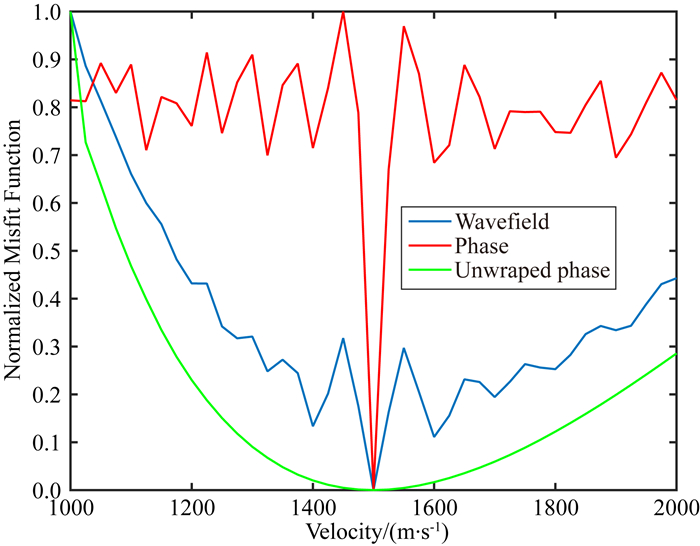
对于一个新的反演问题, 其目标函数的凸性是非常重要的, 它可以反映匹配的变量与介质参数的非线性程度.本文采用一维模型来展示本文提出的新目标函数的凸性, 并与其他形式的目标函数进行比较.真实速度模型是随深度线性变化的:v=v0+0.5×Depth, 而真实的背景速度v0是:1500 m·s-1.目标函数是关于背景速度v0的函数, 并且背景速度均匀变化.图 1所示的曲线是基于不同背景速度的归一化目标函数.基于波场的目标函数曲线(红线)包含许多局部最小值, 且在很小的速度间隔内剧烈波动, 这使得初始速度模型很难确定.对于基于缠绕相位的目标函数(蓝色), 曲线同样存在局部振荡, 并在大尺度上是逐渐逼近最佳解的.说明基于缠绕相位的目标函数凸性较强, 具有解决非线性问题的潜力.而基于解缠绕相位的目标函数曲线(绿色)只有一个整体最小值, 并且显示出非常强的凸性.尽管测试模型相对简单, 但通过对比可以看出基于解缠绕相位的目标函数具有更强的凸性, 可以减弱反演的非线性.
|
图 1 基于不同变量的目标函数性态比较 Fig. 1 The behavior of objective functions for different velocities |
由波场在频域中变换得到的相位都存在缠绕问题.在本节中, 我们将Maier等(2015)提出的基于振幅排列的多聚类解缠绕算法应用于相位解缠绕.对于任意频率的波场, 起始相位在震源位置处具有最大振幅, 该特点非常适合Maier等(2015)提出的解缠相位算法.有关该算法的详细信息, 请参见附录.
图 2为Marmousi速度模型, 图 3是位于(3000 m, 10 m)处震源激发的5 Hz振幅谱和对应的相位谱.可以看到相位被限制在[-π, π], 丢失了真实的相位信息.图 4是基于该算法的解缠绕相位谱.与以2π模态测量并丢失真实相位信息的缠绕相位相比, 解缠绕相位会随着不同的反射点或低波数结构而逐渐增加, 这意味着解缠绕相位可以呈现波场的大尺度信息.

|
图 2 Marmousi模型 Fig. 2 Marmousi Model |

|
图 3 (a) 波场对应的振幅谱; (b)波场对应的相位谱 Fig. 3 (a) Amplitude spectrum; (b) Corresponding phase spectrum of (a) |

|
图 4 解缠绕后的相位谱 Fig. 4 The unwrapped phase of Fig. 3b |
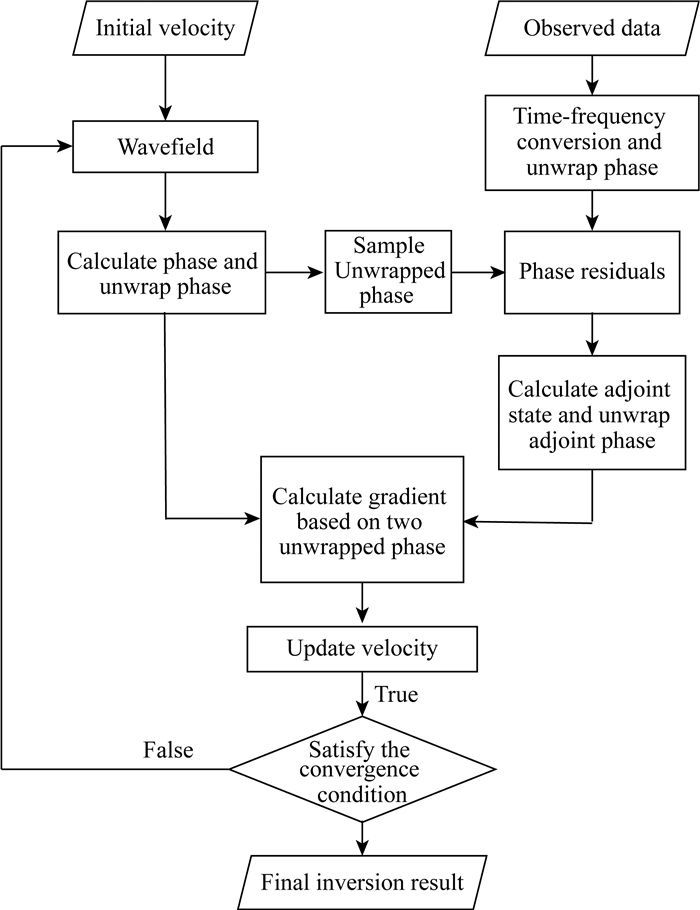
图 5显示了本文提出的解缠绕相位反演方法(Full unwrapped phase inversion, 简称为FUPI)的工作流程, 以及如何在反演中应用上述算法:首先对观测数据进行时频转换, 然后对每炮数据进行解缠绕;接下来使用初始速度进行模拟, 并得到对应的相位信息, 同样使用上述算法对其进行解缠绕.然后基于相位差来计算伴随相位.最后, 可以通过式(13)计算模型梯度, 并通过迭代算法更新模型参数, 直至收敛.
|
图 5 反演流程图 Fig. 5 Flowchart of the proposed method |
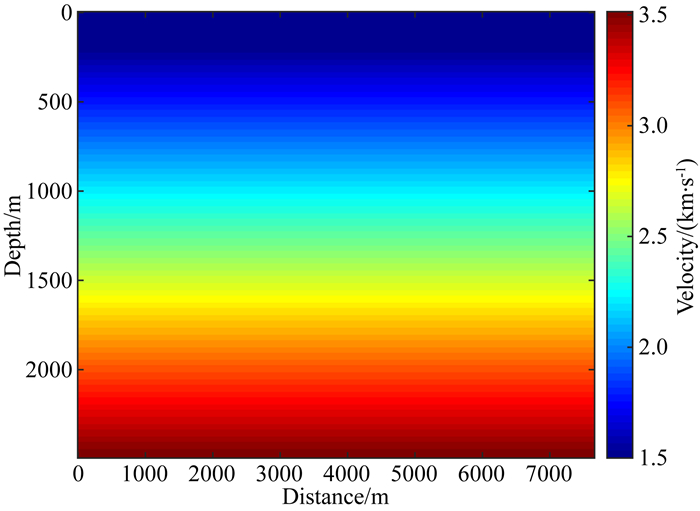
在本节中, 我们使用Marmousi模型(图 2)来证明本文方法的准确性.初始模型采用图 6中所示的不包含任何真实介质信息的线性模型, 该模型网格点为767×250, 水平和垂直方向的网格间隔均为10 m.炮点和接收点分别以20 m和10 m的间隔均匀分布在地表.采用有限差分法进行正演模拟, 震源子波为10 Hz Ricker子波.反演过程根据从低(3 Hz)到高(15 Hz)分为5个频组:3~7 Hz, 5~9 Hz, 7~11 Hz, 9~13 Hz和11~15 Hz(Sirgue和Pratt, 2004).L-BFGS方法(Nocedal, 1980)用于优化和反演加速: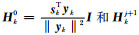
|
图 6 初始介质模型 Fig. 6 Gradient initial model for the test of the Marmousi model |
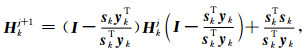
|
(15) |
其中sk=mk+1-mk, yk=gk+1-gk, m是模型参数, g表示梯度, k表示目前迭代次数而j表示L-BFGS内部的迭代次数, I是单位矩阵, T表示矩阵转置而H是Hessian矩阵.
将FUPI方法应用于模拟数据, 图 7a显示了相对较低的频组:3~7 Hz, 5~9 Hz, 7~11 Hz迭代后的FUPI结果.通过对比最终结果(图 7b)与图 7a中的反演结果可以看到, 由于引入了解缠绕相位的约束, 最终反演结果仅部分结果得到了改善, 并且不包含任何高频的信息.接下来将FUPI反演结果作为FWI的输入介质模型, 得到最终的FWI反演结果如图 7c所示.由于FUPI结果作为初始模型已包含精确的低波数分量, FWI方法可提供极其精确的反演结果, 而且没有任何假象, 非常接近真实的Marmousi模型.

|
图 7 (a) 前三个频组的FUPI反演结果; (b) FUPI最终反演结果; (c)基于FUPI的FWI反演结果 Fig. 7 (a) FUPI result after the first three frequency groups; (b) FUPI final result; (c) FWI result with the FUPI result as input |
但是, 基于线性模型(图 6)的反演结果(图 8)并不令人满意:由于缺少合成数据中的低频信息, 并且初始模型与真实模型相差较大, 各个频组的反演结果与真实模型差别较大, 最终的反演结果中浅层中存在一些伪影, 而深层中产生了错误的构造.

|
图 8 (a) 前两个频组的FWI反演结果; (b)前四个频组的FWI反演结果; (c) FWI的最终反演结果 Fig. 8 (a) FWI result after the first two-frequency group; (b) FWI result after the four-frequency group; (c) The final inversion result of FWI |
为了更精确地说明本文方法可以准确反演背景速度, 本文从初始模型、FUPI结果和FWI结果中分别提取了两条速度曲线进行对比, 其中一条位于1.5 km处(图 9a), 另一条位于6.5 km(图 9b)处.其中红线是初始速度, 蓝线是真实速度, 黄线表示前三个频率组之后的FUPI结果, 紫线是最终的FUPI结果, 绿线是FWI基于FUPI速度的反演结果而浅蓝线是基于梯度速度的FWI结果.经过对比可以看出, FUPI方法可以给出Marmousi模型的准确低波数分量, 并获得该模型的粗略轮廓.接下来的FWI可以收敛到合理的反演结果, 表明FUPI可以有效地补偿地下介质的低波数分量.

|
图 9 1.5 km (a)处和6.5 km处(b)速度曲线比较 Fig. 9 Velocity curve comparison at 1.5 km (a) and 6.5 km (b) |
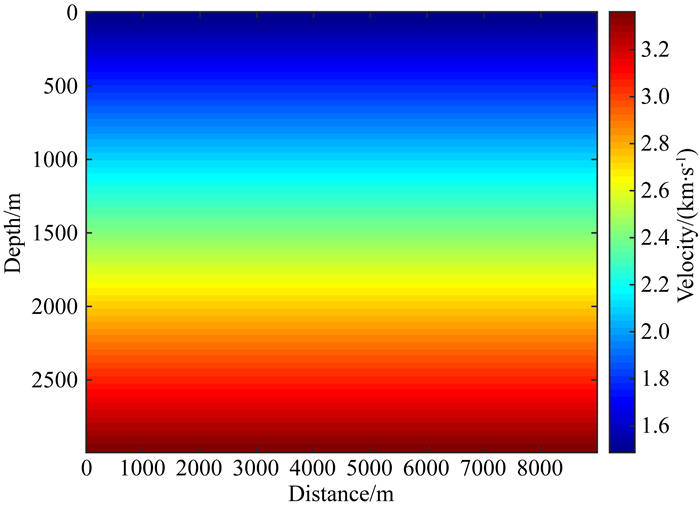
在该小节中, BP模型用于说明FUPI方法处理强非线性问题并进一步恢复模型中大规模低波数分量的能力.图 10是部分BP模型, 其大小为3 km×9 km, 水平和垂直方向的网格间隔均为10 m, 该模型包含大尺度构造和部分小反射点.炮点和接收点位于地表, 间隔分别为40 m和10 m.与上述Marmousi模型测试相同, 线性增加的速度作为初始模型(图 11), 使用10 Hz Ricker子波合成地震数据.

|
图 10 部分BP模型 Fig. 10 Part of the BP model |
|
图 11 线性初始模型 Fig. 11 Gradient initial model for the test of the BP model |
首先基于图 11所示的初始速度模型进行FWI反演, 相应的反演结果如图 12a所示.由于高频部分的数据匹配, 传统的FWI仅恢复了高波数分量, 并且由于初始速度不准确, 还表现出一些假象和错误的构造.而在图 12b中显示的FUPI结果表明, 所提出的方法可以准确地恢复大尺度构造:准确反演出了大型高速的盐丘;部分小构造也得到了反演.但由于解缠绕相位对模型参数的分辨率较低, 只能恢复小构造的大致构造, 难以对其实现精确刻画.

|
图 12 (a) FWI反演结果; (b) FUPI反演结果 Fig. 12 (a) FWI result of the BP test; (b) FUPI result of the BP test |
为了说明该方法的抗噪能力, 我们在观测数据中添加了一定量的高斯噪声, 以测试反演方法的鲁棒性.如Maier等(2015)指出, 当信噪比(SNR)大于4.5时, 解缠绕算法是有效的, 而相位可以进行准确的解缠绕对保证反演方法的稳定性至关重要.因此, 在FUPI测试中分别使用SNR分别为3.0和4.0的炮记录进行测试.
图 13a为位于x=4500 m处震源激发的炮记录, 而图 13b和13c中分别显示了在SNR=4.0和SNR=3.0的炮记录.可以看出随着SNR的降低, 几乎无法准确识别有效反射波.然后我们将噪声数据转换到频域以进行反演.由于时频变换, 减少了每个频组数据中的噪声.经过解缠绕算法后, 我们基本上可以获得如图 14所示的一致相位信息.图 14a, 图 14b和图 14c显示了图 13的相应解缠绕相位.通过比较, 我们可以看到, 随着噪声的增加, 5Hz的解缠绕相位的细节差别较大, 但是基本构造是相同的.

|
图 13 (a) BP模型模拟炮记录; (b) SNR=4.0的模拟炮记录; (c) SNR=3.0的模拟炮记录 Fig. 13 (a) Shot gather; (b) Shot gather with SNR=4.0; (c) Shot gather with SNR=3.0 |

|
图 14 (a) 模拟炮记录在5Hz处的解缠绕相位; (b) SNR=4.0下模拟炮记录在5Hz处的解缠绕相位; (c) SNR=3.0下模拟炮记录在5Hz处的解缠绕相位 Fig. 14 (a) Unwrapped phase of the BP shot gathers at 5Hz; (b) Unwrapped phase of the BP shot gathers at 5Hz with SNR=4.0; (c) Unwrapped phase of the BP shot gathers at 5Hz with SNR=3.0 |
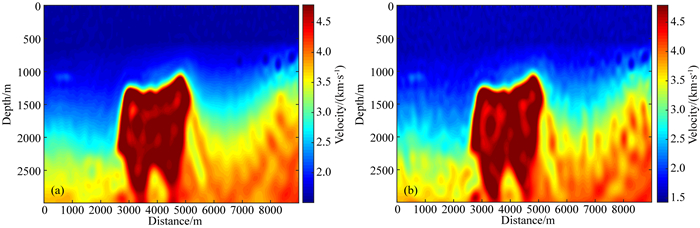
图 15显示了相应的反演结果.在SNR=4.0的情况下(图 13a), FUPI给出了可靠的反演结果, 准确地描绘了只有部分噪声影响的大型高速物体.但是, 当SNR=3时(图 13b), 噪声的影响更为严重:模型的浅层存在大量随机噪声, 深层结构不准确.为进一步说明噪音对反演的影响, 图 16绘制了三个FUPI测试的RMS(均方根)误差历史记录.可以看出随着噪声的增加, RMS误差越来越难以收敛到零, 说明受噪音影响, FUPI难以达到反演的极值点.对比SNR=4.0与常规无噪音影响的曲线, 可以发现当数据信噪比较高时, 解缠绕算法依然准确的情况下, 两者几乎都收敛到了0, 表明了反演算法良好的抗噪性.相应地随着信噪比降低, 解缠绕算法精度下降, FUPI难以完全收敛.标准FUPI、SNR=4.0下的FUPI结果和SNR=3.0下的FUPI的结果说明了FUPI方法和解缠绕算法的鲁棒性.
|
图 15 (a) SNR=4.0下FUPI反演结果; (b) SNR=3.0下FUPI反演结果 Fig. 15 (a) FUPI result of the BP test with SNR=4.0; (b) FUPI result of the BP test with SNR=3.0 |

|
图 16 RMS误差曲线对比:蓝线是标准的FUPI RMS误差曲线;红线是SNR=4.0的FUPI RMS误差曲线;绿线是SNR=3.0的FUPI RMS误差曲线 Fig. 16 RMS error histories comparison of the BP test; the blue line is the standard FUPI RMS error histories, the red line is the FUPI RMS error histories with SNR=4.0 and the green line is the FUPI RMS error histories with SNR=3.0 |
总的来说, 我们的FUPI方法可以有效地缓解反演的强非线性, 并获得收敛的反演结果, 可以为高分辨率FWI提供准确的初始介质参数.
3 结论在本文中, 我们提出了相位空间内的解缠绕相位反演方法, 以减轻反演的强非线性并克服周期跳跃问题.本文将频率域波动方程的相位形式作为约束条件, 并基于相空间中解缠绕相位匹配来重建了一个弱非线性的反演问题.新的约束可以帮助消除伴随状态方程中的链式微分项, 而相位空间内的反演可以充分利用介质参数和解缠绕相位之间的弱非线性, 从而提高低波数反演的精度.同时, 由于将模型空间到波场空间的映射修改为了模型空间到相位空间的映射, 导致反演分辨率降低, 因此, 该反演方法着重于反演地下的大尺度构造, 不适于对地下介质进行高精度刻画.模型测试结果证明了相位空间内的解缠绕相位反演方法的准确性以及解决强非线性问题的适用性.特别是BP模型噪音数据的测试, 说明该反演方法具有一定的抗噪性, 当处理高信噪比的实际资料时, 该方法可以给出准确的反演结果.
附录在本附录中, 我们将介绍基于振幅排列的多聚类解缠绕算法, 其工作流程如附图 1所示.对于每个网格点中的波场, 我们创建两个1D矩阵, 并根据振幅降序对它们进行排序: Ai, Pi, i=1, 2, …, nx×nz.第一步是在每个网格点的每个阶段基于邻居创建不同的群.在2D情况下, 邻居是围绕该相位的8个点.如果相位没有正确的邻居或该相位已经是缠绕的, 我们将创建一个新的群Cj, 并设为相位相同的值.如果邻居是解缠绕的, 则相位将被添加到具有最大权重的相邻群中, 该最大权重是群中所有相位的振幅之和:
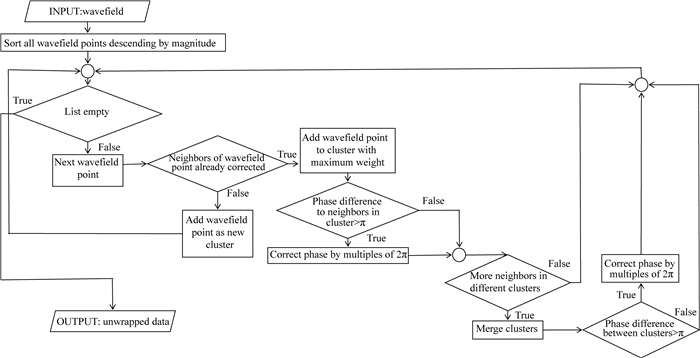
|
图 附图 1 相位解缠绕算法流程 Fig. 附图 1 Flowchart of unwrapping algorithm |
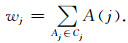
|
建立好群之后, 下一步是在每一个群中进行解缠绕.如群中的相位差大于π:|P(i)-P(i+1)|>π, δ满足:
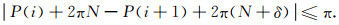
|
当N=N-δ时, 上述流程截止.当存在多个具有多个最大振幅的相邻点时, 在展开后, 将相邻点替换为平均相位.
现在我们需要将群合并到一个未解缠绕的矩阵中.为此, 我们需要确定该群是否在不同群集中有更多邻居.如果该阶段的所有邻居都在一个群集中, 请继续进行下一个阶段.如果不是这种情况, 并且不同群集之间的相位差大于π, 则以2π倍数校正群集.以振幅从大到小的顺序执行上述步骤.如果在一个群中有一个以上具有最大振幅的相邻相位, 则在展开后将其替换为平均相位.
AlTheyab A, Schuster G. 2015. Reflection full-waveform inversion for inaccurate starting models.//85th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 18-22.
|
Ben-Hadj-Ali H, Operto S, Virieux J. 2008. Velocity model building by 3D frequency-domain full-waveform inversion of wide-aperture seismic data. Geophysics, 73(5): VE101-VE117. DOI:10.1190/1.2957948 |
Bertsekas D P. 1996. Constrained Optimization and Lagrange Multiplier Methods. New York: Athena Scientifics.
|
Beydoun W B, Tarantola A. 1988. First Born and Rytov approximations:modeling and inversion conditions in a canonical example. The Journal of the Acoustical Society of America, 83(3): 1045-1055. DOI:10.1121/1.396537 |
Bunks C, Saleck F, Zaleski S, et al. 1995. Multiscale seismic waveform inversion. Geophysics, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
Chen S C, Chen G X. 2016. Full waveform inversion of the second-order time integral wavefield. Chinese Journal of Geophysics (in Chinese), 59(10): 3765-3776. DOI:10.6038/cjg20161021 |
Choi Y, Alkhalifah T. 2011. Frequency-domain waveform inversion using the unwrapped phase.//81st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2576-2580.
|
Choi Y, Alkhalifah T. 2015. Unwrapped phase inversion with an exponential damping. Geophysics, 80(5): R251-R264. DOI:10.1190/geo2014-0498.1 |
De Hoop M V, Van Der Hilst R, Shen P. 2006. Wave-equation reflection tomography:annihilators and sensitivity kernels. Geophysical Journal International, 167(3): 1332-1352. DOI:10.1111/j.1365-246X.2006.03132.x |
Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion. Chinese Journal of Geophysics (in Chinese), 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
Hu W W. 2014. FWI without low frequency data-beat tone inversion.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1116-1120.
|
Li Y Y, Choi Y, Alkhalifah T, et al. 2018. Full-waveform inversion using a nonlinearly smoothed wavefield. Geophysics, 83(2): R117-R127. |
Li Z C, Lin Y Z, Zhang K, et al. 2017. Time-domain wavefield reconstruction inversion. Applied Geophysics, 14(4): 523-528. |
Lin Y Z, Li Z C, Zhang K, et al. 2018. Time domain wavefield reconstruction inversion based on new penalty scalar algorithm. Chinese Journal of Geophysics (in Chinese), 61(10): 4100-4109. DOI:10.6038/cjg2018L0760 |
Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion. Geophysics, 56(5): 645-653. DOI:10.1190/1.1443081 |
Ma Y, Hale D. 2013. Wave-equation reflection traveltime inversion with dynamic warping and full waveform inversion. Geophysics, 78(6): R223-R233. DOI:10.1190/geo2013-0004.1 |
Maier F, Fuentes D, Weinberg J S, et al. 2015. Robust phase unwrapping for MR temperature imaging using a magnitude-sorted list, multi-clustering algorithm. Magnetic Resonance in Medicine, 73(4): 1662-1668. DOI:10.1002/mrm.25279 |
Nocedal J. 1980. Updating quasi-newton matrices with limited storage. Mathematics of Computation, 35(151): 773-782. DOI:10.1090/S0025-5718-1980-0572855-7 |
Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophysical Journal International, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
Pratt R G. 1999. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model. Geophysics, 64(3): 888-901. DOI:10.1190/1.1444597 |
Pratt R G, Sirgue L, Hornby B, et al. 2008. Crosswell waveform tomography in fine-layered sediments-Meeting the challenges of anisotropy.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, F020.
|
Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies. Geophysics, 69(1): 231-248. |
Sourbier F, Operto S, Virieux J, et al. 2009. FWT2D:A massively parallel program for frequency-domain full-waveform tomography of wide-aperture seismic data-Part 1:Algorithm. Computers & Geosciences, 35(3): 487-495. |
Sun D, Jiao K, Cheng X, et al. 2016. Reflection-based waveform inversion.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1151-1156.
|
Symes W W, Carazzone J J. 1991. Velocity inversion by differential semblance optimization. Geophysics, 56(5): 654-663. DOI:10.1190/1.1443082 |
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Van Leeuwen T, Herrmann F J. 2013. Mitigating local minima in full-waveform inversion by expanding the search space. Geophysical Journal International, 195(1): 661-667. DOI:10.1093/gji/ggt258 |
Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. |
Wu R S, Luo J R, Wu B Y. 2014. Seismic envelope inversion and modulation signal model. Geophysics, 79(3): WA13-WA24. DOI:10.1190/geo2013-0294.1 |
Xu S, Lambaré G, Zhang Y, et al. 2012. Inversion on reflected seismic wave.//82nd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1-6.
|
Zhang P, Wu R H, Han L G. 2018. Source-independent seismic envelope inversion based on the direct envelope Fréchet derivative. Geophysics, 83(6): R581-R595. DOI:10.1190/geo2017-0360.1 |
陈生昌, 陈国新. 2016. 时间二阶积分波场的全波形反演. 地球物理学报, 59(10): 3765-3776. DOI:10.6038/cjg20161021 |
董良国, 迟本鑫, 陶纪霞, 等. 2013. 声波全波形反演目标函数性态. 地球物理学报, 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
蔺玉曌, 李振春, 张凯, 等. 2018. 基于新的惩罚因子算法的波场重构反演. 地球物理学报, 61(10): 4100-4109. DOI:10.6038/cjg2018L0760 |
 2020, Vol. 63
2020, Vol. 63


