2. 吉林大学地球探测科学与技术学院, 长春 130021
2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130021, China
时间域航空电磁法具有勘探深度大、工作效率高等优点,可以对高山、沙漠、森林、沼泽等难以开展地面地球物理勘查工作的地区进行快速、高效的电磁探测,已被广泛应用于矿产资源勘查、环境地质调查、地下水和工程勘查等领域(Smith, 2010;殷长春等,2015).然而,随着应用领域的不断拓展和勘探目标的精细化,需要解决的地质问题也越来越复杂.当遇到具有明显层理的沉积岩或裂隙发育地区,导电大地不同方向的导电能力发生变化,地下介质表现出宏观电导率各向异性(Yin and Fraser, 2004).此时,时间域航空电磁响应将受到严重影响,尤其是当三维各向异性异常体存在时,这种影响更为突出(Yin et al., 2016a;刘云鹤等,2018).这导致基于各向同性模型的传统成像和一维反演技术不再适用于各向异性数据的反演解释,时间域航空电磁数据处理和反演必须考虑三维各向异性模型.因此,我们将目光转向三维各向异性大地正反演技术.
正演模拟作为反演的基础,近年来已取得相当的研究成果(Wang and Hohmann, 1993;Commer and Newman, 2004;汤井田等,2007;Oldenburg et al., 2013;孙怀凤等,2013;Yin et al., 2016b;齐彦福等, 2017;周健美等,2018).然而,三维各向异性介质模型电性结构复杂,如何进行合理的网格剖分实现高精度正演模拟仍然是亟待解决的关键问题.在传统的网格剖分过程中,通常采用均匀加密的方式进行网格细化,但是这种网格剖分方式并不能最大程度地提高正演精度,而且还会极大地增加计算量.自适应网格优化算法的出现为进行最优化网格剖分提供了一条有效途径.该算法基于电磁场的传播规律,通过单元后验误差估计,识别剖分不合理的网格单元,然后利用局部网格加密方式降低单元后验误差,实现网格的逐步优化,进而达到提高计算精度的目的.与人为盲目的网格加密方式相比,自适应算法在网格加密过程中更具针对性,可以利用较少的网格获得较高的数值计算精度.因此,前人针对自适应网格优化技术开展了大量研究(Zienkiewicz and Zhu, 1992a;Schwarzbach et al., 2011;Ren and Tang, 2014;Yin et al., 2016),并围绕单元后验误差估计这一自适应算法的核心问题开发出多种自适应网格优化策略.Babuška和Rheinboldt(1979)提出了基于残差的后验误差估计方法,然而Babuška等(1994)通过数值实验发现该方法与基于梯度恢复的自适应方法相比,其计算精度较低,因此并未获得广泛应用.基于梯度恢复的自适应方法首先计算恢复梯度与数值梯度之间的差异,然后采用超收敛碎片恢复技术(Zienkiewicz and Zhu, 1992b)计算后验误差.该方法已被广泛应用于三维稳定电流场和二维电磁场数值模拟当中(Key and Weiss, 2006;Ren and Tang, 2010).然而,当利用该方法处理三维电磁场数值问题时,求解梯度过程过于复杂,为此,Ren(2013)采用法向电流密度和切向磁场的连续性条件定义单元后验误差对三维平面波场进行模拟,获得了很好的应用效果.曹晓月等(2018)在此基础上开发了考虑地形情况下三维大地电磁各向异性自适应有限元算法.Zhang等(2018)利用该方法实现了时间域三维航空电磁响应自适应正演模拟.任政勇等(2018)进一步将该方法应用于直流电场各向异性介质数值模拟当中.
然而,与直流和频率域电磁场正演问题不同,时间域航空电磁各向异性介质模型正演过程中不但要考虑地下各向异性电导率的影响,还需要兼顾电磁波随时间的扩散规律,这使得最优化网格剖分问题变得更加复杂.针对这一问题,本文将自适应算法与非结构时间域有限元方法相结合,通过引入电导率张量,进行各向异性介质模型三维时间域航空电磁自适应正演.为了解决电磁波扩散过程中,电磁响应幅值随时间衰减而产生的巨大差异,本文引入时间加权因子,通过调整不同时刻后验误差的相对权重,实现浅部和深部网格的同步优化.本文首先与一维解析结果对比检验本文算法的准确性,然后以半空间和三维异常体模型为例着重讨论各向异性电导率对自适应网格剖分效果的影响,并分析各向异性对三分量电磁响应的影响规律.最后,利用旋转测量的方式,通过定义全域视电阻率,对大地各向异性进行异常识别.
1 各向异性介质中三维时间域有限元正演理论从时间域麦克斯韦方程组出发,通过消去磁场并忽略位移电流项可以获得电场扩散方程
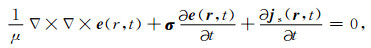
|
(1) |
其中r是位置矢量(x, y, z),t是时间,e(r, t)是r处t时刻的电场,js(r, t)是源电流密度,μ是磁导率,σ为各向异性电导率张量,
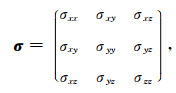
|
(2) |
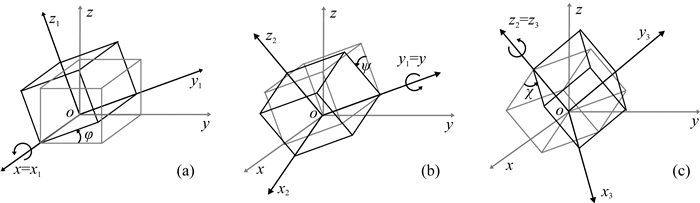
其中非对角元素表示方向电流不仅与同向电场有关,而且受正交方向电场的影响.根据Yin(2000),σ可以由主轴电导率张量σp分别绕x、y和z轴进行三次旋转获得(如图 1所示),即
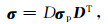
|
(3) |
|
图 1 坐标系旋转示意图(Yin et al., 2016a) (a)绕x轴旋转;(b)绕y轴旋转;(c)绕z轴旋转. Fig. 1 Coordinate system rotation (Yin et al., 2016a) (a) Rotation around the x-axis; (b) Rotation around the y-axis; (c) Rotation around the z-axis. |
其中σp=diag(σx, σy, σz),T表示矩阵的转置,D是旋转矩阵,
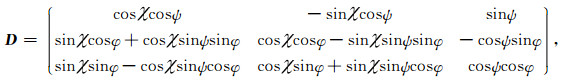
|
(4) |
其中φ、ψ和χ分别为主轴电导率绕x、y和z轴的旋转角度.
引入矢量插值基函数对电场扩散方程进行空间离散,则任意四面体单元内的电场均可表示为
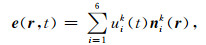
|
(5) |
其中uik(t)是第k单元第i条棱边上的切向电场值,nik(r)是插值基函数,可以自动满足切向电场连续性条件和无散条件.然后利用伽辽金方法建立有限元控制方程
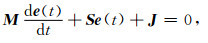
|
(6) |
其中M和S分别为质量和刚度矩阵,J是电流源项,对于任意四面体单元的矩阵元素由(7)式给出(Yin et al., 2016a)

|
(7) |
其中u是电流方向向量,i和j=1,2,…,6.接下来,我们采用二阶后退欧拉离散格式对(6)式进行时间离散,可以得到
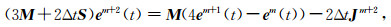
|
(8) |
其中em(t)表示第m时刻的电场,Δt为时间步长.
根据Yin等(2016b),本文中边界条件采用均匀半空间狄利克雷边界条件,而初始电场设为0,这是由于磁性线圈源发射阶跃电流波形时,在供电稳定阶段,根据楞次定律可知空间任意位置的电场均为0.最后,采用多波前并行求解器MUMPS对(8)式进行求解即可得到空间电场分布,再利用法拉第电磁感应定律即可计算接收点处的观测磁场.
2 各向异性模型自适应网格优化算法 2.1 基于法向电流密度连续性条件的加权后验误差估计根据电磁理论,空间任意位置的电磁场均应满足法向电流密度连续性条件,然而由于网格剖分不合理,电磁场数值模拟结果有时并不能满足这一性质,进而产生计算误差.为此,基于相邻单元分界面F上法向电流密度连续性条件,根据Ren等(2013)定义后验误差ηJ为
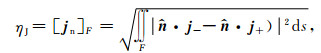
|
(9) |
其中

|
(10) |
由于在电磁扩散过程中,网格质量对正演模拟精度的影响随扩散时间发生变化,为了综合分析网格质量对不同时刻电磁场数值模拟精度的影响,首先计算所有时刻的后验误差,然后进行累加,获得单元的综合后验误差
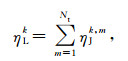
|
(11) |
其中ηJk, m是第k个单元第m时刻的后验误差,Nt是时间道数,ηLk是第k个单元的综合后验误差.然而,时间域电磁场在扩散过程中,随着能量损耗,场值迅速衰减,造成早期和晚期信号强度存在巨大差异.因此在相同的相对误差水平条件下,早期的绝对后验误差在数值上远远大于晚期,使得早期后验误差在综合后验误差中占主导地位,这将导致利用ηLk标记的网格优化单元将集中于地表,无法对地下网格进行有效优化.为了使ηLk能够充分反映网格质量对早、中、晚期信号的综合影响,本文引入扩散时间作为加权因子,平衡不同时刻后验误差的相对权重,得到加权后验误差
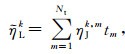
|
(12) |
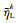
(1) 首先给定自适应参数,利用初始网格正演模拟电磁场,并计算各个单元的加权后验误差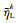
(2) 如果满足下列条件之一则迭代停止(Ren et al., 2013; Li and Pek, 2008):
a) 网格单元数大于事先设定的阈值;
b) 迭代次数达到上限;
c) 相邻两次迭代观测场的改变量足够小.
(3) 如果不满足(2)中的结束条件,根据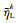
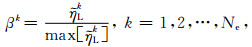
|
(13) |
然后将βk从大到小排序,计算所有单元的相对误差累加和

|
(14) |
找到n使其满足sumβn≤γsumβ≤sumβn+1,其中
(4) 利用新网格重新正演并计算加权后验误差,重新进行(2)(3)步,直到满足结束条件.
自适应流程如图 2.
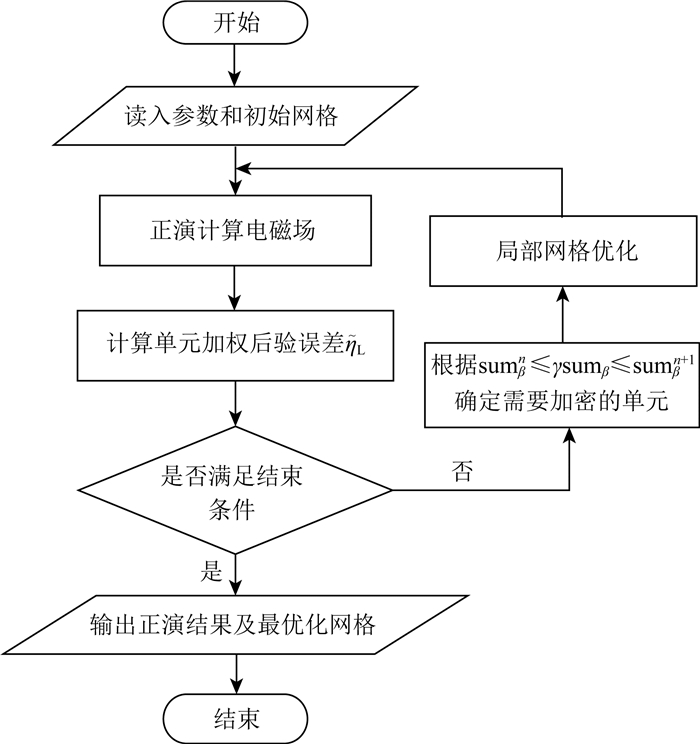
|
图 2 自适应网格优化流程图 Fig. 2 Flow chart for adaptive mesh refinement |
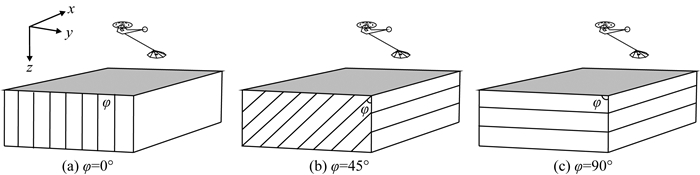
首先,我们设计了如图 3所示的各向异性半空间模型,通过与一维结果对比验证本文自适应算法的准确性.假设各向异性大地的主轴电导率为σp=diag(1, 0.1, 1)S·m-1,并根据(3)式绕x轴分别旋转0°、45°和90°.观测系统采用中心回线装置,设定发射线圈为边长7.95 m的正十二边形,线圈匝数为2匝,采用阶跃发射波形,电流强度为435 A,发射线圈和接收机距地表高度为30 m.为了准确模拟阶跃波形断电后的电磁扩散过程,本文将计算时间分成7段,每段设100个时间步长,各段的时间步长分别为0.02 μs、1 μs、5 μs、2.5 μs、12.5 μss、62.5 μs和312.5 μs.利用非结构四面体网格对计算区域进行离散,三组模型均采用相同的初始网格,其包含6491个四面体单元,共产生7721个未知数.然后采用本文的自适应算法对初始网格进行优化,经过8次迭代,相邻两次迭代观测场的变化量小于阈值,自适应过程收敛,获得如图 4所示的最优化网格(网格参数见表 1).从图 4可以发现随着旋转角度φ的变化,网格加密效果出现较大差异,显示出明显的方向性.为了分析这一特征,我们定义相对网格密度(RMD)来评价网格的疏密程度,即

|
|
图 3 各向异性主轴电导率张量绕x轴旋转模型图 Fig. 3 Anomalous conductivity tensor rotated around the x-axis |

|
图 4 自适应网格 Fig. 4 Adaptive mesh |
|
|
表 1 自适应网格参数 Table 1 Parameters for adaptive mesh |
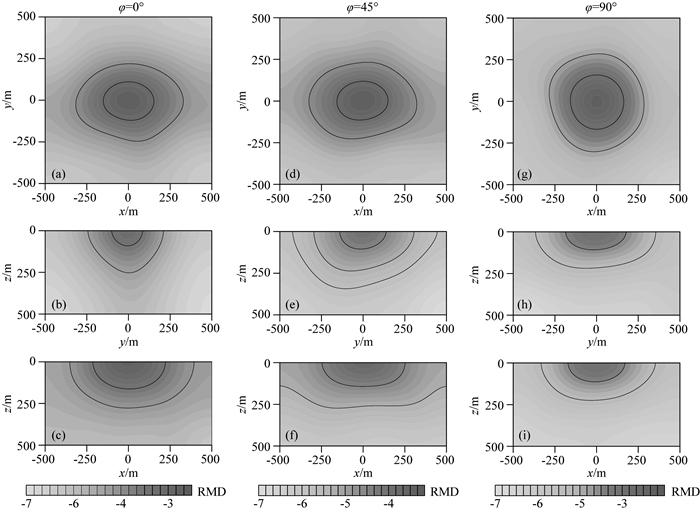
其中vmin为剖分区域的最小网格体积,vi为第i个四面体单元的体积.可以看出,单元体积越小RMD值就越大,说明网格密度越大.图 5为自适应网格图 4的相对网格密度分布.从图中可以看出在xoy面内(图 5a,d,g),当φ=0°和45°时,网格密度呈椭圆状分布,且长轴沿x方向,短轴沿y方向,然而当φ=90°时,网格密度呈对称圆形分布.而在yoz面内(图 5b,e,h),当φ=0°时,网格密度呈半椭圆状分布,高密度网格范围沿z方向拉伸;当φ=45°时,网格密度分布呈现出不对称性,向左下方倾斜;当φ=90°时,网格密度分布呈扁平状,沿y方向拉伸.在xoz面内(图 5c,f,i),网格密度均呈对称分布.之所以出现上述结果是由于发射线圈在地下感应出水平环状涡流,在感应涡流向地下扩散过程中,将沿着最大主轴电导率方向流动,因此对该方向的网格质量十分敏感,需要精细剖分以提高数值模拟精度.图 6展示了本文自适应有限元三维正演结果和一维半解析解(Yin and Fraser, 2004)以及相对误差,可以看出两组结果吻合得非常好,这证明了本文算法模拟任意各向异性大地时间域航空电磁响应的准确性.通过对比不同旋转角度(φ=0°、45°和90°)的时间域航空电磁响应,可以发现大地各向异性对观测信号影响严重,不同旋转角度的电磁响应强度之间存在较大差异.
|
图 5 自适应网格密度分布图 Fig. 5 Adaptive mesh density distribution |

|
图 6 (a) dBz/dt响应;(b)相对误差 Fig. 6 (a) dBz/dt responses; (b) Relative errors |
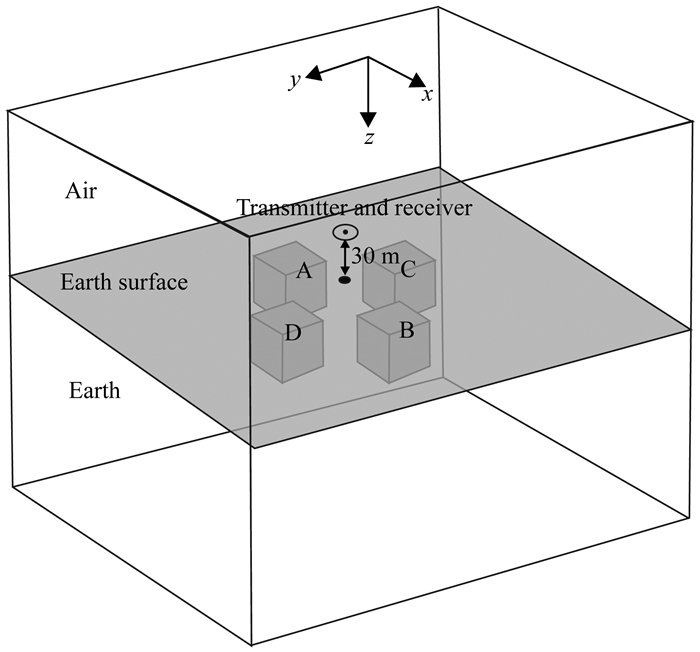
为了进一步分析各向异性对网格剖分效果的影响,本文设计了如图 7所示的多异常体模型.ABCD四个各向异性异常体的尺寸均为100 m×100 m×100 m,顶面埋深50 m,对称分布在原点四周,异常体中心距原点的水平距离均为150 m.围岩是0.01 S·m-1的各向同性介质,异常体各向异性电导率见表 2.采用与图 3相同的观测装置和发射电流.
|
图 7 多异常体模型 Fig. 7 Multiple anomalous body model |
|
|
表 2 异常体电性参数 Table 2 Conductive parameters for anomalous bodies |
经过7次迭代,自适应收敛,获得如图 8所示的自适应网格.从图 8d和f可以看出,本文自适应算法对A和B的网格加密效果十分明显,其中A内网格相对均匀,而B中网格分布不均,其左边界网格加密效果尤为突出.这是由于在xoz平面内地下水平环状涡流主要集中在y方向,因此对y方向电性变化十分敏感.与A相比,B的y方向电导率与围岩电导率差异更大,在异常体边界处需更加精细的网格才能准确描述这一巨大的电性差异对电磁场分布产生的影响.因此,虽然A的x方向电导率与围岩的差异较B大,但并未影响异常体y方向边界的网格加密效果.这说明在最大主轴电导率相同的情况下,自适应网格对异常体边界的加密效果取决于感应涡流方向上异常体主轴电导率和围岩电导率的差异.从图 8e和f可以看出,C的网格加密效果明显优于D,且与A十分接近,这是由于与D相比,C的最大主轴电导率更大,且与A相同.这说明自适应网格对异常体的整体加密效果取决于最大主轴电导率,这与曹晓月等(2018)的结果一致.

|
图 8 (a)—(c)初始网格;(d)—(f) 7th自适应网格 Fig. 8 (a)—(c) Initial mesh; (d)—(f) 7th adaptive mesh |
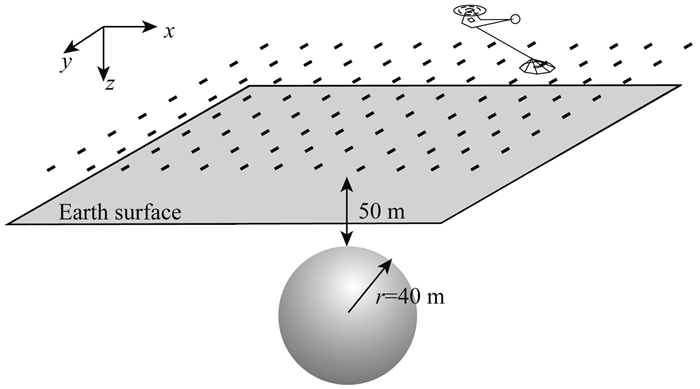
为了分析电导率各向异性对航空电磁响应的影响,本文设计了如图 9所示的球体模型,球体半径为40 m,顶面埋深50 m,采用与图 3相同的观测装置进行面积性测量.我们将分别针对各向异性异常体和各向异性围岩两种情况对三分量时间域航空电磁响应的影响进行讨论.
|
图 9 球体模型 Fig. 9 Sphere model |
假设各向同性围岩电导率为0.01 S·m-1,各向异性球体主轴电导率为σp=diag(1, 0.1, 1)S·m-1,并分别绕x轴旋转0°、45°和90°.图 10展示了当φ=0°时,本文时间加权自适应网格和传统不加权自适应网格的对比结果,两套网格的单元数均为34万.可以看出,当不引入时间加权因子时,后验误差主要由早期信号决定,导致大部分加密网格集中于地表,产生地表过度加密现象,而对地下各向异性球体网格没能进行有效优化.而本文通过引入时间加权因子调整不同时刻后验误差的相对权重,实现了浅部和深部网格的同步优化,尤其针对各向异性球体的加密效果十分明显,可以更加准确的描述各向异性体对地下电磁场分布产生的影响.
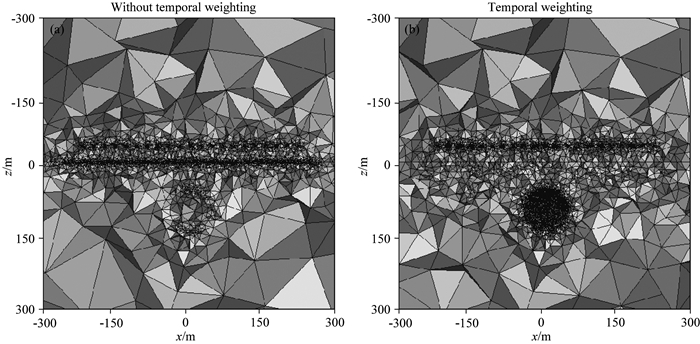
|
图 10 自适应网格加密效果对比 (a)无时间加权;(b)时间加权. Fig. 10 Comparison between adaptive meshes (a) Without temporal weighting; (b) Temporal weighting. |
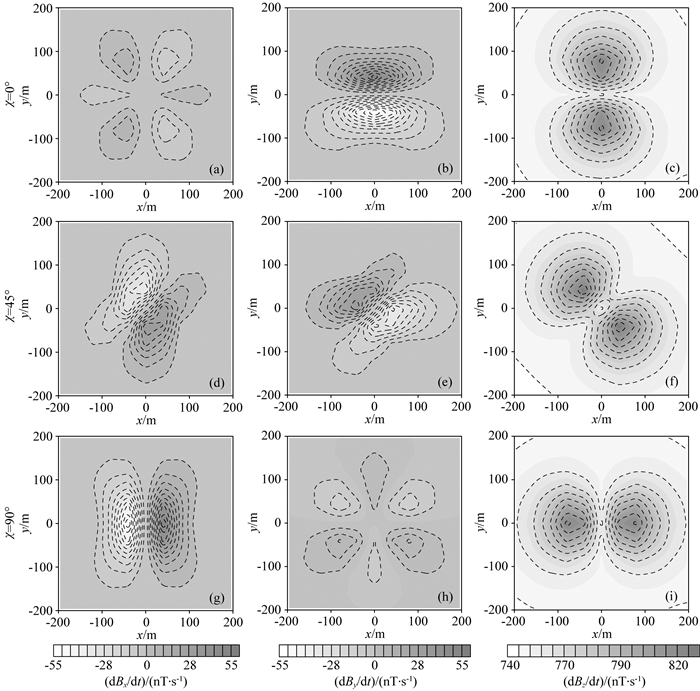
从图 11可以看出,当主轴电导率绕x轴旋转时,三分量航空电磁响应的分布形态和异常幅值均发生明显变化.当φ=0°时,dBx/dt异常响应较弱,分布形态比较复杂;而dBy/dt响应在y轴方向上出现两个对称反号的异常中心,且正异常出现在y轴正方向,这与各向同性情况(图 11b)相反;dBz/dt响应在y轴方向上出现两个对称同号的异常中心,但与各向同性情况(图 11c)相比,异常幅度较小.当φ=45°时,dBx/dt响应出现关于y轴对称的两个反号异常,且异常中心向y轴负方向偏移;dBy/dt响应的异常呈现不对称性,整体向y轴负方向移动;dBz/dt响应呈单峰异常,异常中心在y轴负方向.当φ=90°时,三分量航空电磁响应与各向同性时非常相似,这是由于时间域航空电磁感应涡流主要分布于水平方向,对z方向的电性变化并不敏感.图 12显示,当主轴电导率绕z轴旋转时,三分量电磁响应的异常分布也随着旋转,但是异常中心的连线始终与最小主轴电导率方向保持垂直关系.

|
图 11 各向异性异常体主轴电导率绕x轴旋转三分量航空电磁响应(t=630 μs) Fig. 11 Three-component airborne EM responses for the conductivity tensor of anisotropic body rotated around x-axis (t=630 μs) |
|
图 12 各向异性异常体主轴电导率绕z轴旋转三分量航空电磁响应(t=630 μs) Fig. 12 Three-component airborne EM responses for the conductivity tensor of anisotropic body rotated around z-axis (t=630 μs) |
假设各向同性球体电导率为1 S·m-1,各向异性围岩主轴电导率为σp=diag(0.01, 0.0025, 0.01)S·m-1,并分别绕z轴旋转0°、45°和90°.图 13显示,当χ =0°和90°时,Bx/dt和dBy/dt均出现两个对称异常,但是当χ=45°时,由于各向异性围岩与导电球体相互耦合,导致dBx/dt和dBy/dt响应的分布形态变得十分复杂.与x和y分量响应相比,dBz/dt响应分布较为简单,呈椭圆形,且长轴始终平行于最大主轴电导率方向.
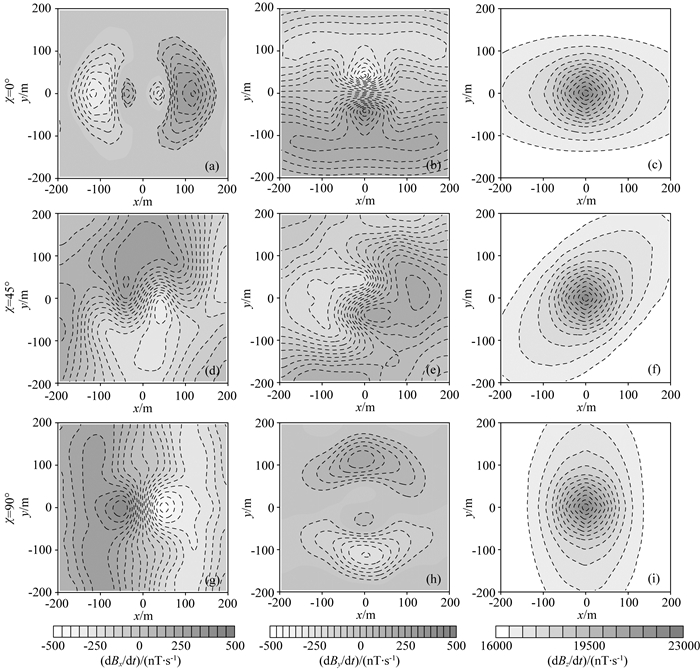
|
图 13 各向异性围岩主轴电导率绕z轴旋转三分量航空电磁响应(t=120 μs) Fig. 13 Three-component airborne EM responses for the conductivity tensor of anisotropic host rock rotated around z-axis (t=120 μs) |
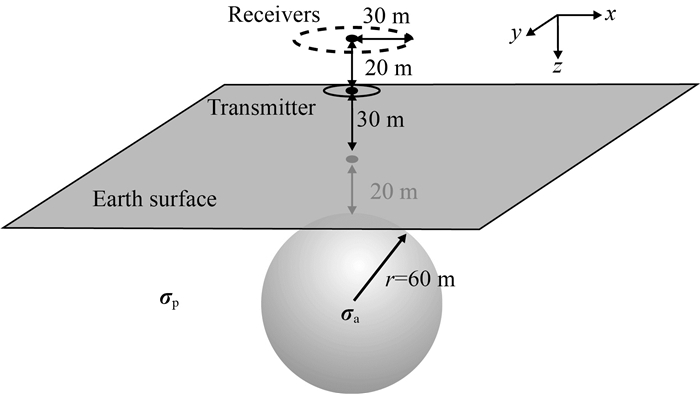
本文采用Yin和Fraser(2004)提出的各向异性识别技术对时间域航空电磁响应中所包含的各向异性信息进行识别,该技术采用环形观测模式进行测量,即发射源保持不动,旋转接收点位置观测.考虑到中心回线装置发射和接收位置重合,无法完成环形测量,为此我们采用分离装置.为了消除航空电磁系统飞行高度、收发距、发射电流等因素的干扰,本文采用全域视电阻率定义方法(张莹莹等,2015;赵越等,2015)计算时间域航空电磁全域视电阻率,提取各向异性信息.建立如图 14所示的球体模型,球体半径为60 m,顶部埋深为20 m,发射源为边长9 m的正十二边形,位于球体正上方距地表高度30 m处,接收点与发射源中心水平距离为30 m,保持距地表 50 m高度进行环形测量.
|
图 14 球体模型及环形观测模式 Fig. 14 Sphere model and circular measurement |
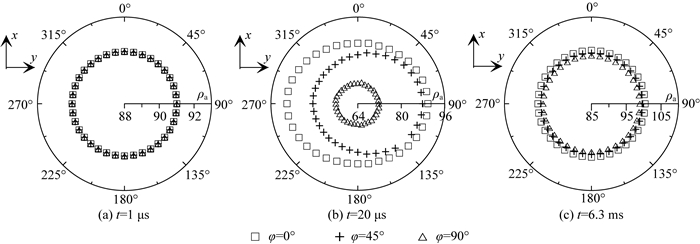
首先考虑各向同性围岩中埋藏各向异性异常体的情况.假设围岩电导率为0.01 S·m-1,各向异性异常体主轴电导率为(1, 0.01, 1)S·m-1,分别绕x和z轴旋转0°、45°和90°.从图 15可以看出,当主轴电导率绕x轴旋转时,早期(t=1 μs)视电阻率呈圆形对称分布(图 15a),随着电磁波向下传播,各向异性异常体的影响逐渐显现(图 15b).当φ=0°时,视电阻率呈椭圆形,且长轴沿y轴方向;当φ=45°时,视电阻率呈现出不对称性,中心向y轴正方向移动;当φ=90°时,异常体水平方向电性不发生变化,此时视电阻率呈对称的圆形,且视电阻率值最小.到了晚期(t=6.3 ms),电磁波穿过异常体,各向异性的影响逐渐消失,视电阻率呈对称的圆形(图 15c),且视电阻率等于背景各向同性围岩电阻率.图 16展示了主轴电导率绕z轴旋转的情况,其中图 16b显示视电阻率的长轴方位随旋转角度发生变化,但始终垂直于最大主轴电导率方向,这为各向异性主轴电导率方向识别提供了依据.
|
图 15 异常体主电导率张量绕x轴旋转时全域视电阻率极性图 Fig. 15 Full field apparent resistivity polar plots for the conductivity tensor of anomalous body rotated around the x-axis |
|
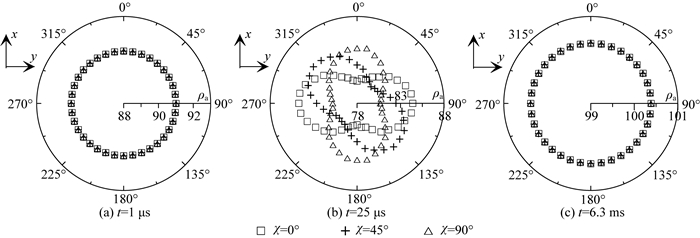
图 16 异常体主电导率张量绕z轴旋转时全域视电阻率极性图 Fig. 16 Full field apparent resistivity polar plots for the conductivity tensor of anomalous body rotated around the z-axis |
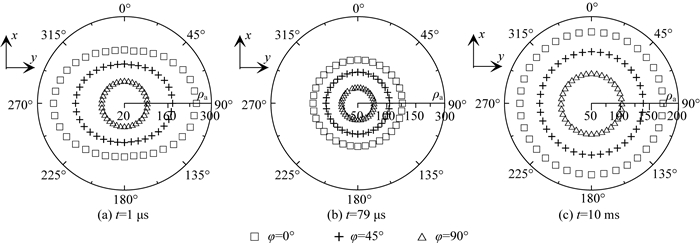
下面我们对各向同性异常体埋藏在各向异性围岩中的情况进行讨论.假设异常体电导率为0.1 S·m-1,各向异性围岩主轴电导率为(0.01, 0.002, 0.01)S·m-1,分别绕x和z轴旋转0°、45°和90°.从图 17可以看出,在早期(t=1μs),各向异性对视电阻率的形状影响严重.当φ=0°和45°时,视电阻率极性图近似呈椭圆形,且长轴沿y轴方向,而当φ=90°时视电阻率呈圆形对称分布,且视电阻率值最小.当t=79 μs时(图 17b),电磁波经过各向同性球体,由于球体内部电性沿各个方向不发生变化,因此视电阻率均呈对称圆形,但是由于背景围岩的影响,导致视电阻率值存在一定差异.到了晚期(图 17c),视电阻率主要反映了地下围岩的电性,但是其形状均为对称的圆形,不随旋转角度发生变化,这表示低阻异常体的影响仍然存在.图 18显示当主轴电导率绕z轴旋转时,视电阻率的长轴方位也随之发生旋转,且与最大主轴电导率方向垂直,这与各向异性异常体模型(图 16b)相同.
|
图 17 围岩主电导率张量绕x轴旋转时全域视电阻率极性图 Fig. 17 Full field apparent resistivity polar plots for the conductivity tensor of host rock rotated around the x-axis |

|
图 18 围岩主电导率张量绕z轴旋转时全域视电阻率极性图 Fig. 18 Full field apparent resistivity polar plots for the conductivity tensor of host rock rotated around the z-axis |
本文通过结合时间域有限元算法和自适应网格优化技术,成功实现了各向异性大地时间域航空电磁自适应正演.利用时间加权算子调整不同时刻后验误差的相对权重,实现了对地下浅部和深部网格的同步优化.数值实验结果表明网格剖分受各向异性电导率影响严重,且存在以下规律:(1)各向异性大地电导率直接影响网格加密效果,且最大主轴电导率方向的网格加密效果最为明显;(2)对于各向异性三维异常体模型,需要对异常体进行整体网格加密,而且加密程度取决于最大主轴电导率与围岩的电性差异;(3)在最大主轴电导率相同的情况下,对异常体边界网格加密效果只取决于感应涡流方向上异常体方向电导率和围岩的电性差异,而与其他方向电导率无关.除此之外,典型地电模型的正演结果显示各向异性对三分量航空电磁响应影响严重,地下各向异性电性结构的改变会导致三分量电磁响应的分布形态和响应幅值出现明显变化.与x和y分量相比,z分量响应的分布形态更加简单,而且对主轴电导率的方向具有良好的反应.利用旋转测量的方式,通过定义全域视电阻率极性图,可以很好地识别各向异性主轴方向,为各向异性识别提供依据.
致谢 我们特别向审稿人和编辑对本文提出的建设性意见表示感谢.
Babuška I, Rheinboldt W C. 1979. Adaptive approaches and reliability estimations in finite element analysis. Computer Methods in Applied Mechanics and Engineering, 17-18: 519-540. DOI:10.1016/0045-7825(79)90042-2 |
Babuška I, Strouboulis T, Upadhyay C S, et al. 1994. Validation of a posteriori error estimators by numerical approach. International Journal for Numerical Methods in Engineering, 37(7): 1073-1123. DOI:10.1002/nme.1620370702 |
Cao X Y, Yin C C, Zhang B, et al. 2018. A goal-oriented adaptive finite-element method for 3D MT anisotropic modeling with topography. Chinese Journal of Geophysics (in Chinese), 61(6): 2618-2628. DOI:10.6038/cjg2018L0068 |
Commer M, Newman G. 2004. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics, 69(5): 1192-1202. DOI:10.1190/1.1801936 |
Key K, Weiss C. 2006. Adaptive finite-element modeling using unstructured grids:The 2D magnetotelluric example. Geophysics, 71(6): G291-G299. DOI:10.1190/1.2348091 |
Li Y G, Pek J. 2008. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media. Geophysical Journal International, 175(3): 942-954. DOI:10.1111/j.1365-246X.2008.03955.x |
Liu Y H, Yin C C, Cai J, et al. 2018. Review on research of electrical anisotropy in electromagnetic prospecting. Chinese Journal of Geophysics (in Chinese), 61(8): 3468-3487. DOI:10.6038/cjg2018L0004 |
Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57. DOI:10.1190/geo2012-0131.1 |
Qi Y F, Yin C C, Liu Y H, et al. 2017. 3D time-domain airborne EM full-wave forward modeling based on instantaneous current pulse. Chinese Journal of Geophysics (in Chinese), 60(1): 369-382. DOI:10.6038/cjg20170131 |
Ren Z Y, Tang J T. 2010. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method. Geophysics, 75(1): H7-H17. DOI:10.1190/1.3298690 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 2013, 194(2): 700-718, doi: 10.1093/gji/ggt154.
|
Ren Z Y, Tang J T. 2014. A goal-oriented adaptive finite-element approach for multi-electrode resistivity system. Geophysical Journal International, 199(1): 136-145. DOI:10.1093/gji/ggu245 |
Ren Z Y, Qiu L W, Tang J T, et al. 2018. 3D modeling of direct-current anisotropic resistivity using the adaptive finite-element method based on continuity of current density. Chinese Journal of Geophysics (in Chinese), 61(1): 331-343. DOI:10.6038/cjg2018K0698 |
Schwarzbach C, Börner R U, Spitzer K. 2011. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics-a marine CSEM example. Geophysical Journal International, 187(1): 63-74. DOI:10.1111/j.1365-246X.2011.05127.x |
Smith R. 2010. Airborne electromagnetic methods:Applications to minerals, water and hydrocarbon exploration. CSEG Recorder, 35(3): 7-10. |
Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time. Chinese Journal of Geophysics (in Chinese), 56(3): 1049-1064. DOI:10.6038/cjg20130333 |
Tang J T, Ren Z Y, Hua X R. 2007. The forward modeling and inversion in geophysical electromagnetic field. Progress in Geophysics (in Chinese), 22(4): 1181-1194. |
Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics, 58(6): 797-809. DOI:10.1190/1.1443465 |
Yin C C. 2000. Geoelectrical inversion for a one-dimensional anisotropic model and inherent non-uniqueness. Geophysical Journal International, 140(1): 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |
Yin C C, Fraser D C. 2004. The effect of the electrical anisotropy on the response of helicopter-borne frequency-domain electromagnetic systems. Geophysical Prospecting, 52(5): 399-416. DOI:10.1111/j.1365-2478.2004.00424.x |
Yin C C, Zhang B, Liu Y H, et al. 2015. Review on airborne EM technology and developments. Chinese Journal of Geophysics (in Chinese), 58(8): 2637-2653. DOI:10.6038/cjg20150804 |
Yin C C, Zhang B, Liu Y, et al. 2016. A goal-oriented adaptive finite-element method for 3D scattered airborne electromagnetic method modeling. Geophysics, 81(5): E337-E346. DOI:10.1190/geo2015-0580.1 |
Yin C C, Qi Y F, Liu Y H. 2016a. 3D time-domain airborne EM modeling for an arbitrarily anisotropic earth. Journal of Applied Geophysics, 131: 163-178. DOI:10.1016/j.jappgeo.2016.05.013 |
Yin C C, Qi Y F, Liu Y H, et al. 2016b. 3D time-domain airborne EM forward modeling with topography. Journal of Applied Geophysics, 134: 11-22. DOI:10.1016/j.jappgeo.2016.08.002 |
Zhang B, Yin C C, Ren X Y, et al. 2018. Adaptive finite element for 3D time-domain airborne electromagnetic modeling based on hybrid posterior error estimation. Geophysics, 83(2): WB71-WB79. DOI:10.1190/geo2017-0544.1 |
Zhang Y Y, Li X, Yao W H, et al. 2015. Multi-component fullfield apparent resistivity definition of multi-source ground-airborne transient electromagnetic method with galvanic sources. Chinese Journal of Geophysics (in Chinese), 58(8): 2745-2758. DOI:10.6038/cjg20150811 |
Zhao Y, Li X, Wang Y P. 2015. Full-domain apparent resistivity definition for large-loop TEM. Progress in Geophysics (in Chinese), 30(4): 1856-1863. DOI:10.6038/pg20150446 |
Zhou J M, Liu W T, Li X, et al. 2018. Research on the 3D mimetic finite volume method for loop-source TEM response in biaxial anisotropic formation. Chinese Journal of Geophysics (in Chinese), 61(1): 368-378. DOI:10.6038/cjg2018K0598 |
Zienkiewicz O C, Zhu J Z. 1992a. Super-convergent patch recovery and a posteriori error estimates. Part 1:The recovery technique. International Journal for Numerical Methods in Engineering, 33(7): 1331-1364. DOI:10.1002/nme.1620330702 |
Zienkiewicz O C, Zhu J Z. 1992b. The superconvergent patch recovery and a posteriori error estimates. Part 2:Error estimatesand adaptivity. International Journal for Numerical Methods in Engineering, 33(7): 1365-1382. DOI:10.1002/nme.1620330703 |
曹晓月, 殷长春, 张博, 等. 2018. 面向目标自适应有限元法的带地形三维大地电磁各向异性正演模拟. 地球物理学报, 61(6): 2618-2628. DOI:10.6038/cjg2018L0068 |
刘云鹤, 殷长春, 蔡晶, 等. 2018. 电磁勘探中各向异性研究现状和展望. 地球物理学报, 61(8): 3468-3487. DOI:10.6038/cjg2018L0004 |
齐彦福, 殷长春, 刘云鹤, 等. 2017. 基于瞬时电流脉冲的三维时间域航空电磁全波形正演模拟. 地球物理学报, 60(1): 369-382. DOI:10.6038/cjg20170131 |
任政勇, 邱乐稳, 汤井田, 等. 2018. 基于电流密度连续性条件的直流电阻率各向异性问题自适应有限元模拟. 地球物理学报, 61(1): 331-343. DOI:10.6038/cjg2018K0698 |
孙怀凤, 李貅, 李术才, 等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049-1064. DOI:10.6038/cjg20130333 |
汤井田, 任政勇, 化希瑞. 2007. 地球物理学中的电磁场正演与反演. 地球物理学进展, 22(4): 1181-1194. DOI:10.3969/j.issn.1004-2903.2007.04.025 |
殷长春, 张博, 刘云鹤, 等. 2015. 航空电磁勘查技术发展现状及展望. 地球物理学报, 58(8): 2637-2653. DOI:10.6038/cjg20150804 |
张莹莹, 李貅, 姚伟华, 等. 2015. 多辐射场源地空瞬变电磁法多分量全域视电阻率定义. 地球物理学报, 58(8): 2745-2758. DOI:10.6038/cjg20150811 |
赵越, 李貅, 王祎鹏. 2015. 大回线源瞬变电磁全域视电阻率定义. 地球物理学进展, 30(4): 1856-1863. DOI:10.6038/pg20150446 |
周建美, 刘文韬, 李貅, 等. 2018. 双轴各向异性介质中回线源瞬变电磁三维拟态有限体积正演算法. 地球物理学报, 61(1): 368-378. DOI:10.6038/cjg2018K0598 |
 2020, Vol. 63
2020, Vol. 63


