地壳应力场的获取大多来自于断层滑动(Angelier, 1979, 1984; Etchecopar et al., 1981; 许忠淮和戈澍谟，1984; Michael, 1984；Gephart, 1990; 万永革，2015)和震源机制(Gephart and Forsyth, 1984; 许忠淮，1985；Michael, 1987; Angelier, 2002; Wan et al., 2016)的约束，因此很多人直接根据少数震源机制或断层滑动信息估计应力场.然而震源机制和应力场是两个不同的概念，虽然两者有一定的联系，然而直接采用震源机制类型判断应力场却是不妥的.震源机制是地震断层错动的运动学描述，在断层错动矢量所在的垂直于断层面的平面内与错动矢量夹角45°的方向为T轴方向，而与错动矢量夹角135°的方向为P轴方向.描述地震震源机制只需要三个独立参数(万永革等, 2000, Li and Tan, 2017).而应力场是对研究地区应力状态的描述，采用对称张量表达，有6个独立参数，如约束膨胀(塌缩)应力为零，则需要5个参数，5个独立参数的物理模型和3个独立参数的物理模型肯定是不同的.求取应力张量的本征值和本征向量，对应于本征值为负的本征向量就是挤压应力方向(这与震源机制的P轴一般是不同的)，反之为拉张应力方向(同样与震源机制的T轴不同).1个应力张量可以有2个拉张轴、1个挤压轴，也可以有1个拉张轴、2个挤压轴，还可以有1个拉张轴、1个挤压轴，而另1个轴的本征值为零，即该轴上既不挤压也不拉张，而地震震源机制是由地震错动得到的，必定有1个P轴、1个T轴，1个B轴(又称N轴).为清楚表明应力场及其作用下产生的震源机制之间的关系，本文模拟挤压、走滑、拉张应力体系下产生的震源机制类型，从而表明一定应力体系可以产生丰富多彩的震源机制类型及其节面上的剪应力和正应力的分布.值得一提的是，Wallace(1951)采用立体投影到施密特网的方式给出了不同应力主值下的剪应力和正应力的空间分布，万永革等(2011)采用应力形因子给出了不同断层面几何形状产生的剪应力、正应力以及不同摩擦系数下的库伦破裂应力的分布，但本模拟是针对不同应力体系下震源机制节面上所表现的剪应力和正应力的分布，目的是理解震源机制所表现的各种类型，从而理解应力张量求解方法所蕴含的一些问题.

应力张量是对称张量，有6个独立参数，但考虑到采用震源机制和断层滑动资料不能求解膨胀(或塌缩)的应力球张量部分，假定这部分为零(Angelier, 1979; Michael, 1984；许忠淮, 1985; 万永革，2015；Wan et al., 2016).加上这个约束后，应力张量的独立变量变为5个.另外即使考虑应力球张量为零，应力偏张量的绝对大小仍然是无法准确得知的(万永革等，2006)，通常采用三个主应力的比例关系归一化应力大小(Gephart and Forsyth, 1984; 万永革等，2008):

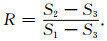
(1)

这里S₁、S₂和S₃是在主轴坐标系下的三个本征值，分别代表主张应力、中间应力和主压应力大小.在只考虑偏应力张量时，必须加上球张量部分为零的约束，即：

(2)

采用震源机制和断层滑动也无法推知偏应力的绝对大小，仿照许忠淮和戈澍谟(1984)的假定，使得应力张量的第二不变量

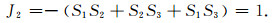
(3)

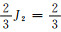
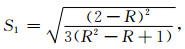
这里相当于规定了八面体面上的剪应力为τ₀²=.在这种情况下，

(4)

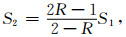
(5)

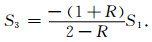
(6)

此时应力张量就简化为4个独立参数，3个参数表示主应力方向，1个参数表示相对大小(即应力形因子).这样在主轴坐标系(主轴方向根据应力值大小排列为拉张轴, 中间轴, 挤压轴)下的应力张量为

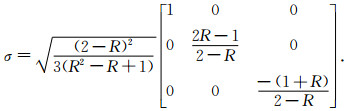
(7)

若已知震源机制一个节面的走向φ，倾角δ，则该断层走向l、倾向m(逆冲为正)在北东下坐标系中可表示为(万永革等，2000)：

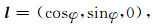
(8)

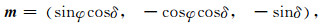
(9)

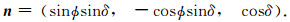
(10)

沿节面剪切方向和倾向方向上的剪应力T₁和T₂可采用下式计算:

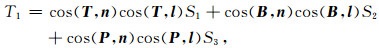
(11)

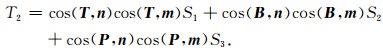
(12)

震源机制节面的正应力为

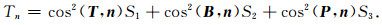
(13)

剪应力方向与节面走向的夹角γ可由下式估计

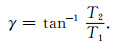
(14)

这就是在给定应力张量情况下计算的震源机制1个节面的滑动角.已知一个节面的走向φ，倾角δ和滑动角γ，另一个节面的对应参数可以相应给出，方法见万永革(2016，第10章)在此不再赘述.

上面只是给出了剪应力的方向，其大小可以表示为

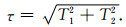
(15)

这里没有采用Wallace(1951)那样假定三个主应力的值，然后计算绝对剪应力和正应力.根据前面的叙述，本研究的应力大小是相对的，为便于比较统一用将(13)式的震源机制解面的正应力和(15)式给出的剪应力统一用最大剪应力(即(S₁－S₃)/2)进行归一化，为相对剪应力和相对正应力，为叙述简单起见，本文也称为剪应力和正应力.

前已述及，一定的应力体系(张量)既有应力3个轴的方向，又有应力形因子R.为全面理解应力张量产生的震源机制表现形式，这里分挤压、走滑和拉张三个应力体系并选择不同的应力形因子进行模拟.对于挤压应力体系，采用挤压轴走向90°，倾伏角为0°；拉张轴走向0°，倾伏角90°，这是1个纯挤压应力体系；拉张应力体系将挤压应力体系的挤压轴和拉张轴交换；走滑应力体系的主压应力轴走向为0°，主张应力轴走向为90°，两个轴的倾伏角均为0°.这里模拟这3种应力体系在不同应力形因子(R)下所产生的震源机制.为理解震源机制的表现，本文假定震源机制的节面走向和倾角按照间隔10°进行全空间取样，采用上节的方法计算滑动角和在该节面上的剪应力和正应力.计算出滑动角后，参照Zoback(1992)世界应力图的震源机制划分标准(表 1)，按照震源机制类型统计展示出各类震源机制的情况.另外，由于震源机制的2个节面相互垂直，应力张量投影到这2个节面的剪应力和正应力在走向0°~180°和180°~360°是对称的，只需两段中的任一段即可知道所有的空间分布.为节省图幅，本文在走向0°~180°范围的底图绘制剪应力的相对大小，而在走向180°~360°范围的底图绘制正应力的相对大小.从而分析应力张量对该地震震源机制的作用.本文分析的各类震源机制(表 1)出现的数量是按照0°~180°进行统计的.

表 1 (Table 1)

表 1 震源机制解分类依据表 Table 1 Categories of tectonics stress regimes for focal mechanism solutions 类型 P轴倾角 B轴倾角 T轴倾角 正断型(NF) ≥52° ≤35° 正走滑型(NS) 40°≤倾角≤52° ≤20° 走滑型(SS) ≤20° ＜40° ≥45° ≥45° ＜40° ≤20° 逆走滑型(TS) ≤20° 40°≤倾角≤52° 逆断型(TF) ≤35° ≥52° 不确定型(U) 上述类型之外的震源机制解

表 1 震源机制解分类依据表 Table 1 Categories of tectonics stress regimes for focal mechanism solutions

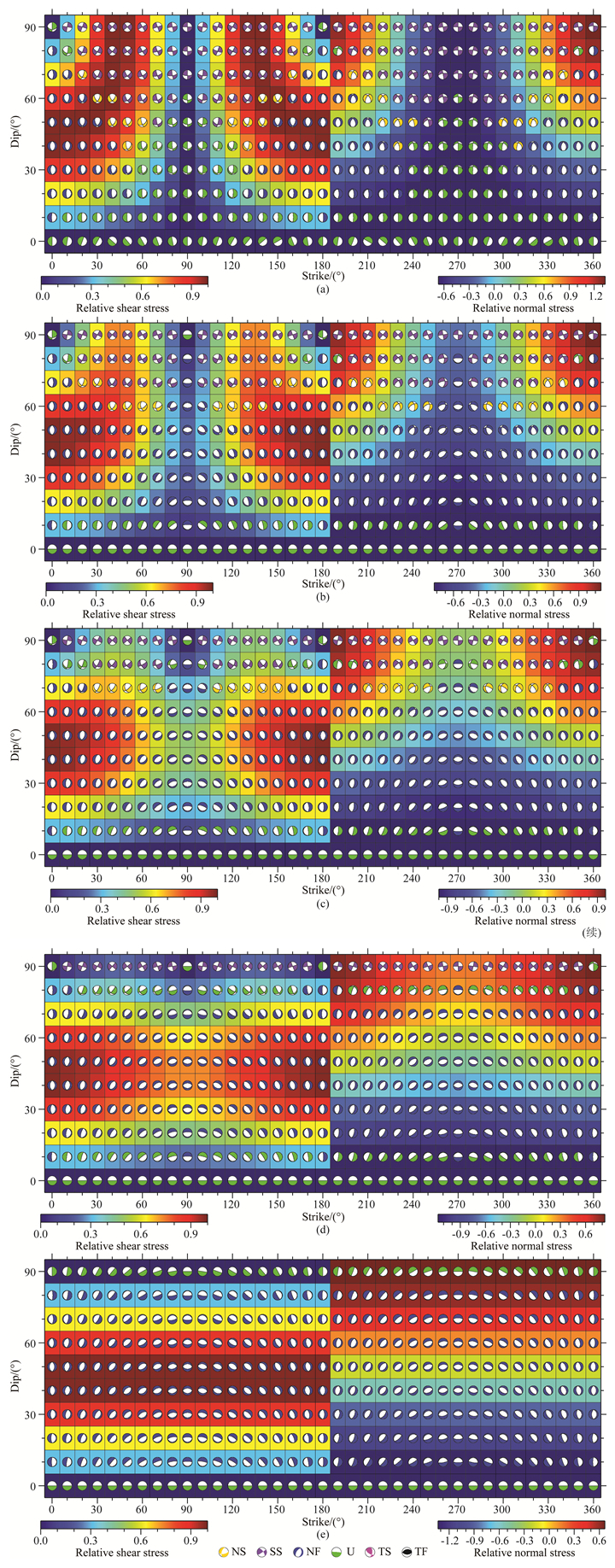
挤压体系产生的震源机制及其断层面上正应力和剪应力大小是以东西向挤压，垂直向拉张为例进行模拟的，不同R值所产生的震源机制、剪应力和正应力分布见图 1.根据理论分析，这种应力情形下的最大剪应力应该在将主压应力轴和主张应力轴平分的断层上，即在走向南北(0°和180°)，倾角为45°的断层上.可以看到，不管R值为多少，剪应力在横坐标的0°和180°，纵坐标的45°均为最大值，并且在这些坐标值上的震源机制节面走向大体上为南北向，这与理论分析一致.但当应力形因子R为不同值时，震源机制、剪应力和正应力分布完全不同.图 1a为R=0的情形，可以看到，在走向为南北(0°和180°)，随着倾角偏离45°，剪应力逐渐减小，震源机制形态也表现很大不同.随着断层走向逐渐偏离南北向，在剪应力较大处仍然为逆冲断层震源机制，但空间形态表现为渐变方式，只有在断层倾角为0°和90°时表现为不确定型断层.这是由于根据式(1)，2个挤压应力(S₂和S₃)相等，根据万永革等(2011)应力状态空间图像结果，S₂和S₃可以相互转换，并且可以在水平面内任意旋转，这就导致任意走向的断层面均可以看作其倾向为挤压应力方向，而垂直方向为拉张，导致了倾角为45°的断层呈现最大剪应力.随着倾角偏离45°，剪应力逐渐减小，这与走向南北(0°和180°)情形的分析一致.当断层倾角为0°和90°时，由于剪应力为零而表现为不确定性震源机制.图 1a的走向180°~360°范围给出正应力的分布.由于R=0的应力状态对应于水平向挤压(方向可任意旋转)，垂直向拉张，导致水平断层(倾角为0°)的正应力为最大值(表现为拉张极值)，垂直断层(倾角为90°)的正应力为最小值(拉张为正，表现为挤压极值)，而倾角自0°到90°正应力逐渐从拉张极值过渡到挤压极值.

图 1

Fig. 1

图 1 挤压应力体系所产生的震源机制及其所产生的相对剪应力和正应力 震源机制为挤压应力体系在对应走向和倾角下产生的.走向0°~180°范围内的底色图为相对剪应力，色标在每幅图左下角给出；走向180°~360°范围内的底图为相对正应力，色标在每幅图右下角给出.震源机制类型图例在子图(e)的下部给出.从上到下五幅图所对应的应力形因子分别为0, 0.25, 0.5, 0.75, 1.0. Fig. 1 Focal mechanisms generated by compressional stress regime and their relative shear stress and relative normal stress Focal mechanisms are generated by the compressional stress regime on the corresponding strike and dip. The relative shear stress is shown in the strike of 0°~180° with color bar in left bottom of each figure, and the relative normal stress is shown in the strike of 180°~360° with color bar in right bottom of each figure. The legend of types of focal mechanism is shown in the bottom of (e). The stress shape ratio of each figure from top to bottom is 0, 0.25, 0.5, 0.75 and 1.0, respectively.

当R逐渐增大时，根据式(1)，挤压应力S₂和S₃的差别逐渐增大，导致走向为90°的断层的剪应力越来越小，逆断型震源机制数目也逐渐减小，而走滑型和逆走滑型震源机制数目逐渐增加(表 2)，正应力的最大值(拉张极值)逐渐减小，最小值绝对值(挤压极值)逐渐增加(参见各幅子图右下方的色棒所展示的取值范围).R自0到1，正应力在走向270°(和90°)的高倾角断层上逐渐增加，呈现拉张，但在走向为180°和360°的垂直断层(倾角为90°)一直为最小值(挤压极值)，这与东西向挤压对南北向的垂直断层的压应力最大的理论分析是一致的.

表 2 (Table 2)

表 2 对应应力体系模拟产生的各类震源机制数量统计 Table 2 Statistics of the number of various types of focal mechanism generated by corresponding stress regimes 类型 应力形因子 正断型(NF) 正走滑型(NS) 走滑型(SS) 逆走滑型(TS) 逆断型(TF) 不确定型(U) 挤压应力体系 0 0 0 0 0 152 38 0.25 0 0 16 0 122 52 0.5 0 0 26 10 110 44 0.75 0 0 40 12 98 40 1 0 0 55 14 56 65 走滑应力体系 0 56 14 55 0 0 65 0.25 44 12 57 2 16 59 0.5 32 8 53 8 24 65 0.75 24 2 57 12 36 59 1 0 0 58 14 48 70 拉张应力体系 0 56 14 55 0 0 65 0.25 98 12 40 0 0 40 0.5 110 10 26 0 0 44 0.75 122 0 16 0 0 52 1 152 0 0 0 0 38

表 2 对应应力体系模拟产生的各类震源机制数量统计 Table 2 Statistics of the number of various types of focal mechanism generated by corresponding stress regimes

当R=1时(图 1e)，根据式(1)，S₁和S₂相等，并且在S₁和S₂组成的平面内可以相互转换和旋转(万永革等，2011)，则既可以看作东西向挤压、垂直向拉张，也可以看作东西向挤压，南北向拉张，这样可以致使在走向南北(0°和180°)的倾角为45°的断层上剪应力最大(对于垂直向拉张情况，对应于逆断层)，也可以导致走向东北—西南(45°和225°)的垂直断层上的剪应力最大(对于南北向拉张情况，对应于走滑断层).由于S₁和S₂轴可以相互旋转，则可以形成最大剪应力以(0°, 90°)和(180°, 90°)为中心的弧形区域，震源机制类型也是逐渐过渡的，此时走滑型和逆走滑型震源机制数目最多(表 2).对于正应力，呈现走向270°和90°的垂直断层(倾角为90°)为拉张应力极值(正应力最大值)，而走向为0°，180°和360°的垂直断层(倾角为90°)为压应力极值(正应力最小值).

对于走滑应力体系，本文采用南北向挤压，东西向拉张的应力状态进行模拟.图 2给出了这种应力状态下的剪应力、正应力及震源机制的分布.根据理论推测，这种应力状态在走向45°和225°的垂直断层[对于图 2中(45°, 90°)和(225°, 90°)]为最大剪应力，应力形因子R值为任何值均是这种情况，这在图中得到体现.然而对于不同的应力形因子R，剪应力、正应力和震源机制类型存在很大差异.对于R=0(图 2a)，S₂和S₃相等，且可以在两者组成的平面内任意旋转和交换.这相当于既可以看作南北向挤压，也可以看作垂直向挤压.如果看作南北向挤压，东西向拉张，则会产生走滑类型震源机制；如果看作垂直向挤压，东西向拉张则会产生正断层类型震源机制.这导致在(45°, 90°)附近为走滑型地震，而在(0°, 45°)和(180°, 45°)附近表现为正断型地震，过渡区的几个震源机制为正走滑型.最大剪应力围绕(0°, 90°)和(180°, 0°)的一个弧形区域.而倾角为零的断层剪应力为零，导致这些点及其周围呈现不确定型震源机制.正应力在南北向垂直断层[表现为(180°, 90°)和(360°, 90°)]最大(拉张极值)，这是由于施加东西向拉张应力导致的.正应力在水平断层(倾角为0°)和走向东西(90°和270°)的断层上最小(挤压机制)，这是由于挤压应力既可以看作南北向(导致水平断层上挤压)，也可以看作垂直向(导致东西走向的断层上挤压).

图 2

Fig. 2

图 2 除了应力体系为走滑应力体系外与图 1相同 Fig. 2 Same as Fig. 1 but for the stress regime of strike-slip

当R逐渐增大时，根据式(1)，挤压应力S₂和S₃的差别逐渐增大，S₂的挤压应力相比于S₃越来越小，导致(0°, 45°)和(180°, 45°)点及其周围的剪应力越来越小.正断型和正走滑型震源机制数目也逐渐减小，逆断型和逆走滑型震源机制数目逐渐增加(表 2).正应力的最大值(拉张极值)逐渐减小，最小值绝对值(挤压极值)逐渐增加(参看每幅子图右下角色棒的取值范围).R自0到1，正应力在走向270°(和90°)的高倾角断层中也逐渐减小，呈现挤压，但在走向为180°和360°(0°)一直为最大值(拉张极值)，这与东西向拉张，南北向挤压的应力状态是一致的.

当R=1时(图 2e)，S₁和S₂相等，并且在S₁和S₂组成的平面内可以相互转换和旋转(万永革等，2011)，则既可以看作南北向挤压，东西向拉张，也可以看作南北向挤压，垂直向拉张.这样可以致使在走向东西(90°和270°)、倾角为45°的断层上剪应力最大(对于垂直向拉张情况，表现为逆断层)，也可以导致走向北东—南西(45°和225°)的垂直断层上的剪应力最大(对于东西向拉张情况，表现为走滑断层).由于S₁和S₂轴可以相互旋转，则可以形成最大剪应力以(90°, 90°)[对称点为(270°, 90°)]为中心的弧形区域，震源机制类型也是逐渐过渡的，此时的逆断型和逆走滑型震源机制数目最多、正断型和正走滑型震源机制数目最少(表 2).对于正应力，呈现走向东西(270°和90°)的垂直断层(倾角为90°)为挤压应力极值(正应力最小值)，而走向为0°，180°和360°的垂直断层(倾角为90°)为拉张应力极值(正应力最大值).

此处的拉张体系是以2.1节的挤压体系的拉张轴和挤压轴交换为例进行模拟的.对应不同R值所产生的震源机制、剪应力和正应力分布见图 3.其分析情况也可以仿照2.1节的分析进行.这种应力情形下的最大剪应力应该在将压应力轴和张应力轴平分的断层面上，即在走向南北(0°和180°)，倾角为45°的断层上，可以看到，不管R值为多少，剪应力在(0°, 45°)和(180°, 45°)均为最大值.但当应力形因子R为不同值时，震源机制、剪应力和正应力分布完全不同.图 3a为R=0的情形，根据式(1)，两个挤压应力(S₂和S₃)相等，可以相互转换，这就导致既可以看作垂直向挤压，东西向拉张，也可以看作垂直向挤压，南北向拉张.第一种情况导致正断型震源机制分布在(0°, 45°)和(180°, 45°)周围，剪应力也以此为最大值中心；第二种情况导致走滑型地震分布在(45°, 90°)周围，剪应力以此为最大值中心.而在水平断层(倾角为零)的剪应力为零，相应的震源机制为不确定型.对于正应力分布，由于垂直向挤压，导致水平断层的正应力为挤压极值(正应力最小值)；由于也可以看成南北向挤压，导致东西向垂直断层(走向为270°和90°)为挤压极值(正应力最小值)，而在南北向垂直断层[对应于(180°, 90°)和(360°, 90°)点]为拉张应力极值(正应力最大值)，其他区域以这些极大值和极小值连续分布.

图 3

Fig. 3

图 3 除了应力体系为拉张应力体系外与图 1相同 Fig. 3 Same as Fig. 1 but for stress regime of extension

当R逐渐增大时，挤压应力S₂和S₃的差别逐渐增大，导致走向为90°的断层的剪应力越来越小，走滑型震源机制数目也逐渐减小，而正断型和正走滑型震源机制数目逐渐增加(表 2).正应力的最大值(拉张极值)逐渐减小，最小值绝对值(挤压极值)逐渐增加(参看每个子图右下方色棒的取值范围).R自0到1，正应力在走向270°(和90°)的高倾角断层中也逐渐增大，呈现拉张，以(180°, 90°)和(360°, 90°)为最大中心值(拉张极值)，这与东西向拉张在南北走向(180°和360°)的垂直断层(倾角为90°)的压应力达到最大的理论分析是一致的.

当R=1时(图 3e)，S₁和S₂相等，并且在S₁和S₂组成的平面内可以相互转换和旋转(万永革等，2011)，则拉张轴可以在任意水平方向，而垂直方向为挤压轴.这样可以在任意走向的倾角为45°的断层上呈现最大剪应力，而随着对倾角45°的偏离剪应力逐渐减小，到倾角为0°和90°时剪应力降为0，此时对应于不确定型震源机制.而其余的均为正断型和正走滑型震源机制.对于正应力，由于施加垂直向挤压，任意水平方向都可作为拉张轴，导致水平断层(倾角为0°)为挤压极值(正应力最小值)，而垂直断层(倾角为90°)为拉张极值(正应力最大值)，自水平断层到垂直断层正应力逐渐过渡.

为理解模拟的各种体系应力张量产生震源机制的情况，本文给出了在全空间取向断层面上产生的震源机制P、T和B轴在施密特网上的分布(图 4).其中，三列图分别对应于前述的挤压应力体系，走滑应力体系和拉张应力体系，自上到下分别对应于应力形因子R=0, 0.25, 0.5, 0.75, 1.其中的红点、蓝圈和黄十字分别表示震源机制P轴、T轴和B轴，对应颜色的五角星为挤压应力轴、拉张应力轴和中间应力轴.从挤压应力体系所产生的震源机制P、T和B轴来看(图 4a, d, g, j, m)，当R=0时，由于S₂和S₃可以相互交换，P轴和T轴是围绕中心对称分布的，而B轴则完全为水平.随着R的增加，P轴逐渐向东西向的应力挤压轴集中，并且集中在外侧，而T轴逐渐沿南北向扩展，集中在内侧，B轴逐渐向南北向集中.这是由于主压应力方向为水平向，而主张应力方向为垂直向，随着R值的增加，主压应力和中间应力的差别越来越大，致使P, T, B轴分别逐渐趋近于主压应力轴，主张应力轴和中间应力轴的缘故.当R=1时，主张应力S₁和中间应力S₂相等，呈现震源机制P轴集中在东西两侧，而T轴分布于南北向的广大区域范围内，B轴集中在南北垂直面和水平方向上.

图 4

Fig. 4

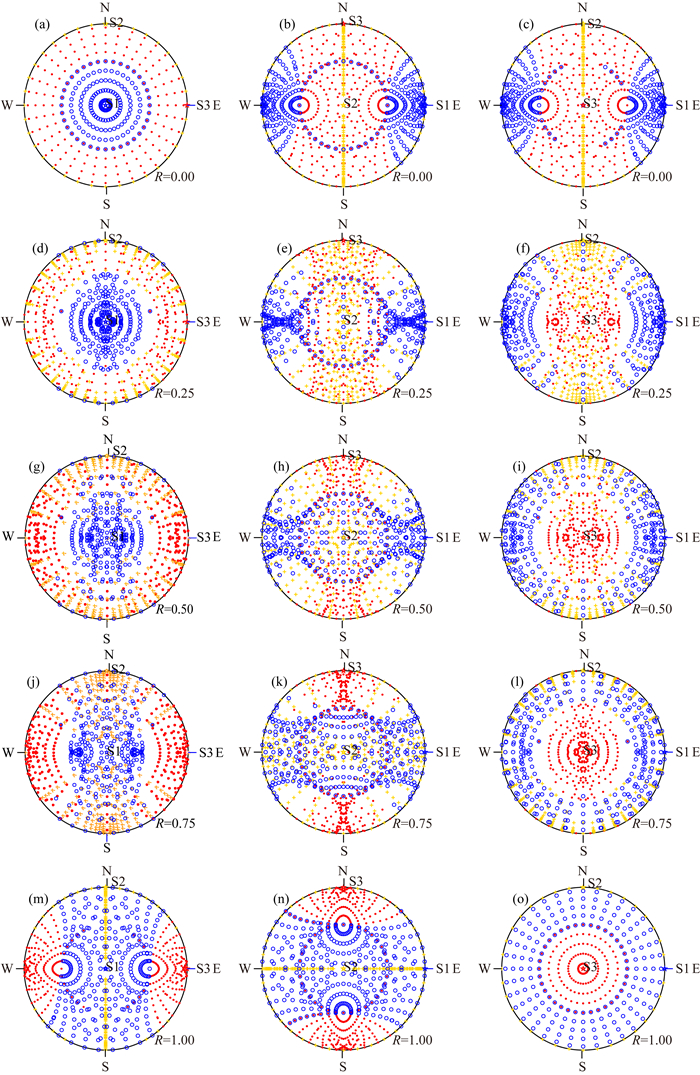
图 4 根据给定应力体系得到的震源机制P, B, T轴的施密特网投影 第一列对应于挤压应力体系，第二列对应于走滑应力体系，第三列对应于拉张应力体系.震源机制P轴投影用红点表示，T轴用蓝色o表示，B轴用黄色+表示.应力轴用五角星表示，红色，蓝色和黄色分别表示主压应力轴，主张应力轴和中间应力轴.从上到下五行图所对应的应力形因子分别为0, 0.25, 0.5, 0.75, 1.0. Fig. 4 Equal area projections of P, T and B axes of focal mechanisms generated by corresponding stress regimes The first, second and third columns correspond to compressional, strike-slip and extensional stress regime, respectively. The projections of P, T and B axes are presented by red point, blue 'o' and yellow '+', respectively. The stress axes are shown by pentagrams, in which, compressional, extensional and intermediate axes are presented by red, blue and yellow. The stress shape ratio of each line from top to bottom is 0, 0.25, 0.5, 0.75 and 1.0, respectively.

由于拉张体系为挤压体系的挤压应力轴和拉张应力主轴交换，此处先分析拉张应力状态(图 4c, f, i, l, o)，以便和挤压应力体系作比较.R=0意味着S₂和S₃相等，均为挤压状态，因此T轴分布于拉张轴周围的东西两侧分布(图 4c)，P轴则分布在施密特网南北及中心的广大区域范围内；B轴分布在南北向的垂直平面及水平方向上.随着R值的增加(图 4f, i, l, o)，震源机制T轴的分布范围逐渐扩大，到R=1时，T轴分布已经在施密特网上的各个方位对称分布，而震源机制P轴则自南北两侧逐渐向中部集中，当R=1时仅分布在中间的对称区域.B轴则由R=0时的南北向垂直面内及水平方向，逐渐弥散到较大的范围，然后逐渐集中在对称的水平方向上.这里需要说明的是，由于拉张应力体系为挤压应力体系的挤压主轴和拉张主轴相互交换，使得拉张体系的每一幅图均可以找到与此对应的挤压应力体系的震源机制的P, T轴交换，即图 4c, f, i, l, o的P, T轴分别图 4m, j, g, d, a的P和T轴位置交换，请读者进行比较.

对于走滑应力体系(图 4b, e, h, k, n)，当R=0时，S₂和S₃相等，震源机制T轴分布于拉张应力轴周围，位于东西两侧，而P轴分布于中间较大的区域范围内，B轴分布于南北垂直面及部分水平方向上.随着R值的增大，T轴范围逐渐扩大，而P轴范围逐渐缩小.R=0.5时，P轴和T轴在施密特网上所占的区域范围对等，分布在南北侧和东西侧.R值再增大时，P轴方向集中在压轴(S₃)附近的集中度大于T轴围绕拉张轴(S₁轴)的集中度.当R=1时，除了P轴集中在南北两侧外，其他区域遍布着T轴.在走滑体系下，B轴在R=0时集中在南北向的垂直面内和水平方向上，在R=1集中在东西向的垂直面内和水平方向外，其他情况分布较为广泛.另外，可以看到，R=0的情况(图 4b)只是R=1情况(图 4o)的P, T轴交换位置，R=0.25的情况(图 4e)只是R=0.75情况(图 4k)的P, T轴交换位置，而B轴不变.这可以从应力场的主压应力轴和主张应力轴交换位置的应力张量对称得到判定.

本文模拟的同一应力张量可以表现为多种震源机制，但震源机制节面上的剪应力是不同的.一般来讲，剪应力最大的震源机制P轴和T轴与应力张量的压轴和张轴分别一致，而其他震源机制的P轴和T轴与应力张量的压轴和张轴并不一致.一般来讲，节面上剪应力越大的震源机制P, T轴与应力张量的压轴和张轴越接近.这对应于一块完整岩石在外力作用下压坏，这时产生的破裂面上就具有最大剪应力.这就引出一个问题，地震是否按照破裂面上具有最大剪应力的震源机制发生？我们按可以看作同一应力张量的较小区域范围内发生的大量地震的震源机制是否具有多样性来进行甄别.大地震之后能计算得到大量余震震源机制，如汶川地震(胡幸平等，2008；易桂喜等，2012)、芦山地震(林向东等，2013；罗艳等，2015)、九寨沟地震(杨宜海等，2017).如果地震按照节面上具有最大剪应力的震源机制发生，则余震震源机制应该有相当一致性.如果忽略了观测和计算误差，则应该只按一种震源机制发生.而实际上，余震的震源机制是多种多样的(如胡幸平等，2008；易桂喜等，2012；林向东等，2013；罗艳等，2015；杨宜海等，2017).这就表明地震不是按着震源机制节面上具有最大剪应力的破裂发生的，而是按照应力张量投影到断层面的方向来错动.这可以解释为由于地质变动，地壳中存在很多薄弱带或小裂纹，往往这些薄弱带或小裂纹随机分布在地壳中.在地壳应力场作用下，虽然这些薄弱带或小裂纹上的剪应力不是最大，但由于相当薄弱，当剪应力超过薄弱带或小裂纹所能承受的极限时，就会沿此薄弱带或小裂纹发生地震.由于这些薄弱带或小裂纹的几何形状的多样性，导致了同一应力张量作用下的震源机制表现为多样性.但需要指出的是，根据前面的模拟结果，挤压应力体系不会产生正断型和正走滑型震源机制，反过来，拉张应力体系不会产生逆断型和逆走滑型震源机制.

震源机制数据是确定应力张量(应力场)的重要数据来源.在早些时候，能确定震源机制的地震数目相对较少，很多学者仅用1个或几个震源机制就分析应力在某某方向挤压，某某方向拉张，其实这只有在地震发生在剪应力最大的断层上才是正确的.如果认为地震发生在随机几何形状的薄弱带或裂纹上，则应力张量不能改变其走向和倾角，只是随着应力张量的不同表现的滑动角不同.因此这种方式只能对应力状态进行大致定性的推断，推断结果具有较大的不确定性.

有些人将震源机制转换为矩张量，将所得到震源机制的矩张量叠加，求解其本征值和本征方向从而得到应力方向(如钟继茂和程万正，2006；盛书中等，2013).这种方法简单，容易实现.但所得到的是地震矩张量释放的主轴方向，不是促使地震发生的构造应力方向.这对于断层上剪切破裂沿着释放最快的方向(即最大剪应力方向)对积累应力进行释放是正确的.但大地震发生后余震震源机制的多样性表明余震的发生不是按照这种方式释放应力的，因此不适合用这种方法.

在比较流行的采用震源机制求解应力场的方法中，Gephart和Forsyth(1984)采用应力张量产生的震源机制的P, T, B轴与实际观测的震源机制P, T, B轴的符合程度，或者旋转角度(万永革，2008)来定义应力张量模拟结果和观测结果的差别的，与多个观测震源机制差别最小的应力张量即为所求解的应力张量.Michael(1987)采用应力张量在给定断层上的剪应力方向与观测的断层滑动方向的差别定义为目标函数，从而找到与观测震源机制最符合的应力张量.这两种方法都不管剪应力的大小，认为较小的剪应力即可以使较为薄弱的裂纹或断裂带发生破裂而设计的方法.这些是本文结果所推荐的方法.

在有些地质断层调查时，通常量取擦痕方法得到断层滑动角.如果断层的走向和倾角差别不大(或者同一断层具有相同的走向和倾角)，而量取的滑动角有很大差别，特别是正断层和逆断层交互出现的情况，则需要特别注意.因为在断层走向和倾角确定的情况下，一定应力张量的剪应力方向是一定的，如果有多个剪应力方向(或滑动方向)，则一种可能是(1)式中的R为1(或0)，即拉张应力S₁(或挤压应力S₃)和中间应力S₂相等，而挤压应力(或拉张应力)作用在断层法向上，另一种可能是震源机制测量存在较大误差(万永革等，2001).对于第一种情况的断层面上的剪应力为0，通常很难发生.另外一种可能是考虑这些滑动不是同一应力张量所导致的，这就需要甄别这些资料分别是哪个时期的应力张量导致的，从而确定不同时期的应力场.因此在反演应力张量中需要特别注意检查数据的有效性.

在有些求解震源机制并分析应力场的文献中，将震源机制的走向、倾角、滑动角、P轴、T轴进行统计给出应力场的压轴和张轴方向的估计，并进行地震发生背景的动力学分析.这里需要说明的是，地震发生所在裂纹是地球上多期地质变动遗留的薄弱带，不随应力场的作用而改变，因此对地震所发生的走向和倾角进行统计是没有意义的，薄弱带的形状不会因为施加的构造应力而改变.如果不管走向和倾角，直接统计滑动角，滑动角只能给出倾滑断层和走滑断层的判断，但其本身不能约束应力方向.因此对断层走向、倾角和滑动角进行统计与应力状态的判定无益.

按照本文的模拟结果，即使在同一应力张量作用下，震源机制P, T轴也有很大的多样性.在R=0时，震源机制的T轴分布在拉张主应力周围，统计大量震源机制T轴或许能估计拉张主应力方向，但P轴分布在很大范围内，通过P轴统计则难以估计应力挤压轴方向.随着R的增大，采用统计方法估计拉张主轴越来越困难，原因是其分布范围逐渐扩大.而P轴的分布范围逐渐集中，估计主压应力轴相对R=0的情况越来越容易.在R=0.5时，P轴和T轴的分布范围均衡.随着R值再增大，震源机制P轴的分布范围逐渐集中在主压应力周围，采用统计P轴的方向估计主压应力的方向越来越容易，而震源机制T轴的分布范围很宽，采用T轴的统计来估计主张应力方向越来越不容易确定.在R=1时，震源机制的P轴范围最小，而T轴的分布范围最大.需要说明的是，这种统计P, T轴估计主压应力和主张应力方向是在统计样本足够多，并且震源机制的断层空间范围较为均匀(或随机分布)的情况下才能得到正确的结果.在进行应力场分析时，最好采用类似于Gephart和Forsyth(1994)与Michael(1987)的方法来确定应力场状态.

我们按照挤压、走滑、拉张三种应力体系模拟了呈现的震源机制类型，节面上的剪应力和正应力以及其震源机制P, T轴的表现，得到如下结论：

(1) 挤压应力体系只能产生逆断型、逆走滑型和走滑型的震源机制；反之拉张应力体系只能产生正断型、正走滑型和走滑型震源机制，而走滑应力体系能产生正断型、正走滑型、逆断型、逆走滑型和走滑型震源机制.各种应力体系产生的各种类型震源机制数目随着应力形因子R而不同.

(2) 对于挤压应力体系，随着R值的增大，走滑型和逆走滑型震源机制数目逐渐增多，而逆断型震源机制逐渐减少；反之对于拉张应力体系，随着R值的增大，正断型震源机制逐渐增多，走滑型和正走滑型震源机制逐渐减少；对于走滑应力体系，随着R值的增大，正断型和正走滑型震源机制数目逐渐减少，而逆断型和逆走滑型震源机制数目逐渐增多.

(3) R=0.5时，应力张量投影到震源机制节面的剪应力在节面位于挤压主应力轴和拉张主应力轴的夹角平分线上时为最大值，随着节面偏离两轴平分线逐渐减小，在两轴上的剪应力为零.当R值自0.5减小时，最大剪应力的节面逐渐扩散至位于挤压应力轴和中间应力轴组成的平面与拉张应力轴夹角为45°的方向上，当R为0时，所有与拉张应力轴夹角为45°的方向上的节面上剪应力均为最大值；反之当R值自0.5增大时，最大剪应力的节面逐渐扩散至位于拉张应力轴和中间应力轴组成的平面与挤压应力轴夹角为45°的方向上，当R为1时，所有与挤压应力轴夹角为45°的方向上的节面上剪应力均为最大值.

(4) R=0.5时，震源机制节面上的正应力在节面与挤压应力轴垂直时最小(挤压)，而在节面与拉张应力轴垂直时最大(拉张).当R值自0.5减小时，最小正应力(挤压)逐渐自以挤压应力为法向的震源机制节面扩展到以中间轴为法向的震源机制节面，当R=0时，与中间应力轴和主压应力轴垂直的震源机制节面均具有最小正应力(挤压应力)；反之当R值自1增加时，最大正应力(拉张)逐渐自以拉张轴为法向的震源机制节面扩展到以中间轴为法向的震源机制节面，当R=1时，与中间应力轴和主张应力轴垂直的震源机制节面均具有最大正应力(拉张应力).

(5) 应力张量所产生的震源机制P, T轴通常与主压应力轴和主张应力轴不重合，而是分布在主压应力轴和主张应力轴周围较大的空间范围内.在R=0.5时，震源机制P, T轴出现震源球(施密特网)的区域范围平衡.当R < 0.5时，P轴所占的范围较大，R=0时P轴在震源球(施密特网)上占据的范围最大；反之，R>0.5时，震源机制T轴在震源球(施密特网)上占据的范围较大，R=1时T轴在震源球(施密特网)上占据的范围最大.

根据本文模拟结果和同一地区观测震源机制多样性，可以推测地震错动不只在剪应力较大的断层面上破裂，地震断层面可能是地球在地质时期变动所存在的随机分布的薄弱面或裂纹，在构造应力作用下，这些薄弱带或裂纹不一定是剪应力最大的面，当剪应力超过薄弱带或裂纹所能承受的剪应力时即会沿着投影到断层面的剪应力方向发生破裂.这预示我们在求解应力场时不要做断层面上剪应力最大的假设.并且通过断层面走向、倾角和滑动角的统计来分析构造应力场是错误的，通过P, T轴的走向和倾伏角的统计来分析应力场也是需要详细论证的.

本文仅采用特定方向的挤压应力体系、拉张应力体系和走滑应力体系模拟应力张量造成的震源机制类型、投影到震源机制节面上的剪应力和正应力，以及P, T轴的分布.但结论是普遍的，只需要对本文所假定的应力体系旋转坐标系就可以转换为读者所希望的任何其他应力体系(Bott, 1959).

本研究研发的根据某地区应力场(包括应力方向和应力形因子R)计算其产生的震源机制及其节面上的剪应力和正应力的程序可向感兴趣的读者提供.