2. 北京应用气象研究所, 北京 100029
2. Beijing Institute of Applied Meteorology, Beijing 100029, China
静力适应过程是大气运动中物理量之间相互调整的重要环节,伴随着垂直加速度的生成和消亡,纷繁多姿的天气现象尽情上演.
对于静力适应过程的研究,最早由Horace(1932)提出,随后Monin和Obukhov(1959)的研究得出静力平衡被破坏后,扰动能量以声波的方式被频散到整个空间,Chao(1962, 1964)和Zeng(1963)也证明频散性质的声波是实现静力适应过程的机制;基于尺度分析,由Ye和Li(1964)等提出研究静力适应过程的线性方程组,并导出波动频散方程,认为频散性质的声波强度可表征大气非静力平衡的程度,同时也讨论了静力适应过程与地转适应过程的关系;Bannon(1995, 1996)从lamb问题出发,研究了一维静态模型中的静力适应过程,Duffy(1997, 2002)利用数值模式研究了二维模型中的适应问题,他认为非静力扰动能量通过声重力波频散出去;Sotack和Bannon(1998)、Chagnon和Bannon(2001, 2004, 2005)从波动理论出发得到热力强迫下静力适应过程的波动响应情况;Fanelli和Bannon(2005)、Edson和Bannon(2008)、Smith和bannon(2008)针对热强迫下的非线性适应问题进行了研究,利用数值模式模拟了等温大气中单个云团、深对流云团和积雨云团中的适应过程,初始强迫激发lamb、声波和浮力波,他们的共同作用使得适应过程最终得以实现;Van Delden(2015)、Cui等(2015)研究了三维静态等温大气中的适应过程,得到结论:声重力波和重力内波是三维静力适应过程得以实现的物理本质.
至此,基于静态大气的假设,科学工作者们从波动和能量的角度描绘了静力适应过程的物理图像.然而,实际大气中常存在着水平基流,且水平基流在垂直方向的分布并不均匀.那么,非静态大气中的静力适应过程如何实现?翻阅历史资料,未曾找到关于此问题的研究文献,作者认为解决这一科学问题的关键便是揭示风垂直切变对静力适应过程的影响.为了清楚全面地揭示风垂直切变对静力适应过程的影响,本研究将构造四种风垂直切变模型,结合模型从波动响应、扰动气块运动规律及适应物理图像和能量转换这三方面进行讨论,第一部分研究非静态大气中的波动响应情况,给出非静态大气静力适应过程的物理机制;第二部分研究风垂直切变对适应过程中扰动气块运动特征的影响,给出适应过程的物理图像;第三部分研究风垂直切变对适应过程中能量转换的影响,给出风垂直切变影响适应过程的物理本质.
本文为第一部分,结构安排如下:第二部分给出研究大气静力适应过程的数学模型,考虑水平基流及其垂直切变作用;第三部分导出模型的波动频散方程、相速度方程和群速度方程; 第四部分构造四种不同的水平基流垂直切变模型,并分析存在水平基流垂直切变时大气静力适应过程中的波动响应;第五部分导出存在风垂直切变情形下的波作用量演变方程,并分析风垂直切变对其的影响;第六部分为结论部分.
1 数学模型数学模型采用在局地直角坐标系中描述完全可压缩等温干大气的原始方程组,忽略运动方程中的科氏力作用项、摩擦力作用和黏性作用,略去由地球旋转引起的惯性波和Rossby波,假定大气运动过程绝热,并满足理想气体状态方程,数学模型表达式为
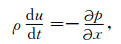
|
(1) |

|
(2) |

|
(3) |
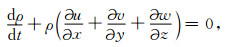
|
(4) |
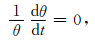
|
(5) |

|
(6) |
其中(u, v, w, p, ρ, T, θ)分别为速度在水平x、y和垂直z方向的分量、大气气压、大气密度、大气温度和位温,cp是空气的定压比热,R是干空气气体常数,g是重力加速度,ps是海平面气压.
利用小扰动法,将物理量写为平均量和扰动量之和的形式(如气压p(x, y, z, t)=p0(z)+p'(x, y, z, t)),其中p0代表气压的基态分量,p'表示气压的扰动分量,假定热力学变量的扰动分量远远小于其基态分量,且热力学基态分量在水平方向分布均匀,保留水平基流在x方向的分量,并假设它只是垂直高度的函数.则线性化后的控制方程组写为
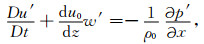
|
(7) |

|
(8) |
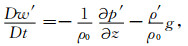
|
(9) |
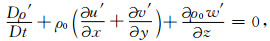
|
(10) |
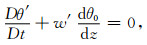
|
(11) |
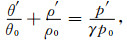
|
(12) |
其中D/Dt≡∂/∂t+u0(z)∂/∂x.
对式(9)和式(12)分别进行D/Dt运算,并结合式(8)和式(11)消去ρ'化简得到:
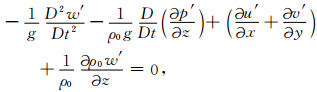
|
(13) |
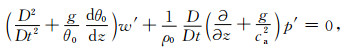
|
(14) |
引入变量:
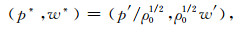
|
(15) |
将式(7)、式(8)代入进行D/Dt运算的式(13)和式(14)中,消去u'和v'得到:
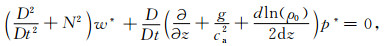
|
(16) |

|
(17) |
由式(16)和式(17)构成了一组闭合的微分方程组,满足方程组的解w'和p'表征了静力适应过程中物理量的相互调整.
2 波动响应由于求解偏微分方程组的解析解具有现实性的困难,故采用正交模方法,假设方程组有波动解,且波动振幅的变化只发生在垂直方向,则有:
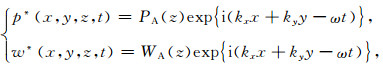
|
(18) |
其中(kx, ky, ω)分别为水平x、y方向的波数和角频率,均为实数;将式(18)代入偏微分方程组则有:
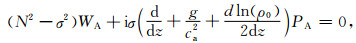
|
(19) |
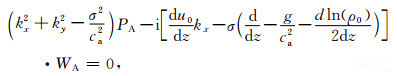
|
(20) |
其中记多普勒频率σ=u0kx-ω,当多普勒频率等于零时有:
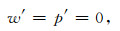
|
(21) |
此时大气处于静力平衡状态,当多普勒频率等于浮力振荡频率时有:

|
(22) |
则得到:
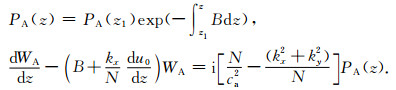
|
(23) |
当多普勒频率既不为零也不等于浮力振荡频率时,利用方程组(19)和(20)消去WA得到:
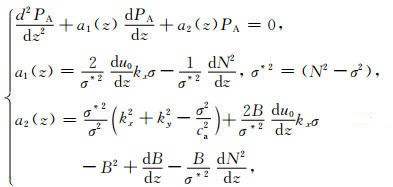
|
(24) |
引入变换:
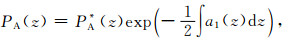
|
(25) |
则式(24)可以化为
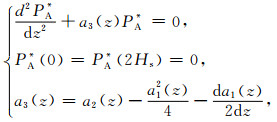
|
(26) |
其中a3称为垂直折射指数,当a3(z)>0时,波动才能在垂直方向进行传播,PA*为一震荡型解,而且波传播总是指向a3(z)大的区域,而当a3(z) < 0时,波的垂直方向传播受阻,PA*有一指数或双曲型解.
当折射指数大于零时,可得到静力适应过程中的波动频散方程为

|
(27) |
其中垂直方向波数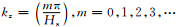
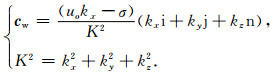
|
(28) |
由式(28)可知,当波动固有频率大于零时,波动传播方向同波矢方向相同,当波动固有频率小于零时,波动传播方向同波矢方向相反.利用隐函数求导原则得到波动固有群速度方程为
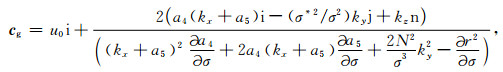
|
(29) |
其中:
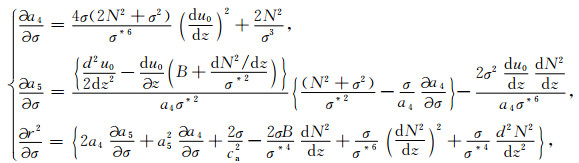
|
(30) |
由式(28)和式(29)可以得到相速度和群速度之间的关系为
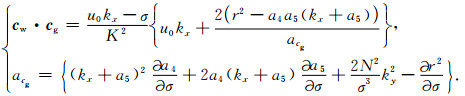
|
(31) |
由式(31)可知,波动形式的传播同波动能量的传播均受水平基流及其垂直切变的影响.当VWS为零时,由式(27)可知,a5等于零,在σ2>N2的条件下,a4=-σ*2/σ2大于零,频散关系为椭球方程,假设水平基流为零,在kxky平面内,相速度和群速度共线,波动呈现Lamb波特征;在kxkz或kykz平面内,相速度分量和群速度分量传播方向均相同,由于在垂直方向受恒定重力的作用,波动呈现各向异性的声波特征;在σ2<N2的条件下,a4小于零,频散关系为双曲型方程,假设水平基流为零,相速度和群速度趋于垂直,两者水平分量符号相同,垂直分量符号相反,波动呈现重力内波性质;实际大气中水平基流不为零,使得波动群速度的kx分量发生变化,但总有相速度和群速度的ky、kz分量符号相反;波动呈现重力内波的特征.假设VWS不为零时,当a4大于零,频散关系为椭圆方程,若a5大于零,频散关系图像向水平波数负方向移动,若a5小于零,频散关系图像向水平波数正方向移动,当水平波数满足关系式:
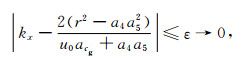
|
(32) |
其中ε为某一固定小量,在式(32)所给的条件下,有σ2 < N2,波动相速度与群速度趋于垂直状态,波动具有重力波的传播特征,在其他波数条件下,有σ2>N2,波动相速度和群速度趋于共线状态,波动具有声波的传播特征;当a4小于零时,频散关系为双曲型方程,当水平波数满足条件:
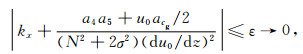
|
(33) |
在式(33)所给的条件下,有σ2>N2,波动相速度与群速度趋于平行状态,波动具有声波的传播特征,在其他波数条件下,有σ2 < N2,波动相速度与群速度趋于垂直状态,波动具有重力波的传播特征;由此可知VWS的存在使得静力适应过程中波动性质发生改变.
3 VWS模型中波动的响应为了计算简单,取水平y方向波数为零,构造四种VWS模型,表示为

|
(34) |
其中(umax, U)为常数,定义水平基流向东为正,随(λ1, λ2)取值的变化表征不同的水平基流垂直结构模型,其中z为垂直高度,本文中选取范围为0≤z≤2Hs,Hs=RTs/g为大气标高,Ts表示地表温度,等温大气中基态量随垂直高度的变化存在关系为
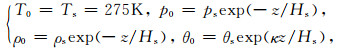
|
(35) |
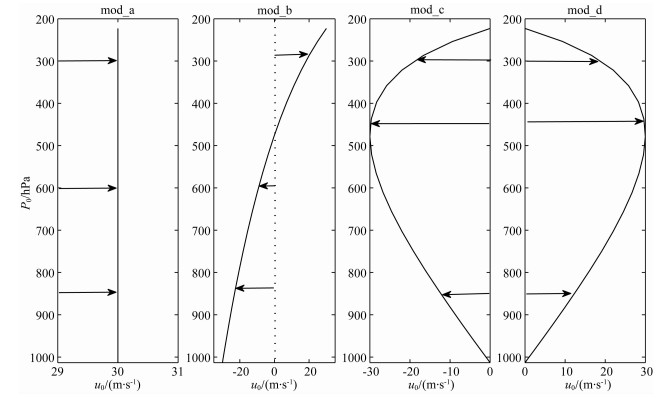
其中κ=R/cp,当取最大水平风速umax=30 m·s-1,则构造所得四种VWS分布模型如图 1所示.
|
图 1 四种基流垂直切变模型 Fig. 1 Four models of VWS |
图 1中mod_a为λ1=λ2=0时,水平基流呈常数分布的西风,无垂直切变;mod_b为λ1=0, λ2=1时,水平基流为随高度呈线性变化的西风,VWS随高度不发生变化,均大于零;mod_c为λ1=-1, λ2=2时,水平基流为随高度呈反气旋式切变的东风急流,先向西增加后减小,急流轴在Hs处,VWS为高度的函数,在急流轴下方小于零,在急流轴上方大于零;mod_d为λ1=1, λ2=2时,水平基流随高度呈气旋式切变的西风急流,先向东增加后减小,急流轴在Hs处,VWS为高度的函数,在急流轴下方大于零,在急流轴上方小于零.
3.1 mod_a水平基流为常数构造一种理想的水平基流场,用于体现水平基流对静力适应过程中波动的作用,也以此作为参照,分析存在VWS时静力适应过程中波动的响应,假设有西风基流在空间均匀分布,取U=umax=30 m·s-1,频散关系式(27)简化为
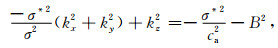
|
(36) |
式(36)为多普勒频率的四阶方程,则代表四支两两成对的波动,每对波动传播方向相反,但性质相似;定义多普勒频率较大的一对波动为σ1,多普勒频率较小的一对波动为σ2,则在mod_a中波动σ1水平正向传播支的速度参数分布如图 2所示.
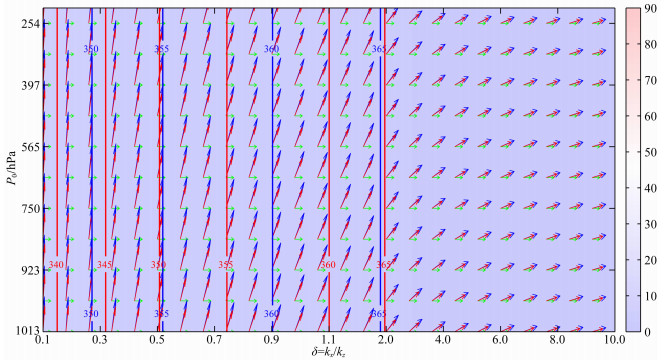
|
图 2 波动σ1水平正传支的速度参数演变 其中横坐标为非均匀分布的垂直水平比,在区间0.1≤δ<1.2内,间隔为0.02,在区间1.2≤δ≤10内,间隔为0.2,取m=1时的垂直波数,纵坐标为大气压强,蓝色、红色和绿色箭头分别表示相速度、群速度和水平基流的方向,蓝色和红色等值线分别表示相速度和群速度的大小;底图颜色表示相速度和群速度之间的夹角,与色标对应. Fig. 2 Velocity distribution for an eastward branch of σ1 The abscissa presents the non-uniform distribution of aspect-ratio δ, the interval is 0.02 for 0.1≤δ < 1.2, and 0.2 for 0.1≤δ < 1.2. The ordinate is the atmosphere pressure. Arrows in blue, red, and green colors represent the directions of phase velocity, group velocity, and the basic flow, respectively. Contours in blue and red colors stand for magnitudes of the phase velocity and group velocity, respectively. The color of base diagram represents the angle between phase velocity and group velocity corresponding to the color bars. |
由图 2可知,正传波动σ1向上向东传播,随着扰动尺度的减小,相速度与铅直轴正方向的夹角变大,向东倾斜,水平基流对正传波动起加速作用,因VWS为零,波动性质未随垂直高度发生变化.波动能量向上向东传播,随扰动尺度和垂直高度的变化与相速度变化趋势一致,群速度方向落于相速度东侧,且两者之间的夹角小于10°,波动传播具有声波特征;波动相速度和群速度的等值线平行于纵坐标轴分布,且等值线间隔不均匀,随着扰动尺度的减小,速度均呈增加趋势,说明扰动尺度越小其耗散速度越快,达到平衡所需的时间越短,当δ<1.2时,波动相速度大于群速度,当δ>2时,波动群速度大于相速度,扰动能量先于扰动传播,产生上游效应,由此可知水平基流对波动相速度与群速度大小的影响和扰动尺度呈非线性关系.对于逆传波动,西风基流起阻滞作用.
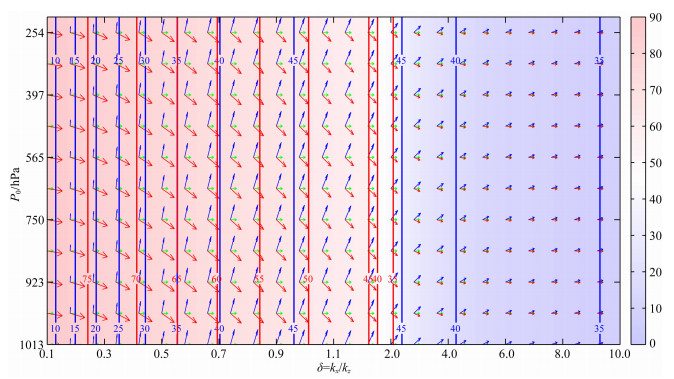
在mod_a中波动σ2水平正向传播支的速度参数分布如图 3所示.图 3显示,动向上向东传播,随着扰动尺度的减小,相速度与铅直轴正方向的夹角变大,向东倾斜,且不随垂直高度发生变化,因VWS为零,则波动性质不随垂直高度发生变化.正传波动能量向下向东传播,随垂直高度的变化与相速度变化趋势一致,随着扰动尺度的减小,群速度与铅直轴正方向的夹角变小,向东倾斜,群速度方向与相速度方向的夹角从垂直向平行渐变;波动相速度和群速度等值线平行于纵坐标轴分布,随着扰动尺度的减小,相速度大小先增加后减小,群速度大小呈减小趋势,说明水平基流对正传波动σ2群速度的加速作用不同于对相速度的加速作用,且与扰动尺度相关.当δ < 1.2时,正传波动相速度小于群速度,扰动能量先于扰动传播,产生上游效应,同时,波动相速度与波动群速度垂直,波动传播具有重力波性质;当δ>2时,波动群速度小于相速度,波动传播逐渐向声波性质转变.水平基流对正传波动的群速度具有加速作用,而对相速度在中小尺度下起加速作用而在微尺度中起阻滞作用.对于逆传情形,西风基流均为阻滞作用.
|
图 3 波动σ2水平正传支的速度参数演变(对应标识同图 2) Fig. 3 Velocity distribution for an eastward branch of σ2 (Explanations are same as Fig. 2) |
当两种相对运动的气块相遇时,较暖的上升,较冷的下沉,在交汇面上往往会形成明显的风切变,这种情形也是造成大气静力平衡被破坏的因素之一,据此构建低层东风,高层西风的水平基流垂直切变模型,假设VWS随高度呈线性变化,取U=umax/H=3.73×10-3 s-1,则式(27)为多普勒频率的8阶方程,其中的四个实数解表征两两成对的波动.
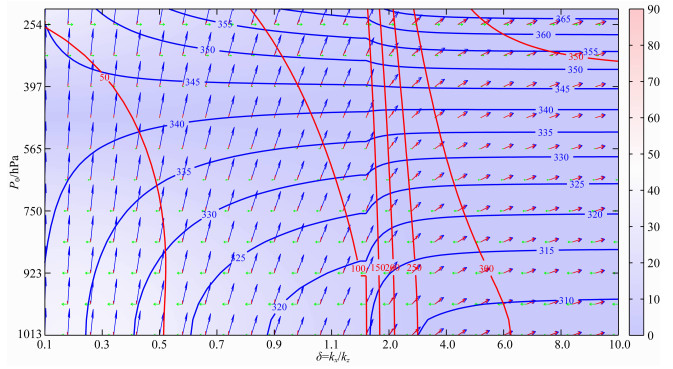
在mod_b中波动σ1水平正向传播支的速度参数分布如图 4所示.由图 4可知,正传波动向上向东传播,在切变线以下,波动水平传播方向与基流相反,在切变线以上,波动水平传播方向与基流相同,随着扰动尺度的减小,相速度与铅直轴正方向的夹角变大,向东倾斜,此时VWS大于零,水平基流向东增加,使得波动传播方向随垂直高度向东倾斜,扰动尺度越小,VWS作用越显著;波动能量向上向东传播,随扰动尺度的减小向东倾斜,随垂直高度的增加逐渐从相速度西侧转向相速度东侧,相速度与群速度之间的夹角均小于35°,波动传播具有声波特征,且随着高度先减小后增大,扰动尺度越大,变化越显著,VWS使得波动性质在垂直向发生了变化.波动相速度等值线在δ>2时呈水平状分布,当δ < 1.2时,相速度等值线在切变线以下呈脊状分布,脊线自下而上向西倾斜,在切变线上层呈槽状分布,自下而上槽线向东倾斜;随垂直高度的增加呈增加趋势,即非静力平衡扰动在高层传播快于低层;群速度等值线自下而上向西倾斜,随着扰动尺度的减小,倾斜程度先减小后增大,群速度大小呈增大趋势,即扰动尺度越小,能量耗散越快,静力适应时间越短.恒定的VWS使得波动能量传播速度发生较大变化,使得波动传播速度随垂直呈线性变化,增大了波动传播方向和能量传播方向之间的夹角.
|
图 4 波动σ1水平正传支的速度参数演变(对应标识同图 2) Fig. 4 Velocity distribution for an eastward branch of σ1 (Explanations are same as Fig. 2) |
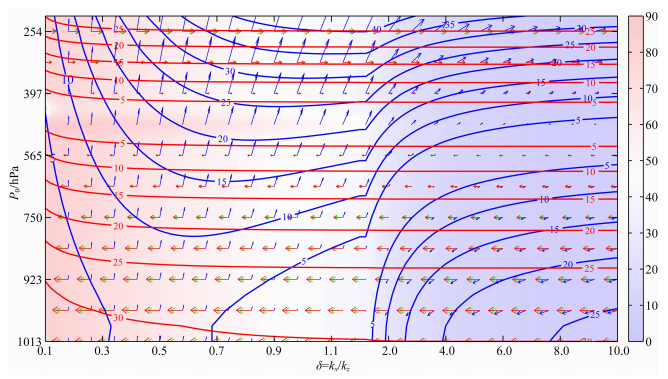
在mod_b中波动σ2水平正向传播支的速度参数分布如图 5所示.图 5显示,在δ < 1.2的区域以及在δ>1.2且垂直高度在切变线上层的区域,波动向上向东传播,随扰动尺度的减小,相速度与铅直轴正方向的夹角变大,向东倾斜,在VWS和水平基流的作用下,相速度等值线呈槽状分布,槽线自下而上向东倾斜,随垂直高度增加相速度大小呈增长趋势,而在δ>1.2且垂直高度在切变线下层的区域,波动向下向西传播,随扰动尺度的减小,相速度与铅直轴负方向的夹角变大,向西倾斜,相速度等值线呈脊状分布,脊线自下而上向西倾斜,随垂直高度增加相速度大小呈减小趋势.群速度传播方向基本与水平基流保持一致,自下而上从向西传播转变为向东传播,群速度等值线呈水平分布,随着垂直高度的增加,群速度大小先减小后增加.在贴近地面的区域,波动群速度大于相速度,能量先于扰动传播,具有上游效应;随着扰动尺度的减小,相速度与群速度从互相垂直向互相平行渐变,波动传播特征也从重力波性质向声波渐变.相比图 3,VWS使得相速度与群速度之间的夹角变小.
|
图 5 波动σ2水平正传支的速度参数演变(对应标识同图 2) Fig. 5 Velocity distribution graph for an eastward branch of σ2 (Explanations are same as Fig. 2) |
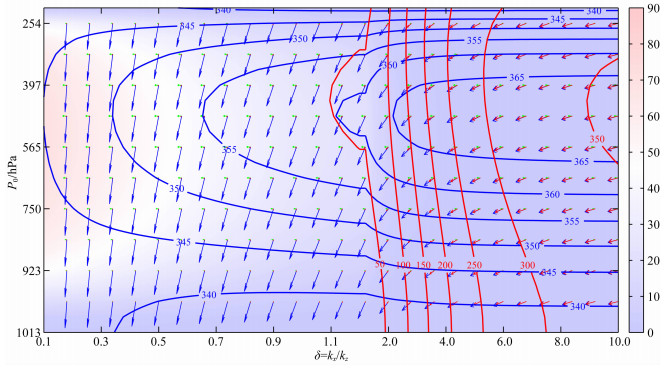
由热力差引起的热带东风急流,在对流层上层有强劲的东风,其平均风速达到30 m·s-1,并伴随有暖性的反气旋;基于此,构造mod_c垂直切变模型,从地面向上东风呈增长分布,在垂直高度Hs处达到最大值,取30 m·s-1,并随垂直高度的继续增加东风逐渐消亡.取U=umax/H2=4.6×10-7 m-1·s-1,在mod_c中波动σ1水平逆向(与水平基流同向)传播支的速度参数分布如图 6所示.
|
图 6 波动σ1水平逆向传播支的速度参数演变(对应标识同图 2) Fig. 6 Velocity distribution for a westward branch of σ1 (Explanations are same as Fig. 2) |
比较图 2、图 4和图 6可知,逆传波动向下向西传播,随着扰动尺度的减小,相速度与铅直轴负方向的夹角变大,向西倾斜,由于水平基流即VWS的作用,随着垂直高度的增加,波动传播方向发生变化,扰动尺度越大,VWS作用越显著;波动能量向下向西传播,变化趋势同相速度类似,相速度与群速度之间的夹角随着垂直高度呈先增大后减小趋势,在急流轴高度处最大,随扰动尺度的减小,波动传播性质向声波趋近.波动相速度等值线呈反气旋状分布,高值中心位于δ大值区且靠近急流轴的高度处,随着垂直高度的增加,相速度呈先增大后减小,即在急流轴高度处扰动传播最快;群速度等值线呈垂直向分布,在急流轴高度处向δ的低值区弯曲;随着δ的增加呈增加趋势,VWS使得能量的传播速度减小,在δ < 2的区域,群速度远小于相速度;VWS使得群速度和相速度之间的夹角增大,在δ→0.1高度趋于急流轴的区域,群速度与相速度趋于垂直,波动传播符合重力波的性质,在δ→10的区域,群速度与相速度趋于平行,波动传播符合声波的性质.
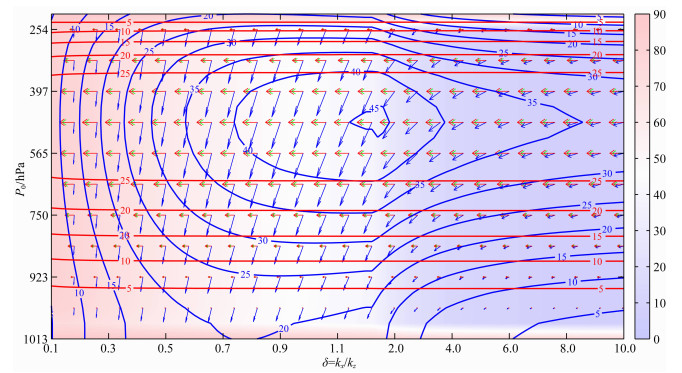
在mod_c中波动σ2水平逆向(与水平基流同向)传播支的速度参数分布如图 7所示.比较图 3、图 5和图 7可知,波动向下向西传播,随着扰动尺度的减小,相速度与铅直轴负方向的夹角变大,向西倾斜;波动能量传播方向同水平基流方向一致,呈准水平向西传播,随扰动尺度基本保持不变,相速度与群速度之间的夹角随扰动尺度的减小呈现减小趋势.波动相速度等值线呈反气旋状分布,高值中心位于δ→2且垂直高度在急流轴的区域,随着垂直高度的增加相速度大小呈先增加后减小;群速度等值线呈水平状分布,随垂直高度的增加呈先增加后减小;随着扰动尺度的减小,波动传播特征从类似重力波特征向类似声波特征渐变.
|
图 7 波动σ2水平逆向传播支的速度参数演变(对应标识同图 2) Fig. 7 Velocity distribution graph for a westward branch of σ2 (Explanations are same as Fig. 2) |
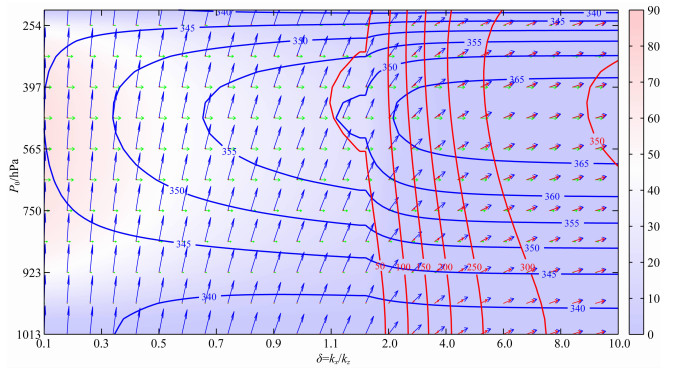
类似西风急流,在对流层上层有强劲的西风,其平均风速达到百米量级,构造mod_d垂直切变模型,从地面向上西风呈增长分布,在垂直高度Hs处达到最大值,为了与mod_c比较,取最大值为30 m·s-1,并随垂直高度的继续增加西风逐渐消亡.取U=umax/H2 =4.6×10-7 m-1·s-1,此时水平风速在各层上的大小同mod_c中相同,而方向相反;在mod_d中波动σ1水平正向传播支的速度参数分布如图 8所示.
|
图 8 波动σ1水平正传支的速度参数演变(对应标识同图 2) Fig. 8 Velocity distribution for an eastward branch of σ1 (Explanations are same as Fig. 2) |
图 8显示波动向上向东传播,其中等值线的分布同图 6完全相同,水平基流的垂直切变对波动相速度和群速度的影响与mod_c中逆传波动情形相似,而波动传播方向和能量传播方向与图 6中相反.
在mod_d中波动σ2水平正向传播支的速度参数分布同图 7相同,其逆向传播支的速度参数分布如图 9所示.图 9显示,在δ < 1.1的区域,波动向下向西传播,相速度等值线自下而上呈对称的双反气旋式分布,高值中心分别位于δ→0.7的地面和高空200 hPa附近,而急流轴附近则为低值中心;群速度水平分量的传播方向同水平基流方向一致,等值线呈水平平行状分布,越靠近急流轴区域群速度越大;相速度与群速度的夹角随垂直高度的增加呈先减小后增加的趋势;在δ>1.1的区域,由于水平基流的作用,波动传播方向由向下向西切变为向上向东,相速度等值线呈反气旋式分布,高值中心位于δ→10靠近急流轴的区域,群速度分布同δ < 1.1的区域相同;随着扰动尺度和垂直高度的变化,波动传播特征从类似重力波特征向类似声波特征渐变.

|
图 9 波动σ2水平逆向传播支的速度参数演变(对应标识同图 2) Fig. 9 Velocity distribution for a westward branch of σ2 (Explanations are same as Fig. 2) |
前面的结论是基于假设波动在均匀介质中的传播,而实际大气是非均匀介质,波参数随时间和空间发生变化,在此,引入缓变波列:
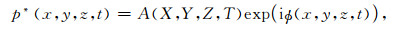
|
(37) |
其中:
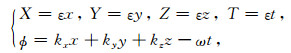
|
(38) |
ε表示参数小量.缓变波列在各平面内的等相位线斜率为

|
(39) |
对于式(16),结合式(17)消去垂直速度变量w*,得到关于扰动气压p*的微分方程为
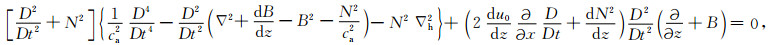
|
(40) |
其中:
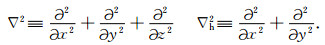
|
(41) |
将式(37)代入式(40)中,并假设:
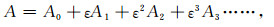
|
(42) |
取零级近似可得到频散关系式:

|
(43) |
式(43)中波参数与式(27)中波参数含义不同,式(43)中波参数均为复数,波动振幅的变化可发生在空间和时间中.若取一级近似并结合频散关系,则可得到:
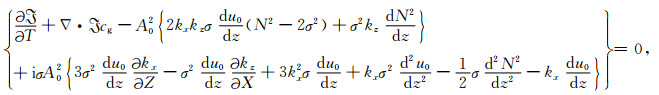
|
(44) |
其中有静力适应过程中波动的波能密度:
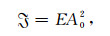
|
(45) |
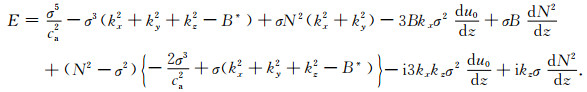
|
(46) |
假设系统闭合,对式(44)在整个空间积分可得:

|
(47) |
在等温大气下,无VWS时式(47)可化为
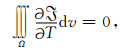
|
(48) |
即在等温大气下,水平基流无垂直切变时,在整个空间内波能守恒,由式(47)可知,在静力适应过程中被激发的波动能否发展起来取决于该波动的空间螺旋结构以及在基本气流上的位置以及大气稳定度参数随高度的变化情况.
在此忽略大气稳定度参数的影响,只考虑VWS的影响,则对于三种VWS模型静力适应过程中波动对VWS的响应情况具体如下.
4.1 mod_b水平基流呈线性切变此种情形下,式(47)取实部,化简为

|
(49) |
由式(49)可知,对于波动频率满足关系σ(N2-2σ2)>0时,若等相位线自下而上向西倾斜,则有kxkz>0,此种情形下波动能量随时间增加,波动呈发展型,若等相位线自下而上向东倾斜,则有kxkz<0,此种情形下波动能量随时间减少,波动呈衰亡型.对于波动频率满足关系σ(N2-2σ2) < 0时,则情形相反.
4.2 mod_c水平基流呈反气旋式切变
在东风急流中,随着垂直高度的变化,VWS发生变化,则在此情形下,波动对于VWS的响应情形之一如图 10所示.由图 10a可知,当σ(N2-2σ2)>0时,在急流轴上方有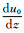
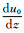
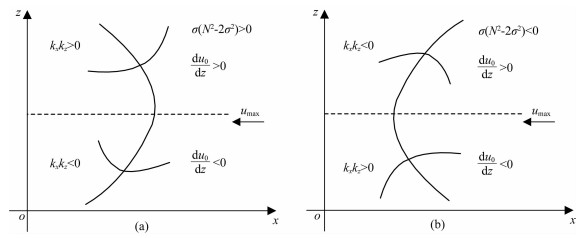
|
图 10 发展型波动螺旋结构及其在基流中的位置 虚线表示急流轴高度,实线表示等位相线. Fig. 10 Spatial structure for a developed wave The dashed line represents the height of jet axis. Solid lines are equiphase lines. |
在西风急流中,随着垂直高度的变化,波动对于VWS的响应情形之一如图 11所示.由图 11a可知,当σ(N2-2σ2)>0时,在急流轴上方有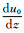
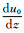
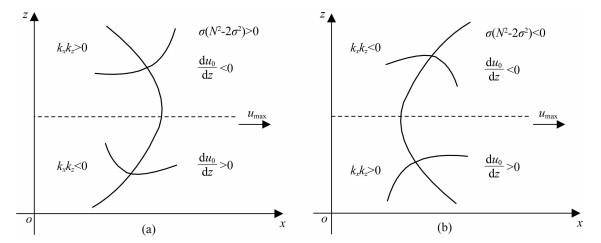
|
图 11 衰亡型波动螺旋结构及其在基流中的位置 虚线表示急流轴高度,实线表示等位相线. Fig. 11 Spatial structure for a decayed wave The dashed line represents the height of jet axis. Solid lines are equiphase lines. |
本文为了研究VWS对静力适应过程中波动的影响,构造了四种VWS模型,分别讨论了均匀介质与非均匀介质中由非静力平衡扰动能量诱发的波动对VWS的响应情况.
在等温大气的假设下,若将大气视为均匀介质,则波动参数不随时间和空间发生变化,从扰动线性方程组得到的波动频散关系显示,当大气静力平衡遭到破坏后,激发出四支两两成对的波动,其中一对波动频率接近声波频率,另外一对波动频率接近重力波频率,非静力扰动能量被这两对波动在整个空间内耗散,使得大气恢复到静力平衡状态.而VWS的存在使得波动频率发生了变化,波动相速度和群速度在波数和垂直空间内的分布发生了改变,同时还改变相速度和群速度的传播方向,使得波动的传播性质发生了变化,在不同的VWS模型中,波动对VWS的响应随垂直高度和扰动尺度的变化不同.
若将大气视为非均匀介质时,波动参数随时间和空间发生演变,引入缓变波列假设,得到的波动能量演变方程显示,当水平基流不随高度发生切变时,有VWS为零,则波能量守恒;当VWS不为零时在不同的基流切变模型中波动能量的演变结构不同,对于发展型的波动螺旋结构和基流配置,扰动能量随时间增长,延长静力适应进程;而对于衰亡型的波动,扰动能量随时间消减,促进静力适应进程.
同时,本文仅从波动理论出发研究了VWS对静力适应过程的影响,而针对非静力平衡扰动激发的这四支两两成对的波动在静力适应过程中所起的具体作用未能给出清晰的物理图像;清晰描述在静力适应过程中,不同VWS模型条件下气块的运动情况,则是理清VWS在静力适应过程中作用的一个有效途径,对于此问题将在本文第二部分进行详细研究.
Bannon P R. 1995. Hydrostatic adjustment:Lamb's problem. Journal of the Atmospheric Sciences, 52(10): 1743-1752. DOI:10.1175/1520-0469(1995)052<1743:HALP>2.0.CO;2 |
Bannon P R. 1996. On the anelastic approximation for a compressible atmosphere. Journal of the Atmospheric Sciences, 53(23): 3618-3628. DOI:10.1175/1520-0469(1996)053<3618:OTAAFA>2.0.CO;2 |
Chagnon J M, Bannon P R. 2001. Hydrostatic and Geostrophic adjustment in a compressible atmosphere:Initial response and final equilibrium to an Instantaneous localized heating. Journal of the Atmospheric Sciences, 58(24): 3776-3792. DOI:10.1175/1520-0469(2001)058<3776:HAGAIA>2.0.CO;2 |
Chagnon J M, Bannon P R. 2004. Wave response during hydrostatic and geostrophic adjustment.Part I:transient dynamics. Journal of the Atmospheric Sciences, 62(5): 1311-1329. |
Chagnon J M, Bannon P R. 2005. Wave response during hydrostatic and geostrophic adjustment.Part II:potentialvorticity conservation and energy partitioning. Journal of Atmospheric Sciences, 62(5): 1330-1345. |
Chao J P. 1962. On some fundamental problems of dynamics of small scale processes in the atmosphere. ActaMeteorologicaSinica (in Chinese), 32(2): 104-118. |
Chao J P. 1964. On the local conditions of convection development. ActaMeteorologicaSinica (in Chinese), 32(1): 86-90. |
Cui X D, Liu Y D, Zhao Z L, et al. 2016. Study of characteristics of the acoustic gravity wave and energy conversion in the three-dimensional hydrostatic adjustment process. Acta Meteorologica Sinica (in Chinese), 74(1): 127-132. |
Duffy D G. 1997. Hydrostatic adjustment in nonhydrostatic, compressible mesoscale models. Monthly Weather Review, 125(12): 3357-3367. DOI:10.1175/1520-0493(1997)125<3357:HAINCM>2.0.CO;2 |
Duffy D G. 2002. Hydrostatic Adjustment in Nonisothermal atmospheres. Journal of the Atmospheric Sciences, 60(2): 339-353. |
Edson A R, Bannon R R. 2008. Nonlinear atmospheric adjustment to momentum forcing. Journal of Atmospheric Sciences, 65(3): 953-969. DOI:10.1175/2007JAS2278.1 |
Fanelli P F, Bannon P R. 2005. Nonlinear atmospheric adjustment to thermal forcing. Journal of the Atmospheric Sciences, 62(12): 4253-4272. DOI:10.1175/JAS3517.1 |
Horace L. 1932. On the theory of waves propagated vertically in the atmosphere. Proceedings of theLondon MathematicalSociety, S2-7(1): 122-141. |
MoninAS, ObukhovAM. 1959. A note on general classification of motions in a baroclinic atmosphere. Tellus, 11(2): 159-162. DOI:10.3402/tellusa.v11i2.9303 |
Smith J W, bannon P R. 2008. A comparison of compressible and anelastic models of deep dry convection. Monthly Weather Review, 136(12): 4555-4571. DOI:10.1175/2008MWR2343.1 |
Sotack T, Bannon P R. 1998. Lamb's hydrostatic adjustment for heating of finite duration. Journal of the Atmospheric Sciences, 56(1): 71-81. |
Van Delden A. 2015.Atmospheric Dynamics.Netherlands: IMAU, Utrecht University, Netherlands, http://www.staff.science.uu.nl/~delde102/AtmosphericDynamics.htm.
|
Ye D Z, Li M C. 1964. A process of generation of strong Nongeostrophic motion by gravitational wave. Scientiasinica, 8: 92-106. |
Zeng Q C, Ye D Z. 1963. the advance in the investigation of the problems of the adaptation processes in the rotating atmosphere, I. Chinese Journal of Atmospheric Sciences (in Chinese), 4(4): 379-393. |
巢纪平. 1962. 论小尺度过程动力学的一些基本问题. 气象学报, 32(2): 104-118. |
巢纪平. 1964. 对流发展局部气象条件的初步理论分析. 气象学报, 32(1): 86-90. |
崔新东, 刘宇迪, 赵增亮, 等. 2016. 三维静力适应过程中声重力波的特性和能量转换研究. 气象学报, 74(1): 127-132. |
曾庆存, 叶笃正. 1963. 旋转大气中运动的适应过程问题的研究(一). 大气科学, 4(4): 379-393. |
 2020, Vol. 63
2020, Vol. 63


