2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3. 中国石油大学CNPC测井重点实验室, 山东青岛 266580
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3. CNPC Key Laboratory for Well Logging, China University of Petroleum, Qingdao 266580, China
水平井钻进过程中,地层边界的准确预测对实时地质导向决策、储层定性乃至定量评价至关重要(Zhang et al., 2008).随钻方位电磁波测井具有探测范围大、对地层界面方位敏感性强等优势,被广泛运用于实时地质导向和储层评价(Omeragic et al., 2006b).2005年,Schlumberger公司首先推出了第一支随钻方位电磁波测井仪器PeriScope,随后各大石油服务公司陆续发布了多支随钻方位电磁波测井仪器,如Halliburton公司的ADR,Baker Hughes公司的AziTrak和Weatherford公司的GuideWave等,如图 1所示(Li et al., 2005, 2014; Bell et al., 2006; Bittar et al., 2007; Wang et al., 2007).尽管各大公司仪器设计与具体参数各不相同,但其探边能力大致相同(小于6 m).与传统随钻电阻率测井仪器相比,随钻方位电磁波测井仪器最大不同之处在于,引入正交线圈或者倾斜线圈设计,测量磁场的正交分量信号(Hzx/Hxz)以增加对邻近地层界面的方位敏感性(王磊等, 2015).正交磁场分量的实现方式包括多种组合(Li and Wang, 2016):(1)轴向发射(接收)线圈和正交接收(发射)线圈组合;(2)轴向发射(接收)线圈和倾斜接收(发射)线圈组合;(3)倾斜发射线圈和倾斜接收线圈组合.

|
图 1 几种商业化随钻方位电磁波测井仪器 Fig. 1 Configurations of commercial azimuthal electromagnetic tools |
随钻方位电磁波测井测量信息为一般为幅度比或相位差等地质信号,而非地层电阻率及地层界面位置等信息,测量信息不直观.同时,受层厚、围岩及井斜等复杂测井环境的影响,其响应较为复杂(Pardo and Torres-Verdin 2015; Hu et al., 2017;许巍等, 2016).因此,该类资料的定性、定量解释必须依靠反演的手段方可实现(Wang et al., 2018a).随钻方位电磁波测井资料的反演包括以下难点:(1)缺乏适用于复杂地层结构的快速正演算法,且高维反演参数过多,测量信息有限,反演可能存在多解性(Habashy and Abubakar, 2004);(2)反演参数类型多样,不仅包含电阻率、地层界面还包括倾角等信息,反演可能存在多个局部解(Wang et al., 2018b);(3)随钻过程中,由于缺乏足够的已知信息,反演初值难以确定,导致反演难度的进一步增大(Omeragic et al., 2006a).
为此,本文给出了一种随钻方位电磁波测井资料实时处理方法.首先介绍了随钻方位电磁波测井的基本原理与典型响应特征.接着,采用等效降维策略和多初值正则化Levenberg-Marquardt最优化算法,结合三层反演模型和分级反演加速方法,实现了地层界面及电阻率的准确、快速提取.
1 随钻方位电磁波测井原理本文以斯伦贝谢公司的PeriScope为例,介绍随钻方位电磁波测井仪器线圈设计、合成方式及典型响应特征等.PeriScope包括两类测量信号:视电阻率信号和地质信号.与传统随钻电磁波测井相同,视电阻率信号基于轴向发射线圈T与两个轴向接收线圈R1和R2.通过测量两接收线圈处的电势VR1和VR2,将其转化为两者的相位差PS和幅度比Att,具体转化方式见式(1):
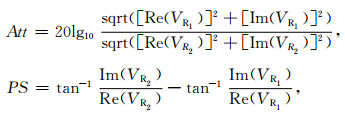
|
(1) |
因视电阻率信息无方位敏感性、地层界面探测能力弱,故在同轴发射线圈的基础上,引入了倾斜线圈,线圈法向方向与仪器轴夹角为45°.利用钻铤旋转,测量不同方位角情况下的接收线圈处的电势,根据式(2)将信息转化为相位差和幅度比地质信号信息:
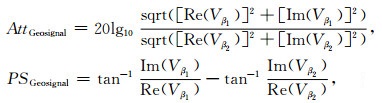
|
(2) |
式中,Vβ1和Vβ2分别为方位角为β1和β2时的倾斜线圈的电势信号,β1和β2可取0°和180°.
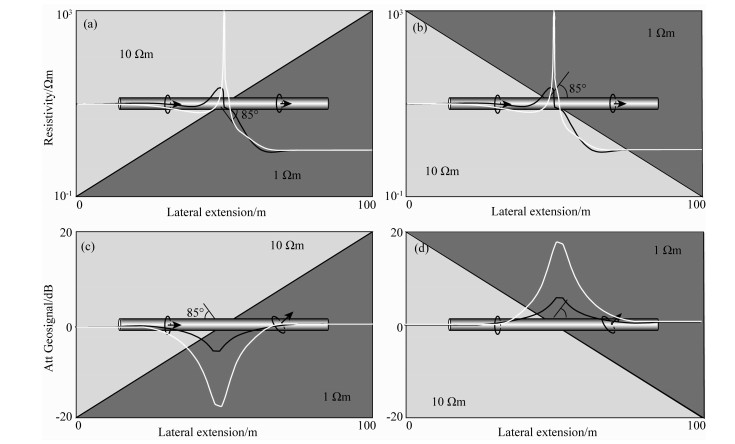
给出随钻方位电磁波测井的典型响应特征,如图 2所示,PeriScope仪器分别自上而下或自下而上由砂岩层钻进泥岩层,其中砂岩和泥岩电阻率分别为10 Ωm和1 Ωm,仪器与地层的相对夹角为85°.(a)和(b)为测量的视电阻率信息,(c)和(d)则为幅度比地质信号响应.可以看出,仪器自上而下与自下而上钻入时,视电阻率曲线相同,这表明其对地层界面方位无敏感性.仪器远离地层界面时,地质信号基本为零,随着与地层界面距离的减小,地质信号幅度不断增加,且在地层界面附近达到最大值.与此同时,地质信号在两种情况下测量值幅度相同,符号相反.综合视电阻率信息与地质信号正负差异等信息,可以定性判断地层界面的位置等参数.
|
图 2 随钻方位电磁波测井典型响应特征 Fig. 2 Classic tool responses of azimuthal electromagnetic measurements |
一般而言,随钻方位电磁波测井资料的处理是一复杂的高维问题(Abubakar et al., 2008; Zeng et al., 2018),但受高维正演速度、计算机内存与反演参数数量等限制,目前高维反演仍不现实.为满足随钻实时资料处理的需要,工业界常采用降维处理的方法进行解决.通过对如图 3a所示的复杂模型进行逐步开窗处理,从而将高维反演问题转化为一系列的1D模型的反演.其中,每个窗口均为多层相互平行且无限延伸的层状TI介质.那么,偶极子源在1D地层中产生的电磁场则可解析获得(Hong et al., 2016; Løseth and Ursin, 2007; Zhong et al., 2008; Gao et al., 2013).对1D解析解而言,每个测量点所需计算时间0.1~1 ms,从而满足随钻方位电磁波测井快速正反演的需要.1D解析解的推导方法见附录,此处不再赘述.

|
图 3 降维处理方法 Fig. 3 Dimensionality reduction of the formation model |
对随钻方位电磁波测井而言,测井响应主要受当前层及两侧围岩影响,故常采用图 3b所示的三层模型进行资料实时处理.三层反演模型中的待反演参数包括:当前层水平和垂直电阻率、两侧各向同性围岩电阻率、仪器距上下地层界面的距离和仪器与地层法向的相对夹角等.
2.2 Levenberg-Marquardt最优化方法测井资料的反演可以转化为求实测资料与模拟响应拟合差最小值,反演所用代价函数C(m)如下:
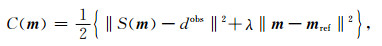
|
(3) |
其中,第一项为模拟响应向量S(m)与实测电磁波测井资料向量dobs之差的L2范数,m为待反演参数向量.代价函数第二项为正则化项,由正则化参数λ和模型向量与参考向量mref之差组成,其主要作用是压制测量噪声,同时减小非线性反演出现的病态问题.
对式(3)进行二阶Taylor展开,忽略二阶导数项,可得:
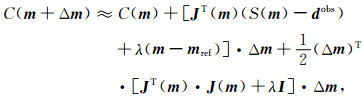
|
(4) |
式中,I为单位矩阵,上标T表示向量或矩阵的转置,Δm为模型向量m附近的扰动.J(m)为雅克比矩阵,如下式所示:
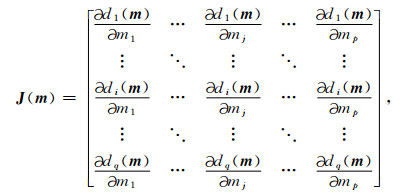
|
(5) |
其中,p和q分别为m和dobs的长度.
令代价函数对反演模型扰动Δm的导数为零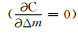
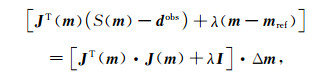
|
(6) |
利用Levenberg-Marquardt和信赖域方法,可将上式求解转化为下列最小二乘问题,第k次迭代时:
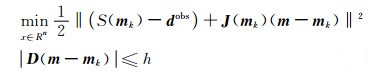
|
(7) |
其中,h为信赖域半径,D为缩放矩阵.上式的解可以表示为

|
(8) |
式中,α为Levenberg-Marquardt正则化参数.采用Moré(1978)给出的方法,确定信赖域半径h、缩放矩阵D和α.在迭代的过程中,模拟响应与实测数据拟合差的二范数是不断减小的,即反演模型不断逼近最优解的过程,利用该性质确定正则化参数λ,具体表示为
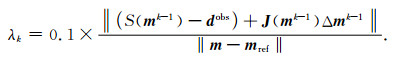
|
(9) |
Levenberg-Marquardt迭代过程中,另一个需要确定的是参考模型向量mref.参考模型向量也存在多组选取方式,这里在第k次迭代过程中,直接令mref=mk-1.这样处理的意义在于,随着迭代的进行,mk与mk-1越来越接近,代价函数中正则化项对代价函数的贡献越来越小.从数学角度而言,经过上述处理,式(3)所示的代价函数可以转化为一系列式(10)所示代价函数.在每次迭代中,只对当前代价函数进行单次Levenberg-Marquardt迭代寻优.
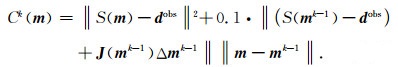
|
(10) |
对随钻方位电磁波测井而言,反演参数包含多种类型信息,其既包括各向异性电阻率,又有地层界面及相对倾角.反演参数类型多样一方面导致代价函数变化剧烈,同时导致多个局部极小值的存在.此时,若采用传统的单一初值的方法,反演结果易困于局部解.为解决该问题,我们采用多初值方法,以保证解的全局最优性.该方法可分为以下几个步骤:(1)随机产生几百个初始模型,计算其正演响应;(2)获取模拟响应与实测数据的拟合差,并选取拟合差最小的30组初始模型;(3)对选取后的模型分别进行Levenberg-Marquardt迭代,最终获取拟合差最小的地层模型.一般而言,随机初始模型和反演迭代过程中所需要的正演次数约2000~3000次,每个测井点耗时小于2 s.而大斜度井/水平井中仪器的前进速度远小于反演速度,故本文给出的反演算法仍旧可以满足资料实时处理的需求.
2.4 反演加速方法
为实现对地层边界的实时探测,随钻过程中通常采集至少一条长源距地质信号和一条电阻率曲线.若多种源距条件的地质信号和电阻率曲线同时存在时,则可以利用不同曲线探测能力的不同,进行分级反演.首先,基于浅探测地质信号和电阻率曲线,建立单界面反演模型,利用多初值方法,获取当前层电阻率、近围岩电阻率和距仪器最近的地层界面.随后,将单界面模型反演结果作为已知信息,利用深探测曲线和双界面反演模型,进一步获取远地层界面和远围岩电阻率等信息.假定每个反演参数取相同数目(m)的随机值且反演参数的数量为n.在分级反演过程中,对单界面模型需要的初值数目为N1=m4;而利用单界面提供的信息,双界面模型仅需要N2=m3个初值.与传统双界面反演相比,分级反演可得到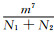
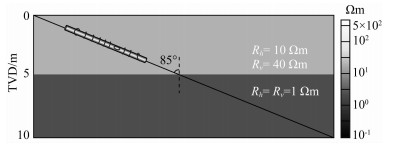
为验证反演算法的准确性,建立图 4所示的单界面地层模型.其中,第一层的水平和垂直电阻率分别为10 Ωm和40 Ωm,第二层为电阻率为1 Ωm各向同性地层,仪器与地层法向的相对倾角为85°.为同时明确反演算法对噪声的适应性,分别对随钻方位电磁波测井响应添加0%、5%、10%和15%的高斯白噪,相应的反演结果见图 5和图 6.
|
图 4 单界面地层模型 Fig. 4 Single-boundary inversion model |

|
图 5 不同高斯噪声情况下反演的电阻率窗帘图 (a)无高斯白噪;(b)添加5%高斯白噪;(c)添加10%高斯白噪;(d)添加15%高斯白噪. Fig. 5 Inverted resistivity curtains for measurements with: (a) 0% Gaussian noise; (b) 5% Gaussian noise; (c) 10% Gaussian noise; (d) 15% Gaussian noise. |
|
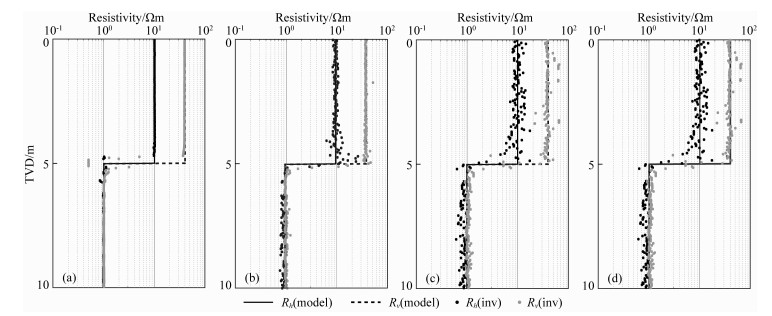
图 6 不同高斯噪声情况下反演得到的地层水平和垂直电阻率值 (a)无高斯白噪;(b)添加5%高斯白噪;(c)添加10%高斯白噪;(d)添加15%高斯白噪. Fig. 6 The estimated horizontal and vertical resistivities for measurements with: (a) 0% Gaussian noise; (b) 5% Gaussian noise; (c) 10% Gaussian noise; (d) 15% Gaussian noise. |
图 5为反演得到的二维电阻率窗帘图,其中每点的颜色代表其电阻率值.图 6为反演的仪器所在层的水平和垂直电阻率.可见反演后的电阻率和地层界面与真实地层模型基本一致,这表明反演算法准确可靠.在高阻层内,随钻方位电磁波测井仪器可准确提取井周4.5 m以内的地层界面,而低阻层内探边能力降低至3 m.噪声的存在造成反演的各向异性电阻率与地层上、下界面在地层模型真值附近波动,且噪声幅度越大,波动越剧烈.当仪器接近地层界面时,噪声对反演的地层水平和垂直电阻率影响影响较大,而其对反演的地层界面影响基本可以忽略不计.这主要是因为地层界面附近,随钻方位电磁波测井资料对地层界面最为敏感,其受噪声的影响也最小.与无噪声反演结果对比,当仪器远离地层界面时,受噪声影响反演的地层界面的稳定性和准确性降低,而地层各向异性电阻率则受噪声影响较小.一般而言,高斯噪声强度小于5%时,噪声对随钻方位电磁波测井的影响基本可以忽略.
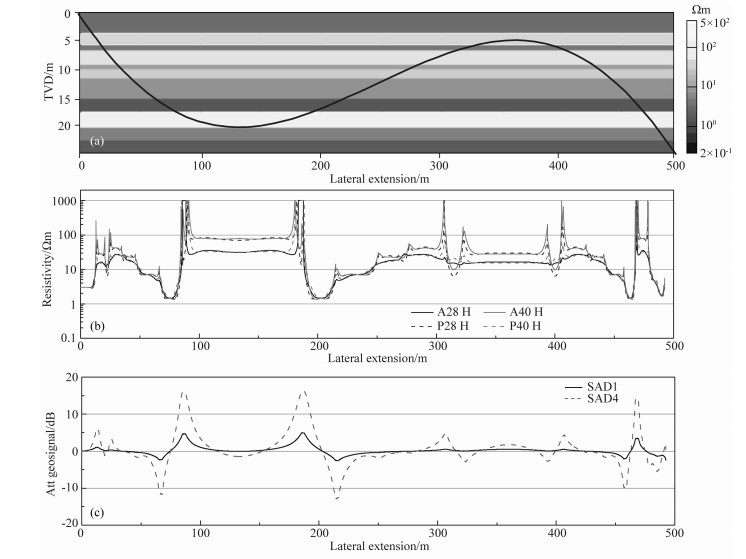
3.2 地层结构重构为进一步明确反演算法对层厚及电阻率范围的适用性,建立1D多层地层模型.该模型包括12个各向同性地层,层厚变化范围为0.8~4.0 m,电阻率变化范围为1.5~100 Ωm,各层具体参数详见表 1.仪器轴与地层法向相对倾角最小为70°,最大相对倾角为105°.这里假定复杂正弦形井眼轨迹,即图 7a黑线,仪器打穿各个地层后上钻,最后调整仪器再次下钻,相应的随钻方位电磁波测井视电阻率与地质信号响应见图 7b-7c.
|
|
表 1 1D多层地层模型各层电阻率参数设置 Table 1 Resistivities of each bed in the 1D multi-layered formation model |
|
图 7 (a) 1D地层模型;(b)视电阻率曲线;(c)幅度比地质信号 Fig. 7 (a) 1D formation model with arbitrary well path; (b) Apparent resistivity; (c) Attenuation geosignals |
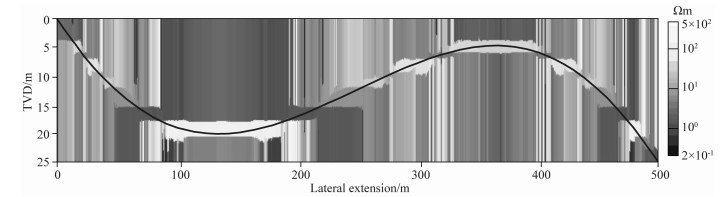
利用双界面反演模型和梯度算法获得的地层电阻率窗帘图见图 8.可以看出,不同层厚及不同电阻率对比度条件下,均可得到准确的上、下地层界面位置.并且,反演结果不受仪器与地层相对倾角的影响,进一步说明了反演算法的适用性强.二维窗帘图不仅直观地显示井眼附近地层的纵向电阻率分布,且从横向延伸可以初步给出地层结构分布.
|
图 8 反演后的二维窗帘图 Fig. 8 Inverted 2D resistivity curtain |
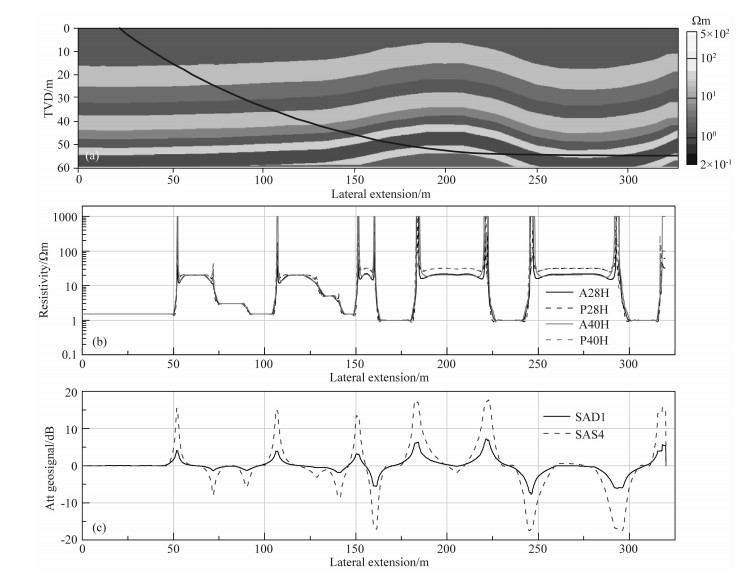
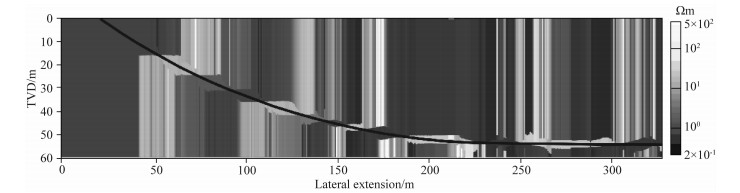
前文仅给出了降维反演算法在简单的1D模型中的地质导向应用.现以一个褶皱模型为例进一步阐述降维反演算法在复杂地层结构中的适用性.为此,建立图 9a所示的复杂地层模型,其中,每个地层均设置为各向同性地层.模型不仅考虑了地层纵向的电阻率变化,同时在横向方向也存在非均质性.相应的视电阻率响应和地质信号曲线见图 9b和图 9c.图 10为反演得到的二维电阻率窗帘图.可以看出,在地层界面附近,反演的地层界面位置点和当前层电阻率准确可靠.这表明反演结果基本不受地层横向非均质的影响,降维反演方法适用性强.通过反演可以很好地重构地层界面的位置和角度变化,再现了地层的结构分布.需要注意的是,由于横向电阻率和地层厚度变化的影响,反演结果的稳定性略有降低,但这并不影响地质导向决策的进行.
|
图 9 (a) 褶皱模型;(b)视电阻率曲线;(c)幅度比地质信号 Fig. 9 (a) Synthetic 2D folding model; (b) Apparent resistivity; (c) Attenuation geosignals |
|
图 10 反演后的二维窗帘图 Fig. 10 Inverted 2D resistivity curtain |
通过降维处理简化复杂三维地层模型,结合Levenberg-Marquardt最优化方法实现随钻方位电磁波测井快速反演,并将其应用于地质导向着陆及地层结构重构,得到以下认识:
(1) 采用逐步开窗方法可实现复杂问题的降维处理,将高维反演问题转化为一系列的1D模型的反演,极大提高随钻资料处理速度,以确保实时地质导向的需要;
(2) 采用多初值方法,随机产生数百组初始模型,避免反演结果陷于局部最优,从而获取真实地层参数;
(3) 反演实例表明,通过随钻方位电磁波测井数据反演,不仅可以为实时地质导向提供仪器距地层界面距离等重要参数,还可实现井周附近地层结构重构.
附录假定发射线圈为时谐偶极子源e-iωt,引入Hertz矢量势Π和标量势ϕ,则磁场矢量H=Hρeρ+Hϕeϕ+Hzez和电场矢量E=Eρeρ+Eϕeϕ+Ezez满足:
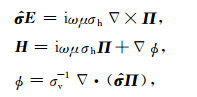
|
(A1) |
式中,
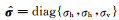

|
(A2) |
式中,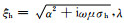
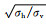
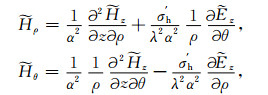
|
(A3) |
式中,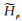
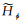
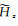
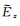
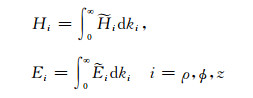
|
(A4) |
任意多层介质中,谱域中磁场和电场的z向分量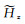
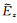
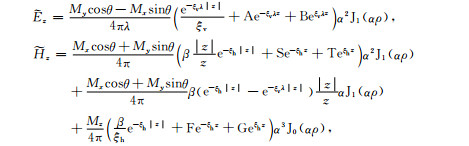
|
(A5) |
式中,A、B、F、G、S和T为上/下行波的幅度.采用广义反射系数方法,通过在地层界面施加边界条件,经递推获得上述系数.获得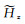
Abubakar A, Habashy T, Druskin V, et al. 2006. Two-and-half-dimensional forward and inverse modeling for Marine CSEM Problems.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Bell C, Hampson J, Eadsforth P, et al. 2006. Navigating and imaging in complex geology with azimuthal propagation resistivity while drilling.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Bittar M S, Klein J D, Randy B, et al. 2007. A new azimuthal deep-reading resistivity tool for geosteering and advanced formation evaluation.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Gao J, Xu C H, Xiao J Q. 2013. Forward modelling of multi-component induction logging tools in layered anisotropic dipping formations. Journal of Geophysics and Engineering, 10(5): 054007. |
Habashy T M, Abubakar A. 2004. A general framework for constraint minimization for the inversion of electromagnetic measurements. Progress in Electromagnetics Research, 46: 265-312. |
Hong D C, Huang W F, Liu Q H. 2016. Radiation of arbitrary magnetic dipoles in a cylindrically layered anisotropic medium for well-logging applications. IEEE Transactions on Geoscience and Remote Sensing, 54(11): 6362-6370. |
Hu S, Li J, Guo H B, et al. 2017. Analysis and application of the response characteristics of DLL and LWD resistivity in horizontal well. Applied Geophysics, 14(3): 351-362. |
Li H, Wang H. 2016. Investigation of eccentricity effects and depth of investigation of azimuthal resistivity LWD tools using 3D finite difference method. Journal of Petroleum Science and Engineering, 143: 211-225. |
Li Q M, Omeragic D, Chou L, et al. 2005. New directional electromagnetic tool for proactive geosteering and accurate formation evaluation while drilling.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Li S J, Chen J F, Tommy L B Jr. 2014. Using new LWD measurements to evaluate formation resistivity anisotropy at any dip angle.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Løseth L O, Ursin B. 2007. Electromagnetic fields in planarly layered anisotropic media. Geophysical Journal International, 170(1): 44-80. |
Moré J J. 1978. The Levenberg-Marquardt algorithm: Implementation and theory.//Watson G A ed. Lecture Notes in Mathematics. Berlin, Heidelberg: Springer, 630: 105-116.
|
Omeragic D, Dumont A, Esmersoy C, et al. 2006a. Sensitivities of directional electromagnetic measurements for well placement and formation evaluation while drilling.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Omeragic D, Habashy T, Esmersoy C, et al. 2006b. Real-time interpretation of formation structure from directional EM measurements.//76th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Pardo D, Torres-Verdín C. 2015. Fast 1D inversion of logging-while-drilling resistivity measurements for improved estimation of formation resistivity in high-angle and horizontal wells. Geophysics, 80(2): E111-E124. |
Wang L, Fan Y R, Huang R, et al. 2015. Three dimensional Born geometrical factor of multi-component induction logging in anisotropic media. Acta Physica Sinica (in Chinese), 64(23): 239301. |
Wang L, Fan Y R, Yuan C, et al. 2018a. Selection criteria and feasibility of the inversion model for azimuthal electromagnetic logging while drilling (LWD). Petroleum Exploration and Development, 45(5): 974-782. |
Wang L, Li H, Fan Y R, et al. 2018b. Sensitivity analysis and inversion processing of azimuthal resistivity logging-while-drilling measurements. Journal of Geophysics and Engineering, 15(6): 2339-2349. |
Wang T L, Chemali R, Hart E, et al. 2007. Real-time formation imaging, dip, and azimuth while drilling from compensated deep directional resistivity.//77th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Xu W, Ke S Z, Li A Z, et al. 2016. Structural effects analysis of an electromagnetic wave propagation resistivity LWD tool by 3D finite element method. Journal of China University of Petroleum (in Chinese), 40(6): 50-56. |
Zeng S B, Chen F Z, Li D W, et al. 2018. A novel 2. 5D finite difference scheme for simulations of resistivity logging in anisotropic media. Journal of Applied Geophysics, 150: 144-152. |
Zhang Z Y, Gonguet C, Rajani V, et al. 2008. Directional LWD resistivity tools and their business impacts.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Zhong L L, Li J, Bhardwaj A, et al. 2008. Computation of triaxial induction logging tools in layered anisotropic dipping formations. IEEE Transactions on Geoscience and Remote Sensing, 46(4): 1148-1163. |
王磊, 范宜仁, 黄瑞, 等. 2015. 各向异性介质多分量感应测井三维Born几何因子理论研究. 物理学报, 64(23): 239301. DOI:10.7498/aps.64.239301 |
许巍, 柯式镇, 李安宗, 等. 2016. 随钻电磁波测井仪器结构影响的三维有限元模拟. 中国石油大学学报(自然科学版), 40(6): 50-56. |
 2020, Vol. 63
2020, Vol. 63


