历史上,早有一些著名的地震学家指出:在一个观测点上,只观测位移不能得到完整的地震波信息,要得到完整的信息还要观测应变(例如Båth,1979).应变变化的张量性质决定了应变地震仪与观测位移变化的摆式地震仪有本质区别.这种新观测技术可以为地震学提供新的数据资源,开辟新的研究领域.
20世纪60年代,Benioff等(1961)最早设计制作了一种应变地震仪,并根据其观测结果进行了地球自由振荡研究.但是其应变仪只给出了线应变变化,没有给出应变张量变化.传统的基线式应变仪,基线一般比较长,是不利于观测高频信号的.近年来,在国际范围内,钻孔应变观测技术得到长足发展(欧阳祖熙,1977;池顺良等,2009;Gladwin,1984;Ishii,2001;Qiu et al., 2013;邱泽华,2017).将这种仪器用于地震波观测已经取得初步进展(Ishii,2001;Barbour and Agnew, 2012;邱泽华和池顺良,2013;Qiu et al., 2015;邱泽华, 2016, 2017;Barbour and Crowell, 2017).
中国地震局地壳应力研究所的欧阳祖熙小组发明的RZB-1型四元件钻孔应变仪,是最早的二维张量应变观测仪器(欧阳祖熙,1977).至今,以池顺良小组研制的YRY-4型四元件钻孔应变仪为代表(池顺良等,2009),中国的二维张量钻孔应变仪已经基本成熟,取得了长达十年的观测数据,已经正式走上国际舞台(Qiu et al., 2013).必须说明的是,中国的四元件钻孔应变仪实现了观测自洽,观测数据可靠,在国际上处于领先地位,最有条件率先开展地震波研究(邱泽华等,2005;Qiu et al., 2013;刘序俨等,2014;邱泽华,2017).
用中国现有的几种钻孔应变仪,已经陆续开展了地震波观测实验.在地壳应力研究所的北京昌平台,进行过RZB-1型四元件钻孔应变仪的高采样率观测(杨选辉等,2011).与附近十三陵台的摆式地震仪观测的远震数据进行对比,发现二者的频谱很相似.但是,一方面当时观测所用仪器出现了坏道,记录不完整;另一方面也未记录到地方震.在山西昔阳台也进行过高采样率的钻孔体应变仪的观测,记录到远震、近震和地方震(郭燕平等,2012).与附近的摆式地震仪记录进行频谱对比,二者也非常一致.但是体应变缺少方向性,与张量应变仪相比,提供的信息很有限.
2008年3月17日,池顺良等在四川姑咱台用YRY-4型四元件钻孔应变仪进行了数小时采样率为100 sps(samples per second)的观测,碰巧记录到发生在康定的三次3级左右的地震.在这样高的采样率下,YRY-4型四元件钻孔应变仪的观测,达到了令人满意的自恰;除YRY-4型四元件钻孔应变仪外,姑咱台还有CTS-1型宽频带摆式地震仪,对这两种仪器观测的功率谱分析的结果表明,YRY-4型钻孔应变仪的频响性能不次于摆式地震仪的水平(Qiu et al., 2015).以姑咱实验为契机,用YRY-4型四元件钻孔应变仪又在甘肃高台、山西神池和大同等地震台站开展了类似的高频实验,结果进一步支持了以上结论(邱泽华和池顺良,2013;邱泽华,2016).甚至对于面波,通过适当的变换,这种仪器记录的曲线与摆式地震仪记录的曲线几乎完全重合(邱泽华,2017).
可以肯定地说,用合格的YRY-4型四元件钻孔应变仪可以开展多方面的地震波研究,包括确定地震的震级、地点和时间.而最有挑战性的、至今未有文献讨论的问题是:如何用钻孔应变观测研究地震的震源机制?
Gilbert(1971)最早用地震矩张量来描述震源机制,并且率先开辟了根据地球自由振荡理论利用地震波形资料求解震源机制的道路.此前,人们讨论的单力偶和双力偶等不过是震源地震矩张量的特殊形式(例如Saito,1967).至今,这种地震矩张量求解已经成为常规操作(Gilbert and Dziewonski, 1975;Dziewonski et al., 1981;Dziewonski and Woodhouse, 1983;ekström et al., 2012).但是,因为这种矩张量震源机制求解方法以有限地球的自由振荡理论为基础,而目前可识别的简正振型的周期至少在数十秒以上,所以只能研究可以产生这种周期波形的比较大(MW>5)的地震.
对于比较小的地震,传统的求解震源机制的方法需要震中周围有大量的观测点.此时可以用格林函数法求矩张量解(例如刘超等,2008),然而很多学者还是根据P波初动分布划分象限来给出双力偶解(例如许忠淮等, 1987, 1989;胡幸平等,2008;崔效锋等, 2011).一般地,对于单个小地震,很难有足够多的观测记录用来准确地给出矩张量解.
应变是张量,地震矩也是张量,二者是有直接联系的.根据惠更斯原理,地震波在传播过程中的每一个点都形成新的震源(例如Stein and Wysession, 2003).重要的是,如果新的点震源与原始震源性质一致,就可以根据一点的观测地震波应变张量,推断原始震源的矩张量性质.但是,P波与S波的分离传播表明,地震波传播过程中一点新生成的震源与原始震源并不一致.即便如此,两种张量之间到底有什么关系,可否用来研究震源机制,仍然是一个需要搞清楚的、引人入胜的问题.
本文首先梳理了地震矩张量的概念,在现行理论基础上,明确了震源应变张量的概念及其与地震矩张量的直接联系,进而给出地震波的应变张量表示,提出了地震矩张量与地震波应变张量的关系,并以双力偶为例对这种关系给出了证明.根据地震矩张量与地震波应变张量的关系,在理想的无限介质中,只要有两个不同地点的应变地震波观测,就可以解得震源矩张量.这为求解震源机制(特别是小震的震源机制)问题开辟了新的途径.
1 震源矩张量与震源应变张量在震源坐标系(x,y,z)中,点源地震矩张量可以表示为
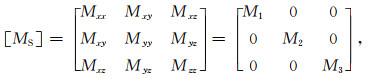
|
(1) |
这里,下角标S表示震源坐标系,M1、M2和M3是地震矩张量[MS]的特征值.地震矩张量是对称的.
一个最常见的近似是,把震源机制看成双力偶,如图 1a所示,其地震矩张量
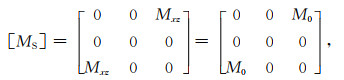
|
(2) |
|
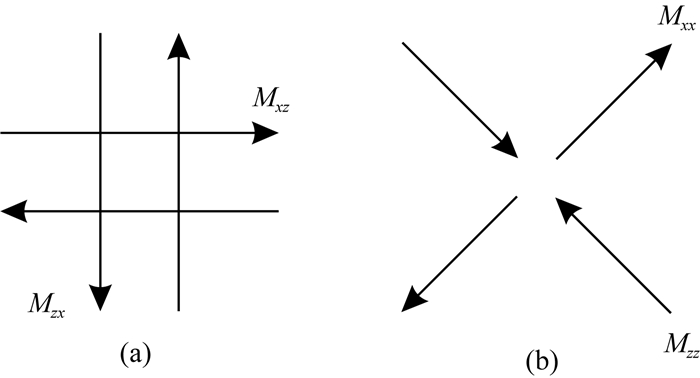
图 1 两种等效的双力偶作用示意 (a)剪应力型;(b)正应力型. Fig. 1 The two equivalent double-couples (a) Shear-stress model; (b) Normal-stress model. |
需要说明的是,式(2)的表示之所以看起来简单,是因为在震源坐标系中进行描述.由张量分析理论可知,在一般的坐标系中,所有分量都可以不为零.
式(2)中的地震矩M0>0,定义为

|
(3) |
其中,μ为剪切模量,D为断层位移量,A为断层面积.令L0代表断层面的特征尺寸,c为由断层面形状决定的常数,断层面积可以记为

|
(4) |
令与断层位移对应的应力
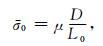
|
(5) |
式(3)可以改写为(例如Stein and Wysession, 2003;万永革,2016)
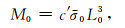
|
(6) |
其中,c′为由震源体形状决定的常数.可以令
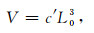
|
(7) |
称为等效震源体积.请注意,式(6)已经将地震矩与应力联系起来.地震矩是张量,应力也是张量.
需要强调的是,图 1a所示并非唯一的双力偶表示.图 1b同时给出了另外一种等效的双力偶表示(Aki and Richards, 1980;Stein and Wysession, 2003;万永革,2016).图 1a和图 1b可以看成在不同坐标系中的双力偶表示,为叙述方便,这里称前者为剪应力型,称后者为正应力型.正应力型双力偶的地震矩张量
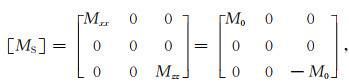
|
(8) |
对于正应力型双力偶,式(3)—(7)依然成立.由此可知,M0=M1以及-M0=M3不过是地震矩张量的特征值.
就作用效果而言,剪应力型和正应力型双力偶性质完全相同.实际上,两种双力偶的差别不过是在不同坐标系中的描述不同.重要的是,在物理解释上,前者对应的是剪应力;而后者对应的是正应力.由此可知,地震矩既可以对应剪应力,也可以对应正应力.
根据以上讨论,将式(6)引入式(1),我们得到一个地震矩张量的等效关系:
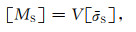
|
(9) |
其中,
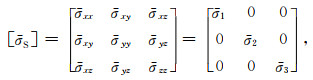
|
(10) |
称为震源应力降张量或震源应力张量,也是对称的.图 2为地震矩张量各分量作用示意,由此可见其与应力张量的一致性.二者的区别仅在于:前者是集中力,作用在一点上;而后者是面力,作用在无限小的面上.

|
图 2 地震矩张量各分量作用示意 Fig. 2 The nine force couples of the components of seismic moment tensor |
既然有应力,就应该有应变.这里定义应变张量
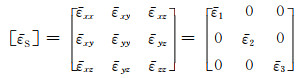
|
(11) |
为等效震源应变张量或震源应变张量,其与[σS]的关系符合胡克定律
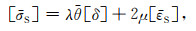
|
(12) |
其中,λ和μ是两个拉梅系数(Lamé′s constants),克罗内科函数(Kronecker Delta)
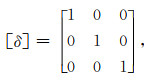
|
(13) |
而体应变
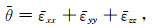
|
(14) |
震源应变张量同样是对称的.
对于双力偶,因为
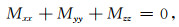
|
(15) |
所以由式(9)知体应力
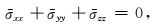
|
(16) |
从而体应变θ=0.于是,由式(9)和式(12),就得到双力偶地震矩张量与震源应变张量的等效关系:
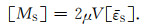
|
(17) |
我们看到,点源的震源机制既可以看成一个矩张量,也可以看成应力张量以及应变张量.更一般地,我们有(Aki and Richards, 1980,p59,3.29)

|
(18) |
其中,cpqrs为广义胡克定律的四阶张量系数.这也就是说,震源应力张量就是地震矩密度(moment-density)张量.
我们需要引入地理坐标系(N,E,D).矩张量震源机制解通常是在地理坐标系中给出的.这里的地理坐标系N轴指北,E轴指东,D轴指深度方向(Aki and Richards, 1980).在地理坐标系中,震源应变张量为

|
(19) |
震源坐标系的震源应变张量
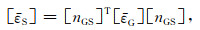
|
(20) |
其中,[nGS]为由地理坐标系变换到震源坐标系的方向余弦张量.由式(1)可知,在震源坐标系中,[εS]由主对角线上的三个特征值构成,其他分量都为0.[nGS]由三个列矢量构成,它们分别为与三个特征值对应的特征矢量.
所谓震源机制求解,主要就是要求解[εG].一旦[εG]已知,剩下的问题就变成求解其本征值和本征矢量的问题.
2 地震波的应变张量把地下的岩石看成理想的弹性介质,其内部传播的地震波只有P波和S波两种,统称为体波.地震波是从震源发出的.对于一个观测点,当其与震源之间的距离比震源体特征尺寸大得多时,其观测的地震波就可以近似看成平面波.这里我们重点分析平面波.
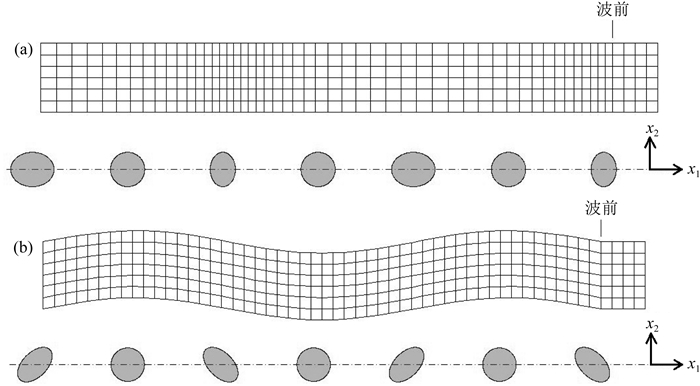
为了区别起见,我们在直角坐标系(x1,x2,x3)中讨论地震波的应变张量.此时平面波沿x1轴传播,图 3a所示是我们熟知的P平面波,其应变变化的特征是,只沿波的传播方向交替出现压缩和拉张.我们可以直接写出P平面波的应变张量:
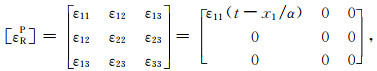
|
(21) |
|
图 3 P平面波(a)和S平面波(b)的传播模式及其应变椭圆变化示意 Fig. 3 Propagation modes of P wave (a) and S wave (b) and their strain ellipses |
其中,t表示时间,α为P波传播速度,下角标R表示射线坐标系.类似地,图 3b所示的在(x1, x2)坐标平面内沿x1轴传播的S平面波也为我们所熟知,其应变变化的特征是,只在(x1, x2)坐标平面(偏振面)内发生交替的剪应变变化,其应变张量为
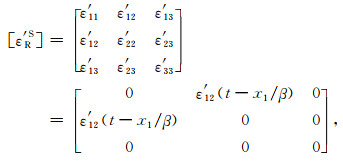
|
(22) |
其中,β为S波传播速度.
通常,为研究的方便,除要求平面波沿x1轴传播外,还要对坐标系(x1,x2,x3)附加一个条件:x3轴与地面平行,此时坐标平面(x1, x2)与地面垂直.我们称这样的坐标系为地震波射线坐标系.地理坐标系与地震波射线坐标系的关系如图 4所示.

|
图 4 地理坐标系(N,E,D)和地震波射线坐标系(x1,x2,x3) x1表示地震波传播的射线. Fig. 4 Geographic coordinate system (N, E, D) and seismic ray coordinate system (x1, x2, x3) x1 indicates the seismic ray. |
在地震波射线坐标系中,P波的应变张量表示式(21)保持不变,但是S波应变张量表示式(22)变为
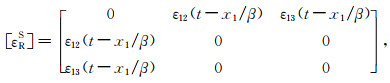
|
(23) |
此时,应变分量ε12与ε13的变化相位相同.
设x′2和x′3为与式(22)对应的坐标轴,S波的偏振面(x1, x′2)位于(x1, x2)和(x1, x3)坐标平面之间(x1轴指向读者),如图 5所示.图中,λ称为S波的偏振角.

|
图 5 S波的偏振角 Fig. 5 Polarization angle of S-wave |
由坐标旋转的应变换算关系
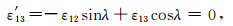
|
(24) |
得到偏振角的计算公式
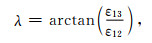
|
(25) |
沿x1轴辐射的地震波应变张量等于以不同速度传播的两种体波应变张量相加:
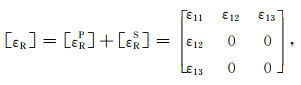
|
(26) |
其中,所有应变分量都是t和x1的函数,参见式(21)和式(23).
3 用应变地震观测求解震源机制的基本假设根据第2节的分析,我们得到一个重要的结论:作为一级近似,从震源向某方向辐射的平面地震波,只能传播三个互相独立的分量ε11、ε12和ε13,其他分量不能传播,参见式(26).
用应变地震观测求震源机制解的基本假设是,震源发出的地震波应变张量[εR]的三个不为0的独立分量ε11、ε12和ε13与震源应变张量的关系符合坐标旋转的张量变换公式:
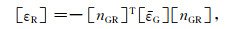
|
(27) |
其中,由地理坐标系变换到地震波射线坐标系的方向余弦张量
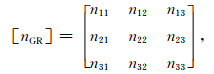
|
(28) |
其中,[nGR]的三个列矢量,分别表示射线坐标系(x1,x2,x3)的三个坐标轴在地理坐标系(N,E,D)中的方向余弦矢量(例如钱伟长和叶开沅,1956).根据式(26),具体给出这三个应变分量的表达式为
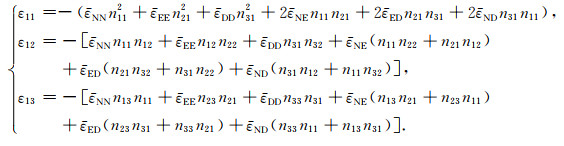
|
(29) |
我们实际上要用的就是式(29).在本节的讨论中,应该把ε11、ε12和ε13看成刚刚要从震源辐射出去的地震波应变,传播距离尚为0.
请注意式(27)和式(29)中的负号.这是由于震源等效应变张量与外围岩体地震波应变张量符号相反:震源应变膨胀的方向就是外围岩体受挤压的方向,震源应变收缩的方向就是外围岩体受拉伸的方向.
一个射线方向只需两个球坐标ϕ和θ即可确定,参见图 4.对于图 4所示坐标系,方向余弦张量各元素与球坐标ϕ和θ的关系为(例如Aki and Richards, 1980;万永革,2016)
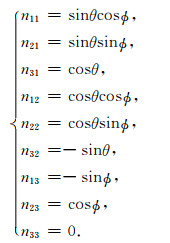
|
(30) |
而入射角i=π-θ.设地理坐标系原点为震中,射线坐标系原点为观测点,则震源距为r,震中距为L,而震源深度为h.在均匀介质中有

|
(31) |
设想我们可以观测到ε11,ε12和ε13,式(29)给出了求解震源矩张量的3个方程.对于一个特定方向,可以认为由地理坐标系变换到地震波射线坐标系的方向余弦张量已知.当有两个方向的观测时,我们就有6个方程,可以全部求出未知震源矩张量的6个分量.这就是用应变地震观测求解震源机制的简单原理.
在任意方向上,都可以建立射线坐标系(x1,x2,x3).由式(27)还可以计算得到另外三个分量ε22、ε23和ε33,这三个应变分量不能沿x1方向传播,只能沿其他方向传播:ε22和ε23与ε12一起沿x2方向传播;ε23和ε33与ε13沿x3方向传播.我们看到,在应变张量具有对称性的假设下,正应变分量ε11、ε22和ε33只能沿一个方向传播,而剪应变分量ε12、ε13和ε23可以沿两个方向传播.
4 双力偶的地震波应变张量如前所述,用应变地震观测求震源机制解的基本假设是,震源发出的地震波应变张量与震源应变张量的关系符合公式(29).这里以双力偶震源机制为例来说明这个假设的合理性.我们要说明,用双力偶产生的理论远场P波和S波位移求出的地震波应变场辐射花样,与由式(29)给出的地震波应变场辐射花样一致.
考察最简单的情况(图 6).对应于式(2)给出的双力偶,等效震源应变张量
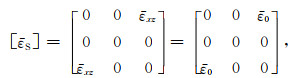
|
(32) |
|
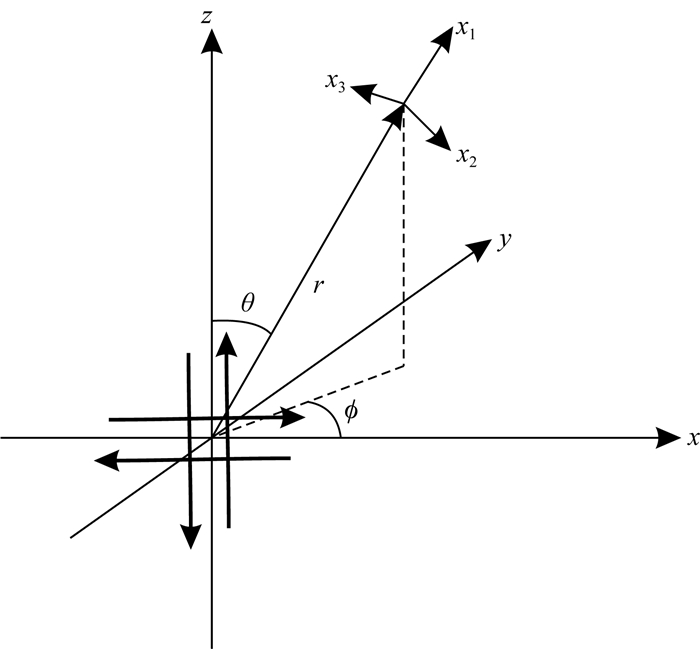
图 6 双力偶震源坐标系和地震波射线坐标系的极坐标关系 x1轴指向r增大的方向;x2轴指向θ增大的方向;x3轴指向ϕ增大的方向. Fig. 6 Relationship between the double couple coordinates and the seismic ray coordinates x1, x2 and x3 point the increasing directions of r, θ and ϕ, respectively. |
其中,ε0称为与地震矩M0对应的等效双力偶应变.
此时,一方面,参照式(29)和式(30),P波应变分量为
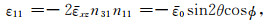
|
(33) |
S波应变分量为
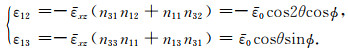
|
(34) |
在式(33)和式(34)中,等式左边的应变都是刚刚要从震源辐射出去的地震波应变,传播距离尚为0.在远离震源的地方,地震波应变是距离的函数,可以记为
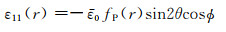
|
(35) |
和
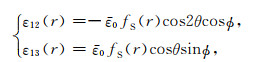
|
(36) |
其中,fP(r)和fS(r)分别称为P波和S波的应变衰减函数.
另一方面,在图 6所示极坐标下,与式(2)给出的双力偶对应的远场P波位移和S波位移分别为(例如Aki and Richards, 1980)
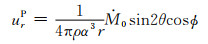
|
(37) |
和
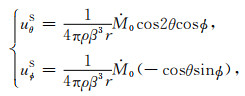
|
(38) |
其中,ρ为介质的密度.作为一级近似,可以把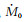
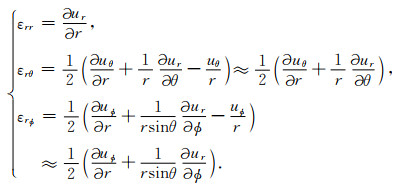
|
(39) |
由此可得P波的应变分量
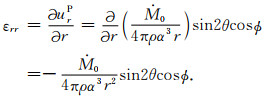
|
(40) |
同时,因为S波没有位移分量ur,所以S波的两个应变分量
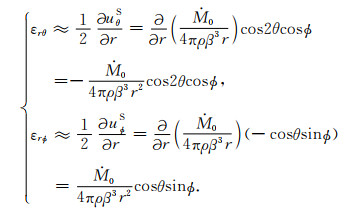
|
(41) |
应变分量(εrr,εrθ,εrϕ)与(ε11,ε12,ε13)是一致的.震源机制解只与震源辐射花样有关,而震源辐射花样只与θ和ϕ有关,与r无关.对照式(35)和式(40)可见,两种应变的P波辐射花样相同;对照式(36)和式(41)可见,两种应变的S波辐射花样也相同.由此可见,用应变地震观测求震源机制解的基本假设符合P波和S波的辐射理论,即震源发出的地震波应变张量与震源应变张量的关系符合张量变换公式(29).
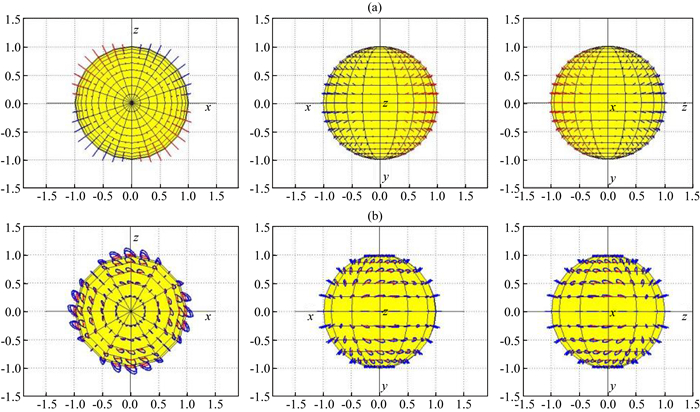
从点源发出的地震波的波前是一个球面.图 7所示为双力偶震源的由式(35)给出的P波应变(a)和由式(36)给出的S波应变(b)在波前球面上的辐射花样.
|
图 7 双力偶震源的P波初动应变(a)和S波初动偏振面(b)辐射花样 Fig. 7 Radiation patterns of P-wave initial strain (a) and S-wave initial polarization (b) for double couple source |
如图 7a所示,在波前球面上,P波应变只有一个与球面垂直的正应变分量,蓝色(负)表示挤压,红色(正)表示拉伸.由图 7a1可见,双力偶震源的P波应变辐射花样呈四象限分布.图 7a2和图 7a3分别给出从z轴正向和x轴正向看的辐射花样.
S波的应变特征是在波前球面内发生剪应变.在图 7b1中,红色直线段示意偏振面与波前球面的交线,蓝色椭圆示意在偏振面内的剪应变(参照图 3b).图 7b2和b3分别给出从z轴和x轴正向看的辐射花样.因为双力偶在(x,z)平面内,所以在(x,z)平面内的偏振面都位于(x,z)平面内,其他偏振面也都接近与(x,z)平面平行.这里需要注意,由图 3b可知,椭圆长轴和短轴都与地震波射线以45°相交.
5 震源机制的求解前面的分析都是以震源处的应变张量为对象进行的,只关心辐射花样,而不需要考虑振幅大小.但是,实际的震源机制求解问题必须考虑应变振幅衰减.
参照式(35)和式(36),一般地,可以将式(29)改写为
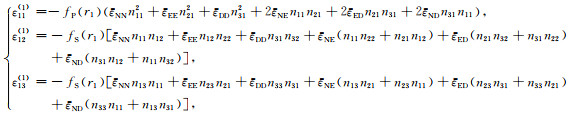
|
(42) |
其中,r1为该观测点的震源距.
假如还有另外一个观测点的数据ε11(2),ε12(2)和ε13(2),类似地,我们有
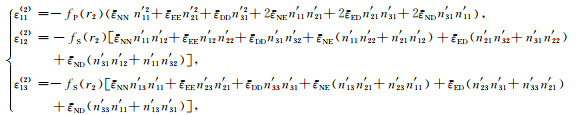
|
(43) |
其中,r2为该观测点的震源距.当衰减函数fP和fS已知时,式(42)和(43)共给出6个线性方程,可据此解出地理坐标系的震源应变张量[εG]中的所有6个分量.
将式(35)和(36)与式(40)和(41)对比,可得地震波应变衰减函数

|
(44) |
令
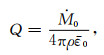
|
(45) |
称为体波衰减系数,式(44)变为

|
(46) |
需要注意的是,Q与体波类型(P波或S波)无关,与距离也无关.
一般地,我们难以事先得知Q.但是,因为α和β以及r1和r2都为已知,所以由式(42)和(43)可以解出视震源应变张量[εQ]=Q[εG].因为震源机制只与地震波辐射花样有关,而[εQ]与[εG]的辐射花样相同,所以[εQ]就可以作为震源机制解.
6 讨论和结语应变地震观测是一种新的地震波观测.因为它与传统的摆式地震仪的观测一样,都与震源过程有确定的联系,所以能用这种观测资料求解震源机制.
虽然目前还没有成熟的三维应变地震仪可以用于震源机制研究,但是已经有二维的水平张量应变地震仪,例如YRY-4型四元件钻孔应变仪.二维应变张量有三个独立分量,经过坐标变换是可以导出求解震源地震矩张量所需的三个地震波应变分量的.
只需要两个应变仪观测点就可以求解震源机制,并且可以给出更加精确的结果,这比需要众多不同地点的摆式地震仪观测才能做出粗略估计高效得多.然而这只是理想情况.以双力偶震源机制为例,在两个垂直相交的节面上,P波幅度为0,观测点一旦落在节面附近,会导致难以求解.要避免这种情况,应该考虑利用尽可能多的观测点的资料.
作为第一步,我们首先研究地方震的情况.此时可以忽略地下岩石的不均匀性,把地震波射线近似看作直线,接近本文讨论的理想情况.本研究的实验即将在山西开展,计划用5个间距只有数十千米的钻孔应变观测点组成台阵,以期首先捕捉地方震来求解其震源机制,并通过多个两点结果的互相校验和与传统求解方法的结果作对比来对新方法进行实践检验.显然,能否捕捉到合适的地方震存在不确定性.
一般地,我们不考虑用应变地震观测的地震波初动分布求震源机制解,而是用地震波形资料.大量观测表明,即使是对于爆炸源,实际的地震波记录也不是简单的脉冲,而是由不同频率的波组成的不断变化的波列.假定仪器响应的问题已经解决,可以设想仪器观测的地震波形是由震源和介质两方面决定的.一方面,一个构造地震的震源过程究竟如何我们并不知道;另一方面,地下的岩石也并非理想的弹性介质.在深入探讨用应变地震观测求解震源机制的过程中,需要借鉴用摆式地震仪观测资料求解震源机制的方法:一方面建立震源时间函数,另一方面建立地震波在实际介质中传播的格林函数.
本文是对用应变观测资料求解震源矩张量原理的分析说明,离实际应用还有相当长的路要走,还有很多工作要做.
致谢 作者感谢池顺良先生对这个工作鼎力支持,感谢两位审稿人提出宝贵意见.
Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods, Vol. Ⅰ and Ⅱ. San Francisco: W. H. Freeman and Co.
|
Barbour A J, Agnew D C. 2012. Detection of seismic signals using seismometers and strainmeters. Bulletin of the Seismological Society of America, 102(6): 2484-2490. DOI:10.1785/0120110298 |
Barbour A J, Crowell B W. 2017. Dynamic strains for earthquake source characterization. Seismological Research Letters, 88(2A): 354-370. DOI:10.1785/0220160155 |
Båth M. 1979. Introduction to Seismology. Basel: Birkhäuser Verlag.
|
Benioff H, Press F, Smith S. 1961. Excitation of the free oscillations of the Earth by earthquakes. J. Geophys. Res., 66(2): 605-619. DOI:10.1029/JZ066i002p00605 |
Chi S L, Chi Y, Deng T, et al. 2009. The necessity of building national strain-observation network from the strain abnormality before Wenchuan earthquake. Recent Developments in World Seismology (in Chinese), (1): 1-13. |
Cui X F, Hu X P, Yu C Q, et al. 2011. Research on focal mechanism solutions of Wenchuan earthquake sequence. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese), 47(6): 1063-1072. |
Dziewonski A M, Chou T A, Woodhouse J H. 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res., 86(B4): 2825-2852. DOI:10.1029/JB086iB04p02825 |
Dziewonski A M, Woodhouse J H. 1983. An experiment in systematic study of global seismicity: centroid-moment tensor solutions for 201 moderate and large earthquakes of 1981. J. Geophys. Res., 88(B4): 3247-3271. DOI:10.1029/JB088iB04p03247 |
Ekström G, Nettles M, Dziewoński A M. 2012. The global CMT project 2004-2010: Centroid-moment tensors for 13, 017 earthquakes. Phys. Earth Planet. Inter., 200-201: 1-9. DOI:10.1016/j.pepi.2012.04.002 |
Gilbert F. 1971. Excitation of the normal modes of the Earth by earthquake sources. Geophys. J. Roy. Astron. Soc., 22(2): 223-226. DOI:10.1111/j.1365-246X.1971.tb03593.x |
Gilbert F, Dziewonski A M. 1975. An application of normal mode theory to the retrieval of structural parameters and source mechanisms from seismic spectra. Philos. Trans. Roy. Soc. A, 278(1280): 187-269. |
Gladwin M T. 1984. High precision multi-component borehole deformation monitoring. Rev. Sci. Instrum., 55(12): 2011-2016. DOI:10.1063/1.1137704 |
Guo Y P, Qiu Z H, Li S H, et al. 2012. On high sample rate of borehole volume strainmeter observation. Journal of Geodesy and Geodynamics (in Chinese), 32(1): 51-55. |
Hu X P, Yu C Q, Tao K, et al. 2008. Focal mechanism solutions of Wenchuan earthquake and its strong aftershocks obtained from initial P wave polarity analysis. Chinese Journal of Geophysics (in Chinese), 51(6): 1711-1718. |
Ishii H. 2001. Development of new multi-component borehole instrument. Report of Tono Research Institute of Earthquake Science, 6: 5-10. |
Liu C, Zhang Y, Xu L S, et al. 2008. A new technique for moment tensor inversion with applications to the 2008 Wenchuan MS8.0 earthquake sequence. Acta Seismologica Sinica (in Chinese), 30(4): 329-339. |
Liu X Y, Wang Z Y, Fang H F, et al. 2014. Analysis of 4-component borehole strain observation based on strain invariant. Chinese Journal of Geophysics (in Chinese), 57(10): 3332-3346. DOI:10.6038/cjg20141020 |
Ouyang Z X. 1977. RDB-1 type electric capacity strainmeter.//Selected Papers of the National Conference on Stress Measurement, Part 2 (in Chinese), 337-348.
|
Qian W C, Ye K Y. 1956. Elastic Mechanics (in Chinese). Beijing: Science Press.
|
Qiu Z H, Shi Y L, Ouyang Z X. 2005. Relative in-situ calibration of 4-component borehole strain observation. Journal of Geodesy and Geodynamics (in Chinese), 25(1): 118-122. |
Qiu Z H, Chi S L. 2013. Shear strains of P wave observed with YRY-4 borehole strainmeter. Earthquake (in Chinese), 33(4): 64-70. |
Qiu Z H, Tang L, Zhang B H, et al. 2013. In situ calibration of and algorithm for strain monitoring using four-gauge borehole strainmeters (FGBS). J. Geophys. Res.: Solid Earth, 118(4): 1609-1618. DOI:10.1002/jgrb.50112 |
Qiu Z H, Chi S L, Wang Z M, et al. 2015. The strain seismograms of P- and S-waves of a local event recorded by four-gauge borehole strainmeter. Earthquake Science, 28: 209-214. DOI:10.1007/s11589-015-0120-5 |
Qiu Z H. 2016. Asymmetric Linear Elasticity (in Chinese). Beijing: Seismological Press.
|
Qiu Z H. 2017. Borehole Strain Observation, Theory and Application (in Chinese). Beijing: Seismological Press.
|
Saito M. 1967. Excitation of free oscillations and surface waves by a point source in a vertically heterogeneous earth. J. Geophys. Res., 72(14): 3689-3699. DOI:10.1029/JZ072i014p03689 |
Stein S, Wysession M. 2003. An Introduction to Seismology, Earthquakes, and Earth Structure. Oxford: Blackwell Publishing.
|
Wan Y G. 2016. Introduction to Seismology (in Chinese). Beijing: Science Press.
|
Xu Z H, Wang S Y, Huang Y R, et al. 1987. Directions of mean stress axes in northwestern China deduced from microearthquake data. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 30(5): 476-486. |
Xu Z H, Wang S Y, Huang Y R, et al. 1989. The tectonic stress field of Chinese continent deduced from a great number of earthquakes. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 32(6): 636-647. |
Yang X H, Yang S X, Zhang B, et al. 2011. Strains recorded by seismic acquisition unit. Earthquake Research in China (in Chinese), 27(1): 65-71. |
Yin X C. 2011. Solid Mechanics (in Chinese). 2nd ed. Beijing: Seismological Press.
|
池顺良, 池毅, 邓涛, 等. 2009. 从5.12汶川地震前后分量应变仪观测到的应变异常看建设密集应变观测网络的必要性. 国际地震动态, (1): 1-13. DOI:10.3969/j.issn.0253-4975.2009.01.001 |
崔效锋, 胡幸平, 俞春泉, 等. 2011. 汶川地震序列震源机制解研究. 北京大学学报(自然科学版), 47(6): 1063-1072. |
郭燕平, 邱泽华, 李素华, 等. 2012. 钻孔体应变高采样率观测实验. 大地测量与地球动力学, 32(1): 51-55. |
胡幸平, 俞春泉, 陶开, 等. 2008. 利用P波初动资料求解汶川地震及其强余震震源机制解. 地球物理学报, 51(6): 1711-1718. DOI:10.3321/j.issn:0001-5733.2008.06.011 |
刘超, 张勇, 许力生, 等. 2008. 一种矩张量反演新方法及其对2008年汶川MS8.0地震序列的应用. 地震学报, 30(4): 329-339. DOI:10.3321/j.issn:0253-3782.2008.04.001 |
刘序俨, 王紫燕, 方宏芳, 等. 2014. 对当前四分量钻孔应变观测的审视——以应变不变量为标尺. 地球物理学报, 57(10): 3332-3346. DOI:10.6038/cjg20141020 |
欧阳祖熙. 1977. RDB-1型电容式地应变计.//全国地应力专业会议论文选编(下), 337-348.
|
钱伟长, 叶开沅. 1956. 弹性力学. 北京: 科学出版社.
|
邱泽华, 石耀霖, 欧阳祖熙. 2005. 四分量钻孔应变观测的实地相对标定. 大地测量与地球动力学, 25(1): 118-122. |
邱泽华, 池顺良. 2013. YRY-4型钻孔应变仪观测的P波剪应变. 地震, 33(4): 64-70. DOI:10.3969/j.issn.1000-3274.2013.04.007 |
邱泽华. 2016. 非对称线弹性理论. 北京: 地震出版社.
|
邱泽华. 2017. 钻孔应变观测理论和应用. 北京: 地震出版社.
|
万永革. 2016. 地震学导论. 北京: 科学出版社.
|
许忠淮, 汪素云, 黄雨蕊, 等. 1987. 由多个小震推断的青甘和川滇地区地壳应力场的方向特征. 地球物理学报, 30(5): 476-486. DOI:10.3321/j.issn:0001-5733.1987.05.005 |
许忠淮, 汪素云, 黄雨蕊, 等. 1989. 由大量的地震资料推断的我国大陆构造应力场. 地球物理学报, 32(6): 636-647. DOI:10.3321/j.issn:0001-5733.1989.06.004 |
杨选辉, 杨树新, 张彬, 等. 2011. 测震数采仪记录的钻孔应变. 中国地震, 27(1): 65-71. DOI:10.3969/j.issn.1001-4683.2011.01.007 |
尹祥础. 2011. 固体力学. 2版. 北京: 地震出版社.
|
 2020, Vol. 63
2020, Vol. 63

