2. 桂林理工大学地球科学学院, 桂林 541006
2. College of Earth Sciences, Guilin University of Technology, Guilin 541006, China
航空电磁法(Airborne Electromagnetic,简称AEM)于20世纪50年代开始研发,由频率域和时间域航空电磁法两部分组成.目前,航空电磁法已被广泛应用于矿产勘查、环境工程、地下水和地热资源探测等诸多领域.然而,由于航空电磁法采用动态飞行平台,噪声干扰严重,给反演解释造成严重困难.因此,采取有效措施抑制噪声,提高数据质量至关重要.
航空电磁数据受到来自飞机机身震动、发射和接收线圈振动、天电、人文等多方面的噪声影响.天电噪声属于准脉冲型信号,其幅值在高频部分很高;运动噪声由发射和接收线圈振动产生,属于低频噪声;人文噪声属于随机噪声,无明显变化规律.近年来,学者们提出了各种去噪方法.Sykes和Das(1998)提出了利用拉东变换提取航空电磁数据中人文噪声的方法.Ridsdill-Smith和Dentith(1999)将小波变换(WT)应用于航空电磁数据处理中.然而,WT的去噪效果与小波母函数及尺度参数的选取有关,在实际应用中存在局限性.Reninger等(2011)提出利用奇异值分解(SVD)对航空电磁数据进行去噪.朱凯光等(2013)利用主成分分析法(PCA)对航空电磁信号进行去噪,去除了高阶主成份中的无关噪声,但低阶主成分中仍然含有部分噪声.杜兴中和陆从德(2016)提出了一种基于奇异值分解和小波变换的航空电磁数据去噪方法,该方法可以同时去除天电噪声和人文噪声,但去噪效果对参数的依赖性较强.
由上所述,传统航空电磁去噪方法虽然取得一定的效果,但均存在局限性.为了弥补这些现有方法的不足,本文提出基于曲波变换的航空电磁数据去噪技术,并使用Sigmoid阈值函数代替传统阈值函数以改善去噪效果.曲波变换具有多尺度性、多方向性和各向异性特征,可将信号分解成多个尺度和方向进行精细分析.因此,曲波变换可以较准确地拟合信号,更适合处理具有曲线奇异性的二维数据(Li et al., 2015),已在地震勘探数据处理领域获得广泛应用(曹静杰等,2018;李继伟等,2019).另外,本文提出的Sigmoid阈值函数可以对曲波系数进行平滑截断,在一定程度上避免了伪吉布斯效应,同时还可提取出部分被传统阈值函数忽略的有效信号.因此,曲波变换方法在全面去除数据中噪声的同时,有效地保留了有用信号.本文在阐述曲波变换原理的基础上,首先通过与传统阈值函数去噪结果进行比较验证Sigmoid阈值函数的有效性,进而通过对理论和实测数据进行处理,并与传统去噪方法进行对比验证所提出的曲波变换方法的技术优越性.
1 曲波变换及去噪理论曲波变换最早由Candès和Donoho(1999)提出,它是对小波变换和脊波变换理论的继承和发展.由于早期曲波变换金字塔式的层式分解导致数据冗余量较大,其计算速度缓慢.2004年,Candès和Donoho提出了第二代曲波变换.下面我们将分别介绍离散曲波变换理论、曲波变换的Wrapping算法及基于阈值法的曲波去噪技术.
1.1 波数域内的窗函数
离散曲波变换在波数域内具有紧支性,可以将信号转换到不同的尺度和角度分量(Candès et al., 2006).定义二维波数域内的径向窗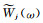
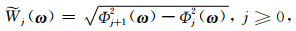
|
(1) |
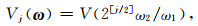
|
(2) |
其中,ω=(ω1, ω2)为波数域内的变量,j为尺度参数,[j/2]表示j/2的整数部分,Φ由两个一维低通窗的乘积定义,可表示为
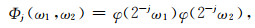
|
(3) |
其中,滤波器φ满足0≤φ≤1.由此,我们可以进一步定义如下“笛卡尔”窗,即
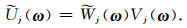
|
(4) |
根据“笛卡尔”窗的定义可知,径向窗和角度窗共同构造出多个楔形支撑区间,波数域在楔形的边缘处{(ω1, ω2)|2j≤ω1≤2j+1, -2-j/2≤ω2/ω1≤2-j/2}被分割(如图 1a所示).接下来引入相同间隔的斜率tanθl=l·2-[j/2],表征了图 1a中角度窗的倾斜程度,其中,角度参数l满足l=-2-[j/2], …, 2[j/2]-1(Candès et al., 2006),则(4)式可写为
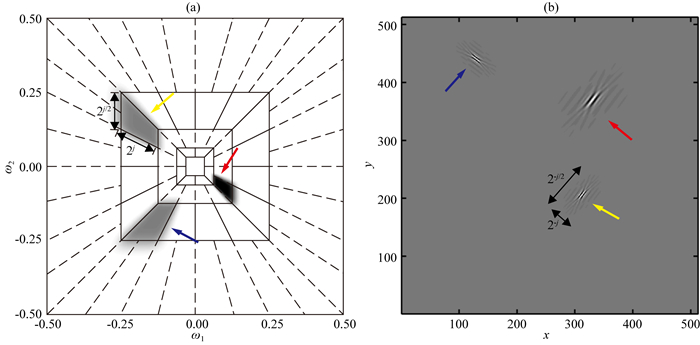
|
图 1 (a) 波数域中的楔形窗;(b)与波数域中楔形窗对应的空间域曲波(参考Herrmann and Hennenfent, 2008) Fig. 1 (a) Wedges in wavenumber domain; (b) Curvelets in spatial domain corresponding to wedges in the wavenumber domain |
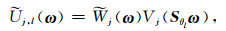
|
(5) |
其中,剪切矩阵Sθl定义为
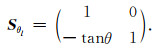
|
(6) |
图 1a为角度窗W和径向窗V支撑得到的波数域内的“笛卡尔”窗
空间域内离散曲波的定义与连续曲波的定义相似(Ying et al., 2005).因此,我们首先引入R2内空间变量为x的连续曲波.我们定义一个“母曲波”为φj(x),其傅里叶变换为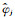
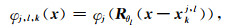
|
(7) |
其中,旋转矩阵Rθl为
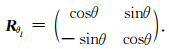
|
(8) |
函数f的曲波系数由φj, l, k(x)与函数f∈L2(R2)的内积定义,可表示为
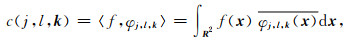
|
(9) |
其中〈f, φj, l, k〉表示φj, l, k(x)与f的内积,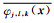
根据Plancherel定理(王丽萍,2006),曲波系数也可以在波数域内由下式计算,即
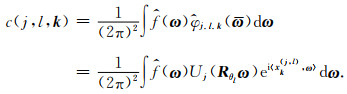
|
(10) |
图 1b中展示了空间域内曲波,其长度2-j/2和宽度2-j满足抛物线尺度关系:宽度∝长度2.因此,曲波变换具有各向异性特征.通过对波数域内的信号进行反变换,图 1a中3个波数域剖分网格内的信号分别转换为图 1b中3个空间域曲波.黄色和紫色箭头分别指向第四尺度内不同方向的楔形窗,而红色箭头指向第三尺度内的楔形窗.黄色和红色箭头指向的楔形窗在波数域内近似平行,而紫色箭头指向的楔形窗与它们近似垂直.由于傅里叶变换的90°旋转特性,使得波数域内的楔形窗和空间域内相对应的曲波方向相互正交.
1.3 基于Wrapping技术的离散曲波变换本文采用Candès等(2006)提出的基于Wrapping技术的离散曲波变换来实现去噪.类似于(9)式,笛卡尔坐标系下离散曲波变换可写为
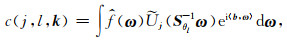
|
(11) |
其中,角度的旋转矩阵Rθl被剪切矩阵Sθl-1代替,而xk(j, l)被矩形网格中的离散值b=(k1·2-j, k2·2-j/2)代替.我们进一步将(11)式离散化,得到如下表达式:
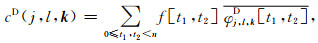
|
(12) |
其中,cD(j, l, k)为离散曲波系数,f[t1, t2]为输入的离散二维信号,φj, l, kD表示离散曲波.
必须指出,公式(11)中窗函数为楔形,无法进行二维傅里叶变换,因此不能实现曲波变换.为此,我们引入Wrapping算法.其实施步骤总结如下:
首先,对f[t1, t2]∈L2(R2)进行二维快速傅里叶变换,得到傅里叶采样
其次,对每一组尺度和角度(j, l),取“笛卡尔”窗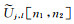
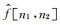
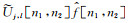
再次,把上面得到的乘积围绕笛卡尔坐标系的原点做包络,得到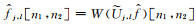
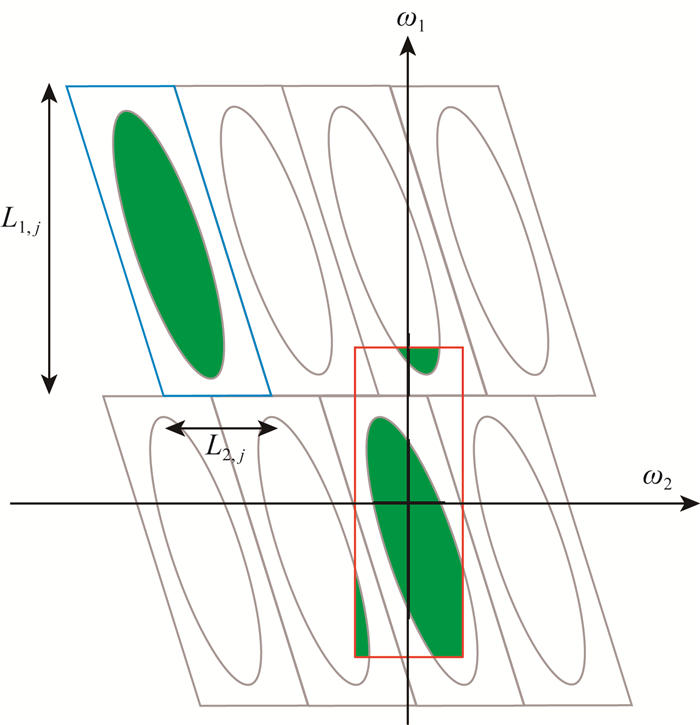
|
图 2 曲波变换中的Wrapping技术 蓝色平行四边形为波数域中的一个支撑区间,绿色区域包含该尺度和方向内的信息,Wrapping过程将该区域内的信息转化到围绕原点的红色矩形支撑区间内(参考Candès et al., 2006). Fig. 2 Wrapping process in curvelet transform The blue parallelogram is a support interval in wavenumber domain and the green area contains the information in this scale and direction. The wrapping process transfers the information to the red rectangular around the origin. |
最后,对每一个
Wrapping技术的核心步骤是围绕原点做包络,目的在于将所有区域都通过平移映射到位于原点的矩形仿射区域,由于二维傅里叶变换具有周期性,故此映射过程不对信息造成损失.经过此步骤,傅里叶变换得以实现.
1.4 曲波域中信号特征分析根据Candès和Donoho(2004),当信号特征与曲波基形态拟合较好时,对应的曲波系数较大,反之则较小.另外,粗尺度(j=1)存储着信号的低频信息,随着尺度参数j增大,对应信息的频率增高.由于有用信号主要成分的变化通常呈现规律性且平滑有序,因此可以用较大的曲波系数对其进行描述,并存放于曲波域内较低频率的尺度中.相反,噪声经常呈现随机振荡特征,由较小的曲波系数描述,并存储于曲波域内较细尺度中.
为检验曲波域中有用信号与噪声的特征差异,对图 3a给出的磁感应强度时间导数理论信号以及图 4a的纯噪声模型进行分析.

|
图 3 理论磁感应强度时间导数信号及其在不同尺度上的重构结果 (a)理论信号;(b)粗尺度重构结果;(c)第二尺度重构结果;(d)第三尺度重构结果;(e)第四尺度重构结果. Fig. 3 Theoretical magnetic induction and its reconstruction results at different scales (a) Theoretical signal; (b) The coarse scale reconstruction result; (c) The 2nd scale reconstruction result; (d) The 3rd scale reconstruction result; (e) The 4th scale reconstruction result. |
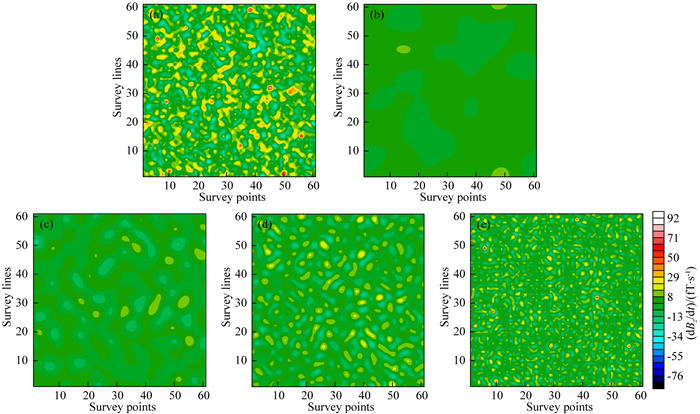
|
图 4 全随机磁感应强度时间导数(噪声)及其在不同尺度上的重构结果 (a)噪声;(b)粗尺度重构结果;(c)第二尺度重构结果;(d)第三尺度重构结果;(e)第四尺度重构结果. Fig. 4 Random noise and its reconstruction results at different scales (a) Noise; (b) The coarse scale reconstruction result; (c) The 2nd scale reconstruction result; (d) The 3rd scale reconstruction result; (e) The 4th scale reconstruction result. |
首先,将理论信号转换到曲波域(分解尺度数为4),并利用各尺度的系数分别进行重构,得到如图 3b—3e所示的重构结果.由图可以看出,通过粗尺度曲波系数进行信号重构可以恢复信号的总体特征(图 3b).另外,由于信号在测区边缘处被截断,在较高频尺度上可以观察到较为明显的边缘效应,这些细节信息在信号重构中发挥着一定的作用(图 3c—3e).图 4为纯噪声在曲波域内逐尺度分解并重构的结果.由图可以看出,随机噪声在j较大的细尺度上有较强的反映.
对比图 3和4可知,有用信号和噪声在各尺度均有分布,然而,有用信号主要分布在j较小的中低尺度,噪声主要分布在中高尺度.另外,由于在各尺度中有效信号对应的曲波系数较大,而噪声对应的曲波系数较小,因此在信号重构前我们可以在各尺度设置阈值,实现信号和噪声的有效分离(齐少华等,2016).
1.5 阈值函数设置由上所述,有用信号在曲波域内通常对应较大的系数,而噪声对应较小的系数.因此,我们在曲波域各尺度上设置阈值,滤除与噪声相关的系数,再将剩余的曲波系数重构回空间域,实现去噪.
阈值函数主要包括硬阈值函数、软阈值函数、线性阈值函数和非线性阈值函数等.我们分别对上述四种阈值函数进行介绍.
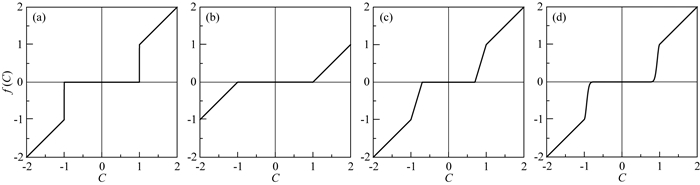
(1) 硬阈值函数
参见图 5a,硬阈值函数可表示为
|
图 5 (a) 硬阈值函数(T=1); (b)软阈值函数(T=1); (c)线性阈值函数(T1=0.8,T2=1); (d)非线性阈值函数(T1=0.8,T2=1) Fig. 5 (a) Hard threshold function (T=1); (b) Soft threshold function (T=1); (c) Linear threshold function (T1=0.8, T2=1); (d) Nonlinear threshold function (T1=0.8, T2=1) |
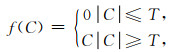
|
(13) |
式中,C为曲波系数,T为阈值,f(C)为阈值函数处理后的输出结果.该阈值函数将大于阈值的系数保留,并将其他系数置零(Donoho and Johnstone, 1994).
(2) 软阈值函数
参见图 5b,软阈值函数是在硬阈值函数的基础上对大于阈值的曲波系数进行适当的衰减(Donoho,1995),即

|
(14) |
式中,sign代表符号函数.
(3) 线性阈值函数和非线性阈值函数
上述硬阈值函数能较好地描述信号的局部特征,但经其处理后的曲波系数是不连续的,这会导致空间域内的信号产生伪吉布斯现象.软阈值函数处理得到的曲波系数相对连续,但会导致信号失真.为了克服这些缺点,学者们提出了线性阈值和非线性阈值函数(Abma and Kabir, 2006;张恒磊等,2010),参见图 5c和5d.假设T1和T2为阈值,且T1<T2,则线性阈值函数定义为

|
(15) |
而非线性阈值函数定义为
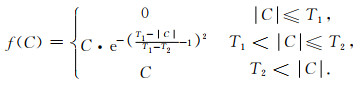
|
(16) |
(4) Sigmoid阈值函数
通过上述讨论,可以看出传统的阈值方法存在两方面问题.首先,在去除小于阈值的曲波系数时,置零的部分仍然包含少量有效信号,这可能导致信号部分失真;其次,线性和非线性阈值函数可在消除伪吉布斯效应的同时在一定程度上减少信号失真,但均需要设置两个阈值,这在实际处理中较难实现.为此,我们引入Sigmoid函数定义新的阈值函数.Sigmoid函数(也称为logistic函数)可表示为
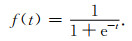
|
(17) |
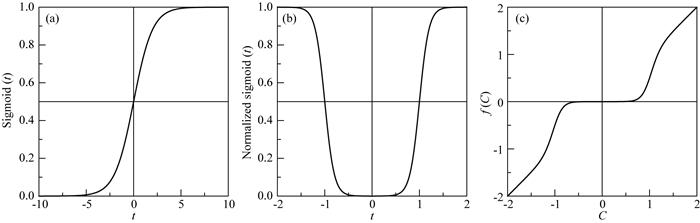
如图 6a所示,当t大于0时,f(t)迅速趋于1.相反,当t小于0时,f(t)迅速趋于0.在构造Sigmoid阈值函数之前,需要对其进行归一化,将其置于所需的区间内,从而得到可用于截断的函数(图 6b).截断位置由阈值T决定.归一化后的Sigmoid函数可表示为
|
图 6 (a) Sigmoid函数;(b)归一化后的Sigmoid函数(T=1);(c) Sigmoid阈值函数(T=1) Fig. 6 (a) Sigmoid function; (b) Sigmoid function after normalizing (T=1); (c) Sigmoid threshold function (T=1) |
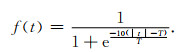
|
(18) |
进而,我们通过将(18)式与曲波系数相乘以构建Sigmoid阈值函数,即
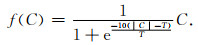
|
(19) |
从图 6c给出的Sigmoid阈值函数可以看出,当|C|大于T时,f(C)迅速趋于C;而当|C|小于T时,f(C)迅速趋于0.其核心思想可解释如下:Sigmoid阈值函数不是一个严格的约束,曲波系数没有完全被消除或保留,而是平滑地被截取.显然,Sigmoid阈值较线性和非线性阈值更加平滑,且仅需设定一个阈值即可实现.
为了验证Sigmoid阈值函数的优越性,我们对图 3a和图 4a相加得到的含噪模型(图 7b)进行去噪,并选取信噪比(SNR)作为去噪效果的评价指标,即
|
图 7 (a) 图 3a中给出的理论信号;(b) 图 3a中的理论信号和图 4a中的随机噪声的叠加结果,SNR=39.61 dB;(c)硬阈值函数去噪,SNR=47.35 dB;(d)软阈值函数去噪,SNR=46.83 dB;(e)非线性阈值函数去噪,SNR=47.47 dB;(f) Sigmoid阈值函数去噪,SNR=48.72 dB Fig. 7 (a) Theoretical signal in Fig. 3a; (b) Addition of the theoretical signal in Fig. 3a and the random noise in Fig. 4a, SNR=39.61 dB; (c) Result of hard threshold function denoising, SNR=47.35 dB; (d) Result of soft threshold function denoising, SNR=46.83 dB; (e) Result of nonlinear threshold function denoising, SNR=47.47 dB; (f) Result of Sigmoid threshold function denoising, SNR=48.72 dB |

|
(20) |
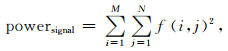
|
(21) |

|
(22) |
式中,f为理论信号,
图 7展示了Sigmoid阈值函数和其他传统阈值函数的去噪结果对比.由图可以看出,硬阈值函数的突然截断导致数据产生了局部振荡(图 7c).软阈值函数去噪得到的信号相对平稳,但它对曲波系数的收缩导致了一定的数据畸变(图 7d).非线性阈值函数的处理结果具有较高的质量(图 7e).然而,利用Sigmoid阈值函数得到的结果信噪比最高,异常特征最接近理论信号,且具有良好的边缘连续性.
2 数值试验 2.1 理论模型试验为了进一步展示曲波变换结合Sigmoid阈值函数去噪方法的有效性,我们利用本文方法对正演计算得到的时间域航空电磁磁感应强度时间导数(dBz/dt)响应进行去噪处理,并与传统的去噪方法(奇异值分解SVD,主成分分析PCA和小波变换WT)的结果比较.我们在理论数据中加入高斯白噪、随机噪声和脉冲噪声(局部突跳值),并进行去噪处理.在曲波变换去噪过程中,首先将数据转换到曲波域的4个尺度内,第二尺度的分解角度数为32,第三、四尺度的分解角度数为64.我们分别在各尺度设置阈值,根据经验,阈值T选取3倍的噪声曲波系数均方根误差为最佳,不同尺度会有细微变化,在实际去噪处理过程中,应根据噪声大小和分布进行适当调整.WT采用硬阈值法去噪,试验表明选取db23作为母波函数去噪效果最佳.图 8给出各种去噪方法的结果对比.由图可以看出,传统去噪方法得到的结果有较明显的畸变,特别是在异常边缘.WT去噪效果较好,但仍存在局部失真.曲波变换去噪效果最佳,重构信号最准确,信噪比最高.
|
图 8 (a) 航空电磁某一时间道理论数据;(b)含噪信号,SNR=40.18 dB;(c) SVD去噪结果,SNR=44.91 dB;(d) PCA去噪结果,SNR=45.19 dB;(e) WT去噪结果,SNR=47.01 dB;(f)曲波变换去噪结果,SNR=50.86 dB. Fig. 8 (a) Theoretical AEM signal; (b) The signal with noise added, SNR=40.18 dB; (c) Result of SVD denoising, SNR=44.91 dB; (d) Result of PCA denoising, SNR=45.19 dB; (e) Result of WT denoising, SNR=47.01 dB; (f) Result of curvelet transform denoising, SNR=50.86 dB |
基于上述讨论我们可以得出结论:电磁去噪方法最初是对数据进行简单的加权平均,不进行精细分析;随后的PCA和SVD等去噪技术将信号分为低频和高频部分,并通过对低频信号进行重构得到对原始信号的估计以实现去噪;基于WT的去噪技术对信号进行多尺度分析,并通过对各尺度设置阈值提取有用信号和滤除噪声.然而,这些方法对信号的分析仍然不够精细,特别是没有对信号进行方向性分析和提取.相比之下,曲波变换在WT的基础上增加了方向特征,除了对信号进行多尺度分析,还对信号多方位描述,因此能更好地识别和拟合二维信号,进而实现有效去噪.
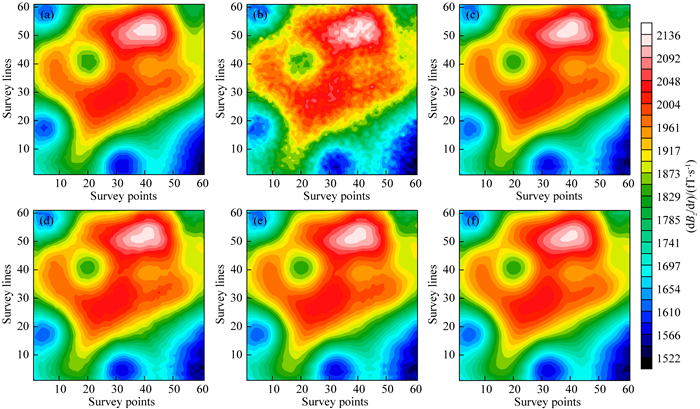
2.2 实测数据去噪本节我们讨论实测航空电磁数据去噪问题.该数据是由CGG公司在爱尔兰Knock和Weston地区利用时间域GENESIS系统观测得到的(https://www.gsi.ie/en-ie/data-and-maps/pages/sics.aspx).测线总长度32141 km,线距为200 m,测线方向N15°W.发射基频为225 Hz,发射电流为方波,峰值为391 A.本次测量得到了11个时间道的归一化垂直分量dBz/dt数据.我们以第五时间道为例进行去噪,图 9a给出了原始数据.首先将数据转换到曲波域的六个尺度内,第二尺度的分解角度数为64,第三、四尺度的分解角度数为128,第五、六尺度的分解角度数为256.图 9d—9i展示了各尺度的重构信号.由图可见,通过对第一尺度信号重构,响应的大致轮廓已较为清楚.第二和第三尺度存在大量的有用信息和少量噪声.从第四尺度开始,噪声的比例逐渐增大,主要表现为沿测线的系列跳点,同时四周边界上残留部分有用信号.我们使用Sigmoid阈值函数进行分尺度去噪.考虑到第一到第三尺度内噪声成分较少,经设定小阈值处理后数据改变很小,文中没有展示第一到第三尺度的去噪结果.由于第四到第六尺度中既含有随机噪声,又含有方向性明显的调平残差,我们首先针对各尺度设计较小的阈值去除随机噪声;进而,针对沿测线方向分布的特殊噪声,我们在测线方向的系数矩阵上设计较大阈值去除该方向的噪声(调平残差).因此,利用曲波变换的多尺度和多方向特征,有效地去除了沿测线方向的噪声和其他随机噪声,同时很好地保存了有用信号(参见图 9j—9l).最后,我们利用各尺度保留下来的曲波系数进行重构,得到如图 9b所示的去噪结果,而图 9c给出了去除的噪声.

|
图 9 爱尔兰Knock和Weston地区实测数据曲波变换重构及去噪结果 (a)原始观测数据;(b)曲波去噪结果;(c)曲波变换去除的噪声;(d)第一尺度重构;(e)第二尺度重构;(f)第三尺度重构;(g)第四尺度重构;(h)第五尺度重构;(i)第六尺度重构;(j)去噪后第四尺度重构;(k)去噪后第五尺度重构;(l)去噪后第六尺度重构. Fig. 9 Reconstruction and denoising of the survey data from Knock and Weston, Ireland by curvelet transform (a) Original survey data; (b) Result of curvelet denoising; (c) Noise removed by curvelet transform; (d) Reconstruction of 1st scale; (e) Reconstruction of 2nd scale; (f) Reconstruction of the 3rd scale; (g) Reconstruction of 4th scale; (h) Reconstruction of 5th scale; (i) Reconstruction of 6th scale; (j) Reconstruction of 4th scale after denoising; (k) Reconstruction of 5th scale after denoising; (l) Reconstruction of 6th scale after denoising. |
为了进一步说明曲波变换多方向性优点,我们将图 9a中的原始观测数据转换到小波域,并将其分解成5个尺度得到高频信息(细节分量)和低频信息(近似分量).图 10d—10i展示了小波域内第五尺度的近似分量和五个尺度的细节分量.由图可见,第一到第三尺度的细节分量包含大量沿测线方向分布的噪声.我们分别设置阈值对各尺度的细节分量和第五尺度的近似分量进行去噪.图 10j—10l给出其中第一到第三尺度细节分量去噪结果.从图可以看出,由于WT仅有三个方向参数,因此经WT去噪后的高频信号失真较严重.另外,由于WT不能对特定方向的小波系数设定阈值,因此为全面地去除噪声,必须去除阈值以下的所有小波系数,故在噪声去除的同时,也造成部分有用信号丢失.图 10b给出剩余小波系数重构得到的去噪结果,而图 10c给出去除的噪声.

|
图 10 爱尔兰Knock和Weston地区实测数据WT重构及去噪结果 (a)原始观测数据;(b) WT去噪结果;(c) WT去除的噪声;(d)第五尺度近似分量;(e)第五尺度细节分量;(f)第四尺度细节分量;(g)第三尺度细节分量;(h)第二尺度细节分量;(i)第一尺度细节分量;(j)去噪后第三尺度细节分量;(k)去噪后第二尺度细节分量;(l)去噪后第一尺度细节分量. Fig. 10 Reconstruction and denoising of the survey data from Knock and Weston, Ireland by WT method (a) Original survey data; (b) Result of WT denoising; (c) Noise removed by WT; (d) Approximation component of 5th scale; (e) Detailed component of 5th scale; (f) Detailed component of 4th scale; (g) Detailed component of 3rd scale; (h) Detailed component of 2nd scale; (i) Detailed component of 1st scale; (j) Detailed component of 3rd scale after denoising; (k) Detailed component of 2nd scale after denoising; (l) Detailed component of 1st scale after denoising. |
对比图 9c和图 10c,我们可以明显看出,曲波变换由于可以在特定方向设定阈值进行去噪,因此在准确去除噪声的同时很好地保留了有用信号.相比之下,WT在去除噪声的同时也造成部分有用信号的损失.
由于实测数据难以确定SNR,因此本文引入均方根误差(RMSE)和平滑度(R)两个参数来定量判别曲波变换和WT的去噪效果.
均方根误差(RMSE)定义为
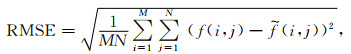
|
(23) |
式中,f为原始信号,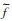
陶珂和朱建军(2012)利用平滑度对一维信号的去噪效果进行了评价,我们将其推广到二维情况并定义平滑度R为
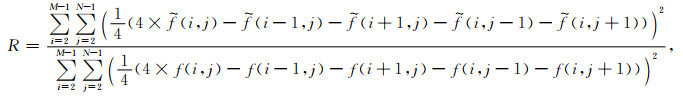
|
(24) |
式中,f为原始信号,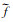
在去噪后的重构信号不失真的前提下,我们认为平滑程度越高去噪效果越好.换句话说,RMSE和R均较小的数据,去噪效果较好.计算表明,针对图 9和10中给出的爱尔兰Knock和Weston地区实测数据,曲波变换和WT去噪后数据的均方根误差RMSE分别为0.3803和0.4414,而平滑度R分别为2.0961×109和5.4840×109.由此可见,曲波变换在保持数据原有形态的基础上,较好地去除了噪声.
本文提出的曲波变换方法面向二维数据,除了对单一时间道的平面数据进行去噪外,还可对多时间道剖面数据进行处理.为此,我们将剖面上各测点对应的各时间道响应作为输入数据进行二维去噪处理.图 11给出加拿大Iroquois Falls地区时间域航空电磁实测dBz/dt(磁感应强度时间导数)去噪结果.本次观测共采集55 off-time时间道.由于发射电流采用半正弦和梯形波两种波形,因此我们将所有时间道数据分为前25道和后30道两组.该测区共有六条测线,每条测线包含1440个测点,间距为5 m.我们选取第一条测线的数据进行去噪试验.图 11给出WT和本文曲波变换去噪的对比结果.由图可以看出:经曲波变换去噪后,局部干扰得到有效压制,各时间道曲线不再出现交叉重叠的反常现象,符合时间域航空电磁信号衰减规律;相比之下,WT去噪结果出现局部过度平滑现象.同时,对比均方根误差RMSE可知,去噪后的数据与原始数据偏差较大.

|
图 11 加拿大Iroquois Falls地区实测数据去噪结果 (a)对应于半正弦波的前25时间道数据去噪结果;(b)对应于梯形波的后30时间道数据去噪结果. Fig. 11 Denoising of survey data from Iroquois Falls, Canada (a) Denoising of the first 25 time channels corresponding to the half-sine transmitting wave; (b) Denoising of the last 30 time channels corresponding to the trapezoidal wave. |
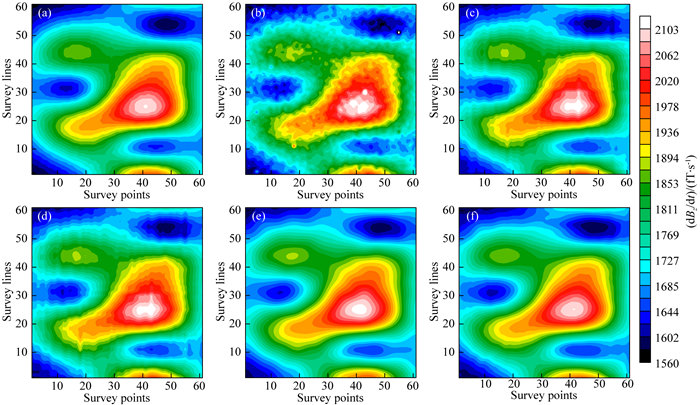
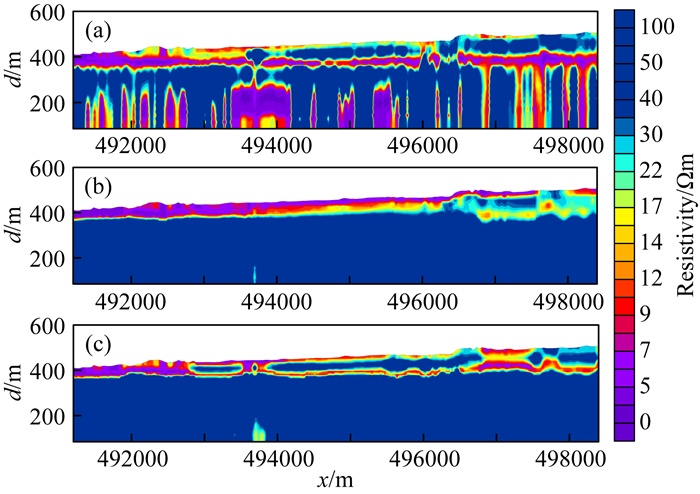
为了更深入了解曲波变换的去噪效果,我们对原始数据及WT和曲波变换去噪后的信号分别进行成像.图 12给出了成像结果.由图可以看出:曲波变换去噪后的数据成像能很好地划分地下电性分界面,特别是两个良导层中间的高阻层得到了有效识别.相比之下,由于WT去噪造成数据过度光滑,地下电性界面难以区分.
|
图 12 加拿大Iroquois Falls地区实测数据成像结果 (a)原始信号成像结果;(b) WT去噪后信号成像结果;(c)曲波变换去噪后信号成像结果. Fig. 12 Imaging results of survey data from Iroquois Falls, Canada (a) Imaging of original signal; (b) Imaging of WT denoised data; (c) Imaging of curvelet transform denoised data. |
本文我们利用曲波变换和Sigmoid阈值函数成功实现了航空电磁数据去噪.较之于传统方法依据噪声的随机性进行加权平均去噪,或者基于信号和噪声频谱成分差异进行去噪(比如SVD和PCA方法),曲波变换的多尺度性使得它可以在各尺度上对信号和噪声进行分离和去除.虽然小波变换也具有多尺度特征,然而其方向参数有限.相比之下,曲波变换方向参数健全,可对复杂二维信号进行有效刻画,同时可对具有一定方向性的噪声(比如调平残差)进行有效去除.引入Sigmoid阈值函数可以平滑地截取曲波系数,进而通过提取部分小值有效系数,可以更完整保留信号中的细节成分.因此,曲波变换结合Sigmoid阈值函数特别适合去除航空电磁数据中的随机噪声和其他具有方向性的残差.理论和实测航空电磁数据处理结果验证了方法的有效性.
致谢 感谢CGG公司前总工Greg Hodges先生和Tianyou Chen博士以及爱尔兰地质调查局提供的实测数据.我们对审稿人和编辑给出的意见和建议表示衷心感谢.
Abma R, Kabir N. 2006. 3D interpolation of irregular data with a POCS algorithm. Geophysics, 71(5): E91-E97. |
Candès E, Donoho D L. 1999. Curvelets:A Surprisingly Effective Nonadaptive Representation for Objects with Edges. Nashville: Vanderbilt University Press: 1-10.
|
Candès E, Donoho D L. 2004. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Communications on Pure and Applied Mathematics, 57(2): 219-266. DOI:10.1002/cpa.10116 |
Candès E, Demanet L, Donoho D, et al. 2006. Fast discrete curvelet transforms. Multiscale Modeling & Simulation, 5(3): 861-899. |
Cao J J, Yang Z Q, Yang Y, et al. 2018. An adaptive seismic random noise elimination method based on curvelet transform. Geophysical Prospecting for Petroleum (in Chinese), 57(1): 72-78, 121. |
Donoho D L, Johnstone J M. 1994. Ideal spatial adaptation by wavelet shrinkage. Biometrika, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
Donoho D L. 1995. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 41(3): 613-627. DOI:10.1109/18.382009 |
Du X Z, Lu C D. 2016-11-09. Singular value decomposition and wavelet analysis-based time-domain aeronautical electromagnetic data denoising method, CN, 106094046A.
|
Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
Li J W, Liu X B, Zhou J H, et al. 2019. A curvelet threshold iteration method based on energy ratio for surface-wave suppression. Oil Geophysical Prospecting (in Chinese), 54(5): 997-1004. |
Li L F, Zhang X C, Zhang H, et al. 2015. Feature extraction of non-stochastic surfaces using curvelets. Precision Engineering, 39: 212-219. DOI:10.1016/j.precisioneng.2014.09.003 |
Qi S H, Liu Q Y, Chen J H, et al. 2016. Attenuation of noise in receiver functions using curvelet transform. Chinese Journal of Geophysics (in Chinese), 59(3): 884-896. DOI:10.6038/cjg20160311 |
Reninger P A, Martelet G, Deparis J, et al. 2011. Singular value decomposition as a denoising tool for airborne time domain electromagnetic data. Journal of Applied Geophysics, 75(2): 264-276. DOI:10.1016/j.jappgeo.2011.06.034 |
Ridsdill-Smith T A, Dentith M C. 1999. The wavelet transform in aeromagnetic processing. Geophysics, 64(4): 1003-1013. DOI:10.1190/1.1444609 |
Sykes M P, Das U C. 1998. Removal of herringbone effects from AEM data maps using the Radon transform. Exploration Geophysics, 29(1-2): 92-95. DOI:10.1071/EG998092 |
Tao K, Zhu J J. 2012. A comparative study on validity assessment of wavelet de-noising. Journal of Geodesy and Geodynamics (in Chinese), 32(2): 128-133. |
Wang L P. 2006. Plancherel theorem in L2(Rn). Journal of the Central University for Nationalities (Natural Sciences Edition) (in Chinse), 15(4): 334-338. |
Ying L X, Demanet L, Candès E. 2005.3D discrete curvelet transform.//Proceedings of SPIE 5914, Wavelets XI. San Diego, California, United States: SPIE, 351-361.
|
Zhang H L, Liu T Y, Zhang Y C. 2010. High order correlation based dip angle scanning noise elimination method in curvelet domain and space domain. Oil Geophysical Prospecting (in Chinese), 45(2): 208-214. |
Zhu K G, Wang L Q, Xie B, et al. 2013. Noise removal for airborne electromagnetic data based on principal component analysis. The Chinese Journal of Nonferrous Metals (in Chinese), 23(9): 2430-2435. |
曹静杰, 杨志权, 杨勇, 等. 2018. 一种基于曲波变换的自适应地震随机噪声消除方法. 石油物探, 57(1): 72-78, 121. |
杜兴忠, 陆从德. 2016-11-09.基于奇异值分解和小波分析的时间域航空电磁数据去噪方法.中国, 106094046A.
|
李继伟, 刘晓兵, 周俊骅, 等. 2019. 基于能量比的Curvelet阈值迭代面波压制. 石油地球物理勘探, 54(5): 997-1004. |
齐少华, 刘启元, 陈九辉, 等. 2016. 接收函数的曲波变换去噪. 地球物理学报, 59(3): 884-896. DOI:10.6038/cjg20160311 |
陶珂, 朱建军. 2012. 小波去噪质量评价方法的对比研究. 大地测量与地球动力学, 32(2): 128-133. |
王丽萍. 2006. 平方可测空间的Plancherel定理. 中央民族大学学报(自然科学版), 15(4): 334-338. |
张恒磊, 刘天佑, 张云翠. 2010. 基于高阶相关的Curvelet域和空间域的倾角扫描噪声压制方法. 石油地球物理勘探, 45(2): 208-214. |
朱凯光, 王凌群, 谢宾, 等. 2013. 基于主成分分析的航空电磁数据噪声去除方法. 中国有色金属学报, 23(9): 2430-2435. |
 2020, Vol. 63
2020, Vol. 63


