2. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室, 北京 100083;
3. 中国石油大学(华东)石油工程学院, 青岛 266580
2. State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology(Beijing), Beijing 100083, China;
3. School of Petroleum Engineering, China University of Petroleum(East China), Qingdao 266580, China
我国有近3×106 km2的碳酸盐岩分布,约占陆上国土面积的1/3,其中塔里木盆地、四川盆地、鄂尔多斯盆地和华北地区广泛发育,已经成为极具潜力的油气勘探区(江怀友等,2008).然而,碳酸盐岩油气藏储集空间比较特殊,具有类型多、次生变化明显、非均质性强、以及成岩作用复杂等特点,使得碳酸盐岩储层地球物理预测成为一项极富挑战的工作(Vanorio et al., 2008;Xu and Payne, 2009; Zhao et al., 2013a).
在对储层进行预测时,需要综合地震、测井、以及实验室岩心测量数据以分析与解释储层的地质特征以及油气聚集性.通常而言,地震数据频段在1~100 Hz之间,声波测井在104 Hz频率附近对原位地层岩石属性进行测量,而实验室纵横波速度的测量是在超声频率(106 Hz)下完成.岩石骨架的非弹性和孔隙流体的存在会导致波通过流体饱和岩石时,在较宽的频带和尺度范围发生速度频散与衰减(Müller et al., 2010;Pride et al., 2004;Zhao et al., 2020).这种波传播的频率依赖性使得不同频率范围内的测量结果会出现差异.因此,深入理解不同频段的波传播物理机制,并综合利用这些不同频率范围内的数据进行碳酸盐岩储层的刻画是非常重要的(Sams et al., 1997;Zhao et al., 2017).
从实验的角度,对于储层岩石进行跨频段速度频散与衰减测量是研究相应物理机制的基础.近年来,国内外学者在新兴的低频岩石物理测量领域进行了大量的探索与研究.Wang等(2012)以及Zhao等(2013b, 2015)在Harris等(2005)的工作基础上,利用差分共振声谱技术开展了低频条件下岩石弹性性质的研究.中国石油勘探开发研究院与休斯顿大学合作开发了低频应力应变等岩石物理测量设备,并完成了四川盆地须家河组致密砂岩(杨志芳等,2014)、阿姆河右岸麦捷让地区灰岩(巴晶等,2013)等的宽频带弹性性质测量及研究,验证了修正White部分饱和模型对地震频段速度预测的适用性,并表明采用双重孔隙介质波动理论建立的多尺度岩石物理解释量板对于各频段数据具有良好的解释能力.中国石油大学(北京)同科罗拉多矿业学院合作建立成低频应力应变岩石物理测量设备后,未晛等(2015a,b)研究了孔隙流体饱和度对砂岩弹性性质的影响;Yin等(2017)通过控制饱和流体类型、饱和度、温度、以及有效压力等实验条件,对致密砂岩的速度频散与衰减的影响因素进行了详尽的研究,在此基础上利用渗流机制和喷射流机制相结合的岩石物理理论对实验数据进行了解释.Sun等(2018)对实验仪器进行了数值模拟,分析了共振现象对于低频应力应变实验的影响,并对应力应变低频设备的机械结构做了相应的改进.
然而,总的来看,目前国际上已发表的针对碳酸盐岩的低频实验测量结果较为稀少.Adam等(2006)在3~3000 Hz和1 MHz频率测量了11块孔隙度与渗透率均递增的中东地区碳酸盐岩,将实验数据与Gassmann流体替换结果进行了对比分析.Adam等(2009)分析了碳酸盐岩在地震频段和超声频段得到的体积模量、杨氏模量、纵波速度以及横波速度与衰减之间的关系,并得到了饱和不同流体(盐水或烃)时的衰减规律.Mikhaltsevitch等(2016)在0.1~120 Hz频段内测量了两块各向同性Savonnieres碳酸盐岩在完全饱和水和癸烷条件下的速度频散与衰减,结果表明样品从地震到超声频段没有明显频散,且饱和不同流体的情况同Gassmann预测的结果相同.Borgomano等(2017)在0.01~10 Hz频段范围内测量了一块含粒间孔与粒内孔的孔隙灰岩样品在饱和不同流体时的速度频散与衰减,得到与全局流动有关的排液、不排液两种流体状态的过渡区,由于没有观测到更高频率的过渡区域以及样品的裂缝型孔隙结构较少,因而排除了喷射流机制的影响.李闯等(2020)运用喷射流模型对一块含裂缝的致密碳酸盐岩频散测量结果进行了描述.Li等(2020)定量化测量了致密砂岩和碳酸岩样品在地震频带(1~1000 Hz)的弹性参数随频率及饱和度的变化规律,并分析了流体饱和度、流体空间分布、孔隙结构类型等对波频散和衰减的影响.
综合国内外跨频段实验测量的研究现状,已有的碳酸盐岩样品测量数据未能充分体现孔隙结构类型的不同对岩样速度频散和衰减规律的影响,从而相应机制的细致研究较少,并导致目前不同孔隙类型碳酸盐岩储层的频散与衰减模型缺乏足够的实验数据验证.本文对不同孔隙类型碳酸盐岩样品进行跨频段岩石物理测量,并试图建立相应的多孔隙类型岩石物理模型来解释碳酸盐岩完全饱和流体时的模量频散与衰减测量结果,从而增强对碳酸盐岩储层速度频散与衰减特征的认识,提升针对碳酸盐岩的储层预测与流体识别水平.
1 跨频段测量装置和数据处理图 1为跨频段(1~1000 Hz, 106 Hz)岩石物理测量所使用的装置示意图.为了充分模拟地下岩石所处的环境条件,并研究流体流动相关的岩石速度频散和衰减,跨频段岩石物理装置需要对岩样的围压、孔压、流体类型、流体饱和度等条件进行控制.

|
图 1 跨频段弹性参数测量系统示意图 (a)低频测量设备;(b)应变片在样品上的分布;(c)超声测量设备. Fig. 1 Cross-frequency band elastic parameters measurement system (a) Low-frequency measurement instrument; (b) Strain gauge alignment on sample; (c) Ultrasonic measurement instrument. |
在围压控制方面,低频及超声测量实验都在承载压力强度高达300 MPa的高压容器中进行.围压由氮气提供,装置单元由空气压缩机、气体增压装置和压缩氮气瓶组成,氮气经由增压泵压缩后注入到容器中,可为样品提供最大80 MPa的均匀围压,满足大部分深层储层岩石物理测量与研究的需求.在高压容器内部装有精度为0.01 MPa的压力传感器,用来监测样品所受的围压.
在孔压及孔隙流体控制方面,使用了独立于围压的控制装置,可以实现对样品的流体饱和与驱替.不同的流体存储在中间容器中,由高精度Teledyne ISCO柱塞泵驱动并经由流体管线注入到岩石样品中.Teledyne ISCO柱塞泵的流体压力控制精度为0.001 MPa,以水为介质由恒压与恒流两种模式控制流体注入,从而决定岩心的饱和状态以及相应的孔隙压力.此外,为了有效隔绝岩石外部的围压气体和内部的孔隙流体,在样品外包裹了一层环氧树脂来对样品表面进行密封.
高频超声测量示意图见图 1c,该测量技术已经较为成熟,因此下面主要介绍低频部分(图 1a)的原理及过程.在设定好围压、孔隙压力、以及流体饱和状态后,整套系统在LabView平台上实现信号的激发、数据的采集和处理.在LabView程序中输入采集参数后,电脑将控制函数发生器发出特定频率和幅度的正弦信号,该电压信号被输入给功率放大器并转化为具有所需功率的简谐波形式的信号,驱动振动台给岩石试样和标准铝样施加一个正弦模式振动,使得被测样品及标准铝块产生轴向与径向应变.
应变信号由粘贴在被测岩石样品及标准铝块上的应变片获取,并以电压信号的形式由信号采集卡完成采集,具体实现过程如下:附着在样品和标准铝表面的应变片接入惠斯通电桥双臂动态检测应变幅值的大小,惠斯通电桥将应变幅值转换为电压波形并输入到信号增益放大器,被增益放大的波形信号由24位多通道AD采集卡采集获取.与此同时,来自函数发生器的原始激励电压简谐波信号也被读入AD采集卡,用作锁定放大器中的参考信号.所有信号在输入到AD采集卡之后转化为数字信号,最终被发送到LabView程序以进行实时处理、记录和显示.使用锁相放大算法获取每个通道(每个通道为附着在试件上的一对应变片组成)的动态应变的幅度和相位后,即可计算测量样品的杨氏模量、泊松比和逆品质因子.
为了获得被测岩石样品的频散及衰减,实际使用的试件由被测岩石样品与已知弹性参数的参考标准样品(本实验选择铝块)制作而成,如图 1b所示,被测岩石样品居中,两端为已知弹性性质(EAl)的参考标准样品,被测标准样品与参考标准样品之间由固化剂连接.动态振动实验中,整个试件(被测样品与参考标准样)受到的应力相等,因此通过测量参考标准样品上的纵向应变εAl,以及被测岩石样品表面的纵、横向应变εrv和εrh,就可以获得不同频率时被测岩石样品的杨氏模量Er与泊松比ν,如公式(1),(2)所示:

|
(1) |
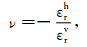
|
(2) |
待测岩石样品的纵波速度VP与横波速度VS可以由公式(3),(4)获得,其中ρr为测量岩石样品的密度.
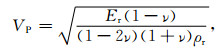
|
(3) |
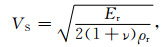
|
(4) |
衰减通常用逆品质因子Q-1表示(Mavko et al., 2020),即
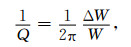
|
(5) |
W是每周期内系统存储的弹性应变能,ΔW是每周期内系统消耗的能量.实验中,杨氏模量逆品质因子可以由应变片记录到的标准样品相位θstdv与岩石样品相位θsamplev的相位差求得(O′Connell and Budiansky, 1978):
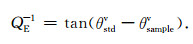
|
(6) |
样品制备的步骤具体为:
(1) 标准测量样品制作.对采集的岩石样品进行钻取与切磨,得到两端光滑平整且直径为3.8 cm、长度在5~7 cm之间的圆柱形岩心样品.为使样品既满足高频超声测量也满足基于“应力应变”的低频岩石物理测量,所钻取的碳酸盐岩样品上下两端面磨平至平行度小于0.01 mm.
(2)“干燥”岩石准备.将钻取好的符合测量仪器规格的岩石样品置于有机溶剂中以除去孔隙中的残余油和盐份,然后置于烘箱中烘干,再将烘干后的样品在空气中放置24 h以上,得到和空气湿度一致的“干燥”岩石.
(3) 样品基本物性参数测量.测量岩心的长度(误差±0.02 mm);称量岩心的质量(误差±0.01 g).用氦气为介质的孔渗测定仪测量岩石的孔隙度及渗透率参数.
(4) 样品孔隙结构微观分析.将制备好的岩心进行CT扫描成像;取岩心顶、底部切割掉的一部分制作成普通薄片及铸体薄片进行镜下岩性鉴定.薄片镜下定名与分类可以确定碳酸盐岩矿物成分、孔隙类型和面孔率等特征.
(5) 样品矿物分析.利用部分岩心碎屑进行X射线衍射矿物分析,得到被测岩石样品的矿物组分及各矿物含量信息.
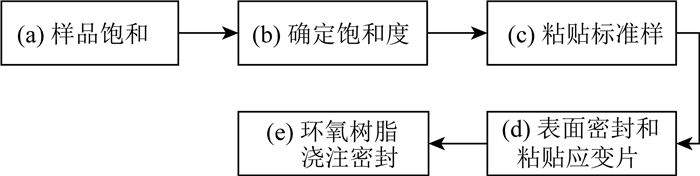
完成样品的制备与基础物性参数测量工作后,开始跨频段弹性性质测量工作.首先对样品进行低频测量,低频实验测量过程分成5个步骤,流程如图 2a-e所示:
|
图 2 岩心制备流程图,顺序为(a)-(e) Fig. 2 Flow chart of core preparation (a)-(e) |
(1) 样品流体饱和.由于本批次碳酸盐岩岩心孔渗较低,不能采用流体驱替的方式进行流体饱和,因此实际将样品浸泡在甘油中进行抽真空后密封加围压饱和.为使岩样达到完全饱和状态,抽真空加压的过程不低于48 h,同时对甘油进行加热以降低黏度使其更易进入岩石孔隙.
(2) 样品饱和度计算.将饱和后的样品称重,和干燥时的样品质量对比后结合孔隙度计算出饱和度,确保样品完全饱和,即孔隙体积对应的流体质量等于称重前后质量差.
(3) 样品标准铝块贴合.在确定样品两端面平整且平行的前提下将两端各粘贴一个标准块,并保证样品和标准块的外径相同且同心(如图 3c所示).

|
图 3 岩心制备实物图,顺序为(a)-(e) Fig. 3 Pictures of core preparation process (a)-(e) |
(4) 样品密封及应变片贴合.为了防止岩心中饱和流体流失,同时也为保证应变片粘贴在一个光滑平整的表面,须在岩心表面涂抹一层环氧树脂胶.在密封完成后,岩心处于不排液的状态.接下来在合适的位置粘贴好应变片并焊接导线与插针,最终完成应变片的粘贴步骤.为了满足根据公式(1)、(2)计算样品杨氏模量、泊松比及衰减因子的要求,需在岩心中间部分粘贴垂直方向和水平方向应变片4对(8片),在上下的标准铝样上沿样品纵向各粘贴两对应变片,如图 1b所示.
(5) 浇筑环氧树脂密封层.将样品整体放入模具并注入环氧树脂,最终形成环氧树脂密封层.密封层的作用是将样品内部的流体和外界围压气体(氮气)隔绝开来.
在完成低频测量后,拆除岩心以外的环氧树脂、标准样等部件,对样品再次进行洗油、干燥,然后进行高频超声测量.为保证测量精度,选用超声测量设备AutoLab 1000进行测量,该设备所使用的纵波、横波换能器的主频均为1 MHz.我们测量了碳酸盐岩样品在干燥条件下的变围压超声速度,测量的起始与终止压力分别为0 MPa与50 MPa,压力间隔为5 MPa.为保证稳定的围压施加,两个围压的压力施加间隔为30 min.
表 1为本实验研究碳酸盐岩样品的岩石物理参数表.岩石的矿物组分由X射线衍射矿物分析得到,岩石基质的体积模量和剪切模量由Voigt-Reuss-Hill平均计算得到.
|
|
表 1 碳酸盐岩样品岩石物理数据 Table 1 Rock physics data of carbonate samples |
碳酸盐岩孔隙类型主要为粒间孔、粒内孔、网格状孔及遮蔽孔、晶间孔、溶孔、洞穴、沟槽(溶沟)和裂缝等(Choquette and Pray, 1970).孔隙类型决定了油气运移和储量,而且决定了碳酸盐岩的地震特性.为了便于岩石物理建模和实际应用,根据不同孔隙类型对弹性性质影响的大小,把碳酸盐岩储层孔隙类型简化为:孔隙、孔洞和裂缝.再根据其含量的组合,进一步将储层划分为:孔隙型、裂缝型、裂缝-孔隙型和裂缝-孔洞型(马永生等,1999).从岩石物理岩心尺度的实验角度,根据孔隙类型描述的资料,最终我们将采集的样品划分成为几乎不含孔隙的致密型(图 4a),与孔隙特征明显的裂缝型(图 4b)、裂缝-孔隙型(图 4c)、孔洞型(图 4d)三类.后续的研究便是针对具有不同孔隙类型的碳酸盐岩样品进行低频岩石物理实验测量,并对它们表现出的不同岩石物理响应特征及其机理进行分析.

|
图 4 岩石样品铸体薄片与扫描电镜照片 (a)灰岩15#铸体薄片(致密型);(b)灰岩12#铸体薄片(裂缝型);(c)灰岩13#铸体薄片(裂缝-孔隙型);(d)白云岩2#铸体薄片(孔洞型);(e)人工碳酸盐岩11#扫描电镜照片(人工孔洞型)(Wang et al., 2015b). Fig. 4 Thin sections and scanning electron microscope image of carbonate samples (a) Thin section of limestone 15# (tight); (b) Thin section of limestone 12# (crack-type); (c) Thin section of limestone 13# (crack-pore-type); (d) Thin section of dolomite sample 2# (pore-type); (e) Scanning electron microscope image of artificial carbonate 11# (artificial pore-type) (Wang et al., 2015b). |
由于天然碳酸盐岩的孔隙结构具有更加复杂的形态,为明确孔隙结构类型对跨频段岩石物理测量响应的影响,在收集到的天然样品外,本次实验研究中制作了一块孔隙结构类型与2#天然碳酸盐岩相近的人工碳酸盐岩样品11#.该人工碳酸盐岩岩样由天然碳酸盐岩岩屑颗粒和环氧树脂胶结剂制成(王子振等,2015),其孔隙结构扫描电镜结果如图 4e所示(岩石骨架参数见表 1).该样品在制备时设计成含有溶孔与粒间孔,并从图中可以观察到该样品的孔隙结构类型与设计一致,因此认为该人工样品可代表孔洞型的碳酸盐岩样品.需要指出的是,由于制作人工碳酸盐岩样品基质用到的环氧树脂的体积模量与剪切模量相比岩屑更小(Wang et al., 2015a),本人工样品的体积模量和剪切模量只近似为天然样品的一半.
本次实验中,受实验工艺的限制,一个样品仅进行一次测量.在实验条件设计上,15#样品在干燥条件下测量,其余的2#、11#、12#、13# 4块样品均在完全饱和甘油的条件下测量.甘油的密度与黏度参考Volk和Kähler(2018)得到,模量由实验室测量得到,如表 2所示.
|
|
表 2 孔隙流体物理属性 Table 2 Physical properties of the pore fluids |
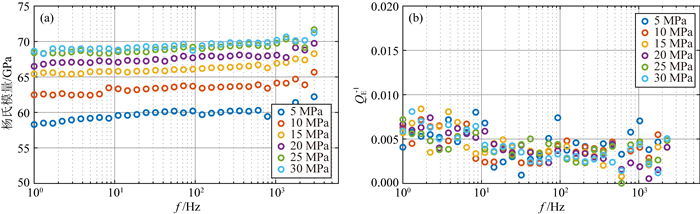
图 5展示了致密碳酸盐岩15#样品在干燥条件下的低频测试结果.在高围压下该样品杨氏模量表现出小到可以忽略的频散,整体呈现近似于岩石基质的性质;另外杨氏模量的衰减QE-1在1~1000 Hz的频带范围内小于0.01.
|
图 5 致密型石灰岩15#干燥条件下的低频测量结果:杨氏模量(a)及其衰减值(b)的围压和频率依赖关系 Fig. 5 Measurement results of frequency dependent (a) Young′s modulus, (b) Young′s attenuations of dry tight limestone 15# at different confining pressures |
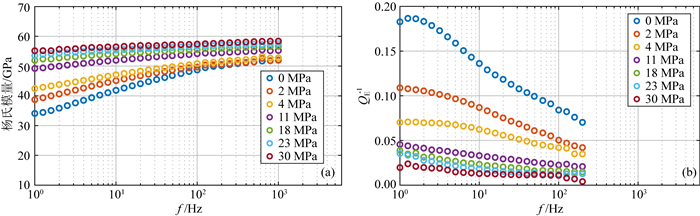
裂缝型样品12#在完全饱和甘油状态下测量.从测量的结果(图 6)可以看到,在0 MPa的围压下,样品的杨氏模量在测量频率段(1~200 Hz)内表现出近47.1%的频散(200 Hz时杨氏模量相对1 Hz时杨氏模量的增加量与1 Hz时杨氏模量的比值),当围压增加到30 MPa时杨氏模量的频散减小到4.6%,仍然表现出一定的频散.当围压从0 MPa增至11 MPa,频率在1 Hz的杨氏模量增加了44.3%,频散的幅度对于围压非常敏感;当围压从18 MPa增至30 MPa,1 Hz的杨氏模量仅增加了6.2%,敏感性降低.由图 6b的衰减峰位置可知,0 MPa时的特征频率在1.25 Hz附近;随着围压的增大,衰减的幅度减小,同时特征频率向着低频方向移动并逐渐移出了低于1 Hz的测量频带范围之外.
|
图 6 裂缝型石灰岩12#在甘油饱和条件下的低频测量结果:杨氏模量(a)及其衰减值(b)的围压和频率依赖关系 Fig. 6 Measurement results of frequency dependent (a) Young′s modulus, (b) Young′s attenuations of glycerol saturated crack-type limestone 12# at different confining pressures |
图 7为裂缝-孔隙型石灰岩13#在甘油饱和条件下的低频测量结果.在1~1000 Hz频段范围内,杨氏模量随着频率的升高而升高,另外,由于该样品同时存在较软的裂缝和较硬的孔洞,可以看到杨氏模量的衰减上出现了两个特征峰值.一个出现在低频1~2 Hz之间,另一个出现在70~110 Hz之间,两个衰减峰的幅度都随着围压的增大而减小.处于1~2 Hz频段的衰减峰值在2 MPa围压下的幅值较大,但随着围压增大,相较于70~110 Hz之间的衰减峰数值减小得更快,在30 MPa时几乎消失;而在70~110 Hz频段里的衰减峰值随着围压减小较慢,在10 MPa之后几乎保持不变.在围压增至30 MPa时,衰减随频率变化曲线只有一个独立的峰值存在且该衰减特征频率在80 Hz附近,而模量的频散曲线则呈现“平缓-上升-平缓”的形状.

|
图 7 裂缝-孔隙型石灰岩13#在甘油饱和条件下的低频测量结果:杨氏模量(a)及其衰减值(b)的围压和频率依赖关系 Fig. 7 Measurement results of frequency dependent (a) Young′s modulus, (b) Young′s attenuations of glycerol saturated crack-pore-type limestone 13# at different confining pressures |
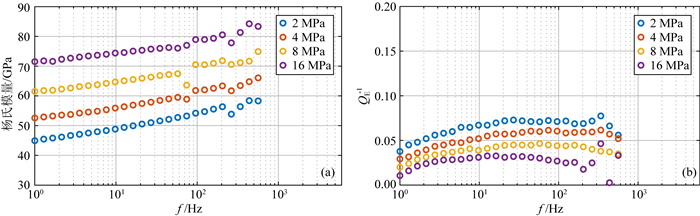
图 8为天然孔洞型白云岩2#完全饱和甘油的低频测量结果.综合分析杨氏模量与衰减随频率的变化特征,可以发现特征频率处在20 Hz至100 Hz之间,随着围压的增大杨氏模量的频散程度与杨氏模量的衰减幅度均减小,且特征频率向着低频移动,在围压16 MPa时特征频率移动至30 Hz附近.
|
图 8 天然孔洞型白云岩2#在甘油饱和条件下的低频测量结果:杨氏模量(a)及其衰减值(b)的围压和频率依赖关系 Fig. 8 Measurement results of frequency dependent (a) Young′s modulus, (b) Young′s attenuations of glycerol saturated dolomite 2# at different confining pressures |
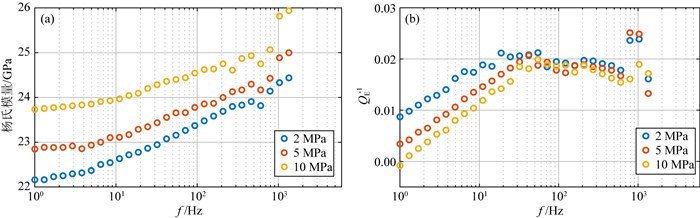
最后,对于孔洞型人工样品11#的低频测量,图 9显示衰减幅值较小且特征频率在100 Hz附近,随着围压的增大衰减数值小幅减小.与天然孔洞型样品2#的测量结果相比,人工样品11#特征频率的位置出现在与之相近的(30~100 Hz)的频段范围内,同时与天然裂缝-孔隙型的碳酸盐岩样品12#(图 4c、图 7)的第二个衰减特征频率位置相近.
|
图 9 人工孔洞型碳酸盐岩11#在甘油饱和条件下的低频测量结果:杨氏模量(a)及其衰减值(b)的围压和频率依赖关系 Fig. 9 Measurement results of frequency dependent (a) Young′s modulus, (b) Young′s attenuations of glycerol saturated artificial pore-type carbonate 11# at different confining pressures |
在已有的描述流体完全饱和岩石的弹性模量频散与衰减的岩石物理理论中,喷射流模型较为常用.在基于喷射流假设的模型中,Gurevich等(2010)推导了在双孔隙(软孔隙ϕC,硬孔隙ϕS)结构假设下,岩石骨架弹性性质随频率与压力变化的理论公式,如下所示:
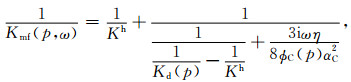
|
(7) |
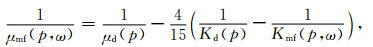
|
(8) |
其中,ω为圆频率,η为流体黏度,αC为软孔隙特征纵横比,Kd(p)、μd(p)和ϕC(p)分别为有效压力p下的干燥岩石体积模量、剪切模量和软孔隙孔隙度;而Kh为岩石骨架在高有效压力作用下所有软孔隙闭合而使岩石骨架仅含有硬孔隙时的等效基质体积模量.公式(7)、(8)中Kh、Kd(p)、μd(p)这3个量可以通过干燥条件超声速度-压力实验获取.上述具有双孔隙(软孔隙,硬孔隙)结构岩石(图 10a)是“湿骨架模量”(或称为“修改的骨架模量”).将此“湿骨架模量”代入Gassmann方程,此时原始Gassmann方程中的Kdry由Kmf(p, ω)替换,再代入岩石基质模量K0与流体体积模量Kf,饱和流体岩石的体积模量Ksat与剪切模量μsat的计算公式变为
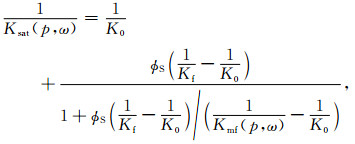
|
(9) |
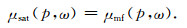
|
(10) |
|
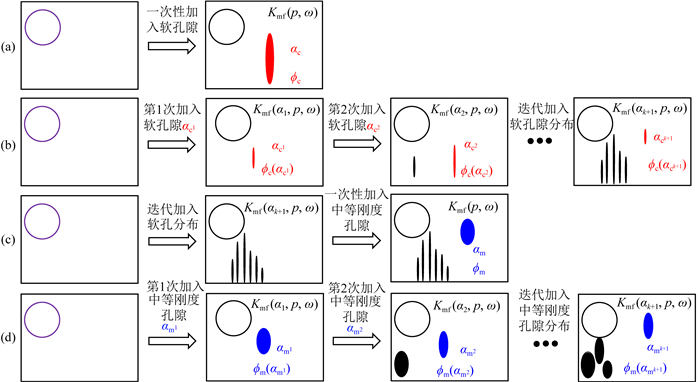
图 10 岩石“湿骨架”建模流程图 (a)含单一纵横比软孔隙的基本情况;(b)含一定分布的软孔隙的裂缝型情况;(c)含一定分布的软孔隙及单一中等刚度孔隙的裂缝-孔隙型情况;(d)含一定分布的中等刚度孔隙的孔洞型情况. Fig. 10 Workflow of building "wet-frame" of rock (a) Basic case with single aspect ratio; (b) Crack-type case with compliant pore aspect ratio distribution; (c) Crack-pore-type case with compliant pore distribution and single intermediate pore; (d) Pore-type case with intermediate pore distribution. |
邓继新等(2015)在Gurevich等(2010)基于单一软孔隙纵横比“湿骨架”的基础上,考虑岩石中所有的软孔隙的纵横比呈一定范围分布的状态,而不是一个单一固定值,对原始喷射流模型进行了改进.该模型以α=0.01作为软硬孔隙的分界,在单一硬孔隙纵横比的基础上,迭代加入具有不同孔隙纵横比的软孔隙,从而可以考虑软孔隙纵横比具有一定分布范围的饱和流体岩石中喷射流的综合效应.改进模型能够得到在地震频段中随频率近似线性递增的频散趋势,这与多数低频测量数据呈现的趋势较为吻合.这种思路更加符合真实的喷射流机理,其中“湿骨架模量”迭代过程如下:
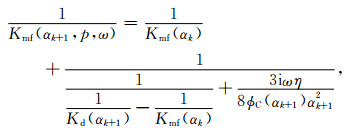
|
(11) |
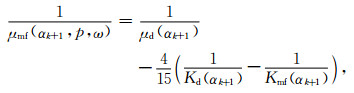
|
(12) |
式中各参数的定义与公式(7)及(8)一致.叠加建模的过程为:在以硬孔隙为背景的基质中逐次加入某一含量和纵横比软孔隙,考虑其喷射流机制的影响,并作为下次计算的背景基质(图 10b黑色部分).叠加直至将反演得到的所有软孔隙按照其对应含量加入到背景基质中,得到最终岩石中的喷射流效应.例如,第k次加入软孔隙αk所计算的Kmf和μmf,将视作第(k+1)次加入软孔隙的Kh和μh;在Kh和μh基础上加入软孔隙即得第(k+1)次的Kmf和μmf,而式中各个软孔隙纵横比αk及其对应的软孔隙度ϕC(αk)采用David和Zimmerman(2012)的方法,根据速度-压力数据及等效介质理论反演得到.图 10b描述了基于此思路对裂缝型岩石的“湿骨架”的建模过程.
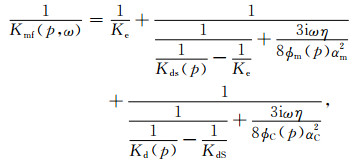
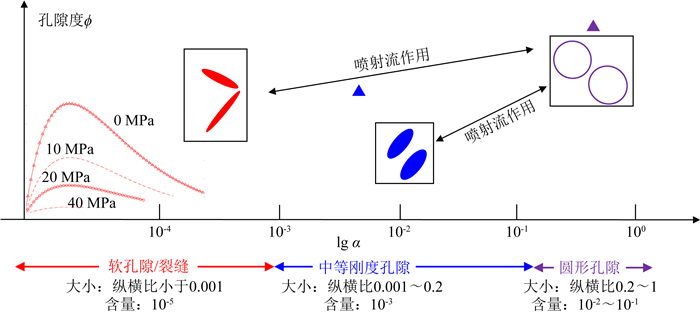
然而Eberhart-Phillips等(1989)和Gurevich等(2010)对于实验数据的分析表明,硬孔隙对于岩石可压缩性随压力变化的贡献在0 MPa到50 MPa压力范围也是显著的.这意味着硬孔隙类型孔隙并不是不会随着围压的改变而改变,硬孔隙整体的可压缩性大于只含有球形或圆形孔隙情况下的可压缩性.所以对于孔隙类型更加复杂的岩石,仅仅考虑用单一纵横比表征硬孔隙也不能全面地反映孔隙结构特征对骨架弹性性质的影响.de Paula(2012)分析表明除了圆形孔隙之外,硬孔隙包含孔隙纵横比小于0.2的部分,进而将硬孔隙ϕS分为两部分:特征纵横比接近1的圆形孔隙ϕe,以及特征纵横比在0.001~0.2范围的中等刚度孔隙ϕm,于是有ϕ=ϕe+ϕm+ϕc.Xu和Payne(2009)在针对碳酸盐岩构建Xu-Payne模型时,将孔隙分成了四类:含黏土的孔隙、粒间孔、微裂隙、硬孔隙(圆形孔隙),从等效介质模型角度使得模型预测数据与实际测量数据更加吻合.因此当进行频散理论建模时,对于不含黏土的情况,根据孔隙类型将微裂缝、粒间孔和硬孔隙分别对应软孔隙(ϕC)、中等刚度孔隙(ϕm)、圆形孔隙(ϕe)也认为是合理的.如图 11所示,当波传播时,中等刚度孔隙与软孔隙分别与圆形孔隙之间存在喷射流机制,de Paula等(2012)根据公式(7)进行拓展后,提出了双尺度喷射流的估计模量计算方法:
|
(13) |
|
图 11 软孔隙分布(红色曲线)、中等刚度孔隙(蓝色三角)与圆形孔隙(紫色三角)相应尺寸与含量示意图 Fig. 11 Schematic diagram of the size and volume of the compliant pore aspect ratio distribution (red curve), intermediate pores (blue triangle) and equant pores (purple triangle) |
其中Kds(p)为不包含软孔隙时随压力变化的骨架模量,Ke是只含有纵横比接近于1的圆形孔隙的骨架模量,KdS是包含圆形孔隙和中等刚度孔隙时候的骨架模量.
公式(13)相当于将公式(7)的Kh分解成为了圆形孔隙与中等刚度孔隙两部分.当同时考虑软孔隙分布以及中等刚度孔隙时,先将由高频速度-压力曲线计算得到的软孔隙纵横比分布加入到骨架模量中,再根据公式(13)将中等刚度孔隙加入到“湿骨架”中.基于此思路的裂缝-孔隙型岩石“湿骨架”的建模过程由图 10c描述.同样的思路,针对含有溶孔与粒间孔的孔洞型岩石建模时,也可以根据公式(11)(12),将一定分布的中等刚度孔隙加入到含有圆形孔隙的骨架模量中,如图 10d描述.最后可通过Gassmann方程(9)(10)得到完全饱和岩石的频散曲线.
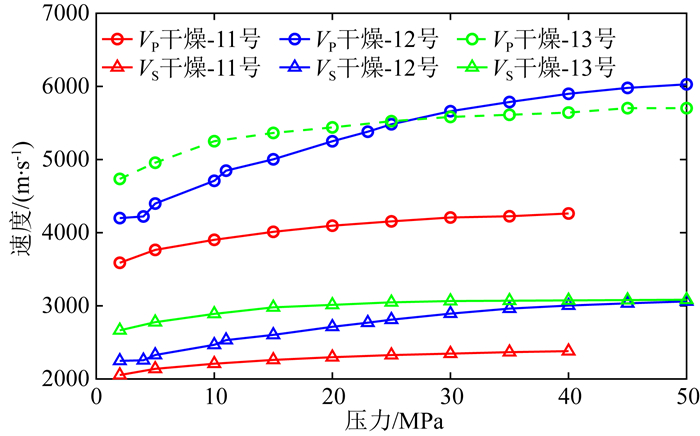
根据实验测量结果的特征,对于11#孔洞型样品、12#裂缝型样品采用考虑孔隙分布的模型进行建模,13#裂缝-孔隙型样品采用三种类型的孔隙模型进行建模.3块样品对应的干燥条件下的纵横波速度随围压的变化数据如图 12所示.样品12#、13#、11#岩石物理建模所用的孔隙分布如图 13所示,其中图 13a,b是用David和Zimmerman(2012)的方法计算得到的12#与13#的软孔隙分布;图 13c为13#建模所用的中等刚度孔隙参数,图 13d为11#建模所用到的服从正态分布的中等刚度孔隙.
|
图 12 样品11#、12#、13#干燥条件超声速度随压力变化 Fig. 12 Pressure dependence of ultrasonic velocities of sample 11#, 12#, 13# under dry condition |

|
图 13 各个压力下模型计算时所使用的孔隙参数 (a) 12#样品软孔隙分布;(b) 13#样品软孔隙分布;(c) 13#样品中等刚度孔隙;(d) 11#样品中等刚度孔隙分布. Fig. 13 Pore distribution parameters for dispersion modeling of samples under different pressures (a) Compliant pore aspect ratio distribution of 12#; (b) Compliant pore aspect ratio distribution of 13#; (c) Intermediate pore aspect ratio of 13#; (d) Intermediate pore aspect ratio distribution of 11#. |
图 14为裂缝型样品12#杨氏模量的频散与衰减的实验和模型计算结果的对比.其中的离散点是实验测量结果,虚线是考虑软孔隙分布喷射流模型的计算结果.该样品的铸体薄片结果显示出主要孔隙结构为裂缝,由于围压增加过程中,岩石结构发生的变化主要体现在裂缝的逐渐闭合,同时样品模量的频散与衰减数值产生较大幅度的降低,可以推断该样品表现出的频散与衰减为裂缝所主导.作为对比,模型得到频散和衰减的特征频率都在1 Hz以下,模型计算的频散与衰减程度小于实验测量结果.从杨氏模量的数值上来看,2 MPa与4 MPa的实验结果高于模型计算结果,而在围压为23 MPa与30 MPa时,模型计算结果高于实验测量结果.随围压的增大,模型计算和实验测量的频散和衰减曲线都呈现减弱趋势.对于该裂缝型样品,以考虑软孔隙分布的喷射流模型进行建模能够一定程度反映实验数据的规律特征.

|
图 14 裂缝型样品12#的(a)杨氏模量与(b)杨氏模量衰减测量与模型计算结果对比 Fig. 14 Comparison of (a) Young′s modulus and (b) Young′s modulus attenuation of crack-type carbonate 12# with rock physics model |
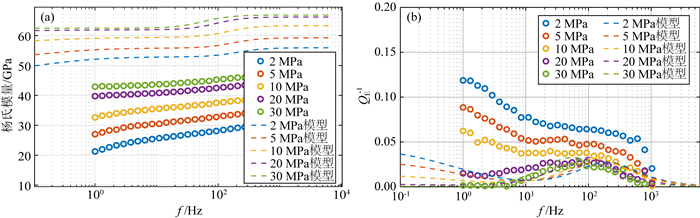
图 15为裂缝-孔隙型13#样品杨氏模量的频散与衰减的实验和模型计算结果间的对比.可以注意到不论频散理论模型还是测量得到的衰减结果中都出现了两个不同位置的峰值,且都随着围压的增大而减小并同时向低频方向移动.低频段1~2 Hz的衰减峰呈现了和裂缝型碳酸盐岩12#相同的规律,即随围压增大显著降低,可以认为是由裂缝主导的衰减.50~200 Hz之间也出现了额外的衰减的峰值,仅靠单孔隙或软孔隙分布的模型无法解释,推断可能存在着两种尺度的喷射流作用.当定义了三种孔隙类型之后,该实验数据趋势可以用软孔和高纵横比圆孔隙,以及软孔和中等刚度孔隙之间的喷射流机制来进行描述:在观测频段中,低频段(1 Hz)的衰减峰与纵横比较小的裂缝(软孔隙)相关,较高频段(100 Hz)的衰减峰与纵横比较大中等刚度孔隙相关.中等刚度孔隙本身和其主导的频散与衰减受到围压的影响并不如裂缝(软孔隙)主导的显著.由从实验和模型的对比结果来看,在低围压下,模型计算得到的模量结果高于实验结果,而随着围压的增大,实验和模型计算得到的频散程度和衰减值更加接近.实验数据中两种尺度孔隙对应的两个特征频率分别为100 Hz与102 Hz,相差两个数量级,而理论模型计算结果得到的两种尺度孔隙对应的特征频率分别为10-1 Hz与102 Hz,相差三个数量级,未能完全重合.但总的来看,模拟结果可以在一定程度上来解释裂缝-孔隙岩石饱和高黏度流体后的频散与衰减的特征.
|
图 15 裂缝-孔隙型样品13#(a)杨氏模量与(b)杨氏模量衰减测量与模型计算结果对比 Fig. 15 Comparison of (a) Young′s modulus and (b) Young′s modulus attenuation of crack-pore-type carbonate 13# with rock physics model |
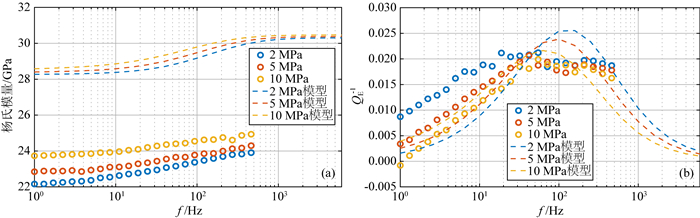
图 16中为人工孔洞型碳酸盐岩样品11#分别在2 MPa、5 MPa、10 MPa下的实验结果和相应的模型结果进行对比.可以看出实验和模拟结果中仅有一个衰减峰,且衰减的特征频率在100 Hz附近,与裂缝-孔隙型样品的第二个衰减峰出现的频段相近.计算得到的杨氏模量结果较实验数据相比偏大,杨氏模量衰减趋势与幅度较为吻合.因此从中等刚度孔隙与圆形孔隙间发生的喷射流作用的角度,能够一定程度解释饱和流体后孔洞型碳酸盐岩样品中发生的频散与衰减现象.与溶孔相比,虽然粒间孔可压缩性较大,围压增大时,岩石颗粒间发生更紧密的接触,粒间孔的纵横比降低,从而衰减在数值上降低,但是从衰减幅度相对变化上来看,压力对孔洞型样品的影响远不如对裂缝型样品的显著.
|
图 16 孔洞型样品11#(a)杨氏模量与(b)杨氏模量衰减测量结果与模型计算结果对比 Fig. 16 Comparison of (a) Young′s modulus and (a) Young′s modulus attenuation of artificial carbonate 11# with round-pore with rock physics model |
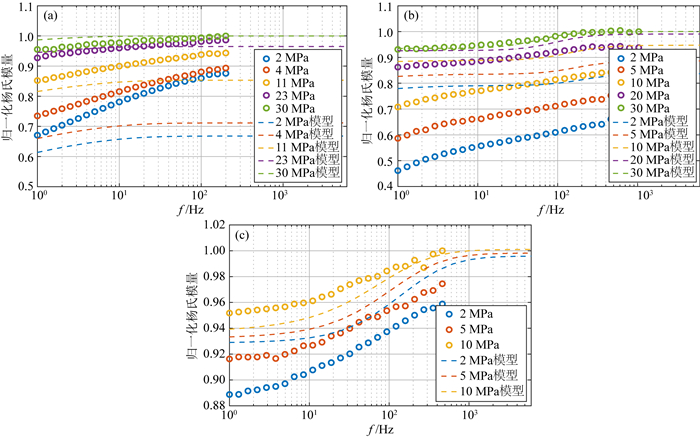
从图 14-16中可以明显发现实验测量结果相对于模型结果总体偏低.造成这种差异的一种原因是在实验工艺中为了隔绝岩石内部流体与围压气体介质,在样品表面浇注了一层环氧树脂密封层,使得岩石表面的应变片所采集到的应变幅度变大.此外,上述各种机制的频散理论都是简化的岩石模型,与实际情况有一定差别,也会造成实际测量结果与理论模型不能完全相符.这也从一个侧面说明部分的频散理论模型只能半定性半定量,而不能完全定量地描述实际饱和流体岩石的频散.因此,在实际研究与应用中应该更侧重于这些理论模型联合实验研究所反映的模量频散与衰减的趋势变化.从不同孔隙结构类型数据的对比中可以发现,无论是仅含裂缝或孔洞的单一孔隙类型样品,还是裂缝-孔隙型样品,模型计算的模量频散与衰减的变化趋势与实验测量数据的变化趋势大体是一致的.为了进一步进行对比,并排除一些实验系统误差的影响,我们将实验测量与理论计算在最高压力及双方重叠频率的最大值处,分别进行归一化,如图 17所示.对比归一化后的实验和模型计算数据,随着围压的增大,理论值和计算值逐渐接近.在高围压下,理论模型计算能够较好的反映相应孔隙类型岩石的频散规律.
|
图 17 归一化的样品(a)12#、(b)13#与(c)11#的实验测量与岩石物理模型计算杨氏模量结果对比 Fig. 17 Comparison of normalized Young′s modulus of experimental measurement and normalized result from rock physics model of sample (a) 12#, (b) 13# and (c) 11# |
根据完全饱和甘油的碳酸盐岩样品测量结果,不同孔隙类型的样品在测量频带表现出了与之对应的频散与衰减的特征,即不同的模量频散“台阶”与衰减峰,且同类孔隙结构对应频散与衰减规律表现一致.其中,对于裂缝-孔隙型样品观测到了两个和喷射流机制相关的衰减峰,出现在较低频率的频散与衰减认为由裂缝主导,与裂缝型样品的测量结果规律一致,而出现在较高频率的频散与衰减则认为由中等刚度孔隙主导,与孔洞型样品的测量结果规律一致.不同类型样品随着围压的增大,都表现出模量频散与衰减变弱的现象,在最高压力时频散与衰减达到最小值,位于较低频率的衰减在低围压下幅度大于处在较高频率的衰减峰,且对于围压变化更敏感.
将由超声测量数据计算得到的纵横比具有一定分布的软孔隙以及选择一定量的中等刚度孔隙加入到喷射流模型中分别针对裂缝型、裂缝-孔隙型、孔洞型碳酸盐岩进行建模,计算结果与各个孔隙类型碳酸盐岩的实验测量结果在测量频带中具有相似的趋势变化.
对碳酸盐岩岩心样品饱和较高黏度流体条件下的测量能够提高我们对于低孔渗致密油储层的认识.当碳酸盐岩储层埋藏深度较深时,有效压力较高时,或主要孔隙类型为圆孔和粒间孔时,由于喷射流机制引起的频散的特征频率会处在较高频段,在地震频段并不明显.对于埋藏深度较浅且裂缝等软孔隙较为发育的碳酸盐岩储层,流体饱和后由于喷射流机制引起的波的频散在地震频带可能会较强,此时在地震频段应谨慎应用Gassmann方程进行流体替换.
Adam L, Batzle M, Brevik I. 2006. Gassmann's fluid substitution and shear modulus variability in carbonates at laboratory seismic and ultrasonic frequencies. Geophysics, 71(6): F173-F183. DOI:10.1190/1.2358494 |
Adam L, Batzle M, Lewallen K T, et al. 2009. Seismic wave attenuation in carbonates. Journal of Geophysical Research:Solid Earth, 114(B6): B06208. DOI:10.1029/2008JB005890 |
Ba J, Yan X F, Chen Z Y, et al. 2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs. Chinese Journal of Geophysics (in Chinese), 56(5): 1696-1706. DOI:10.6038/cjg20130527 |
Borgomano J V M, Pimienta L, Fortin J, et al. 2017. Dispersion and attenuation measurements of the elastic moduli of a dual-porosity limestone. Journal of Geophysical Research:Solid Earth, 122(4): 2690-2711. DOI:10.1002/2016JB013816 |
Choquette P W, Pray L C. 1970. Geologic nomenclature and classification of porosity in sedimentary carbonates. AAPG Bulletin, 54(2): 207-250. |
David E C, Zimmerman R W. 2012. Pore structure model for elastic wave velocities in fluid-saturated sandstones. Journal of Geophysical Research:Solid Earth, 117(B7): B7210. DOI:10.1029/2012JB009195 |
de Paula O B, Pervukhina M, Makarynska D, et al. 2012. Modeling squirt dispersion and attenuation in fluid-saturated rocks using pressure dependency of dry ultrasonic velocities. Geophysics, 77(3): WA157-WA168. DOI:10.1190/geo2011-0253.1 |
Deng J X, Zhou H, Wang H, et al. 2015. The influence of pore structure in reservoir sandstone on dispersion properties of elastic waves. Chinese Journal of Geophysics (in Chinese), 58(9): 3389-3400. DOI:10.6038/cjg20150931 |
Eberhart-Phillips D, Han D H, Zoback M D. 1989. Empirical relationships among seismic velocity, effective pressure, porosity, and clay content in sandstone. Geophysics, 54(1): 82-89. |
Gurevich B, Makarynska D, de Paula O B, et al. 2010. A simple model for squirt-flow dispersion and attenuation in fluid-saturated granular rocks. Geophysics, 75(6): N109-N120. DOI:10.1190/1.3509782 |
Harris J M, Quan Y L, Xu C T. 2005. Differential acoustical resonance spectroscopy: an experimental method for estimating acoustic attenuation of porous media.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Jiang H Y, Song X M, Wang Y J, et al. 2008. Current situation and forecast of the world's carbonate oil and gas exploration and development. Offshore Oil (in Chinese), 28(4): 6-13. |
Li C, Zhao J G, Wang H B, et al. 2020. Multi-frequency rock physics measurements and dispersion analysis on tight carbonate rocks. Chinese Journal of Geophysics (in Chinese), 63(2): 627-637. DOI:10.6038/cjg2019M0294 |
Li H, Wang D X, Gao J H, et al. 2020. Role of saturation on elastic dispersion and attenuation of tight rocks:An experimental study. Journal of Geophysical Research:Solid Earth, 125(4): e2019JB018513. |
Müller T M, Gurevich B, Lebedev M. 2010. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics, 75(5): 75A147-75A164. DOI:10.1190/1.3463417 |
Ma Y S, Mei M X, Chen X B. 1999. Sedimentology of Carbonate Reservoirs (in Chinese). Beijing: Geological Publishing House: 161-166.
|
Mavko G, Mukerji T, Dvorkin J. 2020. The Rock Physics Handbook. Cambridge: Cambridge University Press.
|
Mikhaltsevitch V, Lebedev M, Gurevich B. 2016. Laboratory measurements of the effect of fluid saturation on elastic properties of carbonates at seismic frequencies. Geophysical Prospecting, 64(4): 799-809. DOI:10.1111/1365-2478.12404 |
O'Connell R J, Budiansky B. 1978. Measures of dissipation in viscoelastic media. Geophysical Research Letters, 5(1): 5-8. DOI:10.1029/GL005i001p00005 |
Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow. Journal of Geophysical Research, 109: B01201. DOI:10.1029/2003JB002639 |
Volk A, Kähler C J. 2018. Density model for aqueous glycerol solutions. Experiments in Fluids, 59(5): 75. DOI:10.1007/s00348-018-2527-y |
Sams M S, Neep J P, Worthington M H, et al. 1997. The measurement of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62(5): 1456-1464. DOI:10.1190/1.1444249 |
Sun C, Tang G Y, Zhao J G, et al. 2018. An enhanced broad-frequency-band apparatus for dynamic measurement of elastic moduli and Poisson's ratio of rock samples. Review of Scientific Instruments, 89(6): 064503. DOI:10.1063/1.5018152 |
Vanorio T, Scotellaro C, Mavko G. 2008. The effect of chemical and physical processes on the acoustic properties of carbonate rocks. The Leading Edge, 27(8): 1040-1048. DOI:10.1190/1.2967558 |
Wang S X, Zhao J G, Li Z H, et al. 2012. Differential acoustic responce spectroscopy for the acoustic measurement of small and irregular samples in the low frequency range. Journal of Geophysical Research:Solid Earth, 117(B6): B06203. DOI:10.1029/2011JB008808 |
Wang Z Z, Wang R H, Wang F F, et al. 2015a. Experiment study of pore structure effects on velocities in synthetic carbonate rocks. Geophysics, 80(3): D207-D219. |
Wang Z Z, Wang R H, Qiu H, et al. 2015. A new method for artificial core preparation with multiple pore structures and its application. Geophysical Prospecting for Petroleum (in Chinese), 54(2): 150-156. |
Wang Z Z, Schmitt D R, Wang R H. 2015b. Does wettability influence seismic wave propagation in liquid-saturated porous rocks?. Geophysical Journal International, 203(3): 2182-2188. DOI:10.1093/gji/ggv434 |
Wei X, Wang S X, Zhao J G, et al. 2015a. Laboratory study of velocity dispersion of the seismic wave in fluid-saturated sandstones. Chinese Journal of Geophysics (in Chinese), 58(9): 3380-3388. DOI:10.6038/cjg20150930 |
Wei X, Wang S X, Zhao J G, et al. 2015b. Laboratory investigation of influence factors on VP and VS in tight sandstone. Geophysical Prospecting for Petroleum (in Chinese), 54(1): 9-16. |
Xu S Y, Payne M A. 2009. Modeling elastic properties in carbonate rocks. The Leading Edge, 28(1): 66-74. |
Yang Z F, Cao H, Yao F C, et al. 2014. Seismic rock physical analysis of complex porous reservoir and its application. China Petroleum Exploration (in Chinese), 19(3): 50-56. |
Yin H J, Zhao J G, Tang G Y, et al. 2017. Pressure and fluid effect on frequency-dependent elastic moduli in fully saturated tight sandstone. Journal of Geophysical Research:Solid Earth, 122(11): 8925-8942. DOI:10.1002/2017JB014244 |
Zhao J G, Tang G Y, Deng J X, et al. 2013b. Determination of rock acoustic properties at low frequency:A differential acoustical resonance spectroscopy device and its estimation technique. Geophysical Research Letters, 40(12): 2975-2982. DOI:10.1002/grl.50346 |
Zhao J G, Wang S X, Yin H J, et al. 2015. Differential acoustic resonance spectroscopy:improved theory and application in the low frequency range. Geophysical Journal International, 202(3): 1775-1791. DOI:10.1093/gji/ggv234 |
Zhao L X, Nasser M, Han D H. 2013a. Quantitative geophysical pore-type characterization and its geological implication in carbonate reservoirs. Geophysical Prospecting, 61(4): 827-841. DOI:10.1111/1365-2478.12043 |
Zhao L X, Yuan H M, Yang J K, et al. 2017. Mobility effect on poroelastic seismic signatures in partially saturated rocks with applications in time-lapse monitoring of a heavy oil reservoir. Journal of Geophysical Research:Solid Earth, 122(11): 8872-8891. DOI:10.1002/2017JB014303 |
Zhao L X, Cao C H, Yao Q L, et al. 2020. Gassmann consistency for different inclusion-based effective medium theories:implications for elastic interactions and poroelasticity. Journal of Geophysical Research:Solid Earth, 125(3): e2019JB018328. |
巴晶, 晏信飞, 陈志勇, 等. 2013. 非均质天然气藏的岩石物理模型及含气饱和度反演. 地球物理学报, 56(5): 1696-1706. DOI:10.6038/cjg20130527 |
邓继新, 周浩, 王欢, 等. 2015. 基于储层砂岩微观孔隙结构特征的弹性波频散响应分析. 地球物理学报, 58(9): 3389-3400. DOI:10.6038/cjg20150931 |
江怀友, 宋新民, 王元基, 等. 2008. 世界海相碳酸盐岩油气勘探开发现状与展望. 海洋石油, 28(4): 6-13. |
李闯, 赵建国, 王宏斌, 等. 2020. 致密碳酸盐岩跨频段岩石物理实验及频散分析. 地球物理学报, 63(2): 627-637. DOI:10.6038/cjg2019M0294 |
马永生, 梅冥相, 陈小兵. 1999. 碳酸盐岩储层沉积学. 北京: 地质出版社: 161-166.
|
王子振, 王瑞和, 邱浩, 等. 2015. 一种多重孔隙结构人造岩心的制备新方法及其应用. 石油物探, 54(2): 150-156. |
未晛, 王尚旭, 赵建国, 等. 2015a. 含流体砂岩地震波频散实验研究. 地球物理学报, 58(9): 3380-3388. DOI:10.6038/cjg20150930 |
未晛, 王尚旭, 赵建国, 等. 2015b. 致密砂岩纵、横波速度影响因素的实验研究. 石油物探, 54(1): 9-16. |
杨志芳, 曹宏, 姚逢昌, 等. 2014. 复杂孔隙结构储层地震岩石物理分析及应用. 中国石油勘探, 19(3): 50-56. |
 2020, Vol. 63
2020, Vol. 63


