2. 北京市地质勘察技术院, 北京 100120
2. Beijing Institute of Geo-exploration Technology, Beijing 100120, China
一般而言,面波信息在反射地震数据处理中通常被当作噪声来处理(Sheriff and Geldart, 1995).然而,记录了近地表介质的弹性属性信息的面波频散特性是求取近地表的横波速度结构特征主要手段(Stokoe et al., 1994; Park et al., 1999; Strobbia et al., 2010).如Nazarian等(1983)提出了面波频谱分析方法(SASW),即利用一对检波器通过变化炮检距离,多次接收重锤等冲击震源激发的面波信号,在频率域计算每一对检波器的相位差产生频散曲线用于反演近地表信息.Park等(1999)提出了多道面波分析方法(MASW),即采用多道同时接收可控震源或重锤等冲击震源激发产生的面波信号,构建频散曲线来反演近地表速度结构,进而讨论了检波器间距, 最小/最大偏移距等参数对频散曲线的影响(Park et al., 1999, 2001).Roth和Holliger(1998)从反射地震数据中选取浅表层发育的面波信息,建立瑞利面波频散曲线,并利用遗传算法反演了表层结构.在石油勘探反射地震调查中,曾校丰等(2001)利用准噶尔盆地油气反射波地震记录中的面波信息,通过反演获得的覆盖层横波速度结构可与已知地表地质资料很好地对比.在浅层工程勘查领域,邓小娟等(2017)通过提取浅层反射地震数据中的面波信息反演近地表横波速度结构.目前在浅表工程勘查和石油勘探等领域提取面波频散曲线的方法主要有:F-K频谱(Capon, 1969; 李建平,2018),SPAC法(Aki, 1957),Tau-P变换(McMechan and Yedlin, 1981),高分辨率线性拉东变换(Luo et al., 2009),倾斜叠加(Xia et al., 2007)和频率-贝塞尔变换(吴华礼等,2019)等方法,但其偏移距较小(一般为几十米到几公里),取得了较好的效果.
深反射地震探测技术是研究大陆基底、解决深部地质问题和探测岩石圈精细结构的有效技术手段(王海燕等,2006),具有长排列大偏移距(以16~20 km为主),大药量(以30~50 kg为主, 甚至数百公斤-数吨)等特点(Zhao et al., 1993; Gao et al., 2013; 吕庆田等,2015).其炮集数据中一定蕴含丰富的面波信息.然而,尚未有针对大偏移距(6 km以上)反射地震中的面波信息开展相关研究,即利用其频散特性(Park et al., 2007; Strobbia et al., 2010)揭示近地表浅层速度结构特征.其可能原因之一,是由于深地震反射剖面所经过的地表高程变化较大,往往难以构建用以获取频散曲线的高质量面波F-K频谱.为此, 本文试图在起伏地形条件下,尝试构建共检波点域面波F-K频谱方法,提取高品质的多阶面波频散曲线,获取深地震反射剖面下的近地表横波速度结构特征,将其运用在跨过班公湖-怒江缝合带的SinoProbe深反射地震剖面(Gao et al., 2013)中效果明显.
1 方法主动源反射地震中的面波常用的方法是F-K频谱法(Gabriels et al., 1987; Park et al., 2001; Lu and Zhang, 2004; 李建平,2018),即利用傅里叶变换将其从距离-时间域变换到频率-波数域.鉴于目前深地震反射剖面大多为二维测线(Zhao et al., 1993; Gao et al., 2013; Dong et al., 2020), 为此设反射地震时间域信号为h(x, t),H(k, f)为信号h(x, t)的二维频谱,给定采样间隔,二维离散傅里叶变换公式为
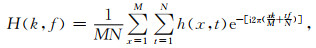
|
(1) |
其中x=1, 2, …, M(M为地震数据记录的道数),t=1, 2, …, N(N为地震数据每道时窗的点数),k=1, 2, …, K(K为地震数据每道波数的点数),f=1, 2, …, F(F为地震数据每道频率的点数).
在复杂地形条件下,利用单炮记录很难获得高质量的F-K频谱.而长排列采集的深反射地震数据中蕴含了丰富的面波信号,在共检波点域采用面波信号F-K频谱叠加的方法,不仅使得面波能量被增强,而且反射波因其非线性特征则会被抵消,进而获取高信噪比的面波F-K频谱.设某一特定检波点,计算其来自不同偏移距地震单炮的F-K频谱H(k, f)(式1),再利用归一化叠加方式(式2)对F-K频谱进行叠加,得到归一化叠加后的F-K频谱G(k, f):
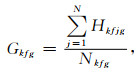
|
(2) |
其中f为频率,g代表共检波点,j代表共检波点域不同偏移距单炮的序数,Nkfg为叠加宽度(叠加次数),代表共检波点域不同偏移距单炮的总个数.然后根据相速度Vr与频率f和波数k之间的关系(式(3)),将频率-波数变换为频率-相速度,在F-K频谱上拾取经二维傅里叶变换得到的频率-波数中能量极大值点,计算后构成了面波频率-相速度频散曲线.
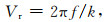
|
(3) |
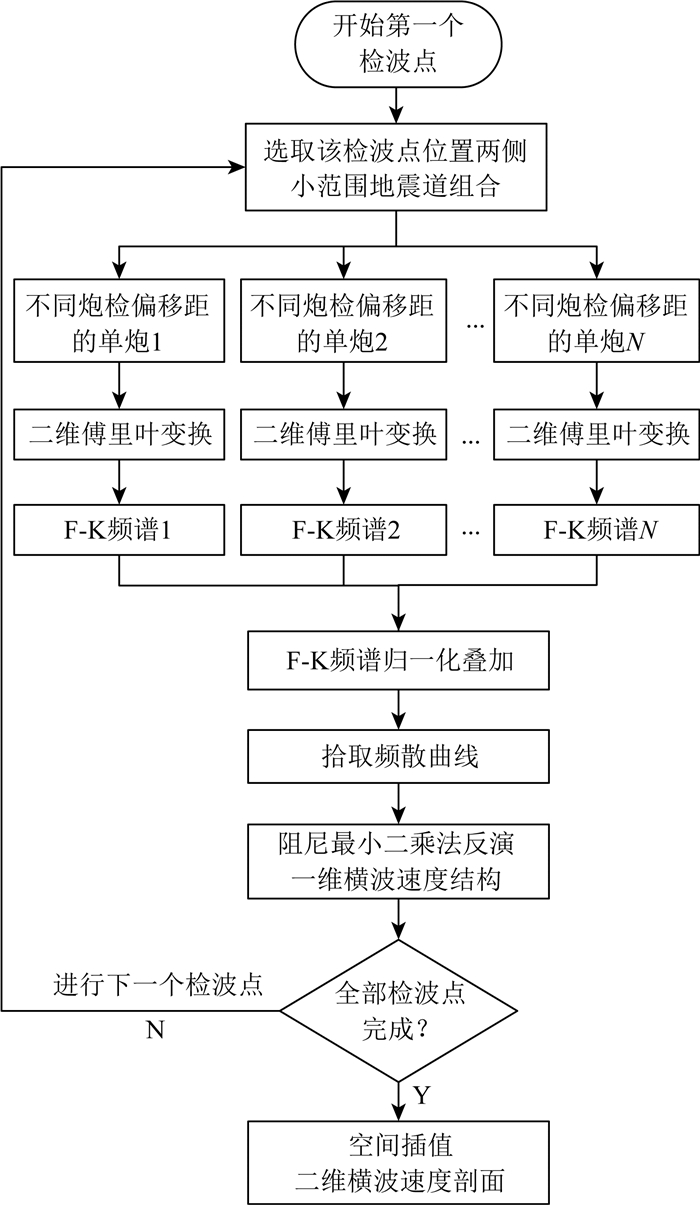
最后通过高信噪比F-K谱来获取频散曲线,利用阻尼最小二乘反演得到近地表横波速度,具体流程如图 1所示.
|
图 1 深反射地震测线中的面波反演处理流程图 Fig. 1 Surface wave inversion processing flowchart for deep seismic reflection profile |
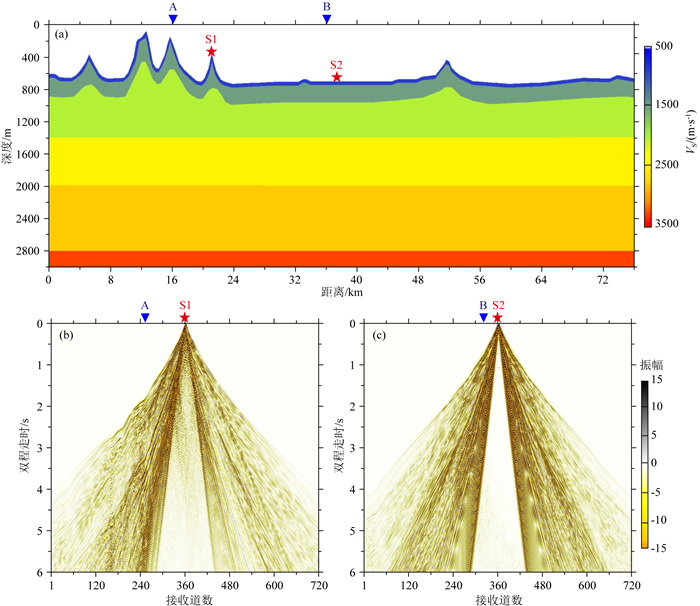
参照深反射地震数据采集的观测系统,构建基于起伏地表的层状介质模型, 如图 2a所示,模型参数如表 1所示.设计检波点位置0~76 km,检波点间距50 m,炮点位置:15.225 km到60.725 km,炮点间距250 m,中间放炮每炮720道,最大偏移距17975 m.采用有限差分弹性波波动方程模拟得到Z分量地震单炮记录(Chopra, 2005),考虑到长排列和较大模型范围,限于计算机性能,采用2.5 m×2.5 m模型网格,主频25 Hz雷克子波,4 ms采样间隔,6 s采样记录,正演模拟得到183炮地震单炮记录,包含地震初至波,面波和反射波等能量,其中面波占据了大部分的能量,反射波能量相对较弱.图 2b和2c所示为地形变化剧烈处(炮点S1)和地势平缓处(炮点S2)模型正演地震单炮记录.
|
图 2 起伏地表地下速度模型及模型正演单炮记录 (a)横波速度模型;(b)地形变化剧烈S1处正演模拟地震单炮记录;(c)地势平缓S2处正演模拟地震单炮记录;A和B为检波点位置,S1和S2为炮点. Fig. 2 Subsurface velocity model with irregular topography and forward modeling seismic records (a) Shear velocity model; (b) Forward modeling seismic records at irregular topography location S1; (c) Forward modeling seismic records at gentle terrain location S2. A, B: receiver location. S1, S2: shot location. |
|
|
表 1 起伏地表层状介质模型参数 Table 1 Layered model parameters with an irregular topography |
面波具有频散的特性,且在同一频率有多个不同的相速度,在单一频率最小传播速度被称为基阶模式,相邻的高于基阶模式的相速度被称为一阶高阶模式,以此类推,所有高于基阶模式传播速度的模式均称为高阶模式(夏江海,2015).为了分析起伏地表对地震面波F-K频谱的影响,选择位于地形变化剧烈的位置A和地形平缓的位置B处(如图 2所示位置)分别进行研究.按照图 1流程所述,以某一特定检波点位置为中心选取其两侧的11道地震道组合,求取不同检波点-炮点偏移距的每一个地震单炮的在该组合处的F-K频谱,然后对不同偏移距地震单炮的F-K频谱进行归一化叠加分析,叠加次数取决于参与叠加的不同偏移距单炮的总个数.
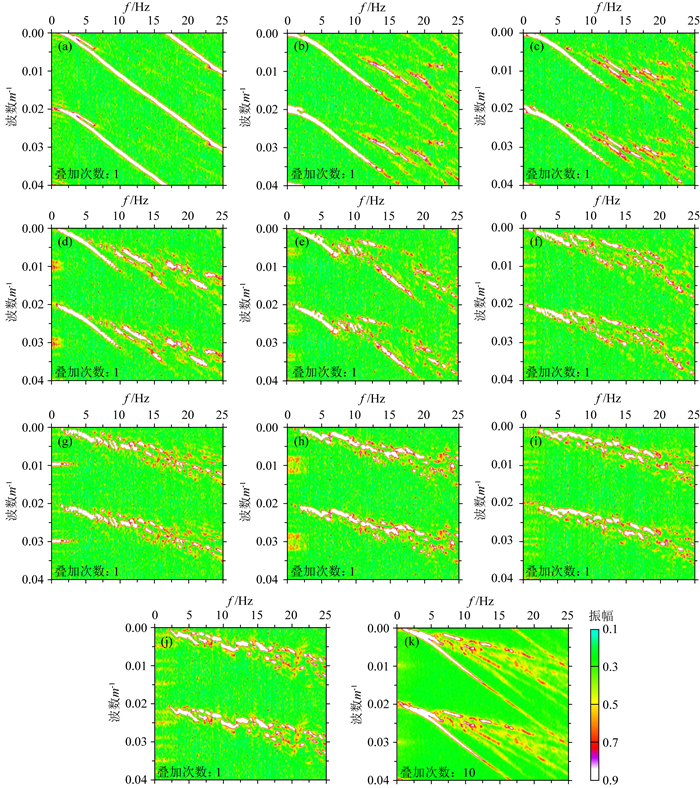
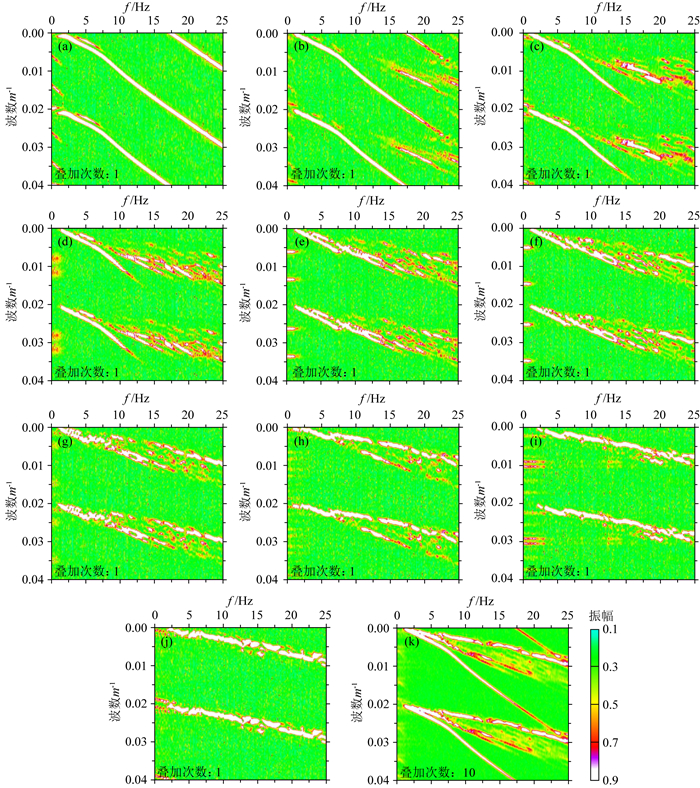
图 3(a-j)展示了距离A点偏移距分别为625 m,1625 m,…,9625 m,每隔1000 m的单炮在A处采用常规单次未叠加方法得到的F-K频谱;图 3k为上述图 3(a-j)所示的10个F-K频谱的叠加,其叠加次数为10次.图 4(a-j)展示了距离B点偏移距分别为625 m,1625 m,…,9625 m,每隔1000 m的单炮在B处采用常规单次未叠加方法得到的F-K频谱,图 4k为上述图 5(a-j)所示的10个F-K频谱的归一化叠加,其叠加次数为10次.
|
图 3 地形变化剧烈A处的F-K频谱 使用距A点不同偏移距的单炮:(a) 625 m;(b) 1625 m;(c) 2625 m;(d) 3625 m;(e) 4625 m;(f) 5625 m;(g) 6625 m;(h) 7625 m;(i) 8625 m;(j) 9625m炮. (k)为(a-j)10个单炮的F-K频谱叠加. Fig. 3 F-K spectrums at irregular topography location A Using single shot of different offset from location A: (a) 625 m; (b) 1625 m; (c) 2625 m; (d) 3625 m; (e) 4625 m; (f) 5625 m; (g) 6625 m; (h) 7625 m; (i) 8625 m; (j): 9625 m. (k): F-K spectrum stack using10 shots from (a) to (j). |
|
图 4 地形平缓B处的F-K频谱 使用距B点不同偏移距的单炮,图注如图 3. Fig. 4 F-K spectrums at gentle terrain location B Using single shot of different offset from location B, figure legends are same as Fig. 3. |
|
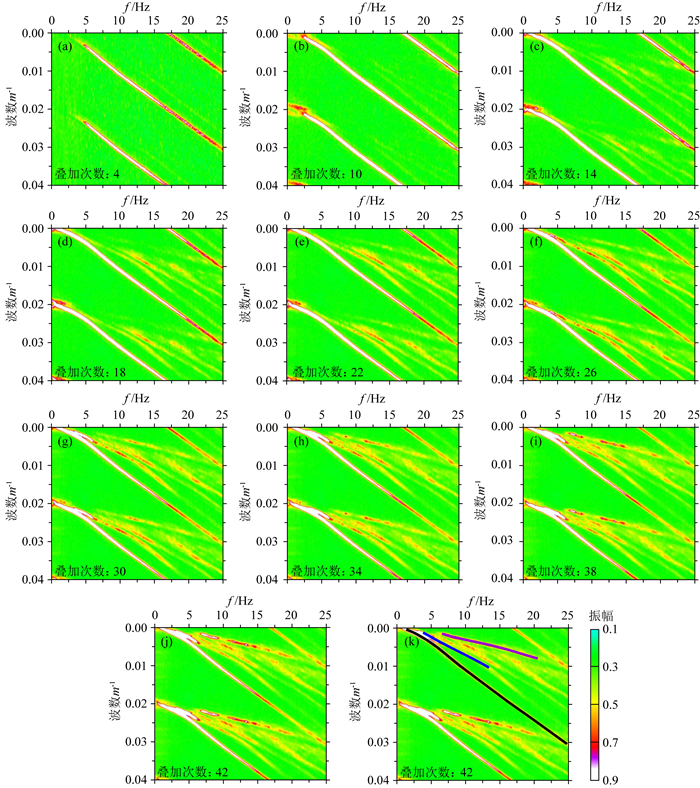
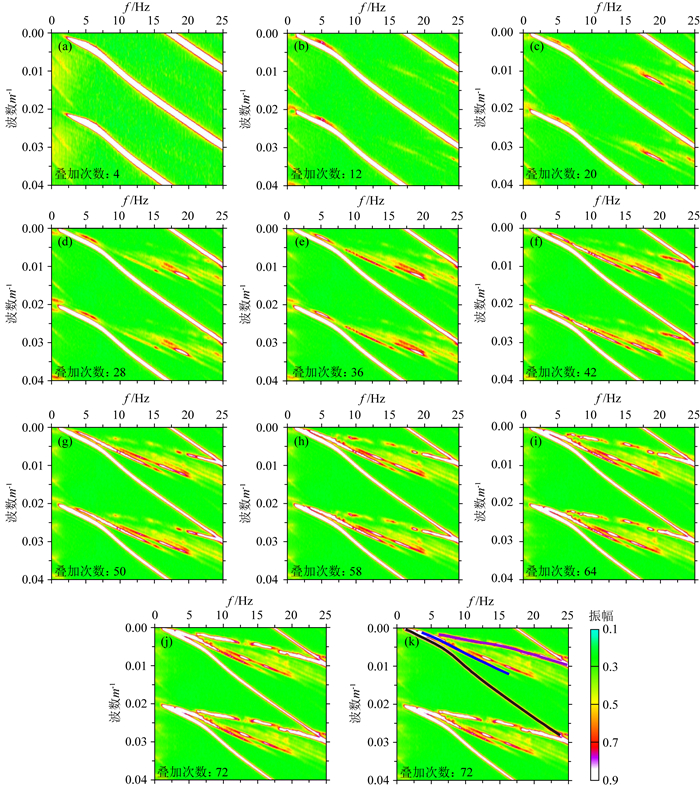
图 5 地形变化剧烈A处的F-K频谱叠加 使用距A点不同偏移距范围内的所有单炮:(a) ±1 km;(b) ±2 km;(c) ±3 km;(d) ±4 km;(e) ±5 km;(f) ±6 km;(g) ±7 km;(h) ±8 km;(i) ±9 km;(j) ±10 km. (k)为在(j)频谱上显示拾取的基阶(黑色),一阶(蓝色)和二阶(紫色)面波信号. Fig. 5 F-K spectrums stacks at irregular topography location A Using all shots within different offset range from location A: (a)±1 km; (b)±2 km; (c)±3 km; (d)±4 km; (e)±5 km; (f)±6 km; (g)±7 km; (h)±8 km; (i)±9 km; (j)±10 km. (k): display picked fundamental mode (black), 1st mode (blue) and 2nd mode (purple) surface waves on F-K spectrum (j). |
此外对一定偏移距范围内的单炮全部用于归一化叠加分析,图 5展示了距离A点偏移距±1000 m,±2000 m,…, ±10000 m范围内所有单炮在A处F-K频谱的归一化叠加.由于中间放炮,A处左侧临近边界炮点较少,主要为A处右侧单炮(+偏移距单炮)叠加,叠加次数如图 5中所示.图 6给出了距离B点±1000 m,±2000 m,…, ±10000 m范围内所有单炮在B处F-K频谱的归一化叠加,叠加次数如图 6中所示.
|
图 6 地形平缓B处的F-K频谱叠加 使用距B点不同偏移距范围内的所有单炮,图注如图 5. Fig. 6 F-K spectrums stack at gentle terrain location B Using all shots within different offset range from location B, figure legends are same as Fig. 5. |
由上述F-K频谱(图 3-6)分析可知:(1)F-K频谱上基阶面波能量强,近偏移距主要表现为基阶面波,高阶面波能量弱;随着偏移距变大,可以看到明显的高阶面波;(2)采用常规单次未叠加方法得到的F-K频谱质量较差(图 3(a-j),图 4(a-j)),不能同时得到可靠的基阶和高阶面波信息,通过在共检波点域对F-K频谱进行叠加构建,可较大程度地提高F-K谱的信噪比,有利于拾取基阶、一阶和二阶甚至更高阶面波相速度频谱信息.(3)尽管地形变化对F-K频谱质量有一定的影响,但是通过对单炮F-K频谱归一化叠加,可以得到高品质的F-K频谱(图 3k,图 5k).
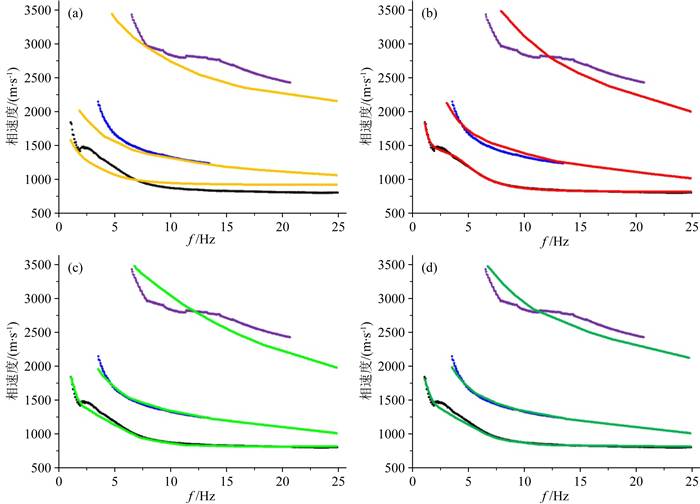
通过不同检炮距的F-K频谱叠加试验,以0~10000 m偏移距范围的F-K频谱叠加(图 5k和6k)为基准,可以较好地拾取强能量处的F-K值,来获取基阶(黑色实线),一阶(蓝色实线)和二阶(紫色实线)面波信号.根据式(3)计算相速度,得到面波频率-相速度频散曲线(图 7).
|
图 7 地形变化剧烈A处拾取和反演的频散曲线 黑色为拾取的基阶频散曲线,蓝色为拾取的一阶频散曲线,紫色为拾取的二阶频散曲线.(a)中橙线为初始速度模型的频散曲线;(b)中红线为仅使用基阶频散曲线反演的频散曲线;(c)中青色线为使用基阶和一阶频散曲线反演的频散曲线;(d)中绿色线为使用基阶,一阶和二阶频散曲线反演的频散曲线. Fig. 7 Picked and Inverted dispersion curves at irregular topography location A Black: picked fundamental dispersion curve, blue: picked 1st mode dispersion curve, purple: picked 2nd mode dispersion curve. (a) Orange line is dispersion curve of initial model; (b) Red line is inverted dispersion curves using fundamental mode dispersion curve; (c) Cyan line is inverted dispersion curves using fundamental mode and 1st mode dispersion curve; (d) Green line is inverted dispersion curves using fundamental mode, 1st mode and 2nd mode dispersion curve. |
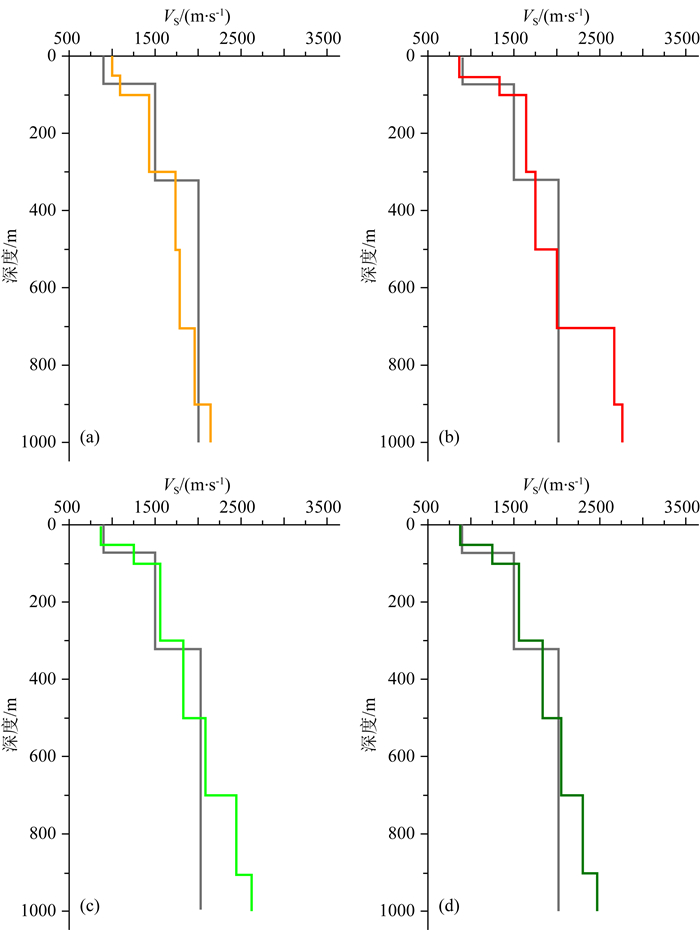
面波频散曲线与地下速度模型结构是一种复杂的非线性关系,主要与纵、横波速度,密度和层厚等参数有关(Horike, 1985; Arai and Tokimatsu, 2005; 徐佩芬等,2013;李巧灵等,2019).通过频散曲线直接反演得到全部介质参数往往显得非常困难,而面波频散与横波速度的敏感性远远高于纵波速度和密度,其次是地层厚度.本文首先利用经验公式(式4)将基阶面波的相速度-频率函数Vr(f)转换为横波速度-深度函数Vs(z)(Stokoe et al., 1994),并依据‘浅层细分和深层粗分’原则建立初始横波速度结构模型,如图 8a中橙线所示.
|
图 8 地形变化剧烈A处反演的横波速度结构 浅灰色为表 1中正演模型的横波速度结构. (a)橙线为初始横波速度结构;(b)红线为使用拾取的基阶频散曲线反演的横波速度结构;(c)青色为使用拾取的基阶和一阶频散曲线反演的横波速度结构;(d)绿色线为使用拾取的基阶,一阶和二阶频散曲线反演的横波速度结构. Fig. 8 Inverted S wave velocity structure at irregular topography location A gray: S wave velocity structure from Synthetic model as listed in Tab. 1. (a) Initial S wave velocity structure model; (b) Red line is inverted S wave velocity structure using fundamental mode dispersion curve; (c) Cyan line is inverted S wave velocity structure using fundamental mode and 1st mode dispersion curve; (d) Green line is inverted S wave velocity structure fundamental mode, 1st mode and 2nd mode dispersion curve. |
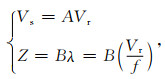
|
(4) |
其中, Vs为横波速度,Vr为面波相速度,Z为深度,λ为波长,f为频率,A和B为系数.A一般取值为1.1~1.2,B一般取值为1/2~2/3.本文选用A=1.2,B=2/3.
本文采用阻尼最小二乘反演算法(Xia et al., 1999; 罗银河等,2008)获得横波速度,并保持模型中的分层厚度不变的情况下利用Ludwig等(1970)的经验公式得到纵波速度和密度,对拾取的基阶和高阶频散曲线进行三种反演:(1)仅使用基阶频散曲线反演;(2)使用基阶和一阶频散曲线反演;(3)使用基阶,一阶和二阶频散曲线反演,反演深度1000 m.反演过程通过对比初始模型的频散曲线和拾取的频散曲线,迭代得到更新后的频散曲线和速度模型,直到均方根差收敛为止.在地形变化剧烈A处,初始模型和三种不同反演结果的频散曲线与拾取的频散曲线对比如图 7所示,初始模型和三种不同反演结果如图 8所示.
上述反演结果(图 7和图 8)显示:(1)仅使用基阶频散曲线反演,反演的频散曲线和拾取的基阶频散曲线吻合性很好,但和拾取的一阶和二阶频散曲线吻合性较差;反演的速度结构在0~300 m以及500~700 m结果很好,但在300~500 m结果较差,700 m以下结果不可信;(2)使用基阶和一阶频散曲线反演,反演的频散曲线和拾取的基阶和一阶频散曲线吻合性很好,但并不与拾取的二阶频散曲线吻合;反演的速度结构在0~700 m效果很好,700 m以下结果不可信;(3)使用基阶,一阶和二阶频散曲线反演,反演的频散曲线与拾取的基阶、一阶频散曲线吻合较好,二阶频散曲线吻合性有一定提高但改进不够明显;反演的速度结构在0~700 m效果很好,在500~700 m有所改善,700 m以下结果不可信.在0~700 m的反演结果比较理想.反演的深度主要与面波波长有关(夏江海,2015),在反演中加入高阶频散曲线,能够改善反演模型的精度(罗银河等,2008).正演模拟数据(图 8)显示,在起伏地形条件下,采用共检波点域面波信号叠加,不仅能够通过高信噪比的F-K谱获取基阶和高阶频散曲线,而且再利用阻尼最小二乘反演快捷地获取近地表横波速度结构.
3 实际数据处理效果 3.1 跨班公湖-怒江缝合带的深反射地震数据班公湖-怒江缝合带是青藏高原中部的一条重要缝合线, 自西向东沿班公湖、改则、东巧、丁青和类乌齐一线分布, 缝合带在平面上呈WE向平缓展布为“S”型(劳熊,2000),以改则、丁青为界可将该带分为西、中、东三段.针对班公湖-怒江缝合带开展了大量的地球物理研究工作,用于研究班公湖-怒江缝合带下莫霍面形态,壳幔结构等深部构造背景及动力学机制(卢占武等,2006;赵文津等,2008;Zhao et al., 2014; Murodov et al., 2018).深部探测技术与实验研究专项(SinoProbe)在青藏高原腹地(跨越BNS和羌塘中央隆起)布设了长约310 km的深反射地震数据(Gao et al., 2013)为本文开展实际数据处理提供了便利条件.
本文所用的实际数据为SinoProbe深反射地震测线(Gao et al., 2013)的南段(见图 9),即南起色林错西岸,经扎根藏布,跨班公湖-怒江缝合带,北止纳江错,约65 km.总炮数192炮(包含1个大炮),小炮使用30 m井深,50 kg药量单井激发,炮点距250 m,最大偏移距17, 975 m,每炮720道;大炮使用50 m井深,总药量1000 kg,10口井组合激发,最大炮检距47975 m,每炮960道.采用主频10 Hz的检波器组合接收,道间距50 m(Gao et al., 2013),共1521个检波点.
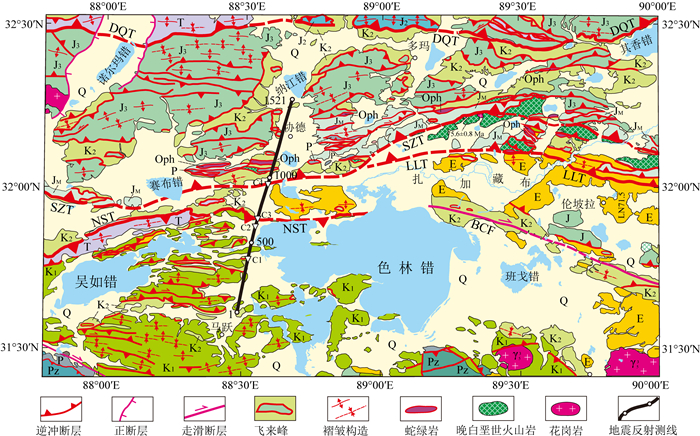
|
图 9 色林错及邻区构造刚要图(吴珍汉等,2016) Q-第四系; E-古近纪河湖相沉积; K2-上白垩统阿布山组红层; K1-下白垩统; J3-上侏罗统; J2-中侏罗统; JM-侏罗纪混杂堆积; T-三叠系; Oph-蛇绿混杂岩; DB-多巴; BCF-崩错走滑断裂; NST:色林错北逆冲断裂SZT:赛布错-扎加藏布逆冲推覆构造;粗黑实线为本文研究深反射地震测线南段检波点位置,数字为检波点序号,C1、C2、C3、C4为在图 15中位置. Fig. 9 Structural outline map of Siling Co and its neighboring areas (from Wu Z H, et al. 2016) Q-Quaternary mud, sands and gravel; E-Paleogene lacustrine, fluvial and alluvial mudstone, sandstone, marl and conglomerate; K2-Upper Cretaceous red beds; K1-Lower Cretaceous limestone and clastic sedimentary rocks; J3-Upper Jurassic limestone; J2-Middle Jurassic limestone, dolomite, sandstone, siltstone and shale; JM-Jurassic mélange; T-Triassic; Oph-ophiolite; DB-Duoba; BCF-Beng co strike fault; NST: North Siling Co thrust; SZT: Serbug Co-Zajiazangbu thrust. The bold dark line refers to south part of seismic reflection profile′s receiver location for this study, the number is receiver sequence number, C1, C2, C3 and C4: locations as shown in Fig. 15. |
原始地震单炮(如图 10)显示:具有较明显的面波频散特征,且有空间假频现象,在大偏移距(10 km)和大双程走时(10 s)仍能见到面波能量.地形平缓处面波线性规律较好,易于观察到基阶和高阶面波,而地形起伏剧烈的山体处的面波视速度范围大,面波频散特征形态较复杂不利于拾取.
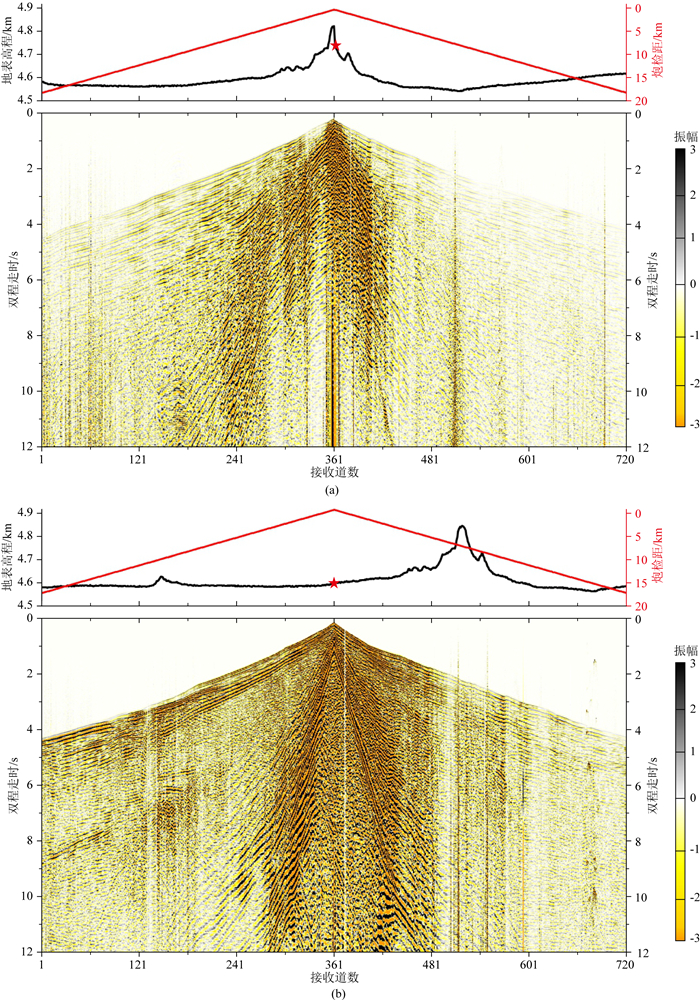
|
图 10 山体处(a)和地形平缓处(b)激发的野外地震单炮 黑线为检波点高程,红线为炮检距. Fig. 10 Field seismic shot gathers at irregular topography location (a) and gentle terrain location (b) Black line: receiver elevation, Red line: source receiver offset. |
实际数据处理过程中, 首先对如图 9所示的检波点自南向北编号(1-1521),然后预处理,如压制异常振幅噪声,对面波范围外的初至波等能量进行切除,并通过频谱分析确定面波频率范围基本上在15 Hz以下.再依据图 1所示的处理流程,求取不同检波点-炮点偏移距的每个单炮的F-K频谱,对不同检波点-炮点偏移距单炮的F-K频谱叠加分析.通过不同检波点-炮点偏移距叠加试验表明,由于班公湖-怒江缝合带及其两侧的近地表大多为未固结的河湖相沉积(图 9), 具有明显的强衰减特性, 导致了实际地震记录的高频信号衰减更快.为此,在低频端使用更远的偏移距单炮进行叠加,而在高频端则需要适当地避免远偏移距单炮,最终在0 Hz端采用±10 km的偏移距范围,15 Hz端采用±6 km偏移距范围的单炮分频叠加.对比山地(图 10a)与地形平缓(图 10b)的实际单炮记录, 显示地表地形变化剧烈面波能量明显弱于平缓地形面波,其类似于正演模型(图 2)的面波特征.图 11(a-h)为最终处理后沿测线不同检波点位置处的F-K频谱.在地势平缓处,F-K频谱的质量高,能够容易地拾取基阶和一阶面波的F-K信息,在检波点(b)和(e)(图 11)处甚至可以得到二阶面波信息.地形起伏变化剧烈的山地地表检波点(c)和(f)(图 11)处尽管其信噪比弱于地形平缓处检波点(b)和(e)(图 11)的面波信号,也能够拾取基阶和一阶面波F-K信息,山地地表检波点(a)(图 11)处也能拾取基阶面波信息,这与模型数据F-K频谱(图 5-图 6)类似.图 12(a-h)为相应的频散曲线,清楚地展示了不同位置的面波频散的空间变化特征,如检波点(a)处为较高的相速度频散,检波点(b)处则为较低的相速度频散,这表明该剖面下的近地表横波速度横向变化较大.
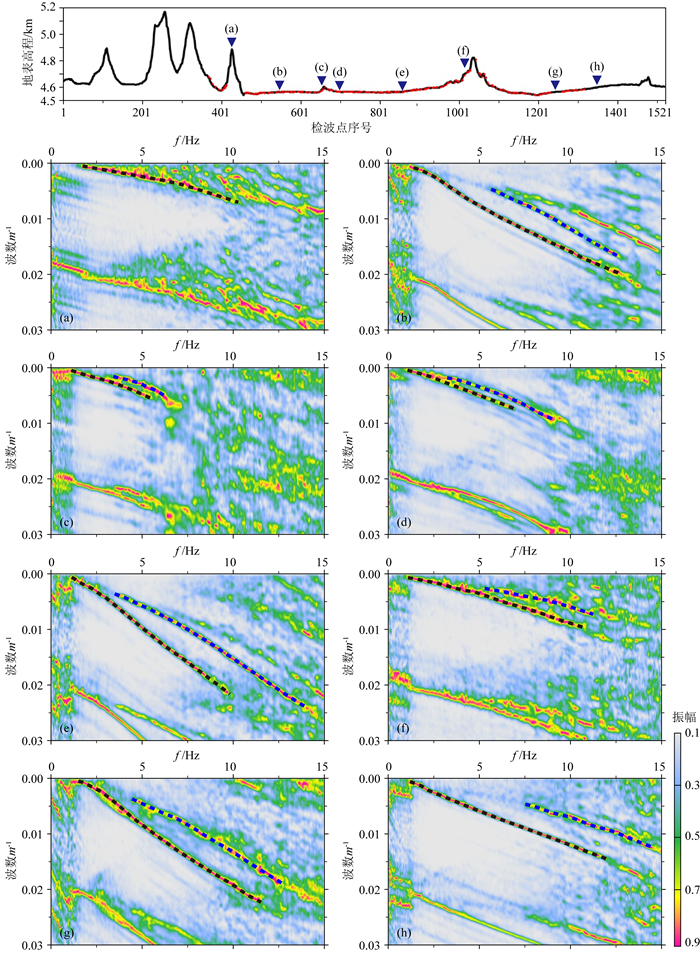
|
图 11 深反射地震测线不同检波点位置处(a)-(h)及F-K频谱 地形线:黑色为检波点高程,红色为炮点高程. Fig. 11 F-K spectrums at different receiver locations along deep seismic reflection profile Topography line: black is receiver elevation, red is shot elevation. |

|
图 12 深反射地震测线不同检波点位置处拾取和反演的频散曲线 Fig. 12 Picked and inverted dispersion curves at different receiver locations along deep seismic reflection profile |
根据经验公式(式(4))建立该测线横波速度初始模型(反演深度1250 m),其中模型空间内的浅部层厚度为25 m共10层,在深部的层厚度为50 m共20层.沿测线大部分位置使用了基阶和一阶频散曲线进行反演,而一阶频散曲线质量很差的位置(图 11a处)仅利用基阶频散信息进行反演.图 13为反演获得的一维横波速度结构.整体而言,反演结果在1000 m以上较为可靠.SinoProbe深反射地震测线检波点距50 m,而本次研究按照每隔一个检波点(即每隔100 m)进行处理,不考虑测线端部处无共中心点位置的检波点,最终通过反演得到检波点编号(273-1423)共576个检波点位置下方的一维横波速度,通过二维线性插值和小尺度300 m空间平滑得到沿测线的二维横波速度剖面,如图 15b所示.
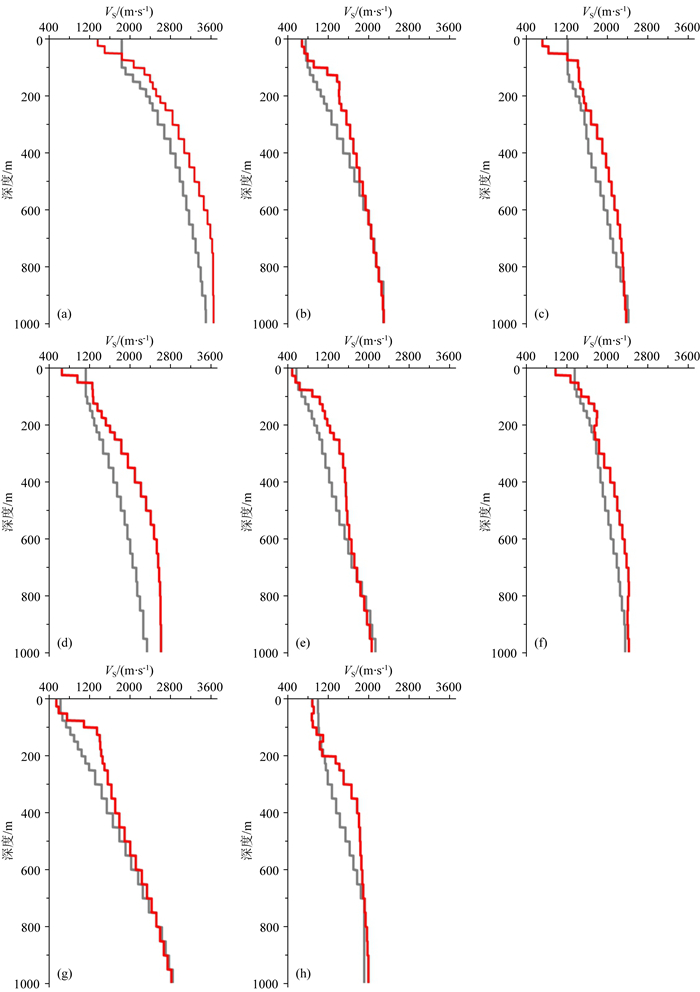
|
图 13 深反射地震测线不同检波点位置处反演的横波速度结构 浅灰色为初始模型的横波速度结构,红色为反演的横波速度结构. Fig. 13 Inverted S wave velocity at different receiver locations along deep seismic reflection profile Gray: initial S wave velocity model; red: inverted S wave velocity model. |
|
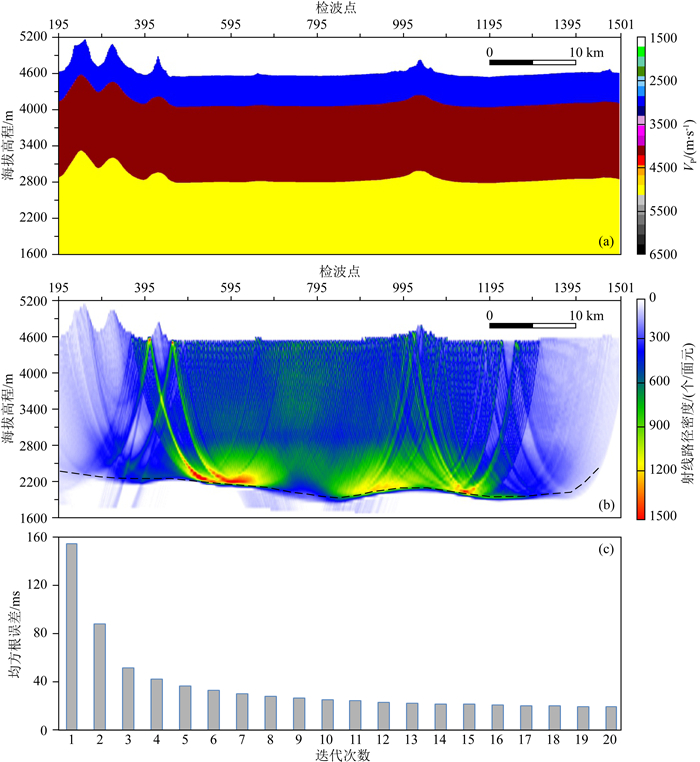
图 14 初至走时层析反演 (a)初始纵波速度模型;(b)射线路径密度;(c)走时均方根误差. Fig. 14 First arrival travel-time tomography inversion (a) Initial P wave velocity model; (b) Ray paths density; (c) Travel-time RMS error. |
|
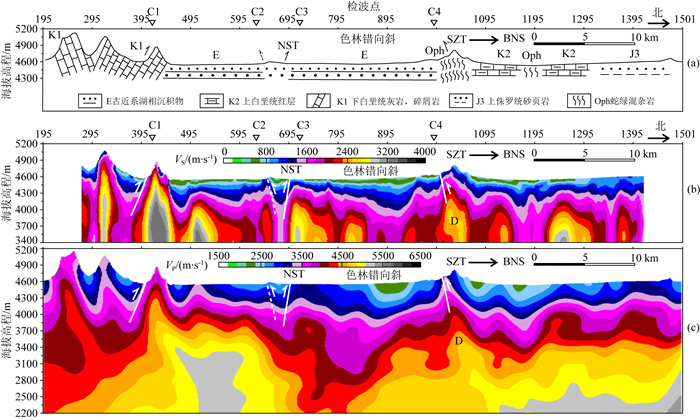
图 15 浅表地质剖面(a),浅部横波(b)和纵波(c)速度结构剖面 NST:色林错北逆冲断裂;SZT:赛布错-扎加藏布逆冲推覆构造;BNS:班公湖-怒江缝合带;C1、C2、C3、C4位置见图 1所示. Fig. 15 Shallow geological profile (a), S wave velocity (b) and P wave velocity (c) structure sections NST: North Siling Co thrust. SZT: Serbug Co-Zajiazangbu thrust. BNS: Bangong-Nujiang Suture Zone. C1, C2, C3 and C4 locations as shown in Fig. 1. |
利用反射地震的初至波走时通过纵波速度层析反演获取近地表的纵波速度结构,其方法技术已较为成熟,广泛运用于石油勘探、工程勘察、煤炭和金属矿探测等(Bishop et al., 1985;罗省贤和李录明,2004;张继国和刘连升,2006;侯贺晟等,2009;孙黄利,2010;李建国等,2012;秦宁等,2014;周衍和饶莹,2019).为了更好地研究跨班公湖-怒江缝合带的近地表速度结构特征,并与反演得到的横波速度(图 15b)对比分析,我们也利用深反射地震单炮的初至波走时信息通过传统的走时层析成像方法(侯贺晟等,2009)获取了测线下方的纵波速度结构(图 15c).
在本文研究中,首先对测线所有单炮进行全排列的初至精细拾取,共计192炮(包含一个大炮),每炮720接收道(大炮960接收道),剔除数据质量差的初至,最终拾取131, 800个初至时用于反演计算,拾取比例达到95%以上.根据偏移距-初至时间信息,计算延迟时和折射波速度建立三层层状初始纵波速度模型(如图 14a).通过试验最终采用横向25 m,垂向25 m地下网格面元,使用偏移距范围0~18 km.当迭代次数达到10次以上时,模型走时和观测初至走时均方根误差趋于收敛(如图 14c),最终采用20次迭代.模型的反演深度与偏移距范围和地下介质的速度相关,往往偏移距越大穿透深度更深,通过射线路径分布密度可以确定本次反演在深度3 km左右(海拔高程2200 m)以上比较可靠(如图 14b黑色虚线所示),临近工区边界由于野外采集没有布设炮点位置,射线密度低,最终反演的纵波速度结构剖面如图 15c所示.
3.4 近地表结构分析面波反演的横波速度在浅层具有较高的分辨能力,而初至波层析反演由于大偏移距采集得到的纵波速度穿透更深.然而,面波反演得到的近地表横波速度(图 15b)和初至波反演得到的近地表纵波速度(图 15c)具有较好的相关性,进而通过近地表速度结构剖面推断表层的构造和岩性特征较为可靠:
(1) 构造:在赛布错-扎加藏布逆冲推覆构造(SZT)附近(图 15:C4),横纵波速度变化剧烈,表现为北向倾斜的逆冲断层.在色林错北逆冲断裂(NST)附近(图 15:C3),速度结构表现为向南倾斜逆冲断层推覆.在SZT和NST之间色林错向斜位置,速度变化趋缓,速度分层整体上较为平缓,显示了清晰的大型色林错向斜结构,盆地内部速度剖面上可以看到较小的向斜和背斜形态,可能是由于受南北两侧逆冲断层(NST和SZT)对冲影响,使得古近系湖相沉积地层发生一定程度的褶皱变形.在NST附近(图 15:C2),发育一向北倾斜的反向逆冲断层,使得局部表现为小型背斜构造.在测线南部边界(图 15:C1)附近,解释为一向南倾斜的逆冲断层.通过横纵波速度结构的断层解释与前人地质研究成果较为吻合(吴珍汉等,2016),总体而言反演得到的横纵波速度结果对盆地结构和逆冲断层构造的展布特征等有更精细的刻画.另外推测测线南部边界(图 15:C1)和NST(图 15:C2)逆冲断层的推覆对冲,使得二者之间的地层也发生了挤压和褶皱变形,从速度结构剖面可以看出色林错向斜部位可以延展到NST以南,一直到测线南部边界(图 15:C1)略北位置.
(2) 岩性:岩性与地震波速度的关系非常密切(闫桂京等,2005).结合大比例尺地质填图认识(吴珍汉等,2016),即在近纳江错南岸高速的横纵波速度为侏罗统砂页岩(图 15);而在赛布错-扎加藏布逆冲推覆构造(SZT)以北表现的整体低速和局部高速,主要与上白垩统红层和局部蛇绿混杂岩出露相关(图 15).而横纵波速度结构剖面(图 15)展示的由深部向上至地表延伸的高速(图 15:D),依据地表地质(图 1;图 15a;吴珍汉等,2016)推测其可能是班公湖-怒江缝合带尚未出露到地表的蛇绿岩岩体.在SZT和测线南部边界附近(图 15:C1)之间,主要为第四系松散堆积物和古近系河湖相沉积的色林错向斜盆地,整体表现为低的P波和S波速度.在测线南部边界(图 15:C1),受到以白垩统灰岩和碎屑岩性为主的一套逆冲推覆构造系形成的陡地形影响,其地震速度变化剧烈.
总之,利用本文提出思路,深度挖掘具有大偏移距特征的深地震反射剖面数据,获得的深地震反射剖面所经过的近地表横纵波速度结构(图 15)与近地表地质特征高度吻合,这表明本文提出的方法与思路是切实可行的.
4 讨论与结论 4.1 讨论准确的近地表速度结构不仅可以提高反射地震资料静校正、速度分析等处理效果,还可以提高深度域速度模型的精度和偏移成像质量(Yilmaz, 2001),是复杂地表构造特征精细刻画的前提,也是准确地解剖深部结构的保证.而长排列、大药量采集的深反射地震数据中蕴含的面波信号研究很少,在复杂地表条件下,难以构建高质量的面波F-K频谱,本文通过研究了在复杂地形条件下基于共检波点域面波F-K频谱构建方法,并对跨越班公湖-怒江缝合带的野外深反射地震数据进行了处理分析,对研究过程中形成的几点认识讨论如下:
(1) 正演模型数据面波反演的误差(图 7和图 8)可能来自以下几个方面:①基于弹性波有限差分正演的地震单炮,由于受到有限差分阶数、震源子波处理、网格大小和边界条件等因素影响,存在一定的数值模拟误差(董良国和李培明,2004;宁刚等,2008);在实际数据反演中,不存在这方面的影响;②在F-K频谱上拾取强能量值时存在一定的拾取误差,可靠的F-K频谱是拾取基阶和高阶频散曲线的基础;③深部700 m以下的反演结果可信度低,皆因受限于面波传播路径的穿透深度,一般来说穿透深度约为一个波长.众所周知,面波波长与其频率和地下介质的速度有关,频率越低,穿透深度越大,而正演的地震数据中缺乏2 Hz以下的低频信息(图 6),故对于深层的反演结果影响较大;④反演的频散曲线和拾取的基阶与一阶频散曲线吻合性很好,二阶频散曲线整体趋势上较为吻合,但细节上吻合性较差,推测是由于高阶瑞利面波较基阶模式波具有更大的穿透深度(Miller et al., 2000),故对较深层的横波速度和层厚度比较敏感,且频率范围分布较大,敏感性强的频段分布比较分散(张明财等,2011).此外,虽然面波频散对介质横波速度的敏感性高于层厚,对纵波速度和密度敏感性较弱,但反演过程中仅考虑横波速度也会引起一定的误差.鲁来玉等(2006)基于高阶模式和基阶模式,采用遗传算法对层状介质模型的横波速度和厚度同时反演,得到了较为可靠的结果,而邵广周和李庆春(2011)通过细化分层方法,将地下介质划分为1 m厚度的薄层,得到的反演结果更接近地下实际情况.
(2) 在实际深反射地震数据的处理中发现:①临近测线端部的位置,野外采集时通常仅有远偏移距单炮贡献,面波的F-K频谱质量相对较差,这是由于在远偏移距时单炮能量较弱,高频信号衰减较快;②复杂地形条件下的深反射地震数据通常信噪比较低,在共检波点域开展F-K频谱叠加,可以较大程度地提高F-K谱的信噪比,有利于拾取基阶和高阶面波信号.但如果采用过多的单炮叠加,则会降低反演结果的横向分辨率,因此需要根据单炮记录的信噪比并通过试验来选择合适的偏移距范围内的单炮叠加,即数据信噪比低则需要适当增加参与叠加的单炮个数,反之适当减少叠加次数.另外由于近地表强衰减特性使得地震高频面波信号衰减更快,因此在低频端尽量使用更大偏移距的单炮叠加,而在高频端则需要适当地避免大偏移距单炮;③面波频散曲线反演方法众多(Herrmann and Al-Eqabi, 1991; Hunaidi, 1998; Xia et al., 1999; Beaty et al., 2002; Pan et al, 2019),其中的阻尼最小二乘SVD算法因其运算速度快以及具有较高精度反演结果而被广泛应用(罗银河等,2008),但其强烈地依赖于初始模型.为此,Stokoe等(1994)和夏江海等(2015)提出通过经验公式(式(4))将面波的相速度-频率函数转换为横波速度-深度函数作为初始模型能够得到较好的反演结果.此外,在建立初始模型时,若能够参考相关的地质地球物理资料,可以更好地降低反演的非唯一性,如利用初至P波走时数据及提取的横波频散曲线进行联合反演(傅磊和刘四新,2016),使得在反演过程中P波速度和S波速度相互约束,或综合利用基阶和一阶瑞利波联合反演(Xia et al., 2003),都能取得较好的效果.
(3) 本研究使用的深反射数据采集中使用了主频为10 Hz的地震检波器,所以实际地震数据的面波频率范围大概在1.25~15 Hz,低频面波信息有限,这直接地影响到了反演深度.而在该测线(图 9)附近布设了较多的被动源宽频带地震台站(吴蔚等,2017)接收到更多的低频信息.通过将两种频散曲线相互补充,得到高精度的频散曲线,进而提高反演的深度和分辨率,来开展更多的研究工作.
4.2 结论(1) 模型数据研究表明,在复杂地形条件下基于共检波点域面波F-K频谱构建新方法,能够较大程度地提高F-K频谱的质量,更利于提取可靠的基阶和高阶面波频散曲线.采用最小二乘SVD算法进行多阶面波联合反演,则可以有效提高速度模型精度,减少反演的多解性.
(2) 选取跨越班公湖-怒江缝合带的深反射地震实际数据,通过共检波点域面波F-K频谱构建方法,处理得到了基阶和一阶面波频散曲线,经反演得到近地表横波速度.该速度与基于初至波走时反演得到的近地表纵波速度具有很好的相关性,且具有更高的浅层分辨力.
(3) 横纵波速度结构剖面较好地揭示了跨越班公湖-怒江缝合带两侧的近地表构造特征,如逆冲断褶带内的色林错盆地结构特征、赛布错-扎加藏布逆冲推覆构造(SZT)和色林错北逆冲断裂(NST)展布特征等,与地质填图成果相吻合且细节更丰富.可靠的近地表横纵波速度结构,可以为静校正、起伏地表叠前深度成像和全波形反演等提供基础数据,进而提高深反射地震数据处理解释的可靠性.
致谢 非常感谢原始地震数据采集的SinoProbe项目组在野外的辛勤付出和中国地质科学院吴珍汉研究员提供的地质图件.更由衷地感谢多位匿名审稿专家提出的宝贵意见和编辑部的大力支持.
Aki K. 1957. Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bulletin of the Earthquake Research Institute, 35: 416-416. |
Arai H, Tokimatsu K. 2005. S-wave velocity profiling by joint inversion of microtremors dispersion curve and horizontal-to-vertical (H/V) Spectrum. Bulletin of the Seismological Society of America, 95(5): 1766-1778. DOI:10.1785/0120040243 |
Beaty K S, Schmitt D R, Sacchi M. 2002. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure. Geophysical Journal International, 151(2): 622-631. DOI:10.1046/j.1365-246X.2002.01809.x |
Bishop T N, Bube K P, Cutler R T, et al. 1985. Tomographic determination of velocity and depth in laterally varying media. Geophysics, 50(6): 903-923. |
Capon J. 1969. High-resolution frequency-wavenumber spectrum analysis. Proceedings of the IEEE, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 |
Chopra S. 2005. Seismic elastic modelling.//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 424-428.
|
Deng X J, Feng S Y, Zuo Y, et al. 2017. Velocity structure of the shallow part of the profile using surface wave of reflection seismic data. Journal of Geodesy and Geodynamics (in Chinese), 37(3): 256-260. |
Dong L G, Li P M. 2004. Dispersive problem in seismic wave propagation numerical modeling. Natural Gas Industry (in Chinese), 24(6): 53-56. |
Dong X Y, Li W H, Lu Z W, et al. 2020. Seismic reflection imaging of crustal deformation within the eastern Yarlung-Zangbo suture zone. Tectonophysics, 780: 228395. DOI:10.1016/j.tecto.2020.228395 |
Fu L, Liu S X. 2016. Joint Inversion of first arrival P waves and Rayleigh waves based on cross-gradient constrain. Chinese Journal of Geophysics (in Chinese), 59(12): 4464-4472. DOI:10.6038/cjg20161209 |
Gabriels P, Snieder R, Nolet G. 1987. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves. Geophysical Prospecting, 35(2): 187-196. DOI:10.1111/j.1365-2478.1987.tb00812.x |
Gao R, Chen C, Lu Z W, et al. 2013. New constraints on crustal structure and Moho topography in Central Tibet revealed by SinoProbe deep seismic reflection profiling. Tectonophysics, 606: 160-170. DOI:10.1016/j.tecto.2013.08.006 |
Herrmann R B, Al-Eqabi G I. 1991. Surface wave inversion for shear wave velocity.//Hovem J M, Richardson M D, Stoll R D eds. Shear Waves in Marine Sediment. Netherlands: Springer, 545-556.
|
Horike M. 1985. Inversion of phase velocity of long-period microtremors to the S-wave-velocity structure down to the basement in urbanized areas. Journal of Physics of the Earth, 33(2): 59-96. |
Hou H S, Gao R, Lu Z W, et al. 2009. First arrival seismic tomographic imaging test of the near-surface velocity structure of central uplift in the Qiangtang basin, Qinghai-Tibet Plateau. Geological Bulletin of China (in Chinese), 28(6): 738-745. |
Hunaidi O. 1998. Evolution-based genetic algorithms for analysis of non-destructive surface wave tests on pavements. NDT & E International, 31(4): 273-280. |
Lao X. 2000. On the formation of the Bangong-Co-Nujiang fault zone. Journal of Geomechanics (in Chinese), 6(1): 69-76. |
Li J G, Zhao B, Sun S W, et al. 2012. Application of seismic first arrival tomographic inversion on the exploration of polymetallic mine. Geoscience (in Chinese), 26(6): 1218-1224. |
Li J P. 2018. Inversion of multi-mode surface waves extracted from the shallow seismic reflection data. Acta Seismologica Sinica (in Chinese), 40(1): 24-31. |
Li Q L, Lei X D, Li C, et al. 2019. Exploring thick overburden structure by microtremor survey:a case study in the subsidiary administrative center. Progress in Geophysics (in Chinese), 34(4): 1635-1643. DOI:10.6038/pg2019CC0128 |
Lu L Y, Zhang B X. 2004. Analysis of dispersion curves of Rayleigh waves in the frequency-wavenumber domain. Canadian Geotechnical Journal, 41(4): 583-598. DOI:10.1139/t04-005 |
Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes. Chinese Journal of Geophysics (in Chinese), 49(4): 1082-1091. |
Lu Z W, Gao R, Li Q S, et al. 2006. Deep geophysical probe and geodynamic study on the Qinghai-Tibet Plateau (1958-2004). Chinese Journal of Geophysics (in Chinese), 49(3): 753-770. |
Ludwig W J, Nafe J E, Drake C L. 1970. Seismic Refraction, the Sea. Vol. 4 (Part 1). New York: Wiley-Interscience, 53-84.
|
Luo S X, Li L M. 2004. The method of ground surface seismic first break tomographic inversion for complicated surface model. Advance in Earth Sciences (in Chinese), 19(S1): 38-42. |
Luo Y H, Xia J H, Liu J P, et al. 2008. Joint inversion of fundamental and higher mode Rayleigh waves. Chinese Journal of Geophysics (in Chinese), 51(1): 242-249. |
Luo Y H, Xia J H, Miller R D, et al. 2009. Rayleigh-wave mode separation by high-resolution linear Radon transform. Geophysical Journal International, 179(1): 254-264. DOI:10.1111/j.1365-246X.2009.04277.x |
Lü Q T, Liu Z D, Dong S W, et al. 2015. The nature of Yangtze River deep fault zone:evidence from deep seismic data. Chinese Journal of Geophysics (in Chinese), 58(12): 4344-4359. DOI:10.6038/cjg20151202 |
McMechan G A, Yedlin M J. 1981. Analysis of dispersive waves by wave field transformation. Geophysics, 46(6): 869-874. DOI:10.1190/1.1441225 |
Miller R D, Park C B, Xia J H. 2000. Advantages of calculating shear-wave velocity from surface waves with higher modes.//70th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1295-1298.
|
Murodov D, Zhao J M, Xu Q, et al. 2018. Complex N-S variations in Moho depth and Vp/Vs ratio beneath the western Tibetan Plateau as revealed by receiver function analysis. Geophysical Journal International, 214(2): 895-906. DOI:10.1093/gji/ggy170 |
Nazarian S, Stoke II K H, Hudson W R. 1983. Use of spectral analysis of surface waves method for determination of moduli and thicknesses of pavement systems. Transportation Research Record Journal of the Transportation Research Board, 930: 38-45. |
Ning G, Xiong Z Q, Chen C X. 2008. An analysis of the error source in the wave propagation forward numerical simulation. Geophysical and Geochemical Exploration (in Chinese), 32(2): 203-206. |
Pan L, Chen X F, Wang J N, et al. 2019. Sensitivity analysis of dispersion curves of rayleigh waves with fundamental and higher modes. Geophysical Journal International, 216(2): 1276-1303. DOI:10.1093/gji/ggy479 |
Park C B, Miller R D, Xia J H. 1999. Multichannel analysis of surface waves. Geophysics, 64(3): 800-808. DOI:10.1190/1.1444590 |
Park C B, Miller R D, Xia J H. 2001. Offset and resolution of dispersion curve in Multichannel Analysis of Surface Waves (MASW).//81st Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Park C B, Miller R D, Xia J H, et al. 2007. Multichannel analysis of surface waves methods (MASW)-active and passive methods. The Leading Edge, 26(1): 60-64. |
Qin N, Li Z C, Sang Y Y, et al. 2014. The research of travel time tomographic velocity modeling method on first break. Progress in Geophysics (in Chinese), 29(1): 255-260. |
Roth M, Holliger K. 1998. Joint inversion of Rayleigh and guided waves in high-resolution seismic data using a genetic algorithm.//68th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Shao G Z, Li Q C. 2011. Study on parameter simplifying in dispersion curves inversion of surface wave based on subdividing layer method. Journal of Earth Sciences and Environment (in Chinese), 33(3): 317-320. |
Sheriff R E, Geldart L P. 1995. Exploration Seismology. 2nd ed. Cambridge: Cambridge University Press.
|
Strobbia C, Vermeer P, Laake A, et al. 2010. Surface waves:processing, inversion and removal. First Break, 28: 85-91. |
Stokoe II, K H, Wright G W, Bay J A, et al. 1994. Characterization of geotechnical sites by SASW method, in Geophysical characterization of sites, ISSMFE Technical Committee #10, edited by R.D. Woods, Oxford Publishers, New Delhi.
|
Sun H L. 2010. The application of the first breaks tomography technique in the seismic exploration of the coal field[Master thesis] (in Chinese). Xi'an: Xi'an University of Science and Technology.
|
Wang H Y, Gao R, Lu Z W, et al. 2006. Precursor of detecting the interior earth:Development and applications of deep seismic reflection. Progress in Exploration Geophysics (in Chinese), 29(1): 7-13, 19. |
Wu H L, Chen X F, Pan L. 2019. S-wave velocity imaging of the kanto basin in Japan using the frequency-Bessel transformation method. Chinese Journal of Geophysics (in Chinese), 62(9): 3400-3407. DOI:10.6038/cjg2019N0205 |
Wu W, Liu Q Y, He R Z, et al. 2017. Waveform inversion of S-wave velocity model in the central Qiangtang in North Tibet and its geological implications. Chinese Journal of Geophysics (in Chinese), 60(3): 941-952. DOI:10.6038/cjg20170309 |
Wu Z H, Zhao Z, Ye P S, et al. 2016. The Siling Co-Lunpola Thrust systems in the central Tibetan Plateau. Acta Geoscientica Sinica (in Chinese), 37(4): 441-448. |
Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh Wave. Geophysics, 64(3): 691-700. |
Xia J H, Miller R D, Park C B, et al. 2003. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 52(1): 45-57. DOI:10.1016/S0926-9851(02)00239-2 |
Xia J H, Xu Y X, Miller R D. 2007. Generating an image of dispersive energy by frequency decomposition and slant stacking. Pure and Applied Geophysics, 164(5): 941-956. DOI:10.1007/s00024-007-0204-9 |
Xia J H. 2015. High-Frequency Surface-Wave Methods (in Chinese). Wuhan: China University of Geosciences Press.: 115-116.
|
Xu P F, Li S H, Du J G, et al. 2013. Microtremor survey method:A new geophysical method for dividing strata and detecting the buried fault structures. Acta Petrologica Sinica, 29(5): 1841-1845. |
Yan G J, Chen J W, Wu Z Q. 2005. Analysis of relation between stratigraphic lithology and velocity of seismic wave. Marine Geology Letters (in Chinese), 21(9): 17-21. |
Yilmaz O. 2001. Seismic data analysis: processing, inversion, and interpretation of seismic data. Society of Exploration Geophysicist.
|
Zeng X F, Qian R Y, Deng X S, et al. 2001. The extraction of surface wave information from the record of oil-gas reflection wave seismic exploration. Geophysical & Geochemical Exploration (in Chinese), 25(6): 443-446. |
Zhang J G, Liu L S. 2006. Static corrections by first breaks tomographic inversion in complex area. Oil Geophysical Prospecting (in Chinese), 41(4): 383-385, 395. |
Zhang M C, Xiong Z Q, Zhang D Z, et al. 2011. Discussion of the sensitivity of each mode dispersion curves Rayleigh wave with the shear wave velocity and depth of stratum. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 33(2): 153-158. |
Zhao J M, Zhao D P, Zhang H, et al. 2014. P-wave tomography and dynamics of the crust and upper mantle beneath western Tibet. Gondwana Research, 25(4): 1690-1699. DOI:10.1016/j.gr.2013.06.020 |
Zhao W J, Nelson K D, Che J, et al. 1993. Deep seismic reflection evidence for continental underthrusting beneath southern Tibet. Nature, 366: 557-559. DOI:10.1038/366557a0 |
Zhao W J, Wu Z H, Shi D N, et al. 2008. Comprehensive deep profiling of Tibetan Plateau in the INDEPTH project. Acta Geoscientica Sinica (in Chinese), 29(3): 328-342. |
Zhou Y, Rao Y. 2019. Tomographic static corrections in loess plateaus. Chinese Journal of Geophysics (in Chinese), 62(11): 4393-4400. DOI:10.6038/cjg2019N0304 |
邓小娟, 酆少英, 左莹, 等. 2017. 利用反射地震资料中的面波研究剖面浅部结构. 大地测量与地球动力学, 37(3): 256-260. |
董良国, 李培明. 2004. 地震波传播数值模拟中的频散问题. 天然气工业, 24(6): 53-56. |
傅磊, 刘四新. 2016. 基于交叉梯度约束的地震初至纵波与瑞雷面波联合反演. 地球物理学报, 59(12): 4464-4472. DOI:10.6038/cjg20161209 |
侯贺晟, 高锐, 卢占武, 等. 2009. 青藏高原羌塘盆地中央隆起近地表速度结构的初至波层析成像试验. 地质通报, 28(6): 738-745. |
劳雄. 2000. 班公湖-怒江断裂带的形成——二论大陆地壳层波运动. 地质力学学报, 6(1): 69-76. |
李建国, 赵斌, 孙少伟, 等. 2012. 地震初至波速度层析反演在多金属矿探测中的应用. 现代地质, 26(6): 1218-1224. |
李建平. 2018. 浅层地震反射资料的多阶振型面波反演. 地震学报, 40(1): 24-31. |
李巧灵, 雷晓东, 李晨, 等. 2019. 微动测深法探测厚覆盖层结构——以北京城市副中心为例. 地球物理学进展, 34(4): 1635-1643. DOI:10.6038/pg2019CC0128 |
鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究. 地球物理学报, 49(4): 1082-1091. |
卢占武, 高锐, 李秋生, 等. 2006. 中国青藏高原深部地球物理探测与地球动力学研究(1958-2004). 地球物理学报, 49(3): 753-770. |
罗省贤, 李录明. 2004. 地面地震初至波层析反演复杂表层速度结构方法. 地球科学进展, 19(S1): 38-42. |
罗银河, 夏江海, 刘江平, 等. 2008. 基阶与高阶瑞利波联合反演研究. 地球物理学报, 51(1): 242-249. |
吕庆田, 刘振东, 董树文, 等. 2015. "长江深断裂带"的构造性质:深地震反射证据. 地球物理学报, 58(12): 4344-4359. DOI:10.6038/cjg20151202 |
宁刚, 熊张强, 陈持逊. 2008. 波动方程有限差分正演模拟误差来源分析. 物探与化探, 32(2): 203-206. |
秦宁, 李振春, 桑运云, 等. 2014. 初至波走时层析速度建模方法研究. 地球物理学进展, 29(1): 255-260. |
邵广周, 李庆春. 2011. 基于细化分层法探讨面波频散曲线反演参数的简化. 地球科学与环境学报, 33(3): 317-320. |
孙黄利. 2010.初至波层析技术在煤田地震勘探中的应用研究[硕士论文].西安: 西安科技大学.
|
王海燕, 高锐, 卢占武, 等. 2006. 地球深部探测的先锋-深地震反射方法的发展与应用. 勘探地球物理进展, 29(1): 7-13, 19. |
吴华礼, 陈晓非, 潘磊. 2019. 基于频率-贝塞尔变换法的关东盆地S波速度成像. 地球物理学报, 62(9): 3400-3407. DOI:10.6038/cjg2019N0205 |
吴蔚, 刘启元, 贺日政, 等. 2017. 羌塘盆地中部地区地壳S波速度结构及构造意义. 地球物理学报, 60(3): 941-952. DOI:10.6038/cjg20170309 |
吴珍汉, 赵珍, 叶培盛, 等. 2016. 青藏高原中部色林错-伦坡拉逆冲推覆构造系统. 地球学报, 37(4): 441-448. |
夏江海. 2015. 高频面波方法. 武汉: 中国地质大学出版社: 115-116.
|
徐佩芬, 李世豪, 杜建国, 等. 2013. 微动探测:地层分层和隐伏断裂构造探测的新方法. 岩石学报, 29(5): 1841-1845. |
闫桂京, 陈建文, 吴志强. 2005. 地层岩性与地震波速度的关系分析. 海洋地质动态, 21(9): 17-21. |
曾校丰, 钱荣毅, 邓新生, 等. 2001. 油气反射波地震勘探记录中面波信息的提取. 物探与化探, 25(6): 443-446. |
张继国, 刘连升. 2006. 复杂区初至层析反演静校正. 石油地球物理勘探, 41(4): 383-385, 395. |
张明财, 熊章强, 张大洲, 等. 2011. Rayleigh面波各阶模式频散曲线对横波速度和层厚的敏感性探讨. 物探化探计算技术, 33(2): 153-158. |
赵文津, 吴珍汉, 史大年, 等. 2008. 国际合作INDEPTH项目横穿青藏高原的深部探测与综合研究. 地球学报, 29(3): 328-342. |
周衍, 饶莹. 2019. 黄土塬覆盖区的层析反演静校正方法研究. 地球物理学报, 62(11): 4393-4400. DOI:10.6038/cjg2019N0304 |
 2020, Vol. 63
2020, Vol. 63


