0 引言

致密气藏通常被定义为含气致密砂岩储层和渗透率低于0.1 mD的碳酸盐岩储层(Holditch，2006；Smith et al., 2009；Ruiz and Cheng, 2010)，其中，致密砂岩天然气藏作为全球非常规资源天然气产量的重要组成部分，同样在国内天然气总储量中占较大比重(Zhu et al., 2008；Khlaifat et al., 2011；Wang et al., 2015).近年来，针对致密砂岩的储层特征、成藏机理、分布规律等，学者开展了大量研究工作(Olson et al., 2009；Laubach et al., 2010；郭梦秋等，2018；Bai et al., 2019；Xiao et al., 2019).有效储层识别被认为是致密砂岩气藏勘探的关键(Stroker et al., 2013；Zou et al., 2013；Liu et al., 2019)，其中的一个重要识别特征是储层内部含有大量的天然裂隙.天然裂隙是控制致密砂岩储层天然气运移、聚集和高产出的重要因素(Olson et al., 2010；Wang et al., 2018a, 2018b；Gong et al., 2019)，天然裂隙的存在，使得裂隙张开连通时储层渗透率显著增加，从而增强储层的流体流动能力(Nelson，2001；Benaafi et al., 2019).致密砂岩储层裂隙的空间分布特征是其天然气地震勘探的重要研究因素(Sanderson and Nixon, 2015；Kong et al., 2018；Zhao et al., 2018).

含微裂隙岩石的弹性性质及其对弹性波的影响，是岩石物理理论模型的研究热点(Crampin and Bamford, 1977；Vernik and Kachanov, 2010；Zhang et al., 2019).Hudson(1986)将裂隙的物理参数与等效弹性参数联系，利用宏观的弹性参数表征微观裂隙的特征.Thomsen(1995)提出了一种在等径孔隙背景下的含裂隙岩石的各向异性表达方式，用于研究裂隙介质的弹性性质.Smith等(2009)对致密砂岩储层进行了物性及弹性研究，认为岩石中裂隙是影响地震波速度的主要因素.唐晓明(2011)探讨了孔隙与裂隙的相互作用，将Biot理论和BISQ理论进行推广, 提出一个可以描述孔隙、裂隙并存的弹性波理论模型.Ba等(2011)基于经典力学Hamilton原理，提出数学物理形式相对严格的波动力学控制方程(Biot-Rayleigh理论)，描述了弹性波在结构非均质性岩石中的传播规律.随后，Ba等(2017)将该方程从饱和单一流体的双重孔隙介质推广到可同时考虑双孔结构及部分饱和双相流体的复杂情况，即双重-双重孔隙结构模型.

岩石物理参数敏感性分析常被用于查明各岩石物理参数或因子对储层、流体的敏感程度(Guo et al., 2015；Zeng et al., 2017)，波的衰减则被认为是对储层物性最为敏感的参数之一(Ba et al., 2018).Toksöz等(1979)使用具有高品质因子的铝块作为参考材料，提出谱比法来估算岩石的品质因子(Q).Quan和Harris(1997)通过假设地震子波的振幅谱满足高斯分布，提出质心频移法估算品质因子(Q).目前的实验和理论研究表明，岩石内部的微裂隙对弹性波频散和衰减有较强的影响(Chapman，2003；Gurevich et al., 2009；Tillotson et al., 2014；Kong et al., 2017；Bouchaala et al., 2019). Hudson(1981)首次研究了裂隙的物理参数对弹性波的速度和衰减的影响，利用宏观的弹性参数表征微观裂隙特征.Ali和Jakobsen(2011)通过测量不同地震频率和方位的速度和衰减数据来预测储层的裂隙含量.Fu等(2018)研究了裂隙对弹性波频散和衰减的影响，其分析结果表明在高频下，衰减和频散受到裂隙密度的控制，而在低频情况下，当裂隙的几何形状不同时，地震波的衰减和频散特性也会发生改变.Guo等(2018)通过实验结果和理论预测的对比，认为裂隙密度对纵波的散射、频散和衰减有显著影响，尤其在低频情况下更为明显.Cao等(2018)结合塔里木盆地研究区储层的地质和测井资料，通过地震正演模拟和反演，得出地震波衰减对裂隙密度敏感性较高的结论.

岩石物理图板能够直观的建立多种弹性性质与不同储层参数之间的联系(Carcione and Avseth, 2015；Hao et al., 2016).Picotti等(2019)分析了不同流体饱和度、孔隙度和渗透率对地震波的影响，给出了常规砂岩储层的地震尺度衰减图板，并开展了敏感性分析，但该研究没有利用实验及地震数据对图板进行校正，也没有付诸实际应用.本文考虑高含气饱和度目的层，基于双重孔隙结构理论模型(Biot-Rayleigh)，选择纵波衰减和波阻抗建立致密砂岩多尺度岩石物理图板，将储层孔隙度、裂隙含量与地震响应联系起来.利用致密砂岩岩心超声波实验、测井和叠后地震数据对图板进行校正，基于校正后的图板对工区地震数据进行应用，进而实现对致密砂岩储层孔隙度和裂隙含量的定量预测.

1 岩石样本及储层地震衰减提取 1.1 超声波谱比法估算衰减

本文利用谱比法估算得到的岩石样品的品质因子Q，使用具有高品质因子的标准铝块作为参考材料(Toksöz et al., 1979；Guo and Fu, 2006)，如下所述：

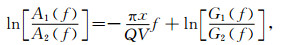
(1)

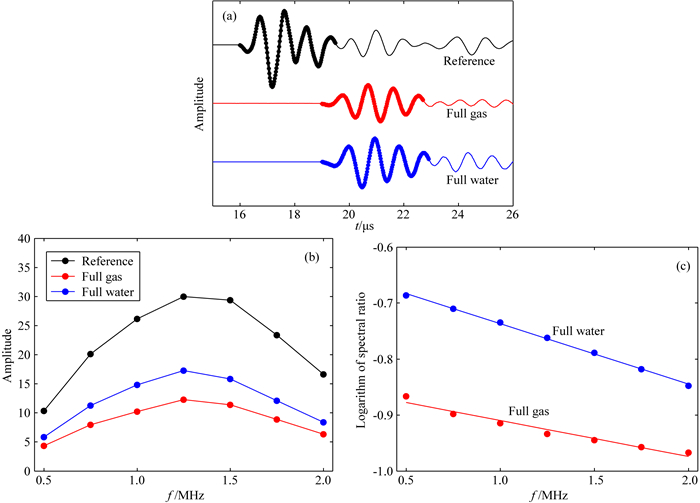
其中f是频率，A₁(f)和A₂(f)分别是岩石样本和参考材料的振幅谱，Q是岩石样本的品质因子，x是波传播距离，V是岩石样本波速，G₁(f)和G₂(f)分别为岩石样本和参考材料的几何因子.如图 1所示，为谱比法的计算过程图，图 1a为参考材料和饱气/饱水岩样的波形，从纵波初至开始选取几个完整周期的波形作为时间窗(图 1a)，进行傅里叶变换得到对应频谱(如图 1b)，求取频谱比曲线，在主频段对曲线进行线性拟合(如图 1c)，求取衰减系数.这种衰减计算方法假定在所分析的较窄频率范围Q不随频率变化，计算结果近似对应中心频率处的Q值.

1.2 超声波实验及样本衰减结果

岩石受到围压的作用下，岩石内部的微裂隙会发生闭合，围压越大，微裂隙含量越少(宋连腾等，2015；魏颐君等，2020).因此，为了观测岩石内部裂隙含量对弹性波的影响，本文通过对致密砂岩岩心施加不同围压，进行了超声波(1 MHz)P波和S波测量.该样本孔隙度为8.64%，渗透率为0.00038 μm²，干燥时密度为2.41 g·cm^-3.样本为直径25.2 mm、长度42.43 mm的圆柱体.实验在20 ℃的温度、10 MPa的孔隙压力下进行.使用Guo等(2009)的实验装置，通过超声波脉冲法测量岩石样本中的波传播速度.

对于饱气实验观测，首先将样本烘干，用橡胶套将岩样密封并置入实验装置中，对样本分别施加20 MPa、25 MPa、30 MPa、35 MPa、40 MPa、45 MPa、50 MPa、60 MPa、70 MPa、80 MPa的围压，然后利用装置内的电热丝加热施加围压的流体，加热至80 ℃并维持半小时，进行超声波实验测量，记录通过岩石样本的超声波波形.对于饱水实验观测，用抽真空加压饱和的方法使致密砂岩样本饱水，然后进行超声波实验测量，记录通过岩石样本的超声波波形.基于提取的纵横波波形的初至计算不同围压下致密砂岩在饱气和饱水条件下的纵、横波速度.

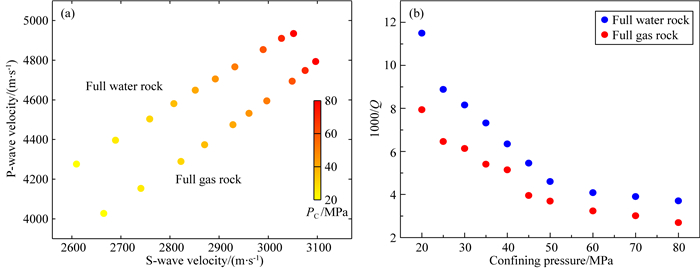
利用公式(1)计算致密砂岩样本不同围压、不同流体时的超声波衰减.如图 2所示是实验样本的结果图，分别给出了纵横波速度和纵波衰减在饱气/饱水时随围压的变化情况.图 2a给出饱气/饱水样本在不同的围压时，纵波速度与横波速度之间的关系，可知纵横波速度随着围压增加而增大，并且纵波速度与横波速度之间有良好线性关系.图 2b给出了样本的纵波衰减与围压的关系，饱水时衰减普遍高于饱气，且两种状态下衰减皆随着围压的增加呈现出减小趋势.

1.3 基于广义S变换的改进频移法

Quan和Harris(1997)提出质心频移法估算品质因子，该方法Q值估算结果具有较好的稳定性，在低信噪比条件下依然可保证质量较高的计算结果.然而由于其假定子波振幅谱是高斯形状，因此在实际资料应用中存在缺陷，且由于高频成分的衰减更快，当介质吸收衰减较强时，振幅谱的形态会愈发区别于高斯形态，此时，使用质心频率进行计算时，会产生较大误差.为此Zhang和Ulrych(2002)提出了一种基于峰值频率的频移的计算方法，其基础假定震源为Ricker子波.该方法适用面更广、误差更小，在实际资料应用中结果也更为精确.但是，此方法结果的稳定性依赖于对峰值频率的精确提取，而在时窗类型及长度的选取、噪声干扰等因素的影响下，峰值频率会产生较大误差.

针对两类频移方法所存在的缺陷，Hu等(2013)、Li等(2015)和Pang等(2019)分别提出并发展了改进的频移方法，结合了两类频移方法的优点，在保证较高精度的Q值估算结果的同时，具有较强的稳定性，在实际地震资料中有更好的适用性.主要思路是在Ricker子波的假设下，推导出基于质心频率的等效峰值频移公式：

(2)

其中，f_C0和f_C1分别表示衰减前和衰减后信号的质心频率，t表示传播时间.

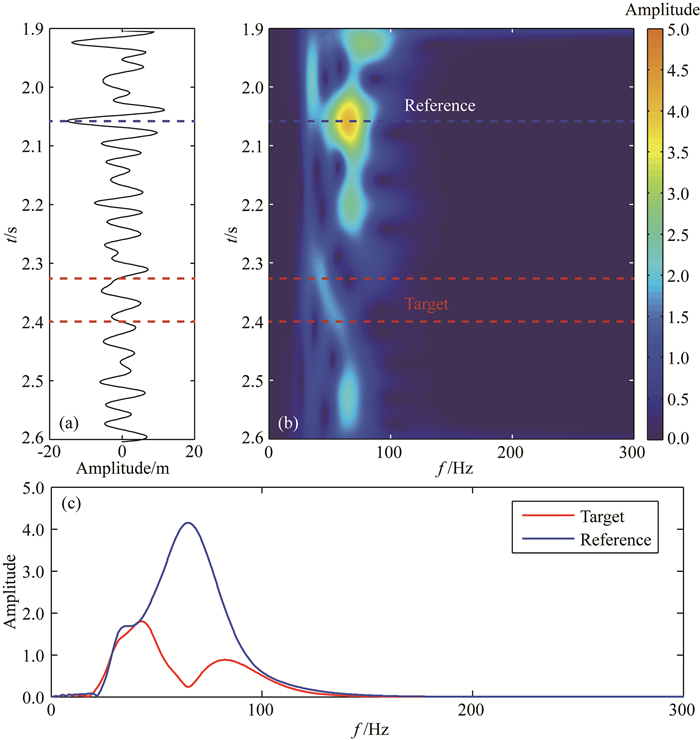
前人在提出并讨论改进的频移法时，是基于短时傅里叶变换开展的，其时窗固定的特性，常不能满足实际资料的非平稳信号在不同区域的时频分辨率的需求.引入广义S变换对此进行改进，获取更合适的频率分辨率，识别短时傅里叶变换所无法识别的层间信息，对储层刻画更精细，在储层应用中有较大的实用价值.图 3a为工区内目的层某地震道数据，蓝线为参考层，红线框内为目的层.该道经过广义S变换后对应的时频图和振幅谱分别为图 3b和3c.由图可知，与目的层相比，参考层反射强烈、质心频率高、频谱结果稳定.

选择参考层时，若参考层离目的层较远，则计算结果中包含较多目的层外的信息.因此估算地层品质因子时，参考层与目的层间的地层层厚越大，结果误差越大(Zhang and Ulrych, 2002).但距目的层越近，选取反射强烈、质心频率高的参考层一般也是困难的，因此参考层的选取要考虑实际资料的具体情况，本文选取的参考层与目的层位置关系如图 3所示.参考层的选取可能影响Q值的计算精度，但这种误差不会抵消基于广义S变换的改进频移法的效果，因为基于广义S变换的改进频移法的主要效果是提高地震资料分析的时频分辨率，进而改善Q值结果.参考层的选取对预测优质储层的精度有影响，但不会影响整体预测结果的分布趋势.基于参考层的衰减提取精度越高，后期储层预测越有利.

1.4 工区概况及储层衰减提取

本文研究工区为四川盆地某探区上三叠统须家河组致密砂岩天然气藏，位于川西坳陷构造区，该区蕴藏有丰富的天然气资源，所在的须家河组埋深较深.其砂岩储层属于辫状河三角洲沉积体系，矿物成分主要为石英、长石、岩屑以及云母、重矿等.矿物颗粒粒径以中-细粒为主，大多数砂岩分选较好，碎颗粒磨圆中等—较差，以次棱角状为主.该地区砂岩储层经历了强烈的成岩作用，普遍致密化，孔渗物性差，形成微观孔隙结构类型多样、裂隙发育以及孔隙流体非均质分布的地质特征(王春梅等，2011).

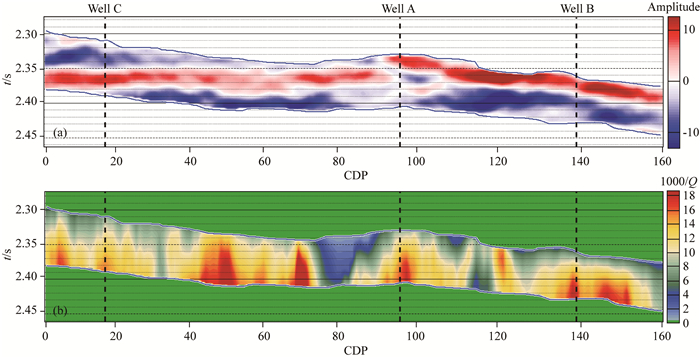
针对研究区内全部地震道数据，开展广义S变换(图 3)进行时频分析，得到参考层和目的层各时深点的结果，采用改进频移法公式(2)估算致密砂岩储层衰减值.如图 4所示，给出该工区储层一条过井A、井B和井C三口含气井的测线，虚线表示三口含气井位置.图 4a和4b分别表示该测线的储层地震振幅剖面和储层衰减剖面，其中红色区域指示储层的衰减较强，蓝色表示衰减较弱.结果显示，三口含气井存在明显的衰减异常.如图 5所示，给出目的层井A的测井孔隙度与井旁道地震衰减结果的交会图.由图可知，该井地震衰减结果与实际储层孔隙度具有一致性趋势，较强衰减指示较高孔隙度储层.

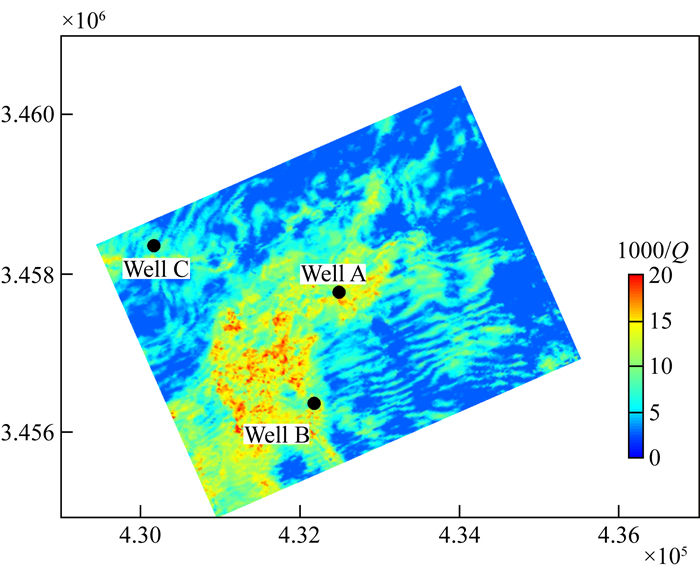
图 6给出研究工区致密砂岩储层的衰减三维切面，该块工区面积为18.75 km².图中显示，井A和井B分布于强衰减区域，井C衰减稍弱.衰减三维切面符合该地区须家河组致密砂岩储层辫状河三角洲沉积体系特征.

2 致密砂岩双重孔隙结构介质模型

由前述超声实验观测及工区储层研究，已知致密砂岩具有复杂的孔隙结构，岩石内部多发育孔隙和裂隙使得致密砂岩具有强烈的结构非均质性.为了描述岩石内部孔隙结构对弹性波的影响，本文建立致密砂岩岩石物理模型.针对致密砂岩目的层岩石微裂隙发育及含高饱和气的特性，采用可以分析岩石内部结构非均质性的Biot-Rayleigh(Ba et al., 2011)方程.首先分析岩石矿物组分，估算岩石基质及骨架的弹性参数与密度.目的层致密砂岩主要为石英砂岩，石英含量较高，含少量长石及岩屑，取石英体积模量K=37 GPa、剪切模量μ=44 GPa，长石体积模量K=75.6 GPa、剪切模量μ=25.6 GPa(Mavko et al., 2009).

岩石由不同矿物颗粒组成，各自的弹性模量不同，各矿物组分组成的复合物的弹性模量与各组分矿物的弹性模量有关.本文使用Voigt-Reuss-Hill(Voigt，1928；Reuss，1929；Hill，1952)平均方程求取岩石基质的体积模量和剪切模量：

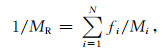
(3a)

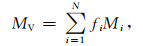
(3b)

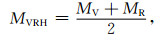
(3c)

式中：f_i、M_i表示第i种矿物组分的体积分数、弹性模量；M_VRH表示基质的弹性模量.

其次，本文基于岩石基质性质、储层孔隙结构、骨架固结程度等因素采用微分等效介质理论(DEM)，将孔隙和裂隙依次加入到岩石基质中，得到岩石干骨架，计算其弹性参数和密度(Norris et al., 1985；Zimmerman, 1991).Li等(Li and Zhang, 2010，2012; 李宏兵和张佳佳，2014)对DEM理论进行了改进，提出了新的解析近似式模型.Berryman(1992)提出等效体积和剪切模量的耦合的微分方程组如下：

(4a)

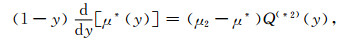
(4b)

其中初始条件是K^*(0)=K₁、μ^*(0)=μ₁，K₁和μ₁分别为初始相的体积模量和剪切模量(相1)，K₂和μ₂分别为逐渐加入包体的体积模量和剪切模量(相2)，y为相2的含量，P^*i和Q^*i是针对具有自相容等效弹性模量K_SC^*和μ_SC^*的背景介质中第i种组分的矿物几何因数.

最后，考虑储层环境下的岩石，采用Batzle和Wang(1992)提出的方程，计算储层流体在不同温度、压力条件下的体积模量和密度.然后利用Biot-Rayleigh方程进行平面波分析，估算含流体的岩石的波响应特征，得到致密砂岩饱和岩石物理模型.该波动控制方程是基于Hamilton原理推导得出的，将不同孔隙区域间的局部流体流动机制相互作用引入应变能、动能，建立了相应的势能函数、动能函数和耗散函数，进而推导出相应的双孔介质波传播控制方程为

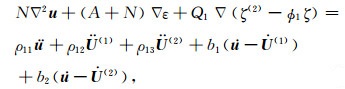
(5a)

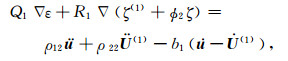
(5b)

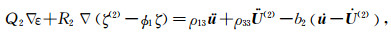
(5c)

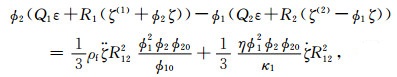
(5d)

式中u，U⁽¹⁾和U⁽²⁾分别为固体骨架的平均颗粒位移、流体相1(主骨架中的流体)、流体相2(微裂隙中的流体)的位移；ε，ζ⁽¹⁾和ζ⁽²⁾是对应的3个位移散度场；ζ表示地震波激励过程中产生的局域流体变形增量.岩石内部由于孔隙结构的非均匀性发育有两类不同孔隙，ϕ₁₀和ϕ₂₀是主体骨架和微裂隙的局部孔隙度；R₁₂为微裂隙的半径.ϕ₁和ϕ₂是两类孔隙的绝对孔隙度.ρ_f、η和κ₁分为流体的密度、黏度与渗透率.A、N、Q₁、Q₂、R₁与R₂为弹性参数，ρ₁₁、ρ₁₂、ρ₁₃、ρ₂₂与ρ₃₃为密度参数，b₁与b₂为耗散参数.

对Biot-Rayleigh波传播控制方程进行平面波分析，解出复波数，得到相速度和品质因子(详见附录A).

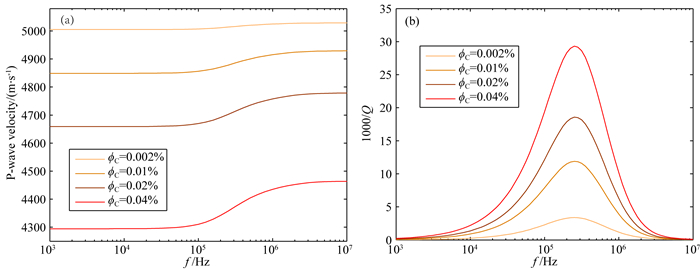
3 孔隙结构的非均质性对纵波频散和衰减的影响 3.1 超声频带下裂隙含量对纵波频散和衰减的影响

本文基于建立的致密砂岩岩石物理模型分析致密砂岩中的纵波频散和衰减特征，模型孔隙度为8%，渗透率为0.0004 μm²，采用的微裂隙半径为50 μm，岩石颗粒和骨架弹性参数分别由Voigt-Reuss-Hill平均方程和DEM公式计算得到.将模型设置为完全饱气，通过调节理论方程中岩石裂隙孔隙度的大小，可以描述岩石内部裂隙含量对致密砂岩中的纵波衰减和频散的影响.将裂隙孔隙度分别设置为0.002%，0.01%，0.02%，0.04%，此时模型中其他参数均保持不变.如图 7所示，给出了在频率段(10³~10⁷Hz)致密砂岩不同裂隙孔隙度的纵波频散(a)和衰减(b)曲线.从图中可以看到，随着致密砂岩岩石内部裂隙含量的增多，纵波频散和对应的衰减峰值逐渐增大，频散和衰减峰位于10⁵~10⁶Hz的超声波频带下.当岩石裂隙含量增加时，岩石内部孔隙结构的非均质性增加，从而导致更强的波频散和衰减.

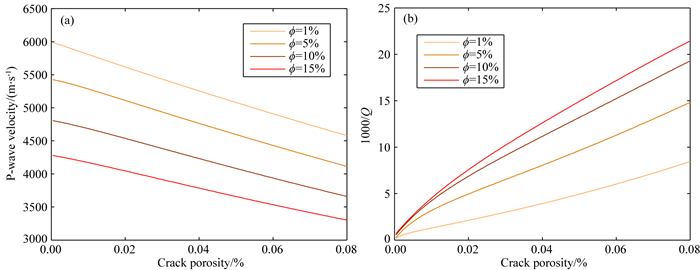
同时，将模型给定为实验室频率1 MHz，裂隙孔隙度设置为变量，给出了分别在总孔隙度为1%、5%、10%及15%时致密砂岩纵波速度和衰减随裂隙含量的变化关系(如图 8).可知随着裂隙含量的增加，纵波速度逐渐降低，衰减逐渐增加，在不同的孔隙度下，规律一致.

3.2 地震频带下裂隙含量对纵波频散和衰减的影响

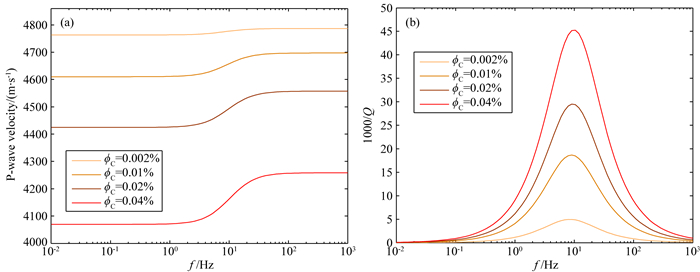
将Biot-Rayleigh模型从微观尺度非均质性推广到中观尺度非均质性(考虑裂隙半径130 mm)，分析在地震频段岩石内部结构非均质性的影响.如图 9所示，给出频率段(10^-2~10³ Hz)致密砂岩不同裂隙孔隙度的纵波频散(a)和衰减(b)曲线.随着致密砂岩岩石内部裂隙含量的增多，纵波频散和对应的衰减峰值增大，频散和衰减峰出现于1~100 Hz的地震频带下.

由于实际储层在各个尺度下都可能存在非均质性裂隙或裂缝，图 7主要分析的是微观尺度非均质性，其对应的纵波频散、衰减有效频段主要在超声频段，图 9主要分析中观尺度非均质性，其有效频段主要在地震频段，至于中间的频段(如1000 Hz)及其对应介于微观与中观之间的尺度的非均质性，由于没有相应观测结果进行对比研究，所以本文没有开展建模、分析.

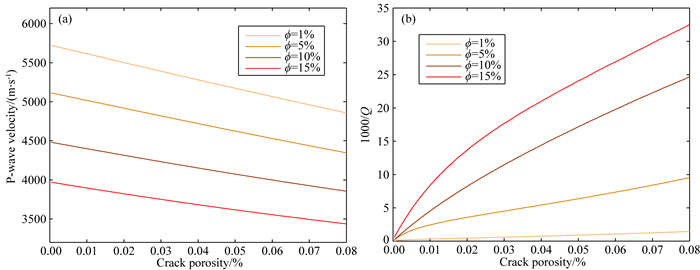
给定地震频率50 Hz，将裂隙孔隙度设置为变量，给出了分别在总孔隙度为1%、5%、10%和15%时致密砂岩纵波速度和衰减随裂隙含量的变化关系(图 10).结果显示，随着裂隙含量的增加，地震频段纵波速度逐渐降低，衰减增加，规律与超声频带一致.由于考虑的岩石内部裂隙的含量、尺度差异，中观尺度下岩石微裂隙联通构成较大裂缝，孔隙结构的非均质性增强，岩石渗透率增加，岩石纵波速度降低，频散和衰减增强.

4 致密砂岩衰减岩石物理图板的建立及校正 4.1 衰减岩石物理图板的构建

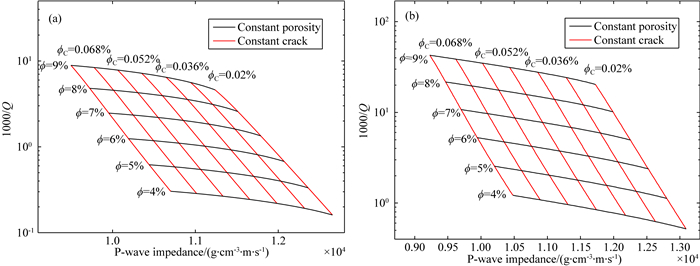
研究工区为高饱和气的致密砂岩天然气藏，因此，本文考虑完全饱气情况下的致密砂岩衰减岩石物理图板，预测储层的裂隙含量.按照前述的岩石物理建模流程，引入纵波衰减和波阻抗参数，分别设置为纵、横坐标.将模型中的裂隙孔隙度和总孔隙度设置为变量，将相应的衰减和波阻抗值进行交汇，得到超声(1 MHz)和地震频率(50 Hz)下关于储层孔隙度、裂隙孔隙度的衰减岩石物理图板.如图 11所示，分别给出超声和地震频率下的衰减岩石物理图板.黑线指在恒定孔隙度时，衰减和纵波阻抗随裂隙孔隙度的变化关系.红线表示在同一裂隙孔隙度下，随着孔隙度的变化，衰减和波阻抗的变化特征.结果显示，超声和地震频率下纵波衰减皆随着裂隙含量和孔隙度的减小呈单调下降趋势，此时波阻抗逐渐增大.

4.2 超声频率下基于实验数据校正图板

本文针对致密砂岩储层建立了基于纵波衰减和纵波阻抗的岩石物理图板.在利用图板对储层进行定量预测之前，需利用实验数据及地震资料对图板进行校正，从而获得最终的储层岩石物理图板，进而在图板的储层参数(文中主要指孔隙度和裂隙孔隙度)范围内，对储层裂隙含量和孔隙度进行定量预测.

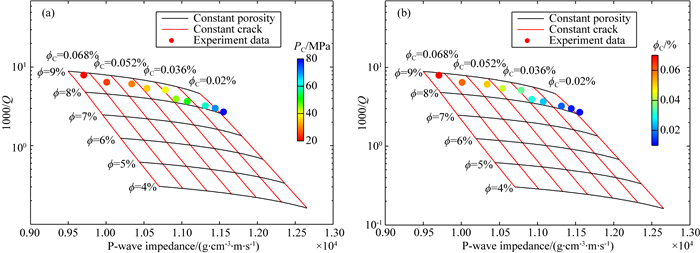
基于实验观测结果，本文采用魏颐君等(2020)、Zhang等(2019)提出的裂隙参数反演方法，根据围压及纵横波速度估算不同围压下饱气岩样裂隙孔隙度，对比上述得到的衰减岩石物理图板进行校正.如图 12给出了校正后的超声频段图板与样本数据的对比情况(色标表示实验数据的围压及裂隙孔隙度).对比样本数据和图板，可知样本的孔隙度与图板吻合良好，数据散点与图板对应的孔隙度基本一致.样本的裂隙孔隙度与图板基本符合，但前者略有偏低，随着裂隙孔隙度减小，数据散点衰减与波阻抗的变化趋势与图板相同.

4.3 地震频率下基于地震数据校正图板

依据工区的测井与地震资料，对衰减岩石物理图板进行地震频率下的校正.利用工区的叠后地震资料，基于改进的频移法公式(2)估算储层衰减，纵波阻抗由地震反演得到，提取对应相关测井数据的井旁地震道衰减和波阻抗，将测井的储层参数(孔隙度)作为对应地震衰减的储层参数.由于地震数据分辨率较低，不能与测井数据储层参数严格对应，因此将测井数据根据相应地震采样取均值，以与地震数据联系，得到对应的储层孔隙度.

如图 13所示，将井旁道的储层地震数据投影到校正后的岩石物理图板，图中孔隙度由颜色深浅表示，颜色越深，孔隙度越高.对比地震数据与岩石物理图板可知，地震数据整体与图板的规律基本吻合，衰减随着孔隙度的增加整体呈逐渐增加的趋势.图板与实际数据对比显示，含气层主要孔隙度分布范围在5%~9%之间.基于该图板对储层裂缝含量、孔隙度的定量预测是可行的.

5 裂隙孔隙度地震预测

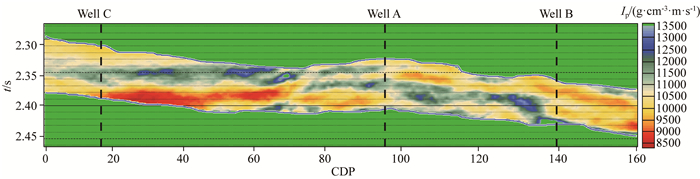
本文对工区一条过井A、井B和井C的测线进行了储层孔隙度、裂隙含量的定量预测.首先使用改进频移法提取该测线的衰减值(如图 4b)，其次提取反演得到的纵波阻抗值，得到该测线的波阻抗二维剖面(如图 14).基于前述得到的致密砂岩衰减岩石物理图板，结合储层地震衰减和波阻抗值，开展对比分析，在图板的储层参数范围内，进行孔隙度、裂隙孔隙度的估算.

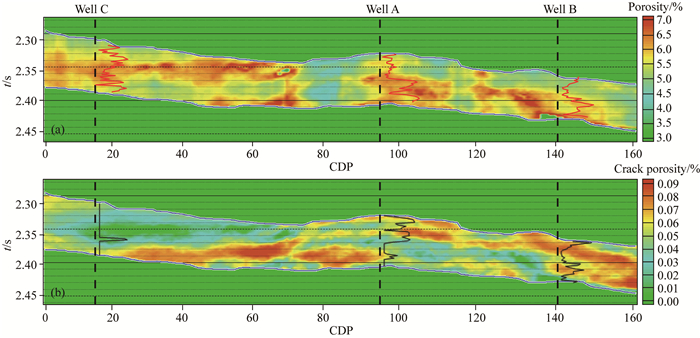
在目的层，反演主要考虑的是主力致密砂岩含气储层, 对数据点与图板的边界差距较大的情况按非储层处理，图板之外裂隙孔隙度、孔隙度过低的致密储层也并非勘探目标.因此，基于地震数据在图板投影的情况，对储层参数进行反演，预测储层孔隙度和裂隙含量.如图 15给出了储层孔隙度和裂隙含量的二维剖面，结果显示，该储层的孔隙度分布范围大致为3%~7%，井A和井B处显示较强的裂隙孔隙度，井C裂隙含量较差.

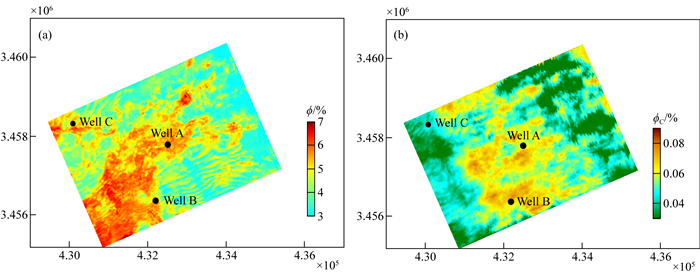
将三口井的孔隙度分别与二维反演结果图进行交会，结果显示，地震预测孔隙度结果与测井解释的孔隙度曲线基本吻合.利用上述方法可得到工区的三维预测结果.如图 16所示，给出了18.75 km²致密砂岩储层孔隙度、裂隙含量的三维预测结果.结果显示，井A和井B分布于孔隙度、裂隙含量较高的区域，这两口井所在区域目的层孔隙连通性较好，且储集空间良好，具有较好的天然气富集条件.基于整个目的层考虑，地震预测结果及测井曲线均显示，井A平均孔隙度高于井B，井A储层条件更好，且目的层主力产气段为上段，井B上段孔隙度明显低于井A.井C位于裂隙含量较低的区域，连通性差.在实际试气结果中，井A为高产气井，产气量为6.833万方/天，井B产气量为0.36万方/天，井C基本不产气.分析表明，储层预测结果与实际试气情况基本符合，孔隙度、裂隙含量预测结果可有效指示储层含气性.

6 结论

本文分析了致密砂岩储层岩石物理特征，基于致密砂岩样本的实验数据，以岩石物理理论模型为依据，利用Biot-Rayleigh方程，提出了微裂隙-孔隙衰减岩石物理模型.实验数据的分析显示，纵波衰减和纵波阻抗对岩石的裂隙含量和孔隙度敏感性较好，可选取这两种参数构建致密砂岩多尺度衰减岩石物理图板，进而应用于储层裂隙含量及孔隙度的预测.分别采用谱比法和改进频移法估算实验样本和地震资料衰减，利用岩石实验观测、测井解释及地震资料对图板进行检验与校正.最终得到的图板能够较好描述致密砂岩储层物性参数与地震波响应特征之间的定量关系.

采用衰减岩石物理图板，基于研究工区的储层地震数据，实现了二维测线和三维地震资料的裂隙含量及孔隙度的定量预测，并且，对比显示，预测结果与三口井的孔隙度测井曲线，以及实际试气结论基本一致.本文基于地震衰减构建的多尺度岩石物理图板，可直接应用于工区致密砂岩天然气检测，并且，这种方法可以仅依赖于叠后地震数据进行储层定量预测，相对于叠前岩石物理预测节省了工作量，对资料处理及品质要求较低，具有更广阔的应用空间.相对于常规叠后预测方法，这种衰减岩石物理模型则同时利用纵波速度、衰减信息进行交会分析，有利于克服来自多解性、资料品质、处理信息等方面的负面影响，具有潜在的重要推广价值.

附录A

将纵波的平面波解析解e^i(ωt-k·x)代入Biot-Rayleigh波动方程中，得到复波数平方k²的复数一元三次方程组，求解方程组：

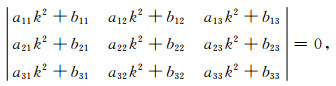
(A1)

其中，k表示波数，且

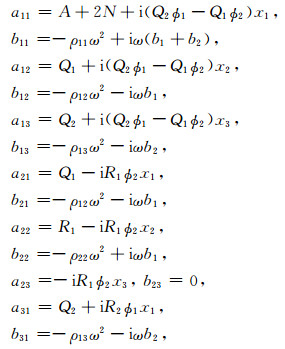
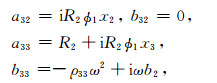
其中，x₁=i(ϕ₂Q₁-ϕ₁Q₂)/Z, x₂=iϕ₂R₁/Z, x₃=-iϕ₁R₂/Z, 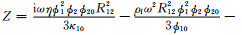(ϕ₂²R₁+ϕ₁²R₂).

复波数平方k²的三个解分别对应于快纵波及两类慢纵波，其中速度最高的快纵波即对应常规勘探的纵波，其频散和衰减可以用复速度来表示v=ω/k(Carcione, 2007),

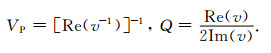
(A2)