2. 中国石油西南油气田公司页岩气研究院, 成都 610051
2. Research Institute of Shale Gas, PetroChina Southwest Oil and Gasfield Company, Chengdu 610051, China
我国页岩气资源丰富,页岩气储量位居世界第一,截止2018年6月,累计探明页岩气地质储量超过1万亿m3(Liu et al., 2019; Ma, 2019).作为一种重要的非常规能源,页岩气的勘探开发对降低我国能源对外依存度,优化能源结构起到了积极的作用.砂岩和碳酸盐岩等常规油气藏往往表现出各向同性的特性,其弹性参数表征仅需2个独立弹性刚度系数(E、v).有别于常规油气藏,页岩表现出典型的横观各向同性特征,其弹性特征表征需要5个独立的弹性刚度系数(c11、c33、c44、c66和c13)(Gui et al., 2018; Ma et al., 2019; Zhang et al., 2020).目前,地球物理测井仪器只能获取5个独立弹性刚度系数中的3个,即c33和c44可通过阵列声波资料提供的纵波、垂向横波和中子密度测井曲线计算,c66可通过斯通利波反演水平横波的方法计算,但剩余2个刚度系数(c11和c13)仍无法通过测井资料直接计算(郭洪志, 2014; 刘忠华等, 2017; 桂俊川等, 2019),目前主要通过室内实验或经验公式获得(Wang, 2002; Vernik and Nur, 1992).但是,室内实验存在周期长、费用高、结果不连续等缺点,而经验公式又缺乏普适性.岩石物理方法是页岩气勘探的重要手段之一,岩石物理建模架接起了岩石微观物性特征与宏观弹性特征的桥梁(Ba et al., 2017; 郭梦秋等, 2018; 巴晶等, 2013; Ba et al., 2016, 2019).
由于黏土和干酪根的含量及定向排列,页岩表现出较强的各向异性特征(Ma and Chen, 2014; Ma et al., 2016; Liu et al., 2020; 桂俊川等, 2019).国内外学者针对页岩以及各向异性特征进行岩石物理建模研究,经过近30年的发展,国内外学者取得了显著的进步.早在1992年,Vernik和Nur(1992)基于Backus平均建立了横观各向同性页岩岩石物理模型.Hornby等(1994)从各向同性自洽模型(SCA模型)和微分等效介质模型(DEM模型)出发,推导了各向异性SCA和DEM模型,在扫描电镜基础上引入高斯分布,模拟了页岩中黏土和干酪根的定向排列分布和成层特性,取得了良好的计算效果.在此基础上,原宏壮(2007)进一步考虑有机质矿物的成层特性,建立了各向异性双重孔隙有效介质模型.Bandyopadhyay(2009)、Wu等(2012)将干酪根视为背景介质,利用Voigt-Reuss-Hill(V-R-H)界限计算除干酪根以外的混合岩石矿物的等效弹性模量,并通过各向异性DEM模型将混合物添加到干酪根中,来模拟富含有机质页岩的弹性属性.通常情况下干酪根含量很少,不足以在地层中形成连续的背景,并且V-R-H界限计算的混合物的等效弹性模量有较大误差.Zhang等(2012)通过将临界孔隙度进行反演,建立了适用于油页岩的岩石物理模型,并用于横波波速的预测.考虑到流体的连通问题,Hu等(2013)利用各向异性SCA和DEM模型模拟得到的黏土和流体混合物作为背景介质,并采用V-R-H界限模拟干酪根、石英、方解石等混合物的等效弹性模量,最后采用各向异性DEM模型将此混合物添加到背景介质中,但由于干酪根和石英等矿物的弹性模量差异较大,该模型仍然存在较大误差.董宁等(2014)在SCA模型和DEM模型的基础上,引入三维孔隙形态及CIZ模型,建立了适用于富有机质泥页岩的岩石物理模型,并讨论了不同孔隙形态、泥质含量对岩石弹性性质的影响.邓继新等(2015)从龙马溪组页岩的岩性和微观结构特征出发,基于SCA模型、微分等效模型和Backus平均的有效组合,建立了龙马溪组页岩的岩石物理模型,并以实验结果和测井数据进行了验证.钱恪然(2016)认为各井段有机质成层特性不同,因此,将描述有机质矿物成层的参数设置为未知数进行岩石物理建模,并通过测井约束进行了反演.李诺(2016)研究了干酪根成熟度以及包含的流体(油、气)对页岩弹性参数的影响,并提出了适用于页岩地层的岩石物理等效模型.针对Wu等(2012)和Hu等(2013)研究存在的局限,刘子淳和郝贺晨(2017)将干酪根视为背景介质,利用SCA和DEM模型将孔隙添加到干酪根中,以保证孔隙和干酪根的相互连通,利用Hashin-Shtrikman(H-S)界限计算除干酪根外矿物等效弹性模量并作为包裹体,然后利用DEM添加到背景介质中,最后进行流体替换得到饱和页岩岩石物理模型,该模型考虑了干酪根及孔隙的连通性,计算精度相对较好.
尽管国内外学者针对页岩开展了大量岩石物理建模研究工作(刘财等,2017;蔡生娟等2020;朱伟,2020),但是,现有的页岩岩石物理模型仍然存在诸多问题需要解决.在页岩各向异性的成因描述方面,当前的岩石物理模型大都采用Backus模型进行描述(刘财, 2018; 张冰, 2018),而Backus模型预测的刚度系数c33存在较大误差;尽管Vernik和Landis(1996)通过引入校正因子对Backus模型进行了修正,但其计算公式仍然为半经验公式,并不具有普适性.同时,矿物混合物的等效弹性的描述也会对模型计算精度产生一定影响,现有的岩石物理模型主要采用V-R-H界限或H-S界限模拟矿物混合物的等效弹性性质(Wu et al., 2012; Hu et al., 2013; 刘子淳和郝贺晨, 2017),但如果各个矿物模量存在显著差异,就会导致矿物混合物等效弹性模量上下限存在较大的差异,这样也会显著影响模型的计算精度.此外,由于岩石物理建模需要结合区域岩石微观物性特征,目前针对龙马溪组页岩建立的岩石物理模型,除了存在上述缺点之外,还存在一些其他不足之处:刘子淳和郝贺晨(2017)将干酪根视为背景介质,然后将孔隙添加到干酪根中,这与页岩实际微观特征存在差异,实际页岩的孔隙广泛存在于干酪根、黏土和脆性矿物之中,这种只考虑干酪根等部分组分微观孔隙的模型显然与实际不符;邓继新等(2015)忽略了干酪根与黏土的相互嵌合,将干酪根作为一种包裹体添加到页岩矿物中,这导致脆性矿物中也分布有干酪根,从而影响了建模结果;Liu等(2017)直接用SCA模型将流体添加到页岩基质当中,这不仅不符合页岩孔隙大多处于离散分布的状况,而且不适用于低频情况,这是因为该模型没有进行流体替换,而是直接进行流体添加.为此,本文针对龙马溪页岩开展了横观各向同性页岩岩石物理建模研究,以期为地球物理和工程地质参数的计算和分析奠定基础.首先,分析龙马溪组页岩的微观物性特征,明确影响页岩弹性性质的微观物性特征;然后,建立一种适用于龙马溪页岩的岩石物理模型,对岩石物理模型框架、建模流程和关键算法模型进行系统阐述;随后,详细论述矿物颗粒和孔隙纵横比参数的确定方法;最后,以四川盆地A井龙马溪组地层为例,计算龙马溪页岩孔隙纵横比、纵横波速和弹性参数,并检验本文模型的准确性.本文模型能够准确计算页岩5个独立的刚度系数,为页岩弹性参数、声波波速、各向异性和脆性分析提供了有效手段,也为后续地球物理和工程地质参数分析提供了重要依据.
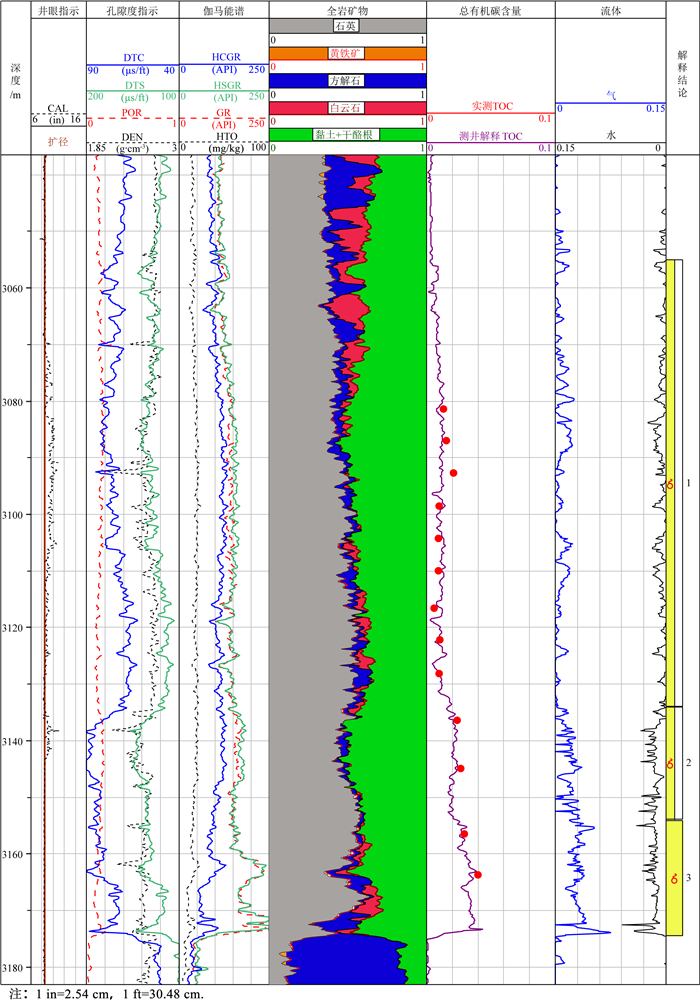
1 页岩物性特征分析影响页岩岩石物理建模的因素较多,岩石矿物组成、矿物含量、矿物性质、孔隙度、孔隙连通关系、孔隙流体、颗粒形态、孔隙形态、矿物及流体性质等都是影响页岩弹性性质的重要因素.为此,首先对页岩基本物性特征进行分析,从而为页岩岩石物理建模提供基础依据.图 1为四川盆地A井龙马溪组页岩地层测井解释成果图.从左至右,第一道为深度道;第二道为井眼指示道,包括井径和扩径指示;第三道为孔隙度指示道,包括纵、横波时差、孔隙度和密度;第四道为伽马能谱道,包括HSGR总伽马、HCGR无铀伽马、GR自然伽马和HTO钍曲线;第五道为全岩矿物,包括石英、黄铁矿、方解石、白云石、黏土+干酪根;第六道为总有机碳含量指示,其中红色散点为实测数据,连续曲线为测井解释结果,经过标定的测井解释总有机碳含量和实测结果吻合度较好.第七道为流体指示,包括含气量和含水率;最后一道为解释结论.
|
图 1 A井龙马溪组页岩测井解释成果图 Fig. 1 Logging interpretation results of the Longmaxi formation shale in well A |
由图 1不难可以看出:A井龙马溪组底部页岩3155~3174.5 m为主力产气层位(龙一段),页岩表现出明显的高自然伽马、高声波时差、高孔隙度、低密度的测井响应特征;龙马溪页岩中矿物以石英和黏土为主,方解石和白云石含量相对较少,并夹杂有少量黄铁矿;龙马溪页岩中总有机碳含量介于0.5%~4%,其中,龙马溪组底部龙一段有机碳含量较高(>2.5%);龙马溪页岩孔隙中所含流体主要为气和水,含气量介于0.5%~12.5%,其中,龙马溪组底部龙一段含气量较高(3%~12.5%).
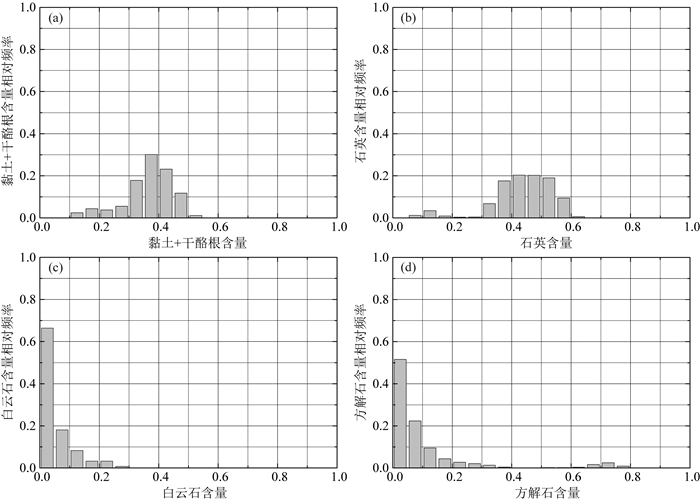
对龙马溪组底部龙一段页岩主要矿物进一步统计分析,结果如图 2所示.由图可知:龙一段黏土和干酪根含量占总矿物含量的10%~55%,并主要分布在30%~50%之间;石英含量占总矿物含量的5%~65%之间,并主要分布在30%~60%之间;白云石含量占总矿物含量的0~25%之间,并主要分布在20%以下;方解石含量占总矿物含量的0~80%之间,并主要分布在30%以下.
|
图 2 A井龙马溪组底部页岩主要矿物含量统计 (a)黏土+干酪根含量;(b)石英含量;(c)白云石含量;(d)方解石含量. Fig. 2 Statistics of content for main minerals at the bottom of Longmaxi formation shale in well A (a) Clay + kerogen content; (b) Quartz content; (c) Dolomite content; (d) Calcite content. |
孔隙和微裂缝是页岩气的主要储集空间,页岩气以吸附态和游离态赋存于页岩中.龙马溪页岩中微纳米孔隙十分发育,孔隙类型主要为有机质孔、粒内孔、粒间孔(邹才能等, 2010).扫描电镜和铸体薄片是研究微观孔隙和结构特征的重要手段,典型的页岩微观结构照片如图 3所示.图 3a为有机质孔隙,有机质孔隙形态以椭球形、球形为主,孔隙间互相分散、互不联通;图 3b为纤维状伊利石粒间孔,其形态为扁平状类裂隙型缝状孔隙,伊利石等黏土矿物的可压缩性非常强,导致黏土颗粒之间的粒间孔呈扁平状,类似于微裂缝;图 3c为相互嵌合的黏土矿物,黏土矿物多以层状、块状的形式定向排列和堆叠,这种定向排列与页岩地层形成的沉积环境历史密切相关;图 3d为页岩铸体薄片,其中亮色为脆性矿物,可以看出,石英等脆性矿物以分散颗粒的形式嵌在黏土和干酪根中.

|
图 3 龙马溪页岩典型微观结构图 (a)有机质孔隙(邹才能等, 2010);(b)纤维状伊利石粒间孔(杨峰等, 2013);(c)片状黏土矿物颗粒相互嵌合;(d)铸体薄片. Fig. 3 Typical microstructure pictures of Longmaxi shale (a) Organic pore (Zou et al., 2010); (b) Fibrous illite intergranular pore (Yang et al., 2013); (c) Flake clay mineral particles intermingled with each other; (d) Casting slice image. |
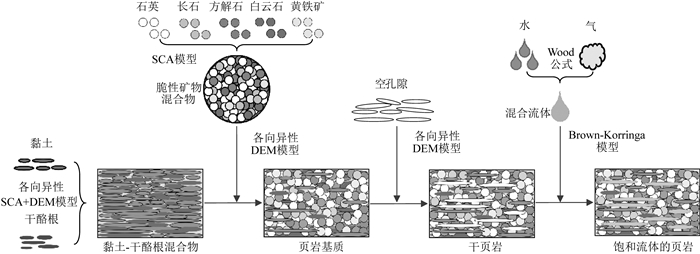
黏土和干酪根混合物通常呈定向排列(Vernik and Nur, 1992; Vernik and Landis, 1996),同时,页岩中水平向分布大量孔隙和微裂缝,这些因素是造成页岩各向异性的主要成因(Sayers, 1994).如何利用恰当的基础岩石物理模型描述黏土、干酪根的定向排列分布以及水平向分布的扁平状孔隙是页岩岩石物理建模的重点和难点.因此,在重点考虑页岩各向异性成因的基础上,针对黏土和干酪根互相镶嵌且定向排列和分布的特征,综合利用各向异性SCA模型和各向异性DEM模型模拟黏土和干酪根混合物,并将其作为背景介质;为了解决脆性矿物力学性质显著差异导致的问题,采用SCA模型对脆性矿物混合物进行模拟,并将脆性矿物混合物利用各向异性DEM模型添加到背景介质中,得到页岩基质模型;考虑到页岩孔隙以有机质孔隙为主(邹才能等, 2016),并且有机质孔隙多呈分散态,此处利用各向异性DEM模型将孔隙添加到页岩基质中;最后,为了使模型适用于低频条件,先利用Wood公式将气和水进行混合,然后利用Brown-Korringa模型进行各向异性条件下的流体替换,最终得到饱和页岩岩石物理模型.
本文提出的横观各向同性页岩岩石物理模型如图 4所示,其具体建模流程如下:
|
图 4 页岩岩石物理模型建模流程 Fig. 4 Modeling procedure of rock physics modeling for shale |
(1) 建立有机质矿物混合物模型:由于页岩矿物中黏土和干酪根互相镶嵌,干酪根又与其他矿物之间弹性参数差异显著,如表 1所示,其他矿物的弹性模量均比较大,而干酪根弹性模量较小,与流体的弹性模量非常接近,并且镶嵌在黏土矿物中,加之黏土和干酪根通常呈现出定向排列和分布特征,因此将黏土和干酪根单独考虑.本文综合利用各向异性SCA模型和各向异性DEM模型模拟黏土和干酪根混合物的等效弹性特征,各向异性SCA模型和各向异性DEM模型见第2.2.2节和第2.3节.为了保证干酪根和黏土的相互连通,先利用各向异性SCA模型计算干酪根和黏土含量各占50%情况下的弹性特征,然后用各向异性DEM模型将两者的体积含量调整至对应的百分比,这既保证了干酪根和黏土的相互连通,又避免了由于干酪根和黏土添加顺序的不同而导致混合物弹性模量的不对称,还考虑了黏土和干酪根的定向排列和分布特征.模拟过程中,黏土和干酪根的颗粒纵横比是计算所需的关键参数,该参数通过各向异性SCA模型和各向异性DEM模型的参数化分析进行确定,具体分析方法和过程见3.1节.此外,处理过程中黏土和干酪根的相对含量由测井资料给出,即图 1中第五道和第六道测井曲线,黏土和干酪根的弹性参数见表 1所示.
|
|
表 1 页岩中主要矿物和流体的弹性参数(Mavko et al., 2009; Carcione et al., 2011) Table 1 Elastic parameters of main minerals and fluids in shale(Mavko et al., 2009; Carcione et al., 2011) |
(2) 建立脆性矿物混合物模型:脆性矿物是指除了黏土和干酪根以外的矿物,包括石英、长石、方解石、黄铁矿等,与黏土和干酪根相比,其弹性模量较大、脆性较强,而且相对比较接近,故将其分为一类矿物进行单独考虑.本文利用各向同性SCA模型模拟石英、长石、方解石等脆性矿物混合物的等效弹性模量,各向同性SCA模型见第2.2.1节.各向同性SCA模型可以避免由于脆性矿物添加顺序不同导致的建模结果差异,并且脆性矿物均为固体,各个脆性矿物的剪切模量差异不大,也不会因为剪切模量的差异导致脆性矿物之间的互不接触,这就克服了传统方法的存在的问题.模拟过程中,石英、长石、方解石、黄铁矿等矿物的颗粒纵横比是计算所需的重要参数,此处通过脆性矿物颗粒图像识别进行提取,其提取和分析的具体方法见3.2节.此外,各脆性矿物的相对含量由测井资料给出,即图 1中第五道测井曲线,石英、长石、方解石、黄铁矿等矿物的弹性参数见表 1所示.
(3) 建立不含孔隙的页岩基质模型:将有机质矿物混合物作为背景介质,利用各向异性DEM模型将脆性矿物混合物添加到背景介质中,从而得到页岩基质模型,各向异性DEM模型见2.3节.考虑到黏土和干酪根混合物颗粒的定向排列受沉积环境和沉积构造历史的影响,而且A井龙马溪页岩地层倾角低(地层倾角分布在0°到5°之间,主频为3°左右),此处主要考虑黏土和干酪根混合物颗粒椭球颗粒长轴为近似水平分布的情况.从图 3d中可以看出,脆性矿物以分散的形式镶嵌在黏土和干酪根混合物当中,而DEM模型能够模拟脆性矿物的这种分散状态,因此将等效后的脆性矿物混合物作为包裹体,利用各向异性DEM模型添加到黏土和干酪根混合物背景介质中,从而得到不含孔隙的页岩基质模型.
(4) 建立含孔隙的干页岩模型:考虑页岩中孔隙主要为不连通孔隙(图 3a、b),利用各向异性DEM模型将空孔隙(不含任何流体)添加到页岩基质中,添加过程中空孔隙的弹性模量设置为0,从而得到含孔隙的干页岩模型.将空孔隙添加到页岩基质中而不是直接将气体和液体的混合物直接添加到页岩中,这是为了让模型适用于低频情况.模拟过程中,孔隙的纵横比是计算所需的关键参数,该参数无法直接获得,此处通过声波测井资料的反演获得,其具体反演方法和过程见3.3节.此外,处理过程中空孔隙的含量由孔隙度曲线给出,即图 1第二道测井曲线.
(5) 建立饱和流体页岩岩石物理模型:由于龙马溪页岩孔隙流体主要为气和水,此处先利用Wood公式计算流体混合物的等效弹性模量,Wood公式见2.4节.为了使模型适用于低频条件,利用Brown-Korringa模型进行各向异性条件下的流体替换(见2.5节),将空孔隙替换为Wood公式计算得到的气和水两相混合物,最终得到饱和流体页岩岩石物理模型.处理过程中气和水的相对含量由测井曲线给出,即图 1中第七道测井曲线,气和水的弹性参数见表 1所示.
2.2 自洽模型(SCA模型) 2.2.1 各向同性SCA模型SCA模型是由Budiansky(1965)和Hill(1965)提出的,并由Berryman(1980a, b)进行了扩展.该模型通过将要求解的多相混合介质放置于无限大的背景介质中,并不断调整背景介质弹性参数,使其最终的弹性参数与多相介质的弹性参数相匹配,当有一平面波入射时,混合介质不会再引起散射,此时背景介质的弹性模量与混合介质的等效弹性模量相等.A井中龙马溪组地层的脆性矿物包括4种:石英、黄铁矿、方解石、白云石,对应的等效自相容近似模型可写为
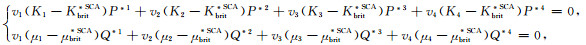
|
(1) |
式中:v1、v2、v3、v4分别为石英、方解石、白云石、黄铁矿的体积分数,无因次;P*1、P*2、P*3、P*4和Q*1、Q*2、Q*3、Q*4分别为石英、方解石、白云石、黄铁矿的形状因子,无因次;Kbrit*SCA为脆性矿物混合物的SCA等效体积模量,单位为GPa;μbrit*SCA为脆性矿物混合物的SCA等效剪切模量,单位为GPa.
由于脆性矿物混合物等效弹性模量Kbrit*SCA和μbrit*SCA是相互耦合的,须通过迭代求解.此外,形状因子P*i和Q*i中包括描述脆性矿物形态的颗粒纵横比,颗粒纵横比是指颗粒的短轴和长轴之比,当颗粒纵横比越接近0时,此时脆性矿物越扁,当颗粒纵横比越接近1时,此时脆性矿物越圆.对于具有任意纵横比的椭球形填充物,其纵横比形状因子P和Q的计算方法请参考附录A.
各向同性SCA模型为对称模型,既可以模拟固体和固体的混合,也可以模拟固体和液体的混合.但当模拟的多相介质的剪切模量差异较大时,例如模拟固-液两相混合,只有当孔隙度介于40%~ 60%时才能保证流体和固体的双相连通(Berryman, 1980b).
2.2.2 各向异性SCA模型页岩中黏土和干酪根是造成页岩各向异性的重要原因之一,各向同性SCA模型无法描述其各向异性.Hornby等(1994)以包裹体理论为基础,将各向同性SCA模型推广到各向异性范畴.页岩中非脆性矿物主要包括黏土和干酪根,并且干酪根通常镶嵌于黏土中.由于干酪根和黏土弹性参数差异较大,为了避免SCA模型存在的连通性缺陷,在模拟黏土和干酪根混合物等效弹性参数时,需结合各向异性DEM模型来使用.
模拟黏土和干酪根混合物等效弹性特征的第一步是利用各向异性SCA模型计算黏土、干酪根含量各占50%的等效弹性刚度.此时只涉及黏土和干酪根,对应的各向异性SCA模型为
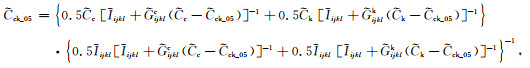
|
(2) |
式中:
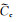
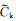
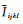

式(2)中Eshelby张量与包裹体纵横比密切相关,通过公式(3)进行计算:

|
(3) |
其中,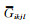
Berryman(1980b)通过向背景介质中逐渐添加包含物来模拟两相混合物的等效弹性模量,建立了DEM模型.DEM模型的基本思想如下:假定有一均匀的背景介质物质1,其体积为v0,从该介质中取出体积为Δv(Δv相对于v0非常小)的材料1,同时在该介质中嵌入相同体积Δv的材料2,这时所形成的复合材料的等效弹性模量产生改变,用等效后的均匀介质代替原先的基质,重复以上过程,直到达到材料1和材料2所占的体积百分比为真实百分比.包裹体被添加到背景介质中时,每一步的替换体积要非常小.不同于SCA模型,DEM模型为非对称模型,其最终等效的岩石弹性模量不仅受到添加物含量及包裹体纵横比的影响,还受到背景材料选择的影响.例如将材料1添加到材料2等效的弹性模量,和将材料2添加到材料1等效的弹性模量会有所差异.
为避免由于添加顺序造成的差异,模拟黏土和干酪根混合物等效弹性特征的第二步是将各向异性SCA模型模拟的
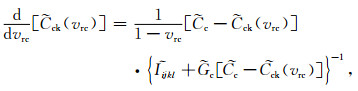
|
(4) |
式中:vrc需要添加到背景介质中的剩余黏土相对含量,且满足vrc=2vc-1,无因次;vc为黏土的真实含量,无因次;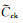
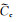
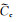
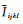
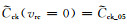
脆性矿物通常以分散态分布于黏土和干酪根混合物中,如图 3d所示.为模拟页岩基质的等效弹性刚度张量,将黏土和干酪根混合物视为背景介质,利用DEM模型将脆性矿物混合物添加到背景介质中.这一步中需要将脆性矿物的等效弹性模量Kbrit*SCA和μbrit*SCA表示为刚度张量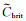

SCA模型和DEM模型适用于高频的实验条件(Mavko et al., 2009),在模拟固体和流体的等效问题时,孔隙中流体不能在孔隙中流动,孔隙压力处于未平衡和绝热状态.而实际地层中,由于声波或地震波穿过地层孔隙造成的孔隙压力扰动有足够的时间平衡.因此,此处先利用各向异性DEM模型将空孔隙(不含有任何流体)添加到页岩矿物中,得到干页岩骨架,其等效刚度张量用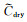
龙马溪页岩孔隙中,流体为页岩气和地层水.为了表征气、水两相混合物的等效弹性性质,利用Wood公式进行模拟(Wood,1955),气、水两相混合物的等效弹性模量可表示为
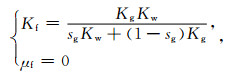
|
(5) |
式中:Kg为气体的体积模量,单位为GPa;Kw为水的体积模量,单位为GPa;Kf为混合流体的等效体积模量,单位为GPa;sg为含气饱和度,无因次;μf为混合流体的等效体积模量,单位为GPa.
2.5 流体替换模型(Brown-Korringa模型)Gassmann方程是研究流体替换问题的重要手段(Gassmann, 1951).但是,由于页岩具有显著的横观各向同性特征,传统Gassmann方程不再适用,Brown和Korringa(1975)将Gassmann方程进行了扩展,建立了适用于各向异性介质流体替换的Brown-Korringa模型,且该模型适用于低频条件.因此,在干页岩模型的基础上,利用Wood公式计算气、水两相混合物的等效弹性模量,然后利用Brown-Korringa模型把空孔隙替换为流体,即得到饱和流体的页岩岩石物理模型:

|
(6) |
式中: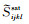

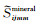

岩石物理建模过程中涉及的物性参数多,如各矿物相对含量、孔隙度、流体类型及其饱和度、各类纵横比等,其中,纵横比又包括各矿物颗粒纵横比、孔隙纵横比、脆性矿物作为包裹体纵横比.这些物性参数中可直接利用地球物理方法测量或解释获得的参数包括:岩石矿物类型及相对含量、孔隙度、流体类型及其饱和度,而其他物性参数(尤其是各类纵横比参数)无法通过地球物理方法直接获得.对于无法直接获得的物性参数,可在合理近似条件下通过测井资料进行反演.
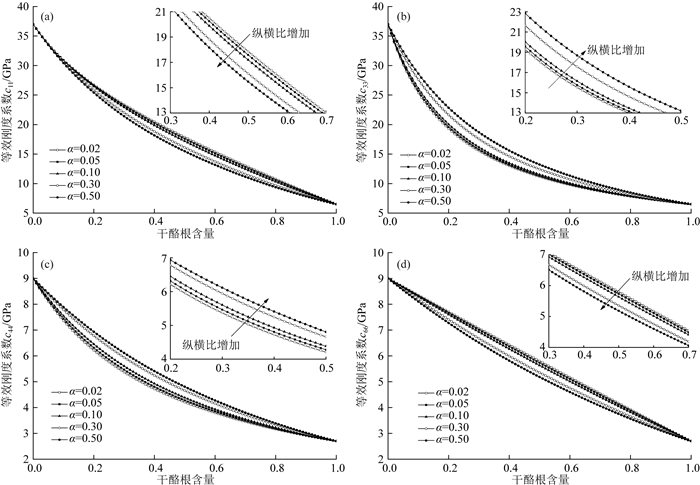
3.1 黏土和干酪根颗粒纵横比的确定黏土和干酪根的可压缩性强、延展性好,并以层状、块状的形式互相堆叠在一起.假定黏土和干酪根为近似椭球形,并具有相同的颗粒纵横比,结合各向异性SCA模型和DEM模型,本文模拟了黏土和干酪根颗粒纵横比分别为0.02、0.05、0.10、0.30、0.50条件下的黏土和干酪根混合物的等效弹性刚度系数,如图 5所示.模拟过程中黏土的体积模量Kclay=25 GPa,剪切模量μclay=9 GPa,干酪根体积模量Kkerogen= 2.9 GPa,剪切模量μkerogen=2.7 GPa(见表 1).
|
图 5 各向异性SCA和DEM模型预测的黏土和干酪根混合物等效刚度系数 (a)刚度系数c11;(b)刚度系数c33;(c)刚度系数c44;(d)刚度系数c66. Fig. 5 Equivalent stiffness coefficients of the mixture of clay and kerogen predicted by anisotropic SCA and DEM models (a) Stiffness coefficient c11; (b) Stiffness coefficient c33; (c) Stiffness coefficient c44; (d) Stiffness coefficient c66. |
由图 5可以看出,当黏土、干酪根的纵横比不等于1时,混合物等效弹性刚度矩阵表现出各向异性特征.随着包裹体(干酪根和黏土颗粒)纵横比增加,包裹体逐渐从椭球形变成球形,在变圆的过程中,水平向刚度系数c11逐渐降低,而垂向刚度系数c33逐渐增加,各向异性程度逐渐降低;当颗粒纵横比为1时,包裹体变成球形,c11和c33将会相互重合.c44和c66有类似于c11、c33的变化趋势.黏土和干酪根颗粒的纵横比在从0.02增加到0.5的变化过程中,各刚度系数的变化趋势分为两个阶段:当纵横比从0.02增加到0.1过程中,各个刚度系数变化不大;纵横比从0.1增加到0.5的过程中,刚度系数c11和c66明显降低,而刚度系数c33和c44明显增加.根据图 5的模拟结果,并考虑黏土和干酪根颗粒纵横比通常很小(如图 3c),实际建模中取干酪根和黏土颗粒的纵横比均为0.05.
3.2 脆性矿物颗粒纵横比的确定脆性矿物的可压缩性差,颗粒较大,磨圆较为接近一致.不同于黏土和干酪根,脆性矿物通常分散在黏土和干酪根混合物当中,并且易于在扫描电镜和铸体薄片等成像资料中识别出来.本文基于数字图像处理和MATLAB软件,对龙马溪页岩脆性矿物的微观特征参数进行提取和统计.以图 3d为例,图中所含脆性矿物颗粒纵横比提取主要步骤如下:(1)利用MATLAB将原图转换为二值图像,所谓的二值图像是指只包含黑白两种颜色的图像,转换后的图像如图 6a所示,其中白色介质的为脆性矿物,黑色背景的为黏土和干酪根混合物;(2)对于图 6a中占据像素较小的矿物,由于无法观测其具体细节,这将对最终的统计结果产生影响,因此将这些点视为噪点予以剔除,剔除后的图像如图 6b所示;(3)对于图 6b,编写相应程序对各个脆性矿物进行识别,同时计算各个脆性矿物的长、短轴,并用短轴除以长轴作为各矿物颗粒的纵横比,处理结果如图 6c.在统计过程中需要剔除由于少数颗粒堆放在一起,从而导致程序将这些颗粒视为整体而引起的误差.例如图 6c中圆圈部分,其中的几个颗粒由于无法从图像上区分,程序将其视为整体进行了识别和分析,这种结果显然是错误的,应予以舍弃.最后对各个颗粒的纵横比进行统计分析,结果如图 6d所示.由图可以看出,龙马溪组地层脆性矿物颗粒的纵横比分布在0.45~1.0之间,并集中分布在0.5~0.85之间.

|
图 6 脆性矿物颗粒纵横比的提取结果 (a)二值化图像;(b)去噪后图像;(c)颗粒纵横比确定;(d)颗粒纵横比统计直方图. Fig. 6 Extraction results of aspect ratio of brittle mineral grains (a) Binary image; (b) Denoised image; (c) Determination of grain aspect ratio; (d) Statistical histogram of grain aspect ratio. |
将各颗粒的纵横比代入式(1),即可计算脆性矿物混合物的等效弹性模量Kbrit*SCA和μbrit*SCA;将等效的脆性矿物混合物视为包裹体,利用各向异性DEM模型添加到黏土和干酪根混合物中,参考钱恪然(2016)的研究结果,脆性矿物包裹体的纵横比取0.8.此时,影响建模结果的物性参数中,只剩下孔隙纵横比没有确定.
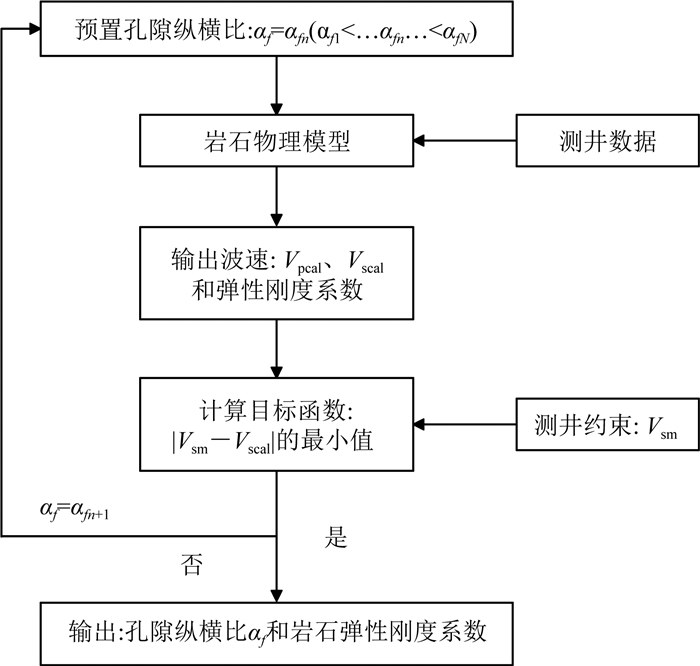
3.3 孔隙纵横比的反演相对于矿物颗粒纵横比,孔隙纵横比不仅受到沉积成岩的影响,地应力、地层孔隙压力等也会对孔隙形态产生较大的影响.一般情况下原生孔隙要比次生孔隙更为扁平.此外,主地应力差异越大,地层孔隙压力越小,则孔隙受到的挤压就越强,内部的孔隙压力对孔隙的支撑作用也就越弱,孔隙也就越扁,孔隙纵横比就越小.因此,各个层位的孔隙纵横比通常不同,在岩石物理建模过程中孔隙纵横比不宜设为定值.本文采用图 7所示的流程和方法,通过声波测井资料中的横波波速作为约束条件,采用遍历搜索方法对孔隙纵横比进行反演:第一步,设定孔隙纵横比初值;第二步,利用测井解释得到的基础物性参数和岩石物理模型计算纵横波波速和弹性刚度系数;第三步,对比横波测井数据和计算横波波速的差值(目标函数);第四步,如果目标函数未达到精度要求则返回第一步,并按一定步长重新赋值孔隙纵横比,直到目标函数达到精度要求退出循环,并输出计算结果,此时得到的即为孔隙纵横比.
|
图 7 孔隙纵横比的反演流程 Fig. 7 Inversion process of pore aspect ratio |
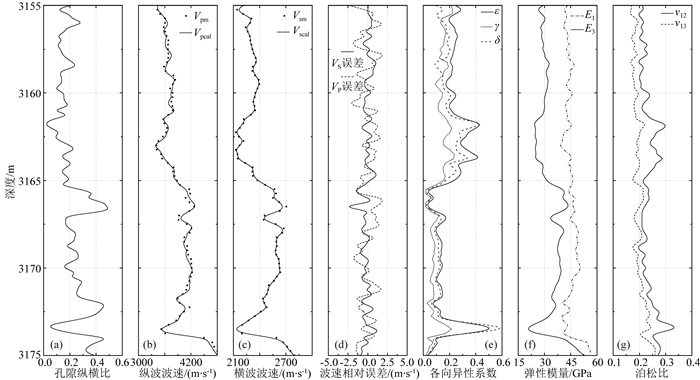
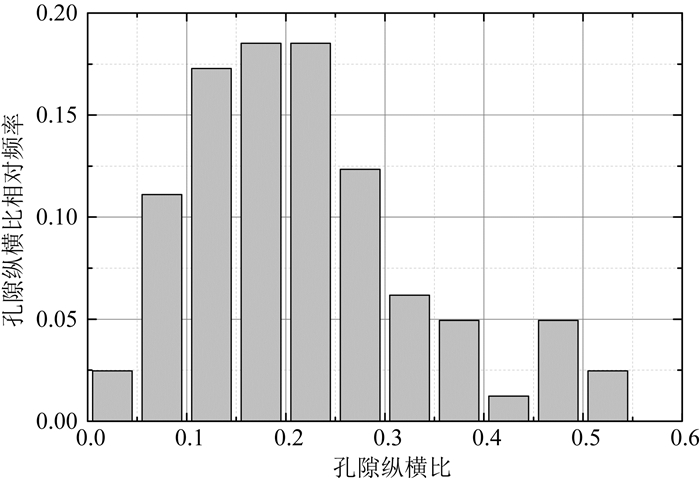
由于建模过程中涉及到多处张量运算,计算量相对较大,处理速度较慢.因此,本文仅对四川盆地A井3155~3175 m井段的龙马溪组页岩地层进行建模分析.采用遍历搜索的方式,对3155~3175 m井段地层的孔隙纵横比进行反演,并同时输出Thomsen各向异性系数和岩石力学参数,建模结果如图 8所示.图 8a为岩石物理建模反演得到的孔隙纵横比.通过对孔隙纵横比的分布进行统计,结果如图 9所示.龙马溪组地层的孔隙纵横比分布在0~0.6范围内,并主要分布在0.1~0.3之间,平均值约为0.22.图 8b、c为实际测井测量的纵横波和岩石物理模型建模得到的纵横波波速,其中Vpm和Vsm分别为测井测量的纵横波波速(散点),Vpcal和Vscal分别为建模得到的纵横波波速(实线).由于建模过程中孔隙纵横比的反演采用测井测量的横波作为约束,因此Vsm和Vscal非常接近,几乎完全一致;如图 8d所示,Vscal和Vsm之间误差介于-1.93%~1.42% (误差绝对值平均0.64%);纵波为岩石物理模型正演参数,因此Vpcal和Vpm存在一定差异,统计发现Vpcal和Vpm之间误差介于-2.40%~2.21%(误差绝对值平均1.20%).纵波和横波的建模结果均与声波测井结果高度吻合,这进一步证明了本文模型的适用性和合理性.
|
图 8 A井3155~3175 m井段龙马溪页岩地层岩石物理模型建模结果 (a)孔隙纵横比;(b)纵波波速;(c)横波波速;(d)波速相对误差;(e)各向异性系数;(f)杨氏模量;(g)泊松比. Fig. 8 Modeling results of rock physical model for Longmaxi shale formation in 3155~3175 m section of well A (a) Pore aspect ratio; (b) P-wave velocity; (c) S-wave velocity; (d) Relative error of wave velocity; (e) Coefficient of anisotropy; (f) Young′s modulus; (g) Poisson's ratio. |
|
图 9 孔隙纵横比统计直方图 Fig. 9 Statistical histogram of pore aspect ratio |
图 8e为龙马溪组地层的Thomsen系数,由图可知:该井段内的纵波各向异性系数ε介于0~0.55之间,平均值为0.20;横波各向异性系数γ介于0~0.24之间,平均值为0.12;δ介于0~0.65之间,平均值为0.16.图 8f为龙马溪组地层的杨氏模量,其中E3和E1分别表示垂直于层理面和平行于层理面的杨氏模量,由图可知:杨氏模量E1介于38.94~56.25 GPa,平均值为33.11 GPa;杨氏模量E3介于33.11~52.64 GPa,平均值为45.07 GPa.图 8g为龙马溪组地层的泊松比,其中ν31和ν12分别表示垂直于层理面和平行于层理面的泊松比,由图可知:泊松比ν31介于0.16~0.26,平均值为0.20;泊松比ν12介于0.19~0.34,平均值为0.24.
5 结论本文首先分析了页岩的微观物性特征,考虑到黏土和干酪根的堆叠成层以及水平向分布的扁平状孔隙是造成各向异性的主控因素,并综合利用测井解释、微观分析资料,基于岩石物理理论建立了龙马溪页岩岩石物理模型,并以四川盆地A井为例进行应用和验证.通过研究得出如下主要结论:
(1) 黏土和干酪根通常相互堆叠、嵌合在一起,为了表征黏土和干酪根在地层中的赋存状态,综合利用各向异性SCA模型和各向异性DEM模型进行了模拟,这保证了黏土和干酪根在不同含量下的相互接触,并避免了由于背景矿物选择的不同而导致的模拟结果差异.不同有机质颗粒纵横比的刚度系数模拟等效结果表明,纵横比在从0.02增加到0.5的变化过程中,各刚度系数的变化趋势分为两个阶段:当纵横比从0.02增加到0.1过程中,各个刚度系数变化不大;纵横比从0.1增加到0.5的过程中,刚度系数c11和c66明显降低,而刚度系数c33和c44明显增加.
(2) 考虑到页岩脆性矿物的剪切模量较为接近,不会因为各矿物剪切模量差异大而导致各个矿物之间互不接触,因此脆性矿物混合物的等效弹性性质可以利用各向同性SCA模型来模拟.利用MATLAB图像识别方法,通过对龙马溪页岩中脆性矿物进行识别、提取和统计,结果表明脆性矿物颗粒的纵横比分布在0.45~1.0之间,并集中分布在0.5~0.85之间.
(3) 孔隙纵横比受地质因素的影响较大,建模过程中不宜设置为定值.利用横波波速作为约束条件,采用遍历搜索的方式,在对孔隙纵横比反演的同时,正演了页岩储层的纵波波速、Thomsen系数和岩石弹性参数,经统计发现:预测和实测纵波波速误差介于-2.40%~2.21%之间(误差绝对值平均1.20%),龙马溪页岩孔隙纵横比在0~0.6范围内,并主要分布在0.1~0.3之间,平均值约为0.22.
(4) 四川盆地A井3155~3175 m井段龙马溪组页岩岩石物理建模分析表明,龙马溪页岩纵波各向异性系数ε介于0~0.55之间,平均值为0.20;横波各向异性系数γ介于0~0.24之间,平均值为0.12;δ介于0~0.65之间,平均值为0.16;杨氏模量E1介于38.94~56.25 GPa,平均值为33.11 GPa;杨氏模量E3介于33.11~52.64 GPa,平均值为45.07 GPa;泊松比ν31介于0.16~0.26,平均值为0.20;泊松比ν12介于0.19~0.34,平均值为0.24.岩石物理建模分析结果为地球物理和工程地质参数的计算和分析提供了重要的基础数据.
(5) 本文综合利用各向同性SCA模型、各向同性DEM模型、各向异性SCA模型、各向异性DEM模型、Wood公式和Brown-Korringa模型,同时优化脆性矿物、孔隙、流体的添加和替换顺序,建立了适合于页岩的横观各向同性页岩岩石物理模型,模型预测精度更高、普适性更强.但是,页岩孔隙成因、类型及其纵横比特征也是影响页岩岩石物理建模的重要因素之一,建议后续对不同孔隙类型及其纵横比进行分类考虑,建立更加精细的页岩岩石物理模型.
附录A 各向同性SCA模型中纵横比系数公式对于具有任意纵横比的椭球形填充物,其纵横比系数P和Q的计算公式为(Mavko et al, 2009):
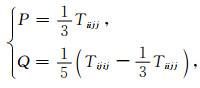
|
(A1) |
式中张量Tiijj与均匀远处的应变场和椭球夹杂物的应变相关,Berryman(1980a, b)推导了计算P、Q所需的相关标量表达式:
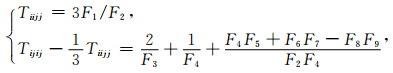
|
(A2) |
其中:
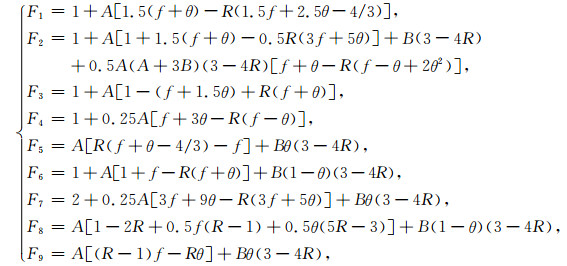
|
(A3) |

|
(A4) |
式(A3)中θ和f是和纵横比相关的函数,其计算公式为

|
(A5) |
式中:α为椭球形包裹体的纵横比,无因次.
附录B 各向异性SCA模型中Eshelby张量各分量公式
式(3)中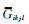
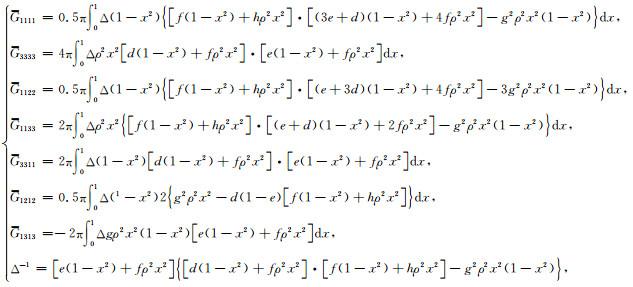
|
(B1) |
并且满足:
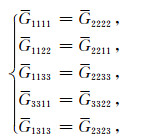
|
(B2) |
式(B1)中过渡参数d、e、f、g、h、ρ的表达式为
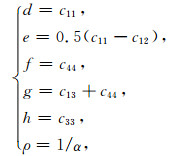
|
(B3) |
式中:c11、c12、c13、c33、c44为包裹体刚度系数,单位为GPa;α为包裹体纵横比,无因次.
Ba J, Ma R P, Carcione J M, et al. 2019. Ultrasonic wave attenuation dependence on saturation in tight oil siltstones. Journal of Petroleum Science and Engineering, 179: 1114-1122. DOI:10.1016/j.petrol.2019.04.099 |
Ba J, Xu W H, Fu L Y, et al. 2017. Rock anelasticity due to patchy-saturation and fabric heterogeneity:A double double-porosity model of wave propagation. Journal of Geophysical Research:Solid Earth, 122(3): 1949-1976. |
Ba J, Yan X F, Chen Z Y, et al. 2013. Rock physics model and gas saturation inversion for heterogeneous gas reservoirs. Chinese Journal of Geophysics (in Chinese), 56(5): 1696-1706. DOI:10.6038/cjg20130527 |
Ba J, Zhao J G, Carcione J M, et al. 2016. Compressional wave dispersion due to rock matrix stiffening by clay squirt flow. Geophysical Research Letters, 43(12): 6186-6195. DOI:10.1002/2016GL069312 |
Cai S J, Li H B, Pan H J. 2020. Construction and application of porosity-insensitive normalized fluid factor based on rock physics template. Progress in Geophysics (in Chinese), 35(3): 932-939. DOI:10.6038/pg2020DD0074 |
Bandyopadhyay K. 2009. Seismic anisotropy: Geological causes and its implications to reservoir geophysics[Ph. D. thesis]. San Francisco: Stanford University.
|
Berryman J G. 1980a. Long-wavelength propagation in composite elastic media Ⅰ. Spherical inclusions. The Journal of the Acoustical Society of America, 68(6): 1809-1819. DOI:10.1121/1.385171 |
Berryman J G. 1980b. Long-wavelength propagation in composite elastic media Ⅱ. Ellipsoida inclusions. The Journal of the Acoustical Society of America, 68(6): 1820-1831. DOI:10.1121/1.385172 |
Brown R J S, Korringa J. 1975. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid. Geophysics, 40(4): 608-616. |
Budiansky B. 1965. On the elastic moduli of some heterogeneous materials. Journal of the Mechanics and Physics of Solids, 13(4): 223-227. |
Carcione J M, Helle H B, Avseth P. 2011. Source-rock seismic-velocity models:Gassmann versus Backus. Geophysics, 76(5): 1-9. |
Deng J X, Wang H, Zhou H, et al. 2015. Microtexture, seismic rock physical properties and modeling of Longmaxi formation shale. Chinese Journal of Geophysics (in Chinese), 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
Dong N, Huo Z Z, Sun Z D, et al. 2014. An investigation of a new rock physics model for shale. Chinese Journal of Geophysics (in Chinese), 57(6): 1990-1998. DOI:10.6038/cjg20140629 |
Gassmann F. 1951. Elastic waves through a packing of spheres. Geophysics, 16(4): 673-685. |
Gui J C, Chen P, Ma T S. 2019. The spatial distribution of elastic parameters of orthotropic rocks. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 41(3): 13-28. |
Gui J C, Ma T S, Chen P, et al. 2018. Anisotropic damage to hard brittle shale with stress and hydration coupling. Energies, 11(4): 926. |
Guo H Z. 2014. Comprehensive logging evaluation for shale gas reservoir in WY area[Ph. D. thesis] (in Chinese). Chengdu: Southwest Petroleum.
|
Guo M Q, Ba J, Ma R P, et al. 2018. P-wave velocity dispersion and attenuation in fluid-saturated tight sandstones:Characteristics analysis based on a double double-porosity structure model description. Chinese Journal of Geophysics (in Chinese), 61(3): 1053-1068. DOI:10.6038/cjg2018L0678 |
Hill R. 1965. A self-consistent mechanics of composite materials. Journal of the Mechanics and Physics of Solids, 13(4): 213-222. |
Hornby B E, Schwartz L M, Hudson J A. 1994. Anisotropic effective-medium modeling of the elastic properties of shales. Geophysics, 59(10): 1570-1583. DOI:10.1190/1.1443546 |
Hu Q, Chen X H, Guo Y. 2013. A rock physics model of kerogen inclusions in shale.//83rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Jakobsen M, Hudson J A, Minshull T A, et al. 2000. Elastic properties of hydrate-bearing sediments using effective medium theory. Journal of Geophysical Research:Solid Earth, 105(B1): 561-577. DOI:10.1029/1999JB900190 |
Li N. 2016. Study on rock physics model for cracked porous medium containing kerogen and application[Master's thesis] (in Chinese). Qingdao: China University of Petroleum (East China).
|
Lin S C, Mura T. 1973. Elastic fields of inclusions in anisotropic media (Ⅱ). Physical Status Solidi: Applied Research, 15(1): 281-285. |
Liu C, Fu W, Guo Z Q, et al. 2018. Rock physics inversion for anisotropic shale reservoirs based on Bayesian scheme. Chinese Journal of Geophysics (in Chinese), 61(6): 2589-2600. DOI:10.6038/cjg2018L0176 |
Liu C, Qiao H Q, Guo Z Q, et al. 2017. Shale pore structure inversion and shear wave velocity prediction based on particle swarm optimization (pso) algorithm. Progress in Geophysics (in Chinese), 32(2): 689-695. DOI:10.6038/pg20170232 |
Liu H, Meng S W, Su J, et al. 2019. Reflections and suggestions on the development and engineering management of shale gas fracturing technology in China. Natural Gas Industry B, 6(6): 539-545. DOI:10.1016/j.ngib.2019.04.003 |
Liu X W, Guo Z Q, Liu C, et al. 2017. Anisotropy rock physics model for the Longmaxi shale gas reservoir, Sichuan Basin, China. Applied Geophysics, 14(1): 21-30. |
Liu Y, Ma T S, Wu H, et al. 2020. Investigation on mechanical behaviors of shale cap rock for geological energy storage by linking macroscopic to mesoscopic failures. Journal of Energy Storage, 29: 101326. DOI:10.1016/j.est.2020.101326 |
Liu Z C, Hao H C. 2017. Basis application for the theory of inclusion in organic shale physics modeling. Progress in Geophysics (in Chinese), 32(6): 2505-2513. DOI:10.6038/pg20170630 |
Liu Z H, Song L T, Wang C S, et al. 2017. Evaluation method of the least horizontal principal stress by logging data in anisotropic fast formations. Petroleum Exploration and Development (in Chinese), 44(5): 745-752. DOI:10.1016/S1876-3804(17)30085-X |
Ma T S, Chen P. 2014. Study of meso-damage characteristics of shale hydration based on CT scanning technology. Petroleum Exploration and Development, 41(2): 249-256. DOI:10.1016/S1876-3804(14)60029-X |
Ma T S, Liu Y, Chen P, et al. 2019. Fracture-initiation pressure prediction for transversely isotropic formations. Journal of Petroleum Science and Engineering, 176: 821-835. DOI:10.1016/j.petrol.2019.01.090 |
Ma T S, Yang C H, Chen P, et al. 2016. On the damage constitutive model for hydrated shale using CT scanning technology. Journal of Natural Gas Science and Engineering, 28: 204-214. DOI:10.1016/j.jngse.2015.11.025 |
Ma X H. 2019. Enrichment laws and scale effective development of shale gas in the southern Sichuan Basin. Natural Gas Industry B, 6(3): 240-249. |
Mavko G, Mukerji T, Dvorkin J. 2009. The Rock Physics Handbook:Tools for Seismic Analysis of Porous Media. 2nd ed. Cambridge: Cambridge University Press.
|
Qian K R. 2016. Anisotropic rock physics modeling and brittleness analysis of shale reservoir[Ph. D. thesis] (in Chinese). Beijing: China University of Petroleum (Beijing).
|
Qian K R, Zhang F, Chen S Q, et al. 2016. A rock physics model for analysis of anisotropic parameters in a shale reservoir in Southwest China. Journal of Geophysics and Engineering, 13(1): 19-34. |
Sayers C M. 1994. The elastic anisotrophy of shales. Journal of Geophysical Research:Solid Earth, 99(B1): 767-774. DOI:10.1029/93JB02579 |
Vernik L, Landis C. 1996. Elastic anisotropy of source rocks:Implications for hydrocarbon generation and primary migration. AAPG Bulletin, 80(4): 531-544. |
Vernik L, Nur A. 1992. Petrophysical analysis of the Cajon Pass scientific well:Implications for fluid flow and seismic studies in the continental crust. Journal of Geophysical Research:Solid Earth, 97(B4): 5121-5134. DOI:10.1029/91JB01672 |
Wang Z J. 2002. Seismic anisotropy in sedimentary rocks, Part 2:Laboratory data. Geophysics, 67(5): 1423-1440. DOI:10.1190/1.1512743 |
Wood A B. 1995. A Textbook of Sound. New York: The MacMillan Co.
|
Wu X, Chapman M, Li X Y, et al. 2012. Anisotropic elastic modelling for organic shales.//82nd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Yang F, Ning Z F, Hu C P, et al. 2013. Characterization of microscopic pore structures in shale reservoirs. Acta Petrolei Sinica (in Chinese), 34(2): 301-311. DOI:10.1038/aps.2012.162 |
Yuan H Z. 2007. Study of anisotropic rock physics model and application[Ph. D. thesis] (in Chinese). Dongying: China University of Petroleum (East China).
|
Zhang B, Liu C, Guo Z Q, et al. 2018. Probabilistic reservoir parameters inversion for anisotropic shale using a statistical rock physics model. Chinese Journal of Geophysics (in Chinese), 61(6): 2601-2617. DOI:10.6038/cjg2018L0086 |
Zhang J J, Li H B, Yao F C. 2012. Rock critical porosity inversion and S-wave velocity prediction. Applied Geophysics, 9(1): 57-64. |
Zhang Q G, Fan X Y, Chen P, et al. 2020. Geomechanical behaviors of shale after water absorption considering the combined effect of anisotropy and hydration. Engineering Geology, 269: 105547. DOI:10.1016/j.enggeo.2020.105547 |
Zhu W. 2020. Rock physics modeling of gas-saturated over-pressured shale. Progress in Geophysics (in Chinese), 35(3): 1116-1121. DOI:10.6038/pg2020DD0197 |
Zou C N, Dong D Z, Wang S J, et al. 2010. Geological characteristics, formation mechanism and resource potential of shale gas in China. Petroleum Exploration and Development (in Chinese), 37(6): 641-653. DOI:10.1016/S1876-3804(11)60001-3 |
Zou C N, Dong D Z, Wang Y M, et al. 2016. Shale gas in China:characteristics, challenges and prospects (Ⅱ). Petroleum Exploration and Development (in Chinese), 43(2): 166-178. |
巴晶, 晏信飞, 陈志勇, 等. 2013. 非均质天然气藏的岩石物理模型及含气饱和度反演. 地球物理学报, 56(5): 1696-1706. DOI:10.6038/cjg20130527 |
蔡生娟, 李宏兵, 潘豪杰. 2020. 基于岩石物理模板的孔隙度非敏感流体因子构建方法及应用. 地球物理学进展, 35(3): 932-939. DOI:10.6038/pg2020DD0074 |
邓继新, 王欢, 周浩, 等. 2015. 龙马溪组页岩微观结构、地震岩石物理特征与建模. 地球物理学报, 58(6): 2123-2136. DOI:10.6038/cjg20150626 |
董宁, 霍志周, 孙赞东, 等. 2014. 泥页岩岩石物理建模研究. 地球物理学报, 57(6): 1990-1998. DOI:10.6038/cjg20140629 |
桂俊川, 陈平, 马天寿. 2019. 正交各向异性岩石弹性参数的空间展布. 西南石油大学学报(自然科学版), 41(3): 13-28. |
郭洪志. 2014. WY地区页岩气藏测井精细评价[博士论文].成都: 西南石油大学.
|
郭梦秋, 巴晶, 马汝鹏, 等. 2018. 含流体致密砂岩的纵波频散及衰减:基于双重孔隙结构模型描述的特征分析. 地球物理学报, 61(3): 1053-1068. DOI:10.6038/cjg2018L0678 |
李诺. 2016.含干酪根的孔、裂隙介质岩石物理模型及应用研究[硕士论文].青岛: 中国石油大学(华东).
|
刘财, 符伟, 郭智奇, 等. 2018. 基于贝叶斯框架的各向异性页岩储层岩石物理反演技术. 地球物理学报, 61(6): 2589-2600. DOI:10.6038/cjg2018L0176 |
刘财, 乔汉青, 郭智奇, 等. 2017. 基于粒子群算法的页岩孔隙结构反演及横波速度预测. 地球物理学进展, 32(2): 689-695. DOI:10.6038/pg20170232 |
刘忠华, 宋连腾, 王长胜, 等. 2017. 各向异性快地层最小水平主应力测井计算方法. 石油勘探与开发, 44(5): 745-752. |
刘子淳, 郝贺晨. 2017. 包裹体理论在富有机质页岩岩石物理建模中的依据因素应用. 地球物理学进展, 32(6): 2505-2513. DOI:10.6038/pg20170630 |
钱恪然. 2016.各向异性页岩岩石物理建模及储层脆性评价[博士论文].北京: 中国石油大学(北京).
|
杨峰, 宁正福, 胡昌蓬, 等. 2013. 页岩储层微观孔隙结构特征. 石油学报, 34(2): 301-311. |
原宏壮. 2007.各向异性介质岩石物理模型及应用研究[博士论文].东营: 中国石油大学(华东).
|
张冰, 刘财, 郭智奇, 等. 2018. 基于统计岩石物理模型的各向异性页岩储层参数反演. 地球物理学报, 61(6): 431-447. DOI:10.6038/cjg2018L0086 |
朱伟. 2020. 气饱和超压页岩的岩石物理建模研究. 地球物理学进展, 35(3): 1116-1121. DOI:10.6038/pg2020DD0197 |
邹才能, 董大忠, 王社教, 等. 2010. 中国页岩气形成机理、地质特征及资源潜力. 石油勘探与开发, 37(6): 641-653. |
邹才能, 董大忠, 王玉满, 等. 2016. 中国页岩气特征、挑战及前景(二). 石油勘探与开发, 43(2): 166-178. |
 2020, Vol. 63
2020, Vol. 63


