2. 地壳动力学重点实验室, 中国地震局地壳应力研究所, 北京 100085
2. Key Laboratory of crustal dynamics, The Institute of Crustal Dynamics, China Earthquake of Academy, Beijing 100085, China
大地电磁测深(MT)是地球深部电性结构探测、油气和地热资源勘探、深部热液成矿系统研究等地学领域的主要地球物理方法之一(刘国栋和赵国泽,1994;赵国泽等, 2007).由于平面扩散场边值问题的良好数学物理特性,MT的正、反演理论及其应用一直是国际电磁法研究的前沿和热点(魏文博,2002;胡祥云等,2012),而三维MT反演更是在复杂地形、地质条件下准确推断地下电性结构的重要前提.得益于近十几年来的持续研究,随着积分方程、有限单元和有限差分等数值计算方法在三维MT正演中的成功应用(如:Hursán and Zhdanov, 2002;Nam et al., 2007;Newman and Alumbaugh, 2000),经典凸优化的反演算法如非线性共轭梯度法(NLCG)(Newman and Alumbaugh, 2000)、高斯牛顿法(GN)的变种OCCAM方法(Siripunvaraporn et al., 2005)、拟牛顿法(QN)(Avdeev,2005)等都已成功引入三维MT反演.与之对应的计算程序如WSINW3DMT(Siripunvaraporn, 2012)和ModEM(Kelbert et al., 2014)也陆续发布,且近年来已广泛用于深部电性结构研究探测的实测数据解释并取得了大量应用结果(Xiao et al., 2017;叶涛等,2018).但大规模数据集和区域电性结构复杂的研究区的三维MT反演算法仍不能有效适应实际需求.具体表现为:(1)最稳定的OCCAM反演方法内存需求巨大、计算时间太长,不适应大规模问题,需要一种高效替代算法;(2)常规三维MT反演通常基于全局最平坦(或最光滑)模型期望,可能会降低反演算法真实电性界面的分辨能力.
对于问题(1),由于OCCAM反演稳定的主要原因在于每次迭代自动搜索合理的正则因子以保证“充分正则”,其内存需求与计算速度与显式求取雅可比矩阵(Siripunvaraporn et al., 2005)有关.因此,高效替代算法的关键在于海塞(Hessian)矩阵的进一步逼近方法,目前的牛顿型逼近方法主要为准线性近似(Zhdanov et al., 2000;Wang et al., 2006)和改进型QN(邓琰等,2019).后者引入了梯度二范数比值自动更新正则因子的机制,实现了稳定性很强的常规L2正则AR-QN反演方法,在玉树地震科考实测数据反演中高效的取得了可靠电性结构模型(邓琰,2019).对于问题(2),因为常规L2正则反演的全局最平坦(或最光滑)的期望与突出局部电性界面的需求相悖,故需要改变正则项的形式以让反演算法允许电阻率空间局部不连续.在重力、地震数据的三维反演中,已有学者利用L1正则反演技术提升分辨率(Gholami et al., 2016;Vatankhah et al., 2017;Wang et al., 2017),作为L1正则反演的一种特例,最小梯度支撑泛函(Zhdanov et al., 2004)的尖锐边界反演(或聚焦反演)也已在二维MT中实现(张罗磊等,2010).但直接对L1正则目标函数求极小的NLCG算法(Zhdanov et al., 2004)有可能因为L1范数零点不可导使得迭代不稳定,且因L1正则对模型的“约束”比L2正则更为宽松,很容易在迭代早期陷入奇异解.构建迭代更稳定的L1正则目标函数极小化方法,同时引入合理的自适应正则因子策略,这二者均是L1正则的稳定三维MT反演算法的重点.
本文首先分析L1正则项(梯度算子)在解空间的取值特征,解释L1正则有利于模型空间梯度向量取得稀疏解的原因,并详细论述此稀疏解对于反演电阻率模型期望的具体意义.引入迭代重加权最小二乘(IRLS)方法(Holland and Welsch, 1977)把L1正则反演问题转换为一系列经典线性最小二乘子问题,并引入AR-QN(邓琰等,2019)方法的下降方向,使用比值法和分段衰减法自适应调整正则因子,从而实现三维MT的自适应L1正则反演方法(AR-QNL1).最后,对标准模型合成数据和实测数据均进行对比测试,以测试AR-QNL1反演的收敛稳定性、电性界面分辨能力、初始模型依赖度、观测噪声稳健性.
1 L1正则反演及其IRLS解法常规三维MT反演的L2正则目标函数Φl2为
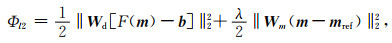
|
(1) |
其中,右边第一个L2范数为数据拟合项,F(m)为模型向量m的三维MT正演响应,m的每个元素均为电导率自然对数,b为观测数据向量,Wd一般为主对角阵,元素为各数据观测误差倒数(为防止除0,其门槛值为期望噪声);第二个L2范数为正则罚项,对m-mref起全局“约束”作用,Wm可取为单位算子(最小模型)、梯度算子(最平坦模型)或拉普拉斯算子(最光滑模型);超参数λ是正则因子(或称正则参数),控制反演更倾向于拟合数据还是让模型更相似于参考模型mref.
类似的,L1正则反演的目标函数为
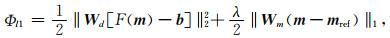
|
(2) |
因篇幅所限,本文仅讨论Wm取单位梯度算子的情况,它可以表示为
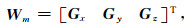
|
(3) |
其中,上标T表示矩阵转置,子矩阵Gx,Gy,Gz分别为沿x,y,z空间方向的单位一阶差分算子.引入编号映射函数p(i, j, k)把三维空间编号(i, j, k)映射为向量m的下标,则稀疏算子矩阵Wm的每个非零元素可表示为
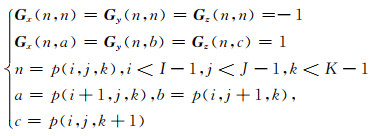
|
(4) |
其中,I、J、K为模型网格三个方向的单元个数,N=I×J×K为m的元素个数,式(3)和式(4)表明Wm为3N×N稀疏阵,每行最多2个非零元素.令向量x=Wm(m-mref),则式(1)和式(2)中可写为以下形式:
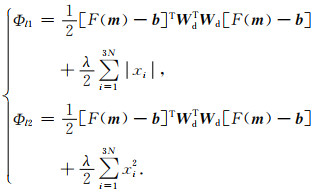
|
(5) |
若mref为均匀半空间模型,取沿x方向的三个相邻单元,设它们在向量m中分别对应m1,m2,m3三个元素,定义两个参数子空间如下:
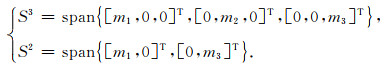
|
(6) |
在子空间S3内,L1和L2正则项可表示为
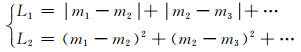
|
(7) |
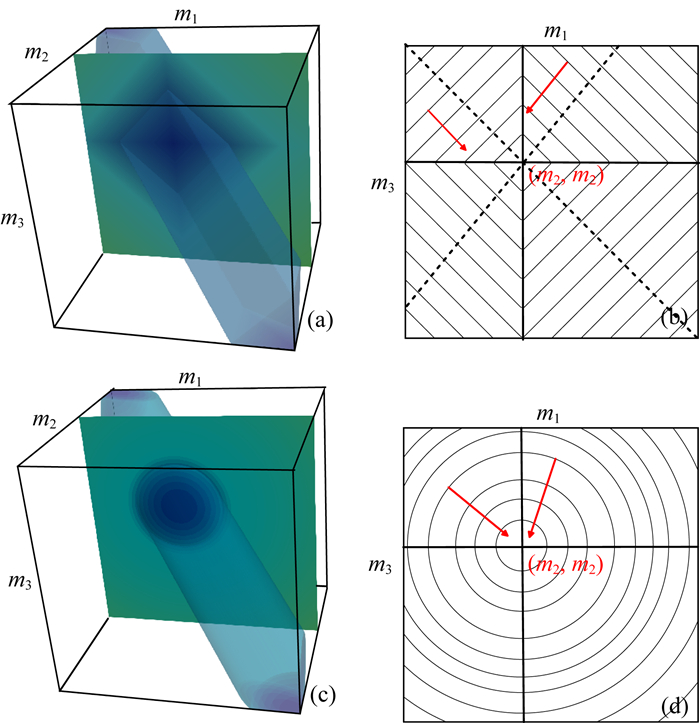
在其他单元格已取收敛解时,L1和L2在子空间S3和S2内的等值线(或面)必然如图 1所示,其中图 1a和图 1c的颜色表示数值大小(绿大蓝小),让L1和L2取最小值的模型m分布在子空间S3的“对角线”上(m1=m2=m3),若反演的正则因子选择合理,则最终模型应位于该对角线的邻域内,即图 1a和图 1c的半透明等值面(此时正则项为某小值)内部.图 1b和图 1d为当m2取定值时L1和L2在S2空间的等值线形态,其最小值位于原点(m2, m2)上.
|
图 1 解空间的L1和L2正则函数示意图(红色箭头指向负梯度方向) (a) S3中的L1正则;(b) S2中的L1正则; (c) S3中的L2正则;(d) S2中的L2正则. Fig. 1 Regularization function value of L1 & L2 in solution sub-space (red arrows point to negative gradient direction) (a) L1-norm in S3; (b) L1-norm in S2; (c) L2-norm in S3; (d) L2-norm in S2. |
为便于论述,定义集合Al1和Al2如下:
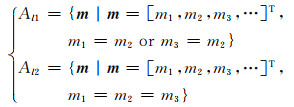
|
(8) |
其中,集合Al1在S2子空间中对应过原点(m2, m2)的两个坐标轴(图 1b和图 1d中实线所示),集合Al2对应原点(m2, m2).用迭代法求Φl1和Φl2的极小时,对于第k次迭代模型mk,除|m1-m2|=|m2-m3|的情况(图 1b中虚线所示),L1正则项的最速下降方向都偏离原点,使mk+1更倾向于落在集合Al1及其邻域内;而L2正则项的最速下降方向一定指向原点,使mk+1更倾向于落在集合Al2及其邻域内.考虑整个解空间,L1正则反演会让模型空间梯度向量x更有机会取得稀疏解,此时“正则约束”更能允许局部位置的电阻率存在突变.
对L1正则目标函数求极小时,若迭代中mk+1∈Al1,正则项不可导,无法得到最速下降方向.因此,取一个很小的正数ξ,将式(2)近似为下式:
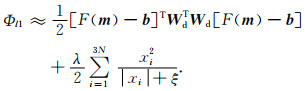
|
(9) |
引言中提到的最小梯度支撑泛函反演的目标函数为
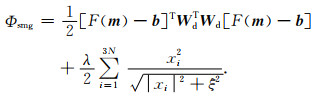
|
(10) |
由式(9)和式(10)可知,所谓最小梯度支撑泛函就是L1正则反演的一种通用近似解法,早期文献(Zhdanov et al., 2004)使用NLCG法直接求解式(10)的非线性最优化问题.但当x向量在迭代中取得稀疏解时,正则项导数的计算仍然不可靠,反演迭代有可能陷入奇异稀疏解“陷阱”.
另一种求解Φl1极小的技术是迭代重加权最小二乘法(IRLS)(Holland and Welsch, 1977),把正则项改写
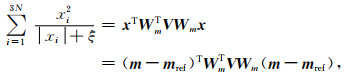
|
(11) |
其中, V是根据模型m计算得到的3N×3N对角加权矩阵,其主对角元素如下:
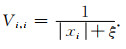
|
(12) |
将式(9)重写为
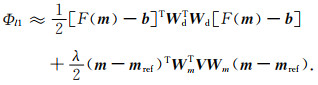
|
(13) |
用牛顿型迭代方法(如GN)求解式(13)的极小时,在第k次迭代模型mk的邻域中引入近似V=Vk≈Vk+1(将V视为常量),此时mk处的反演线性化子问题变为常规加权L2正则问题.利用常规算法得到加权L2正则解mk+1后,更新V=Vk+1,进入下一次迭代,重复这一过程直至收敛.
通常IRLS解法比NLCG直接求解更稳定高效,原因有二:(1)每次迭代的正则项都为线性最小二乘形式,具有更好的数学特性.(2)在IRLS解法中,若正则因子在迭代早期足够大,V非常光滑,此时迭代和常规L2反演迭代一致.随着模型逐渐变得复杂,在迭代后期才接近L1正则反演,整个反演迭代是一个稳定递进过程.但也需指出,IRLS在每次迭代中视V为常量,故要求相邻两次迭代的模型修正量不宜过大.所以,用IRLS求解L1正则反演问题时,每次迭代尽量选取合适的正则因子变得尤其重要,不能过早追求目标函数的快速下降而破坏V=Vk≈Vk+1的假设.
2 IRLS问题的自适应正则因子QN解法 2.1 两种QN海塞逼近方法设第k次迭代模型mk的数据拟合项海塞矩阵为Bk,GN方法使用雅可比矩阵Jk将其逼近为JkTWdTWdJk,视Vk在当前迭代中为常量,目标函数的下降方向dk满足下式:
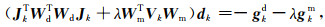
|
(14) |
其中,gkd=JkTWdTWd[F(mk)-b],为模型mk的数据拟合项梯度,通过一次“拟正演”可以隐式求取(Newman and Alumbaugh, 2000),gkm=WmTVkWm(mk-mref)为IRLS线性子问题的正则项梯度.若计算时间和内存空间允许显式计算Jk,则可用式(14)得到L1正则的OCCAM反演方法.但在大规模问题的三维MT反演中,由于Jk的维度巨大,其每行(或列)的计算均需进行一次“拟正演”,在现阶段的计算机上应用仍不现实,QN方法是相对更可行的选择.
以QN的LBFGS更新公式(Byrd et al., 1994)为例,设模型修正量sk=mk-mk-1,拟合项梯度改变量ykd=gkd-gk-1d,总梯度的改变量yk=(gkd+λgkm)-(gk-1d+λgk-1m),对式(14)有两种逼近手段:
(1) 使用前n次(3≤n≤20)的{yk-n+1, yk-n+2, …, yk}和{sk-n+1, sk-n+2, …, sk}逼近总海塞Bk,得到式(15).
(2) 使用前n次(3≤n≤20)的{yk-n+1d, yk-n+2d, …, ykd}和{sk-n+1, sk-n+2, …, sk}逼近数据拟合项海塞Bkd,得到式(16).
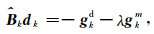
|
(15) |
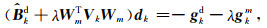
|
(16) |
其中,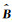
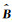
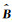
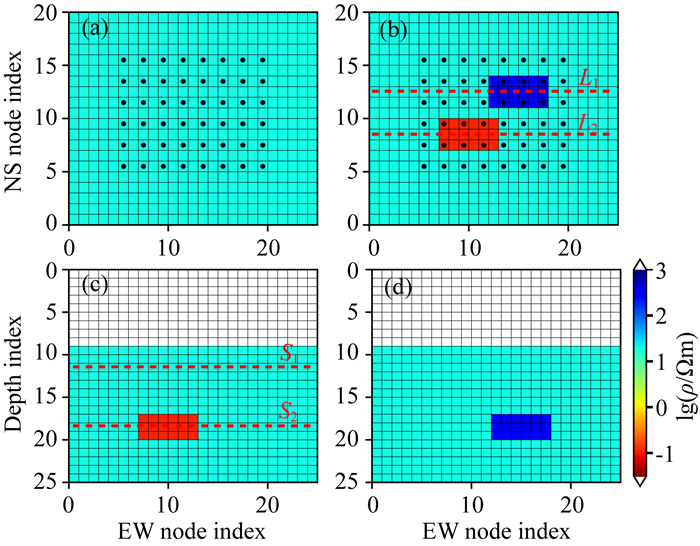
为对比两种QN下降方向的效果,设计了简单模型(CUBES)的合成数据进行对比分析.CUBES模型的电阻率如图 2所示,网格剖分及频率表见表 1,在对比中为兼顾L1和L2正则,令Vk≡I,初始模型设为设为1000 Ωm(背景电阻率的10倍),取正则因子固定为1000.分别用两种QN下降方向对合成数据进行8次反演迭代,反演收敛曲线和迭代结果分别如图 3和图 4所示.
|
图 2 CUBES模型网格电阻率示意图 黑点表示MT测点,绘图坐标为网格编号,红色虚线为水平、垂直切片的位置. (a) S1水平切片,深度0.5 km; (b) S2水平切片,深度10 km;(c)东西向L1剖面;(d)东西向L2剖面. Fig. 2 Resistivity blocks and sites distribution of model CUBES Black dots indicate horizontal sites locations, blocks are projected into unit length scale. (a) Horizontal slice map S1 on depth=0.5 km; (b) Horizontal slice map S2 on depth=10 km; (c) EW profile L1; (d) EW profile L2. |
|
|
表 1 CUBES模型三维网格剖分参数及合成数据频率表 Table 1 Three-dimensional mesh parameters and forward modelling frequencies of CUBES model |
|
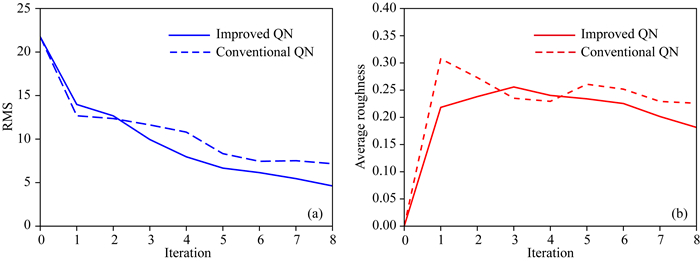
图 3 CUBES模型常规和改进型QN的8次反演迭代收敛曲线 (a) RMS;(b)平均粗糙度. Fig. 3 Convergence curves of 8 inversion iterations using conventional and improved QN descent direction for CUBES model (a) RMS; (b) Average roughness. |
|
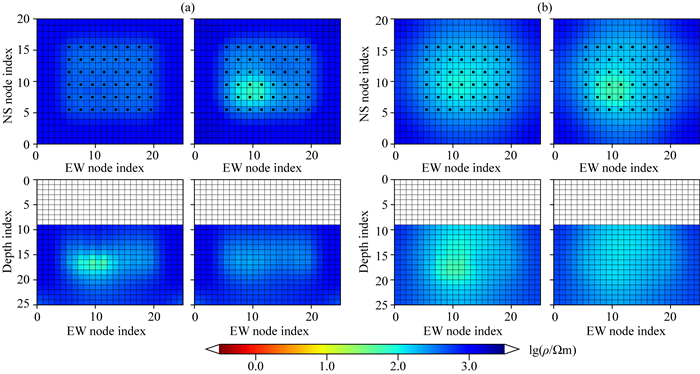
图 4 CUBES模型常规和改进型QN下降方向8次反演迭代结果(绘图参数同图 2) (a)常规QN;(b)改进型QN. Fig. 4 Results after 8 inversion iterations using conventional and improved QN descent direction for CUBES model (same plotting parameters as Fig. 2) (a) Conventional QN; (b) Improved QN. |
试算结果表明,改进型QN有更小的加权残差均方根(RMS)(图 3a)和正则项均方根(平均粗糙度)(图 3b),两条曲线随迭代变化均更加平缓,最终模型更光滑(图 4).这表明当Vk≡I时,改进型QN会得到更光滑、RMS更小的模型,比常规QN更适应Vk随迭代更新的情况.
2.2 自适应正则因子策略在病态线性方程组的求解问题中有很多正则因子择优策略,如Morozov偏差原理(Morozov, 1966)、GCV广义交叉验证(Golub and von Matt, 2012)、L-曲线法(Hansen, 1992)等.应用这些策略时需假定以下方程的解存在,
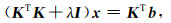
|
(17) |
其中,x为原病态方程组Kx=b的正则最小二乘解,一般需要利用矩阵分解技术(如LU分解)回代得到,然后在一系列x(λ)中根据择优策略(如Morozov偏差原理)选取最佳正则因子,当KTK+λI不正定时,可能需要截断奇异值分解对x(λ)进行近似.
以上策略对某些病态非线性最优化问题也可适用,但与三维MT反演问题的实际需求仍有差距,具体表现为:
(1) 三维MT反演的线性子问题的系统矩阵随迭代变化.若λ对于每次迭代取定值,可能在反演早期因正则“约束”不足而陷入局部奇异解.
(2) GN(或OCCAM)方法数据拟合项海塞的逼近是半正定的,当正则因子很小时,不能保证式(14)左边的矩阵正定,此时用截断奇异值分解近似下降方向非常耗时.
(3) 三维MT反演不仅要保证数据拟合达到某种水平,还需考虑正则项对模型“观测数据盲区”的光滑插值效果.Morozov准则、GCV和L曲线并未考虑这一需求.
鉴于以上三点,在三维MT的非OCCAM反演方法中,常用的自适应更新策略有二:
2.2.1 比值法比值法思想是在每次迭代中均保证数据拟合项和正则罚项的某种平衡(陈小斌等,2005;邓琰等,2019).若目标函数在第k次迭代取极小的条件为gkd+λkgkm=0,考虑两种情况:(1)当λk→0时‖gkd‖2→0;(2)当λk很大时‖gkm‖2→0,但不保证‖gkd‖2→0.若从一个非常光滑的m0开始迭代到第k次结束反演,以满足‖gkd‖2=λk‖gkm‖2且‖gkd‖2+λk‖gkm‖2→0的模型为反演期望解.若反演算法收敛,则mk(λk)为目标函数的一个不动点,根据下式构建不动点迭代:
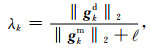
|
(18) |
其中,ℓ为防止除零的门槛值,与式(9)引入的ξ作用类似.本文设定ξ=0.001,其物理意义为相邻网格电阻率之比小于0.1%时可视为相等,即模型梯度向量x的每个元素的容许误差为ξ,在IRLS迭代子问题中,视式(12)为常数矩阵并根据误差传递原理,可得到ℓ=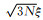
基于改进型QN下降方向和比值法的自适应正则因子策略,笔者于2019年开发了自适应正则因子的L2正则三维MT反演方法AR-QN(邓琰等,2019),在玉树地震区稀疏MT数据集的反演解释中取得了较好效果(邓琰,2019).在AR-QN的算法实现中,为保证不动点迭代稳定,取平均阻尼不动点迭代式如下,
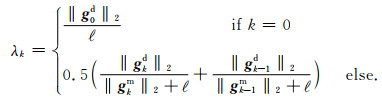
|
(19) |
式(18)基于梯度范数比值构建,其他学者的研究(如陈小斌等,2005)表明数据拟合项和正则罚项的比值也是不错的选择,这一类更新策略均统称为比值法.
2.2.2 分段衰减法分段衰减法则从较大的正则因子随迭代缓慢衰减来模拟OCCAM方法(吴小平和徐果明, 1998;Zhdanov et al., 2004).由于常规QN和NLCG反演的下降方向需保证正则因子不变,当拟合差无法下降时,重启算法并减小正则因子继续迭代.这样做的合理性在于几次QN和NLCG迭代可以等价为一次GN迭代.若正则因子的初始值足够大且其衰减速度适当的小,则反演效果可以接近OCCAM反演.具体过程为:
(1) 根据公式(19)设定λ0以保证初始正则因子足够大.
(2) 对于k>0的所有迭代,若满足不等式(20),则令λk=λk-1,否则令λk=λk-1/w,其中w>1.
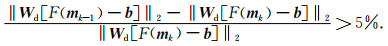
|
(20) |
与比值法相比,分段衰减法更接近OCCAM原理,但需要引进另一个超参数w.若w过大,会因正则因子衰减过快而稳定性减弱;若w过小,极可能导致收敛停滞而陷入局部极小点.本文对复杂模型下两种策略均进行了对比测试,详见后文.
2.3 AR-QNL1三维MT反演在AR-QN算法基础上,对于第k次迭代,首先用比值法或分段衰减法确定λk,用迭代法(如SQMR)求解方程组(16)得到下降方向dk,取初始尝试步长α=1,线搜索一个满足Wolfe条件的步长α(Moré et al., 1994),再利用式(21)得到mk+1.由于AR-QNL1的下降方向为牛顿型,绝大多数情况下,α=1即为最佳步长,这是其相对于NLCG的一个优点.
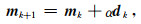
|
(21) |
得到mk+1后,根据公式(12)计算重加权矩阵Vk+1,用LBFGS公式更新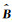
不断重复迭代过程,若满足下列条件之一即可退出反演:
(1) 达到最大迭代次数;
(2)‖gkd‖2 < 10-6;
(3)‖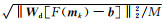
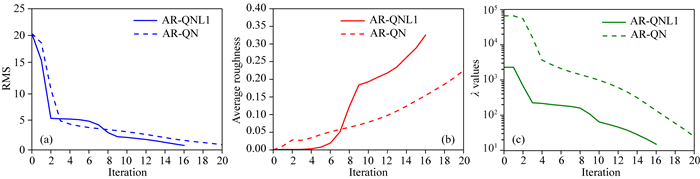
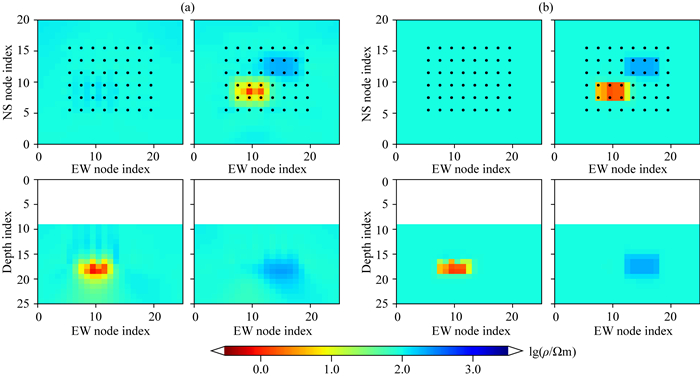
为初步测试反演算法效果,对CUBES模型的合成数据进行了AR-QN和AR-QNL1反演,正则因子使用比值法自适应更新,其他参数与图 3的8次迭代一致,反演收敛曲线及模型结果分别如图 5和图 6所示.对比后可知:AR-QNL1准确清晰的显示了两个异常体边界(图 6b),模型恢复效果强于L2正则;其RMS和平均粗糙度随迭代变化比AR-QN更剧烈(图 5a、图 5b),收敛稳定性弱于L2正则.
|
图 5 CUBES模型合成数据AR-QN和AR-QNL1反演收敛曲线 (a) RMS;(b)平均粗糙度;(c)正则因子. Fig. 5 Convergence curves of synthetic data inversions for model CUEBS by AR-QN and AR-QNL1 (a) RMS; (b) Average roughness; (c) Regularization parameter. |
|
图 6 CUBES模型合成数据AR-QN和AR-QNL1反演结果(绘图参数同图 2) (a) AR-QN;(b) AR-QNL1. Fig. 6 Results of synthetic data inversion for model CUEBS by AR-QN and AR-QNL1 (same plotting parameters as Fig. 2) (a) AR-QN; (b) AR-QNL1. |
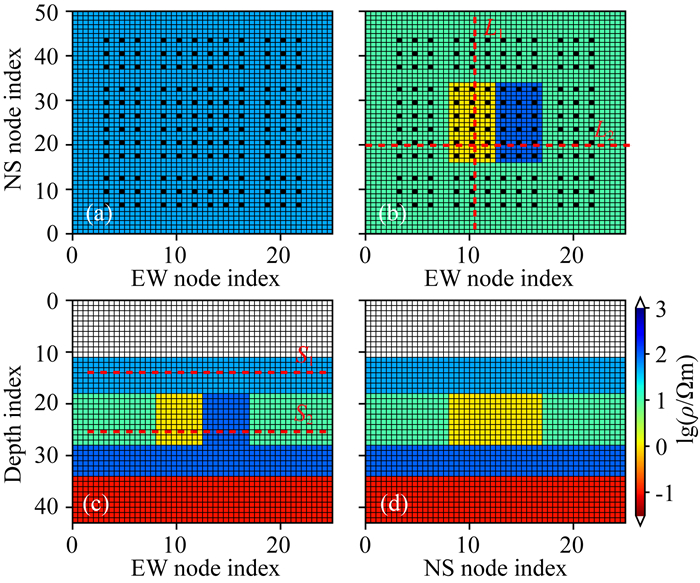
为了进一步测试AR-QNL1算法对复杂模型的反演效果,选择国际标准模型DSM2进行更详尽的反演测试.很多文献都详细介绍了此模型(秦策等,2017),这里不过多描述.为排除反演方法、数据观测误差、MT观测畸变等因素的影响,反演的输入为三维正演合成的无噪、无畸变响应数据.DSM2的网格剖分和频率表如表 2所示,模型电阻率如图 7所示.
|
|
表 2 DSM2模型三维网格剖分及合成数据频率表 Table 2 Three-dimensional mesh parameters and forward modelling frequencies of DSM2 model |
|
图 7 DSM2模型网格剖分示意图 黑点表示MT测点,绘图坐标为网格编号,红色虚线为水平、垂直切片的位置. (a) S1水平切片,深度0.5 km; (b) S2水平切片,深度4 km;(c)东西向L1剖面;(d)南北向L2剖面. Fig. 7 Resistivity blocks and sites distribution of DSM2 Black dots indicate horizontal sites locations, blocks are projected into unit length scale. (a) Horizontal slice map S1 on depth=0.5km; (b) Horizontal slice map S2 on depth=4 km; (c) EW profile L1; (d) NS profile L2. |
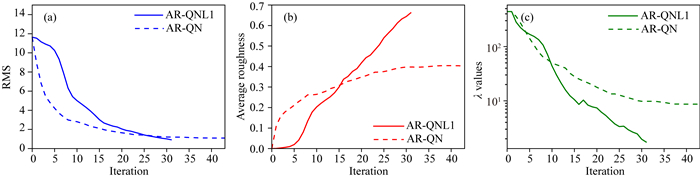
分别使用AR-QN和AR-QNL1对全部合成数据的全阻抗和倾子响应进行反演.反演参数为:初始模型100 Ωm均匀半空间;反演网格与正演相同;比值法自适应更新正则因子;以视电阻率相对误差5%、阻抗相位绝对误差2.5度,倾子绝对误差0.01设定误差门槛.反演收敛曲线和最终模型分别如图 8和图 9所示.
|
图 8 DSM2模型合成数据AR-QN和AR-QNL1反演收敛曲线 (a) RMS;(b)平均粗糙度;(c)正则因子. Fig. 8 Convergence curves of synthetic data inversions for model DSM2 by AR-QN and AR-QNL1 (a) RMS; (b) Average roughness; (c) Regularization parameter. |
|
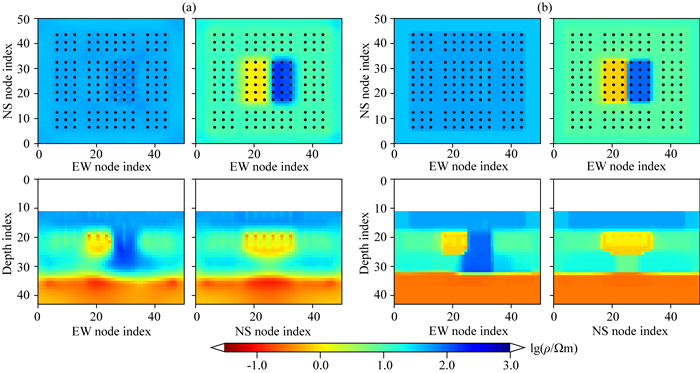
图 9 DMS2模型合成数据AR-QN和AR-QNL1反演结果绘图参数同图 7,(a) AR-QN;(b) AR-QNL1. Fig. 9 Results of synthetic data inversion for model DMS2 by AR-QN and AR-QNL1 Same plotting parameters as Fig. 7, (a) AR-QN; (b) AR-QNL1. |
与CUBES模型的测试结果类似,两个反演均收敛到RMS为1的拟合期望,但AR-QNL1的所有收敛曲线均比AR-QN变化更剧烈(图 8).对比反演结果可见:AR-QN为追求纵向“最平坦”,深部超低阻(0.1 Ωm)界面的水平形态被扭曲,所有电性边界均比较模糊(图 9a);AR-QNL1恢复了深部低阻层的水平顶界,中深度的异常体和电性边界更加清晰(图 9b);两个反演都对深部100 Ωm的水平层分辨不足,这可能因为MT方法本身对高阻不够敏感,在视电阻率误差为5%的门槛噪声下无法清晰分辨.
3.2 AR-QNL1稳定性测试为测试AR-QNL1算法的收敛稳定性和初始模型依赖程度,设计了四种反演参数(表 3)对DSM2合成数据进行反演测试,表 3中未列出的其他参数均与第3.1节一致.四个测试的参数选择依据分别如下:
|
|
表 3 AR-QNL1算法稳定性测试参数对照表 Table 3 Parameters for AR-QNL1 inversion stability tests |
(1) FIX-100用于测试固定正则因子的反演效果.设定λk≡2是取图 8c的迭代后期正则因子极大值,此时由于RMS收敛到1,表明接近Morozov偏差原理估计.
(2) RTO-10和RTO-1000用于检验初始模型偏离背景电阻率时比值法是否稳定.
(3) STP-RND是更严格的随机数初始模型测试.试算中比值法非常不稳定,因此经试验选择了分段衰减法w=2.
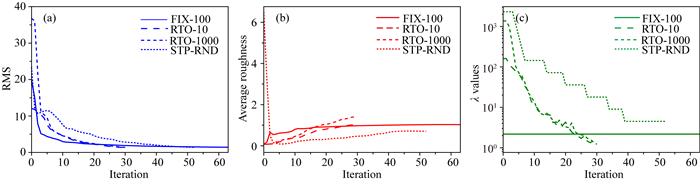
所有反演测试的收敛曲线如图 10所示,迭代早期、中期和最终的模型分别如图 11、图 12和图 13所示.所有反演均收敛到RMS为1的期望数据拟合水平(图 10a),最终模型的平均粗糙度也基本在同一水平(图 10b).其中RTO-10与RTO-1000的收敛曲线形状与图 8型态相似,都在约30次迭代完成收敛.若仅从平均模型粗糙度来评价,比值法AR-QNL1在初始模型为均匀空间时不太依赖初始模型.
|
图 10 DMS2模型合成数据AR-QNL1稳定性测试收敛曲线 (a) RMS;(b)平均粗糙度;(c)正则因子. Fig. 10 Convergence curves of AR-QNL1 inversion stability test for synthetic data of model DMS2 (a) RMS; (b) Average roughness; (c) Regularization parameter. |
|
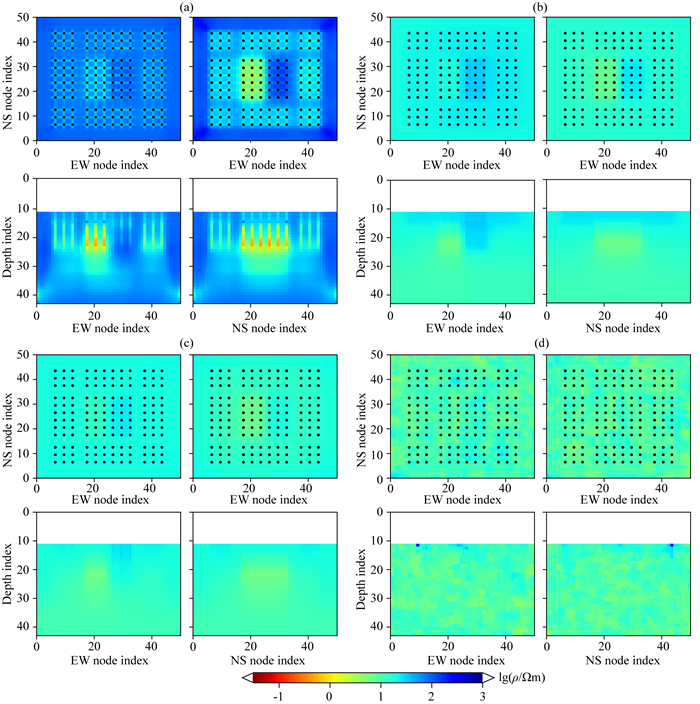
图 11 DMS2模型合成数据AR-QNL1稳定性测试反演迭代早期模型 绘图参数同图 7,(a) FIX-100第4次迭代;(b) RTO-10第4次迭代;(c) RTO-1000第5次迭代;(d) STP-RND第2次迭代. Fig. 11 Resistivity model on early stage of AR-QNL1 inversion stability test for synthetic data of model DMS2 Same plotting parameters as Fig. 7, (a) FIX-100 on iter.4; (b) RTO-10 on iter. 4; (c) RTO-1000 on iter.5; (d) STP-RND on iter.2. |
|
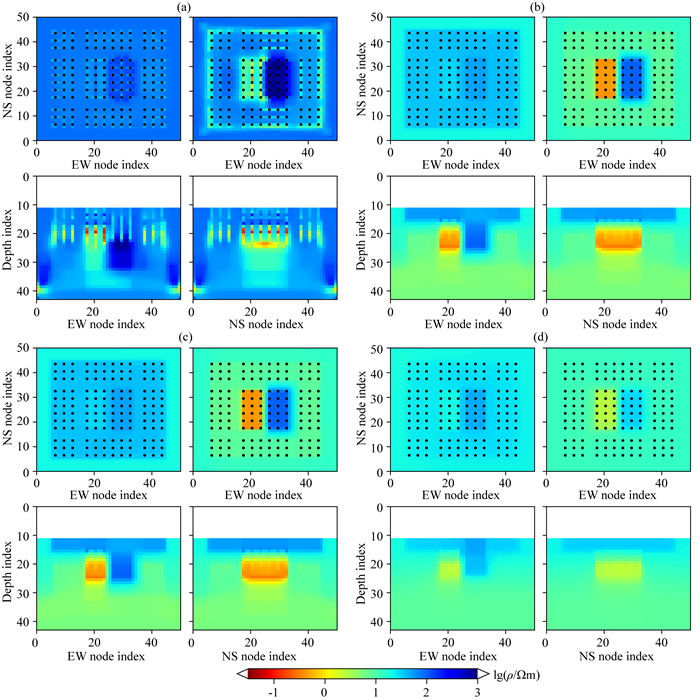
图 12 DMS2模型合成数据AR-QNL1稳定性测试的反演迭代中期模型 绘图参数同图 7,(a) FIX-100第20次迭代;(b) RTO-10第10次迭代;(c) RTO-1000第10次迭代;(d) STP-RND第10次迭代. Fig. 12 Resistivity model on middle stage of AR-QNL1 inversion stability test for synthetic data of model DMS2 Same plotting parameters as Fig. 7, (a) FIX-100 on iter. 20;(b) RTO-10 on iter. 10;(c) RTO-1000 on iter. 10;(d) STP-RND on iter. 10. |
|
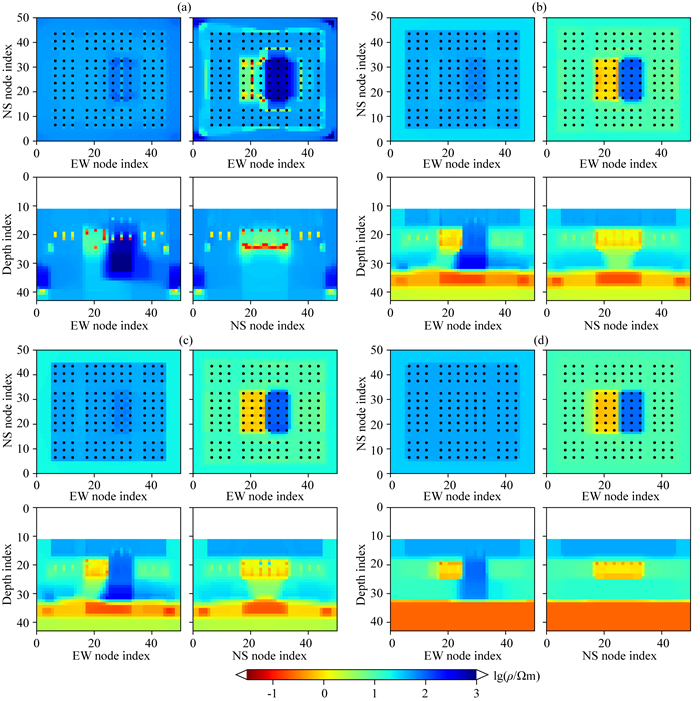
图 13 DMS2模型合成数据AR-QNL1稳定性测试最终反演结果 绘图参数同图 7,(a) FIX-100;(b) RTO-10;(c) RTO-1000;(d) STP-RND. Fig. 13 Results of AR-QNL1 inversion stability test for synthetic data of model DMS2 Same plotting parameters as Fig. 7, (a) FIX-100; (b) RTO-10; (c) RTO-1000; (d) STP-RND. |
特别的,当初始模型单元电阻率为随机数时,STP-RND的RMS不再单调下降(图 10a),迭代初期倾向于让模型光滑(图 10b).随着正则因子的阶梯状递减(图 10c),在第10次迭代之后RMS开始稳定下降.
分析图 11、图 12和图 13可知:(1)FIX-100反演在早期因正则因子过小而过分追求RMS下降,导致迭代很快进入奇异点(图 11a),最终模型出现了很多冗余的方块状假异常(图 13a);(2)RTO-10和RTO-1000的模型修正过程非常稳定,尽管初始模型偏离真实背景,反演结果仍可接受,但深部低阻层的恢复效果仍然不好;(3)STP-RND较好的恢复了真实电性结构,但衰减率w=2是经多次试验选取的.总体来说,AR-QNL1算法具有很强的迭代稳定性,对初始模型的依赖性不强.自适应更新正则因子的策略对反演效果的影响很大,当初始模型选择合理时,比值法的结果较好,反之分段衰减法可能更佳.
3.3 AR-QNL1含噪数据稳健性测试设每种大地电磁数据的实、虚部噪声水平均为l,定义以下函数:
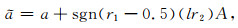
|
(22) |
其中a为无噪数据,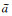
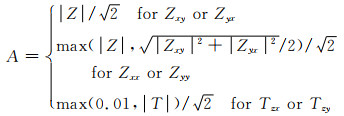
|
(23) |
对DSM2模型合成数据的实、虚部分别按l=5%、l=10%、l=20%和l=30%利用式(22)添加人工噪声以模拟“观测数据”,并分别进行AR-QNL1反演,所有反演参数均与3.2节的STP-RND相同,收敛曲线和最终模型分别如图 14和图 15所示.为保证对比的一致性,所有反演均在第52次迭代截断,此时l=5%的RMS已收敛到1.
|
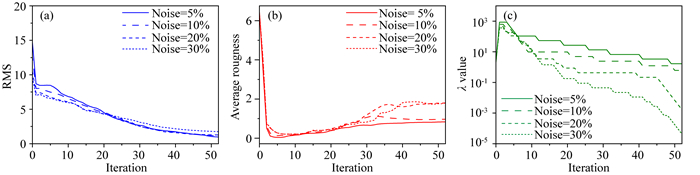
图 14 DMS2模型合成数据AR-QNL1噪声稳健性测试收敛曲线 (a) RMS;(b)平均粗糙度;(c)正则因子. Fig. 14 Convergence curves of AR-QNL1 inversion noise level robustness test for synthetic data of model DMS2 (a) RMS; (b) Average roughness; (c) Regularization parameter. |
|
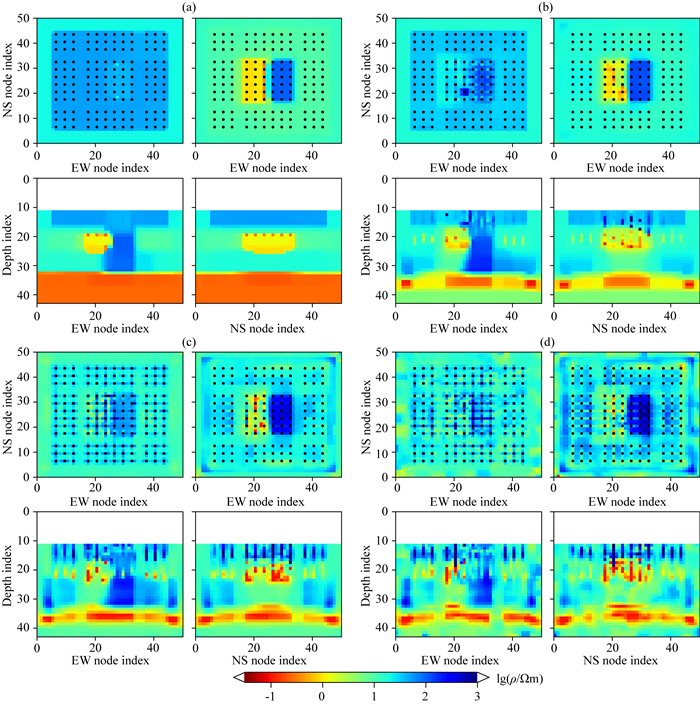
图 15 DMS2模型合成数据AR-QNL1噪声稳健性测试反演结果 绘图参数同图 7,(a) 5%噪声;(b) 10%噪声;(c) 20%噪声;(d) 30%噪声. Fig. 15 Results of AR-QNL1 inversion stability test for synthetic data of model DMS2 Same plotting parameters as Fig. 7, (a) 5% noise; (b) 10% noise; (c) 20% noise; (d) 30% noise. |
从收敛曲线看,即使采用随机数模型,经20次迭代后模型平均粗糙度基本在同一水平(图 14b),此时所有反演均让RMS收敛到4.8左右(图 14a).但随着噪声水平增大,AR-QNL1需要更小的正则因子达到这个效果(图 14c).在20次迭代以后,噪声水平低于10%时的反演收敛曲线基本处于同一数值水平,噪声水平超过20%时迭代后期模型粗糙度急剧增大(图 14b),这表明此时数据噪声已严重影响模型恢复效果.
对比第52次迭代的四个模型(图 15)和STP-RND的反演结果(图 13d)可知:5%的噪声水平对于AR-QNL1算法影响不大;10%的观测噪声已足够影响深部低阻层的恢复;20%和30%的数据噪声已在浅层和中深部造成过多的冗余构造.但也必须指出,测试中对于四种噪声数据AR-QNL1的正则因子均按w=2衰减,可能并不适应强噪声数据的反演.
4 稀疏测点实测MT资料反演对比为对比AR-QN和AR-QNL1在MT实测资料的反演效果,选择青海省20100415-Ms7.1玉树地震的震后科考MT数据集进行测试.该数据集已进行了L2正则的AR-QN反演,得到的电性结构模型已成功用于该区孕震环境解释(邓琰,2019).因篇幅所限,详细的地质背景信息本文不做介绍.两个反演均采用同一反演网格,初始模型均设定为100 Ωm均匀半空间.因实测辅助阻抗和倾子数据干扰严重,仅拟合剔除严重飞点后的Zxy和Zyx数据.唯一不同的参数是AR-QN使用比值法更新正则因子,而AR-QNL1使用更稳健的分段衰减策略(w=2)(见第3.2节),收敛曲线和结果模型分别如图 16和图 17所示.
|
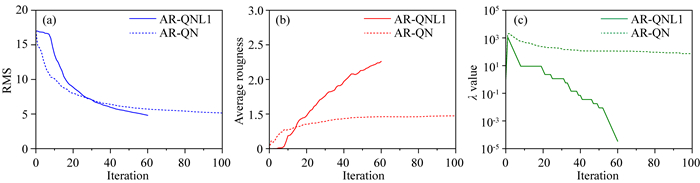
图 16 玉树MT实测资料AR-QN和AR-QNL1反演收敛曲线 (a) RMS;(b)平均粗糙度;(c)正则因子. Fig. 16 Convergence curves of AR-QN and AR-QNL1 inversion for real MT data in Yushu (a) RMS; (b) Average roughness; (c) Regularization parameter. |
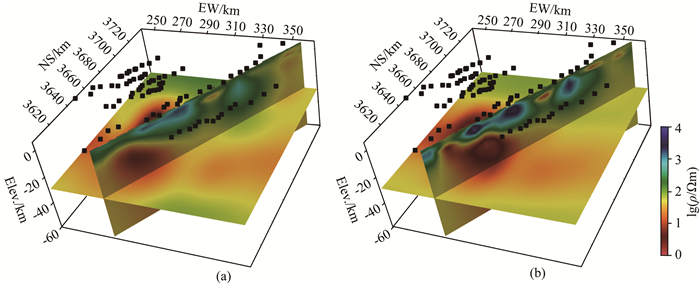
|
图 17 玉树MT实测资料AR-QN和AR-QNL1反演结果对比 黑点表示MT测点,(a) AR-QN;(b) AR-QNL1. Fig. 17 Results of AR-QN and AR-QNL1 inversion for real MT data in YUSHU Black dots shows MT sites′ location, (a) AR-QN; (b) AR-QNL1. |
由于使用了不同的正则因子更新策略,RMS曲线在第20次迭代之前有较大差异(图 16a).正则因子的数值差别很大(图 16c)的原因在于AR-QNL1的正则项与AR-QN具有不同数值特性.在第15次迭代之后AR-QNL1的模型粗糙度逐渐超过AR-QN,这表明此时L1正则已逐渐生效.在相同RMS水平下,AR-QNL1的反演结果与AR-QN基本一致(图 17),不同之处在于海拔-20 km以上AR-QNL1的电性界面更加清晰,整体模型分辨率优于AR-QN.这表明只要保证反演的每个阶段正则因子尽量大,L1正则的结果应优于L2正则.
但也必须指出的是,在AR-QNL1的迭代后期由于RMS难以下降导致分段衰减法的正则因子急剧减小(图 16c),这和第3.3节的强噪数据反演的情况类似(图 14c),使用比值法的AR-QN反演并无这一现象.这表明目前AR-QNL1的正则因子更新策略仍需进一步研究,避免迭代后期因正则因子过小而增加块状假异常.
5 结论本文分析了三维MT的L1正则化反演理论、求解方法和预期效果,建立了AR-QNL1反演算法,经模型合成数据和实测数据的反演对比分析,得到以下结论:
(1) L1正则反演更有利于让模型空间梯度(或二阶导)取稀疏解,允许模型电阻率空间分布函数局部尖锐.若反演的正则因子选取合理,其结果对电性界面的分辨能力应优于L2正则.
(2) L1正则反演问题可通过IRLS方法求解.若每次迭代正则因子足够大,反演早期接近常规L2正则解.随着迭代继续进行,重加权矩阵空间分布逐渐复杂,L1正则的突出界面的能力逐渐体现.为避免出现假异常,每次迭代中选择合理的正则因子非常必要.
(3) 模型合成数据和实测数据的反演对比都表明AR-QNL1算法收敛稳定,具有噪声稳健性.比值法自适正则因子策略不太适应AR-QNL1,分段衰减法的稳定性更强.在含噪数据反演中,分段衰减法后期正则因子减小过快,需进行改进.
(4) 鉴于L1正则在三维MT反演的应用仍是首次,模型合成数据验证和实测资料检验的工作仍不全面,在今后的研究中需更广泛的进行各种地质条件的观测数据反演对比,以发现并改进AR-QNL1算法的不足.
Avdeev D B. 2005. Three-dimensional electromagnetic modelling and inversion from theory to application. Surveys in Geophysics, 26(6): 767-799. |
Byrd R H, Nocedal J, Schnabel R B. 1994. Representations of quasi-Newton matrices and their use in limited memory methods. Mathematical Programming, 63(1-3): 129-156. |
Chen X B, Zhao G Z, Tang J, et al. 2005. An adaptive regularized inversion algorithm for magnetotelluric data. Chinese Journal of Geophysics (in Chinese), 48(4): 937-946. |
Deng Y, Tang J, Ruan S. 2019. Adaptive regularized three-dimensional magnetotelluric inversion based on the LBFGS quasi-Newton method. Chinese Journal of Geophysics (in Chinese), 62(9): 3601-3614. DOI:10.6038/cjg2019M0045 |
Deng Y. 2019. The study of three-dimensional electrical resistivity structure and the seismogenesis in Yushu earthquake area[Ph. D. thesis] (in Chinese). Beijing: Institute of Geology, China Earthquake of Academy.
|
Gholami A, Gheymasi H M. 2016. Regularization of geophysical ill-posed problems by iteratively re-weighted and refined least squares. Computational Geosciences, 20(1): 19-33. |
Golub G, von Matt U. 2012. Generalized Cross-Validation for Large-Scale Problems. Journal of Computational and Graphical Statistics, 6: 1-34. |
Hansen P C. 1992. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Review, 34(4): 561-580. |
Holland P W, Welsch R E. 1977. Robust regression using iteratively reweighted least-squares. Communications in Statistics-Theory and Methods, 6(9): 813-827. |
Hu X Y, Li Y, Yang W C, et al. 2012. Three-dimensional magnetotelluic parallel inversion algorithm using data space method. Chinese Journal of Geophysics (in Chinese), 55(12): 3969-3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 |
Hursán G, Zhdanov M S. 2002. Contraction integral equation method in three-dimensional electromagnetic modeling. Radio Science, 37(6): 1089. DOI:10.1029/2001RS002513 |
Kelbert A, Meqbel N, Egbert G, et al. 2014. ModEM:A modular system for inversion of electromagnetic geophysical data. Computers & Geosciences, 66: 40-53. |
Liu G D, Zhao G Z. 1994. New developments in magnetotellurics. Advance in Earth Sciences (in Chinese), 9(4): 97-100. |
Morozov V A. 1966. On regularization of ill-posed problems and selection of regularization parameter. J. Comp. Math. Phys., 6(1): 170-175. DOI:10.1007/978-1-4612-5280-1_2 |
Moré J, Thuente D. 1994. On Line Search Algorithms with Guaranteed Sufficient Decrease. ACM Trans. Math. Softw., 20(3): 286-307. |
Nam M J, Kim H J, Song Y, et al. 2007. 3D magnetotelluric modelling including surface topography. Geophysical Prospecting, 55(2): 277-287. |
Newman G A, Alumbaugh D L. 2000. Three-dimensional magnetotelluric inversion using non-linear conjugate gradients. Geophysical Journal International, 140(2): 410-424. |
Qin C, Wang X B, Zhao N. 2017. Parallel three-dimensional forward modeling and inversion of magnetotelluric based on a secondary field approach. Chinese Journal of Geophysics (in Chinese), 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
Siripunvaraporn W, Egbert G, Lenbury Y, et al. 2005. Three-dimensional magnetotelluric inversion:data-space method. Physics of the Earth and Planetary Interiors, 150(1): 3-14. |
Siripunvaraporn W. 2012. Three-Dimensional Magnetotelluric Inversion:An Introductory Guide for Developers and Users. Surveys in Geophysics, 33: 5-27. |
Vatankhah S, Renaut R A, Ardestani V E. 2017. 3-D projected L1 inversion of gravity data using truncated unbiased predictive risk estimator for regularization parameter estimation. Geophysical Journal International, 210(3): 1872-1887. |
Wu X P, Xu G M. 1998. Improvement of OCCAM's inversion for MT data. Chinese J. Geophys. (in Chinese), 41(4): 547-554. |
Wang T X, Wang D L, Sun J, et al. 2017. Closed-loop SRME based on 3D l1-norm sparse inversion. Acta Geophysica, 65(6): 1145-1152. |
Wang Z G, He Z X, Liu H Y. 2006. Three-dimensional inversion of borehole-surface electrical data based on quasi-analytical approximation. Applied Geophysics, 3(3): 141-147. |
Wei W B. 2002. New advance and prospect of magnetotelluric sounding (MT) in China. Progress in Geophysics (in Chinese), 17(2): 245-254. |
Xiao Q B, Yu G, Liu Z J, et al. 2017. Structure and geometry of the Aksay restraining double bend along the Altyn Tagh Fault, northern Tibet, imaged using magnetotelluric method. Geophysical Research Letters, 44(9): 4090-4097. |
Ye T, Huang Q H, Chen X B. 2018. Three-dimensional deep electrical structure and seismogenic environment of Nantinghe fault zone in southwestern Yunnan, China. Chinese Journal of Geophysics (in Chinese), 61(11): 4504-4517. DOI:10.6038/cjg2018M0287 |
Zhang L L, Yu P, Wang J L, et al. 2010. A study on 2D magnetotelluric sharp boundary inversion. Chinese Journal of Geophysics (in Chinese), 53(3): 631-637. DOI:10.3969/j.issn.0001-5733.2010.03.017 |
Zhao G Z, Chen X B, Tang J. 2007. Advanced geo-electromagnetic methods in China. Progress in Geophysics (in Chinese), 22(4): 1171-1180. |
Zhdanov M S, Fang S, Hursán G, et al. 2000. Electromagnetic inversion using quasi-linear approximation. Geophysics, 65(5): 1501-1513. |
Zhdanov M S, Ellis R, Mukherjee S. 2004. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics, 69(4): 925-937. |
陈小斌, 赵国泽, 汤吉, 等. 2005. 大地电磁自适应正则化反演算法. 地球物理学报, 48(4): 937-946. |
邓琰, 汤吉, 阮帅. 2019. 三维大地电磁自适应正则化有限内存拟牛顿反演. 地球物理学报, 62(9): 3601-3614. DOI:10.6038/cjg2019M0045 |
邓琰. 2019.玉树地震区三维电性结构及孕震环境研究[博士论文].北京: 中国地震局地质研究所.
|
胡祥云, 李焱, 杨文采, 等. 2012. 大地电磁三维数据空间反演并行算法研究. 地球物理学报, 55(12): 3963-3978. DOI:10.6038/j.issn.0001-5733.2012.12.009 |
刘国栋, 赵国泽. 1994. 大地电磁法新进展. 地球科学进展, 9(4): 97-100. |
秦策, 王绪本, 赵宁. 2017. 基于二次场方法的并行三维大地电磁正反演研究. 地球物理学报, 60(6): 2456-2468. DOI:10.6038/cjg20170633 |
魏文博. 2002. 我国大地电磁测深新进展及瞻望. 地球物理学进展, 17(2): 245-254. |
吴小平, 徐果明. 1998. 大地电磁数据的Occam反演改进. 地球物理学报, 41(4): 547-554. |
叶涛, 黄清华, 陈小斌. 2018. 滇西南地区南汀河断裂带三维深部电性结构及其孕震环境. 地球物理学报, 61(11): 4504-4517. DOI:10.6038/cjg2018M0287 |
张罗磊, 于鹏, 王家林, 等. 2010. 二维大地电磁尖锐边界反演研究. 地球物理学报, 53(3): 631-637. DOI:10.3969/j.issn.0001-5733.2010.03.017 |
赵国泽, 陈小斌, 汤吉. 2007. 中国地球电磁法新进展和发展趋势. 地球物理学进展, 22(4): 1171-1180. |
 2020, Vol. 63
2020, Vol. 63


