2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院大学, 北京 100049;
4. 中国石油大学(华东)深层油气重点实验室, 青岛 266580;
5. 中国石油勘探开发研究院, 北京 100020;
6. 中国科学院地质与地球物理研究所, 中国科学院地球与行星物理重点实验室, 北京 100029
2. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Key Laboratory of Deep Oil and Gas(China University of Petroleum(East China)), Qingdao 266580, China;
5. The Research Institute of Petroleum Exploration and Development, Beijing 100020, China;
6. Key Laboratory of Earth and Planetary Physics, CAS, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
作为石油勘探的重要环节之一,地震观测系统设计和采集参数优化是地震资料品质好坏的先决条件,也是地震资料处理和解释的基础.随着当前油气藏勘探的不断深入,勘探目标逐渐转向深层或超深层的复杂地质目标,对地震数据质量也提出了更高的要求.基于此,勘探界发展了“两宽一高”采集技术(李庆忠,1993),即宽频带、宽方位长排列和高密度的三维地震采集方式及其配套技术.该技术极大地提升了地震勘探的能力和精度,在地层或岩性油气藏地区取得了明显的应用效果(陈志刚等,2018),但相对于常规观测而言,其经济投入也十分高昂.因此,如何在现有的成本限制和装备条件下,根据具体工区的地质地球物理条件来选择合适的“两宽一高”采集观测参数以实现最佳的勘探效益,已成为当前地震勘探中迫切需要解决的瓶颈问题之一.
常规的观测系统设计基于共中心点(CMP)分析(Evans,1997),主要通过覆盖次数、炮检距分布和方位角分布等来判断观测系统设计方案的合理性,详见Cordsen等(2000)、Vermeer(2002).对于倾斜目的层,CMP分析不再有效.因此,勘探界发展出共反射点(CRP)分析方法,它基于宏观速度模型,通过射线追踪手段,得到通过目的面元位置的射线条数、传播距离与反射角度.与CMP分析类似,CRP分析也可以得到目标面元的覆盖次数、炮检距分布和方位角分布信息,详见Slawson等(1994)、Muerdter和Ratcliff(2001)和Chang等(2002).照明分析方法可以进一步实现复杂介质模型下的面元分析,计算其等效覆盖次数、炮检距分布和方位角分布(朱金平等,2011;谢小碧等,2013).但上述方法均立足于叠加效应分析,无法直接反映叠前偏移的效果.基于此,勘探界发展出了多种基于叠前偏移理论的观测系统设计方法,包括:基于Beylkin(1985)理论的分辨率分析(Vermeer,1999;Gibson and Tzimeas, 2002;Schuster and Huang, 2014),基于点绕射成像的角度域照明分析(Wu and Chen, 2006;Xie et al., 2006;Cao and Wu, 2009;Xie and Yan, 2016),直接进行多炮正演模拟加叠前偏移(Jurick et al., 2003;Regone, 2006)等.上述方法能直观的给出目标位置的偏移成像效果,但若采用波动方程延拓的实现方式,其运算效率较低,难以被直接用于三维观测系统方案的分析和比较.聚焦分辨率分析方法(Berkhout et al., 2001)是一种更高效的基于波动方程延拓的观测系统分辨率分析方法,采用分别对检波点与震源点进行聚焦分析的运算方式,能直接用于地震采集设计.聚焦分析方法源于共聚焦偏移理论(Berkhout, 1997a, b),其提供的分辨率结果和偏移成像的分辨率具有等效性(Tzimeas,2004).聚焦分析方法能适用于均匀介质(Volker et al., 2001)、水平层状介质(狄帮让等,2006)或复杂介质(Van Veldhuizen et al., 2008;魏伟等,2009;Wei and Fu, 2014),且能考虑面波(Ishiyama et al., 2015)和多次波(Kumar et al., 2016a, b)的影响.为了进一步提高聚焦分析的效率,Wei等(2012)提出了一种频率-波数域的多频快速聚焦分析算法,只需进行几个单频计算,随后可插值得到全频带聚焦分析结果.但上述研究仅针对稀疏采集情况,缺乏对于“两宽一高”采集的研究,尤其缺乏针对具体地质目标和地球物理条件“两宽一高”采集的研究.
基于此,本文首先回顾了聚焦分析的基本原理,随后给出一种新的水平分辨率和清晰度量化评价方法及其物理意义.基于该理论,我们以一个典型的陆上三维地震勘探方案和速度模型为例,采用复杂介质多频率快速聚焦分辨率分析方法,研究了“两宽一高”采集偏移成像分辨率问题,系统地讨论了水平分辨率随着关键采集参数的变化规律,给出了不同条件下水平分辨率的理论极限值,进而讨论当前采集参数的合理性并给出了进一步的优化建议.本文第1节首先回顾了聚焦分析的基本原理,随后给出一种新的水平分辨率和清晰度定量化方法及其物理意义,第2节给出了复杂介质条件下不同目标深度的水平分辨率和清晰度随排列长度、排列宽度、面元大小、子波频谱的变化规律及其极限值,第3节进一步提出了一种新的采集参数和子波频谱的交汇定量分析方法,证明了采集参数和子波频谱参数之间的可替代性,为复杂接收激发条件下采集观测系统设计提供了新的理论依据.
1 基本理论 1.1 多频聚焦分析如图 1所示,基于WRW波传播模型(Berkhout,1984),WRW分别表示上行传播、反射和下行传播阶段,空间频率域中深度zm处的绕射点k(x, y)(x,y表示水平位置坐标)在地表z0处产生的一次单频谐波响应δkP(z0, z0)可表示为
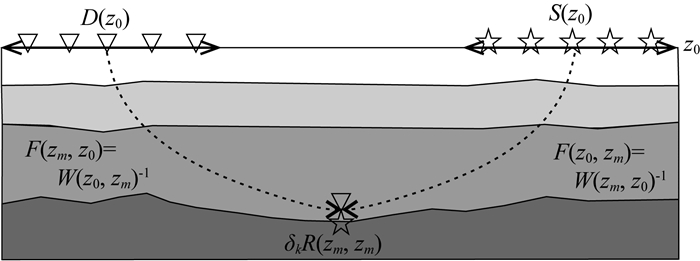
|
图 1 聚焦过程示意图 Fig. 1 Schematic diagram of the focal beams |
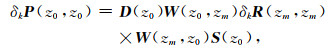
|
(1) |
其中:D(z0)和S(z0)分别是检波点矩阵和震源点矩阵;W(z0, zm)代表从目标深度zm到地表z0的上行波传播矩阵;δkR(zm, zm)表示地表位置(x, y)k在地下深度zm处的网格点角度无关的反射率矩阵;W(zm, z0)代表从地表z0到目标深度zm的下行波传播矩阵.
点绕射响应在所有水平位置及所有深度的叠加响应,即为完整的一次反射波场.为了从地震数据中提取反射率信息,可将地表z0处的地震响应δkP(z0, z0)向下外推到目标深度zm,分别在接收端和激发端应用聚焦算子F(zm, z0)和F(z0, zm)消除传播效应:
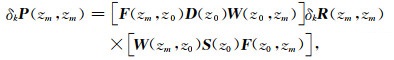
|
(2) |
其中δkP(zm, zm)为目标深度zm处k点的网格点响应.理想的偏移算子应当满足:
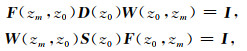
|
(3) |
I为单位矩阵,即
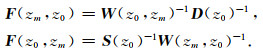
|
(4) |
但在实际偏移中,通常忽略观测系统效应,将聚焦算子F取值为矩阵W的逆,即:F(zm, z0)=W(z0, zm)-1,F(z0, zm)=W(zm, z0)-1.为了研究观测系统布设(D和S)对偏移分辨率的影响,可假设目标点响应是一个角度无关的点绕射δkR(zm, zm),进而可以得到其地表波场响应的成像矩阵δkP(zm, zm).矩阵δkR(zm, zm)为一个仅在k点处有一个非零元素的单位矩阵,可以表示为两个单位向量的矩阵乘积:
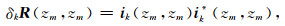
|
(5) |
其中ik(zm, zm)为一个仅在k点处有一个非零元素的单位列向量,星号表示转置.等式(2)可以写成:
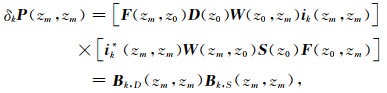
|
(6) |
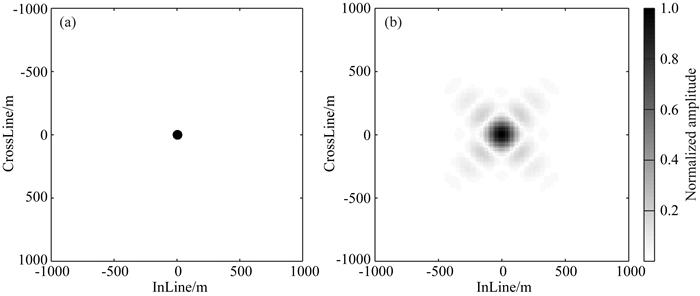
其中,Bk, D(zm, zm)=F(zm, z0)D(z0)W(z0, zm), Bk, S(z0, zm)=W(zm, z0)S(z0)F(z0, zm),分别代表目标深度zm处水平位置k点处的检波点和震源点聚焦矩阵,分别代表检波端和震源端的聚焦效果,可独立地对震源和检波器的采样性能进行评价.将检波点和震源点聚焦结果进行标量乘积,可得到双聚焦结果δkP(zm, zm),它是目标深度zm处水平位置k点处的聚焦分辨率矩阵(Van Veldhuizen et al., 2008),表示整个观测系统条件下目标点绕射的偏移成像效果.理想的情况下,聚焦过程满足公式(3),分辨率矩阵δkP(zm, zm)=δkR(zm, zm),仅在目标点k处取值为1,其他位置均为0值(如图 2a),但在实际情况下,由于地震观测系统的有限范围及其离散性,实际得到的分辨率矩阵结果会发生不同程度的发散,并且在复杂模型条件下还会产生旁瓣(如图 2b).
|
图 2 理想情况下的聚焦分辨率结果(a)和实际情况下的结果(b) Fig. 2 Focal beams resolution results under ideal conditions (a) and actual results (b) |
实现聚焦分析,必须对公式(6)进行恰当的计算,也就是对算子F和W进行波场延拓.在实际计算中,只需进行三次波场延拓操作,即一次W和震源侧和检波点侧的F.波场延拓的精度和效率取决于采取方法,常用的波场延拓通常在空间频率域(Blacquiere et al., 1989;Wapenaar et al., 2014)或空间波数域进行(Fu,2006;符力耘等,2007;王一博等,2016).综合考虑地震采集设计的精度和效率要求,我们选择退化傅里叶大步长延拓+Born-Kirchhoff插值(DF+BK)的方法实现波场延拓.退化傅里叶大步长延拓算子可由广义Lippmann-Schwinger积分方程(Fu et al., 1997)导出:
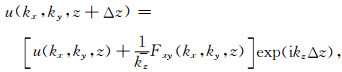
|
(7) |
其中u为压力,kx、ky和kz为波数分量,z为深度,Fxy(kx, ky, z)=FTxy{ik0[n(r)-1]u(r)},FTxy为水平方向的2D傅里叶变换,r为位置,n(r)=v0/v(r)为声波折射率,v0为参考速度,k0=ω/v0.式(7)的频散关系为
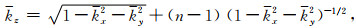
|
(8) |
kx、ky、kz为归一化波数.为避免波场与慢度扰动的褶积运算,可将折射率n(r)取值为不同常数n,在特定深度z下,常数n(x, y)=v0/v(x, y),即特定层参考速度v0与该层空间中各点速度v(x, y)的比值.由于kx≤1, ky≤1,得
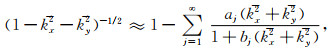
|
(9) |
因为参数aj、bj是与折射率n无关的变量,式(8)可近似为
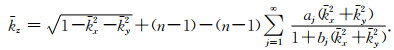
|
(10) |
式(10)即为三维退化傅里叶算子(Fu, 2006; Wei et al., 2012).其中,参数aj、bj的最优值可通过最小二乘法确定,以实现频散误差的最小化.实际应用中,公式(10)的一阶近似或至多二阶近似的精度已经可以满足较大传播角度、较大阻抗对比度的波场模拟需求.
采用指数近似eiξ≈1+iξ,由式(10)可得到以下单向波传播方程:
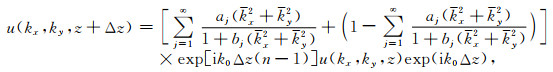
|
(11) |
令Cj=aj(kx2+ky2)/1+bj(kx2+ky2),并取一阶近似,式(11)可以简化为
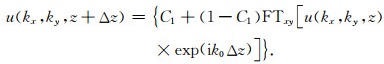
|
(12) |
式(12)即为一阶退化傅里叶(DF)单程波延拓算子,只用傅里叶变换进行波场延拓,且适用于强速度变化和大角度波场传播.式(12)的计算精度显著优于分裂步(SSF)延拓方法,几乎与傅里叶有限差分(FFD)方法接近(符力耘等,2007).
从广义Lippmann-Schwinger积分方程可在空间域导出Born-Kirchhoff插值算子(符力耘,2010):
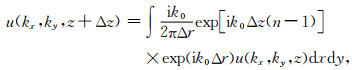
|
(13) |
其中Δr=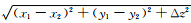
为了进一步提高聚焦分析的效率,Wei等(2012)提出了一种多频快速聚焦分析算法,只需进行一次单频计算,随后可插值得到全频带聚焦分析结果.不同频率下的聚焦分辨率矩阵满足如下近似关系:
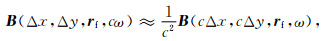
|
(14) |
其中c是常数(0 < c < 1),Δx=x-xf,Δy=y-yf,rf=(xf, yf, zf)为目标点,r=(x, y, z)为目标点附近的点.等式(14)能实现通过内插直接从频率为ω的分辨率矩阵导出频率为cω的分辨率矩阵,分别乘以子波频率振幅系数并求和即可得到全频带分辨率矩阵.利用该算法,仅需进行一次(或少量的)聚焦分析计算,再通过插值直接得到全频带聚焦分析的近似结果,极大提升了聚焦算法的运算效率.
1.2 分辨率定量化方法传统的成像分辨率研究通常采用经典Rayleigh准则(Jenkins and White, 1957),将时间或深度轴上相邻波峰和波谷的间距作为分辨率值.Schoenberger(1974)使用主瓣和旁瓣的峰值比作为分辨率值.Chen和Schuster(1999)基于远场或平面波近似,引入了均匀介质中的叠前偏移公式.Safar(1985)发现两个散射点在观测系统响应的35%振幅处可以分辨,它表示观测系统记录到的地下一个目标点的两个响应互相干涉,当两个响应的间隔小于响应的35%振幅处的宽度时,两个响应将不能分辨.
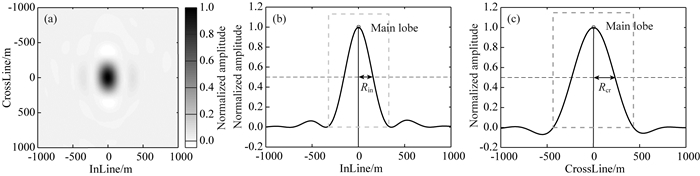
基于类似的方法,对于水平方向,本文采用水平分辨率(horizontal resolution)和清晰度(sharpness)量化三维观测系统对勘探目标的成像能力,下文将水平分辨率简称为分辨率(resolution).如图 3b和3c所示,分辨率数值定义为分辨率矩阵主瓣峰值1/2振幅处水平距离的一半,包括InLine方向和CrossLine方向.聚焦分辨率数值的物理意义为:两个邻近绕射点的水平间隔大于或等于分辨率,则这两个绕射点可分辨.
|
图 3 聚焦分辨率量化示意图 聚焦结果的平面图(a),聚焦结果沿InLine (b)和CrossLine (c)方向的剖面. Fig. 3 Schematic diagram of the focal beam resolution quantization (a) Planar diagram of the focusing results, (b) InLine section, and (c) CrossLine section. |
清晰度(sharpness)按(15)式计算:
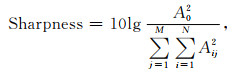
|
(15) |
其中,A0表示峰值振幅,Aij表示全部振幅分量.类似于Widess(1973)定义的参数,清晰度是一个独立于分辨率的物理量,代表了偏移成像结果中有效能量占总能量的比值,单位通常为dB.清晰度的数值与偏移噪声之间呈负相关关系,即较低的清晰度对应于较大的偏移噪声,进而间接地影响分辨率的效果.
根据上述原理,如图 4所示,复杂介质中多频率快速分辨率量化分析包括以下7个步骤:

|
图 4 多频快速聚焦分辨率分析流程示意图 Fig. 4 Schematic diagram of multi-frequency fast focal beams resolution analysis process |
① 建立速度模型,在地下目标处选择一个网格点k;
② 通过DF-BK传播算子对k点到采集地表进行波场延拓,即W(z0, zm)、W(zm, z0);
③ 将观测系统应用于正向波场,即分别对震源侧和检波点侧进行采样,即DW和WS;
④ 从采集地表聚焦到目标点k,通过应用聚焦算子F(zm, z0)聚焦到检波点,F(z0, zm)聚焦到震源点,即FDW和WSF;
⑤ 检波点聚焦束和震源点聚焦束相乘得到空间分辨率函数,即公式(6);
⑥ 用单频聚焦分辨率结果插值计算其他频率分量结果,并对其求和计算宽频(多频)聚焦分辨率结果;
⑦ 将分辨率矩阵定量化为水平分辨率和清晰度数值,定量比较不同采集方案下偏移成像的效果差异,进而反馈采集参数调整及采集设计过程.
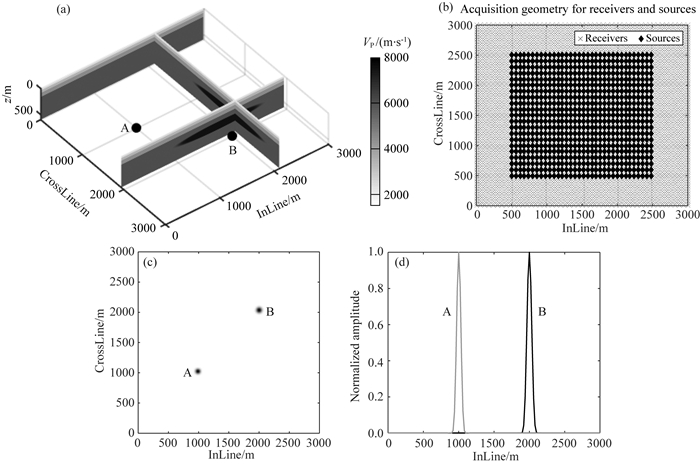
1.3 理论模型分析首先我们建立一个含高速侵入体的地质模型,选取两个目标点A(1000,1000,600)、B(2000,2000,600),A点位于水平地层下方,B点位于高速侵入体下方,如图 5a.检波点距线距分别为20 m、50 m,炮点距线距分别为20 m、100 m(图 5b).聚焦结果如图 5c和5d,其中A点Rcr=35.49 m,Rin=35.19 m,Sharpness=-8.4 dB;B点Rcr=39.86 m,Rin=39.35 m,Sharpness=-9.4 dB.A点的分辨率和清晰度显著高于B点,说明高速侵入体存在一定的屏蔽作用,会降低下伏地质构造的分辨率.另外,该示例也说明本文方法具有分析复杂速度结构的能力.
|
图 5 含高速侵入体不同目标点聚焦分辨率结果 Fig. 5 Focal beam resolution of high speed intrusion model |
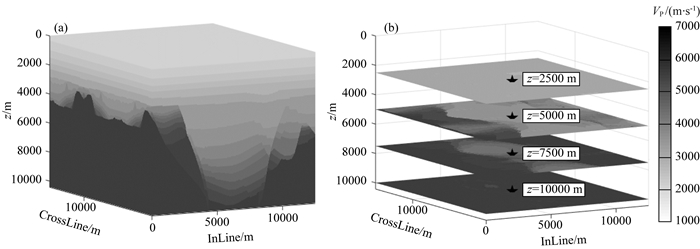
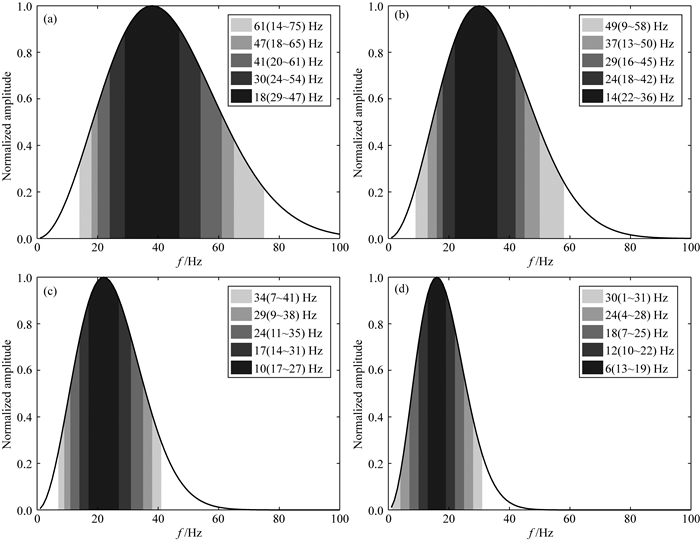
选用如图 6所示的中国某油田的实际复杂速度模型,模型尺寸是15000 m×12500 m×10000 m,网格间距是6.25 m×6.25 m×6.25 m.目标点深度分别选取2500 m(浅)、5000 m(中)、7500 m(深)和10000 m(超深),实际勘探中所采用的采集参数见表 1.不同深度对应地震子波频谱如图 7所示,由于采集设计阶段建立的速度模型精度有限,无法客观反映实际地震子波频谱随深度的变化规律.因此,我们直接从实际层位地震数据中提取出子波作为震源子波.
|
图 6 实际模型(a)和目标点层位切片(b) Fig. 6 Actual model (a) and target point horizon slice (b) |
|
图 7 不同深度目标点对应的子波振幅谱 (a) 2500 m; (b) 5000 m; (c) 7500 m; (d) 10000 m. Fig. 7 Wavelet amplitude spectrum corresponding to target points at different depths |
|
|
表 1 实际采集系统参数(单位:m) Table 1 Parameters of an actual acquisition geometry(unit:m) |
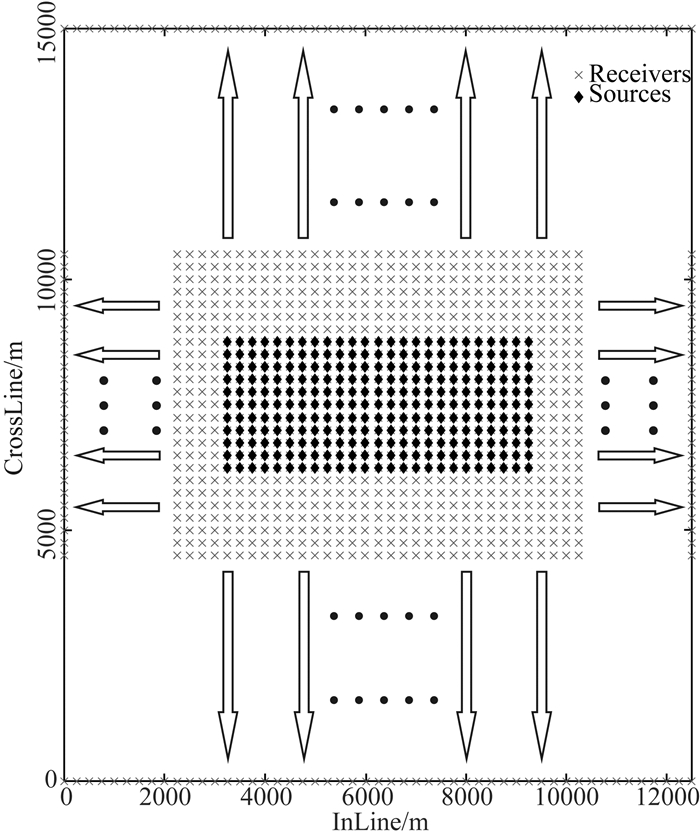
基于上述复杂模型,我们采用不同地震子波频谱,对不同深度的目标点进行了多频快速聚焦分辨率定量分析,得到其空间分辨率和成像清晰度量化结果.随后我们系统地分析了排列长度、排列宽度、面元密度、子波主频、子波频宽5个关键采集参数对聚焦分辨率和清晰度及其理论极限值的影响.分析所用的观测系统如图 8,炮点点距线距均为80 m并保持不变,炮点范围如图 8所示,InLine方向3000~9000 m,CrossLine方向6100~8800 m.
|
图 8 观测系统示意图 Fig. 8 Template of acquisition geometries |
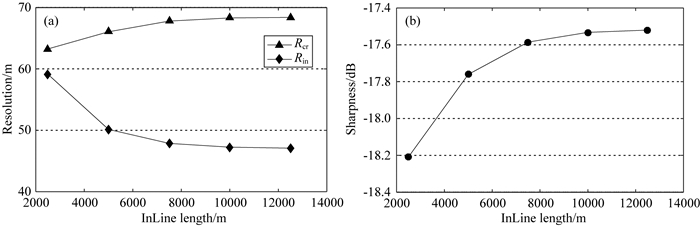
首先以5000 m深度目标点为例,讨论排列长度(InLine方向)对分辨率的影响.分析过程中保持其他采集参数值不变:排列宽度5000 m,面元尺寸6.25 m×6.25 m,主频30 Hz,频宽1~58 Hz,仅改变排列长度值,从2500 m逐步增加至12500 m.分别对这些采集方案进行聚焦分辨率量化分析,得到不同排列长度下的分辨率和清晰度量化结果(图 9).如图 9a所示,随着排列长度的增加,InLine方向分辨率逐步提高,但其提高的幅度逐渐趋缓,特别是在达到排列长度的临界值点(10000 m)以后,其结果趋于稳定,不再发生变化.另一方面,随着排列长度的增加,CrossLine方向分辨率则略有降低.这一结果表明增加一个方向(比如Inline方向)采样长度会降低其正交方向(比如Crossline方向)的分辨率.成像清晰度结果如图 9b所示,随着排列长度的增加而逐步提高,其临界值点出现位置与分辨率结果几乎相同.另外,排列长度达到10000 m之后继续增加,分辨率不再提高,而增加排列长度在实际生产中意味着更多的设备和更多的工时,增加设备和工时投入,均会增加采集成本,降低采集效益,却并不能提高采集质量.综上,10000 m排列长度即为当前条件下的理想排列长度值,是在兼顾采集质量和采集效益条件下的最优采集参数值.
|
图 9 分辨率(a)和清晰度(b)随排列长度(InLine)的变化(目标深度5000 m) Fig. 9 Resolution (a) and sharpness (b) versus InLine length (target depth 5000 m) |
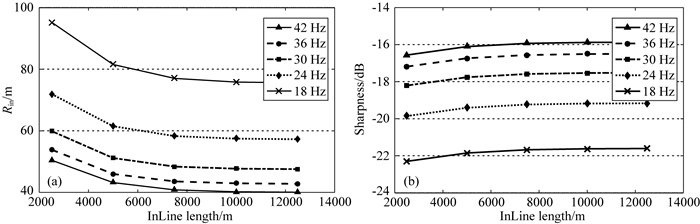
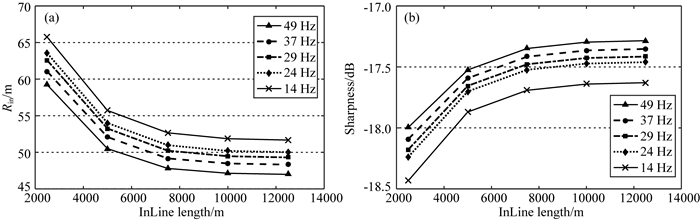
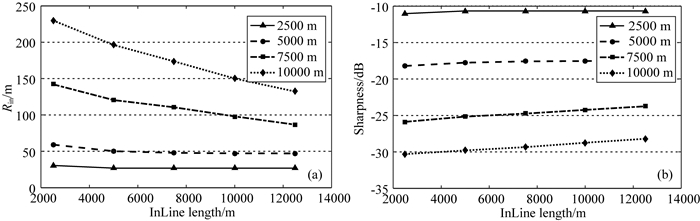
排列长度临界值会随着地震子波频谱(包括主频和频宽)和目标深度的变化而改变.图 10是不同主频下的聚焦分辨率和清晰度随排列长度变化的结果.可以看到,对于某一排列长度而言,地震子波主频越高,分辨率和清晰度明显更高,但分辨率和清晰度临界值点位置几乎相同,均在约10000 m达到最优.其原因是尽管不同主频对应于不同的量化数值,但其分辨率和清晰度变化曲线几乎“平行”,因此其所对应的临界值点位置也几乎相同.也就是说,在地震有效频率范围内,主频并不直接影响排列长度临界值点位置.图 11是不同频宽下聚焦分辨率和清晰度随排列长度变化的结果.可以看到,对于某一排列长度,频宽越宽,则分辨率越高,但分辨率提高并不显著,尤其在频宽从24 Hz增加到29 Hz时,聚焦分辨率几乎不变;同时,清晰度也呈现出相同的变化趋势.不同频宽下分辨率和清晰度变化曲线近似“平行”,其所对应的临界点位置几乎均位于10000 m.也就是说,在地震有效频率范围内,频带宽度也并不直接影响排列长度临界值点位置.图 12是不同目标深度下聚焦分辨率和清晰度随排列长度变化的结果.对于浅中层目标(2500 m和5000 m),其排列长度临界值出现在5000 m之前,随后其分辨率和清晰度不再有明显的变化;而对于深层或超深层目标(7500 m和10000 m),其排列长度临界值出现在12500 m之后,已超出图 12中的最大排列长度(12500 m)范围.综上,当目标点越深时,理想分辨率和清晰度所对应的排列长度临界值也越长,其规律与经典的排列长度取值规律一致,大致为目标深度的2倍.注意:上述聚焦分辨率分析结果不仅代表目标深度对成像的影响,同时也反映了复杂介质(图 5)对成像分辨率和清晰度的影响.因此,聚焦分析结果并不一定满足排列长度是深度的2倍的经典规律(Cordsen et al., 2000).
|
图 10 不同主频分辨率(a)和清晰度(b)随排列长度(InLine)的变化(目标深度5000 m) Fig. 10 Resolution (a) and sharpness (b) versus InLine length with different peak frequencies (target depth 5000 m) |
|
图 11 不同频宽分辨率(a)和清晰度(b)随排列长度(InLine)的变化(目标深度5000 m) Fig. 11 Resolution (a) and sharpness (b) versus InLine length with different bandwidths (target depth 5000 m) |
|
图 12 不同深度目标点分辨率(a)和清晰度(b)随排列长度(InLine)的变化 Fig. 12 Resolution (a) and sharpness (b) versus InLine length with different target depths |
综上:在达到临界值以前,增加InLine方向排列长度能有效地提高InLine方向的分辨率和成像清晰度,同时少量地损失CrossLine方向的分辨率.排列长度临界值位置几乎与主频和频宽等子波频率因素无关,但却与目标深度和介质复杂程度直接相关.目标深度越深,理想的排列长度值越长.
2.1.2 排列宽度同样以5000 m深度目标点为例,讨论排列宽度(CrossLine方向)对分辨率的影响.分析过程中保持其他采集参数值不变:排列长度12500 m,面元尺寸6.25 m×6.25 m,主频30 Hz,频宽1~58 Hz,仅改变排列宽度值,从2500 m逐步增加至12500 m.分别对这些采集方案进行聚焦分辨率量化分析,得到不同排列宽度下的分辨率和清晰度量化结果(图 13).如图 13a所示,随着排列宽度的增加,CrossLine方向分辨率逐渐提高,但其提高的幅度逐渐趋缓,特别是在达到排列宽度的临界值点(10000 m)以后,其结果趋于稳定,不再发生变化.另一方面,随着排列宽度的增加,InLine方向分辨率则略有降低.这一结果再次证明:增加一个方向(CrossLine方向)采样长度会降低其正交方向(InLine方向)的分辨率.如图 13b所示,成像清晰度结果随着排列宽度的增加而逐步提高,其临界值点出现位置与分辨率结果几乎相同.综上,10000 m排列宽度临界值即为当前条件下的理想排列宽度值,与排列长度的结论一致.
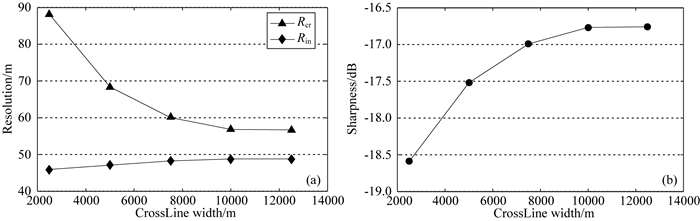
|
图 13 分辨率(a)和清晰度(b)随排列宽度(CrossLine)的变化(目标深度5000 m) Fig. 13 Resolution (a) and sharpness (b) versus CrossLine width (target depth 5000 m) |
与排列长度类似,排列宽度临界值也与地震子波频谱(包括主频和频宽)和目标深度的变化有关.图 14和图 15分别是不同主频和频宽下的聚焦分辨率和清晰度随排列宽度变化的结果.可以看到,在地震有效频率范围内,主频和频宽也不直接影响排列宽度临界值点(约10000 m)的位置.图 16是不同目标深度下聚焦分辨率和清晰度随排列宽度变化的结果.显然,浅中深层目标分别对应于不同排列宽度临界值点位置,其规律与排列长度一致.
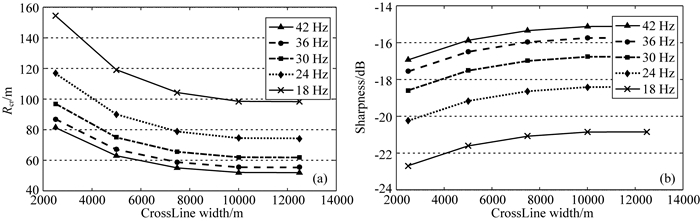
|
图 14 不同主频分辨率(a)和清晰度(b)随排列宽度(CrossLine)的变化(目标深度5000 m) Fig. 14 Resolution (a) and sharpness (b) versus CrossLine width with different peak frequencies (target depth 5000 m) |
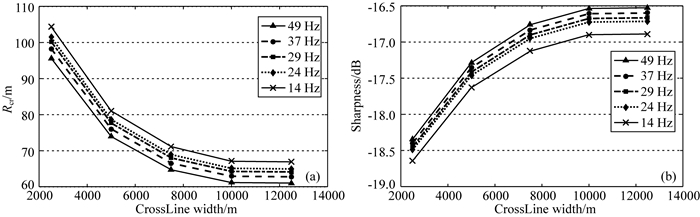
|
图 15 不同频宽分辨率(a)和清晰度(b)随排列宽度(CrossLine)的变化(目标深度5000 m) Fig. 15 Resolution (a) and sharpness (b) versus CrossLine width with different bandwidths (target depth 5000 m) |
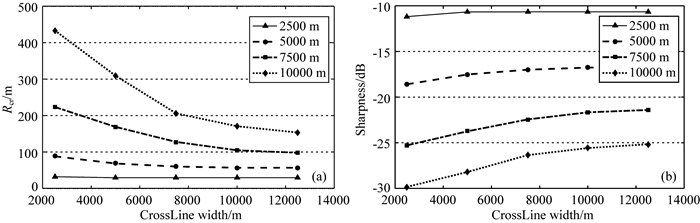
|
图 16 不同深度目标点分辨率(a)和清晰度(b)随排列宽度(CrossLine)的变化 Fig. 16 Resolution (a) and sharpness (b) versus CrossLine width with different target depths |
综上:在达到临界值以前,增加CrossLine方向排列宽度能有效地提高CrossLine方向的分辨率和成像清晰度,同时少量地损失InLine方向的分辨率.排列宽度临界值位置几乎与主频和频宽等子波频率因素无关,但却与目标深度和介质复杂程度直接相关.目标深度越深,理想的排列宽度值越长.
2.1.3 排列长度和排列宽度本节结合排列长度和排列宽度来进行分辨率分析.图 17中,横坐标分母代表排列长度(InLine),分子代表排列宽度(CrossLine).如图 17a所示,保持排列宽度不变,仅增加排列长度时,CrossLine方向的分辨率略有降低,随后保持排列长度不变,仅增加排列宽度时,CrossLine方向分辨率逐渐提高.如图 17b所示,InLine方向的分辨率呈现出与Crossline方向相反的变化规律.如图 17c所示,无论增加排列长度还是排列宽度清晰度都会提高.
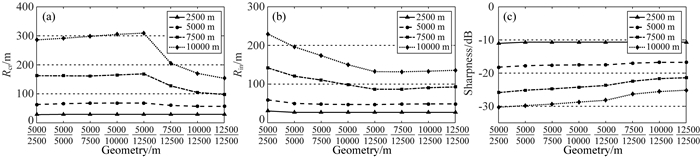
|
图 17 不同深度目标点分辨率(a:CrossLine;b:InLine)和清晰度(c)随排列长度和宽度同时的变化 Fig. 17 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus CrossLine width and InLine length with different target depths |
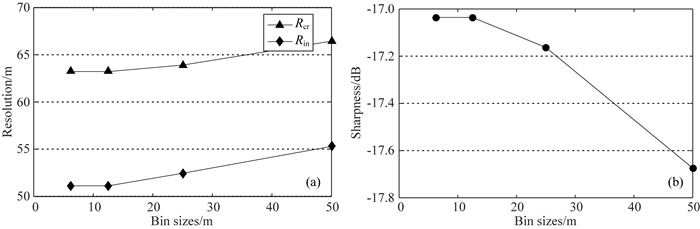
仍然以5000 m深度目标点为例,分析道密度(即面元尺寸)对分辨率的影响.分析过程中保持其他采集参数值不变:排列长宽均为12500 m,主频30 Hz,频宽1~58 Hz,仅改变InLine和CrossLine方向的面元大小:从50 m到6.25 m.分别对不同道密度的采集方案进行聚焦分辨率量化分析,得到不同道密度下的分辨率和清晰度量化结果(图 18).随着道密度的增加,CrossLine和InLine方向分辨率(图 18a)和清晰度(图 18b)均得到改善.当道密度达到12.5 m临界值时,分辨率和清晰度均达到其极限值.注意,随着面元的减小,清晰度的变化幅度要明显地大于分辨率,即小面元能小幅度的提高分辨率,但其主要优势是提高成像的清晰度,而非直接提高分辨率数值.
|
图 18 分辨率(a)和清晰度(b)随道密度的变化(目标深度5000 m) Fig. 18 Resolution (a) and sharpness (b) versus bin sizes (target depth 5000 m) |
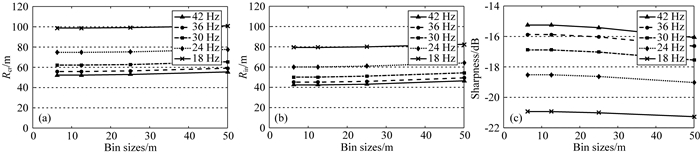
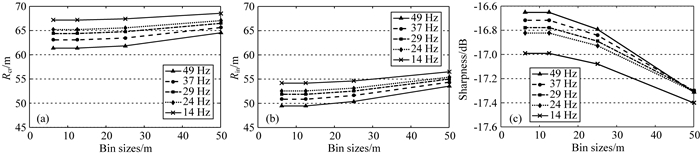
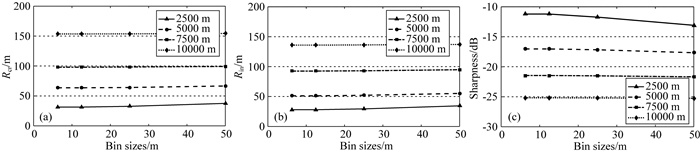
不同道密度下的分辨率也与地震子波频谱(包括主频和频宽)和目标深度的变化有关.图 19是不同主频下的聚焦分辨率和清晰度随道密度变化的结果.可以看到,对于某一道密度而言,地震子波主频越高,分辨率和清晰度明显更高,但在地震有效频率范围内,主频对道密度临界值点位置并无明显的影响.图 20是不同频带宽度下聚焦分辨率和清晰度随道密度的变化规律.显然,频带宽度也不直接影响道密度临界值点的位置.图 21是不同目标深度下聚焦分辨率和清晰度随道密度变化的结果.对于深层目标(7500 m和10000 m),清晰度几乎不随道密度变化,分析中所采用的最大面元(50 m)已能满足成像需求;对于浅中层目标(2500 m和5000 m),清晰度会随道密度的增加而提高,并且深度越浅(如2500 m),清晰度提高越显著.显然,浅层目标对面元大小的要求更高.注意:上述分析结果仅反映了偏移成像对面元大小的需求,如果进一步考虑噪声压制等因素,深层目标对面元大小的要求并不一定低于浅层目标.
|
图 19 不同主频分辨率(a:CrossLine;b:InLine)和清晰度(c)随道密度的变化(目标深度5000 m) Fig. 19 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus bin sizes with different peak frequencies (target depth 5000 m) |
|
图 20 不同频宽分辨率(a:CrossLine;b:InLine)和清晰度(c)随道密度的变化(目标深度5000 m) Fig. 20 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus bin sizes with different bandwidths (target depth 5000 m) |
|
图 21 不同深度目标点分辨率(a:CrossLine;b:InLine)和清晰度(c)随道密度的变化 Fig. 21 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus bin sizes with different target depths |
综上:增加道密度能够显著地提高成像的清晰度,同时小幅度地提高成像分辨率.从分辨率和清晰度的角度,道密度临界值位置几乎与主频和频宽等子波频率因素无关,但却与目标深度和介质复杂程度直接相关,目标深度越浅,道密度临界值越小.
2.2 采集参数与子波频谱的成像效果交汇分析地震子波频谱受多种采集和处理因素的影响,其频谱宽度取决于勘探工区的具体地震地质条件,其中最具决定性因素通常是地震波的激发和接收条件.在地震观测系统设计阶段,一般仅有采集参数是可控的,而子波频谱则是不可控的.基于此,我们拟进一步对采集参数与子波频谱进行交汇分析,通过建立两者之间的定量联系,寻找其可替代性,可为复杂接收激发条件下采集观测系统设计提供新的理论依据.
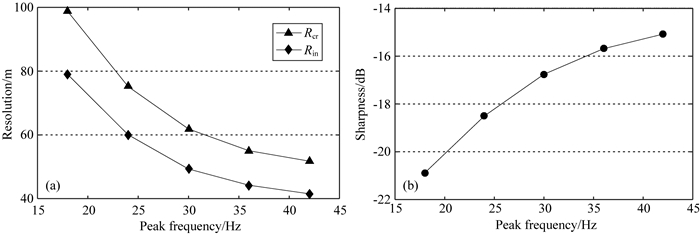
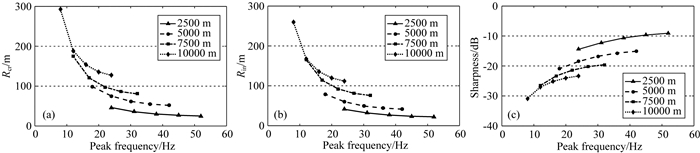
2.2.1 排列长度与主频的交汇分析以5000 m深度目标点为例单独分析子波主频对分辨率的影响.分析中,其他采集参数取值保持不变:排列长宽均为12500 m,面元取6.25 m×6.25 m,频宽1~58 Hz.分辨率和清晰度结果如图 22,可以看到,随着主频的增加,CrossLine和InLine方向分辨率和清晰度均显著提高.当主频从18 Hz增加至42 Hz时,分辨率提高约100%,清晰度提高约40%.与其他采集参数相似,我们可以得到分辨率和清晰度的极限值及其对应的主频临界点位置.在图 22中,主频的临界值应取值为等于或大于42 Hz,可能超出图中的频率范围.为了进一步讨论不同目标点深度对极限分辨率和清晰度及其对应的临界频率值的影响,我们绘制如图 23所示的结果.显然,不管深度如何,提高主频均能显著提高分辨率和清晰度,且深度越深,主频对分辨率和清晰度的影响越显著,比如:对于2500 m深度目标点,主频从24 Hz增加至52 Hz时,目标点分辨率提高约80%,而对于10000 m深度目标点,主频从8 Hz增加至24 Hz时,分辨率能提高约130%.另一方面,目标点深度也能影响临界频率值,但影响幅度较小.
|
图 22 分辨率(a)和清晰度(b)随主频的变化(目标深度5000 m) Fig. 22 Resolution (a) and sharpness (b) versus peak frequencies (target depth 5000 m) |
|
图 23 不同深度目标点分辨率(a:CrossLine;b:InLine)和清晰度(c)随主频变化 Fig. 23 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus peak frequencies with different target depths |
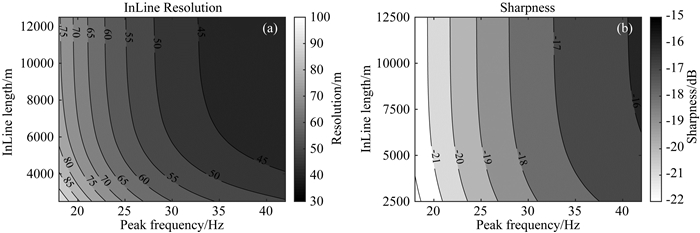
如前所述,增大主频可以同时提高InLine方向和CrossLine方向的分辨率和清晰度;增加排列长度,也可以提高InLine方向的分辨率和清晰度.为了理清两者之间的关系,我们绘制主频和排列长度的交汇分析图(图 24).图中颜色分别代表分辨率和清晰度的量化值,颜色越深表示分辨率和清晰度越高.如图 24a所示,在2500~7500 m排列长度范围内,增加排列长度和提高主频均可以提高InLine方向分辨率;而在7500~12500 m排列长度范围内,排列长度的影响几近消失,提高主频仍能有效地提高InLine方向分辨率;但是当主频无法继续提高,而排列长度较小时,可通过增加排列长度提高InLine方向分辨率,当排列长度达到极限值,继续增加排列长度,也不能使分辨率继续提高.如图 24b所示,在整个排列长度范围内,增加排列长度对提高清晰度作用有限,提高主频是改善清晰度的几乎唯一的选择.综上,排列长度和主频具有替代作用,当无法进一步提高主频时,可通过增加排列长度达到同样的分辨率.
|
图 24 排列长度与主频的交汇量化结果(目标深度5000 m) Fig. 24 Crossplot of InLine length and peak frequencies (target depth 5000 m) |
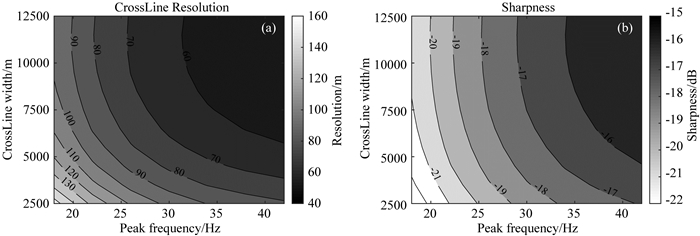
类似于主频和排列长度的交汇分析,以等值线图的方式对主频和排列宽度进行交汇分析.如图 25所示,增加排列宽度和主频均可以有效地提高CrossLine方向的分辨率和清晰度,即从偏移成像的角度,排列宽度和主频具有替代作用,当无法进一步提高主频时,可通过增加排列宽度达到同样的分辨率和清晰度.
|
图 25 排列宽度与主频的交汇量化结果(目标深度5000 m) Fig. 25 Crossplot of CrossLine width and peak frequencies (target depth 5000 m) |
进一步对道密度和主频进行交汇分析,其InLine和CrossLine分辨率和清晰度结果分别如图 26所示.在高频段,道密度与主频之间也具有一定的可替代性,且频率越高,可替代性越强.但在低频段,道密度与主频之间没有可替代性,无法通过加密道来替代频率的影响.
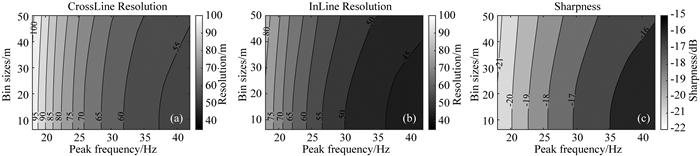
|
图 26 道密度与主频的交汇量化结果(目标深度5000 m) Fig. 26 Crossplot of bin sizes and peak frequencies (target depth 5000 m) |
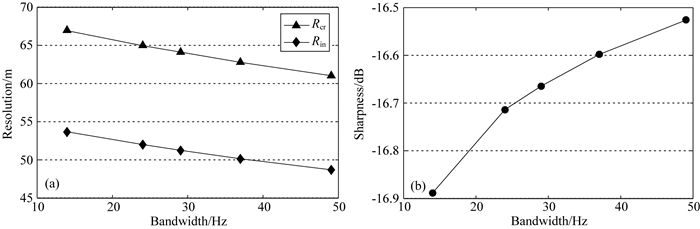
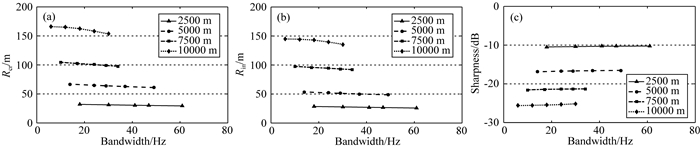
首先单独分析子波频带宽度对分辨率的影响,以5000 m深度目标点为例,保持其他采集参数值不变:排列长宽均为12500 m,面元取6.25 m×6.25 m,主频30 Hz.分辨率和清晰度随频率带宽的变化结果如图 27所示,随着频宽的增加,分辨率和清晰度均有小幅度的提高.进一步对不同深度目标点进行聚焦分辨率分析,结果如图 28所示,频宽对分辨率影响很小,深度越深,分辨率随频宽增加而提高的相对更加明显,而清晰度几乎不随频宽而变化.
|
图 27 分辨率(a)和清晰度(b)随频带宽度的变化(目标深度5000 m) Fig. 27 Resolution (a) and sharpness (b) versus bandwidth (target depth 5000 m) |
|
图 28 不同深度目标点分辨率(a:CrossLine;b:InLine)和清晰度(c)随频带宽度的变化 Fig. 28 Resolution (a: CrossLine, b: InLine) and sharpness (c) versus bandwidth with different target depths |
对排列长度与频宽的交汇分析结果如图 29所示.当排列长度小于其临界值(10000 m)时,排列长度对分辨率和清晰度的影响比频宽因素更明显;当排列长度大于其临界值时,排列长度的影响弱于频宽因素.即从偏移成像的角度,排列长度和频宽均有其优势影响范围,没有明显的替代作用.
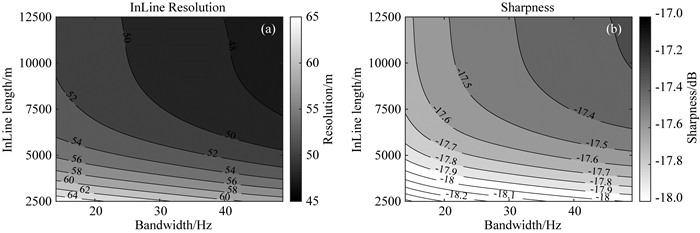
|
图 29 排列长度与频宽的交汇量化结果(目标深度5000 m) Fig. 29 Crossplot of InLine length and bandwidth (target depth 5000 m) |
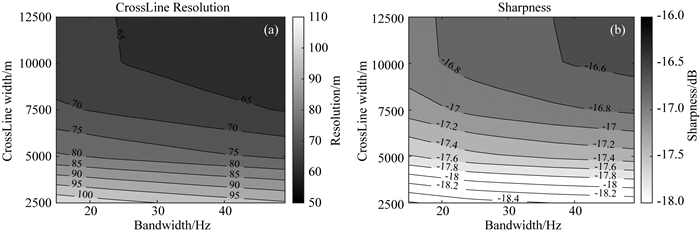
排列宽度与频宽的交汇分析结果如图 30所示,其规律与排列长度相似.当排列宽度小于其临界值(10000 m)时,排列宽度对分辨率和清晰度的影响比频宽因素更明显;当排列宽度大于其临界值时,排列宽度的影响弱于频宽因素.即从偏移成像的角度,排列宽度和频宽均有其优势影响范围,没有明显的替代作用.
|
图 30 排列宽度与频宽的交汇量化结果(目标深度5000 m) Fig. 30 Crossplot of CrossLine width and bandwidth (target depth 5000 m) |
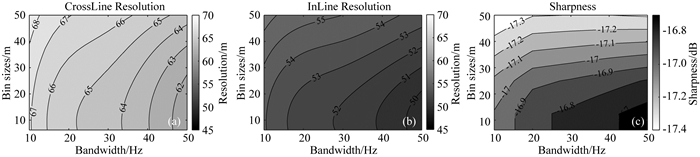
对道密度与频宽进行交汇分析,其InLine和CrossLine分辨率和清晰度结果分别如图 31所示.显然,道密度与频宽之间也具有很强的可替代性.当无法进一步提高频带宽度时,可通过增加道密度达到同样的分辨率和清晰度.
|
图 31 道密度与频宽的交汇量化结果(目标深度5000 m) Fig. 31 Crossplot of bin sizes and bandwidth (target depth 5000 m) |
第2节对观测系统采集参数与子波频谱的成像效果进行了分析,可以发现,地震采样参数中,排列长度和宽度对分辨率和清晰度具有显著影响,增加排列长度或宽度会使该方向的分辨率和清晰度提高,而使与其正交方向上的分辨率略微降低.当地震波以近水平方向入射到目标点,再沿相同方向反射回去将提供最高水平分辨率.长排列有助于提供近水平入射,因而可以提高分辨率,其正交方向分辨率出现降低的原因,可以考虑是波传播算子误差引起,但具体原因还有待进一步研究.此外,考虑到计算效率的问题,本文所采用的退化傅里叶大步长延拓+Born-Kirchhoff插值(DF+BK)的波场延拓方法是单程波算子,并没有选择最高精度的双程波模拟,在大角度的时候会有一定的误差,有可能会影响到最后结果的精度,下一步应采用双程波算子对本文结论做进一步验证.
排列长度和宽度的极限值与子波频率因素无关,但是受目标深度和介质复杂程度的影响,目标点越深,理想分辨率和清晰度所对应的排列长度或宽度的临界值也越长.理论上,地下目标点的水平分辨率极限值会在排列长度和宽度趋近于无限大时出现(水平入射提供最高的水平分辨率,越长的偏移距,入射方向越接近于水平),但是实际上,地下介质往往存在垂向速度梯度,排列长度和宽度无需达到无限大即可实现对目标点的水平入射,达到水平入射后,继续增加排列长宽,水平分辨率也不再继续提高,但是仍然遵循越深的目标点需要越长的偏移距的规律.因此,水平分辨率的排列长度和宽度的极限值与目标点深度和介质速度结构有关.
另外,对于不同深度处目标点的分辨率,其差别还直接与不同深度处的波速有关.目标点越深波速越高,其波长越长,而分辨率和波数成正比,即和波长成反比.因此,相同的观测系统下,目标点越深,其分辨率相应越低.
道密度对提高成像分辨率的贡献较小,但能够显著提高成像的清晰度.道密度临界值位置同样与子波频率因素无关,但与目标深度和介质复杂程度直接相关,目标深度越浅,道密度临界值越小.对于子波频率因素,不管深度如何,提高主频均能显著提高分辨率和清晰度,并且深度越深,主频对分辨率和清晰度的影响越显著.但是提高子波频宽,分辨率和清晰度只有小幅度的提高.从偏移成像的角度,排列长度和宽度与主频之间存在替代作用,当无法进一步提高主频时,可通过增加排列长度或宽度达到同样的分辨率.排列长度和宽度与频宽均有其优势影响范围,没有明显的替代作用.道密度和主频在高频段具有一定的可替代性,但在低频段不存在替代性.但是,道密度和频宽具有很强的可替代性,当无法进一步提高频带宽度时,可通过增加道密度达到同样的分辨率和清晰度.
本文主要研究复杂介质下采集观测参数对水平分辨率的影响,其结论不适合垂直分辨率.本文方法主要考虑偏移成像效应,没有考虑其他处理步骤对采集参数的要求,比如:速度分析可能会对排列长宽提出更高的要求,近地表噪声压制可能会对面元大小提出更高的要求.另一方面,本文结论仅针对一个速度模型和单个目标点位置及其对应的子波频谱,不一定适用于其他地质目标和地球物理条件.此外,为了兼顾效率和精度,我们采用一阶近似退化傅里叶算子进行单程波延拓运算,且仅考虑了一次反射纵波,忽略了多次反射波、横向和转换波的影响.
4 结论本文首先回顾了聚焦分析的基本原理,随后给出一种新的分辨率和清晰度定量化方法及其物理意义.基于该理论,我们选取一个典型的陆上三维地震勘探方案和速度模型,采用复杂介质多频率快速聚焦分辨率分析方法,研究了“两宽一高”采集偏移成像分辨率问题,系统地讨论了偏移成像分辨率随着关键采集参数的变化规律,给出了不同条件下分辨率的理论极限值,进而讨论当前采集参数的合理性并给出了进一步的优化建议.此外,本文也提出了一种新的采集参数和子波频谱的交汇定量分析方法,证明了采集参数和子波频谱参数之间的可替代性,为复杂接收激发条件下采集观测系统设计提供了新的理论依据.
Berkhout A J. 1984. Seismic Resolution: A Quantitative Analysis of Resolving Power of Acoustical Echo Techniques. Worldwide Distributors, Expro Science Publications.
|
Berkhout A J. 1997a. Pushing the limits of seismic imaging, part Ⅰ:prestack migration in terms of double dynamic focusing. Geophysics, 62(3): 937-953. |
Berkhout A J. 1997b. Pushing the limits of seismic imaging, Part Ⅱ:Integration of prestack migration, velocity estimation, and AVO analysis. Geophysics, 62(3): 954-969. DOI:10.1190/1.1444202 |
Berkhout A J, Ongkiehong L, Volker A W F, et al. 2001. Comprehensive assessment of seismic acquisition geometries by focal beams-Part Ⅰ:Theoretical considerations. Geophysics, 66(3): 911-917. |
Beylkin G. 1985. Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform. Journal of Mathematical Physics, 26(1): 99-108. DOI:10.1063/1.526755 |
Blacquiere G, Debeye H W J, Wapenaar C P A, et al. 1989. 3D table-driven migration. Geophysical Prospecting, 37(8): 925-958. DOI:10.1111/j.1365-2478.1989.tb02241.x |
Cao J, Wu R S. 2009. Full-wave directional illumination analysis in the frequency domain. Geophysics, 74(4): S85-S93. DOI:10.1190/1.3131383 |
Chang T S, Kue C W, Canales L, et al. 2002. Forward modeling attribute analysis for AVO and prestack depth migration.//72nd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 48-51.
|
Chen J, Schuster G T. 1999. Resolution limits of migrated images. Geophysics, 64(4): 1046-1053. DOI:10.1190/1.1444612 |
Chen Z G, Li F, Wang X, et al. 2018. Application of prestack anisotropic intensity attribute in prediction of P Buried hill fractured reservoir in Bongor Basin, Chad. Chinese Journal of Geophysics (in Chinese), 61(11): 4625-4634. DOI:10.6038/cjg2018L0640 |
Cordsen A, Galbraith M, Peirce J. 2000. Planning Land 3-D Seismic Surveys. Tulsa: Society of Exploration Geophysicists.
|
Di B R, Cao W P, Gu P C. 2006. Double-focus algorithm of models in different medium. Oil Geophysical Prospecting (in Chinese), 41(2): 123-128. |
Evans B J. 1997. A method for stacking 3-D swath data from a 3-D dipping horizon, without the need for a stacking velocity analysis. Exploration Geophysics, 28(1-2): 48-51. DOI:10.1071/EG997048 |
Fu L Y, Mu Y G, Yang H J. 1997. Forward problem of nonlinear Fredholm integral equation in reference medium via velocity-weighted wavefield function. Geophysics, 62(2): 650-656. DOI:10.1190/1.1444173 |
Fu L Y. 2006. Comparison of different one-way propagators for wave forward propagation in heterogeneous crustal wave guides. Bulletin of the Seismological Society of America, 96(3): 1091-1113. DOI:10.1785/0120050159 |
Fu L Y, Sun W J, Li D P. 2007. Degenerate migrators for imaging fault-related complex structures. Chinese Journal of Geophysics (in Chinese), 50(4): 1241-1250. |
Fu L Y. 2010. Born-series dispersion equations and Born-Kirchhoff propagators. Chinese Journal of Geophysics (in Chinese), 53(2): 370-384. DOI:10.3969/j.issn.0001-5733.2010.02.015 |
Gibson R L, Tzimeas C. 2002. Quantitative measures of image resolution for seismic survey design. Geophysics, 67(6): 1844-1852. DOI:10.1190/1.1527084 |
Ishiyama T, Blacquière G, Verschuur D J, et al. 2015. 3D surface-wave estimation and separation using a closed-loop approach. Geophysical Prospecting, 64(6): 1413-1427. DOI:10.1111/1365-2478.12347 |
Jenkins F A, White H E. 1957. Fundamentals of Optics. New York: McGraw-Hill Publishing Co.
|
Jurick D, Codd J, Hoxha F, et al. 2003. Gulf of Suez acquisition design using 2D and 3D full wave equation simulation.//73rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2136-2139.
|
Kumar A, Blacquière G, Verschuur E. 2016a. Extending illumination using all multiples:application to 3D acquisition geometry analysis. Geophysical Prospecting, 64(3): 622-641. DOI:10.1111/1365-2478.12326 |
Kumar A, Blacquière G, Pedersen M W, et al. 2016b. Full-wavefield marine survey design using all multiples. Geophysics, 81(3): P1-P12. DOI:10.1190/geo2015-0280.1 |
Li Q Z. 1993. A Systematical Analysis of High Resolution Seismic Exploration (in Chinese). Beijing: Petroleum Industry Press.
|
Muerdter D, Ratcliff D. 2001. Understanding subsalt illumination through ray-trace modeling, Part 1:Simple 2-D salt models. The Leading Edge, 20(6): 578-594. DOI:10.1190/1.1438998 |
Regone C J. 2006. A modeling approach to wide-azimuth design for subsalt imaging. The Leading Edge, 25(12): 1467-1475. DOI:10.1190/1.2405331 |
Safar M H. 1985. On the lateral resolution achieved by Kirchhoff migration. Geophysics, 50(7): 1091-1099. DOI:10.1190/1.1441981 |
Schoenberger M. 1974. Resolution comparison of minimum-phase and zero-phase signals. Geophysics, 39(6): 826-833. DOI:10.1190/1.1440469 |
Schuster G T, Huang Y S. 2014. Far-field super resolution by imaging of resonance scattering.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4598-4602, doi: 10.1190/segam2014-0344.1.
|
Slawson S E, Grove K D, Fischer G W. 1994. Model-based 3-D seismic acquisition design.//64th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 919-920.
|
Tzimeas C. 2004. Image resolution analysis: A new, robust approach to seismic survey design[Ph. D. thesis]. Texas A&M University.
|
Van Veldhuizen E J, Blacquière G, Berkhout A J. 2008. Acquisition geometry analysis in complex 3D media. Geophysics, 73(5): Q43-Q58. DOI:10.1190/1.2972029 |
Vermeer G J O. 1999. Factors affecting spatial resolution. Geophysics, 64(3): 942-953. |
Vermeer G J O. 2002. 3-D Seismic Survey Design. Tulsa: Society of Exploration Geophysicists.
|
Volker A W F, Blacquière G, Berkhout A J, et al. 2001. Comprehensive assessment of seismic acquisition geometries by focal beams-Part Ⅱ:Practical aspects and examples. Geophysics, 66(3): 918-931. |
Wang Y B, Zheng Y K, Xue Q F, et al. 2016. Reverse time migration with Hilbert transform based full wavefield decomposition. Chinese Journal of Geophysics (in Chinese), 59(11): 4200-4211. DOI:10.6038/cjg20161122 |
Wapenaar K, Thorbecke J, Van Der Neut J, et al. 2014. On the focusing conditions in time-reversed acoustics, seismic interferometry and Marchenko imaging.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4613-4619, doi: 10.1190/segam2014-1577.1.
|
Wei W, Fu L Y, Jiang T. 2009. Resolution analysis of seismic acquisition geometries by focal beams in 3D complicated media. Chinese Journal of Geophysics (in Chinese), 52(5): 1310-1317. DOI:10.3969/j.issn.0001-5733.2009.05.020 |
Wei W, Fu L Y, Blacquière G. 2012. Fast multifrequency focal beam analysis for 3D seismic acquisition geometry. Geophysics, 77(2): P11-P21. |
Wei W, Fu L Y. 2014. On horizontal resolution for seismic acquisition geometries in complex 3D media. Journal of Applied Geophysics, 108: 43-52. DOI:10.1016/j.jappgeo.2014.06.011 |
Widess M B. 1973. How thin is a thin bed?. Geophysics, 38(6): 1176-1180. DOI:10.1190/1.1440403 |
Wu R S, Chen L. 2006. Directional illumination analysis using beamlet decomposition and propagation. Geophysics, 71(4): S147-S159. DOI:10.1190/1.2204963 |
Xie X B, Jin S W, Wu R S. 2006. Wave-equation-based seismic illumination analysis. Geophysics, 71(5): S169-S177. DOI:10.1190/1.2227619 |
Xie X B, He Y Q, Li P M. 2013. Seismic illumination analysis and its applications in seismic survey design. Chinese Journal of Geophysics (in Chinese), 56(5): 1568-1581. DOI:10.6038/cjg20130515 |
Xie X B, Yan Z. 2016. A Poynting vector-based illumination and resolution analysis method for full-wave RTM.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4372-4377, doi: 10.1190/segam2016-13780002.1.
|
Zhu J P, Dong L G, Cheng J B. 2011. Target-oriented 3D seismic optimal geometry design based on seismic illumination. Oil Geophysical Prospecting (in Chinese), 46(3): 339-348. |
陈志刚, 李丰, 王霞, 等. 2018. 叠前各向异性强度属性在乍得Bongor盆地P潜山裂缝性储层预测中的应用. 地球物理学报, 61(11): 4625-4634. DOI:10.6038/cjg2018L0640 |
狄帮让, 曹卫平, 顾培成. 2006. 不同介质模型的双聚焦计算方法. 石油地球物理勘探, 41(2): 123-128. |
符力耘, 孙伟家, 李东平. 2007. 退化的Fourier偏移算子及其在复杂断块成像中的应用. 地球物理学报, 50(4): 1241-1250. |
符力耘. 2010. Born序列频散方程和Born-Kirchhoff传播算子. 地球物理学报, 53(2): 370-384. DOI:10.3969/j.issn.0001-5733.2010.02.015 |
李庆忠. 1993. 走向精确勘探的道路. 北京: 石油工业出版社.
|
王一博, 郑忆康, 薛清峰, 等. 2016. 基于Hilbert变换的全波场分离逆时偏移成像. 地球物理学报, 59(11): 4200-4211. DOI:10.6038/cjg20161122 |
魏伟, 符力耘, 蒋韬. 2009. 复杂构造三维地震观测系统设计的共聚焦分辨率分析. 地球物理学报, 52(5): 1310-1317. DOI:10.3969/j.issn.0001-5733.2009.05.020 |
谢小碧, 何永清, 李培明. 2013. 地震照明分析及其在地震采集设计中的应用. 地球物理学报, 56(5): 1568-1581. DOI:10.6038/cjg20130515 |
朱金平, 董良国, 程玖兵. 2011. 基于地震照明、面向勘探目标的三维观测系统优化设计. 石油地球物理勘探, 46(3): 339-348. |
 2020, Vol. 63
2020, Vol. 63


