2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
多尺度现象蕴涵于物质世界、科学技术和工程的诸多领域.例如,宇宙形成、生命现象、大气环流以及材料成型与应用等.它们涉及从分子尺度到连续介质尺度的不同物理机制的耦合和关联.跨尺度和跨层次现象以及相应的多尺度耦合反映了物质世界的基本性质.由于不同尺度、不同层次的物理机制相互耦合与关联,只考虑单一尺度上某个物理机制,不可能描述整个系统的复杂现象.因此,研究多物理场耦合和跨尺度关联的多尺度方法已经成为现代科学技术发展的需求和前沿.20世纪70年代,学者们在研究非均匀材料时引入了一种替代的数学方法,Benssousan(1978)称之为均匀化理论.这种方法用于分析具有两个或者多个尺度的物质系统,它可以把含有第二相空间的细观尺度和整体结构上的宏观尺度联系起来.Toledano和Murakami(1989),Guedes和Kikuchi(1990)以及Devries等(1989)成功地把有限元方法和均匀化方法结合起来用于分析复合材料的线弹性问题;李静海(2005)介绍了颗粒流体系统多尺度模拟的能量最小多尺度模型、双流体模型、确定性颗粒轨道模型,并给出了上述多尺度模拟方法数值计算结果.葛蔚(2007)研究了气固、颗粒与散料、多孔介质及纳微多相系统及其耦合过程的多尺度建模.在这些研究当中,通过计算机模拟宏观结构的平均应力和应变场得到了全局的响应,同时借助局部应力和应变场的描述得到了微结构的行为.均匀化方法的思想和过程:对非均质材料(地球)中的某一点进行无限放大,在微观尺度下显示周期性的单胞堆积结构,取出其中一个单胞作为代表性体积单元RVE(Representative Volume Element),建立力学模型,写出能量表达式(势能或余能等),用能量极值原理计算变分,得出基本求解方程,再利用周期性均匀化条件及一定的数学变换(升尺度方法),便可以联立求解,然后渐进展开和平均法得到微观尺度下RVE的场响应平均作为宏观一点的整体性质.
对于地震学来说,给定地球模型和震源参数,获得任一台站的理论地震图一直是正演孜孜以求的目标.目前,谱元法(Spectra Element Method,SEM)可以获得复杂3D地球模型的波场地震图.谱元法结合了有限元法处理复杂结构的几何灵活性和伪谱法高精度、快速收敛的特性,目前已成为进行大尺度、复杂地质结构模型地震数值模拟分析的重要工具,其中以SPECFEM3D-Globe(Komatitsch and Vilotte, 1998)以及CSEM(Coupled Spectral Element Mode,谱元简正模耦合方法)(Capdeville et al., 2000, 2003, 2005, 2008)为代表.
地震图的合成与频段范围[fmin,fmax]以及网格的细化程度密切相关.
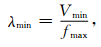
|
(1) |
对于3D模型,地震图合成计算时间tc与最小波长λmin存在tc∞(1/λmin)4.对于非均匀化的介质,最小波长不仅与网格的大小有关,而且与间断面的网格细化密切联系.地球是非均匀的,如果介质的非均匀分布尺度小于最小的理论波长,前人做法是通常忽略或者对区域内的介质参数做简单平均化处理,并没有建立从微观到宏观的升尺度方程以及求解,这也是谱元法在第一步网格离散化时需要面对和解决的难题.即使研究对象是层状的一维地球,简单的参数平均化无法严格满足非线性化的运动方程.
为了建立有效的多尺度方法,需要解决以下几个问题:
(1) 连续与离散的问题:在力学研究中,将宏观物体视为连续体,但是物体在微观尺度下事实上由离散的粒子构成,如何将对于同一物体的两种或多种不同的描述有效的关联起来是多尺度方法需要考虑的重要问题;
(2) 均匀与非均匀的问题:在足够小的尺度上,任何物体都是非均匀的,而且一些复合材料甚至在宏观尺度上都是非均匀的.多尺度方法应该通过均匀化方法获得较大尺度信息的同时,尽可能保存较小尺度的各种信息;
(3) 周期与非周期的问题:被研究的对象在小尺度上被假定具有周期性构造,能大大地简化问题的求解,但实际上物体内部存在大量的非周期性.如何将微观的非周期性与宏观性能关联起来,是发展多尺度方法的需要.
基于此,本文首先介绍基于层状地球模型的均匀化过程,建立从微观到宏观的升尺度均匀化方程以及在不丢失波场计算精度对局部区域的微小尺度进行均匀化;其次通过简正模的计算方法对常微分方程组系数升尺度,合成零阶、一阶改正的理论地震图,与PREM初始模型结果对比,并将之延拓到SEM1D中,为CSEM三维均匀化以及地壳改正等奠定基础.
1 理论和方法对于地球,当其宏观结构受外部负荷作用时,内部的场变量如位移、应变和应力等,将随宏观位置x的改变而发生变化.同时由于微结构的非均匀性,使得这些量在x领域ε内也剧烈振荡,其中ε>0且非常小.由此可以假设一个单位化的微观变量ξ=x/ε,认为所有的场变量都依赖于宏观和微观变量,即在域Vε中有gε(x)=g(x, ε),其中x为宏观坐标,ξ为微观坐标.上标ε表示函数同时具有宏观和微观双尺度特征.假设地球有限范围具有小周期构造,也就是地球可以看做是重复排列的单胞组成.单胞的尺寸与宏观结构的尺度相比很小,可以用ε表示.通过ξ=x/ε的变换,将地球上一点x的ε领域放大成单位单胞Q,从而依赖微观尺度变量ξ也有了周期性.当ε趋近于零时,地球就成为了均质弹性体,从而可以求得等效的弹性势能.
考虑球对称、各向同性、非旋转弹性的SNREI地球模型,采用以流体静力平衡状态作为初始应力状态的地球弹性方程,忽略重力势能的影响,应力平衡方程为
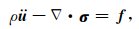
|
(2) |
本构方程(应力-应变)为
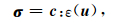
|
(3) |
以及几何方程(应变-位移)为
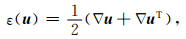
|
(4) |
其中ρ是密度,u是位移场,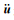
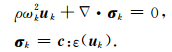
|
(5) |
根据简正模经典理论(Dahlen and Tromp, 1998;Takeuchi and Saito, 1972),SNREI地球模型的位移场解可分为解耦球型场和环型场,解的形式为
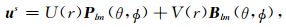
|
(6) |

|
(7) |
其中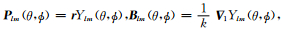
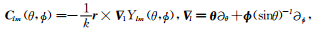
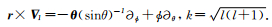

|
(8) |
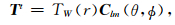
|
(9) |
式(5)通过变量替换得到常微分方程组
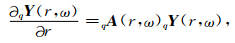
|
(10) |
其中q代表球型解(s)和环型解(t),变量分别为sY(r, ω)=(rU, rTU, rkV, rkTV)T,tY(r, ω)=(rW, rTW)T,常微分方程组矩阵系数为
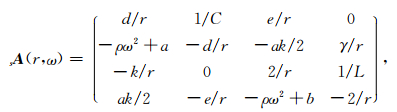
|
(11) |
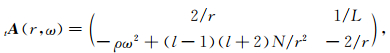
|
(12) |
其中
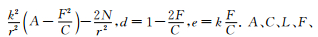
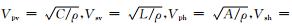
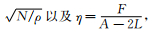

|
(13) |
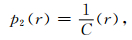
|
(14) |
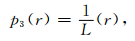
|
(15) |
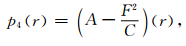
|
(16) |
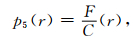
|
(17) |
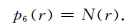
|
(18) |
由于均匀化通常从核幔边界以上开始,因此我们将更加关注(10)式所满足的自由边界条件球型场径向应力、横向应力以及环型场应力在地表(r=R)为0,即
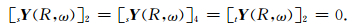
|
(19) |
假设地球的介质参数ρ和地球的弹性系数λ、μ具有周期λc,即ρ(r+λc)=ρ(r),λ(r+λc)=λ(r),μ(r+λc)=μ(r).定义ε=λc/λmin.并采用Capdeville和Marigo(2007)中微观变量的定义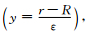

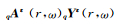
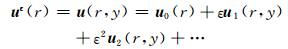
|
(20) |
其中u0(r)是定义在地球上的均匀化解,代表地球的宏观行为. ui(r, y)(i=1,2,…)是具有宏-微观双尺度响应的函数.根据多元函数链式求导法则可得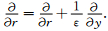

|
(21) |
将(21)和(20)式代入到方程(10)中,整理得到一系列关于ε的幂级数的控制方程(22)式.不失一般性,考虑控制方程的每一项为零,利用周期边界条件化简控制方程求得均匀化结果.

|
(22) |
对于任意函数g(r, y),其在单胞内的平均函数为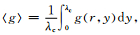
对于周期性介质
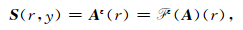
|
(23) |
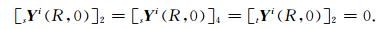
|
(24) |
对于非周期介质,采用对称性延拓到边界外
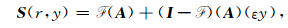
|
(25) |
其中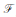
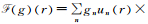
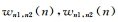
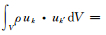
为了验证非周期均匀化在弹性运动方程中的可行性和有效性,我们将从模型的均匀化、简正模方程均匀化计算结果以及SEM1D计算结果三个方面阐述.将均匀化的结果与初始模型得到结果对比分析.
2.1 模型的均匀化
该文采用的初始地球模型是各向同性PREM模型(η≡1).采用Capdeville和Marigo(2007, 2013)文章中的非均匀地球模型(图中简称premt),即在深220 km处间断面存在较强的非均匀性,密度和波速的快速变化(图 3).对模型的均匀化分为正常均匀化和残余均匀化.前者为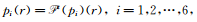
|
(26) |
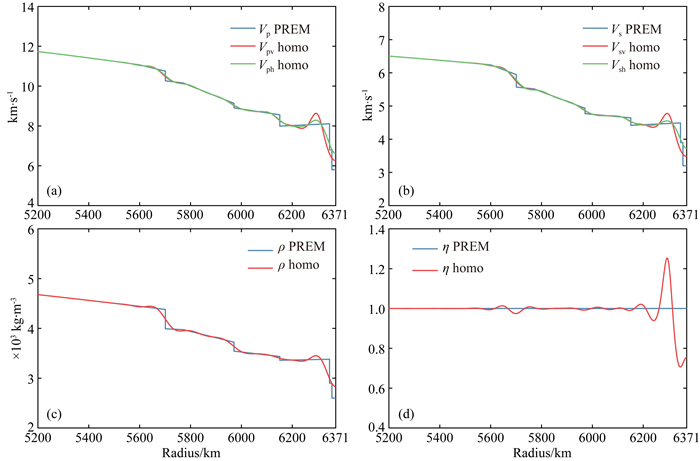
均匀化对象为pi,而并非对A、C、L、F、N简单的平均.本文中所有的模型都是基于残余均匀化得到,通过构建低通滤波,即波速谱在0~1/160 km-1为1,1/160~1/80 km-1为cosine窗函数,大于1/80 km-1为0,这样可将低于80 km尺度结构做均匀化处理,得到零阶均匀化模型(homo),如图 1所示.
|
图 1 参考PREM与零阶均匀化模型的P波波速Vpv、Vph(a),S波波速Vsv、Vsh(b),密度ρ(c)以及η(d)对比.低通滤波波速谱为0~1/160 km-1为1, 1/160~1/80 km-1为cosine窗函数,大于1/80 km-1为0 Fig. 1 Comparison between the Reference PREM model and its order 0 homogenized model. Vph and Vpv (a), Vsh and Vsv (b), density (c) and η (d) for both models are represented as a function of the radius. The lower pass filter chosen here has a flat wave number spectrum between 0 and 1/160 km-1 and cosine taper between 1/160 km-1 and 1/80 km-1 and zero after 1/80 km-1 |
对模型均匀化主要的参数为ε以及w(r),通常使用k11,k12两个参数来控制w(r)的余弦函数区间(Capdeville,2013).对于需要均匀化的模型,一般λmin已定,不同的k11、k12将会得到不同的ε.因此该部分将着重介绍不同的ε得到的均匀化模型.
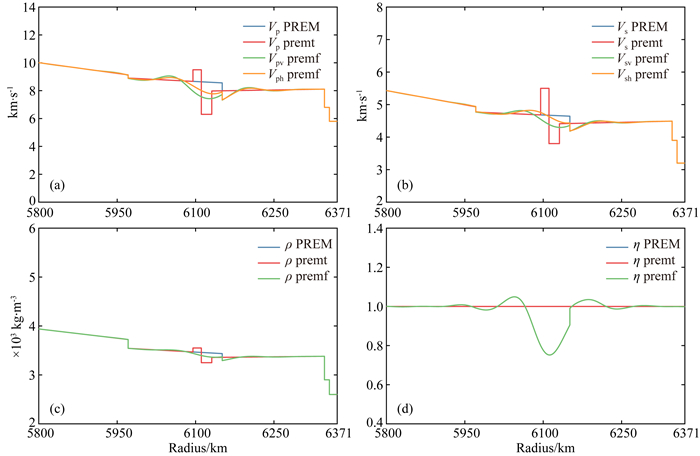
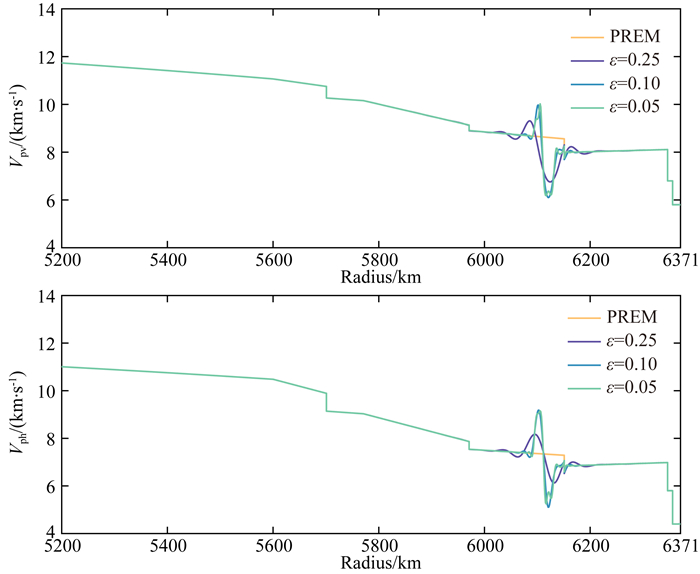
采用残余均匀化,得到ε=0.5的premt模型均匀化结果premf(图 2).从图中发现,对于初始模型为各向同性的premt起始模型,其均匀化结果premf为横向各向同性,即Vsh≠Vsv、Vph≠Vpv,这和Backus(1962)文章中的结果是吻合的.根据(13)—(18)式,得到残余均匀化的pi随半径的分布(图 3).图 4展示了不同的k11、k12参数计算得到w(r)的波数域傅里叶变换,k11越小,对应的ε越小,也就是对220 km间断面刻画的越精细,其波谱宽度越窄,得到的均匀化结果越平滑(图 5).
|
图 2 PREM和premt模型的P波波速(a),S波波速(b),密度ρ(c)以及η(d)分别与残余均匀化(ε=0.5)premf模型对比 Fig. 2 P-wave velocities (a), S-wave velocities (b), density (c) and η parameter (d) from PREM, premt and residual homogenized premf with ε=0.5 are plotted |
|
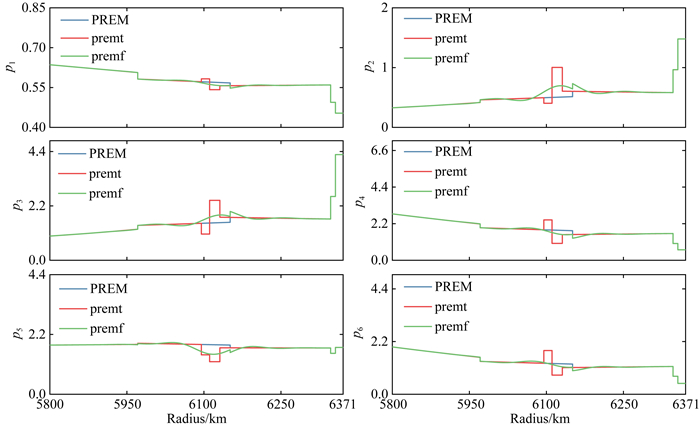
图 3 PREM和premt模型的pi分别与残余均匀化模型premf (ε=0.5)对应参数对比 Fig. 3 pi from PREM, premt and residual homogenized premf with ε=0.5 are plotted |

|
图 4 不同的k11,k12得到的傅里叶小波变换谱比较 Fig. 4 Fourier wavelet spectrum comparison for different k11, k12 parameters |
|
图 5 参考模型PREM分别与残余均匀化premf(ε=0.25,ε=0.10,ε=0.05)模型Vpv、Vph对比 Fig. 5 P-wave velocities comparison among reference PREM model and residual homogenized premf (ε=0.25, ε=0.10, ε=0.05) |
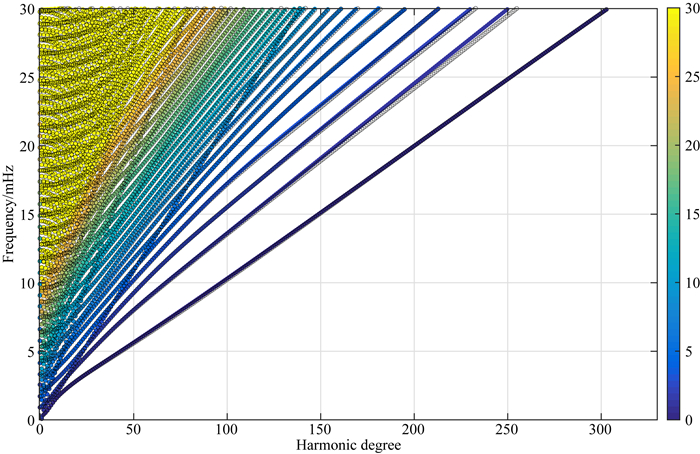
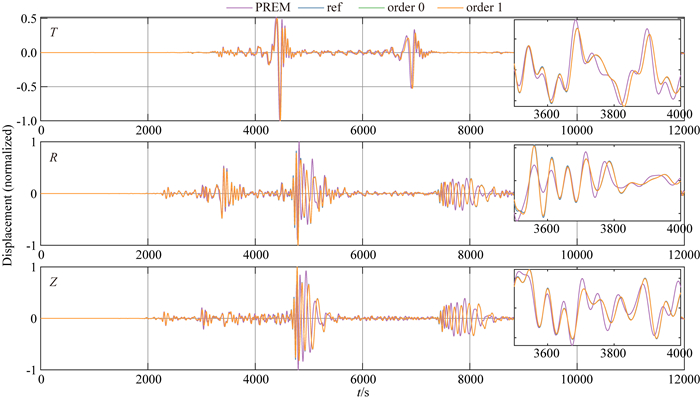
给出均匀化后的地球模型,可计算出相应模型简正模的本征频率和本征函数,进而合成理论地震图.图 6为(0~30 mHz) PREM模型和均匀化模型(ε=0.25)简正模频率随阶数的变化, 其中实心为PREM模型计算结果,空心为均匀化模型计算结果.我们发现:(1)在同样不考虑非弹性、自重力因素情况下,不同的均匀化模型的本征频率接近于PREM模型结果,证明了均匀化计算的可靠性和有效性;(2)PREM 220 km间断面处的不均匀对低频简正模的影响微乎甚微,这与低频简正模的能量分布主要集中于中下地幔密切相关,而高频简正模基本上可看成面波,根据简正模的能量函数曲线,可以得出,对220 km左右深度敏感的基频简正模分布在0S30-0S60,如图 7所示;(3)不同的均匀化模型的本征频率计算结果相比于PREM模型系统性偏小, 为了进一步确认,我们又计算了ε=0.10,ε=0.05的均匀化模型的0S30-0S60本征频率(图 8),结果发现本征频率的计算结果相比于PREM模型的确系统性偏小;(4)ε=0.05相比于ε=0.10和ε=0.25,所计算的本征频率差异并无较强的优异性(图 8),最平滑的模型得到的简正模的本征频率未必具有最小差异性,但如图 9所示,ε=0.05地震图能够很好的和PREM模型符合;(5)考虑浅层震源改正,计算了零阶、一阶改正下的理论地震图,并与PREM结果比较,一阶拥有比零阶更好的符合度.
|
图 6 PREM模型(实心)和残余均匀化模型premf(ε=0.25,空心)球型简正模随球谐阶数变化频散图,频率小于30 mHz Fig. 6 Dispersion diagram showing the spheroidal modes of PREM model (solid) and residual homogenized model premf (ε=0.25, hollow). All the predominantly elastic eigenfrequencies below 30 mHz are plotted versus spherical harmonic degree |

|
图 7 0S40和0S60简正模剪切(红)、压缩(蓝)能量密度函数随归一化半径的变化 Fig. 7 The shear (red) and compress (blue) energy density of 0S40 and 0S60 are plotted versus normalized radius |

|
图 8 PREM模型和premt以及不同残余均匀化模型(ε=0.25,ε=0.10,ε=0.05) 球型简正模0S30-0S60频率差随阶数的变化 Fig. 8 The spheroidal modes′ eigenfrequencies differences between PREM and premt, residual homogenized model with ε=0.25, 0.10, 0.05 respectively that varied with harmonic degree |

|
图 9 震中距Δ=132°台站T,R,Z三通道PREM模型与premt以及不同残余均匀化模型(ε=0.25,ε=0.10,ε=0.05)地震图比较 Fig. 9 The epicenter distance Δ is of 132° and T, R, Z three channel graphs compared with premt and different residual homogenized models (ε=0.25, ε=0.10, ε=0.05) |
|
图 10 震中距Δ=132°台站T,R,Z三通道PREM模型与premt以及零阶、一阶改正地震图比较(ε=0.5) Fig. 10 The epicenter distance Δ is of 132° and T, R, Z three channel graphs compared with premt and different order (ε=0.5) |
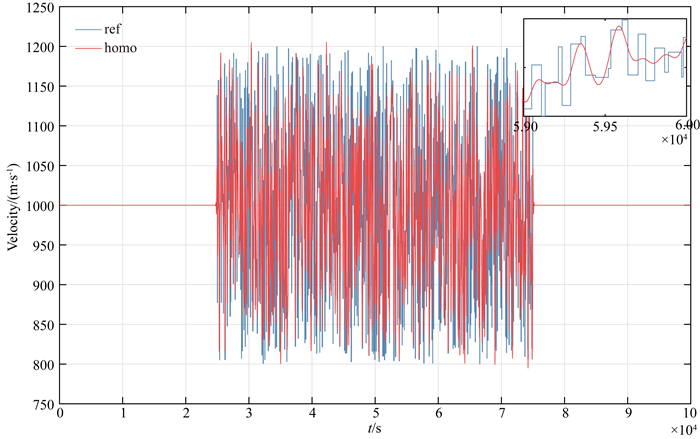
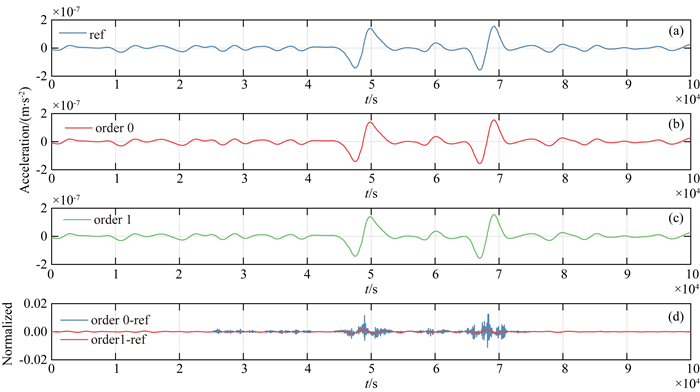
本部分将2.2节中的均匀化理论拓展到SEM1D中.首先产生一个随机的一维模型,并将其均匀化(图 11),此外计算了参考模型、零阶、一阶加速度(snapshot40)以及它们之间的差异(图 12).一阶均匀化改正效果要远远优于零阶改正,这对于CSEM均匀化将有指导性的意义.
|
图 11 随机密度模型及其均匀化结果 Fig. 11 Random density model and its homogenized model |
|
图 12 参考模型(a)、零阶(b)、一阶(c)加速度(snapshot40)以及它们之间的差异(d) Fig. 12 The acceleration of reference model (a), zero-order (b), one-order (c) and their respective difference (d) |
本文简述了非周期均匀化的方法,以PREM模型为例,给出了初始不均匀模型premt随不同ε变化的均匀化模型;建立均匀化方程,利用传统的简正模计算本征频率和本征函数,给出了均匀化的结果,证明了均匀化计算方法的可行性和正确性;并成功将之应用到SEM1D实验中,为下一步CSEM三维均匀化奠定基础.
致谢 感谢法国南特大学Yann Capdeville教授提供的均匀化相关文献和指导以及地球动力学计算基础设施(CIG)提供的MINEOS软件.
Backus G E. 1962. Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res., 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
Bensoussan A, Papanicolau G, Lions J L. 1978. Asymptotic Analysis for Periodic Structures. Amsterdam: North-Holland.
|
Capdeville Y, Stutzmann E, Montagner J P. 2000. Effect of a plume on long period surface waves computed with normal modes coupling. Phys. Earth Planet. Inter., 119(1-2): 57-74. DOI:10.1016/S0031-9201(99)00153-3 |
Capdeville Y, To A, Romanowicz B. 2003. Coupling Spectral Elements and Modes in a spherical earth:an extension to the 'sandwich' case. Geophys. J. Int., 154(1): 44-57. DOI:10.1046/j.1365-246X.2003.01959.x |
Capdeville Y, Gung Y, Romanowicz B. 2005. Towards global earth tomography using the spectral element method:a technique based on source stacking. Geophys. J. Int., 162(2): 541-554. DOI:10.1111/j.1365-246X.2005.02689.x |
Capdeville Y. 2005. An efficient Born normal mode method to compute sensitivity kernels and synthetic seismograms in the Earth. Geophys. J. Int., 163(2): 639-646. DOI:10.1111/j.1365-246X.2005.02765.x |
Capdeville Y, Marigo J J. 2007. Second order homogenization of the elastic wave equation for non-periodic layered media. Geophys. J. Int., 170(2): 823-838. DOI:10.1111/j.1365-246X.2007.03462.x |
Capdeville Y, Marigo J J. 2008. Shallow layer correction for spectral element like methods. Geophys. J. Int., 172(3): 1135-1150. DOI:10.1111/j.1365-246X.2007.03703.x |
Capdeville Y, Guillot L, Marigo J J. 2010. 1-D non-periodic homogenization for the seismic wave equation. Geophys. J. Int., 181(2): 897-910. |
Capdeville Y, Stutzmann E, Wang N, et al. 2013. Residual homogenization for seismic forward and inverse problems in layered media. Geophys. J. Int., 194(1): 470-487. DOI:10.1093/gji/ggt102 |
Dahlen F A, Tromp J. 1998. Theoretical Global Seismology. Princeton: Princeton University Press.
|
Devries F, Dumontet H, Duvaut G, et al. 1989. Homogenization and damage for composite structures. International Journal for Numerical Methods in Engineering, 27(2): 285-298. |
Ge W, Chen F G, Gao J, et al. 2007. Analytical multi-scale method for multi-phase complex systems in process engineering-Bridging reductionism and holism. Chem. Eng. Sci., 62(13): 3346-3377. DOI:10.1016/j.ces.2007.02.049 |
Guedes J, Kikuchi N. 1990. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element solutions. Com. Mech. App. Meth. Eng., 83(2): 143-198. DOI:10.1016/0045-7825(90)90148-F |
Komatitsch D, Vilotte J P. 1998. The spectral element method:an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. Seismol. Soc. Am., 88(2): 368-392. |
Li J, Ge W, Zhang J, et al. 2005. Multi-scale compromise and multi-level correlation in complex systems. Chem. Eng. Res. Des., 83(6): 574-582. DOI:10.1205/cherd.05093 |
Takeuchi H, Saito M. 1972. Seismic surface waves. Methods Comput. Phys. Adv. Res. Appl., 11: 217-295. DOI:10.1016/B978-0-12-460811-5.50010-6 |
Toledano A, Murakami H. 1989. High-order mixture homogenization of fiber-reinforced composites. J. Appl. Mech., 57(2): 388-397. |
 2020, Vol. 63
2020, Vol. 63

