传统的地震波场数值模拟模式将地下介质视为完全弹性介质.这一假设忽略了地震波传播过程中的能量衰减等问题, 造成理论研究结果与实际采集到的地震波记录在振幅、相位等方面有一定差异, 因而简单地使用完全弹性介质模型不能有效解释许多实际地震波传播现象.实际上,地下介质是非完全弹性、各向异性和物性参数连续变化的非均匀介质.相比完全弹性介质, 使用黏弹性介质模型能更好地模拟地震波传播.
黏弹性介质是一种介于固相完全弹性介质和流相黏性介质之间的介质.相应的, 黏弹性方程兼具了波动方程和扩散方程的特点.从而, 不论在理论分析方面, 还是数值模拟方面, 黏弹性方程均比单纯的波动方程或者单纯的扩散方程更复杂.在对黏弹性介质研究过程中, 地球科学研究人员采用的模型有Kelvin介质模型、Maxwell介质模型、标准线性模型等.其中, Kelvin介质模型作为地震学中的一种重要模型, 一直受到广大地球科学研究人员的重视.孙成禹等(2010)基于Kelvin模型对黏弹性波动方程的稳定性进行研究, 得到了Qp较大时的稳定性条件.贺同江等(2010)基于褶积微分算子进行了二维黏弹性介质地震波数值模拟.严红勇和刘洋(2012)基于数值模拟结果分析了时间域和频率域黏弹性介质对地震波的吸收和衰减规律.
模拟地震波在黏弹性介质中传播的数值方法有多种, 常用的有:几何射线法(Červeny and Firbas, 1984)、反射率法(Booth and Crampin, 1983)、有限元法(Chen, 1984;冯德山和王珣, 2017)、有限差分法(Kelly et al., 1976; Dablain, 1986; Virieux, 1984, 1986;董良国等, 2000a;辛维等, 2015;胡自多等, 2016)、谱元法或伪谱法(Komatitsch and Vilotte, 1998; Komatitsch and Tromp, 1999)等.不同的方法各有优劣, 在近些年的研究中许多学者(裴正林和牟永光, 2004;王雪秋等, 2005; Lu and Yang, 2005;李信富等, 2007)都进行了详细的分析.其中, 有限差分法因具有编程简单、计算速度快、存储量小等优势受到地球科学研究人员的青睐.
自1968年Alterman和Karal(1968)第一次采用有限差分方法进行地震波数值模拟到目前为止, 有限差分方法有了很大的发展.从网格划分角度讲,有限差分方法实现了规则网格—交错网格(Madariaga, 1976)—可变网格(Jastram and Behle, 1992)—不规则网格(Moczo, 1989;宋国杰等, 2010;韩颜颜等, 2015;豆辉和张剑锋, 2016)的发展.其中SG方法因在不增加计算量的前提下提高了模拟精度而受到学者们的广泛关注.1976年, Madariaga(1976)首次提出SG方法, 并完成了弹性介质地震波模拟, 精度为O(Δt2+h2).之后, Virieux (1984)提出了代替二阶位移方程的一阶速度-应力方程, 并采用SG方法进行数值模拟.Levander(1988)在Virieux(1984, 1986)的基础上提出了精度为O(Δt2+h4)的SG差分格式.随后, 董良国等(2000b)给出了一阶速度-应力方程更高精度的SG差分格式, 精度达到O(Δt4+h2N).杨庆节等(2014)在董良国等(2000b)的基础上完善了时间4阶、空间2N阶精度的差分格式.但是, 计算精度的提高并不意味着SG方法能在较大空间步长条件下有效压制数值频散.因此, 寻找新的方法以压制较大空间步长条件下的数值频散具有重要的理论价值和现实意义.
2003年, Yang等(2003)提出了近似解析离散化方法(NADM), 该方法与传统方法的不同之处在于对空间高阶偏导数逼近的时候, 采用位移场及梯度场共同逼近, 其中梯度场反映波走势性质, 在计算过程中可以保留更多的波场信息, 从而使得该方法突破了传统差分方法的限制, 可以在较大空间步长条件下有效压制数值频散.之后在NADM基础上发展而来的ONADM(Yang et al., 2004, 2007a)、INADM(Yang et al., 2007b)、SNADM(宋国杰, 2008)、RNADM(Yang et al., 2010)、WNADM(宋国杰等, 2010)、NAIDM(Tong et al., 2011)、NSPRK(Ma et al., 2011)、MNAD(Chen et al., 2014)等方法均保留了NADM能在较大空间步长条件下压制数值频散的特点.汪勇等(2017)基于多种近似解析离散化方法——NADM、RNADM、INADM、WNADM研究了声波在黏弹性介质中的传播规律.值得注意的是NAD-type方法单个时间层内计算比较复杂, 尤其是三维情况下, 单个时间层计算时间较大.
综上所述, SG方法能够在单个时间层计算时间消耗较低的条件下实现高精度模拟, 但是在较大空间步长条件下无法有效压制数值频散; ONADM方法能保证较大空间步长条件下有效压制数值频散, 但单个时间层内计算时间消耗较大.本文集两种方法之长, 提出了一种能在较大空间步长条件下有效压制数值频散且时间消耗较少的黏滞声波波场模拟混合方法(SG-ONADM).在本文中, 我们首先给出了黏滞声波方程的SG方法、ONADM方法和SG-ONADM方法的离散格式, 分析了SG-ONADM方法的算法准确性; 然后在各向同性均匀介质模型中, 比较了SG、ONADM和SG-ONADM三种方法的计算效率; 最后使用SG-ONADM方法研究了黏滞声波在复杂介质中的传播.
1 方法原理 1.1 黏滞声波波动方程黏滞声波波动方程三维分量形式为
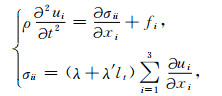
|
(1) |
其中, i=1、2、3, 且1、2、3分别表示x、y、z方向; ui表示相应方向的位移分量, σii表示相应方向的应力分量, fi表示相应方向的体力; lt是关于时间的一阶偏导数算子, 即
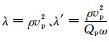
一阶黏滞声波波动方程的具体表达式为
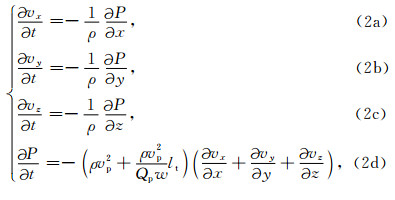
|
其中, vx、vy、vz分别是x、y、z方向的速度, P是应力, 在(2d)式中, 引入加速度场, 可以得到:
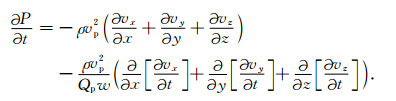
|
(3) |
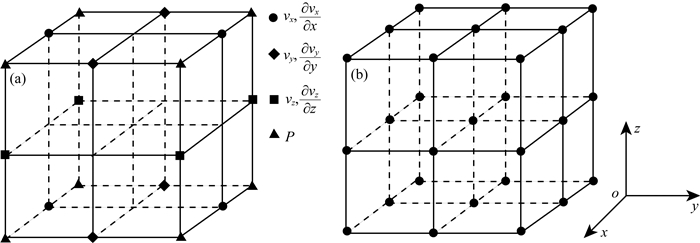
根据SG方法理论可以得到vx、vy、vz、P的离散格式, 其差分模板见图 1a, 其中将应力P定义在整网格(i, j, k)处, 速度分量vx和加速度分量
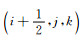

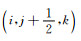
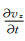
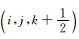
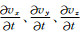


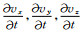
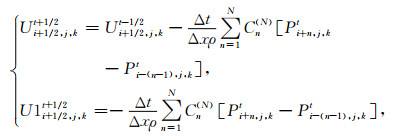
|
(4) |
|
图 1 SG-ONADM方法、SG方法和ONADM方法的差分模板 (a) SG方法及SG-ONADM方法的差分模板; (b) ONADM方法差分模板. Fig. 1 The stencil of the SG-ONADM, SG and ONADM method (a) The stencil of SG and SG-ONADM; (b) The stencil of ONADM. |
其中, Cn(N)为差分系数(严红勇和刘洋,2012).
依次类推, 可写出V、V1、W、W1、P的表达式, 从而得到SG方法的完整离散格式.
1.3 最优近似解析离散化方法为使用ONADM方法进行黏滞声波波场模拟, 需对公式(1)进行变换.考虑到Kelvin介质同均匀弹性各向同性介质一样, 体积应变系数(θ)和位移矢量(u)满足θ=∇·u的关系, 带入式(1)中, 整理得到的二阶黏滞声波波动方程为

|
(5) |
为了避免同时对(5)式右侧的时间和空间混合偏导数进行计算, 我们令
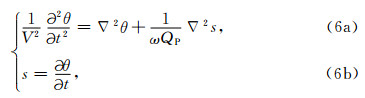
|
其中, ∇2为拉普拉斯算子.
为叙述方便, 将位移场、速度场及其相应的梯度场合写成向量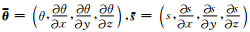
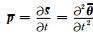
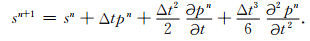
|
(6c) |
在(6a)式中仅含有关于时间、空间的二阶偏导数, 按照ONADM方法在弹性介质中的离散方式处理即可(差分模板见图 1b).为实现位移场和速度场的时间推移, 首先要计算p、θ对时间的高阶偏导数.在此, 我们采用Dablain (1986)的思想将其转换为关于空间的偏导数, 然后采用Yang等(2007a)给出的高阶空间偏导数逼近公式对所涉及到的高阶偏导数进行计算.至此, 我们可以采用ONADM方法对式(6a)和式(6b)进行离散计算, 其中涉及到的高阶空间偏导数逼近表达式见附录.
1.4 SG-ONADM混合方法在SG-ONADM方法中, 对于vx、vy、vz随时间的推移采用SG方法进行计算, 具体参考1.2小节; P随时间的推移同时采用SG方法和ONADM方法.需要注意的是ONADM是一种基于整网格的有限差分方法, 为了保证高阶偏导数在计算时格点位置位于整网格点, 我们在对SG方法的格点分布定义过程中, 将P的空间、时间位置定义在整网格处, 具体做法如下:
根据式(2a)—(2c)给出的速度、应力关系, 将式(2d)中的lt算子转换为应力P关于空间的一阶偏导数, 可以得到:
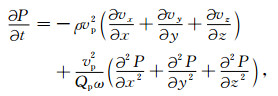
|
(7) |
(7) 式中关于速度场的一阶空间偏导数我们仍采用SG方法进行差分.
接下来我们给出P的具体表达式为
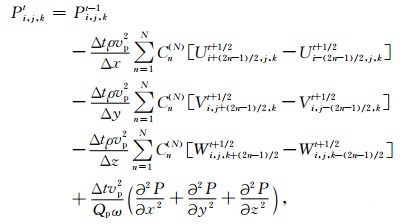
|
(8) |
(8) 式中关于P的高阶空间偏导数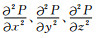
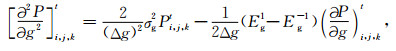
|
(9) |
其中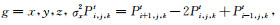
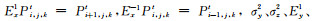
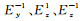
众多学者(Madariaga, 1976;董良国等, 2000a, b ;严红勇和刘洋, 2012)的研究结果表明采用SG方法能够准确模拟地震波在地下介质中的传播过程.我们可以把精细网格下SG方法的模拟结果当作“准解析解”来判断本文所提出的SG-ONADM方法的准确性.因此, 我们设计了二维黏弹性介质模型, 模型大小为3 km×3 km, 纵波速度为v=3 km·s-1, 品质因子Qp=100, 密度为ρ=2.3 g·cm-3.
数值模拟中, SG方法参数为: Δt=1 ms, h=Δx=Δz=5 m, SG-ONADM方法的模拟参数为: Δt=2 ms, h=Δx=Δz=25 m.震源函数为
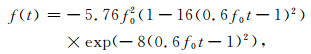
|
(10) |
其中震源主频f0=30 Hz.
在一个波长里, SG方法的采样点数NSG=v/(hSGf0)=3/(0.005×30)=20, 在这样的采样率条件下, SG方法的计算结果已经足够精确, 可以把它的计算结果视为“准解析解”, 而SG-ONADM方法的采样点数仅为NSG-ONADM=v/(hSG-ONADMf0)=3/(0.025×30)=4.
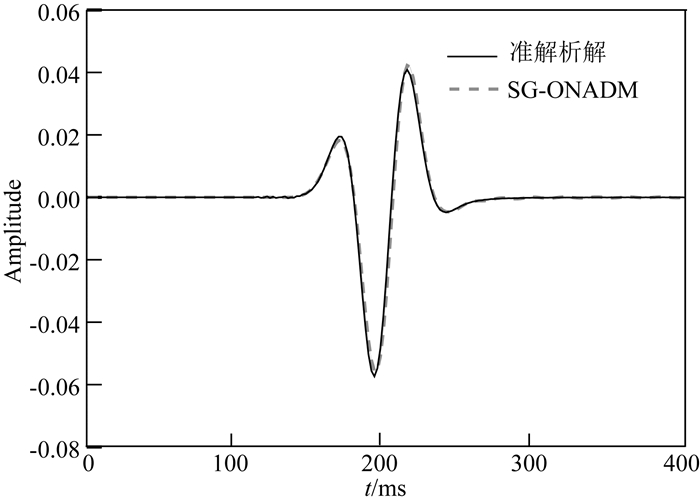
图 2给出了分别采用SG和SG-ONADM方法模拟得到的时长0.4 s, 坐标位置为(1.8 km, 1.8 km)处的波形记录.从图 2可以看出, 采用SG-ONADM方法得到的波形与准解析解(每个波长内采样点数为20的SG网格方法)的波形基本一致.这说明SG-ONADM方法可以在较大空间步长条件下进行黏滞声波波场模拟, 并得到与采用精细网格下SG方法一致的波场模拟结果.
|
图 2 SG-ONADM方法(Δt=2 ms, h=Δx=Δz=25 m)的波形记录与准解析解(精细网格条件下的SG方法, Δt=1 ms, h=Δx=Δz=5 m)对比图 Fig. 2 Comparison between waveform recording simulated by SG-ONADM (Δt=2 ms, h=Δx=Δz=25 m) and quasi-analytical solution (SG method with refined grid, Δt=1 ms, h=Δx=Δz=5 m) |
为了说明本文所提出方法的有效性, 我们设计了以下2个模型.
2.1 模型1我们选择均匀介质模型作为本文的第一个实验模型.模拟区域为3 km×3 km×3 km, 速度为v=4 km·s-1, 介质密度ρ=2.5 g·cm-3, 品质因子Qp=100.模拟过程中, 分别采用ONADM方法, SG方法(时间2阶、空间4阶精度和10阶精度)和本文提出的SG-ONADM进行模拟, 并比较它们的模拟结果.计算参数均采用空间步长Δx=Δy=Δz=30 m, 时间步长Δt=3 ms, 震源位置(1.5 km, 1.5 km, 1.5 km), 震源函数如(10)式所示, 其中震源主频f0=30 Hz.
图 3是使用三种方法在0.3 s时刻的模拟结果.由于本模型是一个均匀各向同性介质模型, 地震波传播过程中波场快照的xoy、xoz、yoz截面具有一致性, 因此我们仅选择xoz截面进行观察.直观地看到, SG-ONADM方法(图 3a)和ONADM方法(图 3b)均得到了清晰、无频散的波场快照.SG方法在4阶(图 3c)、10阶(图 3d)精度条件下均频散严重, 虽然10阶精度模拟结果较4阶精度模拟结果有了一定改善, 但是仍然无法呈现有效的波场快照.这说明提高模拟精度在一定程度上能够有效改善模拟结果, 但并不能使SG方法在较大空间步长条件下有效压制数值频散.

|
图 3 0.3 s时刻波场快照(xoz截面) (a) SG-ONADM; (b) ONADM; (c) 4阶SG; (d) 10阶SG. Fig. 3 Wave field snapshots of xoz section at 0.3 s (a) SG-ONADM; (b) ONADM; (c) 4th-order SG; (d) 10th-order SG. |
为了得到清晰的、无数值频散的波场快照, 现将4阶SG方法的计算参数进行适当的调整: Δx=Δy=Δz=5 m,Δt=1 ms, 得到的无频散波场快照如图 4所示.

|
图 4 4阶SG方法加细网格(Δx=Δy=Δz=5 m, Δt=1 ms)之后的波场快照(xoz截面) Fig. 4 Snapshot of wave field (xoz section) with refined grid by forth-order SG method (Δx=Δy= Δz=5 m, Δt=1 ms) |
上述实验, 从较大空间步长条件下的模拟效果角度对三种方法进行了比较, 说明SG-ONADM方法可以在较大空间步长条件下实现对数值频散的有效压制.接下来我们从计算效率的角度对三种方法进行比较.
理论上影响计算效率的主要因素包括内存需求和计算量两个方面.首先我们来分析三种方法对内存的需求.假设我们模拟M m×N m×L m的计算区域, SG方法在5 m的空间步长条件下, 需要存储11个
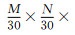
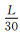

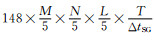

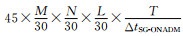
为进一步说明SG-ONADM方法的计算效率较SG方法和ONADM方法高.基于模型1, 我们进行了等时间T的试算(SG方法采用调整之后的参数).试算结果表明, SG方法耗时36310.20 s; ONADM方法耗时305.60 s; SG-ONADM方法耗时26.32 s; 即SG-ONADM方法的计算效率是SG方法的1379.57倍, 是ONADM方法的11.61倍, 依然表明SG-ONADM的计算效率高于SG和ONADM方法.
注意到, SG和ONADM方法的实际计算效率要低于纯粹由计算量比较得到的理论计算效率, 这是因为SG和ONADM方法需要较高的内存来存储计算数组, 而内存存储量的增大又导致内存Cache命中率降低, 从而减慢了计算速度.
图 5给出了SG-ONADM方法结合CPML边界对模型1进行模拟得到的0.45 s时刻波场快照, 此时声波传播到模拟区域边界.可以观察到, 在边界处无任何可见的边界反射, 说明SG-ONADM方法结合CPML边界很好地完成了对边界虚假反射的吸收.

|
图 5 采用SG-ONADM方法结合CPML边界条件对模型1进行模拟得到的0.45 s时刻的波场快照(xoz截面) Fig. 5 Wave field snapshot (xoz section) at 0.45 s of model 1 simulated by SG-ONADM method with CPML boundary |
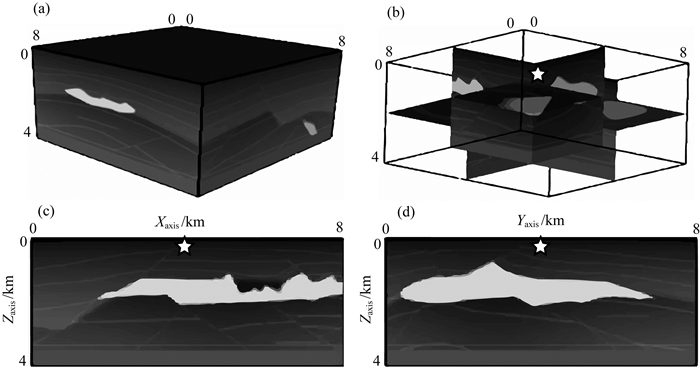
为了验证SG-ONADM方法在复杂介质的有效性, 我们选择了局部盐丘模型(完整盐丘模型大小为676×676×210, 本文所选区域大小为400×400×200)进行数值模拟实验.盐丘模型(图 6)中速度v的变化范围为1.5~4.482 km·s-1, 密度ρ变化范围为2.08~2.58 g·cm-3.震源放置在(4 km, 4 km, 0.2 km)处, 即图中☆所示.空间步长Δx=Δy=Δz=20 m, 时间步长Δt=2 ms, 震源主频、品质因子分别为f0=15 Hz和Qp=150.震源函数见(10)式, 边界采用CPML条件.
|
图 6 三维盐丘速度模型 (a)模拟区域表面渲染图; (b)模拟区域三维截面图; (c) xoz面截面图(y=4 km); (d) yoz面截面图(x=4 km).☆表示震源位置. Fig. 6 Three-dimensional SEG Salt model (a) Surface rendering of the simulated region; (b) 3D slice of simulated region; (c) xoz section (y=4 km); (d) yoz section (x=4 km).The source location is denoted by ☆. |
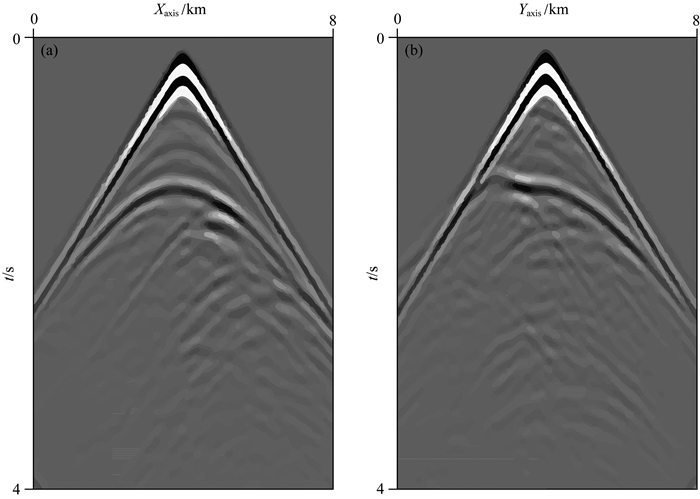
图 7分别是4 s时刻z=0 km, y=4 km和z=0 km, x=4 km处地震记录.其中存在直达波、反射波以及大量的多次波, 无可见数值频散.说明本文提出的SG-ONADM应用于复杂介质中的地震波场模拟是有效的, 同时也说明本方法和CPML可以很好地结合在一起进行复杂介质黏滞声波波场模拟.
|
图 7 4 s时刻地表地震记录 (a) z=0 km, y=4 km处地震记录; (b) z=0 km, x=4 km处地震记录. Fig. 7 Surface seismic records at 4 s (a) Seismic records at z=0 km and y=4 km; (b) Seismic records at z=0 km and x=4 km. |
研究地震波在黏弹性介质中的传播规律具有非常重要的理论指导意义和应用价值.本文在SG方法和ONADM方法的基础上提出了一种新的黏声波波场数值模拟的混合方法——SG-ONADM.该方法中对控制方程中的一阶空间偏导数采用SG方法进行近似; 对高阶空间偏导数采用ONADM的高阶偏导数逼近公式进行计算.理论分析与数值算例均表明SG-ONADM方法计算效率高于SG方法和ONADM方法, 能在较大空间步长条件下有效压制数值频散, 可以用来进行大规模黏滞声波波场模拟.
下一步的研究中, 我们拟将该方法推广至黏弹性地震波场数值模拟.
附录 ONADM方法计算过程中涉及到的高阶偏导数逼近公式为了叙述方便, 我们定义了单位算子符I, 二阶中心差分算子δ2和位移运算符E, 具体表达式为
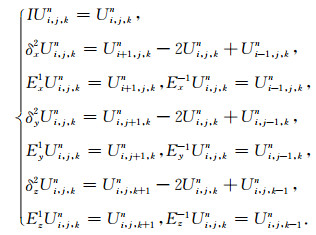
|
(A1) |
ONADM方法计算过程中涉及到的高阶空间导数逼近表达式为
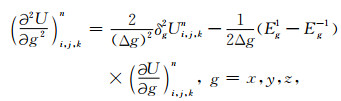
|
(A2) |
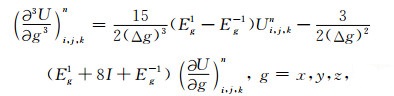
|
(A3) |
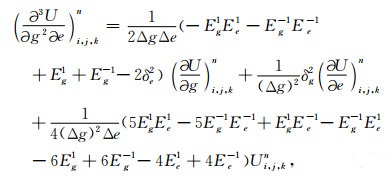
|
(A4) |
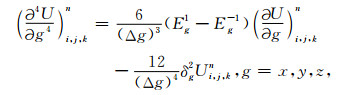
|
(A5) |
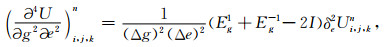
|
(A6) |

|
(A7) |
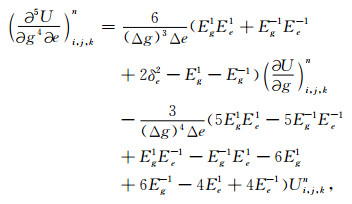
|
(A8) |
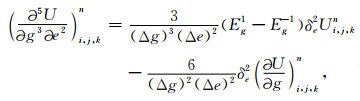
|
(A9) |

|
(A10) |
(A4)中, g, e=x, y, z且g≠e.定义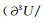
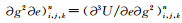
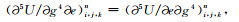

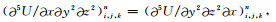

Alterman Z, Karal F C Jr. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of the Seismological Society of America, 58(1): 367-398. |
Booth D C, Crampin S. 1983. The anisotropic reflectivity technique:anomalous reflected arrivals from an anisotropic upper mantle. Geophysical Journal International, 72(3): 767-782. DOI:10.1111/j.1365-246X.1983.tb02832.x |
Červeny V, Firbas P. 1984. Numerical modelling and inversion of travel times of seismic body waves in inhomogeneous anisotropic media. Geophysical Journal International, 76(1): 41-51. DOI:10.1111/j.1365-246X.1984.tb05020.x |
Chen K H. 1984. Propagating numerical model of elastic wave in anisotropic inhomogeneous media-finite element method.//Symposium of 54th SEG. Expanded Abstracts, 54: 631-632.
|
Chen Y S, Song G J, Xue Z H, et al. 2014. An improved optimal nearly analytical discretized method for 2D scalar wave equation in heterogeneous media based on the modified nearly analytical discrete operator. Geophysics, 79(6): T349-T362. DOI:10.1190/geo2014-0092.1 |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
Dong L G, Ma Z T, Cao J Z. 2000a. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation. Chinese Journal of Geophysics (in Chinese), 43(6): 856-864. |
Dong L G, Ma Z T, Cao J Z, et al. 2000b. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419. |
Dou H, Zhang J F. 2016. An irregular grid method for acoustic modeling in inhomogeneous viscoelastic medium. Chinese J. Geophys. (in Chinese), 59(11): 4212-4222. DOI:10.6038/cjg20161123 |
Feng D S, Wang X. 2017. Convolution perfectly matched layer for the finite-element Time-Domain method modeling of Ground Penetrating Radar. Chinese J. Geophys. (in Chinese), 60(1): 413-423. DOI:10.6038/cjg20170134 |
Han Y Y, Zhang Z J, Liang K, et al. 2015. Seismic wave field modeling of wave front healing effect in self-organized media using a heterogeneous multi-scale method. Chinese J. Geophys. (in Chinese), 58(2): 643-655. DOI:10.6038/cjg20150225 |
He T J, Liu H Y, Li X F. 2010. Numerical simulation of seismic wave propagation in viscous-elastic media by the convolutional differentiator method. Northwestern Seismological Journal (in Chinese), 32(4): 318-324. |
Hu Z D, He Z H, Liu W, et al. 2016. Scalar wave equation modeling using the mixed-grid finite-difference method in the time-space domain. Chinese J. Geophys. (in Chinese), 59(10): 3829-3846. DOI:10.6038/cjg20161027 |
Jastram C, Behle A. 1992. Acoustic modelling on a grid of vertically varying spacing. Geophysical Prospecting, 40(2): 157-169. DOI:10.1111/j.1365-2478.1992.tb00369.x |
Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms:A finite-difference approach. Geophysics, 41(1): 2-27. DOI:10.1190/1.1440605 |
Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
Komatitsch D, Vilotte J P. 1998. The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the seismological society of America, 88(2): 368-392. |
Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
Li X F, Li X F, Zhang M G. 2007. Review of seismic wave numerical modeling methods. Journal of Disaster Prevention and Mitigation Engineering (in Chinese), 27(2): 241-248. |
Lu M, Yang D H. 2005. A modified nearly analytic discrete method and wavefield simulations in transversely isotropic media. Science in China Series D:Earth Sciences, 48(8): 1321-1328. DOI:10.1360/03yd0355 |
Ma X, Yang D H, Liu F Q. 2011. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophysical Journal International, 187(1): 480-496. DOI:10.1111/j.1365-246X.2011.05158.x |
Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. |
Moczo P. 1989. Finite-difference technique for SH-waves in 2-D media using irregular grids-application to the seismic response problem. Geophysical Journal International, 99(2): 321-329. DOI:10.1111/j.1365-246X.1989.tb01691.x |
Pei Z L, Mu Y G. 2004. Numerical simulation of seismic wave propagation. Progress in Geophysics (in Chinese), 19(4): 933-941. |
Song G J. 2008. The improved nearly analytic discrete method for 3D elastic equations and its numerical simulation[Master's thesis] (in Chinese). Beijing: Tsinghua University.
|
Song G J, Yang D H, Chen Y L, et al. 2010. Non-uniform grid algorithm based on the WNAD method and elastic wave-field simulations. Chinese J. Geophys. (in Chinese), 53(8): 1985-1992. DOI:10.3969/j.issn.0001-5733.2010.08.025 |
Sun C Y, Xiao Y F, Yin X Y, et al. 2010. Study on the stability of finite difference solution of visco-elastic wave equations. Acta Seismologica Sinica (in Chinese), 32(2): 147-156. |
Tong P, Yang D H, Hua B L. 2011. High accuracy wave simulation-Revised derivation, numerical analysis and testing of a nearly analytic integration discrete method for solving acoustic wave equation. International Journal of Solids and Structures, 48(1): 56-70. DOI:10.1016/j.ijsolstr.2010.09.003 |
Virieux J. 1984. SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 |
Wang X Q, Sun J G, Zhang Z W. 2005. The state-of the-art in numerical modeling including surface topography. Journal of Jilin University(Earth Science Edition) (in Chinese), 35(S1): 13-18. |
Wang Y, Duan Y W, Wang T, et al. 2017. Numerical simulation and the wave field characteristics analysis of viscoelastic acoustic wave equation based on the nearly-analytic discrete method. Geophysical Prospecting for Petroleum (in Chinese), 56(3): 362-372. |
Xin W, Yan Z C, Liang W Q, et al. 2015. Methods to determine the finite difference coefficients for elastic wave equation modeling. Chinese J. Geophys. (in Chinese), 58(7): 2486-2495. DOI:10.6038/cjg20150724 |
Yan H Y, Liu Y. 2012. Numerical modeling and attenuation characteristics of seismic wavefield in Kelvin-Voigt viscoelastic media. Geophysical & Geochemical Exploration (in Chinese), 36(5): 806-812. |
Yang D, Song G, Lu M. 2007a. Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media. Bulletin of the Seismological Society of America, 97(5): 1557-1569. DOI:10.1785/0120060209 |
Yang D H, Lu M, Wu R S, et al. 2004. An optimal nearly analytic discrete method for 2D acoustic and elastic wave equations. Bull. Seismol. Soc. Am., 94(5): 1982-1992. DOI:10.1785/012003155 |
Yang D H, Song G J, Chen S, et al. 2007b. An improved nearly analytical discrete method:an efficient tool to simulate the seismic response of 2-D porous structures. J. Geophys. Eng., 4(1): 40-52. DOI:10.1088/1742-2132/4/1/006 |
Yang D H, Song G J, Hua B L, et al. 2010. Simulation of acoustic wavefields in heterogeneous media:A robust method for automatic suppression of numerical dispersion. Geophysics, 75(3): T99-T110. DOI:10.1190/1.3428483 |
Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seismol. Soc. Am., 93(2): 882-890. DOI:10.1785/0120020125 |
Yang Q J, Liu C, Geng M X, et al. 2014. Staggered grid finite difference scheme and coefficients deduction of any number of derivatives. Journal of Jilin University(Earth Science Edition) (in Chinese), 44(1): 375-385. |
董良国, 马在田, 曹景忠. 2000a. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报, 43(6): 856-864. |
董良国, 马在田, 曹景忠, 等. 2000b. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. |
豆辉, 张剑锋. 2016. 非均匀黏弹性介质中声波模拟的非规则网格方法. 地球物理学报, 59(11): 4212-4222. DOI:10.6038/cjg20161123 |
冯德山, 王珣. 2017. 基于卷积完全匹配层的非规则网格时域有限元探地雷达数值模拟. 地球物理学报, 60(1): 413-423. DOI:10.6038/cjg20170134 |
韩颜颜, 张忠杰, 梁锴, 等. 2015. 基于非均匀化多尺度方法的自组织介质波前愈合效应波场模拟. 地球物理学报, 58(2): 643-655. DOI:10.6038/cjg20150225 |
贺同江, 刘红艳, 李小凡. 2010. 黏弹性介质地震波传播的褶积微分算子法数值模拟研究. 地震工程学报, 32(4): 318-324. DOI:10.3969/j.issn.1000-0844.2010.04.002 |
胡自多, 贺振华, 刘威, 等. 2016. 旋转网格和常规网格混合的时空域声波有限差分正演. 地球物理学报, 59(10): 3829-3846. DOI:10.6038/cjg20161027 |
李信富, 李小凡, 张美根. 2007. 地震波数值模拟方法研究综述. 防灾减灾工程学报, 27(2): 241-248. |
裴正林, 牟永光. 2004. 地震波传播数值模拟. 地球物理学进展, 19(4): 933-941. DOI:10.3969/j.issn.1004-2903.2004.04.038 |
宋国杰. 2008.三维弹性波方程的改进近似解析离散化方法及波场模拟[硕士论文].北京: 清华大学.
|
宋国杰, 杨顶辉, 陈亚丽, 等. 2010. 基于WNAD方法的非一致网格算法及其弹性波场模拟. 地球物理学报, 53(8): 1985-1992. DOI:10.3969/j.issn.0001-5733.2010.08.025 |
孙成禹, 肖云飞, 印兴耀, 等. 2010. 黏弹介质波动方程有限差分解的稳定性研究. 地震学报, 32(2): 147-156. |
王雪秋, 孙建国, 张文志. 2005. 复杂地表地质条件下地震波数值模拟综述. 吉林大学学报(地球科学版), 35(S1): 13-18. |
汪勇, 段焱文, 王婷, 等. 2017. 近似解析离散化方法的黏弹声波方程数值模拟及波场特征分析. 石油物探, 56(3): 362-372. DOI:10.3969/j.issn.1000-1441.2017.03.006 |
辛维, 闫子超, 梁文全, 等. 2015. 用于弹性波方程数值模拟的有限差分系数确定方法. 地球物理学报, 58(7): 2486-2495. DOI:10.6038/cjg20150724 |
严红勇, 刘洋. 2012. Kelvin-Voigt黏弹性介质地震波场数值模拟与衰减特征. 物探与化探, 36(5): 806-812. |
杨庆节, 刘财, 耿美霞, 等. 2014. 交错网格任意阶导数有限差分格式及差分系数推导. 吉林大学学报(地球科学版), 44(1): 375-385. |
 2019, Vol. 62
2019, Vol. 62

