根据记录资料获取震源信息的主要手段是运动学反演，通过计算波形与记录波形的拟合来反演刻画震源过程的参量.由于不涉及震源区的应力分析，因此运动学反演尽管可以提供破裂行为的描述，但不能解释其原因.为了对震源的动力学过程有更深入的了解，必须把震源参数与震源附近的构造应力场结合起来，考察破裂是如何起始、扩展和停止的.这样不仅可以解释近场地震图中的高频分量，而且也可以通过反演，从震源参数了解震源区的背景构造应力场(Yamashita and Fukuyama, 1996)，这是震源动力学的研究范畴.为了实现震源的动力学模拟，需要借助于一些数值方法.有限差分方法(FDM)被较早地引入到破裂传播问题(e.g., Andrews, 1976a, b; Madariaga, 1976), 随后经众多研究者改进(Mikumo and Miyatake, 1978; Madariaga et al., 1998)，现已成为断层破裂传播问题的重要手段之一.除了有限差分方法，有限元方法(FEM, e.g., Oglesby et al., 1998, 2000; Aagaard et al., 2001)和边界积分方程方法(BIEM, e.g., Das, 1980; Fukuyama and Madariaga, 1998)也被广为应用于断层破裂传播问题.有限元方法具有网格划分灵活，不受问题几何形状限制的特点，但计算量巨大；边界积分法是一种半解析半数值方法，计算量较小，但难以应对复杂的介质模型.

BIEM已经被广泛地用于断层的自发破裂过程研究(Das and Aki, 1977; Das, 1980; Fukuyama and Madariaga, 1998; Aochi et al, 2000a, b; Zhang and Chen, 2006a, b).但传统的断层破裂模拟大都是针对较为简单的平面断层，采用结构化网格进行模拟.一方面，平面断层在很多情况下是发震断层的合理近似，另一方面，结构化的离散方案也是简化计算的需要，因为这样不仅可以使积分核形式更简单，还能利用对称性减少计算复杂度.而越来越多的研究表明，真实地震的发震断层往往具有较为复杂的几何形态，并且是一个结构多样化的断层系统，而断层的几何形态对于地震破裂的影响也逐渐被人们所发现.1992年Landers地震的破裂在传播过程中，由于小的Kickapoo断层的存在，导致了破裂传播出现了“跳跃”(Aochi et al., 2002)；对阶跃断层的破裂传播的模拟(Harris and Day, 1993; 袁杰和朱守彪, 2014; Hu et al., 2016)也显示，阶跃的距离以及应力场的分布等都是破裂能否“跳跃”的重要因素.当断层存在弯折时，断层的物理场演化过程会发生变化(Kato et al., 1999; 马瑾等, 1996)，不同的弯折角度对于破裂的传播与停止有着重要的影响(张丽芬等, 2016).当断层面上含有高强度障碍体时，破裂的传播有可能会受到阻挡而停止破裂，也可能会产生“蓄力”，跨过障碍体继续传播，并产生新的子破裂(Zhang and Chen, 2006b; Xu et al., 2016).

对于复杂几何断层的研究已经有过许多尝试，大多采用的是FEM或者FDM.相比较而言，因为求解对象只集中于断层面上的物理量，不需要对一个空间区域求解，BIEM在复杂几何形状断层方面具有独特的优势.当前基于BIEM对破裂过程的研究大多采用结构化网格的平面断层模型，只有少部分研究尝试采用非结构化网格的划分方案.Hok和Fukuyama(2011)，张丽芬等(2016)都曾采用将矩形一分为二的三角形网格去离散化断层，虽然采用的是三角形单元，但其依然存在对称性，并不属于完全的非结构化划分.Ando (2016)通过数学分析对三角形单元的积分核进行了计算的加速与存储的压缩，给出了平面断层的破裂模拟结果，但没有对破裂过程深入研究.

本文中，我们建立了非结构化网格划分下的BIEM去模拟复杂几何断层的自发破裂过程.通过对传统的平面断层以及典型的复杂几何断层模型的模拟，我们验证了方法的正确性，同时展示了非结构化网格划分在特殊的断层模型下的普适性.

本研究采用的方法为BIEM，该方法最早由Das和Aki (1977)引入到震源破裂模拟中，是一种半解析半数值方法.其出发点是震源表示定理：

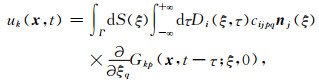
(1)

其中u_k(x, t)为接收点x在t时刻沿着k方向的位移，D_i(ξ, τ)为源点ξ在τ时刻沿着i方向的位错，Γ为断层表面，c_ijpq是弹性常数，n_j(ξ)为ξ点处的法向单位向量，G_kp(x, t-τ; ξ, 0)为位移格林函数，代表的是源点ξ在初始时刻的一个沿p方向上的单位体力，将会在接收点x处在t-τ时刻产生的位移响应.

通过对(1)式求空间导数，并将接收点放置在断层表面，可以得到断层面上的边界积分方程：

(2)

其中T(x, t)为接收点x在t时刻的应力，T⁰(x)为其初始应力，V(ξ, τ)为源点ξ在τ时刻的滑动速率，为应力格林函数，代表的是初始时刻在源点ξ的一个单位速率的滑动，将会在t-τ时刻接收点x处产生的应力响应.

为了将BIE化为便于数值计算的代数方程组，需要对问题的模型、时间和方程进行离散化，离散化后的BIE可以写成如下形式：

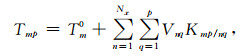
(3)

其中N_x为离散的断层单元总数，T_mp为第m个单元在p时刻的应力累积量，V_nq为第n个单元在q时刻的滑动速率，K_mp/nq为第n个单元在q时刻的滑动对第m个单元在p时刻的应力格林函数，称之为积分核，T_m⁰为第m个单元的初始应力.从离散化形式的边界积分方程可以看到，某个单元的应力累积量是由历史时间内所有单元的的影响和共位单元在当前时刻内的影响叠加而成，这也是运用BIEM计算动力学破裂过程的重要特征.

为了进行非结构化模拟，我们采用的断层模型由三角形单元组成.三角形单元的网格划分已经有了很成熟的方法(Lee and Schachter, 1980; Persson and Strang, 2004)，对于破裂的模拟来说，在保证稳定性的情况下，网格的均匀性会极大地影响破裂模拟的效率，因此，均匀的网格划分对于破裂模拟的效率显得尤为重要.Delaunay三角划分方法(Delaunay, 1934)是最为经典的三角单元划分方法，本研究中我们采用一种基于Delaunay划分方法，利用桁架平衡原理的思想的一种优化网格划分方法(Persson, 2005)，对断层进行网格化.图 1显示的是非结构化剖分的结果，当断层形状规则时，例如图 1a和1c，划分结果具有很好的均匀性，大部分网格都是正三角形.显然，对于规则断层采用结构化网格就可以满足要求，但对于图 1b和1d中所示的断层，由于分别含有圆形的凹凸体(初始破裂区域)和障碍体，采用非结构化的网格划分更容易适应圆形边界.

图 1

Fig. 1

图 1 采用非结构化网格划分的断层模型 (a)弯折断层; (b)弯曲断层; (c)含圆形凹凸体断层; (d)含障碍体断层. Fig. 1 Fault model with unstructured mesh (a) Fold fault; (b) Bend fault; (c) Fault with circle nucleation; (d) Fault with a barrier.

除了方程和模型的离散化，还需要对时间进行离散化，以便进行迭代过程.在本文中我们将时间离散为等步长的时间序列，时间步长的大小由下式决定：

(4)

其中α为介质的纵波波速，Δt, Δs分别为时间步长和网格大小，在正方形单元网格中Δs通常为单元的边长；而在本文中由于采用的是三角形单元，因此Δs取为整个断层面上的三角单元的最小内切圆直径.CFL值为数值算法中用于控制稳定性的参数(Fukuyama and Madariaga, 1998)，我们通过CFL值来限制Δt的大小，为了保证计算的动力学破裂过程的稳定性，在本文中CFL值取值应小于1.

边界积分方程对破裂的数值模拟有两个主要的计算过程，一是由位移格林函数导出的应力格林函数的计算，二是联立边界积分方程与摩擦准则的方程组的时间演化过程.积分核，即应力格林函数，离散化形式如下所示：

(5)

其中为点与点之间的应力格林函数，通过对单元面的积分和历史时间的积分，得到单元与单元之间的离散应力格林函数，它反映了单元与单元间的相互影响的程度，只与介质参数和单元几何信息有关，不随破裂过程而变化.Tada(2005)给出了全空间下矩形单元的积分核解析表达式，随后又对其进行扩展(Tada, 2006)，给出了三角形单元的积分核解析表达式，Feng和Zhang (2017)从另一个角度进行推导给出了形式更为简便、计算更快的三角积分核计算公式，本文我们使用其公式进行积分核的计算.

断层自发破裂过程的模拟需要结合摩擦本构关系.通常采用速率-状态摩擦准则(Dieterich, 1979; Ruina, 1983)或滑动弱化摩擦准则(Ida, 1972).前者通常用于较长时间尺度的震间过程模拟，而同震的动力学破裂过程则多采用后者(Andrews, 1976a, b; Harris et al., 1991).本文，我们采用如下所示的滑动弱化准则：

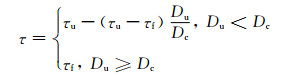
(6)

其中，τ是当前时刻单元的剪切应力值，τ_u是单元的最大静摩擦力，即破裂强度，τ_f是单元的滑动摩擦力，即残余应力，D_c为临界滑动弱化位移，D_u为当前时刻的单元累计滑动量.当断层单元上的剪切应力累积到了破裂强度时，单元开始破裂，其剪切应力随着滑动量线性减小，直至达到稳定滑动后保持不变的摩擦力.

利用前面所描述的方法与流程，我们对不同的断层模型进行了自发破裂的模拟.由于重点是检验非结构化网格的正确性以及在复杂断层上的适用性，因此本文除用于对比的算例外，其余数值算例都采用一致的介质参数和应力参数设置，如表 1所示，其中α, β, ρ分别为介质的P波、S波速度以及密度；T_asp, τ_u, T_e, τ_f分别为初始成核区的初始应力、断层的破裂强度、非成核区的初始应力以及残余应力.值得一提的是，本研究中的残余应力设置为0，这意味着其余应力值都是相对于残余应力而设置的.本研究中积分核是基于全空间介质模型计算得出的，所有的模型均为全空间下的走滑断层模型，且不考虑正应力的影响.

表 1 (Table 1)

表 1 断层应力参数与全空间介质参数设置 Table 1 The shear stress parameters and medium parameters α(km·s-1) β(km·s-1) ρ(kg·m-3) CFL 5.6 3.2 3000 0.98 Tasp(MPa) τu(MPa) Te(MPa) τf(MPa) 120 100 80 0

表 1 断层应力参数与全空间介质参数设置 Table 1 The shear stress parameters and medium parameters

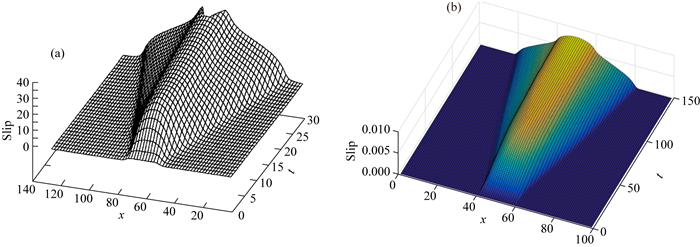
为了验证方法的正确性以及程序的正确性，我们对平面断层进行了模拟.图 2显示的是本文的方法模拟得到的平面断层上的滑动量与Madariaga等(1998)的结果的对比，断层的参数设置大致相同.两个结果刻画的破裂图像基本一致，破裂从初始区域破裂后开始对称地向两边传播，并逐渐加速.固定某个时刻，对断层面上沿破裂传播方向上的一条线上的单元，观察它们的应力分布，对结果进行了对比.如图 3所示，本文的结果与Madariaga等(1998)的结果整体上相似，而细节上存在一些差异.需要说明的是，由于非结构化网格划分与结构化结果的差异，矩形网格有一个固定的网格大小，而三角形网格没有，因此难以取到完全相同的计算参数.这导致了结果在细节上的差异.

图 2

Fig. 2

图 2 平面断层滑动量对比图 (a) Madariaga等(1998)的结果; (b)本文的结果. Fig. 2 Comparison of slip on planar fault (a) Result of Madariaga et al. (1998); (b) Result of our study.

图 3

Fig. 3

图 3 给定时刻断层应力空间分布对比图 (a) Madariaga等(1998)的结果; (b)本文的结果. Fig. 3 Comparison of stress distribution at a given time (a) Result of Madariaga et al. (1998); (b) Result of our study.

在通过与前人结果的对比验证了方法的正确性后，我们就几种常见的复杂几何形状断层进行了模拟.图 4、图 5显示的是一个弯折断层的破裂过程，整个断层由从左到右的三个子平面断层连接而成.三角形单元总数为1073，Δs为0.23 km, Δt为0.041 s, D_c为8.9 cm.最左侧的为主平面，与中间弯折部分的夹角为30°，最右侧的子平面平行于主平面.三个部分的断层尺度为20 km×10 km、10 km×10 km、20 km×10 km.初始破裂区域是位于主平面正中心的一个圆形区域，半径为2.5 km.

图 4

Fig. 4

图 4 弯折断层自发破裂滑动速率快照 Fig. 4 Snapshot of slip rate of spontaneous rupture on a fold fault

图 5

Fig. 5

图 5 弯折断层自发破裂滑动量随时间变化 Fig. 5 The slip of spontaneous rupture on a fold fault

结果显示，在主平面部分破裂的传播方式与平面断层的传播方式差别不大，沿断层走向以椭圆形式对称地向两侧扩展.成核后初始破裂阶段，滑动速率较小，随着破裂的不断加速与扩展，破裂到达第一个弯折部位时已经具有较大的滑动速率，在第一个弯折部分破裂的传播将不再对称扩展，而是出现了明显的阻碍.在经过短暂的延迟之后开始在弯折平面传播扩展，并逐渐加速.当到达第二个弯折部位时破裂传播仍受到阻碍，短暂的延迟之后越过弯折部分从而在平面部分继续传播.为了更细致地考察破裂的行为，我们选取主断层面上的单元与弯折面上的单元，对比其各个物理量的变化，如图 6所示.

图 6

Fig. 6

图 6 断层面上单元间的破裂行为对比 (a) A、B单元位置；(b)滑动量随时间变化图；(c)滑动速率随时间变化图；(d)剪应力随时间变化图. Fig. 6 Comparison of rupture behavior on different elements (a) The position of A unit and B unit; (b) Slip changing with time; (c) Slip rate changing with time; (d) Strain stress changing with time.

A和B分别为主平面的成核区内和弯折面上的单元，图中分别显示了A、B单元的滑动量、滑动速率、剪应力随时间变化的对比.可以看到，两个单元在破裂行为上具有相似性，各个物理量的曲线形状大致相同，但A单元作为成核区上的单元，由于破裂时间更长有着更大的滑动量，而B单元虽然破裂发生的时间较晚，但滑动速率的峰值却要高于A单元，这说明破裂的加速扩展在弯折部分同样出现.为了观察破裂的传播速度以及滑动速率的传播行为，我们选取断层面上的一条线，考察其上的单元随着时间的滑动速率演化情况，如图 7所示.

图 7

Fig. 7

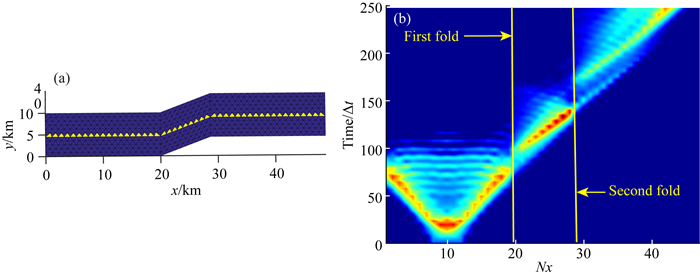
图 7 断层破裂前锋传播图 (a)沿破裂传播方向单元位置示意图；(b)破裂前锋传播图. Fig. 7 Propagation of the rupture front (a) Distribution of units along the rupture propagation; (b) Propagation of the rupture front.

图 7a为我们所选取的单元在断层面上的分布，图 7b为这些单元的滑动速率随时间的变化，其中横坐标为单元的位置，纵坐标为时间步长，颜色深度代表滑动速率的大小.通过颜色最深的线观察破裂前锋的传播，这些线的斜率代表着破裂的传播速率，斜率越小传播速率越大.可以明显看到，破裂从初始区域对称地向两侧传播，传播速度与滑动速率逐渐加大，当遇到第一个弯折部位时，破裂前锋出现了一个短暂的停顿，之后继续在弯折面上传播，并且可以清楚地看到传播速度有一个明显的加速，达到了超剪切速度.当遇到第二个弯折部位时，在同样相似的停顿后，破裂继续在水平面上传播，并且也有一个短暂的加速传播.Bruhat等(2016)曾对微观情况下的破裂传播做过研究，也发现了类似的现象，并将其看成是一种蓄力效应，即破裂在遇到弯折部位时，受到阻碍，但会像弹簧一样蓄力，一旦突破阻碍便会以更大的能量加速传播.

除了弯折断层我们还研究了一些其他类型的复杂断层，不过由于我们的目标是非结构化网格的适用性探索，因此对于其他类型断层上的破裂结果，只简单显示破裂图像，不作细致的分析.图 8显示的是阶跃断层上的滑动速率快照.

图 8

Fig. 8

图 8 阶跃断层自发破裂滑动速率快照图 (a)阶跃距离为0. 5 km；(b)阶跃距离为5 km. Fig. 8 Snapshot of slip rate of spontaneous rupture on step-over faults (a) Step-over distance is 0.5 km; (b) Step-over distance is 5 km.

图 8a和8b分别为阶跃距离0.05 km和0.5 km的断层，断层平面的尺度大小均为20 km×10 km的矩形平面，且断层面之间没有交叠.三角形单元总数为862，Δs为0. 25 km, Δt为0.044 s, D_c为9.6 cm.可以看到破裂从初始区域对称地向两边传播，当到达第一个断层面的边缘时，也就是阶跃点时，破裂的传播发生了一些变化.由于断层的不连续，破裂前锋需要跨过阶跃距离，从而跳到另一个断层面上.图中可以明显地看到，当阶跃距离较小时，破裂在一个短暂的延迟之后跳到了另一个断层面上，并且继续传播下去；而对于阶跃距离较大的断层，破裂的传播则被中断，没能继续在另一个断层面上传播.Hu等(2016)曾专门对阶跃断层的破裂传播行为做过研究，结果表明当阶跃距离较小时，破裂能跨过阶跃部分并继续传播，而随着距离的增大，破裂在跨过阶跃部分后传播的距离将变小，当距离更大时，破裂则难以跨过阶跃部分，这与我们的结果相符.

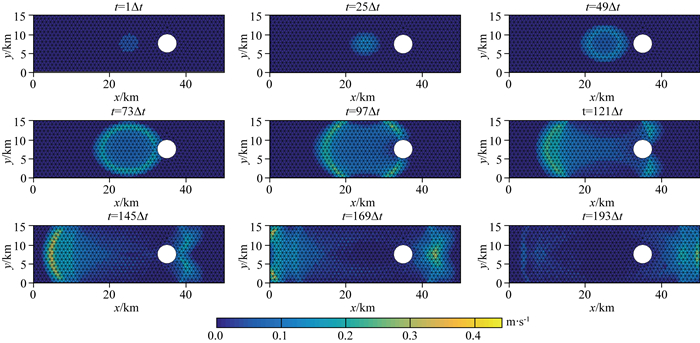
为了显示非结构化网格的优势，我们对含圆形障碍体断层进行了模拟.如图 9所示，断层为一个50 km×15 km矩形平面，在断层的右侧存在一个圆形的障碍体，障碍体是高强度区域，从而不能发生破裂.三角形单元总数为1630，Δs为0.23 km, Δt为0.041 s, D_c为9.0 cm.对于这样存在不规则障碍体的断层模型，无法采用结构化网格进行离散化，只能采用非结构化网格.从破裂模拟的结果可以看到，破裂从初始区域向两边对称传播.当遇到障碍体时，破裂前锋受到了明显的阻碍，以一个缓慢的速度沿着障碍体边缘进行传播；当跨过障碍体后，障碍体上下两侧的破裂前锋又开始向中间缓慢地聚合，并继续向前传播.同时，汇聚后的破裂前锋出现了明显的“一分为二”，有两个破裂前锋在右侧向前传播.Zhang和Chen(2006b)，Xu等(2016)都曾对障碍体对破裂传播的影响做过专门的研究，对于这种强度过高以至于不能破裂的障碍体，他们的研究结果中也发现了在一个破裂前锋通过障碍体后出现了一个新的子破裂，这与我们的结果类似.

图 9

Fig. 9

图 9 含障碍体断层自发破裂滑动速率快照图 Fig. 9 Snapshot of slip rate of spontaneous rupture on a rectangle faults, in which there is a circular barrier zone

本文采用非结构化网格划分下的BIEM去模拟断层的自发破裂，成功地模拟了多种类型的复杂断层模型.通过将采取非结构化网格划分的BIEM的结果与前人的结果就平面断层例子进行对比，验证了本文方法的正确性.除了用于检测正确性的平面断层外，研究中还模拟了多种典型的复杂断层类型模型.对于弯折断层和阶跃断层的研究，模拟的结果显示了复杂几何对于断层破裂的影响，与前人的工作结果相符.对于含圆形障碍体的断层的模拟，非结构化网格的优势得以体现，模拟的结果也显示了障碍体对于破裂传播的影响.

大部分的实际断层都具有复杂的几何形状，并且是一个包含多个子断层的断层系统.本文中的例子都可以看成是某种典型的局部断层，将他们进行组合可以得到更为复杂的断层系统模型.虽然在本文中的大部分例子都可以用结构化网格进行划分，但我们的目的是为了验证非结构化网格在典型断层破裂模拟上的正确性，从而扩展到更复杂的断层系统.采用非结构化网格划分，能对复杂的断层系统更好地离散化.

相比于结构化网格，采用非结构化网格的积分核失去了空间对称性，计算量存储量加大，但能处理更为复杂的断层模型.断层破裂模拟的影响因素很多，除了复杂断层几何形态的影响，正应力、复杂的介质、非均匀应力场分布、自由表面的存在等都是重要影响因素.所以后续的研究会尝试将其他因素考虑进来，使破裂模型更符合实际.