甚低频(VLF)是无线电频谱中极具特点的频段.甚低频波也称超长波，具有波长较长、传播距离远的特点，因此可以在地球-电离层波导内进行远距离传播，在监测地震、太阳耀斑、日食、X射线爆发等引起的电离层扰动方面具有重要意义(Kachakhidze et al., 2012；Sasmal，2018).同时由于VLF波具有传播损耗小且稳定、能穿透一定深度的土壤和海水的特点(底青云等, 2013; 底青云, 2015; Kachakhidze et al., 2012)，也能产生重要的空间波粒相互作用效应(Summers et al., 2007, 2008; Hua et al., 2019; Ni et al., 2008, 2013, 2014, 2017, 2019; Zhao et al., 2019)，其在对潜通信、导航等方面也具有无法替代的作用.因此，对甚低频波传播的研究是十分有意义的.

甚低频波的传播理论研究最早可追溯至20世纪初，随着低频/甚低频导航通信系统的发展，至20世纪中期，逐步出现了比较完善的甚低频波传播模型.Wait(1968)提出了适用于甚低频的地球-电离层波导传播模型，给出了地波传播公式.甚低频波传播理论主要可以概括为两大类：波跳理论和波导模理论.Pal和Chakrabarti(2010)详细介绍了两种传播理论，并提出：由于没有考虑地磁场的影响，波跳理论不能进行较长距离(>4000 km)的甚低频波传播模拟分析.因此，本文选择Ferguson(1995)提出的基于波导模理论的长波传播模型(LWPC)进行甚低频波长距离传播的初步研究.

Pal和Chakrabarti(2011)和Sasmal等(2014)结合LWPC和国际地磁参考场(IGRF, International Geomagnetic Reference Field)模型对VLF波传播路径的损耗率进行了分析.Pal发现夜间相位和衰减率与波跳理论得到的结果有较大的差异性.Sasmal根据位于南极的接收站得到的数据，发现VLF波传播至赤道区域和南极时会有相对较大的损耗率.除了利用LWPC本身进行的甚低频波传播研究，也有大批学者利用LWPC模型的模拟结果作为平静时期结果，进而与地震(Chakrabarti et al., 2010)、闪电(Schmitter，2014; Wang et al., 2019)、耀斑(Grubor et al., 2008；Basak and Chakrabarti, 2013；Bouderba et al., 2016；Šulić et al., 2016)和日食(Pal et al., 2012；Chakraborty et al., 2016；Chakrabarti et al., 2018)等活动发生时的实际接收信号进行比较，从而探讨上述活动对电离层产生的扰动.基于LWPC模型在甚低频波传播研究中具有的重要作用，本文利用国际电离层参考模型(IRI)对LWPC模型中电离层电子密度和碰撞频率做出改进，并利用改进后的模型开展了NWC台站信号传播幅度的建模分析.通过模拟信号与实际接收结果的比较，验证了改进后模型的合理性，模拟了NWC台站在不同区域的幅度分布，并通过比较模型改进前后的变化具体分析了电离层参数对甚低频波传播幅度的具体影响.

基于波导模理论的LWPC模型可以模拟VLF信号传播并得到传播路径上的幅度信息.其基本原理如下：将地球表面和低电离层之间的空间区域视为波导，首先由地面电导率，地磁场大小和方向等因素决定波导参数，根据波导参数将传播路径分段或接受预定的分段列表，从而获得不同段波导参数的特征解，利用沿传播路径水平均匀的波导特征解获得信号强度(Ferguson and Hansen, 1992).本文选择的模型输出为信号在传播路径上的电场强度(E)，进一步利用电场与磁场的关系可以将电场强度转化成磁场强度.

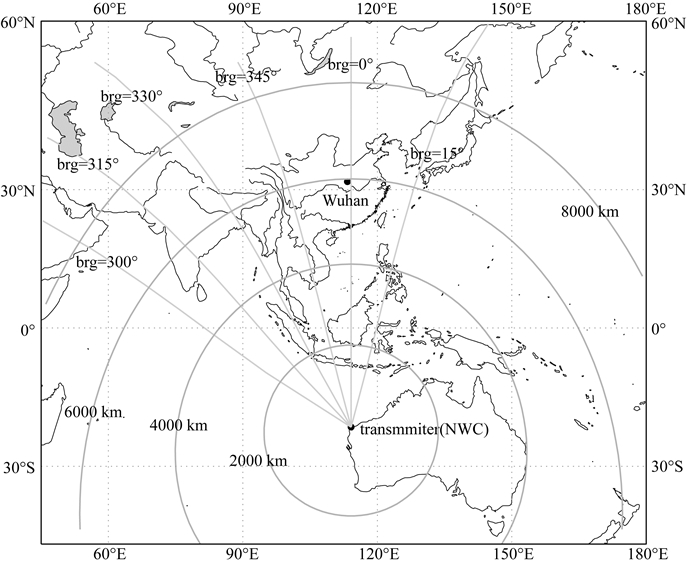
首先利用LWPC模型得到了NWC台站信号传播路径示意图如图 1所示.NWC发射台站位于澳大利亚西北角(21.816°S, 114.16°E)，发射台站信号中心频率为19.8 kHz，功率为1000 kW.图中北向线条表示信号传播的地理方位角(bearing)，圆圈分别表示离NWC台站信号发射点距离为2000 km、4000 km和8000 km的位置.图中黑点表示的是位于北纬30.35°，东经114.17°的武汉大学甚低频接收机位置.可以看出NWC信号传播至武汉接收机点的传播角度可近似为0°(正北方向)，传播距离约为6000 km.正如上文提及的，使用基于波导模理论的LWPC模型分析此较远(>4000 km)的甚低频波传播特性更加合适.

图 1

Fig. 1

图 1 NWC台站信号传播路径图 Fig. 1 The signal propagation path of NWC station

在电离层中影响甚低频波传播的关键因素即包括电离层电子密度和碰撞频率(Ferguson，1985).在LWPC模型中对于这两种电离层参数的计算均采用了一个指数变化的经验公式(Wait and Spices, 1964；Ferguson and Hansen, 1992)：

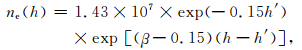
(1)

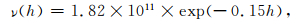
(2)

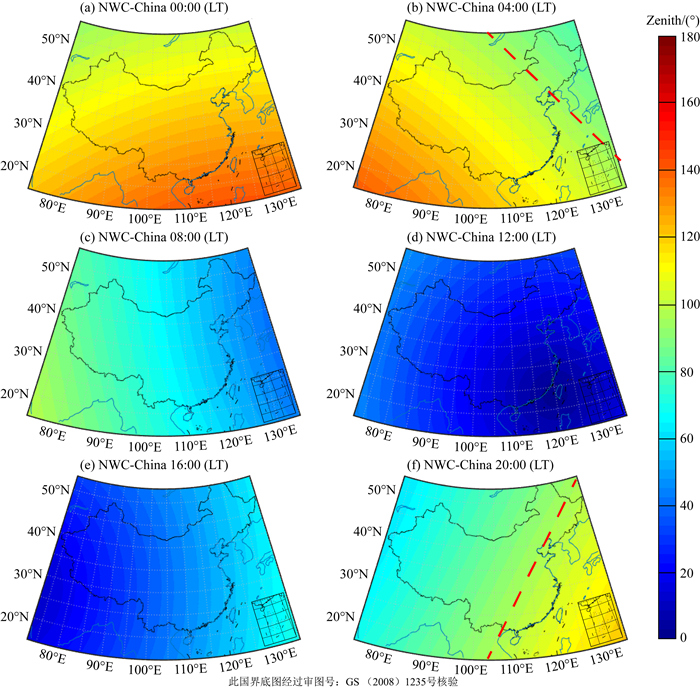
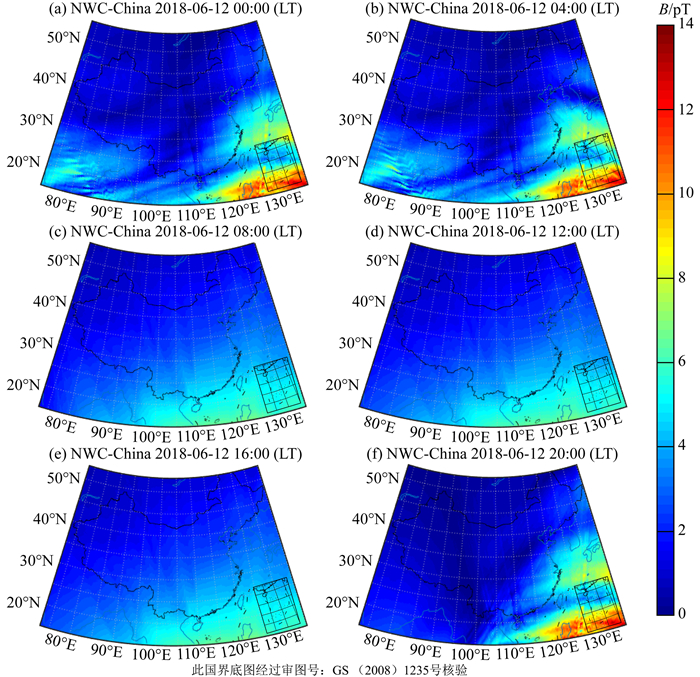
其中，h表示离地面的高度，单位为km；β表示电子浓度随高度变化的梯度参数，单位km^-1；h′为低电离层距地面的参考高度，单位为km.LWPC模型中，β和h′均由太阳天顶角决定，张水仙等(2018)对LWPC中太阳天顶角和β、h′之间的关系进行了详细的介绍.太阳天顶角指的是太阳光线入射方向和天顶方向的夹角，角度范围为-180°~180°，由地理位置、时间等因素决定(谈小生和葛成辉，1995).在LWPC模型中，对于频率为19.8 kHz的NWC台站信号，白天时，天顶角介于-90°~90°之间，β为0.3，h′为74.夜间时，天顶角绝对值大于99°，β为0.4，h′为87.因此，LWPC模型中电子密度和碰撞频率在某一时刻的取值仅取决于离地面的高度及天顶角.本文给出了利用LWPC模型得到的2018年6月12日太阳天顶角绝对值的变化如图 2所示.图 2(a—f)分别表示从零点开始每隔四小时的天顶角的变化，纬度范围为北纬4°~53°，经度范围为从东经73°~135°.从图 2可以明显看出，子图中天顶角最小的区域随时间的推移由西自东又回到西，体现了太阳光照随时间的强度变化.在图 2d给出的北京时间12:00时，天顶角整体最小.图 2b和图 2f中红色虚线表示了天顶角处于90°~99°之间的位置，因此该线表示昼夜变化的分界线，称为晨昏线.在图 2b晨昏线右侧与图 2f晨昏线左侧，天顶角小于90°，属于日间环境，对应的，晨昏线另一侧则属于夜间环境.图 2(c、d、e)给出的天顶角在所研究的区域内基本小于90°，满足日间的条件；而对于图 2(a、b、f)中的大部分区域均满足天顶角大于99°，满足夜间的条件.由于在LWPC模型中，当天顶角满足日间或夜间的条件时，对应的β和h′均为固定值，即电子密度和碰撞频率此时仅与离地面高度有关，而与地理位置无关.因此，对于图中满足日间/夜间条件的区域，其电子密度和碰撞频率随地理位置均无变化，仅与离地面高度相关.这与实际电子密度和碰撞频率的分布情况显然有区别.

图 2

Fig. 2

图 2 2018年6月12日不同区域天顶角随时间的变化 Fig. 2 Variations of zenith angle distribution on June, 12, 2018

IRI模型是一种在给定地理位置、时间和日期的情况下，可以提供电离层高度范围内电子、离子、中性粒子的密度及温度等参数的模型.该模型的电离层下边界与昼夜有关，即日间最低高度80 km，夜间最低高度60 km，存在明显的昼夜变化.本文采用IRI2016版本进行下面的分析.利用何昉和赵正予(2009)给出的计算碰撞频率的公式，对于电子和中性粒子间的碰撞，有

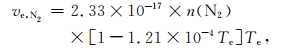
(3)

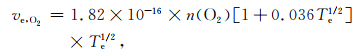
(4)

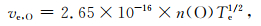
(5)

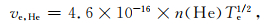
(6)

其中，T_e表示电子温度，利用四种粒子的电子密度可以分别得到电子与这四种中性粒子的碰撞频率.电子与离子的碰撞频率(单位Hz)如下所示：

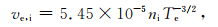
(7)

其中，n_i表示离子密度.可以得到总的电子碰撞频率为

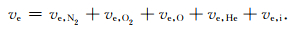
(8)

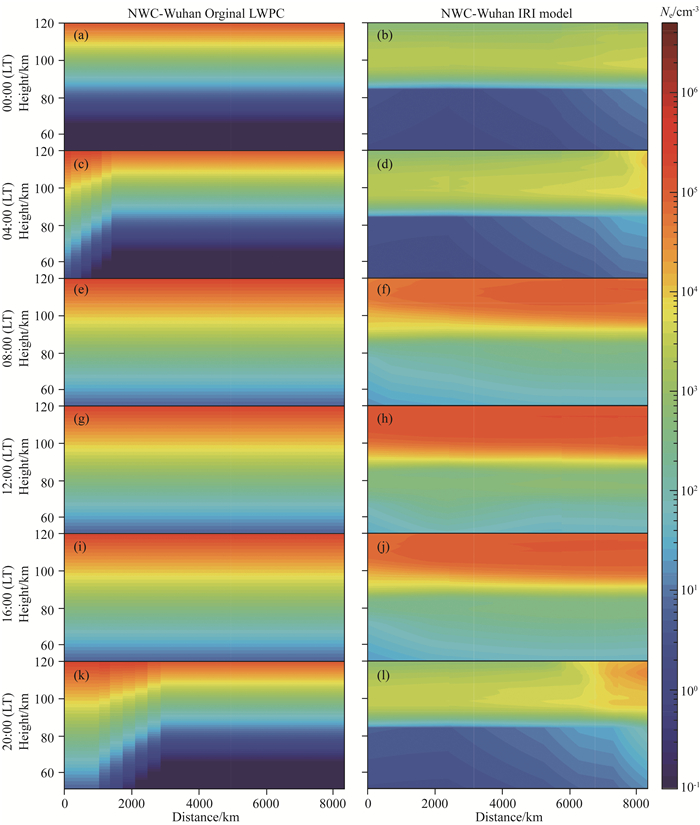
通过IRI模型中的电子、离子、中性粒子的密度及温度可以得到电子密度和碰撞频率在低电离层随高度的分布情况，同时本文采用对数线性插值的方法根据边界处的值分别得到电子密度和碰撞频率在50~60/80 km空间区域上的变化.图 3给出了利用LWPC模型和IRI模型得到的电子密度随离NWC台站的距离和离地面高度的变化示意图，NWC信号传播方位角为0°.从图 3中利用LWPC模型得到的日间电子密度的变化(即图 3(e、g、i))可以看出，电子密度随高度呈指数变化，而随距离无变化，其原因已在上文1.1节中对公式(1)、(2)的介绍中说明.在夜间，图 3(c、k)由于存在区域(距离小于3000 km)处于晨昏交界处，该传播路径上不是日间或夜间的情况，因此电子密度随距离有变化产生.但同样地，在日间或夜间的区域(距离大于3000 km)，电子密度随距离仍未产生变化.相较而言，利用IRI模型得到的电子密度随传播距离具有一定的变化.通过两种模型得到的日间/夜间电子密度的比较可以发现，LWPC模型中的夜间电子密度在较低高度远小于日间，而在较高高度与日间的差异相对较小.而由IRI模型得到的夜间电子密度相对日间在不同高度范围上则有相同量级的减弱.整体来看，两种模拟电子密度主要存在以下两点的差异：1)电子密度随距离是否有变化产生；2)日间和夜间电子密度变化趋势的异同.

图 3

Fig. 3

图 3 LWPC和IRI模型中电子密度随距离和高度的变化示意图 Fig. 3 Variations of the electron density obtained by LWPC and IRI as a function of the distance (X-axis) and the height (Y-axis)

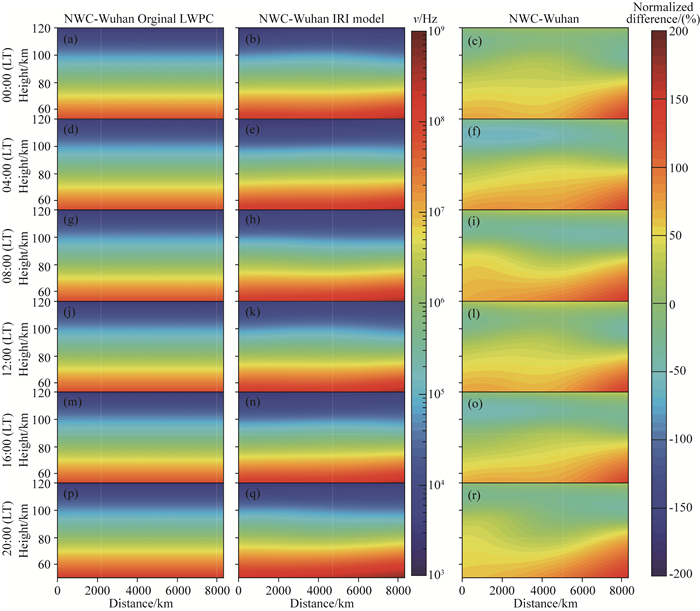
同样地，图 4给出了利用LWPC模型和IRI模型得到的碰撞频率随离NWC台站的距离和离地面高度的变化示意图.由于通过两种模型得到的碰撞频率整体变化差异性较小，图中给出了两种模型碰撞频率的归一化差异.可以发现利用IRI模型计算的碰撞频率随距离、时间均有一定变化.在离NWC台站距离大于4000 km，离地面高度为50~80 km时，利用IRI模型计算的碰撞频率略高于原LWPC模型得到的碰撞频率，此时两者具有最大差异性.但从碰撞频率随高度的分布及变化趋势上看，两种模型得到的碰撞频率整体差异性较小.结合两种模型得到的电子密度随高度的分布及差异性(图 3)，认为模型中由碰撞频率不同引起的幅度区别可以忽略，因此本文主要考虑不同的电子密度对模拟的台站信号传播幅度产生的影响.

图 4

Fig. 4

图 4 LWPC和IRI模型中碰撞频率随距离和高度的变化示意图 Fig. 4 Variations of the collision frequency obtained by LWPC and IRI as a function of the distance (X-axis) and the height (Y-axis)

本文采用位于武汉的甚低频接收机接收NWC台站信号.该甚低频接收机是由武汉大学自主设计研发的一种可以监测自然界闪电辐射和人工台站发射的ELF和VLF无线电磁波信号的数字低频接收机(Chen et al., 2016, 2017).该接收机主要由磁环天线、低噪声模拟前端、数字接收和传输，以及时间保持同步四个部分组成.采用分别为南北方向和东西方向的两路正交磁环天线来连续的接收宽带波数据.接收机的可接收频率范围为200 Hz~50 kHZ，可连续或间隔采样.在1.1节中已经提及，由于NWC信号传播至武汉接收位置处的传播方向为地理正北方向，根据磁环天线接收信号的原理，东西方向接收到的NWC信号将远小于南北方向，因此，本文仅通过南北方向磁环天线接收NWC台站信号并进行分析.通过对接收机信号进行的简单处理(Gross et al., 2018)，利用接收机的相关参数可以将由磁环天线接收到的电压信号(V)转换成实际接收到的信号磁场幅度大小(T).

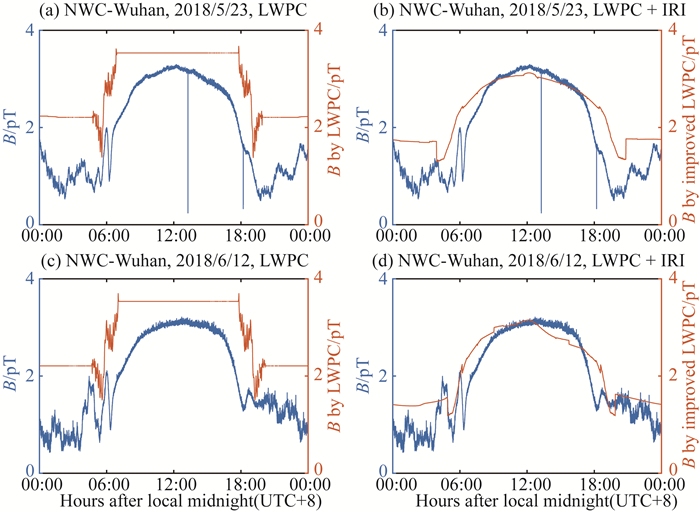
本文选取了2018年5月23日和6月12日武汉接收机的数据，给出了NWC台站信号传播至武汉的实际幅度与模拟结果的日变化比较.图 5中蓝色线表示实际接收的NWC信号幅度，图 5(a、c)中橙色线表示利用改进前LWPC模型得到的NWC台站信号幅度模拟值，图 5(b、d)中橙色线表示利用改进后模型得到的NWC台站信号幅度模拟值.由于LWPC模型中，日间和夜间的情况下，电子密度及碰撞频率等参数完全无变化.因此，可以看到图 5(a、c)基于LWPC模拟的NWC信号幅度在07:00—17:00、00:00—05:00以及19:00—24:00时间段均无变化，这显然与实际接收到的信号变化不符合.而图 5(b、d)得到的幅度呈现明显正午时刻大于其他日间时刻的变化.同时，在12:00(LT)，利用原LWPC模拟的幅度均略高于实际接收幅度.利用IRI模型对LWPC进行改进如图 5(b、d)，可以看到，NWC信号幅度在白天(06:00—18:00)与实际接收的信号幅度变化趋势相同，数值基本一致.由图 5可以得到结论，利用IRI模型对LWPC中电子密度和碰撞频率部分进行改进后，得到了更加接近实际结果的台站信号幅度随时间的变化趋势.

图 5

Fig. 5

图 5 NWC台站信号传播至武汉的实际与模拟幅度比较 Fig. 5 Comparison of the NWC signal amplitude obtained by the observation data (blue) and simulation results (orange) of the LWPC model and the improved LWPC model on May, 23, 2018 and June, 12, 2018

图 5旨在比较利用甚低频接收机接收到的实际信号和改进前后的LWPC模型的模拟结果，主要体现了NWC台站信号在武汉这一地理位置上传播幅度日变化.进一步比较分析改进前后NWC台站信号传播至不同区域的幅值分布情况.图 6为利用原LWPC模型得到的NWC信号传播路径上的幅度分布图.同样地，图 6(a—f)分别表示从零点开始每隔四小时的台站信号幅度值的变化.整体而言，夜间相对日间有较大的信号幅度变化，最大幅度值位于菲律宾海区域，约13.4 pT；而日间最大值位于南海区域，约6.9 pT，其幅度变化基本符合离NWC台站距离越远，幅度越小的趋势.从区域上来看，在大部分位置均可以得到接收信号幅度日间高于夜间的结论，而对于菲律宾海域、南海、黄海、东海和印度附近则有完全相反的结果.在上述区域，日间信号的幅度值大小与相邻区域基本无突变现象，而在夜间，接收信号幅度值有明显增加，这也是引起夜间幅度变化大的原因.上述区域幅度在夜间突然增加的可能原因主要有两点.其一，一般认为低频波在地面-电离层波导传播过程中的反射高度日间为70 km左右，而夜间为90 km左右(Hargreaves，1992；Glukhov et al., 1992；Kumar et al., 2008；姜涛，2014；Chand and Kumar, 2017).结合图 3电子密度的变化分析，在日间70 km处LWPC模型中的电子密度为119 cm^-3，而夜间90 km处，LWPC模型中的电子密度为65 cm^-3.LWPC模型中得到的夜间反射位置处的电子密度低于日间，电子密度减小，碰撞减少，因此夜间信号衰减减小，信号幅度增强.其二，由于陆地和海洋存在的地形差异，海洋区域的电导率远高于陆地，因此衰减会小于陆地，得到信号幅度高于陆地.受上述两种原因影响，夜间部分区域的电子密度会有显著增强现象.

图 6

Fig. 6

图 6 原LWPC模拟的NWC台站信号幅度变化图 Fig. 6 Variations of NWC signal amplitude distribution obtained by the LWPC on June, 12, 2018

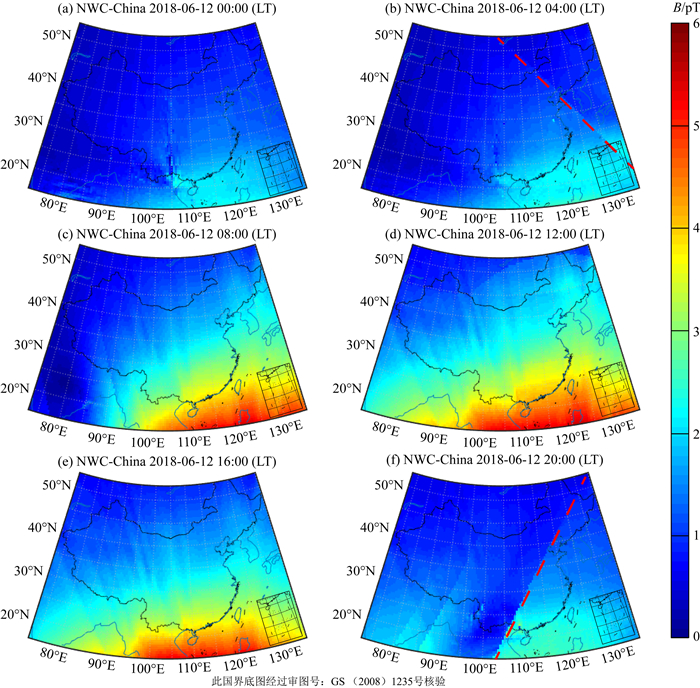
同样的，图 7给出了改进后LWPC模型得到的NWC信号传播路径上的幅度分布，所选区域与时刻均与图 6保持一致.在图中所示区域，接收信号幅度相较于图 6变化范围较小，最大值位于南海区域，约5.51 pT.对于图中所示区域均可以得到接收信号日间幅度基本高于夜间的结论.离NWC台站越近，信号的昼夜变化越明显，不同区域昼夜信号幅度变化在0.4 ~2.3 pT之间变化.同样结合图 3电子密度的变化分析，日间70 km处IRI得到的电子密度为205~330 cm^-3，而夜间90 km处，IRI得到的电子密度为492~811 cm^-3.可以看到夜间发射高度处电子密度略高于日间发射高度处电子密度，电子密度增大，碰撞增加，引起信号衰减增加，因此改进后模型夜间信号幅度低于日间.因此，与图 6相比，改进后模型没有表现出夜间部分区域幅度明显增加的现象.同时，结合图 2对天顶角的分析，可以看到，在晨昏线附近(如图所示的红色虚线)存在幅值突变现象，在图 7f中突变现象更为明显.这种突变现象可能是由于日间和夜间电离层参数有较大的变化，从而导致晨昏线两侧的幅度发生突变.

图 7

Fig. 7

图 7 改进后LWPC模拟的NWC台站信号幅度变化图 Fig. 7 Variation of NWC signal amplitude distribution obtained by the improved LWPC on June, 12, 2018

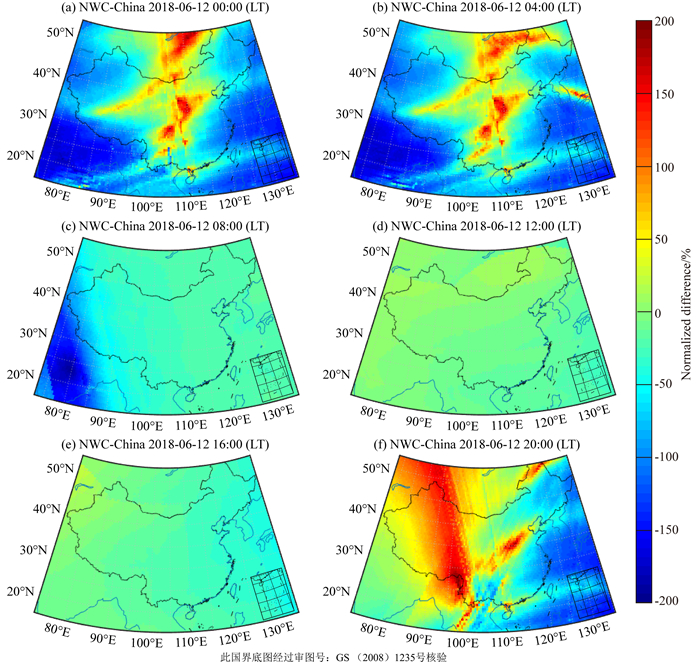
为了更好地说明改变电子密度等电离层参数对LWPC模型产生的影响，本文对两种模型得到的NWC信号幅度进行了归一化处理，如图 8所示.从图 8中可以看出，改进前后模型得到的不同区域NWC台站信号幅度差异在日间较小，且时间越接近正午，差异性越小；而在夜间，信号幅度具有较大差异性.对比图 6，图 7及电子密度的差异(图 3)，可以发现夜间具有较大差异性的原因主要是由于原LWPC模型部分区域的幅度值在夜间有显著增加，造成这种现象的主要原因是夜间反射高度处LWPC模型中的电子密度(65 cm^-3)与IRI模型得到的电子密度(492~811 cm^-3)具有较大差异性，而日间反射高度处LWPC模型的电子密度(119 cm^-3)和IRI模型的电子密度(205~330 cm^-3)相对比较接近.电子密度的变化引起接收的信号幅度产生变化.通过改变电子密度等电离层参数对LWPC模型进行改进后，夜间电子密度随高度、区域的变化更加合理，展示了一个更合适的夜间幅度结果分布.

图 8

Fig. 8

图 8 改进前后模型模拟的NWC台站信号接收幅度归一化图 Fig. 8 The normalized difference of NWC signal amplitude distribution on June, 12, 2018

本文利用IRI模型得到电离层电子密度，并使用该模型中的电离层相关粒子参数计算得到碰撞频率，对LWPC模型中的电子密度和碰撞频率进行改进，得到一个基于IRI模型改进的LWPC甚低频波传播模型.

通过原LWPC模型和IRI模型得到的电子密度和碰撞频率的比较，发现由IRI模型得到的两种电离层参数在日间/夜间条件下随地理位置和时间均产生了变化，且电子密度在夜间反射高度(90 km)处的差异引起了夜间改进前后模型模拟得到的传播幅度的变化.将改进前后的模型计算结果分别与实际接收的NWC台站信号幅度进行比较，发现改进后的模型可以更好地模拟日间的变化趋势，弥补了原模型中日间/夜间状态下幅度等结果完全无变化的不足.基于改进的LWPC模型，对NWC台站信号传播路径上的幅值分布进行了分析，主要有以下结论：

1) 传播路径上的不同区域均体现出了日间NWC台站信号幅度大于夜间的规律.离NWC台站越近，NWC幅度的昼夜变化越明显.

2) 通过结合太阳天顶角分析晨昏效应对NWC台站信号幅度分布的影响，发现由于昼夜突变引起的电离层参数突变，会造成晨昏线附近幅度分布的突变.

本文结合IRI模型改变了原LWPC模型中的电子密度和碰撞频率两种电离层参数，通过对改进前后两种模型结果随时间、地域的变化，验证了改进模型的适用性，建立了一个更合适的甚低频波传播模型，对于快速预测甚低频波的传播场强具有重要意义.