0 引言

岩石物理模版是一门从交会图技术发展起来的、用于定量预测储层参数的地球物理技术(Odegaard and Avseth, 2004).经典的二维岩石物理模版一般选择在声波阻抗和纵横波速度比之间作交会.因此，岩石物理模版通常揭示声波阻抗和纵横波速度比随岩性、孔隙度和饱和度的定量变化关系.岩石物理模版在用于储层预测时，简单直观高效，其预测效果主要依赖于所采用的岩石物理模型.Chi和Han(2009)采用Hertz-Mndlin接触理论模型构建岩石物理模版，将反演得到的弹性参数与岩石物理模版相结合来解释和区分Mexico湾深水未固结砂岩地区的岩性和流体；Gupta等(2012)利用KT模型构建岩石物理模版对Cambay盆地不连续的薄砂岩储层进行描述，并得到了产油层的等厚图，且在实际勘探中得到了验证；张广智等(2015)采用Keys-Xu模型在lamdaRho-muRho交会图上构建能够反映储层孔隙度与含气饱和度的碳酸盐岩岩石物理模版，将岩石物理模版与工区反演提取的参数相结合，确定储层分布范围，并对储层范围内孔隙度和含气饱和度数值进行了定量解释.巴晶等(巴晶等，2013；Ba et al., 2013)基于Biot-Rayleigh方程构建超声波、声波和地震频带的多尺度岩石物理模版，并用来估计碳酸盐岩气藏的孔隙度和饱和度.

现有的二维岩石物理模版只考虑岩石孔隙度和孔隙中所含流体成分对岩石地震特征参数的影响.对常规的碎屑岩储层来说，这样的考虑是合适的，应用结果也比较可信，这是由于常规碎屑岩储层孔隙类型一般比较单一，孔隙结构也比较简单.但是，对于碳酸盐岩以及致密储层来说，储层的孔隙结构非常复杂，通常发育两种乃至两种以上不同类型(如孔隙、裂缝、溶洞等)的孔隙.复杂的孔隙系统使得岩石的速度与孔隙度之间的关系高度分散，具有同一饱和度和孔隙度的数据“点”在模版上并不是紧密“聚焦”，而是“散落”分布(Sayers，2008；Baechle et al.，2008).为此简单的二维岩石物理模型不足以准确表征岩石的弹性性质随孔隙度、饱和度的变化规律，用这样的二维模版来预测储层参数时就有可能将孔隙类型的影响归结为孔隙度或孔隙流体的影响，不可避免地会带来很大偏差.

孔隙结构不仅对岩石的弹性参数有显著影响，对岩石的电阻率和渗透率以及衰减因子也有重要影响(Anselmetti and Eberli, 1999; Ba et al., 2017；Dong et al.，2018).随着数字岩心技术的兴起，岩石孔隙结构可以通过CT扫描获得，并被成功应用于岩石弹性模量和电阻率等参数的模拟.Yin等(2017)利用有限元法计算了数字岩心模型的弹性模量，证实了数字岩心模型与等效介质理论模型的等价性.Dong等(2018)利用有限元方法模拟数字岩心的电阻率，表明水合物微观结构会影响电阻率和水合物的饱和度之间的关系.Anselmetti和Eberli(1999)证实岩石的孔隙类型对其渗透性有显著影响，并试图用之来预测岩石的渗透性.Ba等(2017)指出孔隙结构的非均质性与流体的非均质性都会导致岩石中弹性波传播速度频散与衰减.Duan等(2018)通过数字岩心扫描获得了致密砂岩中裂缝的孔隙纵横比分布，并分析了裂缝对岩石速度频散和衰减的影响.因此，在利用地震资料进行复杂孔隙储层描述时，不能忽略孔隙结构的影响.

本文提出一种适用于复杂孔隙储层的三维岩石物理模版分析方法.首先，分析二维岩石物理模版的适用性；然后，运用Gassmann方程和表征孔隙扁度的干岩石骨架微分等效介质(DEM)解析模型(Li and Zhang, 2011；李宏兵等，2013)模拟地震特征参数(纵横波阻抗、密度)随储层特征参数(孔隙度、流体饱和度和孔隙扁度)的变化过程，建立地震特征参数与储层特征参数间的定量解释关系；接着，建立基于三维岩石物理模版由地震特征参数反演储层的孔隙扁度、孔隙度以及孔隙中所包含的流体饱和度算法；最后，用白云岩储层的实际测井数据和由叠前地震反演获得的地震特征参数基于三维岩石物理模版进行储层特征参数定量预测.

1 二维岩石物理模版及其适用性

二维岩石物理模版(Odegaard and Avseth, 2004)是一种特殊的交会图，其实现步骤一般是：首先为预期中的岩性计算速度-孔隙度趋势；然后计算含水/气的流体体积模量；接着结合上述参数，利用Gassmann方程计算含水/气的岩石的纵横波速度和密度；最后计算出声波阻抗和纵横波速度比.所有计算得到的参数都绘制在同一张图上，就可以分析声波阻抗和纵横波速度比随岩性、孔隙度和饱和度的变化规律.

理想的岩石物理模版解释流程有两步：一是利用测井数据验证所选的岩石物理模版的有效性；二是使用选定和核实的岩石物理模版来解释弹性反演结果，达到预测孔隙度和饱和度的目的.

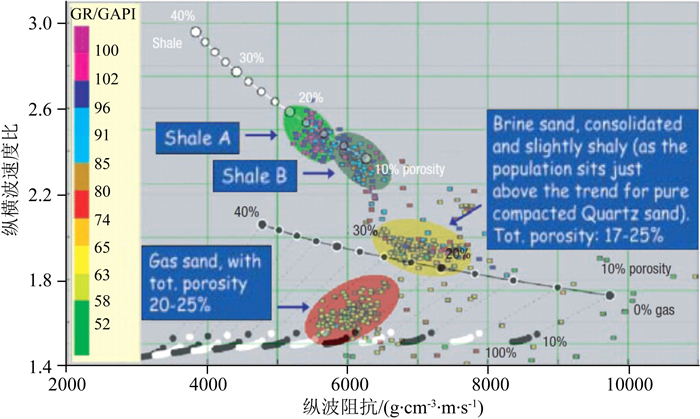
图 1是北海碎屑岩储层测井数据的二维岩石物理模版分析(Odegaard and Avseth, 2004).它包括不同岩性的孔隙度趋势.白色的页岩趋势线代表纯页岩，而黑色的砂岩趋势线代表压实且充填盐水的纯石英砂岩，同时还包含了含气饱和度变化趋势线.注意到，页岩样品均精确地落在页岩的趋势线上，而且这两类页岩具有不同的总孔隙度.盐水砂岩坐落在略高于理论盐水砂岩的趋势上方，说明盐水砂岩中略含泥质.该含气砂岩分布在盐水砂趋势之下，含气饱和度越大越远离虚线.由此，证实二维岩石物理模版所建立的趋势是有效的.

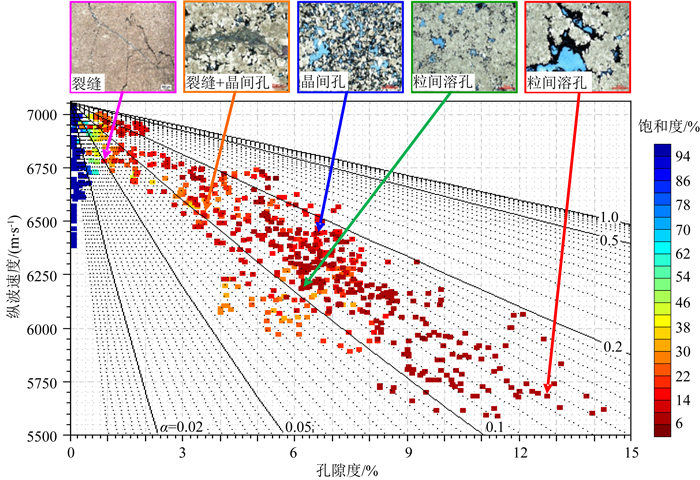
二维岩石物理模版在碎屑岩储层和流体定量预测中已经发挥了积极作用(Odegaard and Avseth, 2004；Chi and Han, 2009)，这是由于常规碎屑岩储层孔隙类型往往比较单一，孔隙结构比较简单.但是，碳酸盐岩储集空间类型多、次生变化大，既有受组构控制的粒间溶孔、粒内溶孔、铸模孔、晶间溶孔等，又有不受组构控制的溶洞、溶缝和构造缝(Odegaard and Avseth, 2004；周进高等，2015).与碎屑岩相比，碳酸盐岩储集层具有很强的非均质性，孔隙结构的复杂性使得用二维岩石物理模版预测储层参数效果不佳.研究区四川安岳气田龙王庙组气藏的储层为白云岩，岩心的孔隙度为2%~10.9%，渗透率为0.001~2 mD(1 mD=0.987×10^-15m²)，具有基质孔渗低，非均质性强，孔洞缝发育的特征(周进高等，2015).通过岩心观察、薄片鉴定及扫描电镜等分析手段，将安岳气田龙王庙组白云岩储层储集空间划分为孔隙(包括粒间溶孔、晶间溶孔、粒内溶孔和残余粒间孔等)、溶洞和缝三种，其中裂缝以网状微缝发育为特点，宏观缝欠发育.图 2是研究区X12井纵波速度与孔隙度的交会图，色标表示含水饱和度，该井段主要是含气层.可以看出，该段储层的速度与孔隙度之间相关性很差，相同孔隙度的纵波速度差值高达750 m·s^-1.从图 2上方展示的该井段储层的岩心薄片可以看到，储层的孔隙结构非常复杂，既发育孔隙扁度较大的溶洞和孔隙，又发育孔隙扁度非常小的裂缝.储层孔隙结构对岩石的弹性性质有很大的影响，它们是导致速度与孔隙度关系发散现象的主要因素(Sayers，2008).图中的黑色线束为储层完全含气时纵波速度随孔隙度和孔隙扁度α变化的二维岩石物理模版，它可以利用等效介质理论(Mavko et al., 1998)或本文下节介绍的复杂孔隙地震岩石物理建模方法计算得到.由此判断X12井白云岩储层的孔隙类型比较复杂，其孔隙扁度在0.01~1.0之间广泛分布.因此，复杂孔隙储层的速度分布可以用岩石的等效孔隙扁度的分布来解释.

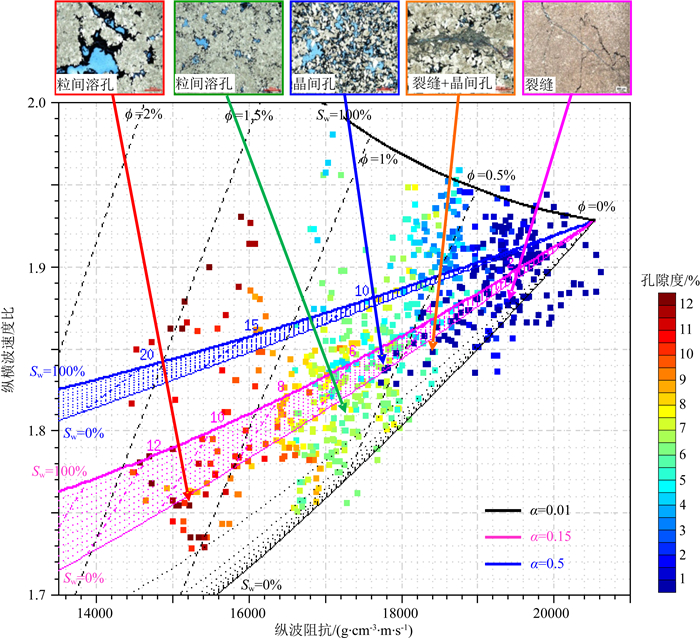
图 3是X12井白云岩储层纵波阻抗与纵横波速度比交会图，图中显示了三种孔隙形状分别为α=0.5、0.15和0.01情形下的二维岩石物理模版，相当于储层孔隙系统发育为溶洞、孔隙和裂缝的情况.图中蓝色二维模版对应的是孔隙扁度为α=0.5时岩石的弹性性质随孔隙度ϕ和饱和度S_w的变化情况，洋红色和黑色二维模版则分别表示孔隙扁度为0.15和0.01的情况，数据点的颜色表示的是孔隙度.可以看出，用具有固定孔隙形状制作的二维岩石物理模版，有相当一部分的储层“点”没有坐落在岩石物理模版区域.随着孔隙扁度的降低，模版覆盖的范围有所扩大，特别是孔隙扁度为0.01时的裂缝型二维岩石物理模版几乎覆盖了整个数据点分布区，但网格点上指示的孔隙度和含水饱和度值与样点的实际测量值难以匹配，说明该储层不仅仅是裂缝发育.

由图 3知，孔隙形状对岩石纵、横波速度及纵横波速度比有很大的影响.实验数据和理论模型已经证实：对于低孔微裂隙岩石，饱含水时泊松比或纵横波速度比具有异常高值，而干燥时则很低(Nur and Simmons, 1969).当孔隙纵横比大于0.1，即岩石发育孔隙时，饱含水情形下的泊松比或纵横波速度比与干燥情形下比较接近，也就是说这种孔隙类型岩石的纵横波速度比对孔隙中的流体相敏感程度较低；而当孔隙纵横比小于0.1，即岩石发育微裂隙时，纵横波速度比对孔隙中的流体相敏感程度非常高(Berryman et al., 2002; Takei, 2002).这主要是由于孔隙中水的存在会增加岩石的弹性模量，其中体积模量增加量比剪切模量要大得多，从而使得纵横波速度比随含水饱和度的增加而增大.然而，孔隙流体引起的岩石弹性模量改变量与孔隙形状和孔隙度有关.对于微裂隙储层来说，裂隙中的水会显著降低微裂隙的可压缩性，而对其剪切模量的贡献几乎为零，这就导致在孔隙度相同情况下，裂隙的孔隙纵横比越小，干燥岩石的纵横波速度比与饱和岩石的纵横波速度比之间的差异越大；同时，孔隙度越大，两者之间的差异会更大.而对于球形孔隙，球孔中的水对孔隙压缩性的修改量几乎可以忽略不计，因此，球孔情况下，干燥岩石的纵横波速度比与饱和岩石的纵横波速度比之间的差异较小；同时，两者之间的差异随孔隙度的增大缓慢增大.

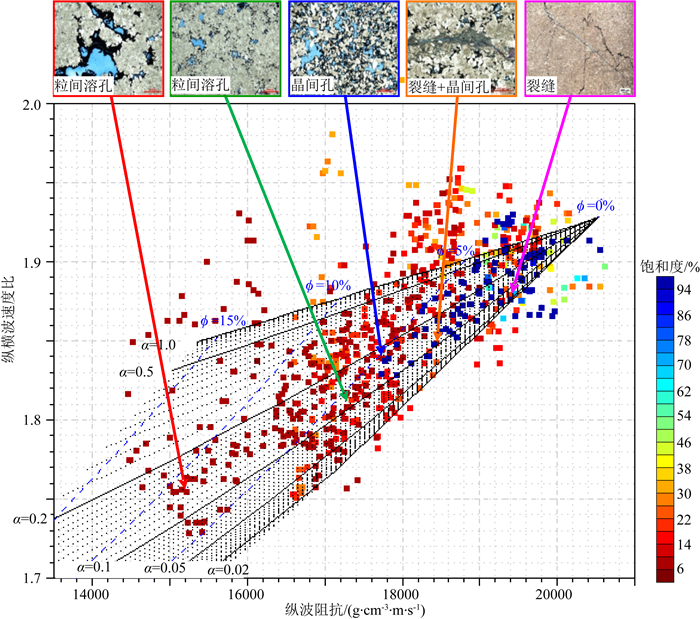
图 4是在与图 3相同数据的交会图上制作的完全含气情形下岩石的弹性性质随孔隙度ϕ和孔隙扁度α变化的二维岩石物理模版，数据点的颜色表示的是含水饱和度.可以看出，大部分点坐落在模版之内，不在模版之内的点可能是矿物的基质模量产生变化所致.对于含气储层来说，其孔隙扁度在0.01~1.0之间都有分布.随着孔隙度的增大，波阻抗和纵横波速度比降低；随着孔隙扁度的降低，波阻抗和纵横波速度比降低.但我们也发现，含水储层的大部分数据“点”也位于“含气”的二维岩石物理模版之内, 而小部分含气储层的数据“点”则位于二维岩石物理模版之外.图 4说明在含气饱和度差异不大的情况下，具有相同纵波阻抗的储层，其纵横波速度比差异非常大，如纵波阻抗为17000 g·cm^-3·m·s^-1时，测井数据的纵横波速度比在1.72~1.9之间，图中岩石物理模版给出的纵横波速度比在1.72~1.87之间.图中岩石物理模版还告诉我们，对于孔隙度相同的储层，其纵横波速度比相差更大，如孔隙度为5%(图中蓝色虚线)时，纵横波速度比在1.7~1.9之间都有分布.这充分说明以裂隙为主的碳酸盐岩也可能具有更高的纵横波速度比，储层孔隙结构的复杂性增加了储层预测的难度.因此，采用一个简单的二维岩石物理模版不足以准确描述所有的岩石样点的弹性参数(I_p、V_p/V_s)随孔隙度、饱和度的定量关系.

2 复杂孔隙地震岩石物理建模

复杂孔隙储层的弹性参数正演模拟通过采用经典的Gassmann方程(Gassmann，1951)和表征孔隙扁度的干岩石骨架DEM解析模型(Li 2010，2011，2012；李宏兵等，2013；李宏兵和张佳佳，2014)来模拟地震特征参数(速度、密度等)随储层特征参数(孔隙度、流体饱和度、孔隙扁度)的变化过程，建立地震特征参数与储层特征参数间的定量解释关系.

2.1 Gassmann方程

在低频假设下，Gassmann(1951)给出了流体饱和岩石的体积模量K_sat和剪切模量μ_sat的计算公式：

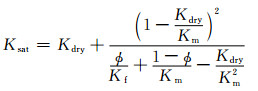
(1)

和

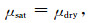
(2)

式中，K_dry为干岩石骨架的体积模量，K_m为岩石基质的体积模量，K_f为流体的体积模量，μ_dry为干岩石骨架剪切模量，ϕ为总孔隙度.

假设岩石孔隙中充填水和天然气的混合体，则在给定的含水饱和度S_w，流体的体积模量K_f可以利用流体均匀分布模型

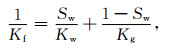
(3)

或流体非均匀分布模型

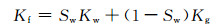
(4)

来计算.式中，K_w为水的体积模量，K_g为天然气的体积模量.相应的流体密度ρ_f可利用(5)式计算

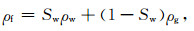
(5)

式中，ρ_w为水的密度，ρ_g为天然气的密度.

由Gassmann方程获得饱和流体岩石的体积模量、剪切模量后，饱和流体岩石的纵、横波速度可表示为

(6)

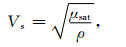
(7)

式中，V_p为纵波速度，V_s为横波速度，ρ为饱和流体岩石的密度.

2.2 多孔岩石干骨架弹性模量

岩石孔隙形态对岩石弹性性质的影响在Gassmann方程中体现在式(1)—(2)中的干岩石骨架模量估计上.多孔岩石的干岩石骨架模量可利用包裹体理论计算.包裹体理论如Kuster-Toksöz理论和微分等效介质(DEM)理论认为干岩石骨架的模量不仅与孔隙度有关，而且与包裹体即孔隙的几何形态有关(Kuster and Toksöz，1974；Norris，1985).与Kuster-Toksöz理论相比，DEM理论更准确有效地模拟了复合材料的等效弹性特性，甚至在包裹体的体积百分比很大时亦如此(Norris，1985；李宏兵和张佳佳，2014).目前，DEM理论已从单孔介质扩展到多孔介质，而且不再受包裹体添加顺序影响(李宏兵和张佳佳，2014).干燥多孔岩石的常微分方程可写成(李宏兵和张佳佳，2014)

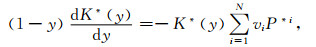
(8)

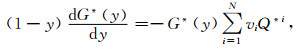
(9)

其中，y是孔隙度，K^*(y)和G^*(y)分别是复合材料的等效体积模量和剪切模量，v_i是第i个包裹体在总孔隙ϕ中的体积百分比，P^*i和Q^*i分别称为等效体积模量和剪切模量的极化因子，取决于包裹体的孔隙扁度(Mavko et al., 1998).N是包裹体的数量.当N=1时，它们与干岩石的经典DEM理论相同.当N=3时，它们变成三重孔隙模型，适合于孔隙系统中含有孔缝洞三种孔隙类型时的等效弹性性质模拟(李宏兵和张佳佳，2014).

干岩石的等效弹性性质不仅可以从式(8)和(9)的数值解中获得，还可以从它们的解析近似公式中获得(Li and Zhang, 2011；李宏兵和张佳佳，2014).他们通过对微分等效介质理论中关于体积模量和剪切模量的两个相互耦合的常微分方程进行解耦，系统地得到关于干岩石骨架的模量比以及体积和剪切模量的解析公式.对于椭球孔，干岩石骨架的弹性模量为

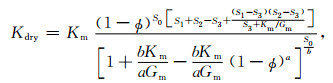
(10)

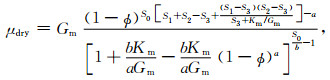
(11)

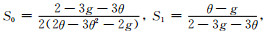
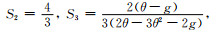
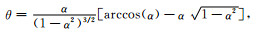
式中，为包裹体的孔隙扁度，亦称为孔隙纵横比(α < 1).常数a和b分别为满足P^*i－Q^*i=a+bK^*(y)/G^*(y)的梯度和截距( and Zhang，2010)，常数b可以简单设置为极化因子之差P^*i－Q^*i的一阶导数在K^*/G^*=Km/Gm时的取值，b已知后常数a就能够由公式P^*i－Q^*i=a+bK^*(y)/G^*(y)来计算得到(李宏兵和张佳佳，2014).椭球包裹体的极化因子之差P^*i－Q^*i及其一阶导数见文献(Li and Zhang, 2011)中的附录A.

2.3 单重孔DEM模型模拟多重孔岩石的有效性

假设式(8)和(9)中所有包裹体的极化因子P^*i和Q^*i的加权求和可以用一个等效包裹体的平均极化因子为P^*I和Q^*I来近似，即其中包裹体i的孔隙扁度为α_i，等效包裹体的孔隙扁度为α_I，则式(8)和(9)变成

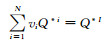
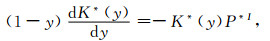
(12)

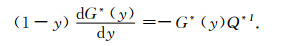
(13)

上述表明，对于具有众多不同孔隙形状的多孔岩石，其弹性性质可以用单重孔隙介质DEM方程来模拟.

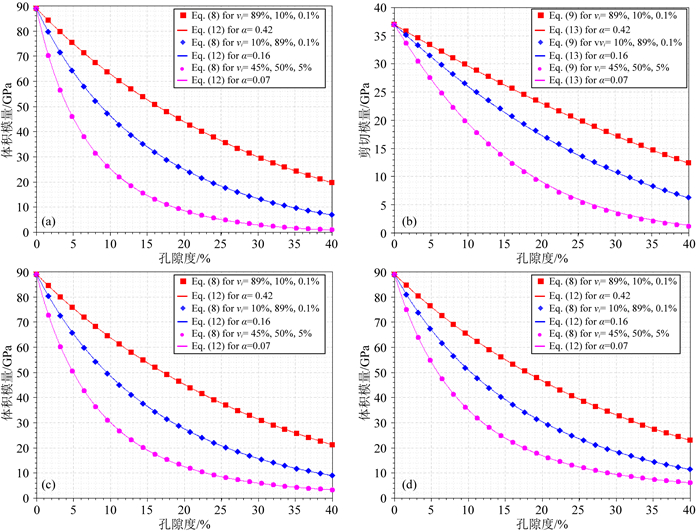
我们对式(8)和(9)与式(12)和(13)进行数值求解并比较其结果.以白云石作为主介质，其体积和剪切模量分别取为K_m=89 GPa和G_m=37 GPa.假设多孔岩石是一个含有孔、缝和洞的三重孔隙系统，即孔隙扁度为0.9的硬圆孔、孔隙扁度为0.15的孔隙和孔隙扁度为0.005的微裂缝.我们还假设孔隙空间中含有三种不同的充填物，分别是油、水和干燥空腔.然后，利用四阶龙格-库塔数值积分法得到式(8)和(9)与式(12)和(13)的数值解，数值积分步长设为Δy=0.1.图 5中的散点代表使用式(8)和(9)模拟的不同孔隙体积的弹性模量.红点代表硬圆孔、孔隙和微裂缝的体积百分比分别为89.9%、10%和0.1%的模拟值，表明多孔岩石的孔隙空间中硬圆孔占主导地位，蓝点代表体积百分比分别为10%、89.9%和0.1%的模拟值，表明多孔岩石的孔隙空间中孔隙占主导地位；粉点代表体积百分比分别为45%、50%和5%的模拟值，表明多孔岩石的孔隙空间中微裂缝占主导地位.图中三种颜色的曲线代表用式(12)和(13)模拟的不同等效孔隙扁度的弹性模量.红色曲线代表等效孔隙扁度α_eff=0.42的模拟值；蓝色曲线代表α_eff=0.155的模拟值；粉色曲线代表α_eff=0.07的模拟值.可以看到，模拟的干岩石、含水和含油饱和岩石的弹性参数曲线与散点吻合得很好.充分说明了用含有等效孔隙扁度的单重孔隙包裹体模型可以等效模拟多孔介质的弹性性质.

3 测井资料三维岩石物理模版分析

三维岩石物理模版RPT3D(three-dimensional Rock Physics Template)的建立包括以下步骤：首先根据测井数据确定储层特征参数(包括孔隙扁度、孔隙度及饱和度)的空间分布，对孔隙扁度、孔隙度及饱和度进行三维网格剖分，使网格中每个节点都对应特定的孔隙扁度、孔隙度及饱和度；然后，根据岩性确定岩石基质的弹性模量，选择合适的岩石物理模型即干岩石骨架模型和流体分布模型，计算网格中每个节点所对应的干岩石骨架模量和流体模量，再运用Gassmann方程计算饱和岩石的速度、密度；接着，在I_p-I_s-ρ构成的三维坐标空间上构建三维岩石物理模版；最后，把测井测量的地震特征参数I_p、I_s和ρ投射到三维岩石物理模版验证三维岩石物理模版的有效性.

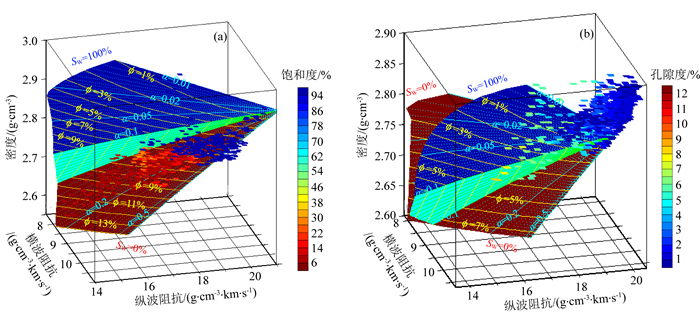
图 6是四川安岳气田龙王庙组储层两口井的三维岩石物理模版分析，其中X12井是一口试气产量达到百万方的高产工业气井，而X203井在目的层上段是孔隙度极低的致密层，下段虽有储层发育但是产水层.在利用第2节提供的方法建立三维岩石物理模版时，需要提供碳酸盐岩地层的骨架矿物成分及流体等弹性模量参数，岩石的骨架矿物成分由测井资料提供，矿物和流体弹性模量可以通过岩石物理实验室测量或由偶极子声波测井数据分析得到.研究区储层主要矿物为白云岩，并含有少量泥质，本次建模岩石基质弹性模量分别取K_m=89 GPa，G_m=37 GPa，密度ρ_m=2.8 g·cm^-3，水的体积模量K_w=2.2 GPa.图 6a为X12井三维岩石物理模版分析图，图中蓝色和棕色曲面分别为储层中完全含水和完全含气时纵、横波阻抗和密度随孔隙扁度和孔隙度变化的趋势面，曲面上的黄色曲线为等孔隙度线，浅蓝色曲线则为等孔隙扁度线.浅绿色曲面为孔隙扁度α=0.1时纵、横波阻抗和密度随孔隙度和饱和度的变化趋势面.蓝色的完全含水曲面始终位于棕色的完全含气曲面之上，这主要是由岩石的密度所控制.图中的长方形散点是龙王庙组地层测井数据，其颜色表示测井解释的含水饱和度值.图 6b为X203井三维岩石物理模版分析图，模版制作所用参数及显示方式与图 6a相同，浅绿色曲面为孔隙扁度α=0.1时纵、横波阻抗和密度随孔隙度和饱和度的变化趋势面.图中的长方形散点颜色表示测井解释的孔隙度值.从图 6可以看出，工业气井X12井中大部分数据“点”的含水饱和度S_w在20%以下，它们位于S_w=0%的完全含气曲面附近，只有极少数据“点”的含水饱和度S_w在80%以上，它们位于S_w=100%的完全含水曲面附近.随着含水饱和度的降低，数据点从完全含水曲面的上方逐渐向完全含气曲面方向移动.而含水井X203井的绝大部分数据“点”位于完全含水曲面附近，图中X12井的数据“点”分布比较均匀，其孔隙度值在0~15%之间，而X203井的绝大部分数据“点”都位于完全含水曲面上方的非储层区域，只有极少数据“点”位于完全含水曲面和完全含气曲面之间，它们的孔隙度低，大部分位于5%以下.这说明制作的三维岩石物理模版与测井解释和钻井结果是吻合的，可以反映纵横波阻抗和密度随孔隙度和含水饱和度的变化规律.此外，从图 6的三维岩石物理模版上还可以发现，两口井的孔隙结构特征互不相同，X12井的孔隙扁度整体上要大于X203井的孔隙扁度.这说明碳酸盐岩储层的纵横波速度不仅受孔隙度和饱和度的影响，也强烈受孔隙扁度的影响，利用纵横波速度、密度数据预测储层孔隙度和饱和度时必须考虑孔隙扁度这一重要因素.

4 三维岩石物理模版储层参数定量预测

利用三维岩石物理模版，可以实现储层特征参数的定量预测.首先把由地震叠前反演得到的地震特征参数I_p、I_s和ρ投射到三维岩石物理模版RPT3D，然后基于最小二乘原理寻找与投影点残差最小的三维模版网格点，该网格点所对应的孔隙扁度、孔隙度和饱和度即为储层位置的反演值.基于这种方法可定量预测储层的孔隙结构和物性参数.

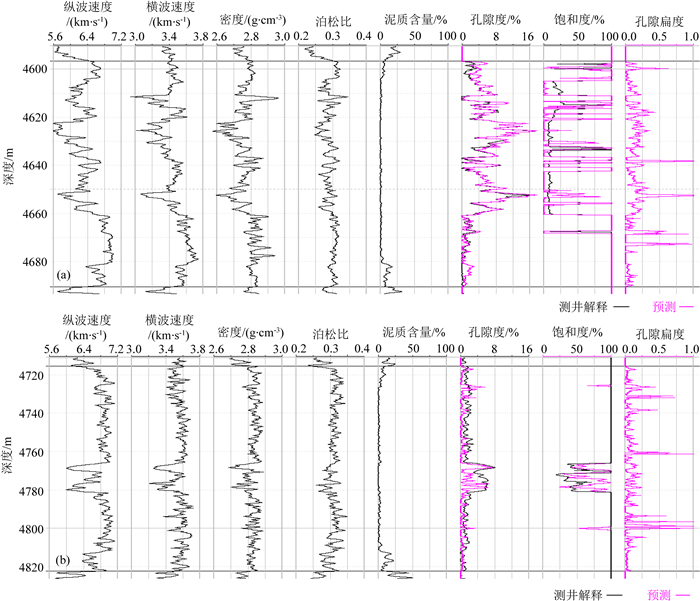
图 7是基于图 6的岩石物理模版计算得到的孔隙度和饱和度及孔隙扁度与测井解释结果对比.图中黑色的曲线分别表示测量的纵横波速度和密度曲线以及测井数据解释的孔隙度和饱和度曲线，洋红色曲线表示的是根据三维岩石物理模版从纵横波阻抗和密度中提取的孔隙度和含水饱和度及孔隙扁度.图 7a是X12井的反演结果与测井解释结果对比.可以看到，X12井储层发育，孔隙度较高，含气性好.在储层孔隙度大于2.5%时，三维模版提取的孔隙度值与测井解释结果非常吻合；三维模版提取的含水饱和度值与测井解释结果有轻微差异，但它们都预测该井的含气饱和度较高，与实际钻探结果一致.这说明由三维模版提取的储层物性参数是可信的.孔隙扁度是本文特有的研究成果，目前的测井解释无法提供，因此无法对比.孔隙扁度大小在一定程度上可以反映储层裂缝的发育情况(Sayers，2008).从反演的结果看，储层段的孔隙扁度变化范围大，大部分位于0.1~1.0之间.图 7b是X203井的反演结果与测井解释结果对比.可以看到，该井只在4765~4780 m之间储层比较发育，三维模版预测的孔隙度和饱和度比测井解释结果更加保守，但与试气结果是吻合的，该井储层段的孔隙扁度普遍较低，基本小于0.25.

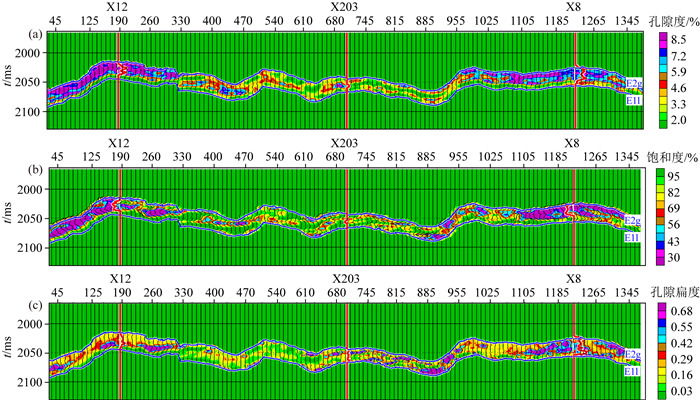
图 8是利用三维岩石物理模版对过研究区X12、X203和X8三口井的连井地震剖面从叠前地震反演数据体中提取的孔隙扁度及孔隙度和含水饱和度，X8井与X12井一样是工区内的一口高产气井.图中红色加粗曲线分别对应为测井解释的孔隙度、饱和度和孔隙扁度.图 8a为反演的孔隙度连井剖面.可以看到，高产工业气井X12和X8都位于局部高点，孔隙度比较高，而产水井X203井位于次高点，孔隙度低.图 8b为反演的含水饱和度连井剖面.可以看到，位于局部高点的高产工业气井X12和X8含气饱和度较高，而位于次高点产水井X203井含气饱和度低.图 8c为反演的孔隙扁度连井剖面.可以看到，位于局部高点的高产工业气井X8孔隙扁度较大，孔隙比较硬，X12井的孔隙扁度相比X8井偏小，孔隙偏软，而位于次高点产水井X203井孔隙扁度更低，孔隙更软.孔隙扁度大小在一定程度上可以反映储层裂缝的发育情况，由于裂缝是扁平和狭长的，它的存在往往导致储层整体的孔隙扁度值偏低.图 8c中在X203井左侧目的层段的等效孔隙扁度在0.03附近，表明此处储层中裂缝比较发育.

5 讨论

需要指出的是，本文的三维岩石物理模版是利用等效介质理论和Gassmann方程构建，而Gassmann方程是基于低频假设提出的，适用于地震频带.三维岩石物理模版中岩石孔隙结构对岩石弹性性质的影响体现在干岩石骨架模量的计算上，本文的干岩石骨架模量估计采用的是等效介质理论，它要求孔隙彼此之间是孤立的，近似高频假设条件，但实验室测量已证明干岩石骨架弹性模量在高频与低频范围内变化不大，可近似相等(Mavko et al., 1998；Adam et al., 2006).目前业界在对Gassmann方程能否用于高频测量的测井数据这一问题有着不同的观点(Adam et al., 2006; Fabricius et al., 2010).由于Gassmann方程不考虑孔隙流体与岩石骨架的相互作用，在应用于测井数据分析时可能会带来一定的误差.因此，对不同频率测量的数据可以考虑用更加复杂的描述速度频散的孔隙弹性理论(Biot，1965；巴晶等，2013；Dong et al., 2017; Ba et al., 2017)来构建适用于各种频率的多尺度三维岩石物理模版，这是一个值得深入研究的新方向.

实际碳酸盐岩储层孔隙结构非常复杂，孔隙形态千姿百态，目前的地震岩石物理建模方法往往采用简化、具有理想规则形态的岩石物理模型来等效，例如本文的三维岩石物理模版构建所使用的岩石物理模型是等效的单重孔隙DEM模型.对于这种等效的合理性很多人也尝试进行了研究，尤其是在3D数字岩心技术发展起来之后.通过微纳米CT扫描，可以得到3D数字岩心图像，并且可以从中提取岩石复杂孔隙结构形态.在数字岩心图像的基础上进行有限元或者有限差分数值模拟，就可以获得准确的岩石弹性参数.Zhang和Toksöz(2012)利用有限元方法计算了不同流体饱和Berra砂岩数字岩心的静态弹性模量，发现Kuster-Toksöz理论模型计算结果与有限元模拟结果比较接近.Yin等(2017)用有限元法计算了三维数字岩心的弹性模量，研究了数字岩心模型与各种岩石物理理论模型的等价性，他们发现基于数字岩心的有限元模拟与边界模型和Gassmann方程可以等价.因此，这些也证实了三维岩石物理模版中采用等效的单重孔隙DEM模型来表征碳酸盐岩孔隙结构是合理的.

6 结论

本文提出利用多孔介质岩石物理DEM解析模型和Gassmann方程由孔隙度、流体饱和度、孔隙扁度三个储层特征参数构建三维岩石物理模版的方法，考虑了孔隙的几何特征，更加准确反映多孔介质岩石的弹性模量随孔隙度和饱和度的变化特征；避免了经典的二维岩石物理模版在预测储层特征参数时有可能将孔隙类型的影响归结为孔隙度或孔隙流体的影响，从而带来很大偏差的问题，可以更加准确地预测孔隙度和饱和度及孔隙扁度.

实际测井数据应用表明，利用三维岩石物理模版预测的储层孔隙度和饱和度与测井解释结果都相吻合，特别是孔隙度大于3%的储层具有很高的吻合度.实际地震数据应用表明，三维岩石物理模版可以准确预测高产气井和含水井的孔隙度和饱和度及其横向分布，并能有效指示储层的软硬孔发育带.

基于三维岩石物理模版的储层孔隙扁度及孔隙度和饱和度的估计方法是一种确定性的岩石物理反演方法，对输入数据有较高的要求，需要准确的纵、横波速度和密度数据.因此，在应用该方法时，需要通过精细的叠前地震反演得到准确的岩石物理反演输入数据，这样才能保证岩石物理反演结果的准确性.

储层孔隙扁度及孔隙度和流体饱和度预测是非均质储层(如碳酸盐岩储层)油气勘探寻找储层甜点必须解决的技术问题.准确建立地震参数与储层参数之间的定量解释关系可以增强储层预测及解释结果的可靠性，提高储层流体识别的能力，减小解释的风险.

致谢  感谢匿名评阅人对本文提出的宝贵修改意见