0 引言

重力坝具有结构简单、安全可靠、对地形和地质条件适应性强等优点，成为水利水电工程中被广泛采用的坝型.然而，我国在建或已建的高混凝土重力坝大多位于地震频发的西部地区，强烈的地震作用是威胁这些高混凝土重力坝安全的主要荷载.多年来，国内外学者在重力坝地震响应分析领域开展了广泛的研究(Lin and Hu, 2005; 龙渝川等, 2008; 苑举卫等, 2011; 徐艳杰等, 2012).在重力坝地震响应分析中，大坝与地基之间的动力相互作用是其应当考虑的重要方面，而波动在半无限地基中传播引起的辐射阻尼效应是该问题的重点和难点.在大坝-地基动力相互作用分析中，通常假定地基为半无限均匀介质，然而在实际工程中，许多重力坝均是坐落于复杂的层状地基之上.与半无限均质地基波传播问题相比，层状地基波传播问题更加复杂，体现在层状地基中同时存在能量向无穷远处耗散的行波和能量在近场衰减耗散的快衰波，这就要求波传播模拟方法具有全频收敛的特性.

在波动传播模拟的众多方法中，有限单元法(徐世浙, 1994; 李伟华等, 2010; 冯德山等, 2012)和有限差分法(Lan and Zhang, 2011; 兰海强等, 2011; 张保庆等, 2016)是其中两种主要的数值方法.但是这两种方法只能离散有限区域，为了避免波动在计算域截断边界上的虚假反射，需要在截断边界上施加人工吸收边界(Givoli, 1991; 邵秀民和蓝志凌, 1995; 廖振鹏等, 2002; Yang et al., 2003; Chen et al., 2010; 冯德山和王珣, 2017)，或者与其他无限域动力模拟数值方法相结合以模拟波动在无限介质中传播引起的辐射阻尼效应.薄层法非常适合于求解水平层状介质中的波传播问题，其主要应用为求解层状地基的格林函数(Kausel and Peek, 1982)；在时域分析方面，该方法存在数值散射问题，需要采取额外的数值措施以保证其计算的稳定(Park and Kausel, 2004).边界元法(Spyrakos and Xu, 2004; Padrón et al., 2008; 胡善政等, 2009)只需对边界进行离散，从而使问题维数降低一维，并且自动满足无穷远处的辐射边界条件，因此在层状介质波传播模拟中得到广泛应用.然而，边界元的求解依赖于基本解，这大大限制了边界元法在实际工程中的应用.

比例边界有限单元法(全称为Scaled Boundary Finite Element Method，简写为SBFEM)是由Wolf和Song提出的一种半解析数值方法(Song and Wolf, 1997, 2000).它只需对边界进行离散而在径向保持解析，不需要基本解即可自动满足无穷远处的辐射边界条件，因此在无限域动力问题模拟中得到了广泛应用.针对层状地基波传播问题，许多学者基于SBFEM开展了探索性研究.Birk和Behnke (2012)采用高频渐近级数方法求解三维层状地基的动力刚度，然而该方法计算复杂、计算量大，精度也不够理想.韩泽军和林皋(2012)采用连分式渐近算法求解三维层状地基的动力刚度，提高了计算精度和计算效率.在时域分析方面，SBFEM的求解主要通过卷积积分计算每个时间点的单位脉冲响应函数实现，计算十分耗时.针对层状地基波传播问题，Chen等(2015)基于截断卷积技术提高了单位脉冲响应函数计算效率.

高阶局部透射边界(Givoli, 2004)同时具有高阶精度和较高的计算效率，其中基于SBFEM发展的高阶透射边界在空间域上具有全局精确特性，但在时间域上实现了局部化，避免了耗时的卷积积分运算，成为了近十多年来无限域动力问题模拟的一个研究热点.Bazyar和Song (2008)、Birk等(2012)基于动力刚度连分式渐近解构建了高阶透射边界，随着渐近阶数的增加，该透射边界具有收敛到动力刚度精确解的高阶精度.Lu等(2016)基于连分式高频渐近解构建了层状地基弹性波传播模拟的高阶透射边界，并与有限元法耦合进行了层状地基波传播模拟研究.然而，上述透射边界属于高频单向渐近边界，在低频处的收敛速度很慢，需要很高的渐近阶数逼近低频部分，不仅增加计算量并且可能导致数值稳定性问题.此外，层状地基中同时存在行波和快衰波，这就要求透射边界具有在全频范围内收敛到动力刚度准确解的特性.

为了克服高频单向渐近透射边界的缺点，Prempramote等(2009)基于动力刚度连分式双渐近解提出了一类标量波传播模拟的高阶双渐近透射边界.随着渐近阶数的增加，该透射边界在全频范围内迅速收敛到动力刚度准确解，具有很高的计算精度和计算效率.Wang等(2011)、高毅超等(2013)进一步将该透射边界应用到层状库水动水压力波的传播模拟，并建立了有限元-高阶双渐近透射边界的时域耦合分析模型，数值算例分析结果表明该透射边界具有很高的计算精度和计算效率，并且具有良好的数值稳定性.Prempramote (2011)进一步将高阶双渐近透射边界推广到均匀层状介质矢量波传播问题，但该透射边界对于大规模自由度问题的时域分析可能存在数值稳定性问题.

本文将高计算精度和高计算效率的高阶双渐近透射边界推广应用到层状地基系统弹性波传播问题的模拟，通过移谱法消除导致系统不稳定的虚假模态，保证该透射边界时域计算的数值稳定性；将该透射边界直接嵌入近场有限元方程，建立了有限元-高阶双渐近透射边界时域耦合分析模型；在开源有限元软件OpenSees上编程实现该时域耦合分析模型，并将其应用到重力坝地震响应分析.

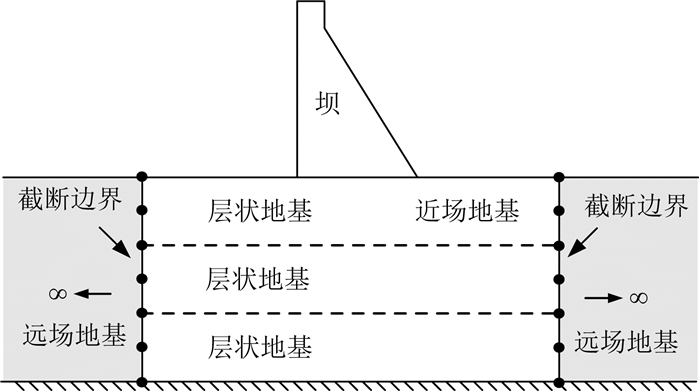
1 重力坝-地基系统运动方程

典型的重力坝-层状地基系统如图 1所示，其中向上下游无限延伸的地基通过竖直截断边界被分割成近场和远场两个部分.具有不规则几何形状的近场地基和混凝土重力坝通过有限单元离散；远场规则地基简化成半无限等高层状介质，采用比例边界有限单元法模拟，相似中心分别取在上下游无穷远处.

鉴于本文主要研究透射边界的影响，不考虑材料阻尼，则重力坝和近场地基系统的有限元控制方程可以写为

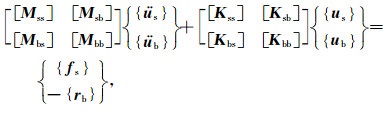
(1)

式中，[M]和[K]分别为质量矩阵和刚度矩阵，{f}为外荷载向量.下标b表示截断边界节点自由度，下标s表示除截断边界节点自由度外的坝体结构和近场地基节点自由度.远场半无限层状地基对近场广义结构的影响通过相互作用力-{r_b}体现.

2 高阶双渐近透射边界

Prempramote (2011)给出了层状介质矢量波高阶双渐近透射边界的构建过程，本文将主要求解算法和流程归纳总结如下，求解算法中涉及到的辅助系数矩阵定义和详细的求解公式详见该文献.

在频域内，等效节点荷载与节点位移幅值的关系可以用动力刚度的定义式表示为

(2)

对于半无限等高层状地基，频域动力刚度表示的比例边界有限单元方程可以写为

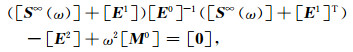
(3)

式中各个系数矩阵的定义详见Prempramote(2011).考虑如下广义特征值分解，即：

(4)

式中[Λ]为对角元素均为正值的对角矩阵，[Φ]为特征向量矩阵，[I]为单位矩阵.对式(3)左乘[Φ]^T，右乘[Φ]，并考虑式(4)可得：

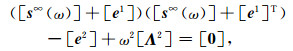
(5)

其中模态动力刚度[s^∞(ω)]、系数矩阵[e¹]和[e²]的定义为

(6)

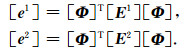
(7)

模态动力刚度的高频连分式渐近解可以表示为

(8)

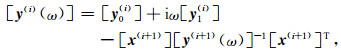
(9)

式中[k_∞]、[c_∞]、[y₀⁽ⁱ⁾]和[y₁⁽ⁱ⁾]为待定系数矩阵，[x⁽ⁱ⁾]是为了提高连分式渐近解构造过程中的数值稳定性而引入的因子矩阵，i=1, 2, …, M_H，M_H为高频渐近阶数.将高频连分式渐近解代入模态动力刚度表示的比例边界有限单元方程，并令其在高频极限ω→∞成立，即可求解得到上述待定系数矩阵，其求解流程如图 2所示.

将高频连分式渐近解的残项[y^(M_H+1)(ω)]作为低频连分式渐近解的起始项[y_L⁽⁰⁾(ω)]，构造[y_L⁽⁰⁾(ω)]的低频连分式渐近解，即：

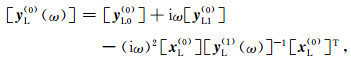
(10)

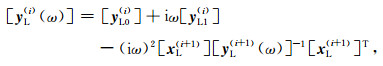
(11)

式中[y_L0⁽⁰⁾]、[y_L1⁽⁰⁾]、[y_L0⁽ⁱ⁾]和[y_L1⁽ⁱ⁾]为待定系数矩阵，[x_L⁽ⁱ⁾]是为了提高连分式渐近解构造过程中的数值稳定性而引入的因子矩阵，i=1, 2, …, M_L，M_L为低频渐近阶数.将低频连分式渐近解带入相应的控制方程，并令其在低频极限ω→0成立，即可求解得到上述待定系数矩阵，其求解流程如图 3所示.

在高频连分式渐近解(式(8)和式(9))和低频连分式渐近解(式(10)和式(11))的基础上引入辅助变量，结合动力刚度的定义式(2)和式(6)，并进行傅里叶逆变换，即可得到如下分块矩阵表示的高阶双渐近透射边界，公式为

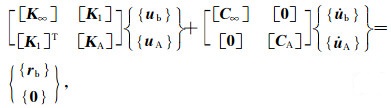
(12)

式中[K_∞]和[C_∞]的定义分别为

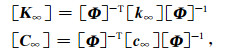
(13)

辅助位移向量{u_A}和分块矩阵[K₁]的定义为

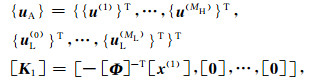
(14)

系数矩阵[K_A]和[C_A]的定义为

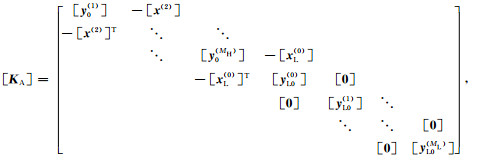
(15)

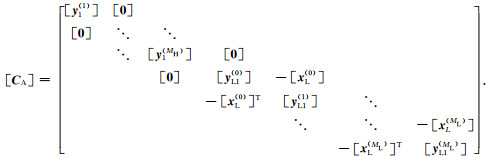
(16)

3 数值稳定性分析及时域耦合分析模型

连分式渐近解的构建过程涉及矩阵的循环求逆，从而引入虚假模态，导致高阶双渐近透射边界时域分析的数值不稳定.为此，Birk and Song (2009)提出了移谱法(Spectral Shifting Technique)用于消除虚假模态，本文将移谱法应用到层状介质矢量波问题的高阶双渐近透射边界，具体算法总结如下.

定义系数矩阵[K_z]和[C_z]为

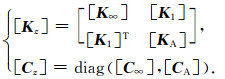
(17)

为了分析式(12)的数值稳定性，考虑广义特征值分解，即：

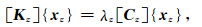
(18)

当所有特征值λ_z的实部均为正值时，式(12)是渐近稳定的.记需要调整的特征值为λ_{z, j}，若λ_{z, j}为实数，记其对应的特征值向量为 {x_z}_j；若λ_{z, j}为成对的共轭复数，其对应的特征向量亦为成对出现的共轭向量，则将其对应的特征向量改写成矩阵形式[X_z]_j(按实部、虚部顺序排列).

通过对[K_z]进行调整([C_z]不需要调整)，即可消除虚假模态，并且不影响其他真实模态，调整公式为

(19)

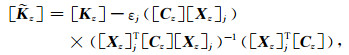
(20)

式(19)和(20)式分别适用于λ_{z, j}为实数和复数的情形，在应用中可取ε_j=2Re(λ_{z, j}).调整后，记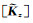的分块形式为

(21)

将时域高阶双渐近透射边界直接嵌入到近场有限元方程，即可得到考虑半无限层状地基辐射阻尼效应的有限元-高阶双渐近透射边界时域耦合分析模型，其表达式如下

(22)

为了实现该时域耦合分析模型，作者基于开源有限元软件OpenSees编写了高阶双渐近透射边界单元，以超单元的形式将该透射边界嵌入到近场有限元方程.高阶双渐近透射边界单元中的刚度矩阵和阻尼矩阵均为常矩阵，在时域分析中只需求解一次，因此可以预先求解并存储以提高计算效率.

4 算例

为了验证本文提出的时域耦合分析模型的计算精度和计算效率，采用以下两个算例进行模型验证.计算中，时步积分法采用Newmark-β法，其中γ=0.5，β=0.25，即平均常加速度法.

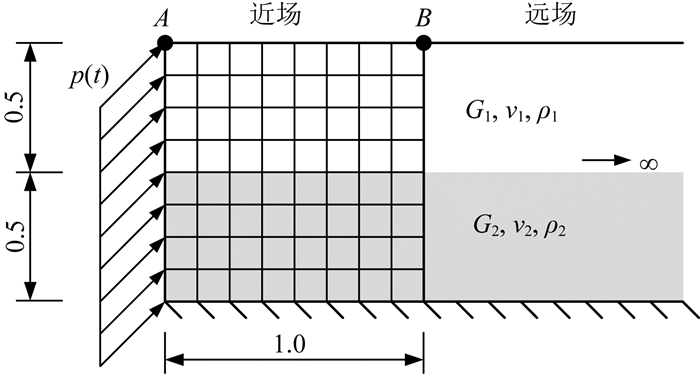
4.1 两层水平层状地基算例

考虑图 4所示的两层水平层状地基，取无量纲模型参数，每层高度均为0.5，底面为固定边界条件，顶面为自由边界条件，左侧受到45°方向均布荷载p(t)的作用.取无量纲材料参数如下：G₁/ρ₁=1，G₂/G₁=3，ρ₂/ρ₁=1，泊松比ν₁=ν₂=0.25.近场域采用有限元法模拟，离散范围为1×1，网格尺寸为0.125×0.125，单元类型为4节点四边形单元，为了同近场有限元网格协调，竖直截断边界采用两节点线单元离散.

为了验证时域耦合分析模型的计算精度，采用有限元扩展网格解作为参考解，其中有限元扩展网格模型的离散范围为60，下层地基中的P波在该范围内往返传播所需的无量纲时间为43.8.算例中，高阶双渐近透射边界的渐近阶数取M_H=M_L=4，为了验证移谱法能够保证时域分析的稳定性，分别采用移谱法与不采用移谱法的进行计算，并与黏性边界的计算结果进行对比.

考虑p(t)为图 5所示的三角脉冲荷载，在三角脉冲荷载作用下，A点的水平向位移和竖向位移响应曲线如图 6所示.

从图中可以看出，若不采用移谱法，时域耦合分析模型解很快发散，因此在时域分析中有必要采用移谱法消除导致高阶双渐近透射边界不稳定的虚假模态.黏性边界解与扩展网格解相差较大，并且在长时间的响应中很快衰减到零；时域耦合分析模型解与扩展网格解基本一致，在长时间的响应中仅伴随有微小的周期延长现象.从计算耗时上看，时域耦合分析模型耗时15.9 s，扩展网格模型耗时175.9 s，黏性边界模型耗时14.5 s，表明时域耦合分析模型与黏性边界模型相比，仍具有较高的计算效率，但极大地提高了计算精度.

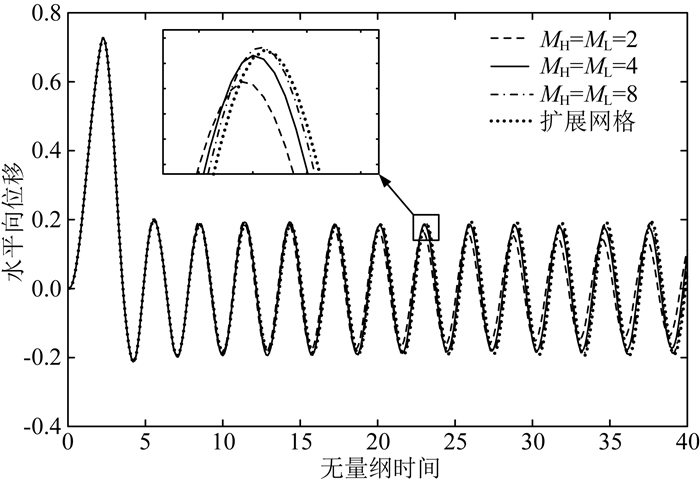
为了分析渐近阶数对高阶双渐近透射边界计算精度的影响，分别选取渐近阶数为M_H=M_L=2，M_H=M_L=4和M_H=M_L=8进行分析，并与有限元扩展网解进行对比.在三角脉冲荷载作用下，A点水平向位移响应如图 7所示.从图中可以看出，M_H=M_L=2的计算结果已经同扩展网格解吻合良好，但在长时间的响应中稍稍偏离参考解；随着渐渐阶数的增加，时域耦合分析模型解的精度进一步提高，M_H=M_L=4的计算结果与扩展网格解基本一致，因此在实际应用中，选取渐近阶数为M_H=M_L=4即可达到良好的计算精度.

4.2 重力坝算例

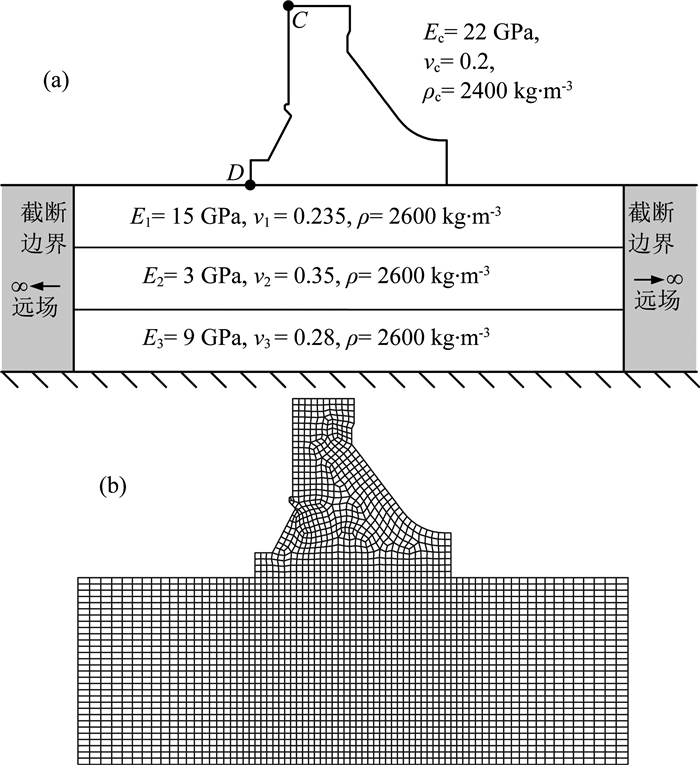
考虑图 8所示的重力坝-层状地基系统，其中重力坝坝高144 m，层状地基总高度150 m，分为3层，每层高度为50 m，近场层状地基向上游和下游方向各延伸150 m.坝体和层状地基材料参数如图 8a所示.近场有限元网格如图 8b所示，其中重力坝采用四节点平面应力单元离散，单元数565；层状地基采用四节点平面应变单元离散，单元数2310；模型节点总数2947.

为了验证的计算精度，采用有限元扩展网格解作为参考解，其中有限元扩展网格模型的离散范围为12000 m，顶层地基中的P波在该范围内往返传播所需的时间为10 s.重力坝算例中，高阶双渐近透射边界的渐近阶数取M_H=M_L=4，并与黏性边界的计算结果进行对比.

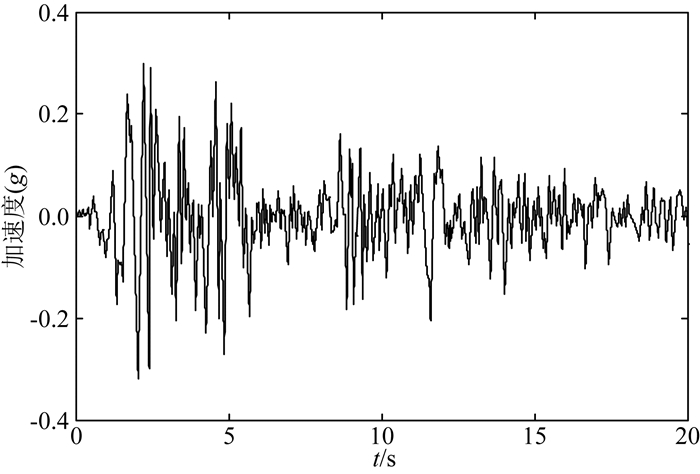
考虑顺河向El-Centro地震波从上游侧截断边界输入，层状地基底部为固定边界条件，地震波从层状地基底部到顶部呈三角形分布.将自由场地震波换算成等效节点荷载实现地震波输入，El-Centro地震波的加速度时程曲线如图 9所示.

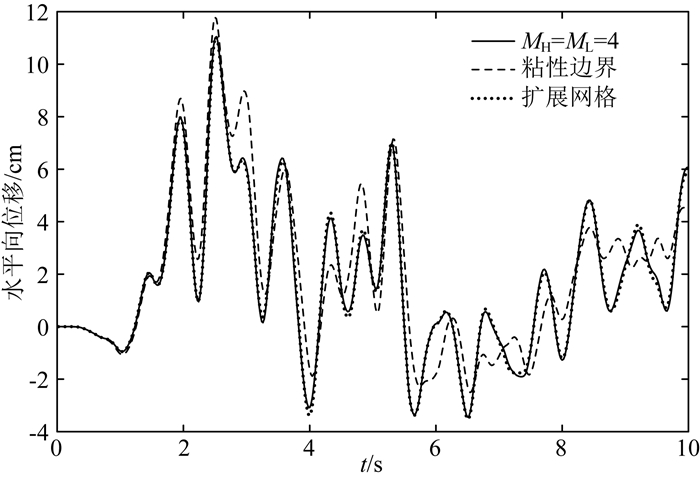
在顺河向El-Centro地震波作用下，C点(坝顶)和D点(坝踵)的水平向位移响应曲线分布如图 10所示.

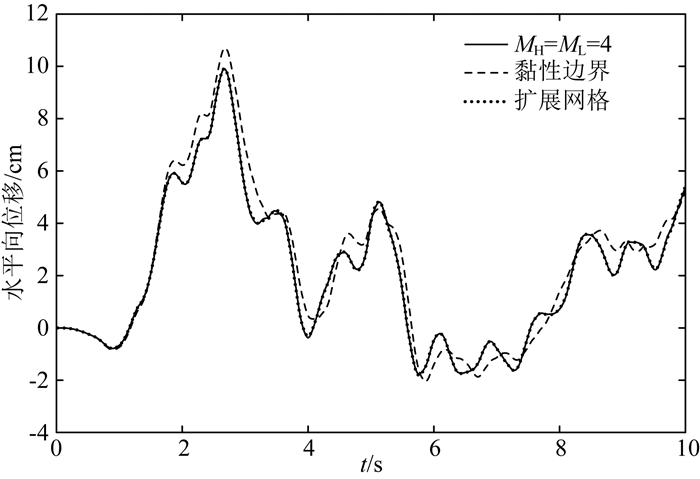
从图中可以看出，黏性边界解扩展网格解相差较大，时域耦合分析模型解与扩展网格解基本一致，重力坝算例同样表明本文提出的时域耦合分析模型具有很高的计算精度.从计算耗时上看，时域耦合分析模型耗时127.4 s，扩展网格模型耗时1487.3 s，黏性边界模型耗时121.4 s，同样表明时域耦合分析模型具有较高的计算效率.

5 结论

高阶双渐近透射边界能够在低频和高频范围内迅速地逼近准确解，具有良好的计算精度和计算效率.本文将层状介质矢量波高阶双渐近透射边界推广应用到多层层状地基系统弹性波传播的模拟，通过移谱法消除导致该透射边界时域计算不稳定的虚假模态.将该透射边界直接嵌入近场有限元方程，建立了有限元-高阶双渐近透射边界时域耦合分析模型，基于开源有限元软件OpenSees编程实现该时域耦合分析模型.两层层状地基算例、重力坝-层状地基算例分析表明，该耦合分析模型具有很高的计算精度和较高的计算效率，适用于长时间地震作用下的重力坝动力响应分析.