2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
所谓的SNREI地球模型是指球对称、非自转、完全弹性和各向同性的地球模型(Dahlen and Tromp, 1998).计算SNREI地球的准静态表面负荷变形的经典数值积分方法是由Longman(1962, 1963),Farrell(1972)等人提出的.在传统理论框架下,计算表面负荷变形的数值方法可以概述为以下三步:首先利用矢量球谐函数作为基函数,将三个二阶偏微分方程组转化为关于六个变量的一阶常微分方程组;然后在半径方向上采用单步积分法(如:四阶龙格库塔法等)得到三组独立解;最后利用表面边界条件确定三组独立解的系数(Longman, 1962, 1963;Farrell,1972).负荷勒夫数是一组表示表面负荷问题位移与引力位解的无量纲量,表面负荷问题最终的格林函数就由负荷勒夫数的加权求和得到.传统单步积分方法的缺陷主要在以下三个方面:(1)由于方程在球心处是奇异的,所以积分的起点需要设在一个事先给出的半径很小的小球表面上;(2)单步积分法的局部精度主要取决于积分步长的大小,然而步长太小会导致误差积累,从而使得全局误差增大;(3)传统方法在数值积分的过程中会出现“数值溢出”,因此需要进行归一化(Longman,1963).
理论力学中的哈密顿变分原理揭示了各种动力学过程中能量的守恒关系.基于动力学变分原理提出了许多数值方法,例如:伪谱法(Fornberg,1988)、有限元方法(Lysmer and Drake, 1972)和谱元法(Komatitsch and Tromp, 1999;Komatitsch, 2002a, 2002b)等.这些方法的数学原理是利用变分原理将偏微分方程的强解转化成Sobolev空间中积分方程的弱解,因此在解决间断问题以及脉冲响应问题上比传统数值积分方法具有更良好的性质.有限元方法的主要思路是在空间上对定义域进行网格划分,利用网格内的线性函数(或高阶多项式)作为基函数,最后利用各个基函数的数值积分求解积分方程.由于只有相邻的基函数之间存在相交的支集,因此有限元方法能够形成对角性好的刚度矩阵,从而具有较快的计算效率.并且由于网格划分灵活,有限元方法能够适用于复杂边界问题当中.然而对于均匀采样的高阶有限元,当解的光滑性不高时,其阶数的增加并不能促进解的收敛,某些时候还会出现“龙格现象”影响计算结果精度(Quarteroni,2009).与有限元方法不同,伪谱法则是采用一组以整个定义域为支集的正交函数作为基函数.与有限元方法相比,伪谱法具有解收敛速度快(指数收敛)的特点.谱元法可以看作有限元方法和伪谱法的结合,其基本思想是:首先将定义域剖分成互不相交的网格,然后在每个网格内利用高阶正交多项式作为基函数(如:Chebyshev多项式,Legendre多项式)进行内插.为了便于积分计算,常采用Gauss-Lobatto-Legendre(GLL)积分方法将函数积分转化为节点处的加权求和.因此,谱元法同时具有有限元方法和伪谱法二者的优点:网格剖分灵活,刚度矩阵为对角矩阵,收敛速度快.
Martinec(2000)针对SNREI地球表面负荷问题提出了一种谱方法(利用球谐函数作为基函数)与有限元方法组合的数值方法(Spectral-finite element approach,FEM).不同于标准谱元法(Spectral element method,SEM),他沿用传统简正模方法的思路:首先将方程的解在球面方向上利用球谐函数进行展开;然后在半径方向上采用有限元方法,在每个半径网格内利用线性样条函数作为基函数进行内插.在地震学谱元法数值计算中,对于重力一般采用Cowling近似,即忽略重力位变化对位移的影响,单纯地将重力场视作恒定的场(Chaljub et al., 2007);然而在Martinec的理论中则严格考虑了重力位的一阶扰动与位移的耦合.Tanaka等(2009, 2011)将Martinec的方法从不可压缩模型发展为可压缩模型.相较于一般有限元中将网格剖分为正四面体和正六面体的情形,Martinec的方法可以理解为将地球剖分为一个个具有厚度的球层.对于不考虑横向不均匀性、椭率以及地形起伏的分层地球模型而言,这种方法充分利用了不同阶次球谐函数之间相互解耦的性质,从而极大地减少了计算量.此外,当我们需要考虑地球模型的横向不均匀性时,Martinec(1989)提出了一种利用快速傅里叶变换(FFT)进行数值积分来解决该问题的方法.
然而,Martinec的方法只适用于固体介质.Chaljub等(2007)指出在液核中,由于缺少对偏应力的约束(μ=0),位移解将无法唯一确定.本文将借鉴Longman(1963)的方法,引入势函数χ=▽·u,并且假设液核初始模型满足Adams-Willianmson条件,从而推导出液核中平衡方程以及其对应的弱解.此外,由于谱元法具有收敛速度比有限元方法快的优良性质,本文将利用谱元法思想发展Martinec和Tanaka的方法:在径向网格内采用高阶拉格朗日多项式作为内插基函数,并利用Gauss-Lobatto-Legendre方法计算基函数的积分.
1 理论基础 1.1 问题的强形式按照Dahlen和Tromp(1998)的理论,假设SNREI地球初始应力状态为静水压力平衡状态.在微小变形的情形下,平衡方程中所有关于位移u一阶以上变分可以忽略不计.那么在欧拉参考系下,对于固体介质,变形后的动量平衡方程为(Dahlen and Tromp, 1998):

|
(1) |
其中ρ0为变形前的密度,ϕ0为变形前引力位,τ为变形后的拉格朗日参考系下的柯西应力张量(Lagrangian Cauchy stress,下简称“应力张量”)的一阶扰动.变形后的泊松方程为(Dahlen and Tromp, 1998):
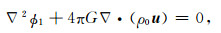
|
(2) |
其中ϕ1为变形后引力位的一阶扰动,G为万有引力常数.对于各向同性、线弹性地球而言,应力张量的一阶扰动本构关系为:

|
(3) |
其中Γ为胡克定律中的四阶弹性张量,λ和μ为拉梅系数,
在液体介质中,应力张量的一阶扰动可以表达为:

|
(4) |
如果假设外核为中性分层流体,那么它满足Adams-Willianmson条件(Longman,1963):
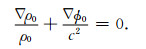
|
(5) |
在准静态问题中,这个条件是隐式包含于平衡方程(1)当中的(Longman 1963).引入势函数χ=▽·u,由(1)、(5)式可以得到关于位移u,势函数χ以及扰动位ϕ1的代数方程:

|
(6) |
然后将(6)式代入(2)式得到关于扰动位的二阶微分方程:

|
(7) |
负荷问题的边界条件见附录A中的(A1)—(A3)式.
1.2 问题的弱形式对于固体介质,按照Dahle和Tromp(1998)给出的修正拉格朗日密度:

|
(8a) |
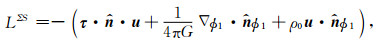
|
(8b) |
这里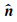
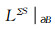

|
(9) |
这里上标中的+,-号分别代表表面∂B的外侧和内侧,σ为负荷质量.g0(a)为变形前地表重力,a为地球半径.
根据哈密顿变分原理,固体介质中的边值问题等价于一个最小值问题:
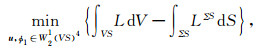
|
(10) |
其中,VS为固体介质部分;ΣS为地球表面∂B、内外核边界ΣICB和核幔边界ΣCMB的并集,W21(VS)4表示Sobolev空间的四次笛卡尔积.如果对(10)式中的位移和引力位扰动求变分,那么最小值问题(10)的驻点对应于边值问题的弱解(Martinec,2000):

|
(11) |
其中(δu, δϕ1)为测试函数,并且在(11)式中

|
对于液体介质,其弱解满足积分方程:
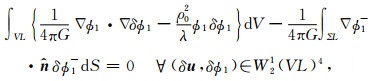
|
(12) |
其中VL为液体介质的定义域,ΣL为其边界.将(11)式和(12)式联立并利用(A1)—(A3)式代入其中,最终得到地球表面负荷问题的弱解为:
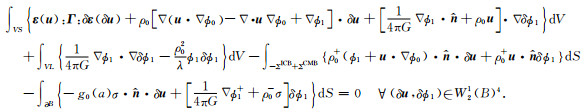
|
(13) |
在式(13)中对于边界上连续的物理量这里不用上标+,-号加以区分.
1.3 空间离散化广义伽辽金(Galerkin)方法的核心思想是将在分布意义上弱解对于任意测试函数在无限维函数空间W21(B)恒成立的问题,转化为在一组有限个基函数扩展成的有限维空间VN⊂W21(B)中寻找满足弱解的投影,并将它作为近似解(Canuto et al., 1988).
在Martinec(2000)谱-有限元方法中,第一步是将地球剖分成多个具有厚度的球层,在球面上对解函数(u, ϕ1)和测试函数(δu, δϕ1)利用球谐函数展开:
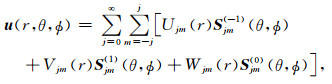
|
(14a) |
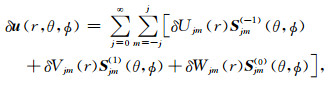
|
(14b) |

|
(14c) |
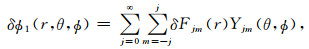
|
(14d) |
其中Yjm(θ, ϕ),Sjm(±1, 0)(θ, ϕ)分别为标量球谐函数和矢量球谐函数(Martinec,2000),r为半径,(θ, ϕ)为球面角.
第二步则是将展开系数中关于半径r的函数Ujm(r), Vjm(r), Wjm(r), Fjm(r)进行离散化.将半径剖分成互不相交的网格单元:
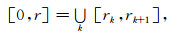
|
(15) |
然后,对每个网格单元中变量r∈[rk, rk+1]与参考变量ξ∈[-1, 1]进行坐标变换:
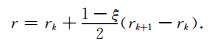
|
(16) |
在Martinec的方法中,每个网格内选用线性样条函数作为内插基函数.这也是经典一维有限元方法的一般做法.本文则选用5阶拉格朗日内插函数作为基函数(Gautschi,2012).为了便于积分计算,采用Gauss-Lobatto-Legendre(下面简称“GLL”)积分方法(Quarteroni,2009),具体的积分过程见附录B.这样关于半径r的任意函数都可以展开为:
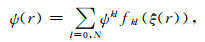
|
(17) |
其中fkl(ξ)的定义见附录B中式(B2).将(14)式和(17)式代入弱形式(13)中, 便可以得到关于系数U=(Ujmkl, Vjmkl, Wjmkl, Fjmkl)的线性方程组:

|
(18) |
其中K为刚度矩阵,U为待求解的系数,F为与非齐次边界条件有关的项.矩阵K的具体形式在附录C中给出.
相较于有限元方法,谱元法的优势在于其收敛速度快(呈指数关系).不妨令待求函数的真实值为u∈W21(Δr),其在N阶样条函数空间SN0(Δr)中的数值解为uδ,我们可以得到关于拟合误差的一个先验估计(Canuto et al., 2007):
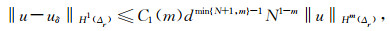
|
(19) |
其中m为待求函数的光滑度,d为最大网格间隔,C1(m)为与N、d无关的常数,此外‖‖H1(Δr), ‖‖Hm(Δr)为希尔伯特空间的范数.由(19)式可知,在待求函数光滑性m一定时,拟合误差随着子区间间隔d减小而呈代数衰减,随着截断阶数N的增加而呈现出指数衰减的特点.因此,在谱元法中我们通过增加截断阶数N,在同等自由度条件下可以获得比经典有限元方法(N=1)更高的精度.这一点在本文的2.1节中将通过数值实验进一步加以说明.
2 计算结果与分析 2.1 均质地球模型负荷勒夫数本节中,我们将正演模拟均质地球模型表面的负荷勒夫数.负荷勒夫数是负荷问题中地球表面位移解和重力位解各阶球谐展开系数的无量纲量,根据Farrell(1972)给出负荷勒夫数的定义,可以推导出如下关系:
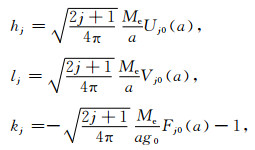
|
(20) |
其中Me为地球总质量.
Wu和Peltier(1982)给出了均质地球模型负荷问题的解析解,我们采用该文中的均质地球模型:密度为ρ=5517 kg·m-3,拉梅系数为μ=1.4519×1011N·m-2,λ=3.5288×1011N·m-2,地表重力为g0=9.82 m·s-2,地球半径为a=6.371×106m.利用不同数值方法计算均质地球模型的负荷勒夫数.然后通过相应数值解相对于解析解相对误差的大小来衡量这些数值方法精度的好坏.
对于内插多项式阶数为N的谱元法,在每个单元内其节点数是有限元方法的N倍.此外,其所形成的刚度矩阵的非零列数为(2N-1),我们可以近似地假设在网格单元数一样时计算量大小与N2成正比.那么我们可以定义一个经验参数——计算消耗指数(Index of computational cost, ICC)作为计算效率的衡量指标,
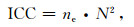
|
(21) |
其中ne为网格单元个数.对于有限元方法,其内插多项式阶数为1,则ICC等于网格单元数.通过比较相同ICC下不同数值方法的计算结果与解析解的相对误差,可以知道在相同内存消耗和计算时间下不同数值方法精度的优劣.下面我们分别采用Martinec的有限元方法(FEM),内插多项式阶数为1, 3, 5, 6的谱元法(SEM)计算上述均质地球模型的负荷勒夫数.然后将数值计算的结果hj与解析解hjana的相对误差取对数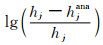
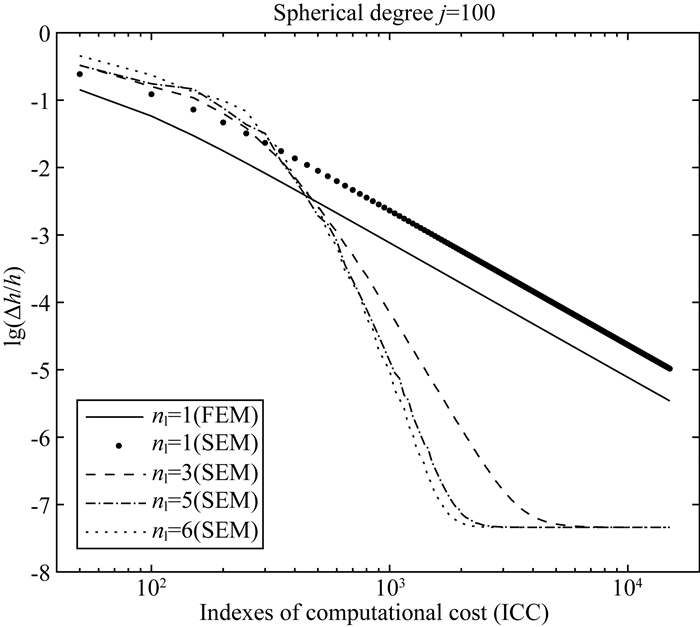
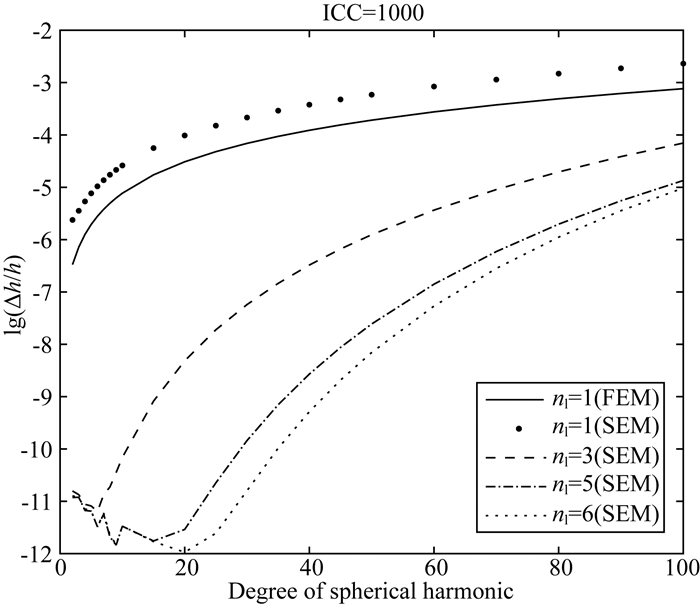
图 1展示了球谐函数阶数为100时,不同数值方法得到的负荷勒夫数的相对误差随计算消耗指数ICC变化的曲线.图 2则展示了当ICC等于1000时,不同数值方法在球谐函数阶数为0到100范围内的相对误差变化曲线.很容易看出,Martinec的有限元方法精度始终高于相同内插阶数(N=1)的谱元法.这是因为Martinec的有限元方法在数值积分时每个单元内都是准确解,而谱元法在每个单元积分时采用的Gauss-Lobatto-Legendre积分是一种近似积分(Maday and Rønquiust, 1990),其精确度(2N-1)小于被积函数的阶数(2N).
|
图 1 在球谐函数阶数为100时,有限元方法(FEM)以及内插多项式阶数分别为1, 3, 5, 6的谱元法的计算精度随计算消耗指数ICC变化的关系 纵轴为数值结果与解析解相对误差的对数. Fig. 1 The relation between the precision and the Index of computational cost (ICC) for Martinec′s finite element method (FEM) and spectral element methods (SEM) with interpolation order of 1, 3, 5 and 6 at spherical harmonic degree of 100 The vertical coordinate denotes the logarithm of numerical results′ relative error in contrast with analytical solutions. |
|
图 2 在ICC为1000时,球谐函数阶数为0到100的有限元方法(FEM)以及内插多项式阶数分别为1, 3, 5, 6的谱元法的相对误差的对数 Fig. 2 The logarithm of numerical results′ relative error in contrast with analytical solutions for Martinec′s finite element method (FEM) and spectral element method (SEM) with interpolation order of 1, 3, 5 and 6 at spherical harmonic degree ranging from 0 to 100 in the case of ICC=1000 |
但是,在网格数目足够的情况下高阶谱元法的计算精度远远高于Martinec的有限元方法.例如图 2中在ICC=1000时,在100阶以内有限元方法的相对误差仅为1×10-5量级左右,而内插多项式阶数为5的谱元法的相对误差为1×10-6~1×10-12.需要注意的是如同公式(19)所反映的那样,高阶谱元方法精度随网格数目的增加而收敛,其收敛速度远高于有限元方法.但是在网格数目不足的情况下,由于高阶谱元法计算内存和时间开销更大,因此在相同的ICC下其计算精度可能不如有限元方法.具体哪种方法更优取决于使用者在计算精度需求和计算效率之间的权衡与取舍.
此外,如果进一步考虑解在半径方向的变化特征,采用不均匀的自适应网格划分也能够有效提高数值收敛速度(Gautschi, 2012).负荷问题的平衡方程属于一类“扩散-输运-反应方程”.这类方程的特点是解在边界层(地表)附近变化较大(Quarteroni, 2009).因此我们采用在靠近地表的部分布设较细网格的策略,可以有效提高计算高阶负荷勒夫数时数值解的收敛速度.
2.2 PREM模型的负荷勒夫数本小节我们将根据Dziewonski和Anderson(1981)给出的PREM模型,计算负荷勒夫数.在每个网格区间r∈[rk, rk+1]内的GLL节点上,按照PREM模型给出的拟合多项式计算相关物性参数.对于PREM模型中的海水层(r=6368~6371 km),按照汪汉胜等(1996)的处理方法,将其与地壳(r=6356~6368 km)看作均一弹性层,密度取ρ=2283.4 kg·m-3,Lame常数取地壳中的值μ=26.624 GPa, λ=34.216 GPa;引力常量取G=6.67259×10-11m3/(kg·s2).
图 3中实线为利用谱元法(SEM)计算的1到1000阶负荷勒夫数,虚线为利用龙格-库塔(Runge-Kutta)积分法(汪汉胜等,1996)得到的计算结果.通过比较可以发现二者的相对误差在0.01%的量级.附录D给出了利用谱元法计算的各阶负荷勒夫数供读者参考.在传统的龙格-库塔法中,即便采用了归一化方法,由于随着阶数的增加,不同线性独立解之间线性相关性变大,从而导致系数方程趋于病态从而产生“数值溢出”的情况.然而如附表D1中可见,谱元法在高于10000阶时仍能得到稳定的结果.

|
图 3 (a)(b)(c)分别表示PREM模型负荷勒夫数hj,jlj,jkj 其中横坐标为阶数j,点线为龙格-库塔方法(汪汉胜等,1996)计算结果,实线为本文谱元法计算结果. Fig. 3 (a) (b) (c) respectively depict the load Love numbers hj, jlj, jkj of the PREM earth The horizontal axes denote the angular degree j. The dotted lines represent the results of Runge-Kutta method (Wang et al., 1996), and the solid lines are obtained by the SEM of this study. |
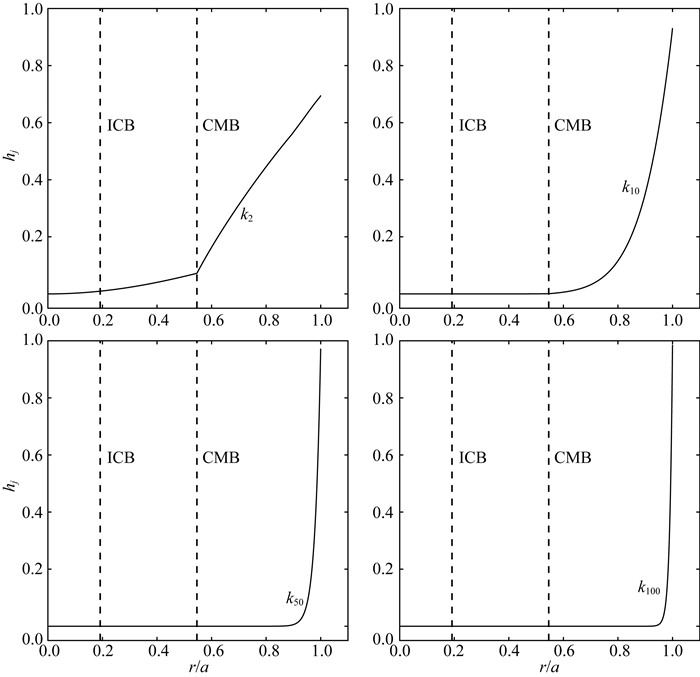
此外,利用谱元法我们可以给出PREM模型负荷勒夫数随半径变化情况.图 4—6展示了PREM模型2、10、50和100阶负荷勒夫数随地球半径的变化.由式(6)(7)可知在液态外核中,我们只能确定扰动位ϕ1,以及一个关于χ和径向位移ur的线性组合的值.由于缺少对偏应力的约束,无法唯一确定液核中的切向位移,也就无法唯一确定它的径向位移.因此在图 4中我们并未给出液核中的表征径向位移和切向位移的负荷勒夫数hj和lj.

|
图 4 负荷勒夫数hj随半径的变化 横坐标为半径的无量纲量(r/a,a为地球半径),纵坐标为负荷勒夫数hj.其球谐函数阶数分别为2, 10, 50, 100. Fig. 4 The variation of load Love numbers hj of different angular degrees over radius The horizontal axes denote the dimensionless radius (r/a, where a is the radius of the Earth), and the vertical axes denote the load Love numbers hj. The angular degrees are 2, 10, 50 and 100. |

|
图 5 负荷勒夫数lj随半径的变化 Fig. 5 The variation of load Love numbers lj of different angular degrees over radius |
|
图 6 负荷勒夫数kj-1随半径的变化 Fig. 6 The variation of load Love numbers kj-1 of different angular degrees over radius |
在图 4—6中可见,低阶球谐函数情况下位移和引力位扰动随深度衰减较慢,而高阶情况下它们随深度衰减较快.由(11)—(16)式可知,低阶情况下的拉格朗日函数
本文利用Dahlen和Tromp(1998)给出的固体介质中一阶微扰平衡方程以及哈密顿变分原理,推导了谱元法计算负荷边值问题的相关理论公式,并且给出了中性分层液体介质中边值问题的弱解.此外我们在Martinec(2000)和Tanaka等(2009, 2011)的谱-有限元方法基础上进行改进,给出了一种在地球径向上以高阶拉格朗日函数作为基函数的谱元法.在一个均质地球模型的算例中,通过比较两种数值方法(Martinec有限元方法与谱元法)与解析解结果的差异,从而证明了本文中所采用的谱元法具有更快的收敛速度.我们计算了PREM模型的负荷Love数,计算结果与汪汉胜等(1996)的龙格-库塔积分法计算结果相比较,相对误差量级为0.01%.此外,谱元法有效解决了偏微分方程在球心处的奇异性问题,并且在10000阶以上时计算结果仍然十分稳定.
从理论力学的角度来说,谱元法是一种利用哈密顿变分原理求解力学问题的方法,因此它具有更深刻的力学背景(Arnold, 1989);从数学分析的角度来说,它是通过数值方法求解二阶偏微分方程在Sobolev空间中弱解的方法,因此在解决间断问题和脉冲响应问题上更具有充分的数学意义(Brezis, 2011);从数值近似的角度来说,它是广义Galerkin方法的应用,结合了谱方法和有限元方法的优点,具有更高的计算效率(Quarteroni, 2009).基于本文弹性变形问题的理论框架,我们可以将其扩展到其他动力学问题(地震波正演、简正模计算、冰后回弹以及震后形变等等).本文的研究结果可以为今后复杂地球动力学数值模拟问题提供参考.
附录A 表面负荷问题的边界条件在地球内部固体-固体边界上,其连续性边界条件为:

|
(A1a) |

|
(A1b) |

|
(A1c) |

|
(A1d) |
在内部液体-固体边界上,其连续性边界条件为:
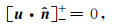
|
(A2a) |
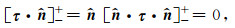
|
(A2b) |

|
(A2c) |

|
(A2d) |
对于表面负荷问题,在地球表面∂B上其边界条件为(Longman,1962; Farrell,1972):
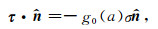
|
(A3a) |

|
(A3b) |
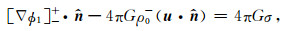
|
(A3c) |
其中+、-号分别代表界面两侧,
在参考变量网格ξ∈[-1, 1]内,选取方程

|
(B1) |
的根ξi(i=0~N)作为GLL控制点,这里P′N(ξ)代表N阶勒让德多项式的一阶导数.然后,选取GGL控制点的拉格朗日多项式作为参考变量网格ξ∈[-1, 1]内的正交基函数fkl(ξ):

|
(B2) |
于是,对于任意(小于或等于)N阶多项式函数ψ(r)∈

|
(B3) |
那么其积分可以表达为

|
(B4) |
其中
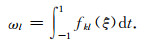
|
(B5) |
在地心处,由于附录C中式(C3g)中积分Iαβ(7)会出现奇异值,因此在球心处第一个网格内我们采用定义域为左开右闭的Gauss-Radau积分方法(Guo et al., 2001),选取

|
(B6) |
的根作为控制点,拉格朗日内插函数以及相应权值的计算如式(B2)(B5)所示.由于此时不在网格左端球心处选取节点,从而也就避免了数值积分的奇异性.
附录C 刚度矩阵K采用5阶GLL积分,可以将(14)式中关于半径r的函数表达为:
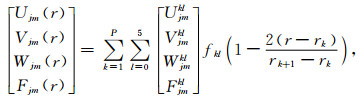
|
(C1a) |

|
(C1b) |
其中k为格网编号,P为格网总数,l为该格网内拉格朗日函数的编号,rk和rk+1分别为第k个格网起点和终点的半径.
由Martinec(2000)一文中的式(80)至(83),更正了其文中的部分笔误,以及结合Tanaka(2011)的式(12)得到:

|
(C2a) |
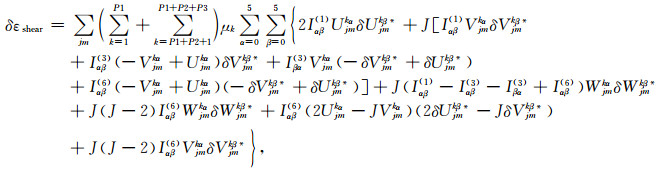
|
(C2b) |
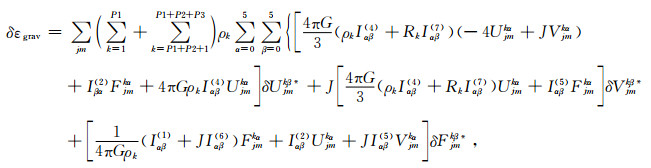
|
(C2c) |

|
(C2d) |

|
(C2e) |

|
(C2f) |

|
(C2g) |
其中J=j(j+1),星号*代表共轭,P1、P2、P3分别代表内核、外核和地幔的总层数,μk, λk, ρk分别为Lame系数以及密度在第k个格网内的取值.rCMB, ρCMB, gCMB分别代表核幔边界上的半径、密度和重力; rICB, ρICB, gICB分别代表内外核边界上的半径、密度和重力.
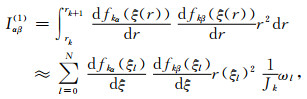
|
(C3a) |
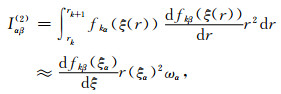
|
(C3b) |
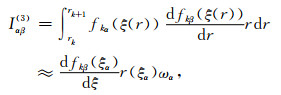
|
(C3c) |
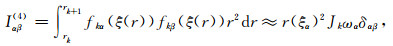
|
(C3d) |

|
(C3e) |
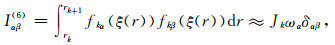
|
(C3f) |

|
(C3g) |

|
这里δαβ为Kronecker符号.
将(C1)、(C2)、(C3)式代入(13)式中可得:

|
(C4) |
分别令测试函数的某个分量为1,其他分量为0,可以得到关于系数的线性方程组(18).
附录D|
|
附表 D1 PREM模型表面负荷勒夫数 Appendix Table D1 The load Love numbers of PREM model |
Arnold V I. 1989. Mathematical Methods of Classical Mechanics. New York: Springer.
|
Brezis H. 2011. Functional Analysis, Sobolev Spaces and Partial Differential Equations. New York: Springer.
|
Canuto C, Hussaini M Y, Quarteroni A, et al. 1988. Spectral Methods in Fluid Dynamics. Berlin Heidelberg: Springer.
|
Canuto C, Hussaini M Y, Quarteroni A, et al. 2007. Spectral Methods:Evolution to Complex Geometries and Applications to Fluid Dynamics. Berlin Heidelberg: Springer-Verlag.
|
Chaljub E, Komatitsch D, Vilotte J P, et al. 2007. Spectral-element analysis in seismology. Advances in Geophysics, 48: 365-419. DOI:10.1016/S0065-2687(06)48007-9 |
Dahlen F A, Tromp J. 1998. Theoretical Global Seismology. Princeton: Princeton University Press.
|
Dziewonski A M, Anderson D L. 1981. Preliminary reference earth model. Physics of the Earth and Planetary Interiors, 25(4): 297-356. DOI:10.1016/0031-9201(81)90046-7 |
Farrell W E. 1972. Deformation of the earth by surface loads. Reviews of Geophysics, 10(3): 761-797. DOI:10.1029/RG010i003p00761 |
Fornberg B. 1988. The pseudospectral method:Accurate representation of interfaces in elastic wave calculations. Geophysics, 53(5): 625-637. DOI:10.1190/1.1442497 |
Gautschi W. 2012. Numerical Analysis. Basel: Birkhäuser.
|
Guo J Y, Ning J S, Zhang F P. 2001. Chebyshev-collocation method applied to solve ODEs in geophysics singular at the Earth center. Geophysical Research Letters, 28(15): 3027-3030. DOI:10.1029/2001GL012886 |
Guo J Y, Li Y B, Deng H T, et al. 2004. Green's function of the deformation of the Earth as a result of atmospheric loading. Geophysical Journal International, 159(1): 53-68. DOI:10.1111/j.1365-246X.2004.02410.x |
Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139(3): 806-822. DOI:10.1046/j.1365-246x.1999.00967.x |
Komatitsch D, Tromp J. 2002a. Spectral-element simulations of global seismic wave propagation-Ⅰ. validation. Geophysical Journal International, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x |
Komatitsch D, Tromp J. 2002b. Spectral-element simulations of global seismic wave propagation-Ⅱ. three-dimensional models, oceans, rotation and self-gravitation. Geophysical Journal International, 150(1): 303-318. DOI:10.1046/j.1365-246X.2002.01716.x |
Longman I M. 1962. A Green's function for determining the deformation of the earth under surface mass loads-Ⅰ. theory. Journal of Geophysical Research, 67(2): 845-850. DOI:10.1029/JZ067i002p00845 |
Longman I M. 1963. A Green's function for determining the deformation of the earth under surface mass loads-2. computations and numerical results. Journal of Geophysical Research, 68(2): 485-495. DOI:10.1029/JZ068i002p00485 |
Lysmer J, Drake L A. 1972. A finite element method for seismology. Methods in Computational Physics:Advances in Research and Applications, 11: 181-216. DOI:10.1016/B978-0-12-460811-5.50009-X |
Maday Y, Rønquist E M. 1990. Optimal error analysis of spectral methods with emphasis on non-constant coefficients and deformed geometries. Computer Methods in Applied Mechanics and Engineering, 80(1-3): 91-115. DOI:10.1016/0045-7825(90)90016-F |
Martinec Z. 1989. Program to calculate the spectral harmonic expansion coefficients of the two scalar fields product. Computer Physics Communications, 54(1): 177-182. DOI:10.1016/0010-4655(89)90043-X |
Martinec Z. 2000. Spectral-finite element approach to three-dimensional viscoelastic relaxation in a spherical earth. Geophysical Journal International, 142(1): 117-141. DOI:10.1046/j.1365-246x.2000.00138.x |
Okubo S. 1988. Asymptotic solutions to the static deformation of the earth-Ⅰ. Spheroidal mode. Geophysical Journal International, 92(1): 39-51. DOI:10.1111/j.1365-246X.1988.tb01119.x |
Quarteroni A. 2009. Numerical Models for Differential Problems. Mailand: Springer-Verlag.
|
Tanaka Y, Klemann V, Fleming K, et al. 2009. Spectral finite element approach to postseismic deformation in a viscoelastic self-gravitating spherical earth. Geophysical Journal International, 176(3): 715-739. DOI:10.1111/j.1365-246X.2008.04015.x |
Tanaka Y, Klemann V, Martinec Z, et al. 2011. Spectral-finite element approach to viscoelastic relaxation in a spherical compressible earth:Application to GIA modelling. Geophysical Journal International, 184(1): 220-234. DOI:10.1111/j.1365-246X.2010.04854.x |
Wang H S, Xu H Z, Li G Y. 1996. Improvement of computations of load Love numbers of SNREI Earth model. Chinese Journal of Geophysics (Acta Geophysica Sinica) (in Chinese), 39(S1): 182-189. |
Wu P, Peltier W R. 1982. Viscous gravitational relaxation. Geophysical Journal International, 70(2): 435-485. DOI:10.1111/j.1365-246X.1982.tb04976.x |
汪汉胜, 许厚泽, 李国营. 1996. SNREI地球模型负荷勒夫数数值计算的新进展. 地球物理学报, 39(S1): 182-189. |
 2019, Vol. 62
2019, Vol. 62

