速度模型的平滑处理对于射线类偏移成像来说有着至关重要的意义(韩复兴等,2011; Gao et al., 2017; Yuan et al., 2017).由于射线类偏移成像采用高频近似的几何射线理论来计算整个地震波场的走时、相位和振幅信息,在实现偏移成像的过程当中,需要求解运动学和动力学射线追踪系统,而在计算的过程当中,为了满足高频近似理论,同时为了满足射线追踪系统的需求,成像空间的速度模型需要满足二阶导数的连续性,而实际处理过程当中的速度模型往往比较复杂,具有许多不连续的速度突变、断面和不同程度的速度梯度,而且横纵向变化不定,无法满足射线追踪系统对模型的需求.为了满足射线类偏移成像对模型的需求,需要对速度模型进行相应的处理,而目前对速度模型的平滑处理都会在一定的程度上改变原有速度模型的空间结构,从而造成成像结果在一定程度上的失真(韩复兴,2009).
如何能够在不破坏原始模型空间结构的前提下实现速度模型的平滑处理来满足射线追踪系统以及高频近似的需求,很多学者做了大量的研究工作(Lailly and Sinoquet, 1996; Gray, 2000; Pacheco and Larner, 2000; 韩复兴等,2011;石秀林等,2016;Gao et al., 2017),同时也证明了速度模型的平滑处理对射线类偏移成像的作用.本研究在前人工作的基础上引入基于速度模型梯度的偏微分方程处理技术来实现速度模型的平滑处理.将偏微分方程应用于数字图像处理可以追溯到1965年Gabor利用反热传导方程进行图像增强(Gabor, 1965).然而真正具有奠基意义的工作是1983年Witkin提出了尺度空间的概念,他将原始图像与不同尺度t的高斯函数卷积所得到的图像序列称为一个尺度空间(Witkin, 1983).1980年,Hummel注意到热传导方程并不是唯一的可以用来构成尺度空间的抛物型方程,他说明了所有满足最大值准则的发展方程都可以定义一个尺度空间(Hummel, 1980).在Hummel的思想指导下,1990年Perona和Malik提出了基于非线性偏微分方程的图像平滑模型(Perona and Malik, 1990),这一模型将各向同性的热传导方程替换为各向异性的偏微分方程,在图像的不同位置实行不同的平滑策略,从而对特征边缘达到了一定的保持作用.该平滑模型根据以下三个准则:因果性(即当尺度由小变大时,不产生新的细节)、即时定位(即在所有尺度上,区域内部要优于区域之间进行平滑)和分段平滑(即在每个尺度上,区域内部的平滑应该优于区域之间的平滑)来实现对速度模型的平滑处理.这三个准则成为了后来利用非线性偏微分方程进行图像平滑的基本准则(丁畅等, 2013; Lopez-Molina et al., 2014; 陈龙, 2015).根据这三个基本准则,在尽可能不破坏原速度模型空间结构的前提下,本研究将从能量泛函的角度着手,基于速度梯度,采用最速下降法推导了基于偏微分方程的速度模型平滑公式.引入控制扩散速度的函数g(x, z, t)实现速度模型的平滑处理,x、z为空间坐标,t为迭代次数,该函数具有这样的功能,即在速度模型的边缘处(速度模型的主要特征),由于模型速度的梯度很大,这时函数应使得扩散速度很慢;而当在模型的非边缘区域中时,模型的速度梯度不大,函数应使得扩散速度很快.该平滑模型以梯度作为自变量构造这个控制速度的函数实现速度模型的光滑处理.
1 基于偏微分方程的速度模型平滑处理算法偏微分方程是借助于物理学中动力学所描述的热扩散过程,以此解释偏微分方程对图像的平滑过程,因此最早的平滑模型借用了热传导方程, 其形式为
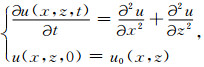
|
(1) |
其中u(x, z, t)为变化过程中的图像,原始图像u0(x, z)为初始条件.偏微分方程的解u(x, z, t)即给出了迭代t次时的图像.在图像的平滑、增强、分割、跟踪和分类等图像处理许多领域中,都可以利用变分方法原理把需要解决的问题转化成某个泛函的最优化问题(姜礼尚和边保军, 2012).变分原理的根本就是将一个物理学或其他学科的科学问题用变分法转化为求解泛函驻值或极值的问题,因此所谓的变分原理就是在一个给定的函数类内求特定泛函的极值,称为求泛函极值的问题为变分问题.而Euler-Lagrange方程是泛函极值条件的微分表达式,求解能量泛函对应的Euler-Lagrange与泛函求极值是等价的.在此基础上根据需要求解的问题,就可以先构建待处理问题的泛函及其约束条件,将求解问题转化为一个泛函最小化问题;然后利用变分法基本原理求泛函对应的Euler-Lagrange方程,引入时间变量t,利用最速下降法获得一个偏微分方程,根据问题初始条件,求解满足约束条件和边界条件的微分方程即可得到所要求解问题的结果.
对于射线类偏移成像当中的速度模型光滑处理问题,采用变分法导出基于速度梯度平滑的偏微分方程模型,其过程如下:
考虑式(2)的能量函数(杨新, 2003),即:
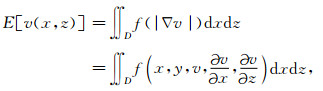
|
(2) |
其中D为速度模型的大小,f(·)≥0为递增函数.在速度模型横向和纵向变化比较剧烈的区域,速度梯度的模就越大,因此,要达到图像平滑的目的就要最小化能量函数E(v).下面用变分方法来求解这个能量极小化问题:
假设上式的极限值为v(x, z),设v(x, z, ε)=v(x, z)+εδv,函数极值在ε=0处取得,即:
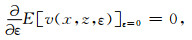
|
(3) |
公式(2)化为
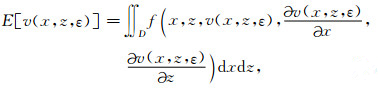
|
(4a) |
令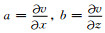

|
(4b) |
将式(4b)及v(x, z, ε)=v(x, z)+εδv代入(4a)式得:
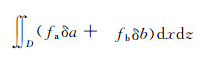
|
(5) |
公式(5)变分为

|
(6a) |
而:

|
(6b) |
将式(6b)代入泛函变分(6a)的第二项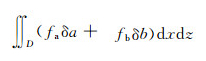

|
(7) |
根据格林公式:
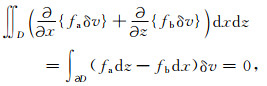
|
(8) |
因此(7)式变为
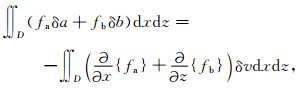
|
(9) |
将(9)式代入(6)式得到:
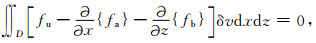
|
(10) |
根据(10)式得到:

|
(11) |
(11) 式即为Euler-Lagrange方程.
对能量泛函的极值的求解可以通过泛函对应的Euler-Lagrange方程求得,然而通常状态下Euler-Lagrange方程是非线性的偏微分方程,通常难以计算,可以通过引入时间变量,使得静态的偏微分方程转化为动态的偏微分方程,当方程达到稳定时就可以得到能量泛函Euler-Lagrange方程的解,即为梯度下降法.根据梯度下降的思想,就可以选择一个合适的v0(x, z),根据时间的迭代进行计算,直到v(x, z)获得稳定的解为止,此时:

|
(12) |
又因为:

|
(13) |
因此:

|
(14) |
即:
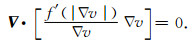
|
(15) |
根据梯度下降可得:
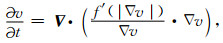
|
(16) |
令
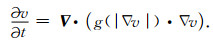
|
(17) |
扩散系数表达式为
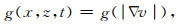
|
(18) |
其中g(s)是单调递减函数,g(0)=1,
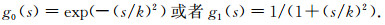
|
(19) |
式中,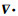
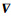


|
图 1 速度模型平滑系数g(s)的示意图 Fig. 1 Sketch of smoothing coefficient for velocity model |
式(17)即为速度模型平滑处理的偏微分方程表示形式,t是人为引入的一个时间维度,表示速度模型的平滑过程.将上边的公式进行离散化以及选择合理的系数分布函数g(| 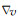

|
图 2 偏微分方程离散格式示意图 Fig. 2 Schematic diagram of discrete scheme for partial differential equation |
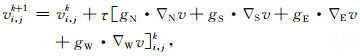
|
(20) |
其中N、S、E、W分别为各个方向North、South、East、West的简写,τ为时间步长,这里的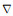
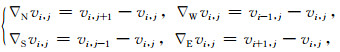
|
(21) |

|
(22) |
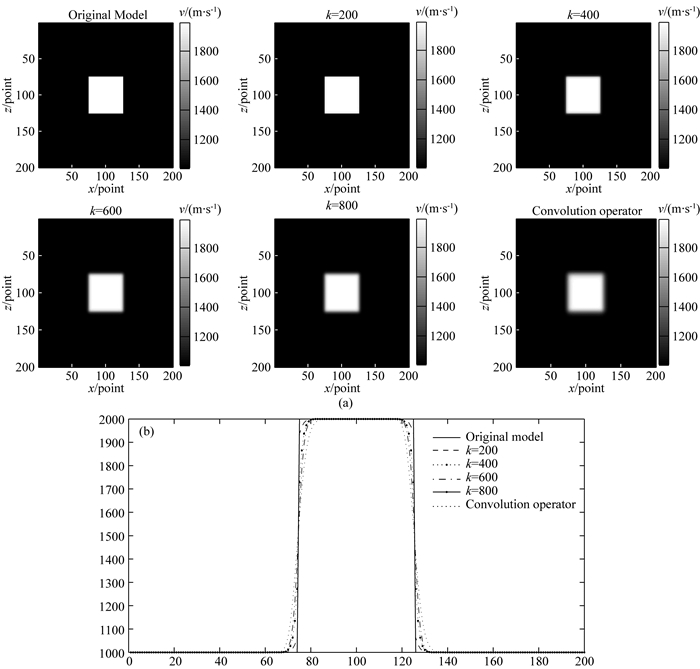
下面以简单的高速体速度模型为例,说明基于偏微分方程的光滑处理对原始速度模型空间结构的影响.速度模型大小200×200,网格间距为1 m×1 m,背景速度v0=1000 m·s-1,高速体速度v1=2000 m·s-1,取dt=0.05,阈值k分别取200、400、600、800时应用PDE算法对原始速度模型迭代处理30次后的速度模型以及应用卷积算子横向和纵向和平滑15次后的速度模型如图 3所示.
|
图 3 PDE模型平滑处理算法、卷积算子对原始速度模型空间结构的影响 (a)原始速度模型及光滑处理后的速度模型;(b)不同k值平滑处理后的速度模型、卷积算子平滑处理后的速度模型与原始速度速度模型空间相对分布. Fig. 3 Influence of PDE smoothing algorithm and convolution operator on the spatial structure of the original velocity model (a) Original and smoothed velocity model using PDE algorithm and convolution operator; (b) Spatial relative distribution of original velocity model and smoothed model after smoothing using different k values and convolution operators. |
通过应用PDE算法对简单的高速体速度模型的光滑处理分析可以看出,在同样平滑次数的前提条件下,随着k取值的增加,PDE算法对速度模型平滑的尺度在逐渐增加,当k取值800时,PDE算法对速度模型的平滑还不到应用卷积类算子对原始速度模型横向和纵向分别平滑15次的结果,通过对比分析,可以根据实际需要采用不同的k值对速度模型进行平滑处理已达到预期的效果.
下面再从射线路径以及时间场的分布来分析偏微分方程模型平滑处理对原始速度模型的影响.如图 4所示,选取k=400处理后的速度模型和应用卷积算子横向和纵向各平滑15次后的速度模型分别计算射线路径和时间场分布.通过射线路径以及时间场的分布可以看出,在满足射线追踪需求的前提条件下,应用偏微分方程处理后的速度模型的时间场比原始速度模型时间场的误差更小,而且随着k取值的减小,应用偏微分对模型进行平滑处理后所得时间场的误差也在逐渐减小.

|
图 4 速度模型射线路径和时间场误差分布图 (a) k=400 PDE处理后的所得的射线路径; (b)卷积算子横纵向平滑15次后所得射线路径; (c) k=400PDE处理后的时间场误差; (d)卷积算子横纵向平滑15次后时间场误差. Fig. 4 Ray paths and time field error distribution of velocity model (a) The ray path after the partial differential equation is processed (k=400); (b) The ray path after smoothing 15 times by the convolution operator; (c) Time field error after partial differential equation processing (k=400); (d) Time field error of convolution operator after smoothing 15 times. |
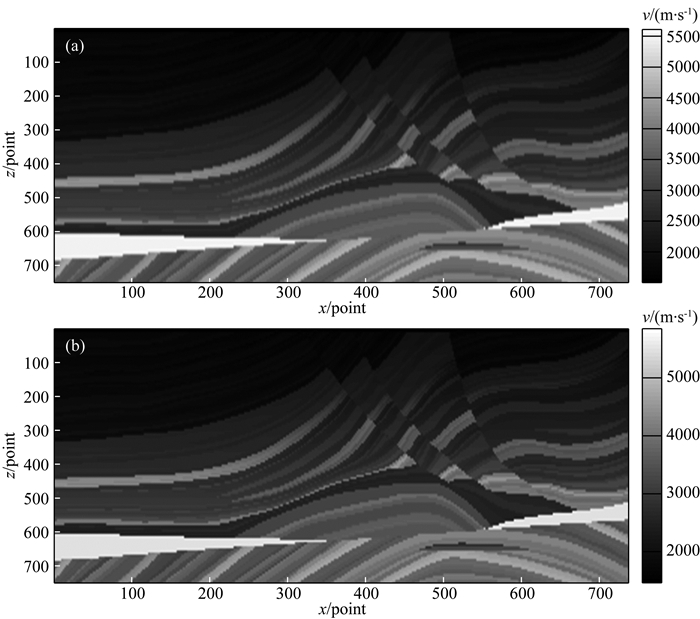
下面以横向纵向速度变化复杂的Marmousi速度模型为例,说明PDE算法在偏移成像速度模型平滑中的对成像的影响作用.Marmousi模型大小为737×750,网格间距为12.5 m×4 m,速度变化从1500 m·s-1到5500 m·s-1,原始速度模型以及应用PDE光滑处理30次后的速度模型如图 5所示.基于Marmousi速度模型模拟的合成数据体由240炮右边放炮方式的地震记录组成.第一炮点的位置为3000 m(240点位处),最后一个炮点的位置为8975 m(718点位处),炮间距为25 m.最小炮检距为200 m,最大炮检距为2575 m,道间距为25 m,道数为96道,时间采样点个数为750,采样间隔为4 ms.
|
图 5 原始速度模型以及应用PDE光滑处理30次后的速度模型 (a)原始Marmousi速度模型; (b) PDE算法光滑处理后的Marmousi速度模型(t=30). Fig. 5 Original and smoothed velocity model using PDE algorithm (t=30) (a) The original Marmousi velocity model; (b) Smoothed velocity model using PDE algorithm (t=30). |
分别在原始Marmousi速度模型以及采用偏微分方程对速度模型进行平滑处理后的模型上进行偏移成像,结果如图 6所示.

|
图 6 原始Marmousi速度模型偏移结果(a)和PDE光滑处理30次后Marmousi模型偏移结果(b) Fig. 6 Migration imaging results of the original (a) and smoothed Marmousi model using PDE algorithm (t=30) (b) |
通过图 6的成像结果可以看出,对于横向和纵向速度变化剧烈的Marmousi模型,PDE对速度模型平滑处理后所获得成像结果其层位清晰可见, 尤其是在速度模型底部,光滑处理后模型所获得成像效果要远远优于原始速度模型的成像效果.
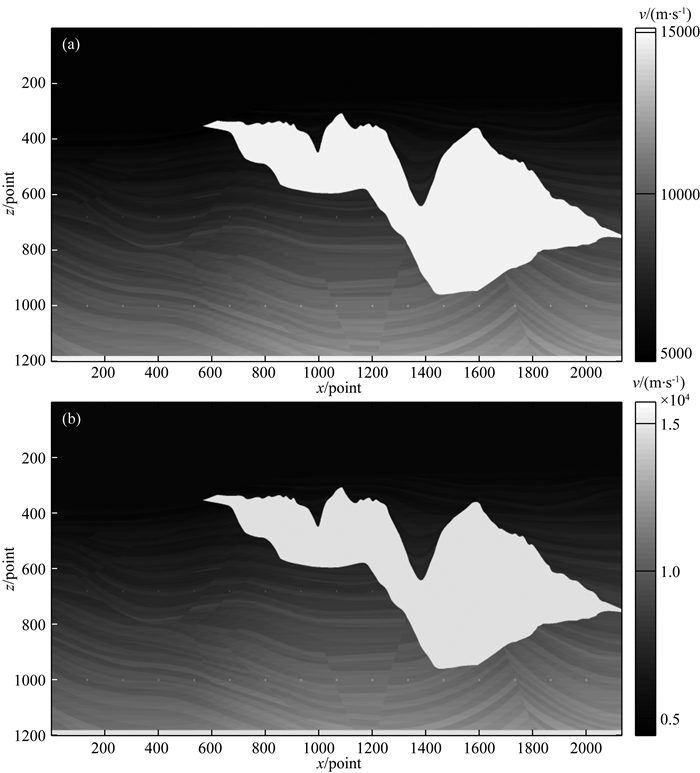
3.2 Sigsbee 2A速度模型平滑前后成像结果Sigsbee 2A速度模型网格大小为2133×1201,网格间距为37.5 m×25.0 m,地震记录共有500炮,每炮对应的接收道数并不完全相同.每道有1500个采样点,采样间隔为8 ms.Sigsbee 2A速度模型在浅层速度变化缓慢,深部较为复杂,除了含有一个又大又复杂的高速体,还包含多个断层,同时还有两列整齐的反射点.原始速度模型及应用PDE平滑处理后的速度模型如图 7所示.
|
图 7 原始Sigsbee 2a速度模型偏移结果(a)和PDE光滑处理30次后Sigsbee 2A模型偏移结果(b) Fig. 7 Migration results of original (a) and smoothed Sigsbee 2A velocity model using PDE algorithm (t=30) (b) |
分别在原始Sigsbee 2A速度模型以及采用偏微分方程对速度模型进行平滑处理后的模型上进行偏移成像,结果如图 8所示.
|
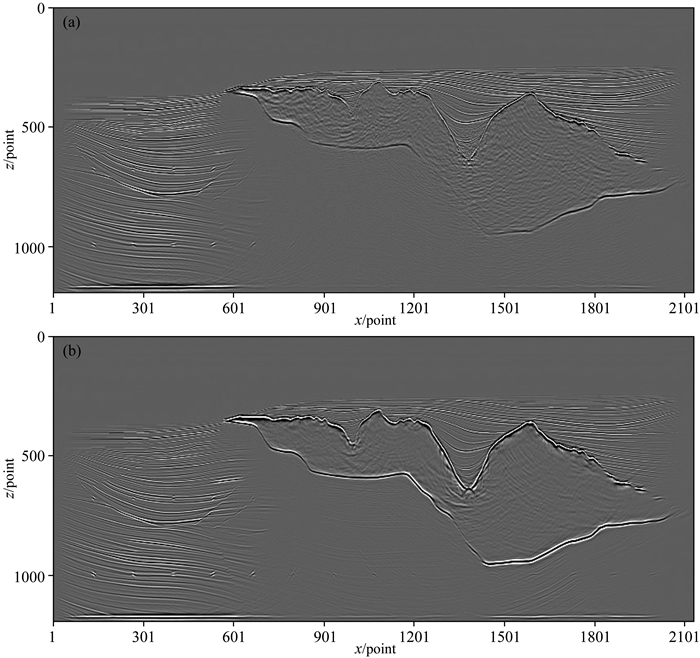
图 8 原始Sigsbee 2A速度模型偏移结果(a)和PDE光滑处理30次后Sigsbee 2A模型偏移结果(b) Fig. 8 Migration imaging results of the original (a) and smoothed Sigsbee 2A velocity model and smoothing using PDE algorithm (t=30) (b) |
通过图 8的偏移成像结果可以看出,对于速度结构较为复杂的Sigsbee 2A模型,原始速度模型成像结果高速体部分较为模糊,而且底层部分的反射点没有得到很好的成像,应用PDE对速度模型平滑处理后所获得成像结果其高速体部分轮廓清晰可见,底层的反射点也得到了较好的成像效果.
4 结论本文从能量泛函的角度着手,基于速度梯度,采用最速下降法推导了基于偏微分方程的速度模型平滑公式.通过在简单的高速体速度模型上采用不同阈值k所得的平滑结果与采用卷积类平滑算子对速度模型进行平滑后其空间结构的变化以及射线路径与时间场的对比分析可以得出:
(1) 基于速度梯度的偏微分方程速度模型平滑处理结果依赖于k值的选取,k值选取越大,其平滑后的速度模型与原始速度模型空间结构的差异就越大.
(2) 射线路径与时间场的误差对比可以得出,偏微分方程对速度模型平滑后所得的速度模型的时间场与原始速度模型更加吻合,与卷积平滑算子对速度模型平滑后的时间场相比其相对误差更小.
(3) 通过在原始Marmousi、Sigsbee 2A速度模型上以及采用偏微分方程对原始速度模型平滑处理后的速度模型上的偏移成像结果可以看出,偏微分方程速度模型平滑处理后能够获得较好的成像结果.
Chen L. 2015. The application of the partial differential equations diffusion model in image de-noising[Master thesis] (in Chinese). Kunming: Kunming University of Science and Technology.
|
Ding C, Yin Q B, Lu M Y. 2013. Summary of partial differential equation (PDE) method on digital image processing. Computer Science (in Chinese), 40(S2): 341-346. |
Gabor D. 1965. Information theory in electron microscopy. Laboratory Investigation, 14(6): 801-807. |
Gao Z H, Sun J G, Sun X, et al. 2017. A fast algorithm for depth migration by the Gaussian beam summation method. Journal of Geophysics and Engineering, 14(1): 173-183. DOI:10.1088/1742-2140/aa52dd |
Gray S H. 2000. Velocity smoothing for depth migration: how much is too much?//70th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1055-1058.
|
Han F X. 2009. On some computational problems in wavefront construction method[Ph. D. thesis] (in Chinese). Changchun: Jilin University.
|
Han F X, Sun J G, Wang K. 2011. Analysis of velocity model smoothing. Journal of Jilin University (Earth Science Edition) (in Chinese), 41(5): 1610-1616, 1645. |
Hummel R. 1987. Representations based on zero-crossings in scale-space.//Fischler M A, Firschein O eds. Readings in Computer Vision. Los Altos, Calif: Morgan Kaufmann Publishers, Inc.
|
Jiang L S, Bian B J. 2012. Concise Course on Equations of Mathematical Physics (in Chinese). Beijing: Higher Education Press.
|
Lailly P, Sinoquet D. 1996. Smooth velocity models in reflection tomography for imaging complex geological structures. Geophysical Journal International, 124(2): 349-362. DOI:10.1111/gji.1996.124.issue-2 |
Lopez-Molina C, Galar M, Bustince H, et al. 2014. On the impact of anisotropic diffusion on edge detection. Pattern Recognition, 47(1): 270-281. DOI:10.1016/j.patcog.2013.07.009 |
Pacheco C, Larner K. 2005. Velocity smoothing before depth migration: Does it help or hurt?//75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1970.
|
Perona P, Malik J. 1990. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7): 629-639. DOI:10.1109/34.56205 |
Shi X L, Sun J G, Sun H, et al. 2016. Depth migration in time domain using wavefront construction:delta packet approach. Journal of Jilin University (Earth Science Edition) (in Chinese), 46(6): 1847-1854. |
Witkin A P. 1983. Scale-space filtering.//International joint conference on Artificial intelligence. Karlsruhe, West Germany, 2: 1019-1021.
|
Yang X. 2003. Principles and Applications of Image Partial Differential Equations (in Chinese). Shanghai: Shanghai Jiao Tong University Press.
|
Yuan M L, Huang J P, Liao W Y, et al. 2017. Least-squares Gaussian beam migration. Journal of Geophysics and Engineering, 14(1): 184-196. DOI:10.1088/1742-2140/14/1/184 |
陈龙. 2015.偏微分方程扩散模型在图像去噪中的应用[硕士论文].昆明: 昆明理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10674-1015641481.htm
|
丁畅, 尹清波, 鲁明羽. 2013. 数字图像处理中的偏微分方程方法综述. 计算机科学, 40(S2): 341-346. |
韩复兴. 2009.论波前构建法中的几个计算问题[博士论文].长春: 吉林大学. http://cdmd.cnki.com.cn/Article/CDMD-10183-2009092298.htm
|
韩复兴, 孙建国, 王坤. 2011. 速度模型的光滑处理分析. 吉林大学学报(地球科学版), 41(5): 1610-1616, 1645. |
姜礼尚, 边保军. 2012. 数学物理方程简明教程. 北京: 高等教育出版社.
|
石秀林, 孙建国, 孙辉, 等. 2016. 基于波前构建法的时间域深度偏移-delta波包途径. 吉林大学学报(地球科学版), 46(6): 1847-1854. |
杨新. 2003. 图像偏微分方程的原理与应用. 上海: 上海交通大学出版社.
|
 2019, Vol. 62
2019, Vol. 62


