0 引言

射线理论曾广泛应用于地震层析和偏移成像中.然而，只有当速度非均匀体的尺度远大于地震波波长及菲涅尔体的宽度时，基于高频近似的射线理论才能成立(Spetzler and Snieder, 2001).当速度非均匀体的尺度小于菲涅尔体的宽度时，地震波散射起主导作用(Spetzler and Snieder, 2004).基于波动方程导出的有限频理论(Woodward，1992；Marquering et al., 1999；Jocker et al., 2006)认为，整个菲涅尔带(体)内的速度扰动都会对地震波的振幅/走时产生影响.有限频理论的核心为波动方程线性化近似，如一阶Rytov近似或一阶Born近似等.

基于一阶Rytov近似，地震波的走时扰动可以表示为速度扰动与一个积分核的体积分(Snieder and Lomax, 1996)，该积分核通常称为走时敏感度核函数(traveltime sensitivity kernel, 简记为TSK；Spetzler and Snieder, 2001，2004；Jocker et al., 2006；Xie and Yang, 2008；刘玉柱等, 2009, 2019；Xu et al., 2015；Feng and Wang, 2015).然而对于非均匀介质，显式计算TSK需要巨大的计算量，导致了基于核函数的走时反演方法(如散射积分法)也需要巨大的计算和存储需求(Zhao et al., 2005；Chen et al., 2007)，限制了该类方法的广泛应用.

另一方面，基于一阶Born近似和互相关时差测量方式也可以导出地震波走时扰动对速度扰动的一阶近似(又称为走时Fréchet导数，Luo and Schuster, 1991；Marquering et al., 1999；Dahlen et al., 2000；Hung et al., 2000；Zhao et al., 2000)，但其成立条件更加苛刻(同时满足走时和波场小扰动假设).由于走时/波场Fréchet导数的计算中都采用了一阶Born近似，走时Fréchet导数也与全波形反演(Tarantola，1984；Rao et al., 2016；Zhang et al., 2016)和环境噪声层析成像(Das and Rai, 2016；Li X X and Li Q C，2016)中的有限频率敏感核具有一定的相似性.基于伴随状态(adjoint state)方法，走时Fréchet导数可以用正向传播的入射波场和逆时传播的伴随波场的时间积分表达(Tromp et al., 2005；Tape et al., 2007；Liu 2006，2008)，可以用逆时偏移(Reverse Time Migration，简记为RTM)算法高效计算走时Fréchet导数及走时目标泛函的梯度，因此被广泛采用(Hung et al., 2004；Montelli et al., 2004；Tape et al., 2009；Yuan et al., 2016).

理论分析可知，由互相关时差测量方式和一阶Born近似导出的走时Fréchet导数经过双重线性化近似，因而对初始速度模型精度的要求很高.此外，虽然基于伴随状态方法可以高效计算走时误差泛函的梯度，但收敛速度慢于散射积分法.过去许多文献从理论分析和数值测试对比了一阶Born近似和一阶Rytov近似的成立条件和适用范围(Brown，1967；DeWolf，1967；Keller，1969；Beydoun and Tarantola；1988；Xu et al., 2015).Wu(2003)指出，Rytov近似更适用于描述前向散射的波场，且不要求小相位扰动假设(但隐含小散射角假设).因此，本文将研究如何在Gauss-Newton反演框架中引入基于Rytov近似的走时核函数，既能保持Rytov近似优点，又有较高的收敛速度.

1 基于Rytov近似及互相关时差测量方式的有限频走时敏感度核函数

在频率域，背景速度场中的波场为u₀=u₀(x_r, ω; x_s)，在真实速度场中的波场为u=u₀(x_r, ω; x_s)expψ(x_r, ω; x_s).其中，ψ为复散射相位，其精确解为(Wu，2003)：

(1)

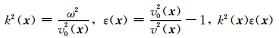
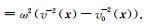
其中， x_s和x_r分别为震源和检波器坐标.v₀(x)为背景速度，v(x)为真实速度.G₀(x, ω; x_r)为背景速度场中从检波器x_r到地下散射点x的格林函数，G₀(x, ω; x_s)为背景速度场中从震源x_s到地下散射点x的格林函数.

(1) 式为非线性方程(Riccati方程；Wu，2003).若将慢度平方扰动记为Δm(x)=v^－2(x)－v₀^－2(x)，并假设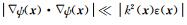 (一阶Rytov近似)，有：

(2)

expψ(x_r, ω; x_s)可视为一个滤波器H(ω)=A(ω)e^iΦ(ω)(其中，A(ω)=e^Reψ(ω)，Φ(ω)=Imψ(ω))，程乾生(2003)给出了滤波器的相位延迟(单频谐波的延迟时间)：

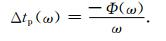
(3)

结合公式(2)和(3)，可以得出单频谐波走时扰动的表达：

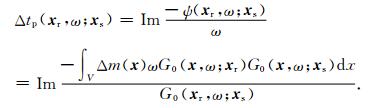
(4)

其中，单频走时敏感度核函数可以定义为：

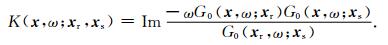
(5)

若震源子波频谱为S(ω)，(5)式也可以写为：

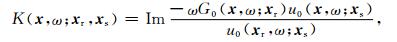
(6)

其中，u₀(x, ω; x_s)=S(ω)G₀(x, ω; x_s)为背景速度场中传播的震源波场.

若观测信号与模拟信号的波形相似，此时可以用互相关函数测量二者的时差.Xie和Yang(2008)指出，单频谐波走时扰动与互相关函数测量得到的带限信号走时扰动有如下关系：

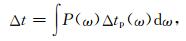
(7)

其中，P(ω)为归一化的加权函数，与子波频谱S(ω)的关系为：

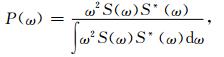
(8)

其中，上标*代表复数共轭.

结合(4)，(6)—(8)式，带限信号的走时扰动为：

(9)

显然，(9)式与Xu等(2015)给出的有限频敏感度核函数相似(区别仅在于模型参数化方式).若记，(9)式中积分核可表示为：

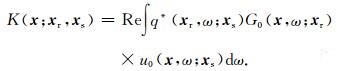
(10)

(10) 式即由Rytov近似及互相关时差测量方式导出的有限频走时敏感度核函数.附录A中给出了(10)式与基于Born近似导出的走时敏感度核函数的差异和联系.

若直接利用(10)式计算核函数，需要计算频率域波场及格林函数(如数值求解Helmholtz方程或者利用Fourier变换将时间域波场变换至频率域)，在三维情况下计算量巨大.考虑到地震信号是平方可积的，本文利用巴什瓦尔等式(Parseval′s theorem，程乾生, 2003, p51 ) 将式(10)中对频率的积分变换到对时间的积分，有：

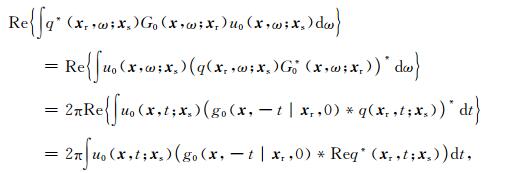
(11)

其中，g₀为时间域格林函数.

若定义单道伴随震源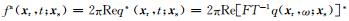，(10)式可以表示为：

(12)

其中，λ₀(x, t; x_r)是逆时传播的伴随波场：

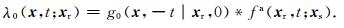
(13)

(10)和(12)式在理论上是等价的，前者在频率域计算，后者在时间域计算.从(12)式可以看出，对于任意一炮检对(x_r, x_s)，核函数的计算需要一次波场正演(计算u₀(x, t;x_s))以及一次波场逆时传播(计算g₀(x, －t|x_r, 0)*f^a(x_r, t;x_s)).显然，这与RTM互相关成像条件相同.由于每个炮检对(x_r, x_s)的核函数的计算需要一次RTM，因此计算量远高于射线(束)或菲涅尔体核函数(Spetzler and Snieder, 2004).

相应的，Rytov近似下波动方程走时层析正问题可以表示为：

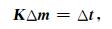
(14)

其中，Δt为用互相关函数测量得到的某个震相的走时残差.对于初至波层析，Δt为初至波时差.

2 基于隐式矩阵向量乘的Gauss-Newton反演算法

基于走时残差L2范数的误差泛函可以表示为：

(15)

其中，m=(m₁, m₂, …, m_N)^T为模型参数向量，在本文中为慢度平方(采用网格参数化方式，N为速度网格数目)，Δt=(Δt₁, Δt₂, …, Δt_M)^T为走时残差向量，M为炮检对的数目.

目标泛函的梯度为：

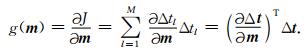
(16)

根据(14)式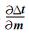，的一阶近似即(10)或(12)式中给出的有限频走时敏感度核函数.此时，泛函梯度可以用核函数与走时残差表示为：

(17)

目标泛函的二阶导数(Hessian矩阵)表示为：

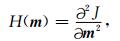
(18)

其中，Hessian的元素可以写为：

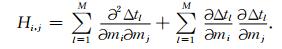
(19)

在线性化正问题的假设下(忽略走时扰动对模型扰动的二阶导数)，Hessian矩阵近似为：

(20)

Gauss-Newton算法的迭代格式为(Nocedal and Wright, 1999)：

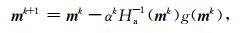
(21)

其中，α^k为步长，可以通过线性搜索方法计算.

由于层析反问题的病态性且Hessian矩阵的规模巨大，通常把对Hessian矩阵的求逆转为求解如下问题的近似解：

(22)

(22) 式可以用直接法或迭代法求解，得到模型扰动的近似解.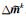

本文采用共轭梯度(conjugate gradient，简记为CG；具体算法见附录B中附表 1)法求解法方程(22).然而若显式计算Hessian矩阵，需要巨大的计算量和存储量.通过分析附表 1中的CG算法可知，求解(22)式的核心为计算Hessian矩阵与模型空间向量p=p(x)的乘积Hp，而无需显式计算核函数K及Hessian矩阵.根据公式(20)，Hessian向量积表示为：Hp=K^TKp=K^T(Kp)，因此需要分别计算如下两类矩阵向量积：

(1) 矩阵向量积Kp(p为模型空间中的向量，p=p(x))：

根据(10)式，Kp可以表示为：

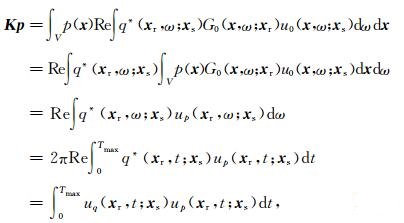
(23)

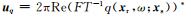
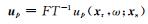
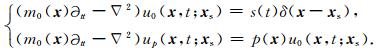
其中，为伴随波场，为反偏移波场，在时-空域满足如下方程：

(24)

矩阵向量积Kp将模型扰动p(x)投影到数据空间中，得到每个炮检对的走时扰动.根据(24)式，u_p，u_q的模拟可以按炮实现.记每炮中检波器数目为Nr，共Ns炮.若显式计算核函数(12)，共需要Ns×Nr次单炮RTM.而采用(23)式直接计算矩阵向量积，只需要2Ns次波场正演(求解(24)式需要两次正演，一次计算入射场，一次计算扰动场)，因此计算量大幅降低且无需存储核函数.

(2) 矩阵向量积K^Tc(c为数据空间中的向量，c=c(x_r, x_s))：

根据(12)式，K^Tc可以表示为：

(25)

若记单炮伴随波场

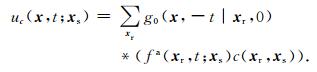
(26)

此时，K^Tc可以用Ns次单炮RTM的求和表示为：

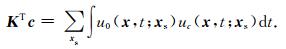
(27)

矩阵向量积K^Tc将走时扰动c(x_r, x_s)投影到模型空间中.根据(27)式，其计算量等同于Ns次单炮RTM，同样无需计算和存储核函数.

通过串联(23)式和(27)式，可以直接计算Hessian向量积Hp，计算量等价于2Ns次波场正演加Ns次RTM.由于避免了显式计算和存储矩阵(即走时敏感度核函数K及Hessian矩阵H)，本文称之为隐式矩阵向量乘方法.同时，以该方法为核心构造的CG算法求解法方程实现迭代反演，称为基于隐式矩阵向量乘的Gauss-Newton反演算法.

3 数值试验

在计算方面，本文重点在于构造了基于隐式矩阵向量乘的CG算法用于实现Gauss-Newton迭代.因此数值试验将验证该方法的有效性.

3.1 走时层析正问题精度测试

为测试敏感度核函数的精度，我们将对比互相关函数测量的时差和用敏感度核函数预测的时差.我们设计了一个棋盘格速度模型，在匀速背景中包含了4个高斯异常(2个正异常和2个负异常交替分布)，速度模型表示为：

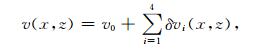
(28)

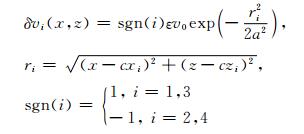
其中，v₀ = 3 km·s^-1，a为高斯球的尺度参数，ε为扰动强度.

速度模型参数为：X，Z方向网格间距dx=dz=10 m，采样点数nx=nz=501. 4个高斯异常的中心坐标(cx, cz)分别为：(1250，1250；3750，1250；1250，3750；3750，3750)，扰动强度为ε=5%，10%，20%，a=600 m.震源坐标(sx, sz)=(1250, 0)，三排检波器分别放置在模型的左右侧和底边.速度模型和观测系统如图 1所示.

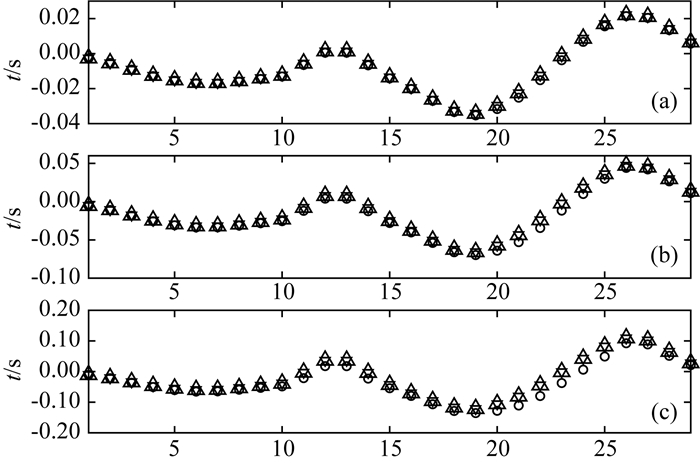
初始速度为v₀=3 km·s^-1的常速模型.首先，本文用时-空域高阶有限差分方法正演，分别得到观测地震记录d和初始地震记录u，并用互相关函数(cross-correlation)测量观测信号和模拟信号的时差Δt^cc=CC(d, u)，作为“观测”时差.接着，用两种方法计算预测走时扰动，分别是：(a)显式计算走时敏感度核函数并预测走时扰动：Δt^tsk=KΔm；(b)用隐式矩阵向量乘方法计算走时扰动：Δt^adjoint=∫u_qu_pdt(公式(23)).图 2a—2c分别为扰动强度ε=5%，10%和20%时预测走时扰动和观测走时扰动的对比.显然，不管扰动强度如何变化，Δt^tsk与Δt^adjoint始终吻合(仅存在计算机浮点误差)，验证了本文隐式矩阵向量乘方法的有效性.随着扰动强度增大，预测结果逐渐偏离观测走时扰动，与前人文献(Mercerat and Nolet, 2013；Xu et al., 2015)的研究结论一致.

3.2 基于隐式矩阵向量乘方法的CG算法测试

根据(21)式，每次Gauss-Newton迭代需要求解法方程(22).为测试文中基于隐式矩阵向量乘的CG算法，我们用3.1节中ε=10%的棋盘格速度模型测试反演算法，初始速度仍采用v₀=3 km·s^-1的常速模型.走时扰动用两种方式测量：分别是互相关测量方式和核函数预测方式(公式(14)或(23)).其中，互相关测量方法代表着实际应用中的时差获取方式，而核函数预测方式仅用于测试反演算法(inversion crime).考虑到观测系统对反演精度的影响至关重要，本文设计了三种观测系统，从理想观测系统(全孔径激发/接收)过渡到井间观测系统.震源函数均为10 Hz主频的Ricker子波(对应的背景波长为λ₀=300 m).

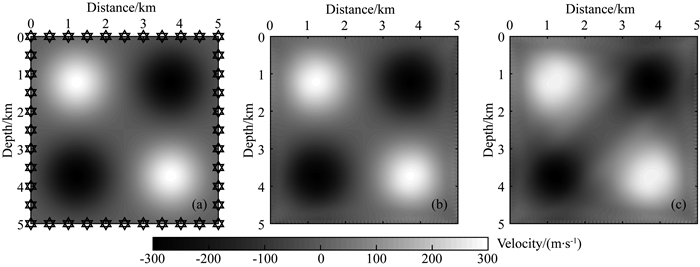
理想观测系统描述为：如图 3a所示，200个检波器均匀分布在模型的四周，道间距100 m.震源坐标同检波器坐标.图 3b和3c分别为核函数预测时差(简称为预测时差)和互相关函数测量时差(简称为互相关时差)对应的反演结果(CG算法求解(22)式并迭代10次).由于采用了全孔径激发/接收的观测系统，由核函数预测走时得到的反演结果(图 3b)基本与真实的模型扰动一致.相比之下，互相关时差的反演结果的分辨率略差(图 3c)，但仍然可以得到较好的反演结果.从图 2b中互相关时差和预测时差对比曲线可以看出，在某些检波器处的时差存在一定偏差(对应大散射角)，导致了互相关时差的反演结果不及前者.

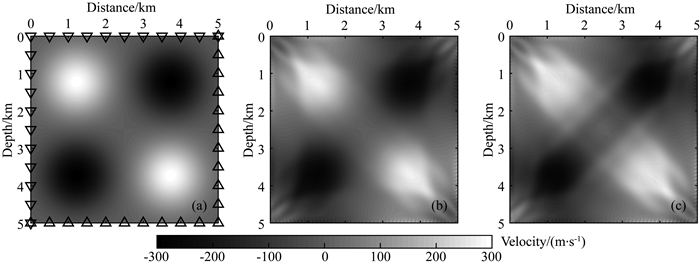
正交观测系统由两束正交的透射观测系统构成：如图 4a所示，第一束观测系统中，震源位于模型左侧，检波器位于模型右侧，震源和检波器纵向间隔均为100 m.第二束观测系统中，震源位于地表，检波器位于模型底边，震源和检波器横向间隔均为100 m.图 4b和4c分别为预测时差和互相关时差对应的反演结果(反演算法的参数不变).与理想观测系统的反演结果相比，由于观测孔径减少，反演结果的分辨率明显降低.

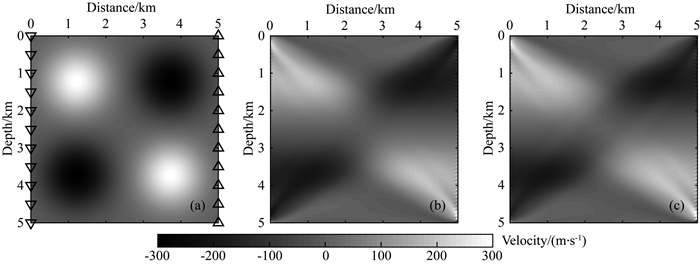
井间观测系统仅保留了正交观测系统中的第一束观测系统，如图 5a所示.图 5b和5c分别为预测时差和互相关时差对应的反演结果(反演算法的参数不变).与正交观测系统的反演结果相比，由于缺少了纵向的照明，反演结果的横向分辨率进一步降低.

4 结论与讨论

基于一阶Rytov近似，本文推导了有限频走时敏感度核函数的两种等价形式：频率积分和时间积分表达式.基于核函数的频率积分形式，可以将核函数与模型空间向量的内积转换为反偏移波场和伴随波场对时间的积分，其计算量与波动方程反偏移(或Born模拟)相仿；基于核函数的时间积分形式，可以将核函数转置与数据空间向量的内积转换为入射波场和伴随波场对时间的积分，其计算量与逆时偏移相当.由于避免了显式计算和存储矩阵(即走时敏感度核函数)，本文称之为隐式矩阵向量方法.

对于走时层析反问题，基于本文提出的隐式矩阵向量方法，可以高效计算Gauss-Newton方向.与传统的敏感度核函数反演方法相比，本文方法无需计算和存储核函数和Hessian矩阵，降低了内存需求并提高了计算效率.与基于Born近似的伴随状态走时层析相比，本文方法适用范围更广，且具有准二阶的收敛速度，因而更适用于背景速度反演.

在数值试验中，由于模型扰动基本满足Rytov近似，因而仅验证了线性反演(即用共轭梯度法求解法方程得到模型扰动的近似值)，而没有迭代更新背景速度.在实际应用中，通常需要迭代反演，并考虑数据预条件、模型正则化及合适的反演策略等.

附录A

为了对比本文导出的走时敏感度核函数与基于Born近似和互相关时差测量方式导出的走时Fréchet导数，我们将相关推导简要列出.首先，观测数据d(t)和模拟数据u₀(t)的互相关函数可以写为：

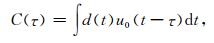
(A1)

观测数据和模拟数据的时差定义为使得(A1)式取得极大值的时移量Δt：

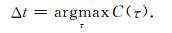
(A2)

假定波场扰动远小于背景波场，观测数据可以表示为：

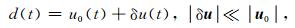
(A3)

其中，δu(t)为波场扰动.

根据(Marquering et al., 1999；Dahlen et al., 2000)，走时扰动的一阶近似为：

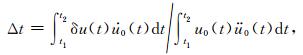
(A4)

(A4) 式假定了波场扰动远小于背景波场，且u₀(t)和δu(t)在区间t₁≤t≤t₂之外为零.

根据巴什瓦尔定理, 公式(A4)可以写为:

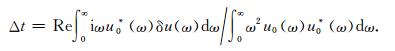
(A5)

在频率域，散射场的一阶Born近似为:

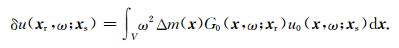
(A6)

结合公式(A5)和(A6)，走时扰动可以表示为：

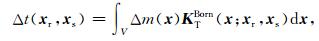
(A7)

其中，K_T^Born为基于Born近似和互相关函数测量得到的走时敏感度核函数:

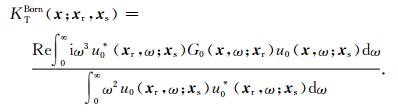
(A8)

为了分析基于Born近似和Rytov近似两种波动方程线性化方式导出的走时敏感度核函数的差异及其内在联系，我们将背景波场的WKBJ近似写为：

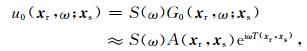
(A9)

其中，A(x_r, x_s)和T(x_r, x_s)分别为震源x_s到检波器x_r的振幅和走时.

对于光滑的背景速度场，(A9)式成立.此时，(8)式中的加权函数可以近似为：

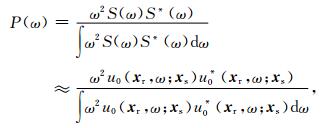
(A10)

其中，

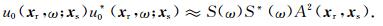
将(A10)式代入(10)式，基于Rytov近似导出的走时敏感度核函数可以表示为：

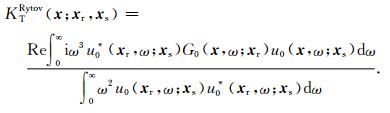
(A11)

显然，(A11)和(A8)式形式上完全一致，即在背景波场的WKBJ近似下，基于Rytov近似和Born近似两种线性化方式导出的敏感度核函数具有相同的形式.然而，它们的成立条件和适用范围却不相同.(A8)式基于一阶Born近似导出，其成立条件要求散射场远小于背景场(速度扰动的强度和尺度都小)，因而只适用于小走时扰动情形.另一方面，本文基于一阶Rytov近似导出的走时敏感度核函数并没有假设走时扰动很小，只要相位扰动是线性的即可.关于Born近似和Rytov近似的对比分析详见本文引言中提及的参考文献，在此不再赘述.

附录B

法方程(22)为一个大型线性方程组，可以用直接法或迭代法求解.考虑到Hessian矩阵的规模巨大，难以直接求逆.因此本文采用附表 1中给出的共轭梯度算法求解其近似解.

致谢  感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持.