0 引言

地震波波场模拟在地球物理中有重要应用，如可以用来探测油气储层和地质构造等.基于声波和弹性波模型的波场模拟理论与应用在石油地球物理勘探中已经取得巨大成功.在这些模型中，多孔流体的性质如流体的黏性、密度、体积模量等都没有考虑.多孔弹性波方程模型则考虑了渗透率、孔隙度及流体黏性等参数的影响，是比声波和弹性波方程更接近实际介质的模型.发展多孔弹性介质中的波场模拟方法几十年来一直都得到重视，研究产生了各种方法，例如：有限差分法(Dai et al., 1995；Özdenvar1997 and McMechan, 1997；Zeng and Liu, 2001；Wang et al., 2003；O′Brien，2010；Zhang and Tong, 2013)；有限元方法(Atalla et al., 1996；Panneton and Atalla, 1997)；谱元法(Morency and Tromp, 2008)；DG方法(de la Puente et al., 2008；Dupuy et al., 2011)；以及，结合有限差分与有限体积的混合法(Zhang et al., 2014)、辛方法(Yang et al., 2014)等.与多尺度方法相对而言，这些方法可都看作直接的(单尺度)波场模拟方法.

地球物理的许多问题都具有多尺度性质，例如从宏观的大地构造到细观的油储结构、不同尺度孔隙介质中的流体流动等(滕吉文，2014).在这些问题中，在计算区域中介质的物理参数(如渗透率和弹性常数)可能在一个很小的尺度(如厘米量级)上不连续或有剧烈变化.当波在这种多尺度非均匀介质中传播时，由于介质的物性参数经常在一个小尺度上有很大变化，直接的波场模拟方法为了能够反映出小尺度上的介质参数变化，在剖分网格时需要采用很细的网格，以使网格大小和参数变化的空间尺度相匹配.这将导致在整个计算区域中的网格点数会达到一个很大的数量，可能会超出计算机计算能力的范围.虽然当前计算机的计算能力和性能在迅速提高，可以用并行实现，但如果不改进算法，不减少网格的自由度，还是会无法满足实际计算的需求.多尺度方法则可以克服这种尺度差异带来的困难，可采用较粗的网格计算，同时又能反映细尺度上物性参数的变化.目前，人们已发展了多种多尺度方法，如均匀化方法(Bensoussan et al., 1978；Nguetseng，1989；Allaire，1992；Owhadi and Zhang, 2008；Abdulle and Grote, 2011；Engquist et al., 2011)，以及求解波动方程的尺度提升方法(Korostyshevskaya and Minkoff, 2006；Vdovina et al., 2005, 2009；Vdovina and Minkoff, 2008)等.均匀化方法通过确定介质的有效物性参数来实现多尺度的计算，但这种方法受到材料或介质结构周期性要求的限制；尺度提升方法也依赖于均匀化理论，对非周期结构或介质也不适合.

Hou等(Hou and Wu, 1997)提出的多尺度有限元方法是一种十分有效的求解多尺度问题的方法，这种方法的核心思想是对传统有限元的多项式基函数作改进.在多尺度有限元中，利用细网格上的局部信息计算出的基函数取代传统的有限元多项式基函数，这种多尺度基函数更能反映出参数的局部信息.这样，在不用加密粗网格的情况下，求出的解在细尺度上会有更高的精确性.随后，多尺度有限元的理论和算法都得到了进一步的发展，进一步可参考文献，如(Efendiev and Hou, 2009).

将有限元基函数应用到波动方程中，需要做一定调整.间断Galerkin方法是一种结合了有限元基函数和有限体积积分的方法(Chung and Engquist, 2009；Zhang et al., 2016).如果将其中传统的多项式基函数替换成多尺度有限元基函数，就可以得到相应的多尺度方法.Gibson等(Gibson et al., 2014)在求解声波方程的过程中就用到了这样的思想，但对于多孔弹性波方程，还未见有研究和应用.

为此，本文研究了多孔弹性波方程的多尺度波场模拟方法.在第1节详细描述了多孔弹性波方程的多尺度方法，推导了多尺度计算格式，包括基函数的计算；在第2节进行了数值实现；最后第3节给出了结论.

1 理论方法 1.1 控制方程——Biot方程

根据Biot理论(Biot, 1956a, 1956b, 1962a, 1962b)，在一定条件下，如地震波波长大于孔隙尺寸、固体介质弹性小变形、流体相位连续等，弹性波在多孔介质中传播可用如下的Biot方程来描述：

(1)

(2)

其中在二维情况下，x₁=x为地面横向坐标，x₂=y为深度纵向坐标.在方程(1)—(2)中，我们需要求解的未知量是向量u和w，在二维情况下它们各有两个分量，其中u_i表示固体位移矢量的第i个分量，w_i表示孔隙中的流体相对于固体位移矢量的第i个分量；λ表示饱和介质的拉梅常数，μ表示干多孔介质的剪切模量；K_s表示固体的体积弹性模量，K_f表示流体的体积弹性模量；ρ_s表示固体的密度，ρ_f表示流体的密度；φ表示孔隙度，κ表示渗透率；表示介质的弯曲度；η表示流体的黏性；σ=▽·u表示固体的膨胀率；ξ=-▽·w表示流体相对于固体的膨胀率；以及

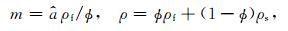
(3)

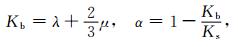
(4)

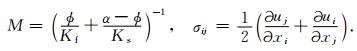
(5)

在非均匀介质中，基本参变量和导出参变量都会随着空间位置而变化；如果在一个粗网格大小的范围里这些参数的变化仍然很剧烈，考虑用多尺度的方法来模拟多孔介质中弹性波的传播会更合适.下面我们将在引入速度变量后将二维Biot方程写成速度-压力形式并描述多尺度模拟方法.

1.2 多尺度计算格式

引入速度变量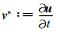及，可将二维形式的Biot方程(1)—(2)改写成如下速度-压力形式的一阶双曲方程组：

(6)

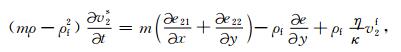
(7)

(8)

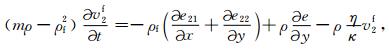
(9)

(10)

(11)

(12)

(13)

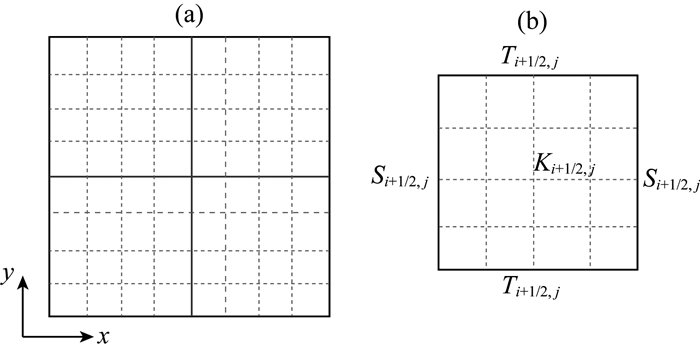
在本文的多尺度算法中，将建立粗细两套网格，如图 1a所示，其中实线表示的是2×2的一套粗网格，每个粗网格由4×4的细网格构成；虚线表示的是8×8的另一套细网格.记空间网格点中心在(i, j)处的一个粗网格为K_{i, j}.在粗网格上的离散将采用交错网格的思想；并通过细网格计算在每个粗网格单元上建立的局部基函数.为了能利用这些局部基函数，我们将首先用有限体积方法来推导方程(6)—(13)在粗网格上的离散形式.

如图 1b所示，又记K_{i+1/2, j}表示以空间网格点(i+1/2, j)为中心的粗网格，S_{i+1/2, j}表示该粗网格的竖向(y)粗网格边，T_{i+1/2, j}表示该该粗网格的横向(x)粗网格边，等等.

在粗网格上，应用一般的交错网格离散思想，即变量e、e₁₁和e₂₂在时间n处与空间(i, j)处离散，变量e₁₂在时间n处与空间(i+1/2, j+1/2)处离散，变量v₁^s与v₁^f在时间n+1/2处与空间(i+1/2, j)处离散，变量v₂^s与v₂^f在时间n+1/2处与空间(i, j+1/2)处离散.在以下的有限体积积分中，我们将速度变量在一个相应的粗网格上视为常数并对方程(6)—(9)在相应的粗网格上直接积分；而对变量e₁₁、e₁₂、e₂₂和e引入多尺度基函数φ₁₁、φ₁₂、φ₂₂和φ，且对方程(10)—(13)两边先乘以相应的基函数再积分.这些基函数在每个1/4粗网格区域上都是1边值的，其具体求法将在下一节中给出.注意这里我们仅对变量e₁₁、e₁₂、e₂₂和e引入多尺度基函数，是因为可以对原方程组中的每个方程进行严格的有限体积积分推导，且所有面积分都可以转化成用边界格点上的值来计算.下面先给出(6)—(9)的离散格式.

对(6)式，在K_{i+1/2, j}上积分，可得

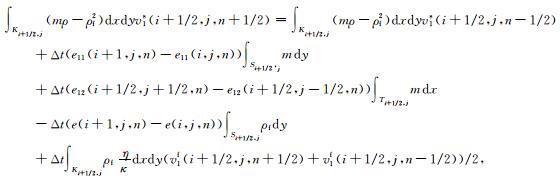
(14)

对(7)式，在K_{i, j+1/2}上积分，可得

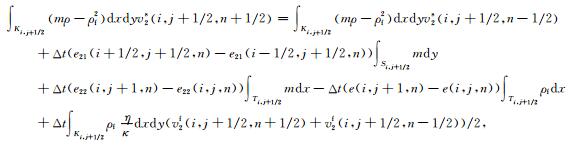
(15)

对(8)式，在K_{i+1/2, j}上积分，可得

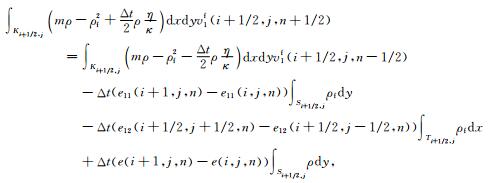
(16)

对(9)式，在K_{i, j+1/2}上积分，可得

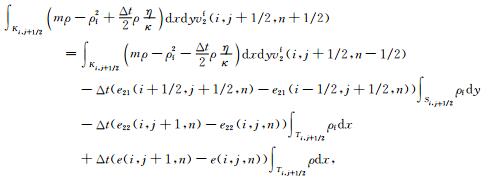
(17)

下面我们考虑方程(10)—(13)的离散格式，在相应的粗网格上将e₁₁、e₁₂、e₂₂和e视为基函数的倍数，在(10)两边乘以基函数φ₁₁，并在一个粗网格单元K_{i, j}上积分，可得

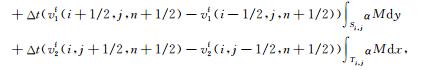
(18)

在(11)两边乘以基函数φ₁₂，并在一个粗网格单元K_{i+1/2, j+1/2}上积分，可得

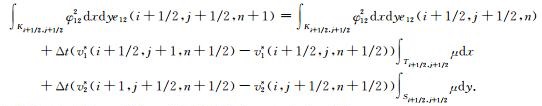
(19)

在(12)两边乘以基函数φ₂₂，并在一个粗网格单元K_{i, j}上积分，可得

(20)

在(13)两边乘以基函数φ，并在一个粗网格单元K_{i, j}上积分，可得

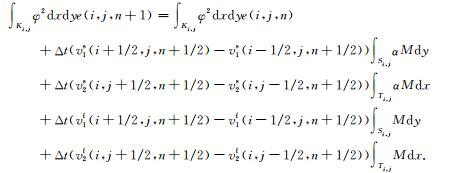
(21)

现在我们已得到式(6)—(13)的完整的计算格式，即式(14)—(21)，这些格式都是在时间方向递推的显式格式，其中的积分直接取细网格点上的值进行数值近似即可；另外，在(18)—(21)中还需要多尺度基函数φ₁₁、φ₁₂、φ₂₂和φ, 下面考虑多尺度基函数的计算.

1.3 基函数的计算

由于在每个粗网格上基函数是相互独立的，因此各个粗网格上基函数的计算是完全并行的.基函数的计算，需要在每个1/4粗网格单元K上求解一个局部问题:

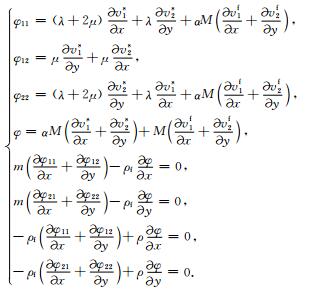
(22)

这种基函数取法的思想来自于多尺度有限元(Hou and Wu, 1997)，反映了K上的局部性质，其中边界条件的取法并不本质，可将边值条件取成φ₁₁、φ₁₂、φ₂₂、φ在粗网格单元K之边界∂K上恒为1.从(22)方程组中的后四个方程中我们可以得到

(23)

现在我们将K做一个三角剖分，将K上的分片线性函数空间记为W，我们将在W空间中求解未知量v₁^s、v₂^s、v₁^f和v₂^f.令w∈W为检验函数，我们首先将(23)中的四个方程两边同时乘以w并在K上积分得到其变分形式，然后将(22)的前四个方程代入其中消去体积分中的φ₁₁、φ₁₂、φ₂₂和φ，并利用边值条件消去边界积分中的φ₁₁、φ₁₂、φ₂₂和φ，最后得到关于v₁^s、v₂^s、v₁^f和v₂^f的变分方程.记∂K_t、∂K_b、∂K_l、∂K_r分别表示网格单元∂K的上下左右边界，内积(f₁, f₂)表示∫f₁f₂dxdy，则对(23)中的第一个方程我们有

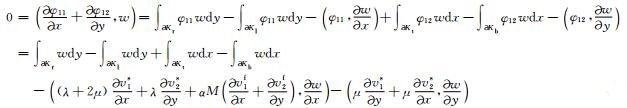
(24)

于是

(25)

同理，对(23)中的后三个方程，推导类似，结果分别为

(26)

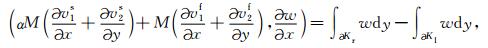
(27)

(28)

于是我们可在空间W中按有限元方法求解变分方程(25)，(26)，(27)和(28).注意到若v₁^s、v₂^s、v₁^f、v₂^f是解，那么v₁^s+k₁y+c₁、v₂^s－k₂x+c₂、v₁^f+k₃y+c₃、v₂^f－k₄x+c₄也是解，这里k₁、k₂、k₃、k₄和c₁、c₂、c₃、c₄是任意常数.于是我们要加上相应的唯一化限制条件.当v₁^s、v₂^s、v₁^f、v₂^f解出后，我们就可以再求出基函数φ₁₁、φ₁₂、φ₂₂、φ.注意到不管对v₁^s、v₂^s、v₁^f、v₂^f所加的唯一化限制条件是什么，求出的φ₁₁、φ₁₂、φ₂₂、φ必然都是唯一确定的；并且在均匀介质的情况下这个唯一的解就是φ₁₁、φ₁₂、φ₂₂、φ均为常数1的解.求出φ₁₁、φ₁₂、φ₂₂、φ后, 我们就可以通过前面给出的(14)—(21)的离散格式来模拟多孔介质中的弹性波的传播了.

2 数值计算

由于数值计算中求解区域都是有限的，计算中需要加吸收边界条件来消除边界反射的影响.吸收边界条件有多种，例如旁轴近似条件(Clayton and Engquist, 1977)、PML边界条件(Berenger，1994；Zeng et al., 2001)和精确吸收边界条件(Zhang et al., 2014).这里，我们采用分裂形式的PML条件(Collino and Tsogka, 2001；Komatitsch and Tromp, 2003)，具体方程见附录.

首先分析一下计算的复杂度，假定粗网格在x方向和y方向的离散网格数分别为M_x和M_y，细网格在x方向和y方向的离散网格数分别为m_x和m_y，则在一个时间步上，粗网格上的计算复杂度约为40M_xM_y次乘除运算，在细网格上的计算复杂度为40m_xm_y；基函数的计算量约为6000m_xm_y.另外，基函数可以预先求解，在每一个粗网格上的计算是互不相关的，不用进行数据交换，且在时间的演化过程中都是相同的.因此，时间步递推的越多，多尺度方法就越节省时间.例如，假设M_x=M_y=m₀，m_x=m_y及m_x=2M_x，则当时间递推200步时，单尺度细网格上的计算复杂度为32000m₀²，多尺度的计算复杂度为32000 m₀²，计算量一样；但当时间递推1000步时，单尺度细网格上的计算复杂度为160000 m₀²，多尺度的计算复杂度为64000 m₀²，可节省96000 m₀².因此当计算规模越大、计算时间步越多及细粗网格比参数m₀越大时，节省的计算量越大.关于计算内存，由于基函数是在每个局部的粗网格上计算，所需内存很小，基本可以忽略，因此多尺度方法可以节省约m₀²倍的内存.

现考虑一个300 m×300 m的非均匀区域，其中含有很多随机分布的小散射体，一种散射体的大小为1.125 m×1.125 m，共有10000个；另一种散射体的大小为0.75 m×0.75 m，共有3000个，模型如图 2所示.背景介质与散射体的物性参数取值见表 1.

震源取在计算区域的中心，震源的时间函数取中心频率f₀为40 Hz的雷克子波：

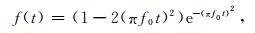
(29)

震源的空间分布取成一个σ=5的高斯分布函数

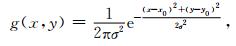
(30)

其中(x₀, y₀)表示求模型的中心点，当σ趋于零时，源函数的空间变成一个奇点.于是完整的震源函数可以表示为

(31)

其中A表示振幅.在实际计算中, 我们只取震源函数在x方向上的分量，在y方向上的分量取为零.计算的CFL稳定性条件为

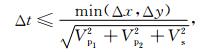
(32)

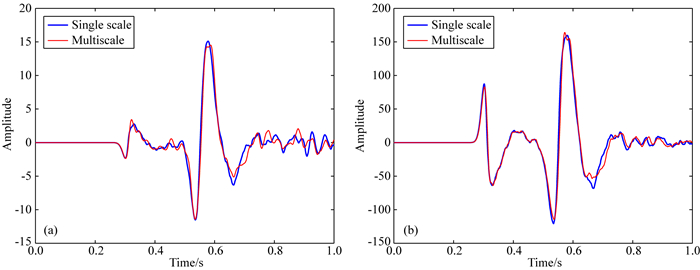
其中V_s、V_p1、V_p2分别为多孔介质中剪切波和两个纵波的波速，Δx和Δy分别为粗网格在x方向和y方向上的空间步长.计算的时间步长Δt取0.5 ms.下面给出0.045 s时刻的波场传播快照.图 3显示了在800×800的单层网格上计算的结果，没有采用多尺度方法，直接用交错网格方法进行计算，其中图 3a和3b分别是固体分量v₁^s和v₂^s，图 3c和3d分别是相对于固体的流体分量v₁^f和v₂^f.图 4显示了在400×400的粗网格和800×800的细网格的两层网格上的多尺度方法计算结果，其中图 4a和4b分别是固体分量v₁^s和v₂^s，图 4c和4d分别是相对于固体的流体分量v₁^f和v₂^f.计算表明，在同样的计算环境下，图 4的cup计算时间仅约为图 3的40%.根据Biot波场传播理论，在多孔介质中存在三种波型，其中有两种是压缩纵波，即快P波和慢P波，快P波类似一般弹性波方程的P波，对应固体液体同相位的位移，慢P波对应固体液体不同相的位移；第三种是剪切横波即S波.这三种波型在流体分量上即图 3c、3d和图 4c、4d上尤其清晰，根据波速大小可知，图中从外至内分别为快P波、S波和慢P波.图 3和图 4中的边界吸收的效果也都很明显，由于介质中有许多非均匀的小散射体，在图中还可见由这些小散射体产生的相对较弱的散射波场.此外，比较图 3和图 4可知，用本文的多尺度方法的计算结果与单尺度细网格上的计算结果非常相似.为了进一步比较两者的差别，取空间某一固定点的振动图形作比较，如图 5所示，选取了空间位置在(93.75 m，93.75 m)处的v₁^f分量和v₂^s分量的振动波形的比较(其他位置和分量也类似)，其中蓝线是单尺度800×800的细网格上的计算结果，红线是在400×400的粗网格和800×800的细网格上用多尺度方法计算的结果，图中振幅均没有作任何标定，比较可见，主要的波形均吻合的较好，能反映出主要的波场特征；在大振幅的波形上的小振幅振动，反映了随机散射体的影响.因此，可以看到本文多尺度计算方法的正确性和有效性.对其他更粗的网格参数的计算结果图形也类似，可得出同样结论.

3 结论

本文研究了二维多孔弹性波方程的多尺度波场模拟方法.波在非均匀介质中的传播涉及到很多不同的尺度，介质的物性参数经常在一个很小的尺度上有很大变化，通常的直接求解方法为了能够反映出小尺度上的物性参数变化，求解中需要很精细的网格剖分，这样大大增加了计算量和计算内存.多尺度方法可采用较粗的网格计算，同时又能反映细尺度上的物性参数的变化信息.基本思想是通过多尺度基函数将细尺度的信息转移到粗尺度上.多尺度基函数通过三角形线性元求解粗网格上的一个局部化问题得到.文中详细阐述了多尺度的方法与算法，推导了计算格式，对具有随机分布散射体的多孔介质模型进行了数值计算，计算区域的边界中应用了PML边界吸收条件，稳定性条件由粗网格步长确定，细网格的步长可以根据问题的需求来确定，数值计算验证了本文方法的有效性.本文的方法可以进一步推广到三维情况.

附录 PML边界条件

在PML吸收边界层内，分别引入在x方向和y方向上的衰减函数d(x)和d(y)，并将每个未知量分裂成x方向和y方向两项之和，通过一个复数变换我们可得带吸收边界层的方程如下：

(A1)

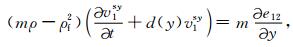
(A2)

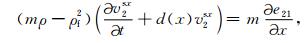
(A3)

(A4)

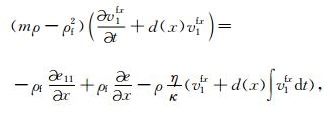
(A5)

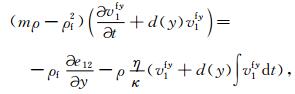
(A6)

(A7)

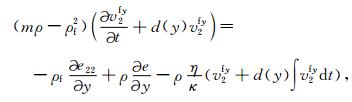
(A8)

(A9)

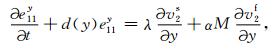
(A10)

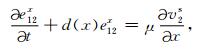
(A11)

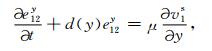
(A12)

(A13)

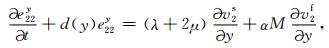
(A14)

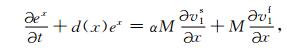
(A15)

(A16)

将上述方程组(A1)—(A16)在粗网格的PML边界层内离散，因其形式较复杂，在此略去其具体的计算格式，其中衰减函数d(x)和d(y)的选择可参考文献(Collino and Tsogka, 2001；Komatitsch and Tromp, 2003).

致谢  计算在“科学与工程计算”国家重点实验室中完成，在此表示感谢.同时也感谢审稿专家的宝贵意见.