2. 地球内部多尺度成像湖北省重点实验室, 武汉 430074
2. Hubei Subsurface Multi-scale Imaging Key Laboratory, Wuhan 430074, China
经过近二十多年的快速发展,海洋可控源电磁法(Marine Controlled Source Electromagnetic Method, MCSEM)已经成为海洋油气资源勘探中必不可少的地球物理勘探技术(Constable,2010).相比于陆地勘探,海洋油气勘探一般所需的投资更大,蕴含的风险更高,因此提高勘探成功率尤为重要.随着海洋电磁仪器和数据采集技术的不断提升,如何对大规模海洋电磁数据进行可靠的定量解释是迫切需解决的问题.一方面,MCSEM所采用的人工场源激发的电磁场是三维的,且真实的海底地电结构也是三维的,通过一维或二维反演解释可能难以获得勘探目标体全方位的空间展布,特别是难以获得海底小尺度目标体的构造信息(Commer and Newman, 2008);另一方面,由于海洋沉积作用,海底地层的宏观电导率常表现为各向异性,如海底泥砂岩薄互层,沿层理方向的电导率通常大于垂直层理方向的电导率(Anderson et al., 1994;Clavaud,2008).大量海洋电磁探测结果已表明,海底沉积地层宏观电性各向异性能够显著改变MCSEM响应(Yu and Edwards, 1992;Li and Dai, 2011).在各向异性程度较高的测区,若仍使用基于电导率各向同性的反演策略来解释海洋电磁资料将很有可能得到不合理甚至是错误的地质解释结果(Mohamad et al., 2010).
在三维正演方面,近年来众多学者就电性各向异性介质对MCSEM的影响进行了比较详细的研究(如殷长春等,2014;周建美等,2014;陈汉波等,2017);而对于MCSEM数据的各向异性反演,目前也已经取得较大的进展.例如Ramananjaona等(2011)、罗鸣等(2016)分别实现了层状垂向各向异性介质中MCSEM反演算法,并通过合成数据的各向同性与各向异性反演对比发现,各向异性反演能够有效消除虚假异常,提高反演精度;Masnaghetti和Ceci(2010)对2.5D情况下MCSEM垂直各向异性反演进行了研究;Key(2016)基于OCCAM反演方法实现了二维轴向各向异性MCSEM反演算法,显著提高了MCSEM数据解释能力;Wiik等(2011)采用对比源(contrast source)方法实现了层状各向异性介质中的MCSEM三维反演,提高了简单背景介质下MCSEM三维反演精度;Newman等(2010)、Sasaki(2013)分别采用非线性共轭梯度法和高斯牛顿算法实现了垂向各向异性MCSEM三维反演,但均采用迭代方法来求解正演问题,计算效率还有待进一步提升;最近赵宁等(2017)结合矩阵直接求解计算,实现了垂向各向异性MCSEM三维拟牛顿约束反演,取得了较好的效果.总体而言,目前对海洋电磁数据的三维各向异性反演研究仍相当有限,提升海洋可控源电磁三维反演算法的性能(如可靠性、稳定性和计算效率)仍是当前研究的重点之一.
本文在海洋可控源电磁三维各向同性反演算法的基础上(彭荣华等,2016a),发展了垂直各向异性海洋可控源电磁三维反演算法,提高了对海底复杂电性结构的反演解释能力,有利于促进MCSEM在海洋油气勘探和地质调查中发挥更重要的作用.
1 三维正演算法 1.1 控制方程由于海水层对电磁波的高衰减作用,MCSEM测量通常所采用的发射场源频率为0.1~10 Hz.在该频率范围内,位移电流的影响可以忽略不计.假定时谐因子为eiwt,则电场E所满足的二阶矢量Helmholtz方程为:
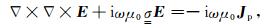
|
(1) |
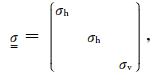
其中,E为电场强度,ω为角频率,μ0为真空中磁导率,Jp为场源电流密度,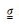
|
(2) |
其中σh为介质水平方向电导率,σv为垂直方向电导率.
对于MCSEM所采用的人工激发场源,其电流密度可视为脉冲函数,在场源点处具有奇异性.为克服场源的空间奇异性对数值结果的影响,本文正演模拟采用广泛使用的散射场(二次场)方法,将待求解的电磁场分解为由背景模型在人工场源激发下所产生的背景场和三维异常体所产生的散射场的叠加.此时,二次电场所满足的控制方程为:
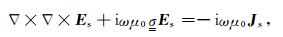
|
(3a) |

|
(3b) |
其中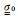
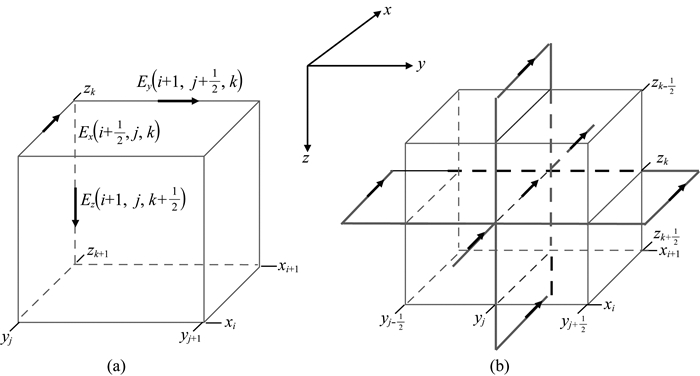
为求解二次电场控制方程(3)式,本文采用交错网格有限体积法(Staggered Finite-Volume, SFV),与常用的有限差分法相比,SFV是在控制体积内对微分方程进行积分.图 1展示了交错网格电磁场采样方式及电场分量的控制体积.考虑到电磁场在发射场源附近存在着剧烈变化,通过积分离散化能更准确地模拟电磁场的分布(Weiss and Constable, 2006).
|
图 1 (a) 电场交错采样网格;(b)电场x分量的控制体积 Fig. 1 (a) Staggered discretization of the electric field; (b) Integration volume for x-component of the electric field |
将方程(3)写成分量的形式:
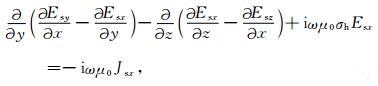
|
(4a) |

|
(4b) |
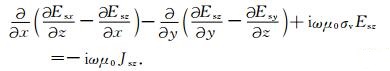
|
(4c) |
可以看出,对于垂直各向异性介质来说,尽管主轴方向上的电导率不再相同,但每个方向上的电流密度仅与该主轴方向上的电导率有关.因此,仍可以采用与各向同性介质相同的离散化方法对(4)式进行离散化.采用类似于彭荣华等(2016b)中的有限体积离散化方法,通过在控制体积内对(4)式进行近似积分,得到待求解的大型线性方程组为:
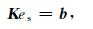
|
(5) |
其中系数矩阵K为稀疏、对称、正定复矩阵.该方程的求解对三维正演的计算精度以及后续三维反演的效率起决定作用.考虑到求解精度和计算效率,本文使用基于矩阵分解的直接法来替代传统的Krylov子空间迭代解法.直接解法相比于迭代解法有两大显著优点:一是求解时间和精度基本不受系数矩阵条件数的影响,使得求解精度更高,正演算法更稳定(韩波等,2015);二是直接解法所消耗的计算资源主要集中在系数矩阵的分解阶段,对于单一频率多个场源位置的问题,只需进行一次矩阵分解加上多次计算量极小的前代-回代过程即可(Streich,2009).本文通过调用MUMPS(Amestoy et al., 2006)线性运算库来实现直接求解.
1.3 正演算法验证为了验证本文正演算法的准确性,考虑具有拟解析解的一维层状垂直各向异性模型进行精度验证.图 2a是MCSEM中用于模拟高阻油气藏的典型模型,其中海水层厚度为1000 m,电阻率为0.33 Ωm;油气储层厚度为100 m,电阻率设为50 Ωm,顶部埋深距海底1000 m;海底沉积层具有垂直各向异性特征,水平电阻率和垂直电阻率分别为1 Ωm和2 Ωm.发射源采用水平电偶极子,位于海底上方50 m处,发射频率为0.25 Hz,电流强度为1 A.电磁接收测点位于海底表面.模型网格剖分为86×42×54,最小网格尺寸为200 m×200 m×50 m.

|
图 2 一维层状垂直各向异性模型MCSEM数值解与准解析解对比 (a)层状模型示意图;(b)电场分量的振幅;(c)电场分量的相位;(d)振幅相对误差;(e)相位误差;(f)各向异性下电场分量相对于各向同性下电场分量的归一场. Fig. 2 Comparison between FV numerical solutions and quasi-analytic solutions for marine 1D layered VTI model (a) Sketch of the layered VTI model; (b) Amplitude and (c) phase responses of the electric field; (d) Relative errors in amplitude and (e) phase difference; (f) Normalized amplitude responses of electric components of anisotropic model with respect to the amplitude responses of 1D isotropic reference model. |
图 2b和图 2c分别给出了inline模式(电场水平分量与发射偶极矩方向平行)和broadside模式(电场水平分量与发射偶极矩方向垂直)下电场分量的振幅-收发距曲线(Magnitude Versus Offset,MVO)与相位-收发距曲线(Phase Versus Offset,PVO)的准解析解与三维数值解的对比.其中准解析利用emmod程序(Hunziker et al., 2014)求得.从图中可以看出,无论inline模式还是broadside模式,电场分量的数值解与准解析均高度一致.图 2d和图 2e分别给出了数值解振幅和相位误差随收发距的分布.除在发射偶极附近外(收发距小于600 m),电场分量的振幅误差均小于1%(图 2d);而从图 2e可以看出,inline模式下相位误差均小于0.5°,而broadside模式相位误差尽管有所增加,但均小于1.0°,表明本文的正演算法能够得到较为精确的数值解.为了评估垂直各向异性对MCSEM响应的影响大小,图 2b和图 2c中还给出了海底沉积层为各向同性(电阻率为1 Ωm)的电场响应曲线(虚线所示),图 2f则给出了垂直各向异性沉积层背景下的电场响应相对于各向同性沉积层背景下的电场响应的归一化场.从图 2f可以看出,沉积层轻微的各向异性特征就会引起MCSEM响应显著的变化,如inline模式的电场响应变化可高达60%;而对broadside模式的影响相对较小,但最大变化也能达到20%.并且电性各向异性对inline模式和broadside模式数据的影响特征不同,如最大影响位置的差别.因此,反演中可同时利用inline模式和broadside模式的观测数据来增强反演的约束.从上述的正演计算结果分析可知,忽略电性各向异性的影响有可能会使得MCSEM数据反演产生较大的偏差,从而影响数据解释的可靠性.
2 三维反演方法 2.1 目标函数的构建由于地球物理电磁反演问题的不适定性(ill-posedness),为获得既拟合观测数据又满足一定先验条件的模型,通常采用Tikhonov正则化方式(Tikhonov and Arsenin, 1977)来构建反演的目标函数.对于垂直各向异性介质,其目标函数可定义为:
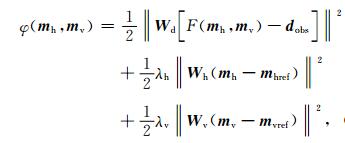
|
(6) |
其中右端第一项为数据拟合项,第二、三项分别为水平参数mh和垂直参数mv的模型正则项;λh和λv分别为水平参数和垂直参数模型的正则化因子,控制着数据拟合项和模型正则项在目标函数中的权重;mhref和mvref分别是水平参数和垂直参数的参考模型,包含着可获得的各类先验信息.Wd为数据协方差矩阵,包含了观测数据中的误差;Wh和Wv分别为水平和垂直方向的模型协方差矩阵,包含了模型先验结构信息,如最小结构模型或最光滑模型等.本文采用最光滑模型泛函来构建模型协方差矩阵(彭荣华等,2016a).
由于目标函数(6)式是非线性的,为获得(6)式的最优化解,通常采用基于线性搜索的迭代法来求解其极小值,其迭代方式为:
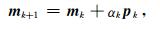
|
(7) |
其中pk为每次迭代的搜索方向,αk为沿着该搜索方向的步长.根据获取搜索方向pk的不同,目前常用于CSEM反演的最优化方法包括拟牛顿法(QN)、高斯牛顿法(GN)、非线性共轭梯度法(NLCG)及这些方法的变种(韩波等,2012).
2.2 高斯牛顿法考虑到正演中使用直接解法求解线性方程组,而反演中每更新一次模型都需要进行新的矩阵分解,即模型更新的次数越多,需要的矩阵分解次数也越多.为减少反演迭代中矩阵分解的次数,充分发挥直接解法的优势,本文采用具有近似二阶收敛性的高斯牛顿算法(Nocedal and Wright, 1999)来对目标函数(6)式进行最优化.
对目标函数(6)式在当前模型处进行二阶Taylor展开,并忽略高阶项,获得GN迭代的正规方程(normal equation):
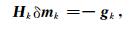
|
(8) |
其中目标函数的梯度向量gk和Hessian矩阵Hk可分别表示为:
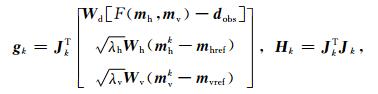
|
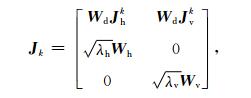
|
(9) |
其中Jhk和Jvk分别是当前模型响应对水平参数和垂直参数的灵敏度矩阵.直接求解(8)式需要显式地计算和存储灵敏度矩阵以及Hessian矩阵,对于三维MCSEM反演来说,需要消耗大量的计算内存以及运算时间,现有计算资源往往无法满足要求.因此,为避免显式地计算和存储灵敏度矩阵与Hessian矩阵,三维反演中通常采用迭代类方法来求解正规方程(8)式(Oldenburg et al., 2012;Jahandari and Farquharson, 2017),本文采用预条件共轭梯度法(PCG)迭代求解(8)式.在迭代求解中,只涉及到求解和存储灵敏度矩阵与模型向量的乘积,以及灵敏度矩阵转置与数据向量的乘积.并且,灵敏度矩阵(或转置)与向量的乘积可以转化为“拟正演”计算(彭荣华等,2016a).由于正演中采用直接解法求解线性方程组(5)式,在同一次GN迭代中,矩阵分解的结果可以多次重复利用.
2.3 模型更新策略求解正规方程(8)式获得每次GN迭代的搜索方向后,还需要确定公式(7)中的步长αk来获得每次GN迭代的模型更新量.步长αk的精确搜索需要求解关于αk的单变量最优化问题.对于三维反演来说,精确线性搜索往往因计算消耗巨大而无法进行.因此通常采用非精确线性搜索方式来确定步长.本文采用Armijo线性搜索法获得步长αk,公式为:
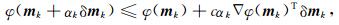
|
(10) |
其中c一般取10-4.
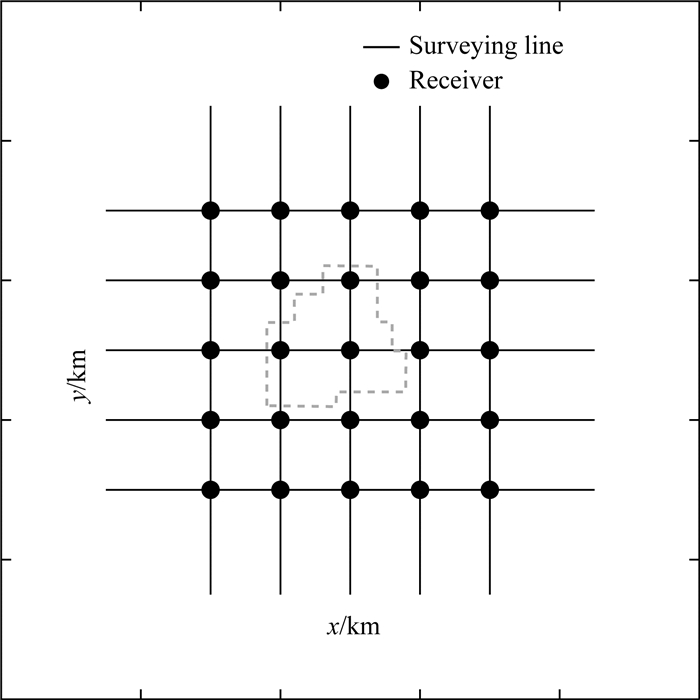
3 三维反演测试为了测试所开发的MCSEM垂直各向异性三维反演算法的有效性,本文考虑海洋油气勘探中常遇到的盐丘构造模型来进行测试.盐丘构造是重要的油气圈闭勘探区域,指示着潜在的油气聚集区.特别是在深水区域,盐丘体地质构造通常预示着油气勘探有利区域位置(Um et al., 2014).但由于盐丘体速度与围岩速度存在较大差异,呈现高波阻特征,造成对地震信号的屏蔽和畸变作用,使得地震勘探难以准确刻画盐丘的构造特征,特别是对于盐丘侧翼及盐下构造成像较为困难(Leveille et al., 2011).为测试所开发的反演算法对于复杂模型的有效性,本文利用地震勘探中的三维盐丘体模型(Aminzadeh et al., 1997)来模拟海洋可控源电磁勘探场景.整个盐丘模型区域大小为6 km×6 km×3 km(含海水层),如图 3所示.由于实际中盐丘体一般呈现各向同性或弱各向异性特征(Yan et al., 2014),本文假定盐丘体为各向同性,其电阻率设为50 Ωm;海底沉积层具有垂直电性各向异性特征,其水平电阻率和垂直电阻率分别为1 Ωm和4 Ωm;各向同性海水层的电阻率为0.33 Ωm,厚度为1 km.
|
图 3 海洋可控源电磁三维采集平面测网示意图 其中圆点为铺设于海底的接收测站,黑色实线为发射源的航行线,虚线方框为盐丘体模型在深度为1700 m时的平面投影. Fig. 3 Sketch of data acquisition grid for MCSEM survey Sea-bottom receivers and transmitter sail lines are denoted by circles and black lines, respectively. The dashed line indicates the projection of the salt dome reservoir at the depth of 1700 m. |
为更好地获得盐丘体的三维空间展布,采用平面测网的MCSEM采集方式,如图 3所示.整个数据采集网包括10条正交的测线,每条测线长为6 km,测线间距为1 km.发射源采用水平电偶极子源,偶极矩方向与测线方向一致,放置于海底上方50 m处.发射偶极子每隔400 m向海底发射电磁信号,频率为0.25 Hz和1.0 Hz,发射电流强度为1 A.25个电磁接收站均匀布设在海底表面,测点间距为1 km.
为得到该模型的MCSEM响应数据,正演网格剖分为72×72×56,正演计算所有收发距大于500 m的电场Ex分量和Ey分量.对正演响应数据添加5%的高斯噪声得到反演的观测数据.为避免反演中振幅较小的数据引起反演振荡,将观测数据中振幅小于5×10-14V·m-1的数据剔除掉,共形成约25100个有效观测数据.反演网格采用不同于正演计算的网格剖分,为46×46×50.对于垂直各向异性反演,根据(6)式,在反演前,需要设置合适的水平参数和垂直参数模型的正则化因子λh和λv,为了平衡反演迭代中数据拟合项与模型正则项的权重,本文采用松弛策略(cooling approach)来自动选取反演迭代中的正则化因子(彭荣华等,2016a).反演初始正则化因子λh和λv设为0.005,初始模型中的海底沉积层电阻率设为1 Ωm.反演迭代中,空气层和海水层电导率均保持不变.此外,为了研究电性各向异性结构对反演结果的影响,本文对该数据进行了常规的各向同性反演.在各向同性反演中,反演初始参数设置与垂直各向异性反演均一致.
图 4及图 5分别给出了各向同性反演和垂直各向异性反演在不同方向上的垂直剖面结果.从图中可以看出,基于各向同性的反演结果与基于垂直各向异性的反演结果相差较大.在各向同性反演中(见图 4与图 5第一行结果),反演所得到的高阻异常主要集中于海底沉积地层的浅部,这与真实的盐丘体分布区域(图中黑色实线所示)有很大的偏差;并且在高阻异常区域的下方,出现了明显的“虚假”低阻异常区.与之对比,基于垂直各向异性的反演结果并未见明显的“虚假”低阻异常区,其所得到的高阻异常区域也很好地刻画了盐丘目标体的空间展布.另外,对比垂直各向异性反演中水平方向(图 4与图 5第二行结果)与垂直方向(图 4与图 5第三行结果)的电阻率反演结果可以发现,垂直各向异性反演所得到的海底沉积层的电阻率在水平方向和垂直方向上均与真实模型的海底沉积层电阻率较为一致,但所获得的盐丘目标体的水平方向电阻率与垂直方向电阻率差异较大,其中垂直方向的电阻率反演结果在电阻率数值上与异常区域范围上都更接近于真实的盐丘目标体.这主要是由于MCSEM对不同方向电阻率的灵敏度不同所造成的.由于采用水平电偶极子源,MCSEM对高阻薄层垂直方向电阻率的灵敏度要远远大于对其水平方向电阻率的灵敏度(Brown et al., 2012).图 6给出了各向同性反演和垂直各向异性反演在不同深度上的水平切片结果.从图中可以看出,各向同性反演结果在深部出现了大范围的“虚假”低阻异常分布.与之对比,垂直各向异性反演所获得的水平电阻率高阻异常区域尽管要小于盐丘目标体的真实分布范围,但垂直方向电阻率反演结果却很好地刻画了盐丘目标体在水平方向上的展布,展示出垂直各向异性反演在电性各向异性环境下对高阻目标体良好的分辨能力.

|
图 4 不同XZ垂直剖面的MCSEM三维各向同性及垂直各向异性反演结果 图中黑色实线框为盐丘体真实位置.(a—c)各向同性反演结果;(d—f)垂直各向异性反演水平方向电阻率结果;(g—i)垂直各向异性反演垂直方向电阻率结果. Fig. 4 Comparisons in different vertical XZ cross-sections between isotropic inversion results and VTI inversion results Isotropic inversion results (a—c); VTI inversion results for horizontal resistivities (d—f) and vertical resistivities (g—i). The location of the salt dome reservoir is indicated by the black line. |

|
图 5 不同YZ垂直剖面的MCSEM三维各向同性及垂直各向异性反演结果 图中黑色实线框为盐丘体真实位置.(a—c)各向同性反演结果;(d—f)垂直各向异性反演水平方向电阻率结果;(g—i)垂直各向异性反演垂直方向电阻率结果. Fig. 5 Comparisons in different vertical YZ cross-sections between isotropic inversion results and VTI inversion results Isotropic inversion results (a—c); VTI inversion results for horizontal resistivities (d—f) and vertical resistivities (g—i). The location of the salt dome reservoir is indicated by the black line. |

|
图 6 不同深度水平切片的MCSEM三维各向同性及垂直各向异性反演结果 图中黑色实线框为盐丘体真实位置.(a—c)各向同性反演结果;(d—f)垂直各向异性反演水平方向电阻率结果;(g—i)垂直各向异性反演垂直方向电阻率结果. Fig. 6 Comparisons in different depth slices between isotropic inversion results and VTI inversion results Isotropic inversion results (a—c); VTI inversion results for horizontal resistivities (d—f) and vertical resistivities (g—i). The location of the salt dome reservoir is indicated by the black line. |
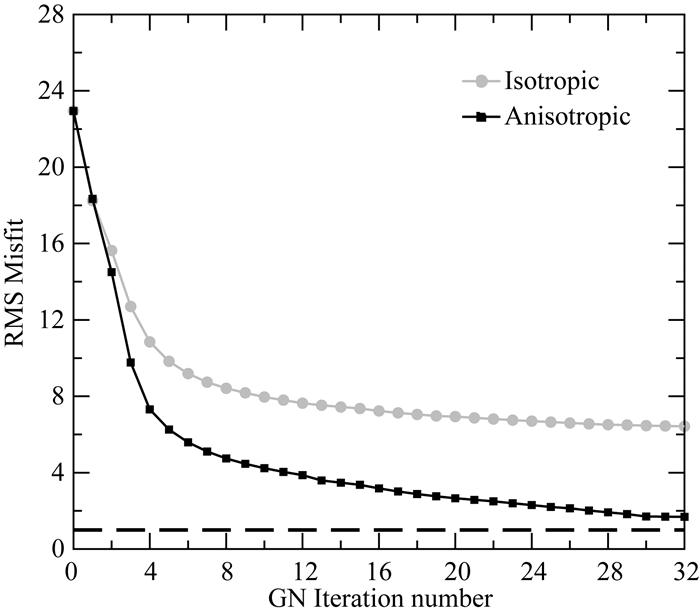
图 7展示了各向同性反演和垂直各向异性反演过程中数据拟合差的变化情况.从图中可以看出,当对受电性各向异性结构影响的海洋可控源电磁数据采用各向同性反演时,反演的数据拟合差在前几次迭代降低后陷入停滞状态,迭代次数的增加并未能有效降低数据拟合差,最终收敛至6.42;与之对比,当采用垂直各向异性反演时,反演的数据拟合差随迭代次数的增加逐步降低,最终收敛至1.68,尽管与目标拟合差(RMS=1)有一定偏差,但要远低于各向同性反演的数据拟合差.
|
图 7 各向同性及垂直各向异性反演数据拟合差随迭代次数变化(虚线为目标数据拟合差) Fig. 7 RMS misfit plots with iterations for isotropic and VTI inversion. The target misfit is indicated by the dashed line |
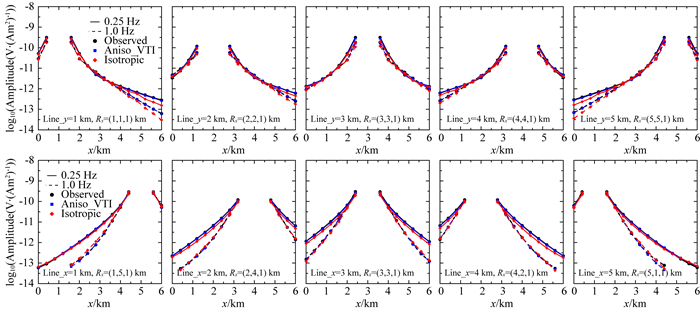
图 8给出了每条测线上单个接收站的数据拟合情况.其中第一行为沿x方向测线上特定接收站电场x分量的数据拟合,第二行为沿y方向测线上特定接收站电场y分量的数据拟合.从图中可以看出,基于垂直各向异性反演的响应数据与观测数据拟合得很好,而基于各向同性反演的响应数据在大收发距区域与观测数据存在较大偏差,这主要是由于大收发距的数据受沉积层电性各向异性结构影响较大,各向同性反演无法搜索出合适的模型参数来拟合这些数据.这也说明了当MCSEM数据受到电性各向异性结构影响时,对数据进行各向异性反演是十分必要的.
|
图 8 不同测线上不同测点的各向同性及垂直各向异性反演数据拟合曲线 Fig. 8 Comparisons between observed data and predicted data for different receivers for isotropic inversion model and VTI inversion model |
海底地层的宏观电性各向异性会显著影响海洋可控源电磁数据.针对海底地层电导率各向异性情况,本文实现了垂直各向异性介质中频率域海洋可控源电磁三维反演算法.三维正演利用交错网格有限体积法对二次电场Helmholtz控制方程进行离散化;考虑到海洋可控源电磁中多场源发射情况,采用直接矩阵分解技术求解离散所得的大型线性方程组,提高正演计算效率.三维反演采用具有近似二次收敛性的高斯牛顿最优化算法,保证反演算法稳定及高效.在此基础上,通过对受电导率各向异性结构影响的MCSEM合成数据分别进行各向同性三维反演及垂直各向异性三维反演,反演结果表明,相比于常规的各向同性三维反演,基于电导率垂直各向异性介质的三维反演能够获得更为可靠的地下电阻率结构和异常体分布,展现出对海底电性各向异性结构更为优良的反演解释能力.
随着海洋电磁勘探精度要求的提高,特别是为获得海底小尺度目标体的构造信息,对海底构造地电模型的假设将越来越接近真实情况,研究更为复杂的电导率各向异性情况(如倾斜各向异性介质)将会成为精细MCSEM数据反演解释的重要内容.本文将各向同性三维反演算法扩展到垂直各向异性三维反演中,但仍有大量的工作有待完成.
致谢 感谢MUMPS线性运算库的开发者们的无私贡献.向匿名审稿人对本文提出的宝贵修改意见表示衷心感谢.
Amestoy P R, Guermouche A, L'Excellent J Y, et al. 2006. Hybrid scheduling for the parallel solution of linear systems. Parallel Computing, 32(2): 136-156. DOI:10.1016/j.parco.2005.07.004 |
Aminzadeh F, Brac J, Kuntz T. 1997. 3-D salt and overthrust models.//67th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Anderson B, Bryant I, Luling M, et al. 1994. Oilfield anisotropy:Its origins and electrical characteristics. Oilfield Review, 6(4): 48-56. |
Brown V, Hoversten M, Key K, et al. 2012. Resolution of reservoir scale electrical anisotropy from marine CSEM data. Geophysics, 77(2): E147-E158. DOI:10.1190/geo2011-0159.1 |
Chen H B, Li T L, Xiong B, et al. 2017. Finite-element modeling of 3D MCSEM in arbitrarily anisotropic medium using potentials on unstructured grids. Chinese Journal of Geophysics (in Chinese), 60(8): 3254-3263. DOI:10.6038/cjg20170830 |
Clavaud J B. 2008. Intrinsic electrical anisotropy of shale:The effect of compaction. Petrophysics, 49(3): 243-260. |
Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion. Geophysical Journal International, 172(2): 513-535. DOI:10.1111/gji.2008.172.issue-2 |
Constable S. 2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics, 75(5): 75A67-75A81. DOI:10.1190/1.3483451 |
Han B, Hu X Y, He Z X, et al. 2012. Mathematical classification of magnetotelluric inversion methods. Oil Geophysical Prospecting (in Chinese), 47(1): 177-188. |
Han B, Hu X Y, Huang Y F, et al. 2015. 3-D frequency-domain CSEM modeling using a parallel direct solver. Chinese Journal of Geophysics (in Chinese), 58(8): 2812-2826. DOI:10.6038/cjg20150816 |
Hunziker J, Thorbecke J, Slob E. 2014. The electromagnetic response in a layered vertical transverse isotropic medium:A new look at an old problem. Geophysics, 80(1): F1-F18. |
Jahandari H, Farquharson C G. 2017. 3-D minimum-structure inversion of magnetotelluric data using the finite-element method and tetrahedral grids. Geophysical Journal International, 211(2): 1189-1205. DOI:10.1093/gji/ggx358 |
Key K. 2016. MARE2DEM:A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophysical Journal International, 207(1): 571-588. DOI:10.1093/gji/ggw290 |
Leveille J P, Jones I F, Zhou Z Z, et al. 2011. Subsalt imaging for exploration, production, and development:A review. Geophysics, 76(5): WB3-WB20. DOI:10.1190/geo2011-0156.1 |
Li Y G, Dai S K. 2011. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophysical Journal International, 185(2): 622-636. DOI:10.1111/gji.2011.185.issue-2 |
Luo M, Li Y G, Li G. 2016. Frequency-domain inversion of marine CSEM data in one-dimensional vertically anisotropic structures. Chinese Journal of Geophysics (in Chinese), 59(11): 4349-4359. DOI:10.6038/cjg20161134 |
Masnaghetti L, Ceci F. 2010. Analysis of the sensitivity to anisotropy of CSEM data using 2.5D modeling and inversion.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Mohamad S A, Lorenz L, Hoong L T, et al. 2010. A practical example why anisotropy matters: A CSEM case study from south east Asia.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Newman G A, Commer M, Carazzone J J. 2010. Imaging CSEM data in the presence of electrical anisotropy. Geophysics, 75(2): F51-F61. DOI:10.1190/1.3295883 |
Nocedal J, Wright S. 1999. Numerical Optimization. New York, USA: Springer-Verlag.
|
Oldenburg D W, Haber E, Shekhtman R. 2012. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics, 78(1): E47-E57. |
Peng R H, Hu X Y, Han B. 2016a. 3D inversion of frequency-domain CSEM data based on Gauss-Newton optimization. Chinese Journal of Geophysics (in Chinese), 59(9): 3470-3481. DOI:10.6038/cjg20160929 |
Peng R H, Hu X Y, Han B, et al. 2016b. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method. Chinese Journal of Geophysics (in Chinese), 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
Ramananjaona C, MacGregor L, Andréis. 2011. Sensitivity and inversion of marine electromagnetic data in a vertically anisotropic stratified earth. Geophysical Prospecting, 59(2): 341-360. DOI:10.1111/gpr.2011.59.issue-2 |
Sasaki Y. 2013. Resolution of shallow and deep marine CSEM data inferred from anisotropic 3D inversion.//83rd Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics, 74(5): F95-F105. DOI:10.1190/1.3196241 |
Tikhonov A N, Arsenin V. 1977. Solutions of Ill-Posed Problems. Washington, D C, USA: John Wiley and Sons.
|
Um E S, Commer M, Newman G A. 2014. A strategy for coupled 3D imaging of large-scale seismic and electromagnetic data sets:Application to subsalt imaging. Geophysics, 79(3): ID1-ID13. DOI:10.1190/geo2013-0053.1 |
Weiss C J, Constable S C. 2006. Mapping thin resistors and hydrocarbons with marine EM methods, Part Ⅱ-Modeling and analysis in 3D. Geophysics, 71(6): G321-G332. DOI:10.1190/1.2356908 |
Wiik T, Löseth L O, Usrin B, et al. 2011. TIV contrast source inversion of mCSEM data. Geophysics, 76(1): F65-F76. DOI:10.1190/1.3524270 |
Yan F Y, Han D H, Yao Q L, et al. 2014. Seismic velocities of halite salt: Anisotropy, dispersion, temperature and stress effects.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Yin C C, Ben F, Liu Y H, et al. 2014. MCSEM 3D modeling for arbitrarily anisotropic media. Chinese Journal of Geophysics (in Chinese), 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
Yu L M, Edwards R. 1992. The detection of lateral anisotropy of the ocean floor by electromagnetic methods. Geophysical Journal International, 108(2): 433-441. DOI:10.1111/gji.1992.108.issue-2 |
Zhao N, Wang X B, Qin C, et al. 2017. 3D frequency-domain MCSEM constrained inversion in VTI media. Chinese Journal of Geophysics (in Chinese), 60(5): 1946-1954. DOI:10.6038/cjg20170527 |
Zhou J M, Zhang Y, Wang H N, et al. 2014. Efficient simulation of three-dimensional marine controlled-source electromagnetic response in anisotropic formation by means of coupled potential finite volume method. Acta Physica Sinica (in Chinese), 63(15): 159101. DOI:10.7498/aps.63.159101 |
陈汉波, 李桐林, 熊彬, 等. 2017. 基于Coulomb规范势的电导率呈任意各向异性海洋可控源电磁三维非结构化有限元数值模拟. 地球物理学报, 60(8): 3254-3263. DOI:10.6038/cjg20170830 |
韩波, 胡祥云, 何展翔, 等. 2012. 大地电磁反演方法的数学分类. 石油地球物理勘探, 47(1): 177-188. |
韩波, 胡祥云, 黄一凡, 等. 2015. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812-2826. DOI:10.6038/cjg20150816 |
罗鸣, 李予国, 李刚. 2016. 一维垂直各向异性介质频率域海洋可控源电磁资料反演方法. 地球物理学报, 59(11): 4349-4359. DOI:10.6038/cjg20161134 |
彭荣华, 胡祥云, 韩波. 2016a. 基于高斯牛顿法的频率域可控源电磁三维反演研究. 地球物理学报, 59(9): 3470-3481. DOI:10.6038/cjg20160929 |
彭荣华, 胡祥云, 韩波, 等. 2016b. 基于拟态有限体积法的频率域可控源三维正演计算. 地球物理学报, 59(10): 3927-3939. DOI:10.6038/cjg20161036 |
殷长春, 贲放, 刘云鹤, 等. 2014. 三维任意各向异性介质中海洋可控源电磁法正演研究. 地球物理学报, 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
赵宁, 王绪本, 秦策, 等. 2017. 基于VTI各向异性介质的频率域海洋可控源电磁三维约束反演. 地球物理学报, 60(5): 1946-1954. DOI:10.6038/cjg20170527 |
周建美, 张烨, 汪宏年, 等. 2014. 耦合势有限体积法高效模拟各向异性地层中海洋可控源的三维电磁响应. 物理学报, 63(15): 15901. DOI:10.7498/aps.63.159101 |
 2019, Vol. 62
2019, Vol. 62


