2. 广西隐伏金属矿产勘查重点实验室, 广西桂林 541004
2. Guangxi Key Laboratory of Hidden Metallic Ore Deposits Exploration, Guilin Guangxi 541004, China
吸收边界条件是探地雷达(Ground Penetrating Radar, GPR)波动方程数值模拟的研究热点(Giannopoulos, 2005; Drossaert and Giannopoulos, 2007; 冯德山等, 2012).由于计算机内存空间的有限性,利用数值模拟方法求解GPR波动方程时,不完善的空间数值截断会产生明显的虚假反射,严重影响GPR数值模拟的精度(Irving and Knight, 2006; Li et al., 2012; 张彬等, 2017).为此,国内外学者对吸收边界条件进行了深入研究,提出并发展了多种边界条件,如旁轴近似边界条件(Clayton and Engquist, 1977; Engquist and Majda, 1977)、Sarma边界条件(Sarma et al., 1998)、Mur吸收边界条件(Mur, 1981a, b).这些边界条件虽然对模型截断边界产生的超强反射能量具有一定的吸收效果,但在计算区域外边界处仍有0.5%~5%的反射系数(冯德山等, 2016b).由Berenger (1994)提出的完全匹配层(Perfectly Matched Layer, PML)通过在计算网格外边界加载一种非物理的吸收介质,从而达到电磁波在PML层内按指数规律衰减的目的.理论上PML边界条件对所有入射角度和频率的电磁波都具有零反射系数,将边界条件研究向前推进了一大步.其后Chew和Liu等(1996)通过引入复数伸展坐标系对PML边界条件进行公式化,证明了PML的本质是在复拉伸坐标系中进行坐标变换.近年来,PML边界条件被广泛应用于GPR数值模拟中(Roberts and Daniels, 1997; Lee et al., 2004; 刘四新和曾昭发, 2007; Millington and Cassidy, 2010; 李静等, 2010).但Berenger提出的PML理论体系是非Maxwell方程且物理机制模糊,同时其电磁场分裂计算增加了计算内存与数值实现的难度(冯德山等, 2016b; Hu et al., 2017).为此,Sacks等(1995)和Gedney(1996)通过在PML层内引入各向异性介质,提出了单轴各向异性完全匹配层(Uniaxisal PML, UPML)边界条件.相比于传统PML边界条件,UPML边界条件虽然与传统PML边界条件具有等价的吸收性能(Rappaport, 1995),但避免了电磁场分裂,减弱了数值实现的难度(Lu et al., 2005; Bernard et al., 2010; Feng and Dai, 2011; 冯晅等, 2011).然而,PML和UPML边界条件只对行波吸收效果好,对入射角度较小的低频波、掠角波和隐失波吸收效果差.为此,Kuzuoglu和Mittra(1996)在复拉伸坐标函数中,引入频移因子和收缩因子,提出了一种复频移完全匹配层(Complex Frequency Shifted PML, CFS-PML)边界条件,实现了低频波、掠角波和隐失波地有效吸收.Wrenger(2002)比较了PML和CFS-PML边界条件的吸收效果,验证了CFS-PML边界条件可有效吸收倏逝波,提高了模拟精度;Roden和Gedney(2000)为弱化CFS-PML边界条件的数值实现难度,提出了卷积完全匹配层(Convolutional PML, CPML)边界条件(Correia and Jin, 2005),在保证计算精度的同时,提高了计算效率;Irving和Knight(2006)采用非分裂CPML边界条件,在GPR正演模拟中有效吸收了临界入射波;Drossaert和Giannopoulos(2007)在弹性波模拟中将递归积分代替卷积积分,提出了一种递归积分完全匹配层(Recursive Integration PML, RIPML)边界条件,相比于CPML边界条件的数值实现,节约了计算内存;Giannopoulos(2008)将RIPML边界条件应用于GPR正演模拟问题中.
上述PML及其改进的边界条件大都是在时域有限差分法(Finite Difference Time Domain, FDTD)正演模拟中提出并得到广泛应用.FDTD是一种基于一阶波动方程的数值计算方法,然而时域有限元法(Finite Element Time Domain, FETD)求解的波动方程大都以二阶形式出现(徐世浙, 1994; Matzen, 2011; 刘有山等, 2013; Liu et al., 2012).相比于一阶波动方程,二阶波动方程涉及的场分量更少,因此利用FETD求解二阶波动方程可有效减少内存占用量、提高计算效率(唐文等, 2014).此外,FETD具有应用非规则网格离散复杂介质模型和自然满足自由边界条件的优点.近年来,基于二阶电磁波动方程的FETD被引入到GPR正演模拟研究中:Lu等(2005)将基于PML边界条件的FETD应用于Debye频散介质的GPR正演模拟中;戴前伟等(2012a, b)为提高模拟精度,将双二次插值及三角剖分的FETD应用于GPR正演模拟;冯德山等(2012)通过分析透射边界条件和Sarma边界条件的各自优势,提出了一种适合FETD的混合边界条件,改善了GPR正演模拟的精度;Varela-Ortiz等(2013)利用FETD模拟分析了GPR探测混凝土桥梁的电磁响应特征;冯德山等(2016a)将基于小波插值基函数的FETD应用于GPR正演模拟中,提高了正演模拟精度;Zarei等(2016)采用正交插值基函数的FETD实现了GPR正演模拟,弱化了数值频散对信号的影响;冯德山等(冯德山和王珣, 2017; Feng et al., 2018)推导了非规则四边形网格的FETD正演算法及FETD/FDTD混合算法,实现了复杂地质体的GPR正演.
由于FETD与FDTD求解的波动方程形式不同,广泛应用于FDTD的各种PML边界条件不能直接应用于FETD正演模拟中.因此,如何高效地将PML边界条件以变分形式加载到二阶电磁波动方程的FETD正演算法中,成为当前波动方程数值模拟的研究热点.Komatitsch和Tromp(2003)根据一阶弹性波方程FDTD正演算法中构建PML边界条件的思想,首次推导了适用于二阶弹性波动方程的分裂PML边界条件,正演模拟结果表明在人工截断边界上,以变分形式将PML边界条件引入到FETD方程组中,可取得良好的吸收效果.刘有山等(2012, 2013)和刘少林等(2015)将该PML边界条件应用于三角网格的FETD的弹性波正演模拟中.然而,该PML边界条件的公式中存在波场关于时间的三阶导数,且需对波场进行分裂,使得计算时间和存储空间大大增加.为此,Basu等(Basu and Chopra, 2004; Basu, 2009)通过构建辅助微分方程,给出了一种二阶弹性波FETD正演模拟的非分裂PML边界条件,大大提高了计算效率.目前,基于二阶波动方程的PML边界条件在声波(邢丽, 2006, 2011; 马友能等, 2013)、弹性波(Li et al., 2010; Liu et al., 2014; 刘少林等, 2015; 周凤玺和高贝贝, 2016)、面波(Zhao and Shi, 2013)的FETD数值模拟中得到广泛应用,并得到不断发展(Martin and Komatitsch, 2009; Matzen, 2011).
本文依据复拉伸坐标变换和引入辅助变量,合理构建辅助微分方程,提出了一种适合二阶GPR电磁波动方程FETD正演模拟的PML边界条件.采用Galerkin法,详细推导了PML区的时域有限元方程及其详细的求解步骤.数值算例验证了PML边界条件的良好吸收效果,实现了PML边界条件在二阶电磁波动方程GPR时域有限元正演模拟中的应用.
1 复拉伸坐标系下的二阶电磁波动方程及其PML边界条件由电磁波理论可知,GPR电磁波在地下介质中的传播规律满足Maxwell方程组(冯德山等,2012),考虑二维地电结构的走向为y轴,则TM模式下的二阶时间域电磁波波动方程为
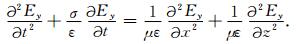
|
(1) |
式(1)中,Ey为y方向电场强度(V·m-1); t为时间(s);μ, σ, ε分别是介质的磁导率(H·m-1)、电导率(S·m-1)和介电常数(F·m-1).
式(1)转化到频率域可得
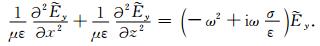
|
(2) |
其中,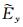
以x方向为例,PML边界条件的主要思想是对PML层内的波动方程进行重构,使得解的形式为Aexp[i(kxx+kzz-ωt)-γx],γ>0.该解表示电磁波沿x递增方向(z方向同理)呈指数衰减,从而使得计算区域和PML区域之间的反射系数趋于零(邢丽, 2011).为此,引入复坐标变量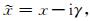
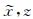
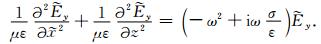
|
(3) |
式(3)的平面波解形式为
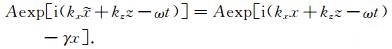
|
(4) |
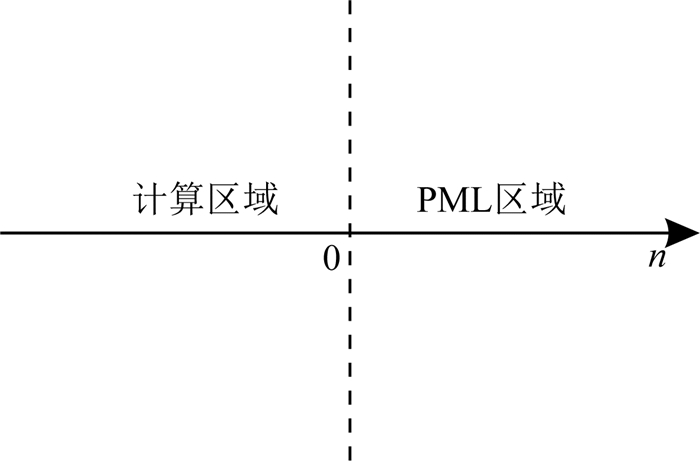
根据Chew和Liu(1996)提出的复拉伸坐标推导PML边界条件的思想:假设计算区域和PML区域的边界位于n=0(n=x, z)处,计算区域和PML区域分别位于n < 0和n>0处,如图 1所示.定义衰减系数dn,使其在计算区域为0,在PML区域大于0,设新复坐标函数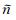
|
图 1 计算区域与PML区域示意图 Fig. 1 Schematic diagram of calculated and PML area |
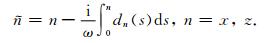
|
(5) |
式(5)两边求导可得
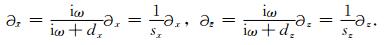
|
(6) |
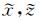
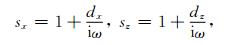
|
(7) |
式(7)为传统PML边界条件对应的复拉伸函数,只对行波有效,对平行于PML和计算区域交界处传播的隐失波和低频波吸收效果差.为解决该问题,Sacks等(1995)和Gedney(1996)在传统复拉伸函数的基础上,通过增加坐标收缩因子kx和kz,提出了UPML边界条件(Bernard et al., 2010).其复拉伸函数可写为
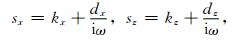
|
(8) |
式(8)中,kx≥1, kz≥1,收缩因子的引入可使电磁波进入PML区域后传播方向沿法线方向弯曲,使得大角度入射波能够更加深入PML区域中并逐渐衰减(Zhang and Yang, 2010).
将式(6)代入式(2),可推导复数拉伸坐标系下的二阶频率域电磁波动方程为
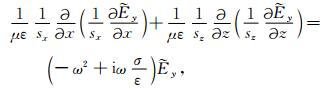
|
(9) |
式(9)两边同乘以sxsz,并整理可简写成为
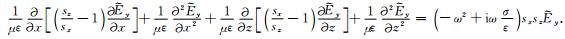
|
(10) |
引入中间变量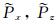
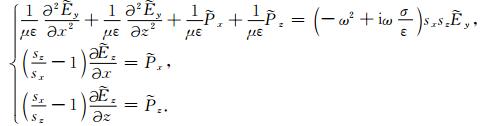
|
(11) |
将式(8)代入式(11),并引入中间变量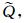
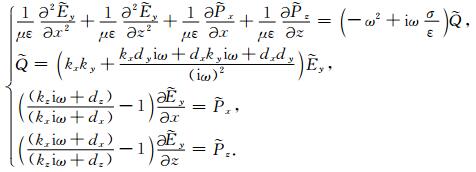
|
(12) |
式(12)转化到时间域,并整理可得
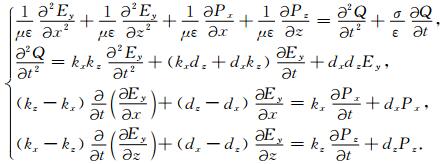
|
(13) |
式(13)中,Px, Pz, Q是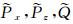
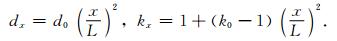
|
(14) |
式(14)中,x表示网格节点到PML层内界面的距离;L为PML层的厚度;d0, k0为常数,通常取d0=-3vlogRc/2L, v为电磁波在介质中传播的最大速度,Rc为理论反射系数(Collino and Tsogka, 2001).沿z方向的衰减系数和收缩因子的计算公式与x方向类似.
2 基于PML边界条件的二阶电磁波时域有限元方程根据Galerkin法原理(徐世浙, 1994),式(14)的弱形式为
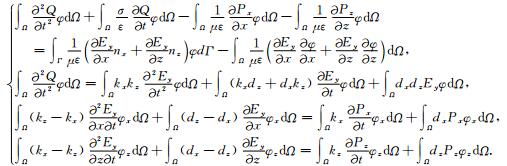
|
(15) |
其中,Γ, Ω分别为计算区域及其边界;n=(nx, ny)T为计算区域的边界外法线向量;φ=(φx, φy)T为测试向量.在PML边界上利用位移为0的Dirichlet边界条件.利用Galerkin法可推导式(15)对应的有限元方程为
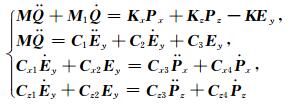
|
(16) |
其中,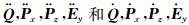
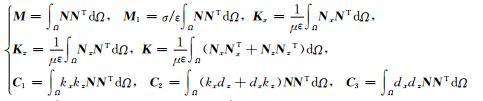
|
(17) |
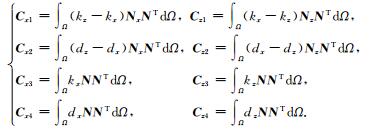
|
(18) |
其中,N是计算区域内的形函数,Nx和Nz分别是形函数关于x和z的导数.由于参数kx, kz, dx, dz一般是赋值于网格节点上,且作用于PML层内的Ey值.因此,需将对应的衰减系数和收缩因子与相应的形函数或形函数的导数对应相乘.由式(16)可知,PML层内的电磁波波动方程求解增加了三个辅助变量,以致需要更多的内存空间.但PML区域相比计算区域的规模较小,总体来说内存消耗不会明显增加.
式(16)中的各式具有的一般形式为
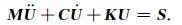
|
(19) |
M为质量矩阵,C为阻尼矩阵,S为荷载向量,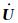
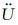
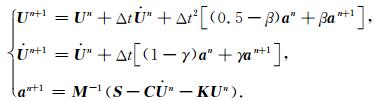
|
(20) |
其中,n为时间步数,a为加速度,β为常数,当且仅当β=0,γ=1/2为保能量的.上述有限元形成的系数矩阵通常为大型稀疏矩阵,若全部存储需要很大的内存空间.为此,本文对系数矩阵采用压缩存储行(CSR)格式,只需存储其非零元素,可极大减少所需存储空间(刘有山等, 2013).此外,采用集中质量矩阵技术(刘少林等, 2015),以避免矩阵M的求逆运算,提高计算效率.
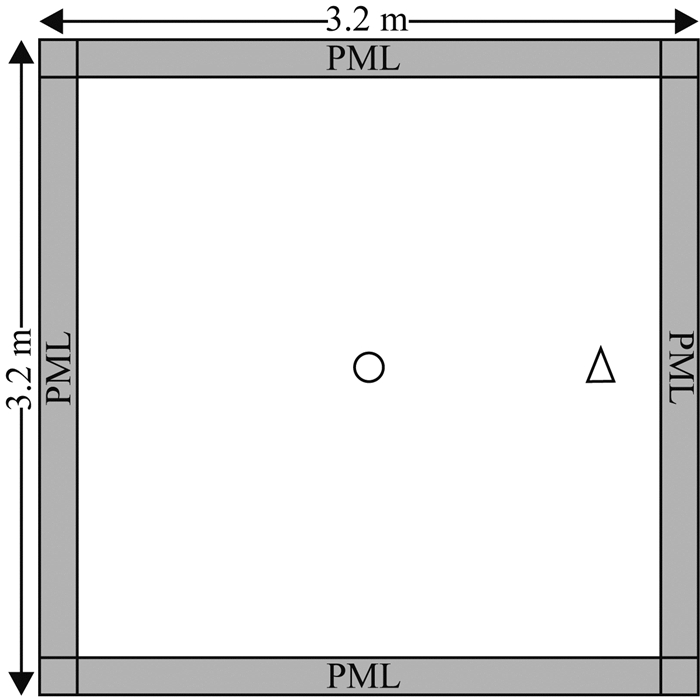
3 计算实例 3.1 PML边界条件吸收效果及计算效率分析为验证本文提出的二阶电磁波动方程的PML边界条件的吸收效果,建立了一个均匀介质模型,利用基于PML边界条件的GPR时域有限元正演算法对其进行正演计算,并与无边界条件和Sarma边界条件的吸收效果及计算效率进行对比分析.图 2是大小为3.2 m×3.2 m的均匀介质模型,背景介质的相对介电常数为10.0,电导率为0.001 S·m-1.为简便起见,模型空间离散采用四边形网格进行,共有320×320个单元,网格单元大小0.01 m×0.01 m,PML层占20个网格.为保证显示时间迭代的稳定性,时间步长取为0.01 ns,模拟计算时间为50 ns.采用中心频率为500 MHz的零相位Ricker子波作为激励源,且位于模型正中心(1.6 m, 1.6 m),如图中圆圈所示;接收点的坐标位置为(2.9 m, 1.6 m),如图中三角形所示,距离PML层的水平距离为0.1 m.
|
图 2 施加PML边界的均匀介质模型 Fig. 2 Homogenous model with PML boundary condition |
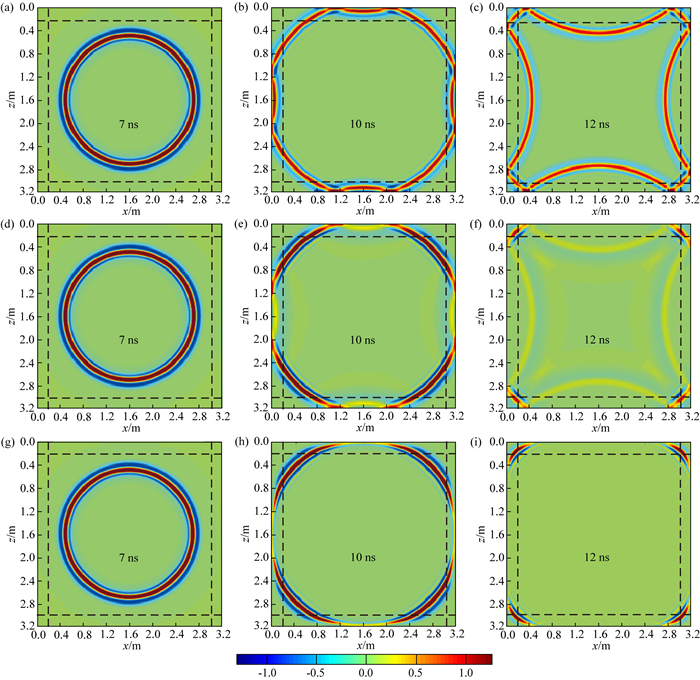
分别利用无边界条件、Sarma边界条件和PML边界条件的FETD正演算法对该模型进行计算,获得不同时刻的雷达波场快照如图 3所示,黑色虚线表示PML层与计算区域的边界.图 3(a,b,c)为无边界条件的波场快照;图 3(d, e,f)为施加Sarma边界条件的波场快照;图 3(g,h,i)为施加PML边界条件的波场快照.由图可见:当电磁波传播到7 ns时刻,电磁波波前面以同心圆扩散传播未遇到模型边界,三种边界条件下的波场快照相同.当传播到10 ns时刻时,电磁波传播到模型边界处,无边界条件下四条人工边界的电磁波反射强烈,如图 3b所示;Sarma边界条件虽然对人工边界产生的反射波能量有一定的吸收,但反射波依然清晰可见,如图 3e所示;PML边界条件对模型边界处的反射波吸收最好,未见明显的反射波,如图 3h所示.当电磁波传播到12 ns时刻时,无边界条件和Sarma边界条件下人工截断边界处的反射波向模型中间扩散传播,对计算区域内的电磁波传播干扰非常严重,如图 3c和f所示.而PML边界条件下,各种入射角度的电磁波都有理想的吸收效果,没有明显的虚假反射波出现.
|
图 3 均匀模型无边界条件(a, b, c)、Sarma边界条件(d, e, f)和PML边界条件(g, h, i)下Ey分量不同时刻的波场快照 Fig. 3 Snapshot of field component Ey of homogenous model at different times without boundary condition (a, b, c), with Sarma boundary condition(d, e, f) and PML boundary condition (g, h, i) |
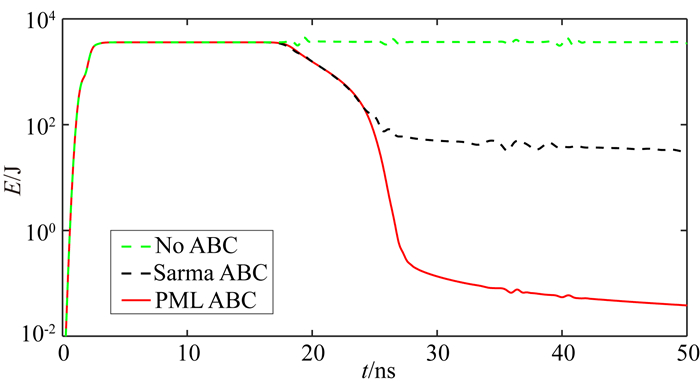
图 4为施加不同边界条件的计算区域内电场能量随时间变化曲线,由图可见:在0 ns到18 ns之间,由于电场在计算区域内传播,施加三种边界条件时的电场能量随时间变化相同.无边界条件时,电场能量一直在5800 J左右震荡.Sarma边界条件下,电场能量在18 ns后一直衰减到约60 J,可见Sarma边界条件对电磁波能量有一定的吸收.施加PML边界条件时,电场在18 ns以后逐渐传播到PML层内,能量迅速衰减更快;传播时间到达30ns以后,电场能量迅速衰减至0.03 J.由此可见,PML边界条件的吸收效果要远优于Sarma边界条件的吸收效果.
|
图 4 电场能量随时间的变化曲线 Fig. 4 Curves of electric-field energy evolution with the time |
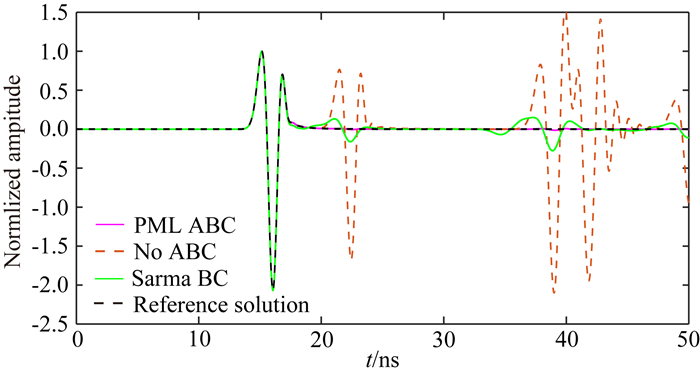
分别利用无边界条件、Sarma边界条件和PML边界条件的GPR时域有限元法计算得到的接收点处的GPR信号与参考解对比图,如图 5所示.本文采用的参考解是在不施加边界条件下,为保证在模拟时间内虚假反射不会到达接收点,将计算模型扩大5倍后采用相同数值方法计算得到的,激励源和接收点的相对位置保持不变.由图可见:无边界条件和Sarma边界条件下的GPR信号中人工边界产生的虚假反射波清晰可见,而施加PML边界条件的GPR信号与参考解吻合较好,未见明显的虚假反射波.
|
图 5 不同边界条件下接收点处获得单道波形与参考解对比 Fig. 5 Compared reference solution and single signal with different boundary condition at receiving point |
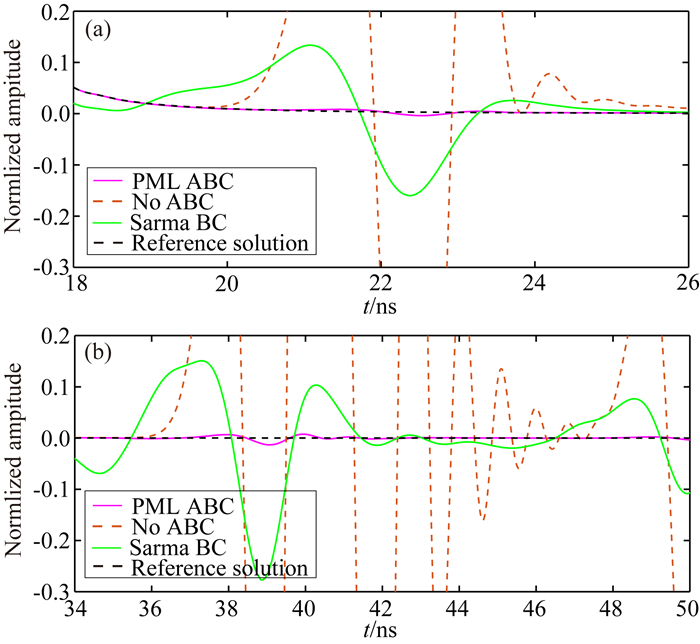
为更好地对比施加PML边界条件的GPR信号和参考解,将图 5中的18~26 ns和36~48 ns之间的信号进行局部放大,获得的波形对比如图 6所示.由图可见:与无边界条件和Sarma边界条件相比,施加PML边界条件之后GPR信号与参考解大部分拟合较好,局部有微弱反射误差,约为0.2%.由此可见:本文构建的PML边界条件的吸收效果要远优于Sarma边界条件,具有近似零反射系数.
|
图 6 图 5中18~26 ns和34~48 ns的放大图 (a) 18~26 ns; (b) 34~50 ns. Fig. 6 Local enlarged image of Fig. 5 at 18~26 ns and 34~48 ns |
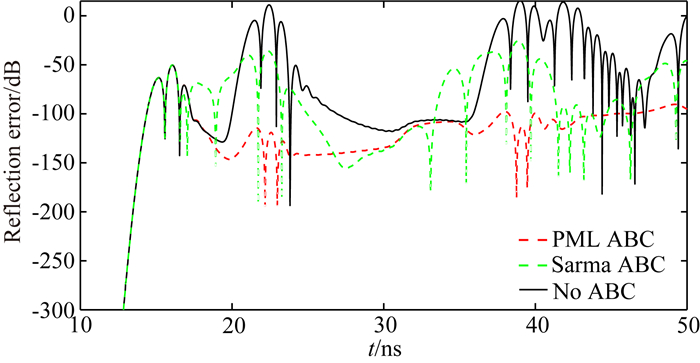
为定量分析PML和Sarma边界条件的吸收效率,利用反射误差计算公式Errordb=20×log(|ES-Eref|/|Erefmax|),计算了图 5中不同边界条件的时域反射误差,如图 7所示.其中,ES为利用不同边界条件计算得到的GPR信号,Eref为参考模型计算得到的GPR信号,|Erefmax|为参考模型计算得到的GPR信号的最大值取绝对值.分析图 7可知,相比Sarma边界条件,PML边界条件下接收点的反射误差均有明显的减少,反射误差平均下降了约50 dB.
|
图 7 不同边界条件的反射误差对比 Fig. 7 Reflection error comparison of different boundary conditions |
为对比PML和Sarma边界条件的计算效率,在同一台电脑上进行计算.无边界条件、Sarma边界条件和PML边界条件的CPU耗时统计和内存占用统计,如表 1所示.相比于无边界条件,施加Sarma和PML边界条件下的计算速度降低了约2倍;虽然PML边界条件下的内存占用约为Sarma边界条件的2倍,但两者的计算速度相差不大.综合考虑边界条件的吸收效果和计算效率,PML边界条件在GPR模型的FETD正演模拟方面具有显著优势.
|
|
表 1 无边界条件、Sarma边界条件和PML边界条件的CPU耗时和内存占用统计 Table 1 Statistical table of computational CPU time and computer memory allocation with Sarma boundary condition, PML boundary condition and without boundary condition |
为充分说明基于二阶电磁波动方程的PML边界条件在复杂结构GPR正演模拟中的良好吸收效果,建立了一个大小为5.0 m×1.8 m的复杂GPR地电模型,如图 8所示.模型被一条起伏界面分为上、下两层介质,埋深约为0.5 m;起伏界面的上层为混凝土,相对介电常数为5.0,电导率为0.0001 S·m-1;下层为土壤,相对介电常数为10.0, 电导率为0.0002 S·m-1.下层介质中埋有一个圆形空洞和一个正方形空洞,其中圆形空洞的直径为0.2 m,圆心坐标为(1.7 m, 1.15 m);正方形空洞的边长为0.2 m,中心坐标分别为(3.3 m, 1.15 m).采用四边形网格对该模型进行剖分的网格数为500×180,网格间距为0.01 m,其中PML层占20层,计算区域与PML层的分界线如图中黑色虚线所示.应用基于PML边界条件的FETD正演算法对该模型进行计算时的时间步长为0.02 ns,计算时间为35 ns,激励源是中心频率为500 MHz的零相位Ricker子波,激励源与接收点距离为0.02 m,移动步长为0.02 m.

|
图 8 复杂GPR模型示意图 Fig. 8 Sketch map of complex GPR model |
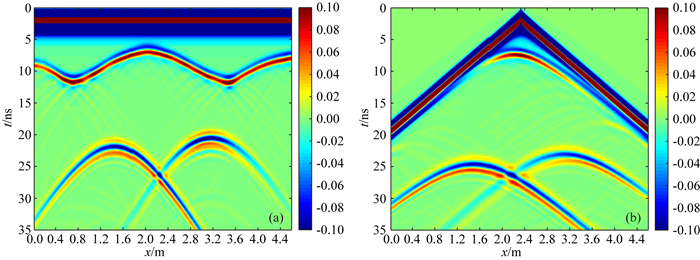
图 9a为利用基于PML边界条件的FETD算法对复杂GPR模型进行计算,获得的GPR正演剖面图.由图可见:在5~13 ns之间出现了一条非常明显的起伏反射波,从左至右有3处较为明显的绕射,分别对应起伏界面的最低点、隆起的最高点和起伏界面的次低点,起伏界面的起伏形态位置在剖面图中清晰可辩,且与真实起伏形态非常吻合.由于圆形空洞和立方体空洞的反射和绕射,20 ns后出现了两条明显的双曲线绕射波,绕射波两翼延伸较宽;两条双曲线顶部的出现时间不同,这是由于空洞异常体上部的起伏反射界面所致.与图 9a相比,采用宽角法进行正演获得的雷达剖面图 9b中,起伏界面的反射波没有剖面法中那样明显,只有起伏界面的隆起部分的反射波清晰可见.由于观测方式的影响,下层介质中的空洞产生的双曲线反射波出现时间、形状和顶点位置均与剖面法中的不同,但两个空洞产生的双曲线反射波依然清晰可见.正演剖面图中未出现明显的人工截断边界的干扰,说明PML边界条件对人工截断边界产生的超强反射波具有较好地吸收效果.
|
图 9 复杂模型GPR正演剖面图 (a)剖面法; (b)宽角法. Fig. 9 Simulated GPR profile of complex model common offset profile (a) and common source profile (b) |
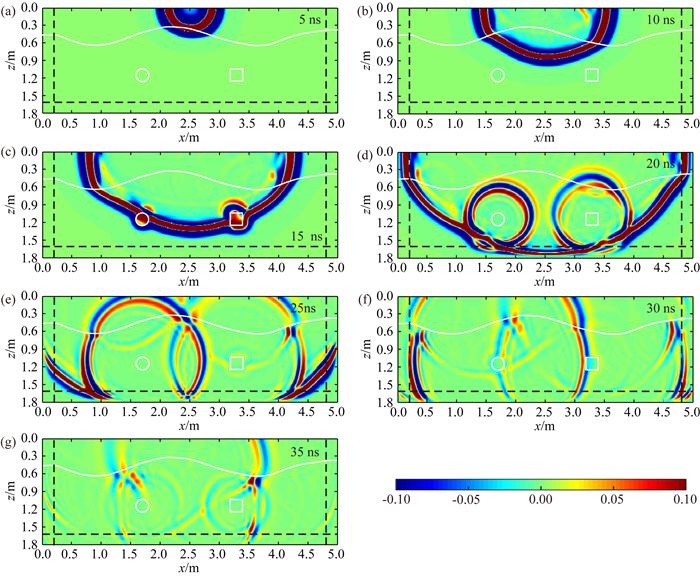
为进一步加强PML边界条件对模型边界处超强反射波吸收和电磁波在复杂结构中传播规律的理解,将发射源置于地表正中心位置,并利用基于PML边界条件的FETD正演算法进行计算,获得的不同时刻的波场快照如图 10所示.图中白线和白色区域为模型中异常体位置,黑色虚线为计算区域与PML层的分界线.5 ns时刻,电磁波以半同心圆向外扩散传播,并遇到起伏界面的隆起部位,如图 10a所示.10 ns时刻,电磁波遇到起伏界面产生反射,反射波向上传播到模型区域外,只有部分反射波可见,如图 10b所示.10 ns之后,波前面继续向前传播,由于界面的起伏,波前不规则,且波前面遇到两个空洞异常体并产生反射,如10c所示.20 ns时刻,波前继续向外扩散传播,并进入到PML层内,几乎没有能量返回到计算区域内;同时两个空洞异常体产生反射波不断扩大,如图 10d所示.25 ns时刻,大部分波前面传播至PML层内,电磁波能量被PML边界条件所吸收,未见明显的反射波;同时空洞异常体产生的反射波继续向外扩散传播,由于遇到起伏反射界面,波前面不规则,在起伏界面与波前面的交点处出现不连续现象,如图 10e所示.30 ns和35 ns时刻,透射波波前面几乎都进入PML层被充分吸收,空洞产生的反射波波前也开始进入到PML层,并无明显的虚假反射波出现,如图 10f和10g所示.通过分析上述正演剖面图和波场快照图可知,本文提出的二阶电磁波动方程的PML边界条件具有良好地吸收效果,可用于复杂GPR模型的FETD正演模拟中.
|
图 10 激励源位于模型表面中心位置时不同时刻的波场快照 Fig. 10 GPR snapshots of different time with shot point located at center of surface of the model |
(1) 从二阶电磁波动方程出发,基于复拉伸坐标系,通过合理构建辅助微分方程,推导了PML区域满足的二阶时域波动方程.在此基础上,利用Galerkin法将PML边界条件以变分形式加载到GPR时域有限元方程,并给出了系数矩阵计算公式、Newmark时间迭代格式等详细求解步骤.
(2) 对比分析均匀模型在无边界条件、Sarma边界条件和PML边界条件下的波场快照、单道波形、时域反射误差及能量衰减曲线,结果表明:相比于Sarma边界条件,PML边界条件可较好地吸收来自模型截断边界处的虚假反射波,具有近似零反射系数.一个复杂GPR模型的正演剖面图和不同时刻的波场快照,验证了PML边界条件在复杂地电结构电磁波传播模拟中的良好吸收效果,实现了PML边界条件在二阶电磁波动方程GPR时域有限元模拟中的应用.
Basu U, Chopra A K. 2004. Perfectly matched layers for transient elastodynamics of unbounded domains. International Journal for Numerical Methods in Engineering, 59(8): 1039-1074. DOI:10.1002/nme.896 |
Basu U. 2009. Explicit finite element perfectly matched layer for transient three-dimensional elastic waves. International Journal for Numerical Methods in Engineering, 77(2): 151-176. DOI:10.1002/nme.2397 |
Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
Bernard L, Torrado R R, Pichon L. 2010. Efficient implementation of the UPML in the generalized finite-difference time-domain method. IEEE Transactions on Magnetics, 46(8): 3492-3495. DOI:10.1109/TMAG.2010.2045357 |
Chew W C, Liu Q H. 1996. Perfectly matched layers for elastodynamics: a new absorbing boundary condition. Journal of Computational Acoustics, 4(4): 341-359. DOI:10.1142/S0218396X96000118 |
Clayton R W, Engquist B. 1977. Absorbing boundary conditions for wave-equation migration. Geophysics, 45(5): 895-904. DOI:10.1190/1.1441094 |
Collino F, Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics, 66(1): 294-307. DOI:10.1190/1.1444908 |
Correia D, Jin J M. 2005. A simple and efficient implementation of CFS-PML in the FDTD analysis of periodic structures. IEEE Microwave and Wireless Components Letters, 15(7): 487-489. DOI:10.1109/LMWC.2005.851583 |
Dai Q W, Wang H H, Feng D S, et al. 2012a. Finite element method forward simulation for complex geoelectricity GPR model based on triangle mesh dissection. Journal of Central South University (Science and Technology) (in Chinese), 43(7): 2668-2673. |
Dai Q W, Wang H H, Feng D S. 2012b. Finite element numerical simulation for GPR based on quadratic interpolation. Progress in Geophysics (in Chinese), 27(2): 736-743. DOI:10.6038/j.issn.1004-2903.2012.02.041 |
Drossaert F H, Giannopoulos A. 2007. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves. Geophysics, 72(2): T9-T17. DOI:10.1190/1.2424888 |
Engquist B, Majda A. 1977. Absorbing boundary conditions for numerical simulation of waves. Proceedings of the National Academy of Sciences of the United States of America, 74(5): 1765-1766. DOI:10.1073/pnas.74.5.1765 |
Feng D S, Dai Q W. 2011. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. NDT & E International, 44(6): 495-504. DOI:10.1016/j.ndteint.2011.05.001 |
Feng D S, Chen C S, Wang H H. 2012. Finite element method GPR forward simulation based on mixed boundary condition. Chinese Journal of Geophysics (in Chinese), 55(11): 3774-3785. DOI:10.6038/j.issn.0001-5733.2012.11.024 |
Feng D S, Yang B K, Wang X, et al. 2016a. Daubechies wavelet finite element method for solving the GPR wave equations. Chinese Journal of Geophysics (in Chinese), 59(1): 342-354. DOI:10.6038/cjg20160129 |
Feng D S, Yang L Y, Wang X. 2016b. The unsplit convolutional perfectly matched layer absorption performance analysis of evanescent wave in GPR FDTD forward modeling. Chinese Journal of Geophysics (in Chinese), 59(12): 4733-4746. DOI:10.6038/cjg20161232 |
Feng D S, Wang X. 2017. Convolution perfectly matched layer for the finite-element time-domain method modeling of Ground Penetrating Radar. Chinese Journal of Geophysics (in Chinese), 60(1): 413-423. DOI:10.6038/cjg20170134 |
Feng D S, Wang X, Zhang B. 2018. Specific evaluation of tunnel lining multi-defects by all-refined GPR simulation method using hybrid algorithm of FETD and FDTD. Construction and Building Materials, 185: 220-229. DOI:10.1016/j.conbuildmat.2018.07.039 |
Feng X, Zou L L, Liu C, et al. 2011. Forward modeling for full-polarimetric ground penetrating radar. Chinese Journal of Geophysics (in Chinese), 54(2): 349-357. DOI:10.3969/j.issn.0001-5733.201.02.011 |
Gedney S D. 1996. An anisotropic perfectly matched layer-absorbing medium for the truncation of FDTD lattices. IEEE transactions on Antennas and Propagation, 44(12): 1630-1639. DOI:10.1109/8.546249 |
Giannopoulos A. 2005. Modelling ground penetrating radar by GprMax. Construction and Building Materials, 19(10): 755-762. DOI:10.1016/j.conbuildmat.2005.06.007 |
Giannopoulos A. 2008. An improved new implementation of complex frequency shifted PML for the FDTD method. IEEE Transactions on Antennas and Propagation, 56(9): 2995-3000. DOI:10.1109/TAP.2008.928789 |
Hu Y P, Egbert G, Ji Y J, et al. 2017. A novel CFS-PML boundary condition for transient electromagnetic simulation using a fictitious wave domain method. Radio Science, 52(1): 118-131. DOI:10.1002/2016RS006160 |
Irving J, Knight R. 2006. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Computers and Geosciences, 32(9): 1247-1258. DOI:10.1016/j.cageo.2005.11.006 |
Komatitsch D, Tromp J. 2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449. DOI:10.1109/75.544545 |
Lee K H, Chen C C, Teixeira F L, et al. 2004. Modeling and investigation of a geometrically complex UWB GPR antenna using FDTD. IEEE Transactions on Antennas and Propagation, 52(8): 1983-1991. DOI:10.1109/TAP.2004.832501 |
Li J, Zeng Z F, Wu F S, et al. 2010. Study of three dimension high-order FDTD simulation for GPR. Chinese Journal of Geophysics (in Chinese), 53(4): 974-981. DOI:10.3969/j.issn.0001-5733.2010.04.022 |
Li J, Zeng Z F, Huang L, et al. 2012. GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD. Computers & Geosciences, 49: 121-130. DOI:10.1016/j.cageo.2012.06.020 |
Liu S L, Li X F, Wang W S, et al. 2015. A Lax-Wendroff lumped mass finite element method for seismic simulations. Oil Geophysical Prospecting (in Chinese), 50(5): 905-911, 924. DOI:10.13810/j.cnki.issn.1000-7210.2015.05.013 |
Liu S X, Zeng Z F. 2007. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium. Chinese Journal of Geophysics (in Chinese), 50(1): 320-326. |
Liu Y S, Liu S L, Zhang M G, et al. 2012. An improved perfectly matched layer absorbing boundary condition for second order elastic wave equation. Progress in Geophysics (in Chinese), 27(5): 2113-2122. DOI:10.6038/j.issn.1004-2903.2012.05.036 |
Liu Y S, Teng J W, Liu S L, et al. 2013. Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition. Chinese Journal of Geophysics (in Chinese), 56(9): 3085-3099. DOI:10.6038/cjg20130921 |
Liu Y S, Teng J W, Lan H Q, et al. 2014. A comparative study of finite element and spectral element methods in seismic wavefield modeling. Geophysics, 79(2): T91-T104. DOI:10.1190/geo2013-0018.1 |
Lu T, Cai W, Zhang P W. 2005. Discontinuous Galerkin time-domain method for GPR simulation in dispersive media. IEEE Transactions on Geoscience and Remote Sensing, 43(1): 72-80. DOI:10.1109/TGRS.2004.838350 |
Ma Y N, Yu J H, Wang Y Y. 2013. Unsplit perfectly matched layer for second-order acoustic wave equation. Acta Acustica (in Chinese), 38(6): 681-686. |
Martin R, Komatitsch D. 2009. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophysical Journal International, 179(1): 333-344. DOI:10.1111/j.1365-246X.2009.04278.x |
Matzen R. 2011. An efficient finite element time-domain formulation for the elastic second-order wave equation: A non-split complex frequency shifted convolutional PML. International Journal for Numerical Methods in Engineering, 88(10): 951-973. DOI:10.1002/nme.3205 |
Millington T M, Cassidy N J. 2010. Optimising GPR modelling: a practical, multi-threaded approach to 3D FDTD numerical modelling. Computers and Geosciences, 36(9): 1135-1144. DOI:10.1016/j.cageo.2009.12.006 |
Mur G. 1981a. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Transactions on Electromagnetic Compatibility, EMC-23(4): 377-382. DOI:10.1109/TEMC.1981.303970 |
Mur G. 1981b. The modeling of singularities in the finite-difference approximation of the time-domain electromagnetic-field equations. IEEE Transactions on Microwave Theory and Techniques, 29(10): 1073-1077. DOI:10.1109/TMTT.1981.1130501 |
Rappaport C M. 1995. Perfectly matched absorbing boundary conditions based on anisotropic lossy mapping of space. IEEE Microwave and Guided Wave Letters, 5(3): 90-92. DOI:10.1109/75.366463 |
Roberts R L, Daniels J J. 1997. Modeling near-field GPR in three dimensions using the FDTD method. Geophysics, 62(4): 1114-1126. DOI:10.1190/1.1444212 |
Roden J A, Gedney S D. 2000. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters, 27(5): 334-339. DOI:10.1002/(ISSN)1098-2760 |
Sacks Z S, Kingsland D M, Lee R, et al. 1995. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE transactions on Antennas and Propagation, 43(12): 1460-1463. DOI:10.1109/8.477075 |
Sarma G S, Mallick K, Gadhinglajkar V R. 1998. Nonreflecting boundary condition in finite-element formulation for an elastic wave equation. Geophysics, 63(3): 1006-1016. DOI:10.1190/1.1444378 |
Tang W, Wang S X. 2012. Perfectly matched layer of finite element prestack reverse time migration in rugged topography. Science Technology and Engineering (in Chinese), 12(31): 8154-8157. DOI:10.3969/j.issn.1671-1815.2012.31.005 |
Varela-Ortiz W, Cintrón C Y L, Velázquez G I, et al. 2013. Load testing and GPR assessment for concrete bridges on military installations. Construction and Building Materials, 38: 1255-1269. DOI:10.1016/j.conbuildmat.2010.09.044 |
Wrenger J P. 2002. Numerical reflection from FDTD-PMLs: a comparison of the split PML with the unsplit and CFS PMLs. IEEE Transactions on Antennas and Propagation, 50(3): 258-265. DOI:10.1109/8.999615 |
Xing L. 2006. Absorbing boundary conditions for the numerical simulation of acoustic waves. Journal of Shanghai Second Polytechnic University (in Chinese), 23(4): 272-278. DOI:10.3969/j.issn.1001-4543.2006.04.002 |
Xing L. 2011. An effective method for handling the corner reflections of PML absorbing boundary condition. Science Technology and Engineering (in Chinese), 11(16): 3769-3771. DOI:10.3969/j.issn.1671-1815.2011.16.035 |
Xu S Z. 1994. Finite Element Method in Geophysics (in Chinese). Beijing: Science Press.
|
Zarei S, Oskooi B, Amini N, et al. 2016. 2D spectral element modeling of GPR wave propagation in inhomogeneous media. Journal of Applied Geophysics, 133: 92-97. DOI:10.1016/j.jappgeo.2016.07.027 |
Zhang B, Dai Q W, Yin X B, et al. 2017. Global reflection errors in the time-frequency domain for GPR simulation in an attenuation interlayer. Chinese Journal of Geophysics (in Chinese), 60(3): 1168-1178. DOI:10.6038/cjg20170327 |
Zhang W, Yang S. 2010. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling. Geophysics, 75(4): T141-T154. DOI:10.1190/1.3463431 |
Zhao J G, Shi R Q. 2013. Perfectly matched layer-absorbing boundary condition for finite-element time-domain modeling of elastic wave equations. Applied Geophysics, 10(3): 323-336. DOI:10.1007/s11770-013-0388-y |
Zhou F X, Gao B B. 2016. A non-splitting PML for transient analysis of poroelastic media and its finite element implementation. Applied Mathematics and Mechanics (in Chinese), 37(2): 195-209. DOI:10.3879/j.issn.1000-0887.2016.02.008 |
戴前伟, 王洪华, 冯德山, 等. 2012a. 基于三角形剖分的复杂GPR模型有限元法正演模拟. 中南大学学报(自然科学版), 43(7): 2668-2673. |
戴前伟, 王洪华, 冯德山, 等. 2012b. 基于双二次插值的探地雷达有限元数值模拟. 地球物理学进展, 27(2): 736-743. DOI:10.6038/j.issn.1004-2903.2012.02.041 |
冯德山, 陈承申, 王洪华. 2012. 基于混合边界条件的有限单元法GPR正演模拟. 地球物理学报, 55(11): 3774-3785. DOI:10.6038/j.issn.0001-5733.2012.11.024 |
冯德山, 杨炳坤, 王珣, 等. 2016a. Daubechies小波有限元求解GPR波动方程. 地球物理学报, 59(1): 342-354. DOI:10.6038/cjg20160129 |
冯德山, 杨良勇, 王珣. 2016b. 探地雷达FDTD数值模拟中不分裂卷积完全匹配层对倏逝波的吸收效果研究. 地球物理学报, 59(12): 4733-4746. DOI:10.6038/cjg20161232 |
冯德山, 王珣. 2017. 基于卷积完全匹配层的非规则网格时域有限元探地雷达数值模拟. 地球物理学报, 60(1): 413-423. DOI:10.6038/cjg20170134 |
冯晅, 邹立龙, 刘财, 等. 2011. 全极化探地雷达正演模拟. 地球物理学报, 54(2): 349-357. DOI:10.3969/j.issn.0001-5733.2011.02.011 |
李静, 曾昭发, 吴丰收, 等. 2010. 探地雷达三维高阶时域有限差分法模拟研究. 地球物理学报, 53(4): 974-981. DOI:10.3969/j.issn.0001-5733.2010.04.022 |
刘少林, 李小凡, 汪文帅, 等. 2015. Lax-Wendroff集中质量有限元法地震波场模拟. 石油地球物理勘探, 50(5): 905-911, 924. DOI:10.13810/j.cnki.issn.1000-7210.2015.05.013 |
刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟. 地球物理学报, 50(1): 320-326. DOI:10.3321/j.issn:0001-5733.2007.01.040 |
刘有山, 刘少林, 张美根, 等. 2012. 一种改进的二阶弹性波动方程的最佳匹配层吸收边界条件. 地球物理学进展, 27(5): 2113-2122. DOI:10.6038/j.issn.1004-2903.2012.05.036 |
刘有山, 滕吉文, 刘少林, 等. 2013. 稀疏存储的显式有限元三角网格地震波数值模拟及其PML吸收边界条件. 地球物理学报, 56(9): 3085-3099. DOI:10.6038/cjg20130921 |
马友能, 余锦华, 汪源源. 2013. 二阶声场波动方程的非分裂完全匹配层算法. 声学学报, 38(6): 681-686. |
唐文, 王尚旭. 2012. 起伏地表有限元叠前逆时偏移完全匹配层. 科学技术与工程, 12(31): 8154-8157. DOI:10.3969/j.issn.1671-1815.2012.31.005 |
邢丽. 2006. 地震声波数值模拟中的吸收边界条件. 上海第二工业大学学报, 23(4): 272-278. DOI:10.3969/j.issn.1001-4543.2006.04.002 |
邢丽. 2011. PML吸收边界条件中的角点处理方法. 科学技术与工程, 11(16): 3769-3771. DOI:10.3969/j.issn.1671-1815.2011.16.035 |
徐世浙. 1994. 地球物理中的有限单元法. 北京: 科学出版社.
|
张彬, 戴前伟, 尹小波, 等. 2017. 衰减夹层GPR模拟的时频域全局反射误差. 地球物理学报, 60(3): 1168-1178. DOI:10.6038/cjg20170327 |
周凤玺, 高贝贝. 2016. 多孔介质瞬态分析中非分裂PML及时域有限元实现. 应用数学和力学, 37(2): 195-209. DOI:10.3879/j.issn.1000-0887.2016.02.008 |
 2019, Vol. 62
2019, Vol. 62


