2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;
3. 中铁工程设计咨询集团有限公司, 北京 100055;
4. 东北大学资源与土木工程学院, 沈阳 110819;
5. 江苏华东八一四地球物理勘查有限公司, 南京 210014
2. The Key Laboratory of Metallogenic Prediction of Nonferrous Metals of Ministry of Education, Central South University, Changsha 410083, China;
3. China Railway Engineering Consulting Group Company Limited, Beijing 100055, China;
4. School of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China;
5. East China 814 Geophysical Prospecting Company Limited, Nanjing 210014, China
勘探地球物理方法包括重力、磁法、电磁法和地震等多种勘探方法(Ren et al., 2017b; Li et al., 2018, 2019).近年来,高精度重力及其梯度测量已广泛应用于目标导航与定位(乔中坤, 2017;Tang et al., 2017; 戴伟铭等, 2018;Tang et al., 2018)、环境监测评估(Benson, 2011)及岩石圈结构的揭示(Cevallos, 2016; 彭江英,2016)等领域.其中基于重力及其梯度张量的边界识别方法是揭露深部地质结构、圈定隐伏岩体和预测深部找矿靶区的重要组成部分(宁津生等,1996;Ren et al., 2017a; Chen et al., 2018).
重力梯度张量曲率广泛应用于地下密度异常体的处理和解释,取得了不错的效果.Pedersen和Rasmussen(1990)率先提出了梯度张量曲率的概念.Phillips等(2007)首次将梯度张量曲率应用于位场数据解释中,估算出源的位置和深度,并且通过墨西哥阿尔伯克基美国盆地航磁资料进行了验证.Chowdhury和Cevallos等(2013)尝试利用航空重力梯度的张量曲率来确定地下异常体的几何形态.Lee等(2013)将梯度张量曲率成功应用于加拿大西北地区古元古代的Wopmay造山带航磁数据的解释.Cevallos等(2013)将梯度张量曲率应用到石油勘探中,取得了良好的效果.Zhou等(2013)讨论了一种新的重力梯度张量曲率法,并用于密度源的边缘检测. Cevallos(2014)利用梯度张量曲率,结合航空重力梯度数据,反演得到了地下密度模型.Wang等(2015)利用主成分分析改进重力梯度张量曲率在边界识别中的应用效果.Cevallos(2016)利用梯度张量曲率估计了地下异常源的位置和深度,并且将其成功应用于澳大利亚坎宁盆地的航空重力梯度数据解释.
上述曲率的应用工作中,大部分工作并没有从曲率基本定义出发,而是直接在笛卡尔坐标系下应用曲率计算公式.然而,曲率计算公式只有在基于等位面的局部坐标系下才有效(Li, 2018).坐标系的不一致可能会导致结果出现显著的错误.Slotnick早在1932年就从数学上就曲率问题进行了讨论,指出了曲率的计算必须在z方向垂直于等位面的局部坐标系下进行,并给出了此坐标系下多种曲率的计算公式.Li(2015)虽然比较了几何面和等位面上各种曲率的效果,但也没有明确指出这一错误.并且现有的工作很少有将重力梯度张量曲率应用到重力数据的边界识别中.
鉴于此,本文回顾曲率的基本定义(Slotnick,1932;Li,2018),建立一个局部坐标系,使坐标系的z方向垂直于重力场产生的等位面;在该坐标系下计算各种曲率,与直接在笛卡尔直角坐标系下计算的曲率进行对比,通过球体和棱柱体模型验证和说明两者之间的差别.然后,在正确计算曲率的基础上,将重力梯度张量曲率应用到重力数据的边界识别中,拓宽重力梯度张量曲率的应用范围,并通过构建一个2D模型比较笛卡尔坐标系下和局部坐标系下重力梯度张量曲率对边界的识别效果.最后,通过理论模型和实际数据分析,详细比较了局部旋转坐标系下各种曲率在重力边界识别中的应用效果.
1 重力梯度张量曲率的计算 1.1 笛卡尔坐标系下重力及其梯度张量在笛卡尔坐标系下,设地面上某点O为坐标原点.根据万有引力定律,一个剩余质量为m,剩余密度为ρ的地质体Ω,其在外部空间任意一点P产生的引力位为(Blakely, 1995; Ren et al, 2018):

|
(1) |
其中r为观测点P(x,y,z)到异常点Q(ξ, μ, ζ)的空间矢量,G为万有引力常量.对引力位V(r)做一阶导数,得出重力三分量:

|
(2) |
重力梯度是重力场的空间变化率.对引力位V(r)做二阶导数,得出重力梯度9个分量,写成矩阵形式,则:
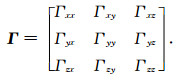
|
(3) |
Slotnick(1932)定义了一个代表等位面的几何函数z′=f(x′, y′),这个函数与重力位函数不一致,因此等位面的偏导数与重力位的偏导数不同,因而我们可以直观地理解局部坐标系中等位面的曲率(Slotnick, 1932; Li, 2018).
定义(x, y, z)笛卡尔坐标系,(x′, y′, z′)为我们所称的局部坐标系.假设两个坐标系有相同的坐标原点,我们则可以通过一个3D的旋转矩阵将两个坐标系下的重力梯度张量可以联系起来,即:
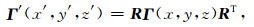
|
(4) |
式中Γ′(x′, y′, z′)局部坐标系下的重力梯度张量,R为旋转矩阵,通常用欧拉角(ϕ, θ, ψ)来表示.这个旋转矩阵可以表示为

|
(5) |
|
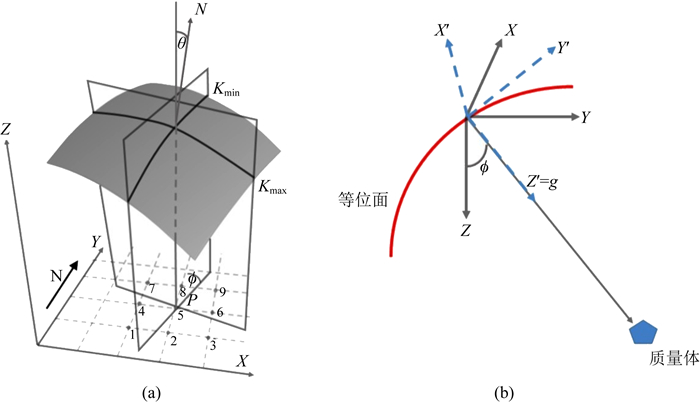
图 1 等位面的曲率(a)和局部坐标系(b)示意图 Fig. 1 Sketches showing curvature of the equipotential surface (a) and the relationship between the local rotational coordinate system and the Cartesian coordinate system (b) |
在旋转坐标系下应用公式(3)和公式(4),旋转空间直角坐标系使得ẑ=ĝ,Γx′y′的绝对值最小,得到旋转后的局部旋转坐标系中的Γ′为
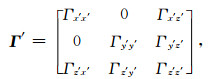
|
(6) |
并且g=gz′=∂V/∂z′,gx′=gy′=0,Γx′z′和Γy′z′远小于主对角线元素的幅值,特别是当观测点附近异常等位面关于ẑ′局部对称(如质点、无限长圆柱体等)时,Γx′z′和Γy′z′都等于0(Li, 2018).
目前为止,确定局部坐标系的方法主要分为两种,一种方法是通过寻找欧拉角来求出所对应的旋转矩阵,最后通过坐标旋转将笛卡尔坐标系下的重力梯度张量旋转到局部坐标系下.另一种方法即特征值分解法,Cevallos(2016)通过理论推导证明特征向量和校正后的局部坐标系之间有较好的对应关系,并且最大特征值所对应特征向量指向物体的质心,本文采用此方法.
对梯度张量Γ进行特征值分解,公式为
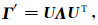
|
(7) |
式中,U是特征向量矩阵,Λ为对角特征值矩阵.比较公式(4)和(7),对角特征值矩阵可以用来估计局部参考坐标系下的Γ′,并且特征向量的转置与旋转矩阵近似,即:
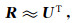
|
(8) |
因此可以采用重力梯度张量的特征值来计算不同的曲率.
1.3 各种曲率计算在得到局部坐标系之后,可以用局部坐标系中的张量分量来定义曲率.Li(2015)给出了在x′和y′处的曲率的定义公式为
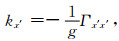
|
(9) |
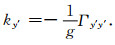
|
(10) |
同时,其他曲率的定义如下所示:
高斯曲率为
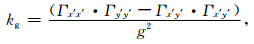
|
(11) |
平均曲率为

|
(12) |
曲度为
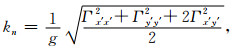
|
(13) |
最大曲率为

|
(14) |
最小曲率为

|
(15) |
差分曲率定义为最大曲率和最小曲率之间的差为
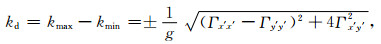
|
(16) |
式中,正负号由两个坐标轴与两个主轴方向的夹角所决定,g为异常重力场的强度.
随着重力梯度张量曲率理论不断地完善,越来越多的曲率定义随之出现(Li, 2015).尽管曲率的表达形式不同,但是经典的重力测量中的曲率理论必须在局部坐标系下定义,其数值计算必须在特定的局部坐标系下进行,而不是在笛卡尔参考坐标系中.
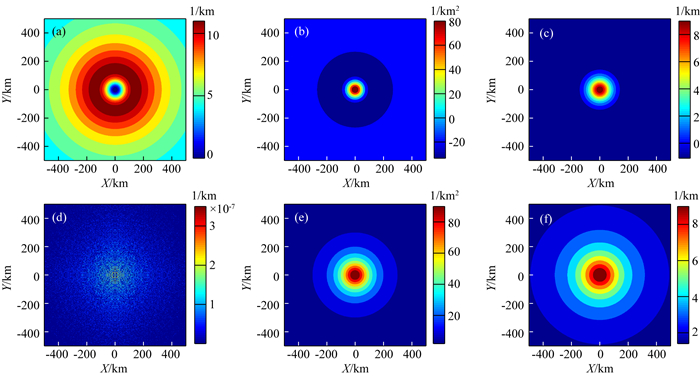
2 理论模型验证为了直观的了解笛卡尔坐标系下和局部旋转坐标系下所计算曲率的差别,本文计算了由一个球体产生的重力场向量的三个分量以及重力梯度张量的六个分量.图 2展示了密度为1g·cm-3球体的两种坐标系下的曲率.由于球体重力场的等位面是球形的,其差分曲率应该等于0.从图中可以看出,在基于等位面的局部坐标系下,其差分曲率等于0,这符合球形等位面曲率的定义,说明基于等位面的局部坐标系是正确计算曲率的先决条件.相比较而言,笛卡尔坐标系下计算的视差分曲率明显偏离0,说明直接在笛卡尔直角坐标系下计算曲率这种方式是错误的.同样,局部旋转坐标系下和笛卡尔直角坐标系下计算的高斯曲率与平均曲率也存在明显的差别.因此,不能简单地把两种坐标系下所计算的曲率混为一谈.
|
图 2 单个球体曲率计算结果对比 (a)笛卡尔坐标系下计算的差分曲率;(b)笛卡尔坐标系下计算的高斯曲率;(c)笛卡尔坐标计算的平均曲率;(d)局部旋转坐标系下计算的差分曲率;(e)局部旋转坐标系下计算的高斯曲率;(f)局部旋转坐标系下计算的平均曲率. Fig. 2 Comparison of calculated curvatures results of single sphere (a) The differential curvature calculated in Cartesian coordinates; (b) Gaussian curvature calculated in Cartesian coordinates; (c) Mean curvature calculated in Cartesian coordinates; (d) The differential curvature calculated in local rotational coordinates; (e) Gaussian curvature calculated in local rotational coordinates; (f) Mean curvature calculated in local rotational coordinates. |
为了进一步直观地了解两种方法差别,本文计算了由一个薄水平矩形体产生的重力场向量的三个分量以及重力梯度张量的六个分量.棱柱体位于网格的中心,在南北方向长400 m,在东西方向宽200 m,密度为1 g·cm-3.利用该模型产生的重力梯度张量的分量在局部旋转坐标系下和笛卡尔直角坐标系下计算差分曲率、平均曲率和高斯曲率.对比差分曲率,从图 3d中可知,局部坐标下所计算的差分曲率的极大值点正好位于棱柱体模型的长边边界正上方,平均曲率(图 3e)和高斯曲率(图 3f)的极大值点位于模型体短边的边界正上方,这符合重力梯度张量曲率所应该提供的信息规律,并为利用重力梯度张量曲率进行边界识别提供了依据.然而在笛卡尔直角坐标系下所计算的视差分曲率正好相反(图 3a),所计算的视平均曲率和高斯曲率更多地反映了模型体的中心位置.

|
图 3 单个棱柱体曲率计算结果对比 (a)笛卡尔坐标系下计算的差分曲率;(b)笛卡尔坐标系下计算的高斯曲率;(c)笛卡尔坐标系下计算的平均曲率; (d)局部旋转坐标系下计算的差分曲率;(e)局部旋转坐标系下计算的高斯曲率;(f)局部旋转坐标系下计算的平均曲率. Fig. 3 Same as Fig. 2 but for a single prism |
因此我们认为,正确的曲率计算应该是在基于z方向垂直于位场等位面的局部坐标系下进行,而不是我们常用的直角坐标系.
3 曲率在边界识别中的应用 3.1 二维理论模型设计 3.1.1 二维模型设计为了直观、量化地比较局部坐标系下各种曲率的识别效果,建立了如图 4所示的一组二维模型.6 km×6 km观测面下有一个x、z为1 km×1 km的截面,且y方向无限延伸长方体场源,其编号为1,异常体的顶、底面深度为0.1 km、1.1 km.1号棱柱体代表地下y方向无限长目标体,密度为1 g·cm-3, 其模型分布如图 5所示.

|
图 4 二维理论模型图 Fig. 4 2D theoretical model |

|
图 5 理论模型的平面图 Fig. 5 Planar diagram of theoretical model |
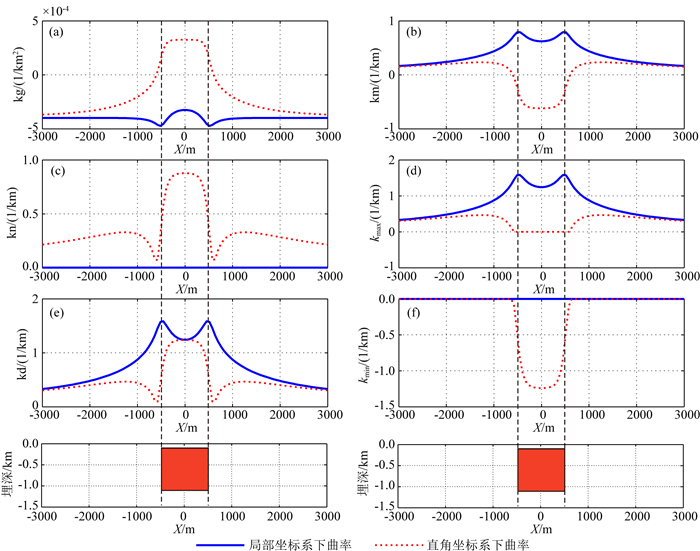
图 6示为分别给出了理论上的局部旋转坐标系下高斯曲率、平均曲率、曲度、最大曲率、差分曲率和最小曲率的计算结果.对比图 6a、b、c、d、e、f曲率计算结果图,笛卡尔坐标下所计算的曲率识别出的边界误差较大,特别是高斯曲率、平均曲率和最小曲率不能反映地下2D模型体的边界,其很大程度上反映了2D模型体的中心位置.而局部坐标系下所计算的高斯曲率、平均曲率、最大曲率和差分曲率可以清晰的勾勒出和突出地下2D模型体的边界,对于边界识别误差更小.另外,从图 6c和图 6f可以看出,在局部坐标系下,2D模型体的重力梯度张量曲率中的曲度和最小曲率趋近于0,这是因为2D模型体所产生的重力梯度张量所形成的等位面沿2D模型体的走向方向近似为一条直线,其曲率本身就趋近于0,更符合一般事实,进一步验证了局部坐标下曲率计算的正确性.
|
图 6 笛卡尔坐标系下和局部旋转坐标系下剩余密度为1 g·cm-3的模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)差分曲率;(f)最小曲率. Fig. 6 The calculated curvatures of the 2D model as shown in Fig. 4 and Fig. 5 with residual density of 1 g·cm-3 in the Cartesian coordinate system and the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Differential curvature; (f) Minimum curvature. |
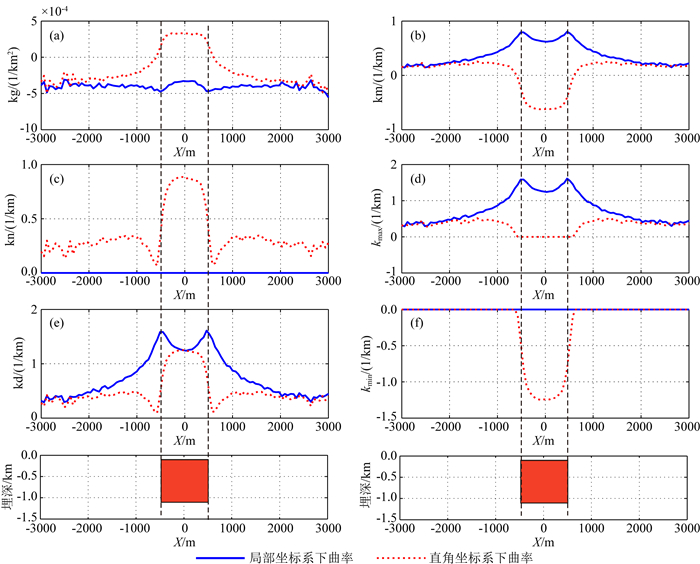
为了测试算法的稳定性,对无限长长方体模型中加了3%的高斯随机噪声,分别计算了前文所述的多种曲率来进行目标体的边界识别,计算结果如图 7.
|
图 7 笛卡尔坐标系下和局部旋转坐标系下加入3%的高斯噪声图 6所示模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)差分曲率;(f)最小曲率. Fig. 7 The calculated curvatures of the 2D model as shown in Fig. 6 contaminated with 3% Gaussian random noise in the Cartesian coordinate system and the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Differential curvature; (f) Minimum curvature. |
由图 7的计算结果可以看出,分别在上述模型中加入噪声之后,在局部旋转坐标系下计算的六种曲率受影响程度均不大,其中高斯曲率(7a)、平均曲率(图 7b)、最大曲率(图 7d)以及差分曲率(图 7f)的识别效果受影响相对较小,基本上没有产生额外的边界,明显优于笛卡尔坐标下曲率所识别的边界效果.并且对异常体周边的噪声压制范围大,在低背景噪声下显著的突出异常体的边界位置.因此,可以看出该方法具有一定的抗噪能力.
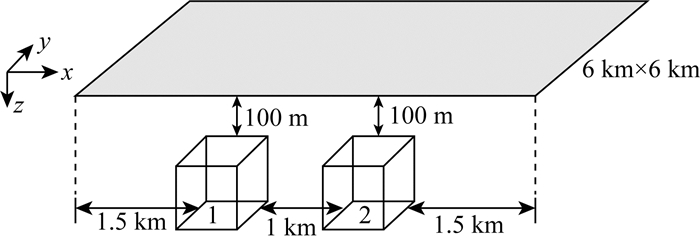
3.2 三维理论模型设计 3.2.1 三维模型设计为了进一步比较局部坐标系下各种曲率的识别效果,参照Cevallos等(2013)的模型,建立了如图 8所示的一组模型.假设在6 km×6 km的平面范围内分布有两个1 km×1 km×1 km正方体场源,其编号为1、2,各异常体的顶、底面深度全部分别为0.1 km、1.1 km.
|
图 8 三维理论模型图 Fig. 8 3D theoretical model |
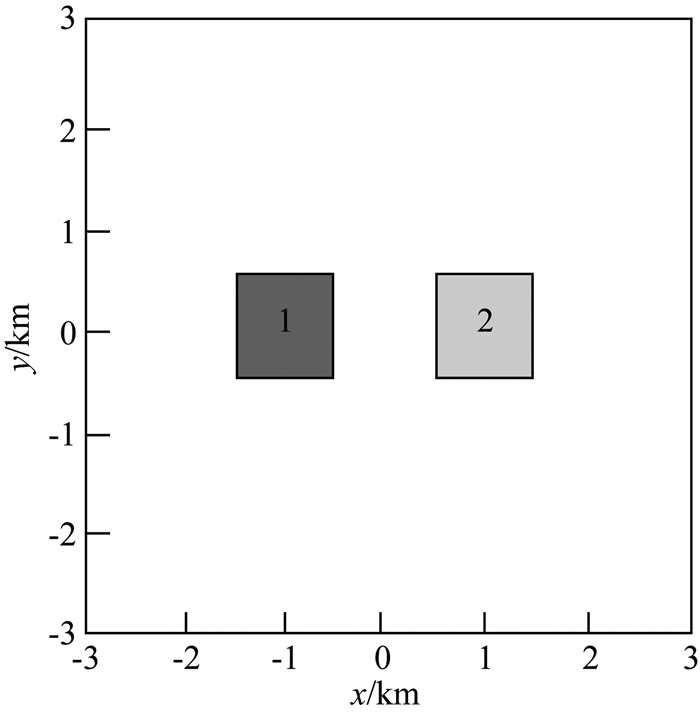
模型考虑到三种情况:(1)模型中正方体的剩余密度均为正,各正方体剩余密度均设为1 g·cm-3,图 10为由此模型计算的曲率结果.(2)模型中正方体的剩余密度均为负,各正方体剩余密度均设为-1 g·cm-3,图 11为由此模型计算的曲率结果.(3)模型中正方体的剩余密度同时含有正、负,设1号正方体的剩余密度为1 g·cm-3,2号正方体的剩余密度为-1 g·cm-3,图 12为由此模型计算的曲率结果.两个棱柱体代表地下两个目标体,其模型分布如图 9所示.
|
图 9 理论模型的平面图 Fig. 9 Planar diagram of theoretical model |

|
图 10 局部旋转坐标系下剩余密度为1 g·cm-3的模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 10 The calculated curvature of the synthetic model as shown in Fig. 8 and Fig. 9 with residual density of 1 g·cm-3 in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |
|
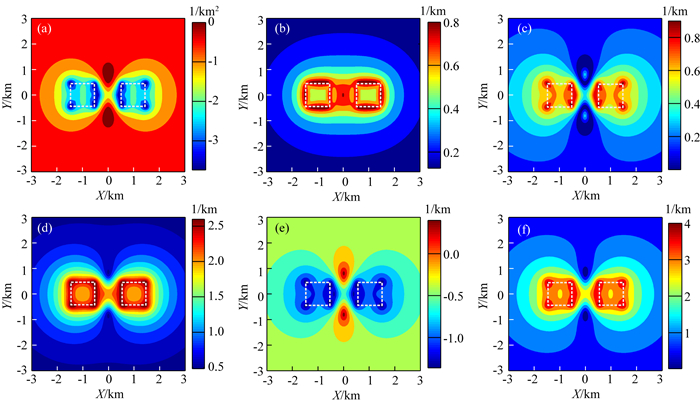
图 11 局部旋转坐标系下剩余密度为-1 g·cm-3的模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 11 The calculated curvature of the synthetic model as shown in Fig. 8 and Fig. 9 with residual density of -1 g·cm-3 in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |
|
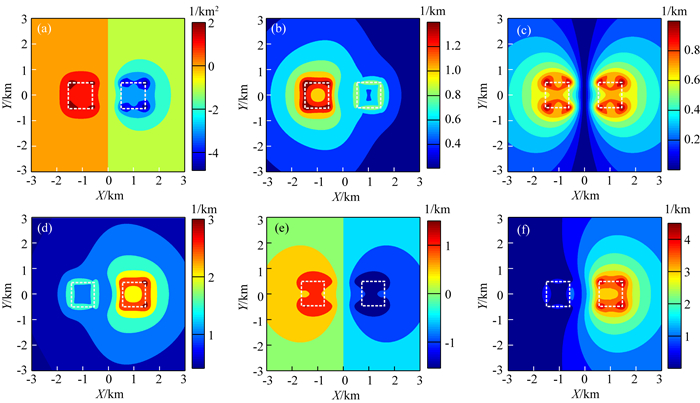
图 12 局部旋转坐标系下左右两侧剩余密度分别为1 g·cm-3和-1 g·cm-3的模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 12 The calculated curvature of the synthetic model as shown in Fig. 8 and Fig. 9 with residual density of -1 g·cm-3 and 1 g·cm-3 in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |
图 10示为分别给出了理论上的局部旋转坐标系下高斯曲率、平均曲率、曲度、最大曲率、最小曲率和差分曲率的计算结果.对比图 10a、b、c、d、e、f曲率计算结果图,可以清晰的看到六种曲率在地下目标体边界识别中都具有一定的效果,高斯曲率(图 10a)、平均曲率(图 10b)、最大曲率(图 10d)的计算结果要优于其他三种曲率.相比于其他五种曲率,高斯曲率的识别效果最佳,不仅能够准确识别地下目标体的边界,而且识别出的背景假异常最少,误差最小;差分曲率(图 10f)的识别效果最差,不能准确识别异常体的边界,增加了多余的假异常.最后,通过比较六种曲率识别效果可知,局部旋转坐标系下计算的高斯曲率的识别效果最佳;而且可以发现,对于正密度差的目标体来说,局部旋转坐标系下计算得到的曲率同样都为正,而且背景场曲率计算结果近似接近0.
对比图 11中的曲率计算结果同样可以发现六种曲率在地下目标体边界识别中都具有一定的效果.通过图 11 b、d,可以发现,当正方体的剩余密度为-1 g·cm-3,平均曲率(图 11b)与最大曲率(图 11d)对于目标体边界的圈定最为准确,但是背景场的曲率计算值相对不均匀;差分曲率对于识别剩余密度为负的异常体,效果较正异常体提高明显.再次比较图 11a、b、c、d、e、f曲率的计算结果,当两个正方体剩余密度都为-1 g·cm-3时,高斯曲率与最小曲率的异常体附近的曲率计算结果都为负,而背景场的曲率计算结果接近0.
图 12中的曲率计算结果有效地验证了图 10、11中得到的结论的正确性.对于剩余密度为正的异常体来说,高斯曲率、平均曲率、曲度、最大曲率、最小曲率都能相对准确的圈定异常体的边界;而对于地下目标体的剩余密度同时存在正负时,高斯曲率和最小曲率能够有效地区分异常体的剩余密度,而高斯曲率的识别总体效果较最小曲率更好一些.观察图 10、11、12中的差分曲率对于正、负剩余密度异常体的边界识别效果,可以发现差分曲率对于剩余密度为负的异常体边界识别效果要更好一些.
3.2.3 三维模型含噪情况下不同曲率的边界识别效果对比为了测试算法的稳定性,对三维模型中两个正方体的剩余密度为正、为负和正负三种情况叠加了3%的高斯随机噪声,分别计算了前文所述的多种曲率来进行目标体的边界识别,计算结果如图 13、14、15.
|
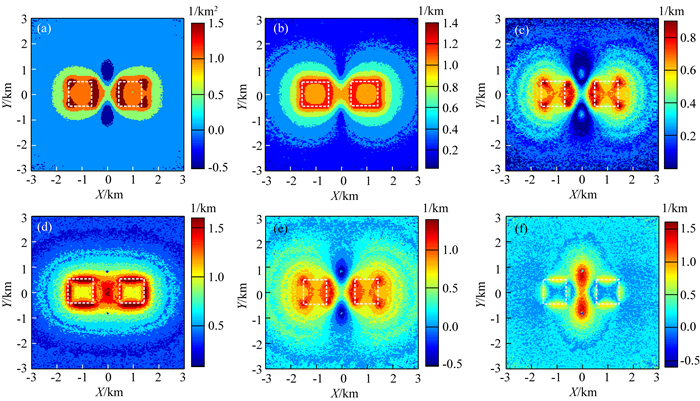
图 13 局部旋转坐标系下加入3%的高斯噪声图 10所示模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 13 The calculated curvatures of the 3D model as shown in Fig. 10 contaminated with 3% Gaussian random noise in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |

|
图 14 局部旋转坐标系下加入3%的高斯噪声图 11所示模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 14 The calculated curvatures of the 3D model as shown in Fig. 11 contaminated with 3% Gaussian random noise in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |

|
图 15 局部旋转坐标系下加入3%的高斯噪声图 12所示模型曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 15 The calculated curvatures of the 3D model as shown in Fig. 12 contaminated with 3% Gaussian random noise in the local coordinate system (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |
由图 13、14、15的计算结果可以看出,分别在上述模型中加入噪声之后,在局部旋转坐标系下计算的六种曲率受影响程度都不大.在异常体的剩余密度为正值时,加入噪声后的六种曲率计算结果受影响程度最小,高斯曲率几乎不受影响;而当存在剩余密度为负值异常体时,平均曲率、曲度、最大曲率、最小曲率和差分曲率在背景场区域有一些影响,局部变得模糊;而高斯曲率图像受到的影响相对较小,基本上没有产生额外的边界,而且对异常体周边的噪声压制范围最大,在低背景噪声下显著的突出异常体的边界位置.基于二维以及三维模型的抗噪测试,验证了本文方法具有一定的抗噪能力,且高斯曲率稳定性最好.
3.3 实际数据试验实际重力梯度数据经过处理之后,通过本文算法可实现地下异常体边界识别.为了验证方法的有效性,本文选取了美国路易斯安那洲西南部文顿盐丘(X440000~445000 m,Y3332500~3337500 m)重力梯度数据进行实际数据测试,数据来源于美国德州休斯顿Bell Geospace公司,图 16为文顿盐丘地区重力梯度分布.

|
图 16 文顿盐丘地区重力梯度 Fig. 16 Gravity gradients in the Vionton Dome area |
为了降低背景场噪声,将g向上延拓200 m,重力梯度张量向上延拓100 m,其张量曲率的计算结果如图 17所示.通过对比图 17中各曲率圈定的文顿盐丘岩盖的边界分布范围,可以看出局部旋转坐标系下计算的各种曲率在边界识别中都具有一定的识别效果,都能对地下异常体边界进行初步的划分,但是参照重力异常分布,比较图 16中重力梯度的范围和大小,高斯曲率背景场分布更加均匀,能够突出异常,更加符合重力异常的分布规律,因此可以初步判断局部旋转坐标系下的高斯曲率对于文顿盐丘地区实测重力梯度数据的识别效果更佳.

|
图 17 文顿盐丘地区曲率计算结果 (a)高斯曲率;(b)平均曲率;(c)曲度;(d)最大曲率;(e)最小曲率;(f)差分曲率. Fig. 17 The results of curvature in the area of Vionton Dome shown in Fig. 16 (a) Gaussian curvature; (b) Mean curvature; (c) Curvedness; (d) Maximum curvature; (e) Minimum curvature; (f) Differential curvature. |
本文研究了笛卡尔坐标系下中重力矢量及其梯度张量的表达式,然后讨论了正确计算曲率的测量参考系和局部旋转的相关理论,并且在此基础上计算了几种不同的曲率,对比了笛卡尔坐标系下和基于等位面的局部坐标系下曲率的特征,说明正确的曲率计算应在基于等位面的局部旋转坐标系下进行;将张量曲率应用到重力的边界识别中,通过理论模型和实际数据分析了其在边界识别中的效果:差分曲率的识别效果相对最差,不能有效识别出地下高密度体;平均曲率、曲度和最大曲率的效果稍好一些,但是识别出的背景假异常体较多,而且不能有效的识别出地下目标体为高密度体或低密度体;高斯曲率和最小曲率能够识别出地下目标体为高密度体或低密度体,其中高斯曲率边界圈定最准确,识别效果最佳.
致谢 感谢Bell Geospace公司提供的实测数据,感谢审稿专家及地球物理学报编辑老师对本文提出的宝贵的修改意见.
Benson S. 2011. Carbon Dioxide Capture and Sequestration-Part Ⅱ. Nonrenewable Energy Sources. //Ginley D S, Cahen D eds. Fundamentals of Materials for Energy and Environmental Sustainability. Cambridge: Cambridge University Press, 90-104.
|
Blakely R J. 1995. Potential Theory in Gravity and Magnetic Applications. .
|
Cevallos C. 2014. Automatic generation of 3D geophysical models using curvatures derived from airborne gravity gradient data. Geophysics, 79(5): G49-G58. |
Cevallos C. 2016. Interpreting the direction of the gravity gradient tensor eigenvectors: Their relation to curvature parameters of the gravity field. Geophysics, 81(3): G49-G57. |
Cevallos C, Kovac P, Lowe S J. 2013. Application of curvatures to airborne gravity gradient data in oil exploration. Geophysics, 78(4): G81-G88. |
Chen C J, Ren Z Y, Pan K J, et al. 2018. Exact solutions of the vertical gravitational anomaly for a polyhedral prism with vertical polynomial density contrast of arbitrary orders. Geophysical Journal International, 214(3): 2115-2132. |
Chowdhury P R, Cevallos C. 2013. Geometric shapes derived from airborne gravity gradiometry data: New tools for the explorationist. The Leading Edge, 32(12): 1468-1474. |
Dai W M, Huang D N, Li T L, et al. 2018. The edge detection method and its application in the south China sea based on the gravity gradient structure tensor eigenvalue. Chinese Journal of Geophysics (in Chinese), 61(6): 2494-2507. DOI:10.6038/cjg2018M0018 |
Lee M, Morris W, Leblanc G, et al. 2013. Curvature analysis to differentiate magnetic sources for geologic mapping. Geophysical Prospecting, 61(S1): 572-585. |
Li J, Zhang X, Gong J Z, et al. 2018. Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals, 26(2): 1840011. |
Li J, Zhang X, Tang J T, et al. 2019. Audio magnetotelluric signal-noise identification and separation based on multifractal spectrum and matching pursuit. Fractals, 27(1): 1940007. DOI:10.1142/S0218348X19400073 |
Li X. 2015. Curvature of a geometric surface and curvature of gravity and magnetic anomalies. Geophysics, 80(1): G15-G26. DOI:10.1190/geo2014-0108.1 |
Li Y G. 2018. Understanding curvatures of the equipotential surface in gravity gradiometry. Geophysics, 83(4): G35-G45. DOI:10.1190/geo2017-0612.1 |
Ning J S, Luo Z C, Chao D B. 1996. The present situation on satellite gravity gradiometry and its vistas in the application of physical geodesy. Journal of Wuhan Technical University of Surveying and Mapping (in Chinese), 21(4): 309-314. |
Pedersen L B, Rasmussen T M. 1990. The gradient tensor of potential field anomalies; Some implications on data collection and data processing of maps. Geophysics, 55(12): 1558-1566. |
Peng J Y. 2016. Gravity anomaly derivative identification configuration application in Qiong Dongnan basin [Master′s thesis](in Chinese). Chengdu: Chengdu University of Technology.
|
Phillips J D, Hansen R O, Blakely R J. 2007. The use of curvature in potential-field interpretation. Exploration Geophysics, 38(2): 111-119. |
Qiao Z K. 2017. The study on joint inversion of gravity and gravity gradient data and its application in Vinton Dome area [Master′s thesis](in Chinese). Changchun: Jilin University.
|
Ren Z Y, Chen C J, Pan K J, et al. 2017a. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surveys in Geophysics, 38(2): 479-502. DOI:10.1007/s10712-016-9395-x |
Ren Z Y, Tang J T, Kalscheuer T, et al. 2017b. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. Journal of Geophysical Research: Solid Earth, 122(1): 79-109. DOI:10.1002/2016JB012987 |
Ren Z Y, Zhong Y Y, Chen C J, et al. 2018. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics, 83(1): G1-G13. |
Slotnick M M. 1932. Curvature of equipotential surfaces. AAPG Bulletin, 16(12): 1250-1259. |
Tang J T, Hu S G, Ren Z Y, et al. 2017. Analytical formulas for underwater and aerial object localization by gravitational field and gravitational gradient tensor. IEEE Geoscience and Remote Sensing Letters, 14(9): 1557-1560. DOI:10.1109/LGRS.2017.2722475 |
Tang J T, Hu S G, Ren Z Y, et al. 2018. Localization of multiple underwater objects with gravity field and gravity gradient tensor. IEEE Geoscience and Remote Sensing Letters, 15(2): 247-251. |
Wang J, Meng X H, Li F. 2015. Improved curvature gravity gradient tensor with principal component analysis and its application in edge detection of gravity data. Journal of Applied Geophysics, 118: 106-114. |
Zhou W N, Du X J, Li J Y. 2013. The limitation of curvature gravity gradient tensor for edge detection and a method for overcoming it. Journal of Applied Geophysics, 98: 237-242. DOI:10.1016/j.jappgeo.2013.09.008 |
戴伟铭, 黄大年, 李桐林, 等. 2018. 基于重力梯度结构张量特征值斜导数边界识别方法及其在南海的应用. 地球物理学报, 61(6): 2494-2507. DOI:10.6038/cjg2018M0018 |
宁津生, 罗志才, 晁定波. 1996. 卫星重力梯度测量的研究现状及其在物理大地测量中的应用前景. 武汉测绘科技大学学报, 21(4): 309-314. |
彭江英. 2016.重力异常导数在琼东南盆地构造识别中的应用[硕士论文].成都: 成都理工大学.
|
乔中坤. 2017.重力及张量数据联合反演研究及在Vinton Dome地区的应用[硕士论文].长春: 吉林大学.
|
 2019, Vol. 62
2019, Vol. 62


