时移地震(Nur，1982；Nur et al., 1984；Nur and Wang, 1987；Greaves and Fulp, 1987；Pullin et al., 1987；Stang and Soni, 1987；Jack，1997；Calvert，2005；Foster，2007; 蔡志东等, 2016)的直接目的是对比一段时间间隔的地质对象的差异，它的基础就是两次地震成像.重复性在其中扮演重要的角色.重复性的起源是地震成像的重复性，被广为引用和使用的衡量指标是NRMS(Kragh and Christie, 2002; Cantillo, 2011).虽然有针对单次采集观测系统依例如陈中山等(2017)和李列等(2016)的阐述而优化的普通三维地震的非一致性时移地震技术(王延光等，2015)，而且一般而言地震数据的重复性，可以通过适当的处理而得到提高(Helgerud et al., 2011a; 李蓉和胡天跃，2004；金龙等, 2005a, 2005b; 赵桂玲等, 2016；熊艳梅等, 2017；王彦军等，2016；潘军等，2016；薛国强等，2017)，采集过程中震源和信号接收的重复性也可以在设计上、采集过程中以一般性技术(林彬华等，2017；于富文等，2017；)单独得以追求，但是由于观测系统重复性对地震数据重复性的影响(Landrø, 1999; Eiken et al., 2003; Smit et al., 2005; Misaghi et al., 2007)，非重复性仍不能被彻底消除，因而前人通过控制观测系统的重复性，从根本上提高时移地震的重复性，通过采集中的观测系统重复性优化对策(Widmaier et al., 2003, 2005; Ebaid et al., 2008; Ridsdill-Smith et al., 2008; Helgerud et al., 2011b)，来优化时移地震的重复性.在早期文献和实践中，监测(monitor)的单道观测系统与基线(baseline)单道观测系统之间的偏离作为观测系统的重复性，具体的是炮点偏离与检波点偏离之和(Johnston，2013)，因此单道对单道的观测系统重复性，表示为

(1)

其中|ΔS|为监测炮点位置与基线炮点位置偏离的模，|ΔR|为监测检波点位置与基线检波点位置偏离的模.

而在实时采集过程中，人们还用单独的monitor与baseline之间的单独炮点偏离、羽角偏差预评估和监控观测系统重复性，然后在采集过程中不断积累的观测系统数据上，对单炮检距观测系统进行单道对单道的观测系统重复性衡量(Johnston，2013)，这样进行逐步的观测系统重复性监控.由于地震资料的处理和成像是基于面元的(周小平等，2015)，为了确保成像的重复性，我们需要针对面元的观测系统重复性评价. 图 1是以从实际观测系统数据中提取的部分数据按Johnston(2013)的例子所做的单炮检距重复性的分布图.

图 1

Fig. 1

图 1 基于面元的单炮检距观测系统重复性原始数据 (a)数据空白处用纯黑色标识；(b)数据空白用纯白色标识. Fig. 1 Raw data of single-trace geometry repeatability for bins (a) Vacancy of data indentified by pure black; (b) Vacancy of data indentified by pure white.

近来，董凤树(2016)和董凤树等(2016)提出多道重复性，而(1)式表示的单道对单道的观测系统重复性也就被称为单道观测系统重复性，并在NRMS计算公式的基础上，以能量均衡为条件，获得了多道地震数据与各单道地震数据间重复性的关系，再依据地震数据单道重复性与观测系统单道重复性之间的关系数据(Landrø，1999；Eiken et al., 2003；Smit et al., 2005；Misaghi et al., 2007)建立了地震数据与观测系统重复性的线性关系模型，得出了多道观测系统重复性及其与单道重复性之间的关系，另外还针对数据大小的不同及对应匹配的不确定性提出了失配构造处理方法和最佳匹配求取方法.多道观测系统重复性成为地震数据观测系统重复性的等价评价工具.在该研究中，地震数据与观测系统重复性关系的线性模型的精确度受到制约而且受数据选取范围的主观性影响，然而整个理论关系和结论为多道观测系统重复性的量度提供了基本方法.本文深入该理论，具体分析了线性模型的关键性和局限性，给出了改进方案，得出了更加合理的数据抽象模式，建立了基于地震数据成像与观测系统重复性关系新模式的多道观测系统重复性度量方法并面向面元进行了应用与实际数据分析，给出了应用方案和参考标准.

时移地震成像的重复性的度量在数据的部分区域取得，而这样的区域对应着勘探对象在两次地震观测之间未发生变化的区域.被文献普遍援引的重复性的度量是归一化均方根差异(normalized rms difference，NRMS)(Kragh and Christie, 2002; Cantillo, 2011)，对于baseline地震数据和monitor地震测数据，NRMS表示为

(2)

其中rms算子定义为

(3)

求和遍及时窗内的N个采样x_i.

多道重复性理论根据(2)和(3)式以及理想的能量均衡假设条件，得到多道间地震数据重复性

(4)

其中D_i为单对地震道的成像重复性，f代表匹配关系，可以是一个向量的形式，p_i是各道参与运算的数据量所决定的道的加权系数.

变量f代表可能的监测与基线的匹配关系，而且其匹配中包含对失配的单道观测系统重复性的处理，包含对失配基线观测系统的重复性的分配和对失配监测观测系统的剔除处理，由图 2和图 3示意，其中剔除的监测道和分配的监测道被标识和画出.剔除的道将不被计入重复性计算，而对失配的基线道和所分配的监测道而言，重复性则为一个常数D₀.

图 2

Fig. 2

图 2 剔除剩余监测道的匹配 剩余的监测道被剔除，被剔除的道随着匹配的不同而不同. Fig. 2 Match with rejection of redundant monitor traces The redundant monitor traces are rejected and the traces rejected will be different among different matches.

图 3

Fig. 3

图 3 含有分配的虚拟道的匹配 在为寻找对应于最佳匹配的重复性的匹配变化过程中，虚拟道将被分配到任何失配的基线道. Fig. 3 Match with assigned imaginary monitor traces During the process of seeking multi-trace geometry repeatability of best match, an imaginary trace will be assigned to any mismatched baseline trace.

概括起来，最佳匹配和失配外推方法的该多道匹配观测系统重复性方法实际上是基于地震成像重复性与观测系统重复性关系的实验数据的，所建立和依据的地震成像重复性与观测系统重复性的关系是线性的，如下面(5)式所示.如果观测系统重复性范围足够小，这一关系模式是满足的.

(5)

其中k为常数，d_i表示第i对匹配道的观测系统重复性.利用(4)式和上式，得到

(6)

其中的

(7)

为匹配关系f下反映NRMS的多道观测系统重复性.由此可见，多道数据重复性是各单道重复性的加权均方根.其中p_i根据动校拉伸系数上限β的不同与检炮距Offset具有不同的关系.需要注意到的是只有在(5)式成立的情况下(6)和(7)式才合理地存在.但是从Landrø(1999)的数据上看，在无限制的范围内，线性模型就不能很好地符合了，而只有在d_i的一定范围内的关系拟合和应用较为精确.当通过拟合取得该线性关系的时候，如果采用的数据范围扩大，虽然对大范围整体拟合更好，但是k值会变小，在小观测系统重复性范围内与实际数据的偏离就更大，并且增加拟合数据中观测系统重复性的数值范围，直接导致k单调减小，使k值的选取不够客观.因此，在该方法的文献中的地震数据的重复性与观测系统重复性的线性关系，较好地适用于有限的单道观测系统重复性范围，或者在采用大范围拟合的线性关系的情况下，使误差增大.注意到前面的分析结论，只有在(5)式表示的正比例线性关系成立的情况下(6)和(7)式才合理地存在.在这种情况下，整体趋势一致的非线性拟合不适应(6)和(7)式的关系的应用.文本针对该问题，根据随着观测系统重复性数值增大而地震数据重复性的变化变小这一趋势特点，提出了分部拟合的方法，形成成像与观测系统重复性关系的我们所称之为的X模式.如图 4，在0到一定偏离量d_m之间拟合一条正比例曲线，斜率为k，基于d在d_m到理论上的无穷大(∞)之间的成像重复性整体变化较小的特点，对d值属于d_m到无穷大或实际数据的最大值之间的数据拟合一条水平线，与正比例线相交于X点.当单道重复性在[0, d_x]上，视地震数据重复性与观测系统重复性之间的关系为所拟合的正比例关系；当单道重复性在(d_x, ∞)上，其地震数据重复保持定值，即与观测系统重复性无关.这样拟合出的作为单道观测系统重复性函数的单道NRMS不具备单值反函数.由于NRMS最终衡量重复性，NRMS相同则重复性相同，所以我们不妨把对应相同NRMS值的单道观测系统重复性用一个相同的值表示，即可把(d_x, ∞)上的单道观测系统重复性收缩为X处的d_x值，单道观测系统重复性的原定义域[0, ∞)收缩为[0, d_x]，使得单道间的地震数据重复性与观测系统重复性保持为[0, d_x]上的正比例线性关系，这样使(5)、(6)和(7)式普遍成立.上覆地层的不均匀性在观测系统差异的情况下导致成像的非真实差异，就处理面元的多道观测系统而言，当量值为0时，对应着每道的观测系统的重复性值为零，也就是监测线观测系统与基线的观测系统完全重合，这样上覆地层的非均匀性通过观测系统差异造成的成像差异噪声就会消失.实际情况下，监控观测系统重复性的目的就是提高观测系统的重复性使重复性量值最小化，因此多道观测系统重复性和单道观测系统重复性的小值及其变化幅度更为重要，而单道大值的观测系统对仍处于小量值的多道观测系统有干扰作用.在本文的X关系模式的多道观测系统重复性下，小值的多道观测系统重复性被更精确地刻画，向大的方向超过X节点的单道重复性量值的出现被合理权衡计入，同时对小值的干扰淹没效应被很好地屏蔽.因此，就上覆地层通过观测系统差异导致成像噪声的机理而言，X关系模式的多道观测系统重复性比线性关系模型下的多道观测系统重复性更适合以提高重复性为目的观测系统重复性评价.另外按照失配外推方法，当基线单道失配的情况下，地震数据重复性为特殊的D₀(取噪声的重复性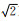)，观测系统重复性外推为D₀/k.这样在计算多道观测系统重复性时，失配的重复性与超大值重复性可以区分，失配形成更大的重复性值具有更低的重复性，失配道的多少可以被量化反映.

图 4

Fig. 4

图 4 成像与观测系统重复性关系模式拟合 一部分数据拟合一条正比例线，大偏差范围内拟合一条水平线. Fig. 4 X mode fitting of relationship between seismic imaging repeatability and geometry repeatability of single-traces One part of data is utilized for fitting a linear section of the relationship and the data with big geometry repeatability is selected for fitting a horizontal line whose a section will be incorporated to the entire pattern of the relationship.

原始的单道观测系统重复性数据部分地显示为图 1，图中数据的空缺表示为纯白或纯黑色.这对单道表示没有什么问题.而在计算多道重复性时，单道的重复性值空缺的重复性该如何计入度量就是一个问题，并可以用外推法解决.

式(4)、(6)和(7)中的加权系数在现有理论中通过动校正拉伸系数上限确定.根据我们采用的研究实例中的地震记录长度(2.5 s)，采用特定地震波速度函数和拉伸系数β=0.2计算了p值与检炮距Offset的关系应用在本文的研究中.

最佳匹配下的多道重复性，即各种匹配下所计算得到的所有多道重复性中的最小值为

(8)

被称为观测系统失配外推最佳定向匹配加权均方根重复性，对应的匹配f为最佳匹配.在不引起混淆的情况下，d_b在本文中其余部分仍书写为d.本文所提出的X模式拟合、关系和度量，会很好地区分重复性值大的单道匹配与失配在多道重复性中的影响，有利于选取最优化的匹配.在匹配后，对于空余的基线道，对应的观测系统重复性为由下面(9)式所确定的d₀(称为观测系统失配外推)，而空余的监测道则被剔除.

记Baseline单道与Monitor中对应虚拟道之间重复性的值为D₀(=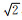，因不相关或相关为零)，并定义d₀为失配的单道观测系统的重复性，满足

(9)

图 5显示部分和全部X模式化的图 1所示单道观测系统重复性数据.

图 5

Fig. 5

图 5 单道观测系统重复性X模式处理过程中数据显示 (a)仅X节点收缩处理(失配用纯黑色标识)；(b)仅X节点收缩处理(失配用纯白色标识)；(c)仅失配外推；(d)完全X模式. Fig. 5 Single-trace geometry repeatability in X-mode processing (a) Only collapse to X node (mismatch indentified by pure black); (b) Only collapse to X node (mismatch indentified by pure white); (c) Only extrapolation for mismatch; (d) Full X-mode processing.

我们从海上某区域的时移地震拖缆采集过程形成的数据中提取部分数据，按照本文描述的地震数据与观测系统重复性关系模式(X模式)，针对面元进行重复性计算并研究观测系统重复性的表现特征.观测系统重复性的量值属于时移地震噪声数据，观测系统重复性是对这种噪声水平的度量，特别是本文的X关系模式下，适合分析在单道分布上动态性强的这种噪声.拖缆方式采集的时移地震噪声水平变化大，适合应用本文的方法.方法的应用独立地限制在每个面元对应的中心点落在其中的多道观测系统.计算中根据实际情况，进一步缩小了匹配搜索范围，避免大量的可避免的计算.如前所述，计算中采用β=0.2所对应的加权系数. 图 6中给出了本文基于X关系模式的多道重复性计算结果的图像显示，由已知的计算方法可知，观测系统重复性大于X节点值的面元一定存在基线失配的情况发生.大值的单道观测系统重复性和失配都会使多道观测系统重复性增大，但是在多道观测系统重复性不超过X节点值的情况下，从面元总体的多道观测系统重复性上无从判断是否存在失配或单道观测系统重复性达到其X节点值的情况.而当面元的多道观测系统重复性超过其X节点值，就能表明一定有失配存在，并且当所有单道对的观测系统重复性达到X节点值，多道重复性也会是X节点值.因此对于多道重复性，X节点值是一个特殊的临界点，达到或超过这一值表示重复性落入一种特殊的范围，而这个特殊的范围可以被视为质量控制中不可接受的范围.另一方面，由于我们依据的理论关系，多道观测系统的重复性的值与单道观测系统重复性值的意义是相同的，达到X节点值代表重复值最差，超过该值的重复性值代表重复性已经超过了最差的观测系统重复性而失配性已经占据主导.因此，我们可以在工程的质量控制中，视X节点值为一个质量等级分界点，并有理由对观测系统重复性达到或超过该值的面元的观测系统重复性要求改进，更具体的是认为在基线的覆盖必要的情况下总体重复性达到和超过X节点值的面元是重复性需要改进的面元.在原方法的研究中表明，含失配外推的最佳匹配多道观测系统重复性与覆盖次数图(图 7)有一定的吻合性，本文改进的方法所形成的重复性计算结果仍然保持这一特征，这是由于方法中考虑了覆盖次数的影响，同时大的偏离代表了点位控制不佳而与覆盖不均匀或不理想有一定关系.我们在计算结果中识别了一定大值区域，并用纯黑色做了标识在图 6b中显示并在图 6c中做了单独显示.单独显示更容易比较与图 7覆盖次数显示的吻合程度.然而，这里数值大小的界定及区域选择是主观的或是根据区域吻合的程度而反向确定的(当然仍然不失为对吻合性的反映).结合本文改进方法的特点，我们把计算后的数据做了一个特定的筛选，大于X观测系统重复性值的重复性被筛选出，在图 6d和e中相应的位置用纯黑色和纯白色标识出.我们还可以把数据中按此原则视为“合格”的其他数据过滤掉，而显示“超标”的数据及其程度的区分，如图 6f.本文所用原始数据来自于已经完成的时移地震，按照以往通行的办法，已经做出了重复性的评价并达到了满意的水平.虽然图 6a、b和c显示出重复性差的区域，但没有相对客观的区分标准，而通过本文方法的评价和分析，以确定的相对客观的标准显示出了少量局部区域的观测系统重复性仍然有待改进. 图 6d、e和f显示的大于X节点观测系统重复性值的区域在显示控制上是客观明确的，与主观确定和感觉的重复性不佳的分布区域的区别显著，给出了新的信息，依据它可以确定明确而不同的重复性改进的目标区域，与所对应的重复性图上的色标依赖性视觉上的低重复性区域和覆盖次数图中低覆盖区域有了明显不同，给出了明确的不同的重复性改进目标.这一判断依据是基于地震数据的重复性(NRMS)相对于观测系统重复性的关系的分布特征而自然得出的客观结果，是抽象后的规律的客观输出.这就为观测系统评价提供了一个自然客观的依据.这种重复性如所引用的方法的评价结果一样能同时反应资料的覆盖，但是由于覆盖次数的影响最终反映为多道重复性，并由于计算方法的改变和定量差异，与覆盖次数图有一些一致的地方也有差异.

图 6

Fig. 6

图 6 面元分布的基于X模式的观测系统重复性 (a) X模式重复性；(b)大值标为黑色的重复性显示；(c)重复性大值的单独显示；(d) X节点值以上标为纯黑色的重复性显示；(e) X节点值以上标为纯白色的重复性显示；(f)筛选出来的X节点值以上重复性值显示. Fig. 6 Bin X-mode multi-trace geometry repeatability (a) X-mode multi-trace geometry repeatability; (b) X-mode multi-trace geometry repeatability with the bigger value spotted by pure black; (c) X-mode multi-trace geometry repeatability with the bigger value displayed in isolation; (d) The value bigger than X-node value is spotted by pure black; (e) The value bigger than X-node value is spotted by pure white; (f) Display of screened repeatability value bigger than X node value.

图 7

Fig. 7

图 7 与观测系统重复性对照的覆盖次数图 (a) Monitor覆盖次数图；(b)扩展面元Monitor覆盖次数图. Fig. 7 Fold of coverage of monitor in the area corresponding to where the geometry repeatability displayed in Fig. 6 (a) Unflexed coverage of monitor; (b) Flexed coverage of monitor.

对比之下，如果我们不对X节点以上的单道重复性做收缩处理，就会出现重复性数值自X节点增长变大并或有超过外推点的观测系统重复性值，使原失配产生的X节点与外推点之间的反映失配的观测系统重复性值及其所处位置被淹没在其中. 图 8a显示了这种情况. 图 8b和图 8c为分别用纯黑和纯白颜色标记了外推点外的重复性数值区域的显示结果，而在图 8d中显示了过滤筛选出的这些数据. 图 8e和f分别显示了过滤出的X节点外面元多道观测系统重复性值及其分布和X节点与外推点之间的面元多道观测系统重复性值及其分布.

图 8

Fig. 8

图 8 无X节点收缩的多道观测系统重复性 (a)在X模式基础之上没有X节点收缩的观测系统重复性；(b)对外推点观测系统重复性数值以上区域用黑色标出的无X节点收缩的观测系统重复性；(c)对外推点观测系统重复性数值以上区域用白色标出的无X节点收缩的观测系统重复性；(d)对筛选出来的外推点值以上的观测系统重复性的单独显示；(e)对筛选出来的X节点值以上的观测系统重复性的单独显示；(f) X节点与外推点之间的面元多道观测系统重复性值及其分布. Fig. 8 Multi-trace geometry repeatability without X node collapse (a) X-mode geometry repeatability without X node collapse; (b) The same display of Fig. 8a with value bigger than extrapolation value indentified by pure black; (c) The same display of Fig. 8a with value bigger than extrapolation value indentified by pure white; (d) The special display of the screened data bigger than extrapolation value; (e) The special display of the screened data bigger than X-node value; (f) The special display of the screened data between X-node and extrapolation value.

我们也对数据进行了无失配外推方式的处理. 图 9显示了没有做失配外推的数据，相对在图 6a中的一些红色，在该图 9a中反转为低值区，也并没有显示出原有的数据空白(图 9b和c).对失配的忽略使多道重复性中形成了高重复性(低值)区域，事实上对应着处在失配情况的区域，也是覆盖欠缺的区域. 图 9d给出完全的X模式与其无失配外推多道观测系统重复性的差，与monitor覆盖次数图形成了对照.在这样的差值图中，所有发生失配的区域连同失配的程度都可以显示.

图 9

Fig. 9

图 9 无失配外推的X模式观测系统重复性 (a)无失配外推的多道观测系统重复性；(b)无失配外推的多道观测系统重复性(失配试图用纯黑色标出)；(c)无失配外推的多道观测系统重复性(失配试图用纯白色标出)；(d)完全的X模式与其无失配外推多道观测系统重复性的差. Fig. 9 X-mode geometry repeatability without extrapolation for mismatch (a) Original display of X-mode geometry repeatability without extrapolation for mismatch; (b) X-mode geometry repeatability without extrapolation for mismatch (mismatch is try to identified with pure black); (c) X-mode geometry repeatability without extrapolation for mismatch (mismatch is try to identified with pure white); (d) Difference between full X mode and non-extrapolation geometry repeatability.

多道观测系统匹配可能存在不确定性和缺失性，因此最佳定向匹配原则和失配外推理论技术与之适应，而利用归一化均方根差异计算公式可以推导出总体对各道的加权均方根方法.本研究所基于的地震数据重复性与观测系统重复性的前研究，建立了简单局部和有代表性的线性关系模型，据此能获得多道观测系统的度量方式.本文对地震数据重复性与观测系统重复性的关系进行了进一步的研究，提出了该关系的X模式.这一方法的引入，使得多道观测系统重复性的研究得到更合理的应用，使其适用范围得到普遍化，总体精度更高.另外，按本文提出的X关系模式计算的多道观测系统重复性，不仅保持了基于面元内的观测系统失配外推最佳定向匹配加权均方根重复性的同时反映monitor采集的全部观测系统的有效重复性和覆盖程度的特点，而且还使自身包含了更丰富的信息，能够透露一定程度的失配，还能自然地给出多道重复性评价的标准.用此方法获得的数据的原始显示自然地解决了此类数据显示中的数值显示限制的一般技术性问题.

此方法的多道观测系统评价结果，具有一定的科学意义和工程技术价值.