2. 中国科学院大学, 北京 100049;
3. 中国电子科技集团公司第三研究所, 北京 100015;
4. 中国船舶工业系统工程研究院, 北京 100094;
5. 北京和德宇航技术有限公司, 北京 100085;
6. 华北水利水电大学资源与环境学院, 郑州 450046
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. The 3rd Research Institute of CETC, Beijing 100015, China;
4. Systems Engineering Research Institute of CSSC, Beijing 100094, China;
5. China Head Aerospace Technology Co., Ltd., Beijing 100085, China;
6. School of Resources and Environment, North China University of Water Resources and Electric Power, Zhengzhou 450046, China
地震数值模拟方法是研究复杂介质条件下地震波传播的重要手段.一般而言,地震数值模拟主要分为时间域和频率域模拟.频率域地震数值模拟最初是由Lysmer和Drake(1972)提出的,Marfurt(1984)、Marfurt和Shin(1989)、Pratt和Worthington(1990)、以及Hustedt等(2004)和Operto等(2007)亦对其进行了研究及发展.相比较于时间域地震数值模拟而言,频率域地震数值模拟有几个方面的优势.首先是频率域数值模拟可以很方便地应用于黏弹性介质(Hustedt et al, . 2004);其次频率域可同时模拟多震源下的波场响应;更为重要是,频率域模拟可模拟单频波场,便于根据需要对所研究问题的波场频率组分进行取舍.
频率域数值模拟的关键在于求得经波动方程离散化后得到的大型稀疏线性方程组的数值解.考虑到波速、密度等参数的影响,离散化得到的线性方程组的稀疏矩阵是非对称和非正定的,方程组的病态亦很强,导致该线性方程难以准确、高效地求解.直接法和迭代法是求解大型方程组的两种主要方法.直接求解法在求解大规模问题时需占用大量的存储空间,无法避免所谓胖节点问题;而迭代法则易于避开此问题,更适用于大规模问题的求解.近年来,迭代算法在科学计算领域占有举足轻重的地位,比较常用的迭代法包括梯度法(Magnus et al., 1952)、拟牛顿法(Broyden, 1965, 1970; Fletcher, 1970; Davidon and William, 1991)等,这些方法在求解方程系数矩阵为对称正定或M型时具有较高的效率和精度.然而,当系数矩阵为非正定或非对称情况时,仅仅利用上述迭代算法会导致收敛缓慢甚至不收敛.
针对以上问题,引进预条件技术是一种有效的解决方案.近年来随着科学问题的复杂化,预条件技术在科学计算领域发挥着越来越重要的作用,针对不同的科学问题,提出了多种行之有效的预条件方法.但目前来看,并没有可以应用到所有问题的普适的预条件存在.简言之,预条件技术即是将一个难以求解的问题转化为相对可简易求解的等价形式,以达到节约存储空间、加快收敛速度的目的.通常一个高质量的预条件必须满足以下条件:添加预条件后的方程较原始方程计算量小,计算时间明显减少,内存消耗无明显增加.
一般而言,形式上较为简单的预条件,如雅克比(Jacobi)预条件和对称超松弛(Symmetric Successive Over Relaxation: SSOR)预条件,其构建是以系数矩阵的分裂为基础的.以SSOR预条件为例,针对线性方程组Ax=b,首先令系数矩阵A=D+E+F,其中D为系数矩阵A的严格主对角部分,E为矩阵A的严格下三角部分,F为矩阵A的严格上三角部分,则SSOR预条件M为M=(D+ωE)D-1(D+ωF),其中ω表示松弛因子,在计算中一般取1.0(Saad, 2003; 芮平亮, 2007).由预条件形式可知,SSOR预条件构造简单,应用于对称正定矩阵有着很好的效果.但包含矩阵分裂,矩阵-矩阵相乘等运算,计算较为耗时.不完全分解(Meijerink and Van Der Vorst, 1977)预条件(Incomplete Factorization Preconditioner)是较为常用的预条件.以不完全LU分解预条件(Incomplete LU Factorization Preconditioner: ILU(p))为例:首先预条件算子定义为M=LU,其中M表示预条件,L和U是系数矩阵的近似下三角和上三角矩阵,系数p表示预条件矩阵中非零元素的个数,一般而言,p越大,需要的计算量越多,得到的预条件越接近系数矩阵的逆,效果也会越好.但以上结论并无严格的数理逻辑证明,而且在实际运用中,p越大并不能保证预条件效果越好(Benzi and Tuma, 1998).系数矩阵为M型矩阵或者对称正定矩阵情况,ILU(p)预条件会有较理想的效果.然而,当方程系数矩阵具有非对称或非正定等复杂特征时,ILU(p)预条件很不稳定.另一类被广泛应用的是近似逆(Approximate Inverse Preconditioner: AINV)预条件(Benzi and Tuma, 1998, 2000; Saad, 1994; Rafiei, 2014).该类预条件依据算法不同可分为两种,一种是稀疏近似逆(Sparse Approximate Inverse Preconditioner: SPAI)预条件(Grote and Simon, 1992; Benson et al., 2007),该种预条件是基于目标函数‖I-GA‖的范数最小化,G表示稀疏系数矩阵的近似逆,I表示单位矩阵.依据目标函数的行(或列)可将目标函数分解为n个独立的线性最小平方问题,这样有利于并行计算,但该种预条件计算量很大,而且多个最小平方问题并非都容易求解,很容易构造失败.另一种是基于不完全双共轭处理的预条件,与矩阵LU分解类似,不完全双共轭处理预条件能够给出近似上三角和下三角矩阵.当系数矩阵为对称正定或者M型矩阵时,该预条件可以被很好的确定.然而,一方面,双共轭过程计算量大,很不稳定;另一方面为了减少计算量,通常使用双阀值(Saad, 1994)进行限定.双阀值的运用给预条件技术带来方便的同时,又带来了在应用中的复杂性.
正则化方法在求解大型方程组问题中占有很重要的地位.该方法主要是以减少矩阵条件数为目的,使得正则化后的方程较原始方程条件数降低,容易求解.Tikhonov (Tikhonov, 1943; Tikhonov and Arsenin, 1977)正则化方法已广泛应用于求解大型方程组问题,同时,正则化方法也被应用在地震学中.例如,Clapp等(2004)利用正则化算法将地质信息加到成像算法中,以此来提高成像精度;崔岩和王彦飞(2015)将Tikhonov方法应用到地震反演问题,取得了良好的效果;王薇等(2013)提出非线性正则化稀疏约束方法来克服传统正则化方法带来的过度平滑问题.本文基于正则化的思想构建一个高效的预条件算法对大型稀疏方程进行求解.主要思路为:首先选择几组优化的正则化参数,根据系数矩阵特征,运用数学算法将参数加到稀疏矩阵中,此时的方程被称作“正则化方程”;进而将得到的正则化方程的近似解作为原始方程的初始迭代值;最后利用拟牛顿迭代法进行求解.在数值模拟实验的同时,引入ILU(0)预条件(即是p=0预条件算子的稀疏性与系数矩阵相同)来进行数值模拟实验,与本文所述方法对比.同时,我们在均匀介质模型数值模拟中引入LU分解算法来进行结果对比.本文的研究结果,可为今后频率域地震波高效大规模模拟研究提供一种新的选择和途径.
1 方法技术 1.1 频率域声波方程的有限差分离散在某些情况下,地震波可用二维频率域声波方程近似描述:
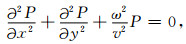
|
(1) |
其中P表示波场, ω表示角频率, v表示声波速度.本文采用九点有限差分格式(Jo et al., 1996)对方程(1)进行差分离散.在二维直角坐标系下,设定二维模型的大小为n1×n2,n1和n2分别是水平和垂直方向的网格数.最终方程(1)差分为一大型稀疏线性方程组:
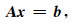
|
(2) |
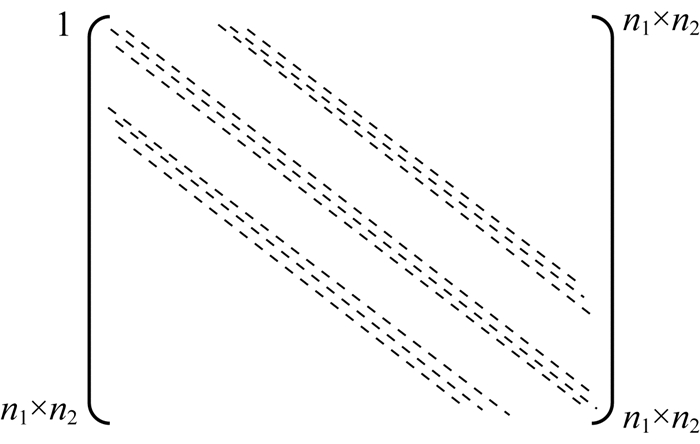
其中A是(n1×n2)×(n1×n2)的系数矩阵,具有非对称和非正定特征;b是(n1×n2)×1阶包含震源信息的向量,x是所要求解的波场向量.通过求解隐性方程(2)就可以得到一炮或多炮的单频波场.系数矩阵的性质是求解方程(2)的关键,九点差分格式得到系数矩阵A如图 1所示,有以下特点:整个系数矩阵最多有9×(n1×n2)个非零元素,分布在主对角以及邻近主对角的九条线上,矩阵整体表现出非对称性、非正定性以及稀疏性.这些复杂特征导致大型稀疏方程(2)难以求解.
|
图 1 系数矩阵的非零元素分布.虚线表示非零元素所在位置,其余均为零元素 Fig. 1 The distribution of nonzero elements. Dotted line shows the position of nonzero elements |
由于方程系数矩阵的复杂性,仅仅用迭代算法来求解方程(2)是非常低效的一种方式.而正则化技术可改善系数矩阵的性质,使得方程更易于求解.在应用正则化方法时,选择合适的正则化系数是关键的一步,若所选系数过大,虽然可以使得矩阵条件数明显改善,但得到的解就偏离了真解;系数太小又会导致条件数得不到改善,方程收敛效率依然很低.故寻找一个适当的正则化系数是加快方程收敛速度的关键所在.
Tikhonov方法是常用的正则化方法之一,根据Tikhonov正则化算法可将方程(2)转化为求解最小平方问题:
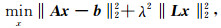
|
(3) |
其中L表示一个与系数矩阵阶数相同的矩阵,λ表示正则化参数,该参数为正数.通常假定L为单位矩阵I.(3)式等价于求解方程:
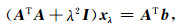
|
(4) |
这里AT表示系数矩阵A的转置,xλ是经正则化后的波场值.在求解方程(4)过程中,若系数λ太大,则会造成方程(4)的系数矩阵ATA+λ2I与原方程(2)的系数矩阵ATA相差很远,最终所求得的波场向量xλ与真实波场值相差很大;反之若λ过小,正则化算子ATA+λ2I与ATA太过接近,起不到加速收敛的作用.而且,方程(4)在实际操作中,ATA会导致计算量增加,条件数增大,导致方程更不容易收敛.因此,应根据原方程系数矩阵的性质适当调整正则化方程.
鉴于ATA算子会引起条件数的增大,本文中利用ATA+λ2I算子并不是一个最佳选择.然而,可将方程(4)转化为等价形式:
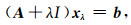
|
(5) |
这里方程(4)中的λ2用正实数λ代替.方程(5)中适当的正则化参数λ是求解的关键.由上可知,λ越大,方程(5)越接近主对角占优,条件数越小,方程越容易求解.方程(5)中的A+λI算子与原系数矩阵的算子的差别恰恰在于主对角元素,故λ的选择与系数矩阵紧密相关.若已知额外的矩阵信息,如特征值和条件数等,则正则化参数λ就比较容易求得,然而求解大型矩阵的特征值或条件数,无疑会耗费更多的计算量和内存空间,得不偿失.根据图 1所示,系数矩阵A的非零元素分布于九条线上,其中三条位于主对角上,其余六条均远离主对角位置.基于以上分析,本文通过对主对角线以及两相邻对角线上的三条非零元素分析,选择正则化参数.
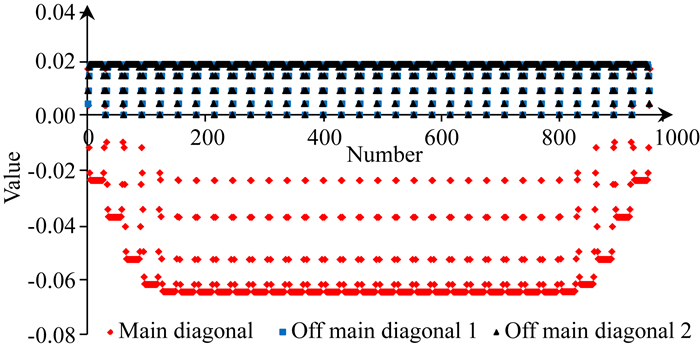
设定一个二维均匀介质模型,波速度为2000 m·s-1,边界为5层PML吸收边界条件,水平方向和垂向网格间距均为6 m,网格点数为nx×nz=31×31,则经9点差分离散得到系数矩阵为312×312的线性方程组,系数矩阵的元素可表示为ai, j,其中i, j=1, 2, 3…n,主对角三条线上元素分别记为ai, i+1,ai, i和ai-1, i,图 2给出了三条线上元素大小分布,可以看出,三条线的元素大小具有“分层”的相对规则的分布特征.然而,分析每条线上元素大小发现,几乎所有的ai, i元素均为负实数,而ai, i+1和ai-1, i元素均为非负实数.这就意味着该系数矩阵性质较为复杂,必须采取措施改善矩阵的性质.
|
图 2 主对角线以及两相邻对角线上元素大小分布示意图 其中“*”表示元素ai, i,“■”|表示元素ai-1, i,“▲”表示元素ai, i+1. Fig. 2 The distribution of elements size of three main diagonal "*" indicates the elements of ai, i, "■" presents the elements of ai-1, i, "▲" gives the elements of ai, i+1. |
Benzi等(2000)的数值实验结论指出:当所构建的预条件矩阵远非主对角占优时,会导致结果不够稳定,精度难以保证;反之,越接近主对角占优,预条件结果越稳定,效率也随之提升.本文基于以上结论并结合频率域波动方程数值模拟系数矩阵的特点,对于方程(5)的处理,有两种方案可供选择.
(1) 系数矩阵主对角线元素比例常数法
引入一个比例常数r,使得正则化前后系数矩阵主对角线元素有固定的比例关系(林胜良,2005).设方程(2)的系数矩阵主对角元素组成的新矩阵为Amd:
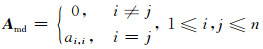
|
(6) |
其中ai, i即为系数矩阵的主对角元素.由此,方程(5)可化为
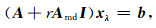
|
(7) |
其中,比例常数通常的取值范围为:0<r≪1.方程(7)为方程(5)经正则化后的方程,与原始方程相比最终效果是主对角线元素整体的改变.
(2) 基于对主对角元素分布范围分析法
以图 2为例,主对角元素ai, i可分为几部分,因此可根据分布范围进行适当操作.首先引入比例常数r,am表示一个正实数.基于以上论述得到正则化方程:
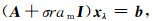
|
(8) |
其中参数σ被定义为

|
(9) |
式(9)中的c表示临界点,c的选择决定了被修正元素的范围.以c=0为例:当c=0时,系数矩阵主对角元素中大于零的部分不变,而所有满足ai, i≤0转变为ai, i+ram.通常设定参数am为
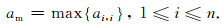
|
(10) |
方程(7)和方程(8)是以两种不同的方式构建正则化算子.算子A+rAmdI是对系数矩阵主对角元素统一按比例改变,每个主对角元素ai, i被(1+r)ai, i代替;算子A+σramI是依据系数矩阵具有的细节特征而灵活做出的部分改变.
式(7)、(8)中的优化参数可由同类研究问题的小规模模型方便而快捷地优化求得(既可采用优化试算,也可采用现有成熟的优化算法).Benzi等(2000)、林胜良(2005)等人的工作表明,对于同类问题或模型,模型的规模对上述优化参数的影响不敏感,即同类问题由小模型优化所得的参数对该类问题的各尺度、规模的模型均具有普适性.
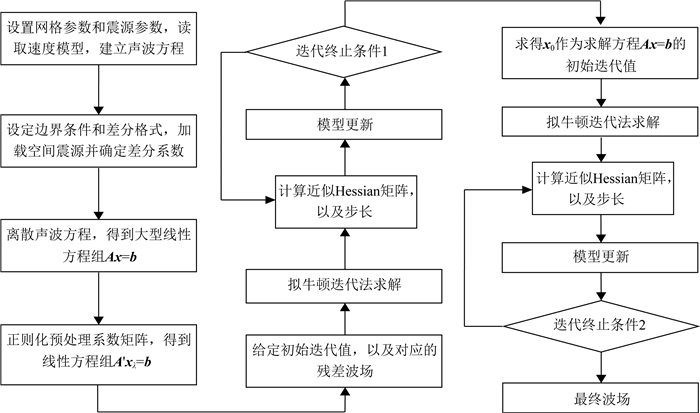
本节所讨论的“正则化预条件迭代算法”具体流程见图 3.
|
图 3 数值模拟算法流程图 Fig. 3 The flow diagram of numerical simulation algorithm |
流程图中方程Ax=b表示原始方程,指频率域声波方程经差分离散后得到的大型稀疏线性方程组,即公式(2);A′x=b表示正则化方程,即是原始方程经预处理方案一或预处理方案二处理后得到的方程组,对应于方程(7)或方程(8).为了在求解两个方程时具有统一性和可比性,流程图中利用的“拟牛顿迭代算法”均采用Broyden拟牛顿算法(Broyden, 1965; Leary, 1993),又称Broyden第一公式进行求解,其基本迭代格式为
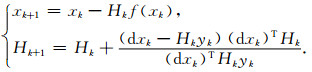
|
(11) |
其中
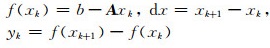
|
式中xk表示第k次迭代值.
2 数值实验 2.1 均匀介质模型在均匀介质模型中,给定网格数为nx×nz=71×71(包括10层PML吸收边界层)网格间距为dx=dz=6 m,波速为2000 m·s-1,时间为512 ms,采间隔为1 ms,激发点位置位于(xs, zs)=(0.5×nx×dx+2, 0.5×nz×dz+2)处,震源子波为主频为30 Hz的雷克子波,单频波场的频率为43.9 Hz.所有的数值模拟程序均使用Fortran 90语言编写,并进行了单、双精度模拟测试.所有的数值实验均在同一工作站上完成,初始迭代值设为-0.05.终止条件包括两个:一是ε1 < 10.0和ε < 0.1,其中ε1和ε分别表示迭代法求解正则化方程和原始方程时的残差二范数,定义为
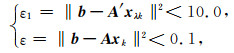
|
(12) |
其中xλk表示求解正则化方程的第k次迭代值,xk表示原始方程的第k次迭代值;第二个终止条件定义为:迭代总次数大于1000次.二者满足其一,迭代即结束.
在上一节中,讨论了两种正则化预条件方案.这里依据两种方案来给出对应的预条件算子:首先经过多次基于不同规模,不同性质模型下的数值实验得出正则化参数r的范围在0.035≤r≤0.065时,对提高求解速度较为明显,这里给定正则化系数r=0.04;给出方程(8)三个临界值分别为c=0, -0.02, -0.06.同时,作为对比算法,Jacobi预条件、SSOR预条件和ILU(0)预条件亦被用来解决该线性问题.
表 1给出不同算法下单频的数值模拟结果:包括不同阶段的迭代次数和总时间消耗.算子①是基于方案一对整个主对角元素做出的0.04的修正,算子②,③和④基于方案二对部分主对角元素做出的修正,⑥算子是用拟牛顿迭代法直接求解.上述数值实验结果表明:基于方案一的算子①在单精度下结果是不收敛的,而基于方案二的算子②,③和④在单精度条件下均能够得到良好的结果.迭代次数与⑥算子相比,②,③和④明显减少迭代次数,减少了时间消耗,尤其是算子④中260次迭代相较于算子⑥中的768次而言,效率明显提高.
|
|
表 1 基于预条件方法的数值模拟实验结果 Table 1 Numerical experiment results based on regularized preconditioning iterative method |
表 1中显示出基于Jacobi预条件和SSOR预条件下的数值模拟结果并不收敛,说明两种预条件方法并不适用于本文研究的问题.且两种预条件的构建均涉及到矩阵分裂和矩阵-矩阵相乘运算,尤其是SSOR预条件在系数矩阵分裂的基础上还要进行两次矩阵-矩阵相乘,计算量和时间代价均较高.
在本算例中,相对于Jacobi预条件和SSOR预条件的表现不佳而言,ILU(p)预条件的效果与参数p的大小有关.p越大越接近系数矩阵的逆,加速效果也越明显,但对内存的消耗亦急剧增加.在本数值算例中,我们采用ILU(0)预条件算子⑤进行数值模拟,发现该算法在构建预条件矩阵过程中不仅占用数倍于迭代法的内存空间,而且消耗了4425 s的时间进行不完全LU分解和求逆等运算.由上述算例可知,对于大规模迭代求解问题,ILU(p)预条件本身固有的额外高内存消耗量和求逆所需运算量无法避免,很大程度上限制了ILU(p)预条件在大规模问题上的应用.除此之外,ILU(p)预条件本身具有不稳定性.
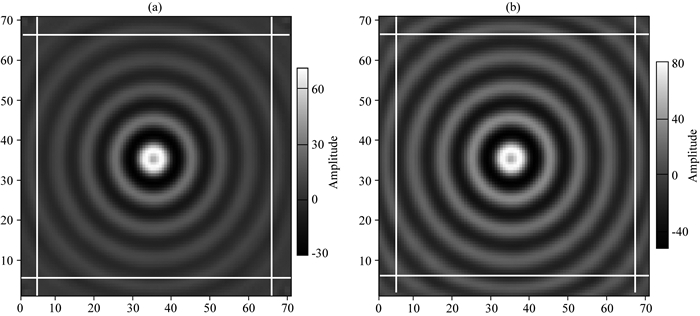
图 4给出基于算法④得到的单频43.9 Hz下的波场示意图.(a)图表示基于正则化方程得到的近似波场,(b)图表示最终波场.对比显示,二者在大致轮廓上基本一致,但在细节刻画方面,波场(b)明显优于波场(a),而且有以震源为中心,二者的差别向四周逐渐增大的特征.
|
图 4 单频43.9 Hz均匀模型下的波场示意图 (a)近似波场; (b)最终波场.模型水平和垂直方向均是420 m,白色实线以外为PML吸收边界区域. Fig. 4 Graphs of wavefield under the homogeneous medium with the single frequency 43.9 Hz The graph (a) shows the approximate wavefield, (b) shows the final wavefield. The horizontal and vertical interfaces are at a same distance 420 m. The white line delineates the PML layers. |
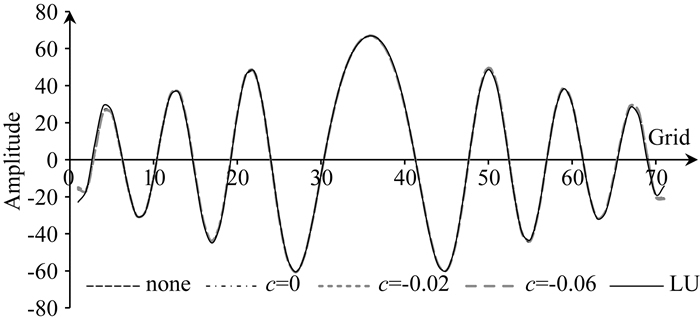
图 5给出不同算法结果准确性估计.分别对应算法②、③、④和⑥结果的第25个网格点处的水平方向波剖面.同时,给出经LU分解算法得到的相同位置波剖面作为参照.对比可知,显示出五种算法下得到的波剖面拟合程度很高,波形基本一致.基于算法②、③、④和⑥的结果与LU分解结果数值差异满足数值精度要求.说明在本文所论述正则化不同算法下,得到的数值结果均是可靠的.
|
图 5 基于不同算法下的波剖面对比 “none”对应于算子⑥,用长虚线表示;“c=0”对应于算子②,用点虚线表示;“c=-0.02”对应于算子③,用短虚线表示;“c=-0.06”对应于算子④,用加粗虚线表示;实线表示LU分解结果. Fig. 5 Results of wave profiles based on different algorithms "none" shows the operator ⑥ with long dashed line; "c=0" presents the result of ② algorithm with dashed line; "c=-0.02" gives the operator ③ with short dotted line; "c=-0.06" shows the result under the operator ④ with bold dashed line; The solid line gives the result of LU decomposition. |
表 1给出时间消耗的明显规律是时间随迭代次数的增多而上升,但很难确定构造预条件算子需要的时间百分比.为了近似估计构造预条件算子所需时间.首先根据表 1将每种方法消耗的总时间平均分配到每次迭代上,得到每次迭代所需时间均在1.24~1.25 s之间.说明预条件迭代算法与直接迭代算法二者每次迭代所消耗的时间几乎相等,表示构建预条件的时间消耗可以忽略不计.这也是该预条件迭代算法的优势之一.
2.2 高非均匀度介质模型:Marmousi模型设定二维Marmousi模型网格数为700×700,水平网格间距为dx=12.5 m,垂直网格间距为dz=4 m,速度模型如图 6所示,采样间隔为1 ms,震源位于表层中心处,子波设定为主频为30 Hz的Ricker子波,单频波场的频率为9.766 Hz.终止条件为:(1) ε1 < 10.0和ε < 1.0时,迭代终止.其中ε1和ε定义同均匀介质模型(式(12));(2)总迭代次数大于1000次时,迭代终止.这里我们给出运用表 1中的算子②和⑥来进行数值模拟实验.

|
图 6 Marmousi速度模型示意图 Fig. 6 Marmousi velocity model |
表 2给出了基于Marmousi模型两种算法下的迭代次数统计.算子①表示将系数矩阵主对角线元素中所有小于零的修正4%,该算法仅需要316次便能收敛到所要求的精度.而算子②无预条件情况下直接迭代算法求解难以收敛(超过1000次).图 7给出了两种方法对应的残差曲线,注意到在初始的几十次迭代中,残差曲线具有很高的一致性,但随着迭代次数的增加,两条残差曲线就逐渐分开.说明预条件技术在处理复杂模型时是很有必要的,适当的预条件在不增加计算量的同时能够很好地改善收敛性,减少迭代次数,加快收敛速度.

|
图 7
Marmousi模型数值模拟中两种方法的迭代残差曲线
实线“Reg_Num”表示基于算子①下的迭代残差曲线;虚线“None”表示算子②求解得到的残差曲线(前1000次). 图中小坐标系中的曲线是红框部分的放大显示. Fig. 7 Residual curves based on two different numerical algorithms "Reg_Num" and "None" present the residual curves under the operator ① and ②, respectively. The residual number range from 300 to 330 of iteration is magnified display. |
|
|
表 2 基于Marmousi模型速度模型的数值模拟实验结果 Table 2 Numerical experiment results based on Marmousi model |
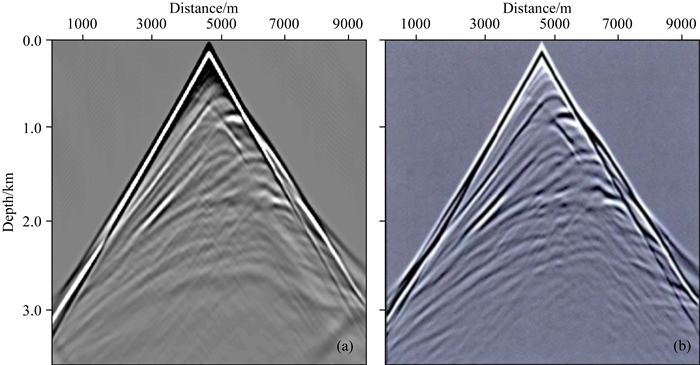
基于表 2中的算子①得到多个频段的波场,进而反傅里叶变换得到混合频率的时间域波场,并生成以中点激发的理论地震记录(图 8a).通过与唐祥德等(2015)通过有限差分时间域得到的正演数值模拟波场(图 8b)进行对比,得到二者的反射同相轴空间形态基本一致,在中深层处的反射仍具有很好的一致性,轻微的差别是由边界条件的不同引起的.理论地震记录的对比充分证明了本文方法的准确性.
|
图 8 Marmousi模型理论地震记录 (a)正则化预条件迭代算法得到; (b)有限差分时间域数值模拟得到(唐祥德等,2015). Fig. 8 Theoretic synthetic records based on the Marmousi model (a) Shows the result under the regularized preconditioning iterative method; (b) Presents the record based on the finite difference numerical modeling (Tang et al., 2015). |
在数值模拟实验中,对于一个80×80的模型网格,正则化预条件迭代算法仅需要0.2 GB的计算空间,但LU分解却需要8 GB的计算空间,前者约是后者的40倍,这就充分证明了正则化预条件迭代方法较LU分解法更适用于大型频率域地震波场问题的处理.
就性能与实现途径而言,本文提出的正则化预条件技术与Wong(1988)、Benzi等(2000)以及Al-Attar等(2012)根据各自研究问题的背景特征所提出的具有针对性的预条件方案,可谓异曲同工.以上数值算例之结果表明:本文所述预条件技术在应用于大规模频率域波动方程数值模拟问题时具有很好的效果.
2.3 数值频散分析数值模拟中的数值频散是一个关键的问题,直接影响到模拟结果的好坏(董良国和李培明,2004).数值频散的原因本质上归结于利用有限的离散网格来近似逼近连续的无限介质,导致不同频率的地震波具有不同的相速度.最初由Alford等(1974)和Dablain(1986)对声波二阶空间差分的数值频散进行了分析,得出影响数值频散的两个因素包括网格大小和声波传播方向,数值正演模拟的效果很大程度上取决于数值频散程度.为简单起见,两个方向离散网格设为相同,即是Δx=Δz.根据二维声波空间差分数值频散公式为

|
(13) |
其中θ表示声波传播方向与坐标x轴的夹角,λ为声波波长,Cn(N)为差分系数,v0为无频散情况下的声波速度,v为相速度.
(13) 式直观地给出了影响频散关系的两个主要因素.图 9给出了传播方向与水平坐标轴之间的夹角θ在0°到60°之间时,每15°传播方向上,随着网格波长比的变化而绘制的曲线.可以发现,一方面同一传播方向上,Δx/λ越小,相速度和真速度越接近,当比例在Δx/λ≈0.1以内时,几乎不发生频散;另一方面,声波传播方向与水平方向的夹角大小对频散也有显著的影响.上述频率域数值模拟实验中参数设置均满足Δx/λ≈0.1条件,得到的结果并没有发现有数值频散现象,得到的波场结果均是可靠的.

|
图 9 不同传播方向上,依据网格波长比的变化而绘制的频散曲线 Fig. 9 Varied dispersion curves based on the grid wavelength ratio and direction of propagation |
本文基于不同介质模型,利用正则化技术和迭代算法相结合,对频率域声波传播进行了数值模拟.本文着重介绍了一种新的正则化预条件迭代算法.通过对均匀介质模型和高度非均匀模型的数值模拟结果分析表明,该算法可满足复杂模型下的波场数值模拟精度,与单独使用迭代算法求解相比,收敛速度明显提高,显著减少迭代次数,适合大规模数值波场模拟问题.而且,通过数值模拟实验可知,在计算量方面,该方法与直接迭代算法求解相比,仅增加了一次矩阵-矢量相乘;在内存消耗方面,与直接法如LU分解算法相比,同样是80×80的网格模型,内存消耗仅为后者的约1/40.综合数值模拟结果的精度、效率、计算量和存储量方面的因素说明,正则化预条件迭代算法可以作为求解大规模频率域地震波场问题的一种新的选择.
致谢 感谢刘洪研究员对本文的指导,感谢审稿人提出的意见和建议.
Al-Attar D, Woodhouse J H, Deuss A. 2012. Calculation of normal mode spectra in laterally heterogeneous earth models using an iterative direct solution method. Geophysical Journal International, 189(2): 1038-1046. DOI:10.1111/j.1365-246X.2012.05406.x |
Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. DOI:10.1190/1.1440470 |
Benson M, Krettmann J, Wright M. 2007. Parallel algorithms for the solution of certain large sparse linear systems. International Journal of Computer Mathematics, 16(4): 245-260. |
Benzi M, Tuma M. 1998. A sparse approximate inverse preconditioner for nonsymmetric linear systems. SIAM Journal on Scientific Computing, 19(3): 968-994. DOI:10.1137/S1064827595294691 |
Benzi M, Haws J C, Tuma M. 2000. Preconditioning Highly Indefinite and Nonsymmetric Matrices. Society for Industrial and Applied Mathematics, 22(4): 1333-1353. |
Broyden C G. 1965. A class of methods for solving nonlinear simultaneous equations. Mathematics of Computation, 19(92): 577-593. DOI:10.1090/S0025-5718-1965-0198670-6 |
Broyden C G. 1970. The convergence of a class of double rank minimization algorithms, Part Ⅰ'. Journal of Applied Mathematics, 6(1): 76-90. |
Clapp R G, Biondi B, Claerbout J F. 2004. Incorporating geologic information into reflection tomography. Geophysics, 69(2): 533-546. DOI:10.1190/1.1707073 |
Cui Y, Wang Y F. 2015. Tikhonov regularization and gradient descent algorithms for tomography using first-arrival seismic traveltimes. Chinese Journal of Geophysics (in Chinese), 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
Davidon and William C. 1991. Variable metric method for minimization. SIAM Journal on Optimization, 1(1): 1-17. |
Dong L G, Li P M. 2004. Dispersive problem in seismic wave propagation numerical modeling. Natural Gas Industry (in Chinese), 24(6): 53-56. |
Fletcher R. 1970. A new approach to variable metric algorithms. The Computer Journal, 13(3): 317-322. DOI:10.1093/comjnl/13.3.317 |
Grote M, Simon H D. 1992. Parallel preconditioning and approximate inverses on the connection machine.//Proc. Sixth SIAM Conference on Parallel Processing for Scientific Computing. Williamsburg, VA: Philadelphia, PA, 519-523.
|
Hustedt B, Operto S, Virieux J. 2004. Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling. Geophysical Journal International, 157(3): 1269-1296. DOI:10.1111/gji.2004.157.issue-3 |
Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2D scalar wave extrapolator. Geophysics, 61(2): 529-537. DOI:10.1190/1.1443979 |
Leary D. 1993. Why Broyden's Nonsymmetric Method Terminates On Linear Equations. University of Maryland at College Park.
|
Lin S L. 2005. Studying the algorithm for solving Ill-conditioned linear system of equations[Master's thesis] (in Chinese). Hangzhou: Zhejiang University.
|
Lysmer J, Drake L A. 1972. A finite element method for seismology.//Bolt B A ed. Methods in Computational Physics, volume 11: Seismology: Surface Waves and Earth Oscillations. New York: Academic Press Inc., 181-216.
|
Magnus. R. Hestence and Stiefel. 1952. Methods of Conjugate Gradients for solving linear systems. Journal of Research of the National Bureau of Standards, 49(6):409-436.
|
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(4): 533-549. |
Marfurt K J, Shin C S. 1989. The future of iterative modeling in geophysical exploration.//Eisner E ed. Handbook of Geophysical Exploration: I Seismic Exploration, volume 21: Supercomputers in seismic exploration. New York: Pergamon Press, 203-228.
|
Meijerink J A, Van der Vorst H. 1977. An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix. Mathematics of Computation, 31(137): 148-162. |
Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver:A feasibility study. Geophysics, 72(5): SM195-SM211. DOI:10.1190/1.2759835 |
Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography:Part Ⅰ:Acoustic wave-equation method. Geophysical Prospecting, 27(6): 287-310. |
Rafiei A. 2014. Left-looking version of AINV preconditioner with complete pivoting strategy. Linear Algebra and its Applications, 445: 103-126. DOI:10.1016/j.laa.2013.11.046 |
Rui P L. 2007. Fast iterative techniques for electromagnetic scattering analysis[Ph. D. thesis] (in Chinese). Nanjing: Nanjing University of Science and Technology.
|
Saad Y. 1994. ILUT:A dual threshold incomplete LU factorization. Numerical Linear Algebra with Applications, 1(4): 387-402. DOI:10.1002/(ISSN)1099-1506 |
Saad Y. 2003. Iterative Methods for Sparse Linear System. Philadelphia: Society for industrial and mathematics.
|
Tang X D, Liu H, Zhang H. 2015. Frequency-space domain acoustic modeling based on an average-derivative and GPU implementation. Chinese Journal of Geophysics (in Chinese), 58(4): 1341-1354. DOI:10.6038/cjg20150421 |
Tikhonov A N. 1943. On the stability of inverse problems. Dolk.akad.nauk Sssr, 39(5): 176-179. |
Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-posed Problems. Wiley.
|
Wang W, Han B, Tang J P. 2013. Regularization method with sparsity constraints for seismic waveform inversion. Chinese Journal of Geophysics (in Chinese), 56(1): 289-297. DOI:10.6038/cjg20130130 |
Wong Y S. 1988. Preconditioned gradient type methods applied to nonsymmetric linear systems. International Journal of Computer Mathematics, 23(2): 141-165. |
崔岩, 王彦飞. 2015. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法. 地球物理学报, 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
董良国, 李培明. 2004. 地震波传播数值模拟中的频散问题. 天然气工业, 24(6): 53-56. DOI:10.3321/j.issn:1000-0976.2004.06.016 |
林胜良. 2005.病态线性方程组解法研究[硕士论文].杭州: 浙江大学.
|
芮平亮. 2007.电磁散射分析中的快速迭代求解技术[博士论文].南京: 南京理工大学.
|
唐祥德, 刘洪, 张衡. 2015. 基于加权平均导数的频率-空间域正演模拟及GPU实现. 地球物理学报, 58(4): 1341-1354. DOI:10.6038/cjg20150421 |
王薇, 韩波, 唐锦萍. 2013. 地震波形反演的稀疏约束正则化方法. 地球物理学报, 56(1): 289-297. DOI:10.6038/cjg20130130 |
 2019, Vol. 62
2019, Vol. 62


 ,
张欢1,2,4,
李冰非1,2,
马晓娜1,2,
鹿璐1,2,5,
陈世仲6
,
张欢1,2,4,
李冰非1,2,
马晓娜1,2,
鹿璐1,2,5,
陈世仲6