当传统单个震源的药量增加到一定程度时，激发产生的地震波能量将不再相应增加(张智等，2003).在近地表散射源较多的西部山前断裂带和近地表土质疏松的沙漠地区，激发接收条件差，普通单震源激发难以获得满意的高性噪比地震数据.震源组合技术能够实现某一方向上各子震源地震波场能量的同相叠加，提高地震资料性噪比和地震波照明度(黄洪泽，1984；Evans，1997；熊翥，2005；Ramsden et al., 2005).

早在20世纪70年代，Arnold(1977)在Oklahoma的Tulsa地区成功地进行了地震波束形成试验，该试验使用单频液压震源，通过设置在地表和地下的检波器证实了可控震源能够形成定向地震波束.20世纪80年代，胡启宇(1981)详细介绍了时序激发等间隔震源组合获得指向性波束的原理和方法.姜弢等(2006, 2008, 2009)，葛利华等(2012)研究了不同震源个数和不同延迟时间参数的相控震源对地震资料信噪比的改善程度.徐峰等(2011)，汪仁富等(2011)建立起了针对目标地层的入射能量判别函数，定量分析了不同震源组合参数情况下震源附近的能量分布.刘福烈等(2013)从能量判别函数出发给出了组合震源理论信噪比的定义及计算方法，定量地分析了震源数目、组内距、地震子波波长等参数与地震资料信噪比之间的关系.Gong等(2014)基于爆炸理论建立了与组合震源激发等价的单震源雷克子波的理论计算公式，在保证总药量不变的条件下，根据新的雷克子波公式定量地分析了不同震源组合个数对地震资料信噪比的影响.Smith(1984)，Moldoveanu(2000)，Robertsson等(2008, 2012)，刘福烈等(2014)，Shen等(2014)提出将震源布设在不同深度并采用不等时激发的组合方式，这种组合方式对虚反射、面波以及地表散射干扰起到了明显的压制作用.巩向博等(2014)指出，对于特定的目标层位，组合震源激发的主波束方向垂直于其构造走向能够对目标地层进行最大能量的照明并获得能量最强信噪比最高的地震记录.

然而，震源组合在提高聚焦方向上地震波场传播能量的同时，削弱了非聚焦方向上地震波场的传播能量.如果聚焦方向选择不当，不仅不能提高地震资料信噪比反而会降低采集质量.因此，组合震源地震波场定向传播方向的正确选择就显得尤为重要.但是，目前对组合震源定向方面的研究大多集中在计算给定聚焦方向的组合震源延迟激发时间上，并没有讨论对于特定的地下构造，如何准确计算最佳的组合震源地震波场定向传播方向.姜弢等(2009)利用多种不同延时参数的组合震源分别进行试验，从而确定较好的组合震源延时参数.但是，该延时参数的准确程度严重依赖于延时参数的模拟间隔，要获得最佳的延时参数需要多次模拟实验，非常耗时.同时，该方法也没有考虑炮间延迟时间参数的差异性.

近年来，地震波场方向性分解越来越受到地球物理工作者们的重视，地震波场方向性分解在地震定向照明和逆时偏移低频噪声压制中得到了广泛的应用(Yoon et al., 2004；陈生昌等, 2007, 2009；裴正林，2008；谢小碧等，2013).地震波场方向性分解通过局部角度域分解算子能够将模拟地震波场分解为不同传播方向上的地震波，这就使得地表方向统计成为了可能.秦龙等(2016)利用地表方向统计的方法计算水平地表组合震源的延迟激发时间.但在应用时为了实现地表能量统计，只是在照明阴影区单点激发地震波，不能保证组合震源波场垂直入射到目的层界面上.本文对该方法进行了改进，根据爆炸反射面原理：水平叠加剖面等价于自激自收剖面也等价于在反射界面上同时激发震源产生地震波，以半速度向外传播，在地面上观测到上行波剖面.根据这一原理，在界面上均匀布置震源同时激发地震波，能够产生垂直于地层界面传播的平面波.如果只在目的层界面激发地震波，当初至波传播至地表时进行地表方向统计，根据互易性原理，沿初至波传播方向的反方向传播的地震波将垂直入射到目的层界面，从而实现了对目的层最大程度的照明并获得能量最强信噪比最高的地震资料.

此外，组合震源理论基本都是基于水平地表条件，国内外对起伏地表条件下组合震源理论的研究相对较少.本文从惠更斯-菲涅尔原理出发，提出一种在已知聚焦方向的情况下求取起伏地表组合震源延迟激发时间的方法.即根据炮点坐标建立起炮点向量，计算炮点向量在聚焦方向上的投影，通过投影的长度即可确定组合震源的延迟激发时间.水平地表和倾斜地表作为起伏地表的特殊形式，同样能够利用此方法求取组合震源沿指定方向定向传播地震波场的延迟激发时间.

坡印廷矢量等于电场强度与磁场强度的叉积，矢量大小代表单位时间内垂直穿过单位面积的电磁场能量，矢量方向代表电磁波的传播方向.地震波场与地磁场类似也存在能流密度矢量，声波方程的能流密度矢量(坡印廷矢量)可表示为(Yoon et al., 2004)

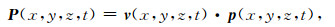
(1)

式中，P(x, y, z, t), v(x, y, z, t), p(x, y, z, t)分别代表(x, y, z)位置处t时刻的坡印廷矢量，质点震动速度矢量和压力场.

通过坡印廷矢量公式可以计算出任意位置任意时刻地震波场的传播方向和沿该方向传播的地震波能量大小.根据爆炸反射面原理，在目的层界面上均匀布置炮点激发地震波，能够形成与地层界面平行的平面波，该平面波传播方向与地层界面垂直.当该平面波传播至地表时，通过坡印廷矢量公式计算并记录地震波的传播方向.根据互易性原理，如果将地表统计方向的反方向作为震源组合的聚焦方向来激发组合震源，则组合震源的主波束传播至目的层时为垂直入射(或近似垂直入射).这样一来可以最大限度的提高目的层的照明能量，同时提高野外采集地震资料的信噪比.

如图 1所示，在目的层界面上均匀布置炮点进行波场上传，当地震波经过上覆地层透射传播至地表时，将其坡印廷矢量记为P(x).为了更加直观的显示地表方向统计结果，将P(x)与x方向的夹角α(x)作为地表方向统计结果的另一种形式进行记录.计算公式如下

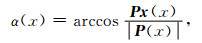
(2)

图 1

Figure 1

图 1 地表方向统计示意图 Figure 1 Diagrammatic diagram of the surface direction statistic

公式中Px(x)代表坡印廷矢量在x方向上的分量.

起伏地表条件下，组合震源的各个子震源位置高低起伏，并不能保证震源布置在同一条直线上.此时组合震源的延迟时间参数是非线性的，传统的归一化方向因子公式也就不再适用了.为此，本文从惠更斯-菲涅尔原理出发提出了一种解决方案.惠更斯-菲涅尔原理指出“行进中的波阵面上任一点都可看作是新的次波源，而从波阵面上各点发出的许多次波所形成的包络面，就是原波面在一定时间内所传播到的新波面”.惠更斯-菲涅尔原理提供了组合震源定向地震波场的计算思路，即若原始波前为定向的地震波场，其新波前仍为同方向的定向地震波场(巩向博等，2014).根据这一理论，在均匀模型条件下，任意两个时刻组合震源形成的定向地震波场方向不会发生改变.因此，在进行组合震源延迟时间参数设计时，只需要确定任意一个时刻组合震源的定向传播方向沿着地表统计方向的反方向传播即可.假设过左边第一个炮点位置坐标并与地表统计方向垂直的平面(二维情况下为一条直线)为某个时刻的波前面.通过计算组合震源激发的地震波传播至该波前的走时确定震源组合的延迟激发时间.

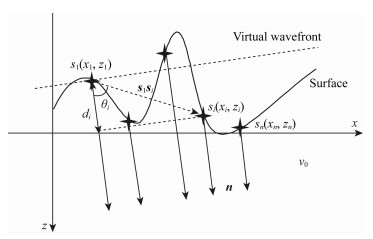
将水平方向依次排列的炮点集合设为{s₁, s₂, …, s_n}；组合震源的各子震源位置坐标集合标记为{(x₁, z₁), (x₂, z₂), …, (x_n, z_n)}；组合震源各子震源到虚拟波前的距离记为{d₁, d₂, …, d_n}；第一个子震源与其他子震源组成的炮点向量记为{s₁s₂, s₁s₃, …, s₁s_n}；炮点向量与定向传播方向的夹角记为{θ₂, θ₃, …, θ_n}；组合震源各子炮点的延迟激发时间记为{t₁, t₂, …, t_n}；n为组合震源个数；n代表组合震源定向地震波场的传播方向；v₀表示近地表地层速度.各参数的关系如图 2所示：

图 2

Figure 2

图 2 起伏地表组合震源激发示意图 Figure 2 Diagrammatic diagram of the source array explosion with undulating surface

通过计算各炮点向量在组合震源聚焦方向上的投影确定各震源间的延迟激发时间.在构造较复杂的地区，组合震源各个子震源位置的地表方向统计结果可能存在一定差异，通过初至波的平均出射方向作为组合震源的聚焦方向，从而提高聚焦方向的可靠性：

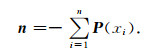
(3)

炮点向量可根据各炮点所在坐标位置来确定：

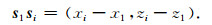
(4)

根据余弦定理可以计算出炮点向量与组合震源聚焦方向夹角的余弦值：

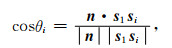
(5)

炮点向量在组合震源聚焦方向上的投影可表示为

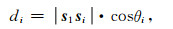
(6)

将公式(5)代入公式(6)中，可得

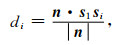
(7)

进而计算出各炮点相对于第一个炮点的延迟激发时间：

(8)

然而，计算出的延迟激发时间为相对于第一个炮点(即s₁)的延迟激发时间.由于炮点位置设置是任意的，该延迟激发时间可能会出现负数.因此，筛选出延迟激发时间最小的炮点作为激发的零时刻，其余炮点延迟激发时间调整为

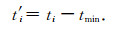
(9)

为了验证本文提出的面向目标的起伏地表组合震源延迟激发时间确定方法的正确性，设计了如图 3所示的起伏地表模型进行测试.模型宽度为800 m，最大深度为800 m，起伏地表最大高低落差达102 m，三套地层层速度由浅至深分别为2500 m·s^-1、3000 m·s^-1、3500 m·s^-1，将最底层视为此次测试的目的层.采用双程波动方程时域有限差分进行数值模拟，水平方向与竖直方向的网格步长均为2 m，时间采样间隔为0.25 ms.由于模型较小，我们选用80 Hz的雷克子波作为震源子波，以减小子波波长.

图 3

Figure 3

图 3 起伏地表模型 Figure 3 Undulating model

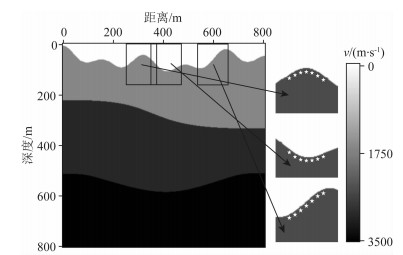
在目的层顶界面上均匀布置炮点进行面炮激发，当激发产生的平面波经过上覆地层透射到达地表时，通过坡印廷矢量进行地表方向统计.由于目的层界面左右两侧基本对称并且呈轻微“凹”状，在不考虑上覆地层界面透射对传播角度影响的情况下，地表出射角统计结果应该成中心对称；目的层左侧倾斜界面产生的平面波在地表的出射角应该为锐角，右侧倾斜界面产生的平面波在地表的出射角应该为钝角；目的层左右两端及目的层中部近似为水平界面，产生的平面波在地表的出射角应该在90°附近.通过公式(2)将传播方向转化为出射角进行显示，如图 4，与预测结果基本相符.因此，利用坡印廷矢量进行地表方向统计的方法是完全可行的.

图 4

Figure 4

图 4 地表方向统计结果 Figure 4 The result of surface direction statistic

根据地表方向统计结果和炮点向量，可以计算出任意起伏地表组合震源的延迟激发时间.我们分别选择了“凸”型，“凹”型和倾斜地表布置了三个包含七个子震源的组合震源，各子震源在水平方向等间隔排列，水平方向组内距为10 m.三个组合震源的水平中心位置分别在320 m，410 m和600 m处(几何放大图中五角星代表各个子震源点)，单个组合震源内最大高低落差达62 m，最大延迟激发时间为19.74 ms.根据地表方向统计结果和炮点向量计算出三个组合震源的延迟激发时间如表 1所示.

表 1 Table 1

表 1 组合震源位置及延时参数表 Table 1 The coordinates and delay explosion time of source array 炮点序号 第一个组合震源 第二个组合震源 第三个组合震源 位置坐标(m) 延迟时间(ms) 位置坐标(m) 延迟时间(ms) 位置坐标(m) 延迟时间(ms) 1 (290, 58) 0 (380, 96) 5.92 (570, 90) 0 2 (300, 52) 3.19 (390, 104) 2.88 (580, 80) 3.29 3 (310, 48) 5.60 (400, 110) 0.64 (590, 68) 6.58 4 (320, 46) 7.22 (410, 112) 0 (600, 56) 10.66 5 (330, 48) 7.29 (420, 112) 0.16 (610, 44) 14.74 6 (340, 56) 5.00 (430, 108) 1.92 (620, 34) 18.03 7 (350, 64) 2.72 (440, 104) 3.68 (630, 28) 19.74

表 1 组合震源位置及延时参数表 Table 1 The coordinates and delay explosion time of source array

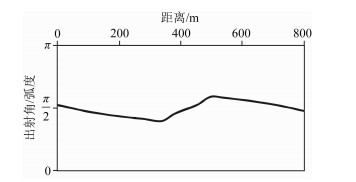
根据计算得到的各子震源的延迟时间参数设计组合震源，可以得到如图 5所示的三个组合震源在225 ms时的波场快照.无论是地表凸起(图 5a)，凹陷(图 5b)或者倾斜(图 5c)，根据地表方向统计和炮点向量设计出的组合震源都形成了垂直于目的层传播的定向地震波场.

图 5

Figure 5

图 5 组合震源225 ms时的波场快照 (a)地表凸起; (b)地表凹陷; (c)地表倾斜. Figure 5 The snapshot of source array at 225 ms (a) The convex Topography; (b) The concave topography; (c) The dipping topography.

波场快照只能反映某一个时刻的地震波场传播情况.为了获得震源能量的传播“轨迹”，我们进行了不同激发方式的多炮照明模拟(图 6)，组合震源均包含七个子震源，除激发时间不同外其余参数相同，单震源与组合震源总药量相等，激发振幅按照经验公式E=(Q/s)^1/3计算，其中E表示单震源激发振幅，Q表示炸药药量，s表示震源组合个数.从照明结果中可以看出，组合震源照明能量大于普通单震源照明能量，定向激发组合震源照明能量大于同时(非定向)激发组合震源照明能量，聚焦方向竖直向下的组合震源主波束入射到目的层界面时通常不是垂直或近垂直入射，并且往往地层倾角越大，入射角越大，检波器接收到的可能性就越小.本文方法设计的组合震源主能量，经过上覆地层透射以后，垂直地入射到了目的层界面上.这就说明本文提出的面向起伏地表模型目的层的组合震源延迟时间参数计算方法的正确性和优越性.

图 6

Figure 6

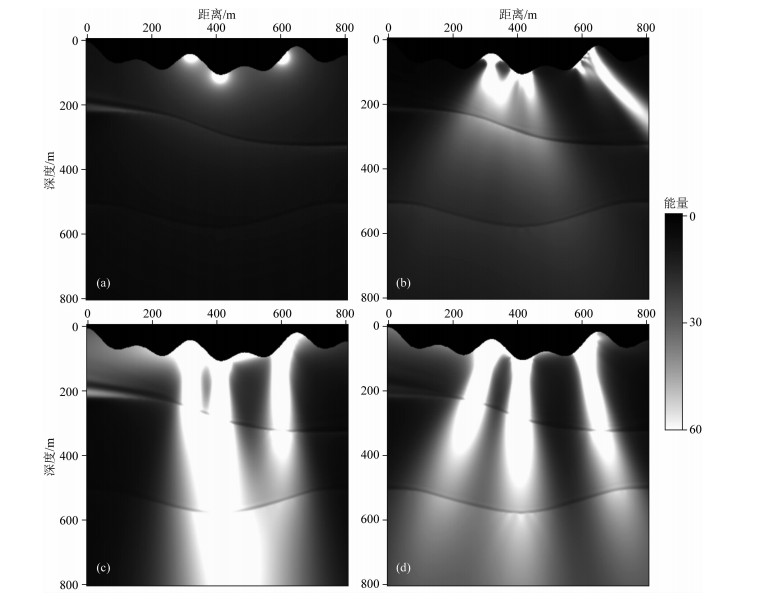
图 6 多炮照明结果 (a)普通单震源多炮照明; (b)同时激发组合震源多炮照明; (c)聚焦方向竖直向下的组合震源多炮照明; (d)本文方法组合震源多炮照明. Figure 6 The result of multiple sources illumination (a) Conventional sources illumination; (b) The illumination by source array explosion at the same time; (c) The illumination that source array focused direction is vertical downward; (d) The source array illumination using the method in this paper.

本节中采用国际上广泛应用的SEG起伏地表模型(如图 7)进行测试，其模型原型来自加拿大英属哥伦比亚东北部的逆掩断层构造，由Amoco和BP公司设计.该模型近地表条件复杂，速度横向变化剧烈，地表高低起伏大，逆掩断层与地层褶皱发育.速度模型剖面全长25 km，模型深度10 km，地层速度3600~6000 m·s^-1，地形最大高低落差达1530 m.

图 7

Figure 7

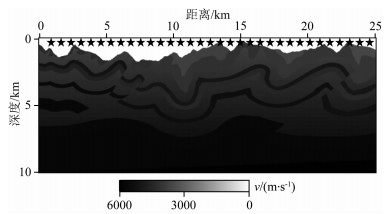
图 7 SEG起伏地表模型 Figure 7 The SEG undulating surface model

地震照明模拟参数：x方向网格步长15 m，z方向网格步长10 m，采样间隔4 ms，单个震源传播时间8 s，炮间距750 m，共计33炮.我们将该模型最底层的倾斜界面视为此次研究的目的层界面，在该界面上利用爆炸反射面原理进行波场上传，得到地表方向统计结果如图 8.

图 8

Figure 8

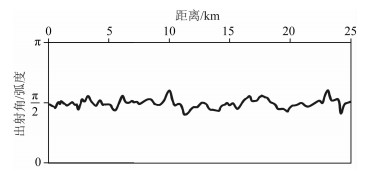
图 8 地表方向统计结果 Figure 8 The result of surface direction statistic

此次模型测试采用了四种不同的震源激发方式进行地震照明模拟，模型(图 7)中五角星为震源横向中心位置.图 9(a—d)依次为单震源照明、同时激发组合震源照明、聚焦方向竖直向下的组合震源照明、采用本文方法设计的组合震源照明.组合激发与普通单震源激发总药量保持不变，根据经验公式计算各震源类型的激发振幅(经验公式为E=(Q/s)^1/3，其中E表示单震源激发振幅，Q表示炸药药量，s表示震源组合个数).

图 9

Figure 9

图 9 地震照明分析 (a)普通单震源照明; (b)震源组合同时激发照明; (c)聚焦方向竖直向下的震源组合照明; (d)按照本文方法设计的组合震源照明. Figure 9 Seismic illumination analysis (a) Conventional sources illumination; (b) The illumination by source array explosion at the same time; (c) The illumination that source array focused direction is vertical downward; (d) The source array illumination using the method in this paper.

从照明结果中可以看出，组合震源激发效果明显优于普通震源激发效果，定向激发效果优于同时激发效果，面向目标的定向激发效果略优于垂向激发效果.图 10是四种激发条件下目的层的照明能量曲线，该曲线更加清晰地反应了各种震源激发类型对目的层照明能量的贡献情况.虽然采用本文方法设计的组合震源激发照明效果与垂向激发照明效果大致相当，但对目的层的照明主要为更有效的垂直入射，相比于另外两种激发方式效果提升明显.值得注意的是，在模型试验过程中，组合震源激发具有一定的能量聚焦能力，而导致目的层照明曲线的均匀性变差.我们可以通过减小组合震源组内距、高密度采集或者进行局部炮点加密的方法解决这一问题.

图 10

Figure 10

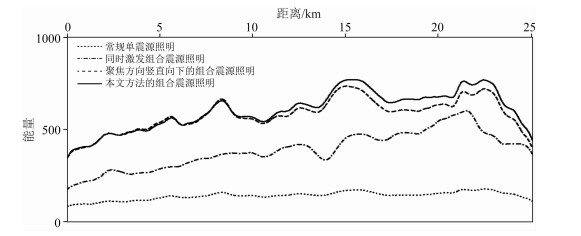
图 10 目的层照明曲线 Figure 10 The illumination curve on the target layer

组合震源定向激发技术对提高地震资料信噪比和地震照明度有着至关重要的作用.本文方法不仅能够确定任意起伏地表情况下沿给定地质模型的目的层界面垂直入射的组合震源聚焦方向，也能够计算形成沿该聚焦方向定向传播地震波场的组合震源延迟激发时间.通过上述理论分析和模型试验可以得出如下结论和认识：

(1) 无论是地表凸起、凹陷或是倾斜，按照本文方法设计的组合震源均能形成沿目的层垂直入射的定向地震波场.水平地表作为起伏地表的特殊形式，同样能够利用本文方法计算基于特定模型目的层的最优组合震源延迟激发时间；

(2) 组合震源照明能量大于普通单震源照明能量，定向激发组合震源照明能量大于同时(非定向)激发组合震源照明能量，聚焦方向竖直向下的组合震源主波束入射到目的层界面时通常不是垂直或近垂直入射，并且往往地层倾角越大，入射角越大，检波器接收到的可能性就越小；

(3) 本文方法只改变组合震源的延迟激发时间，不改变井深等参数，因此，本文方法不会增加组合震源的采集成本；

(4) 速度模型精度对基于模型的方法都具有决定性的影响，定量的评价速度误差对方法的影响程度非常困难.速度模型误差主要来自两个方面，一是层速度误差，由于层速度误差对地震波的传播路径影响较小，对本文方法的影响也就比较小.二是地层倾角误差，如果不考虑上覆地层对地震波传播方向的影响，则可基本认为地层倾角误差小于目的层有效入射角时本文方法有效；

(5) 如果按照地表方向统计结果进行基于组合震源的常规观测系统采集(等炮间距采集)，目的层的“凹型”区域可能会存在照明不足的情况.这是因为在地表方向统计时，目的层的“凹型”区域产生的是汇聚的平面波，在地表占据的区域较窄，导致沿“凹型”区域定向激发的组合震源数目较少，从而造成照明不足.而目的层的“凸型”区域形成的是发散的平面波，在地表占据更多的位置，导致沿“凸型”区域定向激发的组合震源数目较多.因此，在进行观测系统设计时，要充分考虑到特定模型的构造特征，在目的层照明阴影区对应的地表方向统计区域进行适当的炮点加密，有针对性地进行地震资料采集.