2. 中国工程物理研究院研究生院, 四川绵阳 621900;
3. 核废物与环境安全国防重点学科实验室, 四川绵阳 621010;
4. 清华大学数学科学系, 北京 100084
2. Graduate School, China Academy of Engineering Physics, Mianyang Sichuan 621900, China;
3. Fundamental Science on Nuclear Wastes and Environmental Safety Laboratory, Mianyang Sichuan 621010, China;
4. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China
全波形反演吸引了越来越多地球物理学家的注意(Pratt et al., 1998; Virieux and Operto, 2009).无论频率域还是时间域基于伴随原理的波形反演,都需要数值求解地震波运动方程(Tarantola, 1984; Tape et al., 2010).对于时间域求解地震波运动方程而言,在过去40余年已发展了诸多方法,如有限差分法(FDM)(Alford et al., 1974; Marfurt, 1984; 刘伊克和常旭, 1998)、有限元法(FEM)(De Basabe, 2009; Smith, 1975; 杨顶辉, 2002)、伪谱法(PSM)(Fornberg, 1988, 1990; Wang et al., 2010)和谱元法(SEM)(Komatitsch et al., 2002; 严珍珍等, 2009; Liu et al., 2017).其中FDM具有编程简单、易于并行化以及内存消耗小等优点,但有限差分法不能较好处理起伏地表(Moczo et al., 2000)、面波模拟精度低(Liu et al., 2014)以及在粗网格情形下数值频散明显等问题(Zhang and Yao, 2013; 刘有山, 2015).对于FDM地震波数值模拟精度不足,Sun等(2015)提出了交错网格褶积微分算法,该方法较大幅度提高了地震波场的计算精度,且计算效率几乎与经典有限差分方法相同,但该方法仍然较难运用至具有起伏界面的复杂模型.针对有限差分法数值频散大的问题,Yang等(2003, 2006, 2007)提出了一种改进的有限差分方法,即近似解析离散化(Nearly Analytic Discrete, NAD)方法,该方法用位移及位移梯度的线性组合来逼近空间高阶偏导数.由于NAD包含了更多的波场信息,使得该方法极大地压制了数值频散(Yang et al., 2006).前人对FDM的改进主要集中在FDM数值频散的压制,如Zhang和Yao(2013)提出了一种优化的显式有限差分格式、Wang等(2016)提出利用正则化最小二乘方法确定声波方程的有限差分系数等,但这些方法在速度间断模型中的数值模拟精度较差(Shragge, 2014).FEM克服了FDM部分不足,如FEM能自动满足自由地表边界条件,FEM采用三角网格能较好刻画起伏速度间断面等(Marfurt, 1984; Liu et al., 2014).随着计算机计算能力的增强,有限元法吸引了众多研究者的关注(Meng and Fu, 2017; 刘少林等, 2014; 刘有山, 2015).FEM的精度、数值频散、稳定性以及计算效率与单元插值阶数、网格形状、单元刚度矩阵的合成方式以及质量矩阵的组成密切相关(Marfurt, 1984; Mullen and Belytschko, 1982; Wu, 2006 ; Mazzieri and Rapetti, 2012),如何利用FEM高效地模拟地震波传播需要进一步研究.PSM基于Fourier变换原理近似空间微分算子,是一种全局方法,具有计算精度高、数值频散小等优点,该方法适用于规则网格中的地震波场模拟,难以处理起伏地表以及自由边界条件(Fornberg, 1988).SEM常被认为是一种高阶的FEM(Cohen, 2002),该方法具有谱方法的高精度性和指数收敛性(刘有山等,2014).现今在大尺度地震波模拟与成像研究中,SEM已成为较为流行的选择(Komatitsch et al., 2002; Tape et al., 2009; Liu et al., 2017).基于Legendre正交多项式的SEM插值点与Gauss-Lobatto-Legendre (GLL)积分点重合,因此该方法可形成对角质量矩阵,在计算过程中避免了大型稀疏矩阵求逆,提高了计算效率.但经典SEM在二维模型中采用的四边形网格单元(三维情形为六面体)较难准确刻画精细起伏地表和复杂界面.
FEM用于地震波场模拟时,研究者往往采用集中质量矩阵替代一致质量矩阵以提高其地震波模拟效率(Cohen, 2002; Zhebel et al., 2014).当单元尺寸相对于地震波长较小时,假定单元内波场加速度无明显变化( Wu, 2006 ),可以近似认为相邻节点惯性项相同,相邻节点间加速度解耦,基于质量守恒原理可获得对角质量矩阵.采用集中质量矩阵可以减少内存,更重要的是成倍提高计算速度.对于FEM离散后得到的稀疏大规模刚度矩阵,通常采用按行压缩存储(CSR)(Saad, 2001; Sonneveld, 1989; 刘有山等, 2014)的方式来节省内存,类似的压缩策略也被用于解决逆时偏移大规模波场存储(Sun and Fu, 2013).为了减少FEM刚度矩阵内存开销,Liu等(2014)提出了一种核矩阵存储方案(Kernel Matrix Storage, KMS),该方法不再需要组合大型总体刚度矩阵,仅仅只需要存储有限个核矩阵.在计算刚度矩阵与解向量的乘积时,该方法容易通过逐元的方式并行计算.但KMS只适合规则单元,对非规则界面处理时精度较低(Cohen, 2002).Meng和Fu(2017)对KMS进行了改进,提出了改进的KMS(IKMS).IKMS可以采用任意非规则单元(二维为三角单元,三维为四面体单元)进行网格剖分,大幅降低了FEM的计算内存.
相比于空间离散,研究者对时间离散讨论的较少.对于弹性波方程中时间二阶导数,常采用的离散方法是二阶中心差分.二阶中心差分具有简单、速度快的特点,但当采用大时间步长时数值频散严重、精度低和数值误差累积明显,不适合长时间计算和大尺度地震波模拟问题(Gao et al., 2016; 刘少林等, 2015).为了降低时间离散对计算精度的影响,最直接的方法是采用高阶时间离散格式.Dablain(1986)运用Lax-Wendroff方法(Lax and Wendroff, 1964)将高阶时间导数转化为高阶空间导数以获得任意偶数阶时间精度.基于Lax-Wendroff方法,Tong等(2013)将NAD空间离散方法与两步Stereo-Modeling Method相结合获得了时间四阶-空间八阶的模拟方法.Chen(2007)在全面分析了Lax-Wendroff方法、Nyström方法和分裂辛方法这三种高阶时间离散格式之后,认为高阶辛RKN与辛Partitioned-Runge-Kutta(PRK)能有效压制长时间计算的积累误差.Li等(2011, 2012)将波动方程转化成Hamilton形式,在时间离散上采用三阶辛算法,同样验证了辛算法具有长时间计算的优点.Liu等(2017a)将多种辛算法与NAD相结合,并讨论了辛算法模拟效率,阐述了无耗散Newmark格式与二阶辛PRK等价.Cai等(2017)利用共形辛算法求解带耗散项的声波和弹性波方程,对于分解出的保守项利用四阶的辛Nyström算法与SEM空间离散相结合来求解.
二阶辛格式相比高阶辛格式每一个时间更新所需的中间迭代步数少,因此具有计算速度快的优点,但长时间计算能力以及计算精度相对于常用的三阶辛格式要差(Liu et al., 2017a; 刘少林等, 2015).基于最小截断误差原理(McLachlan and Atela, 1992)、频率对比误差最小原理(刘少林等, 2015)得到的优化二阶辛格式具有较高精度,但精度仍然远逊于三阶辛格式(Li et al., 2011; 刘少林等, 2015).为了尽量保持二阶辛格式的计算速度,同时提高计算精度,Liu等(2015)首次提出了适用于地震波模拟的修正辛算法,其核心思想是通过添加空间离散算子,达到修正原格式的目的.该方法构造出的格式具有稳定性高、频散弱、精度高和长时间计算能力强的优点.本文将修正辛策略用于二阶辛格式的修正,得到一种新的修正辛对称格式.该格式一方面保持二阶辛格式迭代步数少的优点,另一方面实现了精度、稳定性以及长时计算能力等方面的全面提升.本文将修正辛格式与改进的FEM空间离散格式相结合,得到适用于高效地震波场模拟的修正辛-FEM.通过理论分析和数值实验验证该方法能够高效率模拟复杂模型中地震波传播.
1 改进的有限元法 1.1 弹性波运动方程的FEM空间离散实际地球介质较为复杂,地壳、地幔以及整个地球不仅广泛存在着不同尺度的非均匀性(Tape et al., 2009; Zhao et al., 2013; Amaru, 2007),而且各向异性以及黏性也非常明显(Chen et al., 2011; Wang et al., 2017).对于区域尺度地震波传播问题而言常用各向同性弹性波运动方程来描述地震波在地球介质中的传播(Komatitsch and Vilotte, 1998).非均匀介质中各向同性弹性波方程可写为
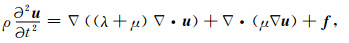
|
(1) |
其中u为位移场,f为震源项,ρ为质量密度,λ和μ为拉梅常数.对方程(1)两端乘以任意向量函数v并在求解区域Ω内积分,利用分部积分和格林公式可以得到方程(1)的弱形式:
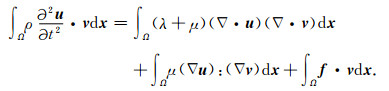
|
(2) |
将积分区域Ω划分为N个非重叠的三角形单元,在单元内选取插值节点,并对u和v利用Lagrange多项式近似,方程(2)离散后的常微分方程组为
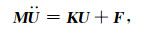
|
(3) |
其中U是位移向量,Ü表示位移对时间的二阶导数,F震源向量. M和K分别表示质量矩阵和刚度矩阵,M和K具体形式为
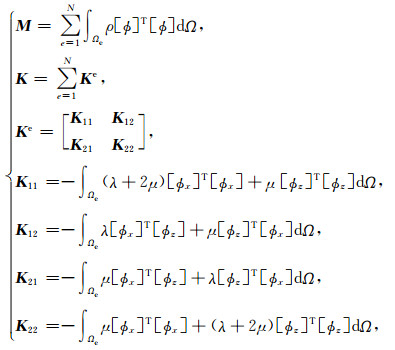
|
(4) |
其中求和算子Σ在这里表示矩阵组装(Liu et al., 2014).
1.2 刚度矩阵的改进存储策略为了在非规则三角形单元上进行数值积分,利用方程(5)将物理单元坐标(x, z)映射到等参坐标(ξ, η)(Meng and Fu, 2017):
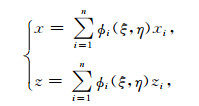
|
(5) |
其中n表示单元中的离散节点个数,ϕi(ξ, η)和(Xi, zi)分别为单元的第i个形函数和第i个节点空间坐标.由求导的链式法则有
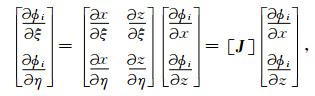
|
(6) |
其中单元的雅克比矩阵J为
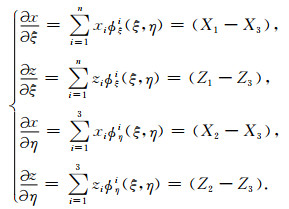
|
(7) |
(X1, Z1)、(X2, Z2)和(X3, Z3)为三角形单元的顶点坐标.由方程(7)知单元雅克比矩阵J为常矩阵,其值由单元顶点坐标决定.由坐标变换关系可得

|
(8) |
为了减少内存消耗,Meng和Fu(2017)提出了IKMS方法,该方法只需要存储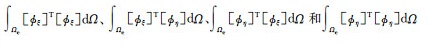
为了提高计算效率,通常采用集中质量矩阵替代一致质量矩阵.一般采用方程(9)和方程(10)作为对角
质量矩阵(Padovani et al., 1994):
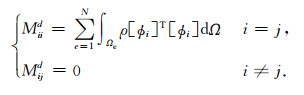
|
(9) |
或

|
(10) |
由方程(9)得到的质量矩阵可能导致质量矩阵对角元出现负值,方程(10)在保证质量守恒的条件下,按对角线上元素的比例集中,该方法构造的质量集中矩阵更符合物理实际(杨亚平和沈海宁, 2010).本文采用方程(10)构造集中质量矩阵.
2 时间离散常用的时间离散方法有二阶中心差分方法(Virieux, 1984, 1986)、Newmark方法(Kane et al., 2000)、Runge-Kutta方法(Butcher, 1996)以及辛算法(Chen, 2007).辛算法是求解Hamilton系统问题而构造的数值离散方法,它使离散化后的方程保持原有系统的辛结构,因此辛算法具有长时间的稳定性(Li et al., 2011).二阶辛算法每一时间更新所需的迭代步数较少,效率较高,但计算精度比高阶辛格式差.Liu等(2015)在传统辛格式基础上加入额外空间离散算子,在不增加迭代步数的情况下,构造出高稳定性、低频散、具有长时计算能力的修正辛格式,但Liu等(2015)的时间格式精度仅达到三阶,为了进一步提高时间离散精度,本文构造一种对称修正辛格式,在相同计算量的条件下,获得四阶时间精度.
对于方程(3),引入中间变量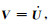

|
(11) |
方程(11)的Hamilton形式为
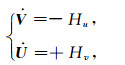
|
(12) |
其中

|
(13) |
为了保证修正格式满足辛性且具有对称性,本文在(13)式第三项加入Gv1,以修正二阶RKN的精度,得到
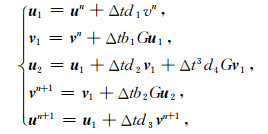
|
(14) |
其中,b1、b2和d1-d4六个系数满足三阶精度的条件为

|
(15) |
(15) 式是不定方程组,用d3表示其他系数,即有下式:

|
(16) |
直接由(16)式可验证(14)式是辛的,即当阶条件满足时辛条件自然满足.为了确保修正辛的系数大于零,(16)式d3的限定条件为d3 < 1/3,为了使(14)式的系数对称,令b1=b2.结合(16)式可得对称辛格式的系数为

|
(17) |
事实上(14)式采用系数(17)所对应的对称格式的精度为四阶,即三次离散算子与解向量的乘积获得四阶时间精度.
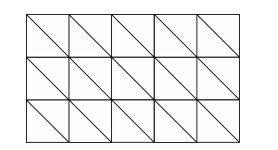
3 理论分析为了理论分析的需要和方便讨论,选择边长为h的等腰直角三角形对无限空间进行网格剖分(如图 1所示).空间周期出现的规则三角单元使得关于有限元频散分析的无限维问题简化为有限维问题(De Basabe and Sen, 2007; 刘少林等, 2014; Liu et al., 2017b).
|
图 1 等腰直角三角形单元网格 Figure 1 FEM element mesh constructed by isosceles right triangles |
为了推导修正辛-FEM的稳定性,设在t=nΔt时刻方程(11)的谐波解表达式为(Moczo et al., 2000)

|
(18) |
式中Δt为时间步长,ω为角频率,k为波数,x j为第j个节点的坐标,Bj和Dj分别为第j个节点上的位移和速度振幅.将(18)式带入修正辛格式(14)得到一般的特征值问题为
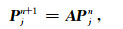
|
(19) |
其中A为修正辛-FEM格式(14)的增长矩阵.设增长矩阵A和空间离散算子G的特征值分别为ψ和λ,可得A的特征多项式为
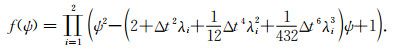
|
(20) |
为使(14)式稳定,需满足|ψ|≤1(Moczo et al., 2000),稳定性条件等价为
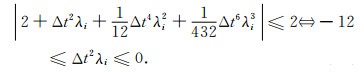
|
(21) |
|Δt2λi|max与库朗数相关,值越大则表示格式越稳定.表 1给出了二阶PRK辛格式、三阶辛格式(Li et al., 2011)和本文提出的修正辛格式的|Δt2λi|max值.从表 1可知,修正辛格式的|Δt2λi|max值为12,在三种辛格式中最大,说明在空间离散相同时,修正辛格式能够取得最大的时间步长,其稳定限大约是二阶PRK辛格式的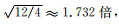
|
|
表 1 三种辛格式的| Δt2λi |max值 Table 1 The values of | Δt2λi |max for three symplectic schemes |
理论推导稳定性条件的解析表达式较为困难,借助Liu等(2015)的讨论,可以利用非线性拟合得到近似表达式:
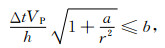
|
(22) |
式中VP为纵波波速,r=VP/VS是纵横波波速比,a和b为待定常数.a只与空间离散有关,当FEM空间插值为一阶时其为1,当为高阶插值时其值几乎为0.b的大小决定了稳定性,b越大则稳定性越强.表 2为三种辛格式在空间离散使用有限元1阶至3阶插值时稳定性范围b值.
|
|
表 2 三种辛格式的稳定性范围b值 Table 2 The stability parameter b for three temporal schemes |
数值频散由数值格式空间和时间离散共同决定.数值频散的强弱是评价数值计算方法的重要指标(Li et al., 2013).为了讨论修正辛时间离散对数值频散的影响,我们采用空间三阶插值来压制空间离散对数值频散的干扰.另外由于S波的波长比P波波长短,因此P波数值频散小于S波,故本文仅讨论S波的数值频散.根据Moczo等(2000)给出的数值频散关系为数值速度与物理速度之比,可得修正辛格式(14)的数值频散为
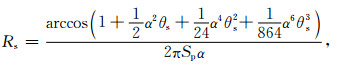
|
(23) |
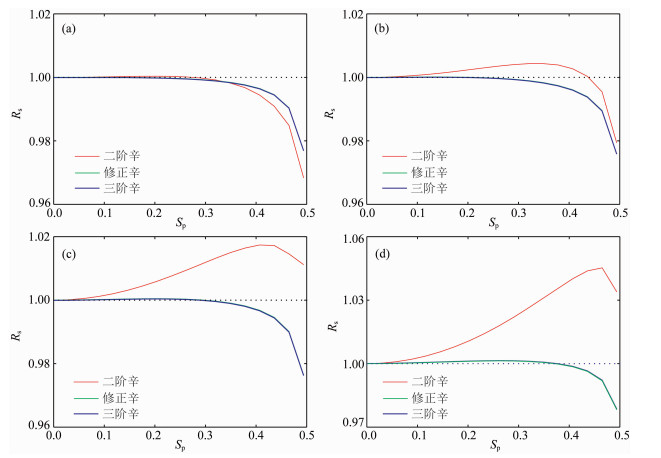
其中Sp为采样率,α为库朗数,θs为(19)式求得的绝对值最小的特征值,该特征值对应于S波的特征值(De Basabe and Sen, 2007).图 2给出了α分别取0.1、0.2、0.3和0.4时S波的频散曲线.从图 2可以看出,在四种库朗数情况下二阶PRK辛格式的数值频散都大于修正辛格式和三阶辛格式,且随着库朗数的增大,差距越明显,而修正辛格式和三阶辛格式的数值频散相当.
|
图 2 三种辛格式的数值频散曲线 (a), (b), (c)和(d)分别为α取0.1、0.2、0.3和0.4时S波的数值频散曲线.红色、绿色和蓝色曲线分别对应二阶PRK辛格式、修正辛格式和三阶辛格式的数值频散曲线.横轴为采样率, 纵轴为归一化数值波速. Figure 2 Numerical dispersion curves of three symplectic schemes Plots (a—d) are numerical dispersion curves with Courant numbers 0.1, 0.2, 0.3 and 0.4, respectively. Red, blue and green curves are second-order symplectic PRK scheme, modified symplectic scheme and third-order symplectic scheme, respectively. The horizontal axis is the sampling rate; the vertical axis is the normalized velocity. |
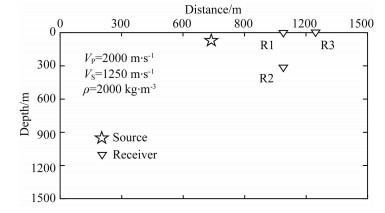
为了定量讨论修正辛有限元法弹性波模拟的内存消耗度、计算效率和数值精度,本节设计了如图 3所示的二维均匀介质模型,模型大小为1500 m× 1500 m,模型中P波和S波的波速分别为2000 m·s-1和1250 m·s-1, 介质密度为2000 kg·m-3.集中力震源采用主频为25 Hz的Rick子波,位于靠近地表处(750 m, 50 m),三个接收器分别为R1 (1050 m, 0 m)、R2(1050 m, 350 m)和R3(1250 m, 0 m).为了避免边界截断所产生的虚假反射波,模型采用完美匹配层吸收边界(Perfectly matched layer, 简称PML)(Berenger, 1994; Gao et al., 2015; 刘有山等, 2014),模型左、右和下部设置厚度为150 m的PML吸收层.
|
图 3 二维均匀介质模型 震源位于(750 m, 50 m)处, 三个接收器分别为R1 (1050 m, 0 m)、R2 (1050 m, 350 m)和R3 (1250 m, 0 m). Figure 3 2D homogeneous model for benchmark One source is located at (750 m, 50 m). Three receivers are labeled as R1 (1050 m, 0 m), R2 (1050 m, 350 m) and R3 (1250 m, 0 m), respectively. |
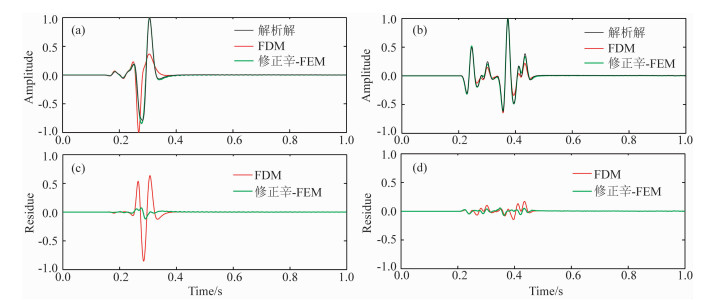
FDM离散格式具有计算效率高和内存消耗少的优点.本算例对比FDM和修正辛-FEM在计算内存、计算时间以及计算精度等方面的差异.FDM模拟时所采用的自由地表边界条件离散格式是通过在地表之上加一层虚拟点的方式实现(Nilsson et al., 2007; Lan and Zhang, 2011),具体参见附录A.FDM的空间网格步长为3 m,修正辛-FEM采用空间三阶插值,两者的时间步长都为0.6 ms.图 4a和4b分别为接收器R1与R2处位移垂直分量归一化合成波形与解析解波形对比图.接收器R1由于其位于地表,可以检验FDM和FEM自由地表处理的数值精度.接收点R2远离自由地表,用于检测其受自由地表影响的情况.由图 4可看出不论接收器在地表还是远离地表,接收器处修正辛-FEM得到的合成波形与解析解高度接近,图 4a和4c显示在地表处FDM格式的数值模拟精度比修正辛-FEM数值精度要差,表现为Rayleigh面波波形与解析波形出现明显偏差.当接收器远离自由地表时,FDM的精度明显改善,原因在于自由地表离散所引入的数值误差在远离自由地表处变弱(图 4b和4d).
|
图 4 R1 (a)和R2 (b)处位移垂直分量合成波形与解析解波形对比; (c)和(d)分别对应于(a)和(b)图中的波形误差 Figure 4 Comparison of synthetic waveforms obtained by analytic method (black curve), FDM (red curve) and symplectic FEM (green curve). (a) and (b) show vertical component of synthetic waveform at R1 and R2, respectively. (c) and (d) show waveform misfits in (a) and (b), respectively |
表 3显示了修正辛-FEM与FDM的计算效率和总体误差对比,总体误差定义为
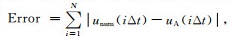
|
|
表 3 修正辛-有限元和有限差分法计算效率和总体误差对比 Table 3 Computational efficiency and accuracy of the modified symplectic FEM and FDM |
采用三角形单元进行空间离散时,为了定量分析修正辛-FEM的内存消耗,设一阶、二阶和三阶的单元直角三角形边长分别为5 m、10 m和15 m,插值后模型总的节点数相同.以2D均匀介质模型采用一阶插值为例,总的三角形单元个数2×300×300=180000个,节点个数为301×301=90601个,采用CSR存储刚度矩阵需要12.3963 MB内存,而修正辛-FEM采用一阶插值时,仅需要0.6868 MB内存.表 4给出了修正辛-FEM采用一阶、二阶和三阶插值时刚度矩阵理论上所需的内存,为了对比也给出了CSR存储所需要的内存.从表 4可知存储内存在一阶插值情形下CSR是IKMS的18.05倍,二阶插值为29.30倍,三阶插值为47.39倍.从1至3阶,CSR与IKMS两种方法实际运行内存之比为4.02倍、3.02倍和3.83倍.实际运行内存改进的优势没有理论分析明显,主要因为实际计算内存要考虑PML吸收边界以及其他计算消耗,该部分共同消耗的内存削弱了IKMS对内存的贡献.总体而言,采用IKMS可以成倍节约计算机内存.值得注意的是,由于IKMS没有组合形成总体刚度矩阵,在计算时需要计算雅克比矩阵和核矩阵,因而耗时比CSR方式要稍多.
|
|
表 4 1至3阶插值时不同存储策略内存消耗对比 Table 4 Memory requirements of two storage schemes with three interpolation orders |
当修正辛-FEM空间上为三阶插值时,讨论其长时间计算的稳定性以及计算效率和精度.接收器为R3,时间步长Δt=0.6 ms,模拟时长为10 s.图 5a和5b分别为归一化数值解与解析解位移的水平分量和垂直分量波形对比.图 5显示三种辛算法得到的数值解与解析解接近,即三种辛格式(二阶辛PRK格式、修正辛格式和三阶辛格式)在模拟弹性波传播时总体上都具备长时程的稳定计算能力.表 5显示了三种数值格式的计算效率和精度.从运行内存来看,三种格式内存消耗基本相当,二阶PRK辛格式所需计算时间最少,三阶辛格式需要的计算时间最多,修正辛格式计算时间比三阶辛格式约少2.60%.接收器R3处二阶PRK辛格式水平分量误差总量约为修正辛格式的2.15倍,垂直分量误差总量约为1.50倍;而修正辛格式与三阶辛格式无论在水平分量还是垂直分量误差总量都接近,修正辛格式误差总量略小于三阶辛格式.综合而言,修正辛格式在几乎不增加计算内存的情况下,获得了计算时间与精度之间的平衡.

|
图 5 R3处合成波形的水平分量(a)与垂直分量(b)和解析解波形对比 Figure 5 The synthetic waveforms of horizontal (a) and vertical (b) components at R3. Black curve is generated by analytic solution; red curve by second-order symplectic PRK; green curve by modified sympectic scheme; blue curve by third-order symplectic scheme |
|
|
表 5 三种时间离散方法的计算效率和总体误差对比 Table 5 Computational efficiency and total error of three temporal methods |
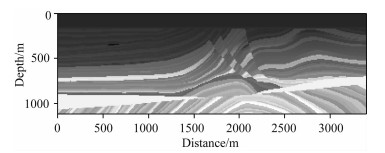
为了验证修正辛-FEM在非均匀复杂介质中的地震波模拟能力,选用Marmousi模型做测试.图 6为Marmousi模型的P波速度结构,模型由171×57个网格点组成,网格间距为20 m.速度变化范围为1500~5500 m·s-1,S波速度由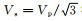
|
图 6 Marmousi模型的P波速度结构 Figure 6 P-wave velocity structure of Marmousi model |

|
图 7 二阶PRK辛-FEM(a)与修正辛-FEM(b)得到的地表合成记录; (c)与(d)分别为二阶PRK辛-FEM与修正辛-FEM地表合成记录与参考解的残差 Figure 7 Synthetic seismograms generated by the second-order PRK symplectic FEM (a) and modified symplectic FEM (b); (c) difference between synthetic record in (a) and the reference solution; (d) difference between synthetic record in (b) and the reference solution |
本文发展了高效模拟弹性波传播的修正辛-FEM.在传统二阶RKN辛格式中额外加入空间离散算子构造出修正辛格式,该格式迭代步数与二阶辛格式相同,但计算精度和稳定性比二阶辛格式有大幅提升.当FEM采用三角形单元对区域离散时,物理单元映射到参考单元的雅克比矩阵只与三角形单元的顶点坐标有关,因此只需存储有限个核矩阵,而不需要组装总体刚度矩阵,该空间改进可成倍减少内存.在二维均匀介质模型中,有限差分格式与修正辛有限元在计算效率、内存消耗以及计算精度等方面做了对比,发现修正辛格式有限元方法虽然内存和时间消耗大于有限差分法,但是计算精度明显优于后者.随后将二阶辛-FEM、三阶辛-FEM和修正辛-FEM计算结果与解析解对比,发现修正辛-FEM的计算精度与二阶辛-FEM相比有显著提高,且高于三阶辛-FEM的计算精度.最后强烈非均匀介质Marmousi模型中的波场模拟结果表明修正辛-FEM适用于复杂模型中高精度波场模拟.本文发展的修正辛-FEM为研究大尺度、复杂模型中地震波传播与波形成像问题提供了有效的正演模拟工具.
附录A对于二维模型,j=0表示自由地表层,j=-1为地表之上的虚拟层(附图 1).有限差分在j=0处需要满足的自由地表条件(Nilsson et al., 2007):

|
图 附图 1 自由地表网格点示意图 Figure 附图 1 Schematic of grid points around free surface in FDM |

|
(A1) |
(A1) 式中的u和w分别表示水平和垂直方向的位移,在二维均匀介质中自由地表条件(A1)可采用以下方法离散(Lan and Zhang, 2011):
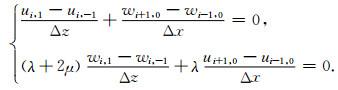
|
(A2) |
其中i是水平横坐标节点编号,Δx和Δz为有限差分网格间距.由公式(A2)可以得到虚拟层水平和垂直方向的位移ui, -1和wi, -1:

|
(A3) |
该位移分量用于计算地表层(j=0)处二阶中心差分

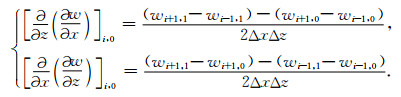
|
(A4) |
将j=0处二阶导代入公式(1),实现自由地表边界条件的有限差分离散.
Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. DOI:10.1190/1.1440470 |
Amaru M L. 2007. Global travel time tomography with 3-D reference models[Ph.D.thesis]. Netherlands: Utrecht University.
|
Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
Butcher J C. 1996. A history of Runge-Kutta methods. Applied Numerical Mathematics, 20(3): 247-260. DOI:10.1016/0168-9274(95)00108-5 |
Cai W J, Zhang H, Wang Y S. 2017. Dissipation-preserving spectral element method for damped seismic wave equations. Journal of Computational Physics, 350: 260-279. DOI:10.1016/j.jcp.2017.08.048 |
Chen J B. 2007. High-order time discretizations in seismic modeling. Geophysics, 72(5): SM115-SM122. DOI:10.1190/1.2750424 |
Cheng B, Zhao D P, Zhang G W. 2011. Seismic tomography and anisotropy in the source area of the 2008 Iwate-Miyagi earthquake (M7.2). Physics of the Earth and Planetary Interiors, 184(3-4): 172-185. DOI:10.1016/j.pepi.2010.11.006 |
Cohen G C. 2002. Higher-Order Numerical Methods for Transient Wave Equations. Berlin: Springer-Verlag.
|
Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. DOI:10.1190/1.1442040 |
De Hoop A T. 1960. A modification of Cagniard's method for solving seismic pulse problems. Applied Scientific Research, Section B, 8(1): 349-356. DOI:10.1007/BF02920068 |
De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations. Geophysics, 72(6): T81-T95. DOI:10.1190/1.2785046 |
De Basabe J D. 2009. High-order finite element methods for seismic wave propagation[Ph.D.thesis]. Texas: University of Texas at Austin.
|
Feng K, Qin M Z. 2010. Symplectic Geometric Algorithms for Hamiltonian Systems. Berlin: Springer.
|
Fornberg B. 1988. The pseudospectral method; Accurate repre sentation of interfaces in elastic wave calculations. Geophysics, 53(5): 625-637. DOI:10.1190/1.1442497 |
Fornberg B. 1990. High-order finite differences and the pseudospectral method on staggered grids. SIAM Journal on Numerical Analysis, 27(4): 904-918. DOI:10.1137/0727052 |
Gao Y J, Song H J, Zhang J H, et al. 2015. Comparison of artificial absorbing boundaries for acoustic wave equation modelling. Exploration Geophysics, 48(1): 76-93. |
Gao Y J, Zhang J H, Yao Z X. 2016. Third-order symplectic integration method with inverse time dispersion transform for long-term simulation. Journal of Computational Physics, 314: 436-449. DOI:10.1016/j.jcp.2016.03.031 |
Kane C, Marsden J E, Ortiz M, et al. 2015. Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems. International Journal for Numerical Methods in Engineering, 49(10): 1295-1325. |
Komatitsch D, Vilotte J P. 1998. The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88(2): 368-392. |
Komatitsch D, Ritsema J, Tromp J. 2002. The spectral-element method, Beowulf computing, and global seismology. Science, 298(5599): 1737-1742. DOI:10.1126/science.1076024 |
Lan H Q, Zhang Z J. 2011. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation. Journal of Geophysics and Engineering, 8(2): 275-286. DOI:10.1088/1742-2132/8/2/012 |
Lax P D, Wendroff B. 1964. Difference schemes for hyperbolic equations with high order of accuracy. Communications on Pure and Applied Mathematics, 17(3): 381-398. DOI:10.1002/(ISSN)1097-0312 |
Li J S, Yang D H, Liu F Q. 2013. An efficient reverse time migration method using local nearly analytic discrete operator. Geophysics, 78(1): S15-S23. |
Li X F, Li Y Q, Zhang M G, et al. 2011. Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method. Bulletin of the Seismological Society of America, 101(4): 1710-1718. DOI:10.1785/0120100266 |
Li X F, Wang W S, Lu M W, et al. 2012. Structure-preserving modelling of elastic waves:A symplectic discrete singular convolution differentiator method. Geophysical Journal International, 188(3): 1382-1392. DOI:10.1111/gji.2012.188.issue-3 |
Liu S L, Li X F, Liu Y S, et al. 2014. Dispersion analysis of triangle-based finite element method for acoustic and elastic wave simulations. Chinese Journal of Geophysics (in Chinese), 57(8): 2620-2630. DOI:10.6038/cjg20140821 |
Liu S L, Li X F, Wang W S, et al. 2014. A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modelling. Journal of Geophysics and Engineering, 11(5): 055009. DOI:10.1088/1742-2132/11/5/055009 |
Liu S L, Li X F, Wang W S, et al. 2015. A symplectic RKN scheme for solving elastic wave equations. Chinese Journal of Geophysics (in Chinese), 58(4): 1355-1366. DOI:10.6038/cjg20150422 |
Liu S L, Li X F, Wang W S, et al. 2015. A modified symplectic scheme for seismic wave modeling. Journal of Applied Geophysics, 116: 110-120. DOI:10.1016/j.jappgeo.2015.03.007 |
Liu S L, Yang D H, Dong X P, et al. 2017. Element-by-element parallel spectral-element methods for 3-D teleseismic wave modeling. Solid Earth, 8(5): 969-986. DOI:10.5194/se-8-969-2017 |
Liu S L, Yang D H, Lang C, et al. 2017a. Modified symplectic schemes with nearly-analytic discrete operators for acoustic wave simulations. Computer Physics Communications, 213: 52-63. DOI:10.1016/j.cpc.2016.12.002 |
Liu S L, Yang D H, Ma J. 2017b. A modified symplectic PRK scheme for seismic wave modeling. Computers & Geosciences, 99: 28-36. |
Liu Y K, Chang X. 1998. The implicit multigrid method for the secondary hydrocarbon migration drived by water. Acta Geophysics Sinica (in Chinese), 41(3): 342-348. |
Liu Y S, Teng J W, Xu T, et al. 2014. Numerical modeling of seismic wavefield with the SEM based on Triangles. Progress in Geophysics (in Chinese), 29(4): 1715-1726. DOI:10.6038/pg20140430 |
Liu Y S. 2015. Seismic wavefield modeling using the spectral element method and migration/inversion[Ph.D.thesis]. Beijing: Institute of Geology and Geophysics, Chinese Academy of Sciences.
|
Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. DOI:10.1190/1.1441689 |
Mazzieri I, Rapetti F. 2012. Dispersion analysis of triangle-based spectral element methods for elastic wave propagation. Numerical Algorithms, 60(4): 631-650. DOI:10.1007/s11075-012-9592-8 |
McLachlan R I, Atela P. 1992. The accuracy of symplectic integrators. Nonlinearity, 5(2): 541-562. DOI:10.1088/0951-7715/5/2/011 |
Meng W J, Fu L Y. 2017. Seismic wavefield simulation by a modified finite element method with a perfectly matched layer absorbing boundary. Journal of Geophysics and Engineering, 14(4): 852-864. DOI:10.1088/1742-2140/aa6b31 |
Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes:Stability and grid dispersion. Bulletin of the Seismological Society of America, 90(3): 587-603. DOI:10.1785/0119990119 |
Mullen R, Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. International Journal for Numerical Methods in Engineering, 18(1): 11-29. DOI:10.1002/(ISSN)1097-0207 |
Nilsson S, Petersson N A, Sjögreen B, et al. 2007. Stable difference approximations for the elastic wave equation in second order formulation. SIAM Journal on Numerical Analysis, 45(5): 1902-1936. DOI:10.1137/060663520 |
Padovani E, Priolo E, Seriani G. 1994. Low and high order finite element method:Experience in seismic modeling. Journal of Computational Acoustics, 2(4): 371-422. DOI:10.1142/S0218396X94000233 |
Pratt R G, Shin C, Hick G J. 1998. Gauss-newton and full newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
Saad Y. 2001. Parallel Iterative Methods for Sparse Linear Systems. Studies in Computational Mathematics, 8: 423-440. DOI:10.1016/S1570-579X(01)80025-2 |
Shragge J. 2014. Reverse time migration from topography. Geophysics, 79(4): S141-S152. DOI:10.1190/geo2013-0405.1 |
Smith W D. 1975. The application of finite element analysis to body wave propagation problems. Geophysical Journal International, 42(2): 747-768. |
Sonneveld P. 1989. CGS, a fast Lanczos-type solver for nonsymmetric linear systems. SIAM Journal on Scientific and Statistical Computing, 10(1): 36-52. DOI:10.1137/0910004 |
Sun W J, Fu L Y. 2013. Two effective approaches to reduce data storage in reverse time migration. Computers & Geosciences, 56: 69-75. |
Sun W J, Zhou B Z, Fu L Y. 2015. A staggered-grid convolutional differentiator for elastic wave modelling. Journal of Computational Physics, 301: 59-76. DOI:10.1016/j.jcp.2015.08.017 |
Tape C, Liu Q Y, Maggi A, et al. 2009. Adjoint tomography of the southern California crust. Science, 325(5943): 988-992. DOI:10.1126/science.1175298 |
Tape C, Liu Q Y, Maggi A, et al. 2010. Seismic tomography of the southern California crust based on spectral-element and adjoint methods. Geophysical Journal of the Royal Astronomical Society, 180(1): 433-462. DOI:10.1111/gji.2010.180.issue-1 |
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
Tong P, Yang D H, Hua B L, et al. 2013. A high-order stereo-modeling method for solving wave equations. Bulletin of the Seismological Society of America, 103(2A): 811-833. DOI:10.1785/0120120144 |
Virieux J. 1984. SH-wave propagation in heterogeneous media; Velocity-stress finite-difference method. Geophysics, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
Virieux J. 1986. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method. Geophysics, 51(4): 889-901. DOI:10.1190/1.1442147 |
Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
Wang Y B, Takenaka H, Furumura T. 2010. Modelling seismic wave propagation in a two-dimensional cylindrical whole-earth model using the pseudospectral method. Geophysical Journal of the Royal Astronomical Society, 145(3): 689-708. |
Wang Y F, Liang W Q, Nashed Z, et al. 2016. Determination of finite difference coefficients for the acoustic wave equation using regularized least-squares inversion. Journal of Inverse and Ill-posed Problems, 24(6): 743-760. |
Wang Z W, Zhao D P, Liu X, et al. 2017. P and S wave attenuation tomography of the Japan subduction zone. Geochemistry, Geophysics, Geosystems, 18(4): 1688-1710. DOI:10.1002/2017GC006800 |
Wu S R. 2006. Lumped mass matrix in explicit finite element method for transient dynamics of elasticity. Computer Methods in Applied Mechanics and Engineering, 195(44-47): 5983-5994. DOI:10.1016/j.cma.2005.10.008 |
Yan Z Z, Zhang H, Yang C C, et al. 2009. Spectral element analysis on the characteristics of seismic wave propagation triggered by Wenchuan MS8.0 earthquake.. Science in China Series D:Earth Sciences, 52(6): 764-773. DOI:10.1007/s11430-009-0078-z |
Yang D H. 2002. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese Journal of Geophysics (in Chinese), 45(4): 575-583. |
Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2): 882-890. DOI:10.1785/0120020125 |
Yang D H, Peng J M, Lu M, et al. 2006. Optimal nearly analytic discrete approximation to the scalar wave equation. Bulletin of the Seismological Society of America, 96(3): 1114-1130. DOI:10.1785/0120050080 |
Yang D H, Song G J, Lu M. 2007. Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3d anisotropic media. Bulletin of the Seismological Society of America, 97(5): 1557-1569. DOI:10.1785/0120060209 |
Yang Y P, Shen H N. 2010. The rationality and limitation on the substitution of the concentrated mass matrix for the consistent mass matrix. Journal of Qinghai University (Natural Science) (in Chinese), 28(1): 35-39. |
Zhang J H, Yao Z X. 2013. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. Journal of Computational Physics, 250: 511-526. DOI:10.1016/j.jcp.2013.04.029 |
Zhao D P, Yamamoto Y, Yanada T. 2013. Global mantle heterogeneity and its influence on teleseismic regional tomography. Gondwana Research, 23(2): 595-616. DOI:10.1016/j.gr.2012.08.004 |
Zhebel E, Minisini S, Kononov A, et al. 2014. A comparison of continuous mass-lumped finite elements with finite differences for 3-D wave propagation. Geophysical Prospecting, 62(5): 1111-1125. DOI:10.1111/gpr.2014.62.issue-5 |
刘少林, 李小凡, 刘有山, 等. 2014. 三角网格有限元法声波与弹性波模拟频散分析. 地球物理学报, 57(8): 2620-2630. DOI:10.6038/cjg20140821 |
刘少林, 李小凡, 汪文帅, 等. 2015. 求解弹性波方程的辛RKN格式. 地球物理学报, 58(4): 1355-1366. DOI:10.6038/cjg20150422 |
刘伊克, 常旭. 1998. 盆地模拟水动力油气二次运移隐式多重网格法. 地球物理学报, 41(3): 342-348. DOI:10.3321/j.issn:0001-5733.1998.03.007 |
刘有山, 滕吉文, 徐涛, 等. 2014. 三角网格谱元法地震波场数值模拟. 地球物理学进展, 29(4): 1715-1726. DOI:10.6038/pg20140430 |
刘有山. 2015.谱元法地震波场数值模拟与偏移成像[博士论文].北京: 中科院地质与地球物理研究所.
|
严珍珍, 张怀, 杨长春, 等. 2009. 汶川大地震地震波传播的谱元法数值模拟研究. 中国科学:地球科学, 39(4): 393-402. |
杨顶辉. 2002. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报, 45(4): 575-583. DOI:10.3321/j.issn:0001-5733.2002.04.015 |
杨亚平, 沈海宁. 2010. 集中质量矩阵替代一致质量矩阵的合理性与局限性. 青海大学学报(自然科学版), 28(1): 35-39. DOI:10.3969/j.issn.1006-8996.2010.01.009 |
 2019, Vol. 62
2019, Vol. 62

