2. 中国石油新疆油田分公司, 新疆克拉玛依 834000
2. Xinjiang Oilfield Company, PetroChina, Karamay Xinjiang 834000, China
地球物理反演是获得地球信息的重要手段.所以反问题的求解是地球物理学中的核心问题(杨文采, 1997).其求解的理论与方法,不仅能用于解决地球物理的问题,而且还能用于其他领域(如图像处理、气象预测、医学成像和遥感成像等等)中的问题,具有广泛的适用性(姚姚, 2002).
地球物理反问题具有的病态性、不适定性等特性(Tarantola, 2005)是地球物理反演工作者不可回避的问题,这是由所求解问题的本质所决定的.为获得稳定的、有意义的结果,地球物理学家的通常做法是在反问题目标函数中加入正则化约束项.地球物理学家在最开始采用吉洪诺夫正则化(Aster et al., 2013; Tikhonov and Arsenin, 1977)来克服地球物理反问题中的不适定性.例如,在求解地震数据的最小平方反褶积时,为减小地震数据自相关矩阵的条件数,在该矩阵的主对角线上加入预白化因子,使得反褶积的求解稳定(Yilmaz, 2001);在层析成像反演中,对模型参数施加平滑度约束,降低层析成像的不适定性(Aster et al., 2013; 崔岩, 王彦飞, 2015; 戴前伟等, 2014; 张风雪等, 2014; 朱小三等, 2014);全波形反演时,在反演目标函数中加入模型参数L2模极小正则化约束项,降低全波形反演的多解性与病态性(Sen and Stoffa, 1991; Sirgue and Pratt, 2004; Tarantola, 2005; 董良国等, 2013).随着地球物理反问题的日趋复杂,地球物理学家针对各自的不同问题又提出了许多其他的正则化约束方法.例如,为了使反演结果具有“块状化”的特点,许多学者在反问题目标函数中加入模型参数全变差正则化约束项(Aster et al., 2013; Gholami, 2015; Li and Zhang, 2017; Zhang et al., 2014);在求解稀疏脉冲反褶积时,在目标函数中加入稀疏性约束项(例如模型参数L1模约束、柯西正则化约束等等),使得反褶积的结果具有脉冲形状,从而拓宽反褶积结果的频带(Claerbout and Muir, 1973; Dai et al., 2016; Sacchi, 1997; Zhang and Castagna, 2011; Zhang and Dai, 2016),等等.
对于正则化约束下的地球物理反问题,其成败在很大程度上取决于合理的正则化参数(Dai et al., 2016; Li and Zhang, 2017; Sen and Biswas, 2015; Zhang et al., 2014).目前最常用的正则化参数选取方法是L曲线准则法(Hansen, 1992; Aster et al., 2013).以零阶吉洪诺夫正则化约束为例,当正则化参数减少时,正则化约束项对目标函数的贡献就会相对减小,求解出的模型参数的方差会变大,形象地说,就是模型参数会变得相对更“粗糙”,而目标函数中的观测数据失配项对目标函数的贡献就会相对增大,因此求解出的模型参数会相对地更忠实于观测数据(王家映, 1998).因此, 通过调整正则化参数可描绘出正则化项与观测数据失配项的变化曲线.该曲线的轮廓呈现出带拐点的“L”形状.对不同的反问题,拐点的清晰度不同,但它始终具有明确意义(但不同的学者对拐点的定义不一样).正则化参数的最佳选择则位于L曲线拐点附近.另一种可选的方法是广义交叉检验法(GCV: Generalized Cross-Validation)(Aster et al., 2013; Craven and Wahba, 1979; Golub and von Matt, 1997; Wahba, 1990).这种方法在理论上具有较大价值,但在实际操作上还具有一定的困难(Aster et al., 2013).除了上述方法外,还有矛盾准则法(Eldar, 2009)、质量控制法(Dai et al., 2016)等等.对于矛盾准则法,需要预先估计出观测数据中误差的方差,这在实际数据中很难实现,因此多用于模型分析或数值试验中,而在实际应用中很少用到(Eldar, 2009).另一种可选的方法,即质量控制法的具体思路是(以地震阻抗反演为例),如果在实际工区里有测井资料,则可在井位置处做质量控制,即对井旁地震道试验不同的正则化参数并进行反演,然后选出与实际井数据最匹配的反演结果所对应的那一个正则化参数,并将该正则化参数应用于整个工区.
从以上叙述可知,目前常用的正则化参数选取方法,都要根据大量的试验来确定合适的正则化参数(Yilmaz, 2001),工作量十分巨大,并且存在很大的经验性(例如,如何定义L曲线的拐点,观测数据中误差的方差的估计等等), 很难得到最优的正则化参数.针对这个问题,本文提议一种基于广义Stein无偏风险估计(G-SURE: Generalized Stein′s unbiased risk estimate)(Donoho and Johnstone, 1995; Eldar, 2009; Stein, 1981)的正则化参数求取方法.广义Stein无偏风险估计是对经典Stein无偏风险估计的拓展,在一定程度上克服了经典Stein无偏风险估计方法只适用于同分布线性高斯模型、以及为了减少优化参数而尽量使用与真实模型有着相近基本结构的初始模型的局限.本文方法的具体思路是通过求解依赖于正则化参数的无偏估计函数(该无偏估计函数从模型参数均方误差(MSE: Mean-squared error)的G-SURE函数推导而来),在反问题求解过程中直接求取正则化参数.模型测试结果表明, 相比于目前常用的正则化参数选取方法,基于G-SURE法求取的正则化参数是最优的.
1 方法原理求解地球物理的正问题意味着预测与给定模型相应的没有误差的数据,可用下式(1)表示这种理论预测
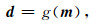
|
(1) |
其中,g是模型参数m与数据d的正演映射.
一般地,正演映射g既可以是线性的也可以是非线性的,范围非常宽泛.在地球物理学中,绝大多数观测数据和模型参数之间都不满足线性关系.但在一定近似条件下,这些非线性关系均可简化或近似简化为线性关系(王家映, 1998),再通过迭代得到反问题的解,例如全波形反演中采用的波恩近似法等(Tarantola, 2005)、AVO或AVA反演中所采用的Aki-Richards近似式(Aki and Richards, 2002)等等.另一方面,实际的地球物理数据处理中,都是在计算机上以离散形式进行操作.因此,为不失一般性,本文重点讨论如下形式的离散线性反问题:
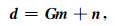
|
(2) |
其中,G是模型参数矢量m与观测数据矢量d的正演矩阵,n是由于数据离散化、地球物理试验的不精确性以及其他原因造成的误差矢量.
1.1 广义Stein无偏风险估计根据最小二乘理论,在没有正则化约束的情况下,地球物理反问题一般采用如下形式的目标函数(Tarantola, 2005; 王家映, 1998; 杨文采, 1997):
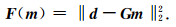
|
(3) |
其中,‖m‖22是矢量m的L2模.
从统计估计的观点来看,上式求得的解等价于观测数据误差服从下式(4)的零均值高斯分布假设条件下的最大似然估计(Tarantola, 2005),

|
(4) |
其中,K是与高斯分布有关的常数,C为高斯分布的协方差矩阵.对于最小二乘问题,C取为单位矩阵I.
为方便G-SURE公式的推导,将式(4)改写为

|
(5) |
容易验证,式(5)与式(4)在C取为单位矩阵I情况下是等价的(Eldar, 2009).
由Rao-Blackwell定理(Kay, 1993)可得,在给定式(5)形式的统计分布时,式(6)是模型参数m的一个充分统计量:

|
(6) |
那么,关于模型参数m的任何一个合理估计都应该是x的函数(Kay, 1993).设

|
(7) |
例如,若目标函数取为式(3),则对应的最小二乘解为

|
(8) |
G-SURE寻求的是与真实模型参数m的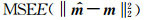

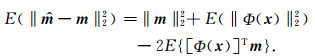
|
(9) |
由于真实模型参数m的L2模是一个常数,因此,为最小化MSE,只需要准确地评估

|
(10) |
明显地,式(10)依赖于未知的真实模型参数m,因此不能被直接地估计.作为替代,G-SURE寻求h(Φ, m)的无偏估计.式(10)中只有E{[Φ(x)]Tm}项明确依赖于真实模型参数m,因此只需讨论该项的无偏估计.
假设已经构建出一个仅依赖于Φ(x)的函数u[Φ(x)]使得下式(11)成立
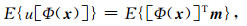
|
(11) |
那么,
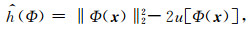
|
(12) |
是h(Φ, m)的无偏估计.因此,一个合理的策略就是选择Φ(x)使得这个无偏估计取得极小,从而得到G-SURE的解.这种思想最先由Stein(1981)提出.Stein所求解的问题是假设观测数据误差服从独立同等的高斯分布,且正演矩阵G为单位矩阵I.本文将该思想推广至更一般的地球物理反问题,因此称为广义Stein无偏风险估计.
现在来讨论函数u[Φ(x)]的具体形式.在推导u[Φ(x)]的具体形式时,需要用到下面的关于x的分布函数.
容易验证,通过简单的参数代换,式(5)可转化成下式(13)关于x的分布函数
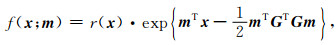
|
(13) |
其中,
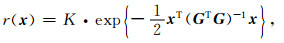
|
(14) |
由式(13)可得,
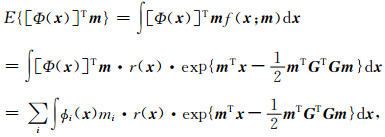
|
(15) |
其中, ϕi(x)与mi是Φ(x)与m的第i分量.
由指数函数的求导性质可得,
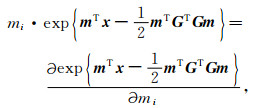
|
(16) |
将式(16)代入式(15)中的相关项,则有

|
(17) |
其中,xi是x的第i分量.采用分部积分法,并结合式(18)(因为E{|Φ(x)|}是有界的,因此,当|xi|→∞时,由简单的积分运算可推得式(18)).
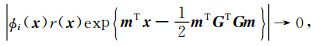
|
(18) |
可得

|
(19) |
由求导的乘积运算关系可得,
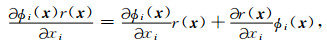
|
(20) |
将式(19)和式(20)代入式(15),可得
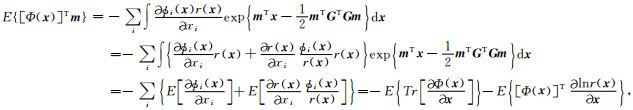
|
(21) |
其中,
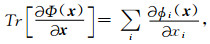
|
(22) |
是Φ(x)关于x的雅可比矩阵的迹.
通过以上推导可知,u[Φ(x)]的具体形式为

|
(23) |
将式(14)代入式(23)可得

|
(24) |
因此,

|
(25) |
上式就是G-SURE核心公式.选择具体的模型参数估计函数Φ(x),并求解该式可得到相应模型参数估计算法的最小MSE无偏估计解.Stein在他的开创性文章中指出,无论真实模型参数的取值如何、具体的模型参数估计函数Φ(x)的形式如何,通过求解模型参数MSE极小得到的解总是最优的(Eldar, 2009; Stein, 1981).
1.2 正则化参数的求取本文推导的G-SURE公式的一个最重要应用就是地球物理反问题中正则化参数的求取.不同的正则化约束具有不同的反问题目标函数,另一方面,对于同一个目标函数,同时还存在着不同的求解算法.因此,模型参数估计函数Φ(x)的形式也是不同的.下文推导了地球物理反问题中常用的吉洪诺夫正则化与L1模正则化约束下的G-SURE正则化参数求取方法.虽然本文中的模型参数估计函数Φ(x)所采用的形式也许和现有文献中的其他模型参数估计方法不同,但基于G-SURE求取正则化参数的基本思路可推广至其他类型的正则化约束方法以及其他形式的模型参数估计函数.
为清楚地阐述G-SURE法求取正则化参数的基本思路,本文采用临近目标函数优化算法(POFA:proximal objective function optimization algorithm)求解反问题目标函数.这是因为,利用POFA求解反问题目标函数时,模型参数估计函数的形式具有显式结构.由于该算法不是本文的主要内容,因此,下文直接给出利用POFA求解相应目标函数的具体步骤,以及相应的模型参数估计函数Φ(x).关于POFA的详细推导过程可见相关参考文献(Beck and Teboulle, 2009; Dai et al., 2016).
1.2.1 吉洪诺夫正则化基于吉洪诺夫正则化约束的地球物理反问题目标函数取如下形式(Aster et al., 2013; Tikhonov and Arsenin, 1977):

|
(26) |
其中,λ为正则化参数,L为关于模型参数m的某种性质的矩阵.例如,若L取为单位矩阵、一阶差分矩阵和二阶差分矩阵等,则分别对应于在目标函数中要求模型参数的方差、平缓度和光滑度极小(王家映, 1998).在通常情况下,L取为单位矩阵I,即阻尼最小二乘,例如最小平方反褶积中的预白化.不失一般性,本文考虑L取单位矩阵下的吉洪诺夫正则化,即
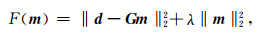
|
(27) |
对于其他类型的吉洪诺夫正则化情形,可根据本文的推导思路很容易地得出相应的结果.
基于POFA的算法原理(Beck and Teboulle, 2009; Dai et al., 2016),容易推导出利用POFA的求解式(27)的具体步骤为,
输入:观测数据矢量d,矩阵G,正则化参数λ,初始解m0;
(1) 计算矩阵GTG的最大特征值ζ,并令k= 1;
(2) 计算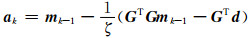
(3) 计算
(4) 判断是否收敛,若收敛,则停止迭代,否则令k=k+1,转步骤2.
因此,POFA求解式(26)的模型参数估计函数Φ(x)为
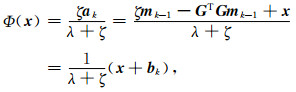
|
(28) |
其中,
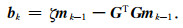
|
(29) |
从上述的求解步骤可知,在算法运行前需要预先确定一个合理的正则化参数,例如最小平方反褶积中预白化因子的大小.目前常用的正则化参数选取方法(例如L曲线法则、矛盾准则法等等),都是根据大量的试验来确定合适的正则化参数,工作量十分巨大,并且存在很大的经验性,很难得到最优的正则化参数.为得到合理的正则化参数,本文基于上文推导的G-SURE,提议一种新的正则化参数求取方法.其基本思路是将具体的模型参数估计函数Φ(x)代入G-SURE公式中,通过求解模型参数MSE的G-SURE关于正则化参数λ的最优化问题,在反问题求解过程中直接求取最优的正则化参数.
对于吉洪诺夫正则化约束问题,具体地说,就是将式(28)代入到式(25)中,得到
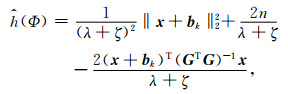
|
(30) |
其中,n是模型参数矢量m的维数.从而有
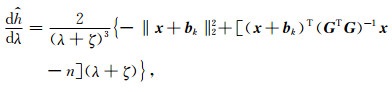
|
(31) |
令式(31)等于零,可求得使ĥ(Φ)取极小时的正则化参数为
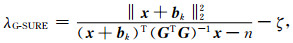
|
(32) |
即为基于G-SURE得到的最优正则化参数.
通常,正则化参数都是大于零的.因此,最终的正则化参数为

|
(33) |
通过以上论述,基于G-SURE正则化参数直接求取的POFA求解式(27)的具体步骤为
输入:观测数据矢量d,矩阵G,初始解m0;
(1) 计算矩阵GTG的最大特征值ζ,并令k= 1;
(2) 计算
(3) 计算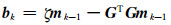
(4) 通过式(32)与式(33)计算正则化参数λ;
(5) 计算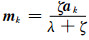
(6) 判断是否收敛,若收敛,则停止迭代,否则令k=k+1,转步骤2.
1.2.2 L1模正则化基于模型参数L1模极小正则化约束的地球物理反问题目标函数取如下形式(Beck and Teboulle, 2009; Zhang and Castagna, 2011):
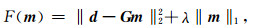
|
(34) |
其中,λ为正则化参数.
Beck和Teboulle (2009)给出了利用POFA的求解式(34)的具体步骤:
输入:观测数据矢量d,矩阵G,正则化参数λ,初始解m0;
(1) 计算矩阵GTG的最大特征值ζ,并令k= 1;
(2) 计算
(3) 计算mk=St(ak),其中,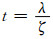
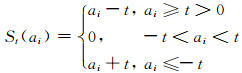
|
(35) |
(4) 判断是否收敛,若收敛,则停止迭代,否则令k=k+1,转步骤2.
上述求解方法就是所谓的迭代阈值收缩算法(ISTA:iterative shrinkage-thresholding algorithm).从上述求解步骤可知,POFA求解式(33)的模型参数估计函数Φ(x)为:

|
(36) |
假设在第k次迭代,矢量ak中有p个分量大于t,有q个分量小于-t,再分别将它们排列在一起组成两个维数分别为p和q的矢量,记为v和w.同时,将(GTG)-1x中与v、w在ak中的指标相对应的分量分别排列成两个矢量,并记为θ和η.那么则有,
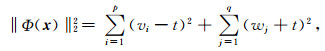
|
(37) |
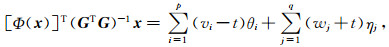
|
(38) |

|
(39) |
将式(37)、(38)和(39)代入到式(25)中,得到
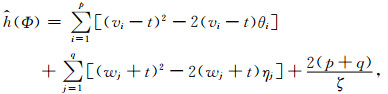
|
(40) |
其中,vi、wj、θi和ηj是矢量v、w、θ和η的分量.从而有
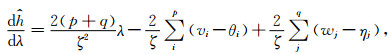
|
(41) |
令式(40)等于零,可求得使ĥ(Φ)取极小时的正则化参数为
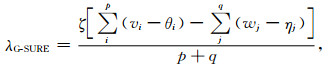
|
(42) |
即为基于G-SURE得到的最优正则化参数.
同1.2.1节类似,求取最终的正则化参数为
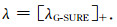
|
(43) |
通过以上论述,基于G-SURE正则化参数直接求取的POFA求解式(34)的具体步骤为
输入:观测数据矢量d,矩阵G,初始解m0;
(1) 计算矩阵GTG的最大特征值ζ,并令k= 1;
(2) 计算
(3) 通过式(42)与式(43)计算正则化参数λ;
(4) 计算mk=St(ak);
(5) 判断是否收敛,若收敛,则停止迭代,否则令k=k+1,转步骤2.
2 模型试验下面采用两个模型对G-SURE正则化参数求取方法进行数值测试,并与其他常用的方法进行对比,以说明该方法的适用性与优势.第一个模型采用王家映(1998)给出的一个反演实例,对吉洪诺夫正则化约束的反问题进行数值试验.第二个模型测试为一个稀疏脉冲反褶积实例,对L1模正则化约束的反问题进行数值试验.
2.1 模型试验1模型1为式(44)所示的连续函数(王家映, 1998):
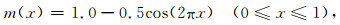
|
(44) |
所采用的正问题为

|
(45) |
其中,
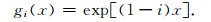
|
(46) |
这是一组人工合成的理论数据,把di视为第i个观测数据.由于计算机实现是离散化的,因此需要对模型进行参数化.本文的具体做法是把在区间[0, 1]上的x等分成10个区间,使得
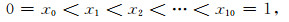
|
(47) |
这时,式(44)可被离散化为

|
(48) |
写成矩阵与矢量形式为

|
(49) |
式(48)与式(49)中,mj为模型m(x)在xj处的值,组成的矢量m为模型参数矢量,di组成的矢量d为观测数据矢量,
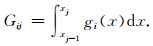
|
(50) |
式(49)即为离散化的正问题方程.
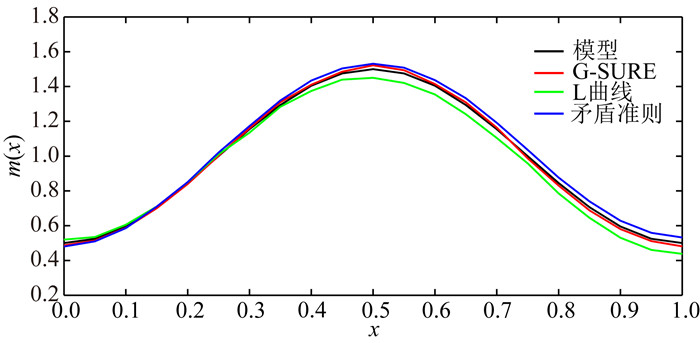
为说明本文提议的G-SURE法在处理地球物理反问题时对噪声的稳健性,对人工合成的理论数据d加入10%的零均值高斯随机噪声.由于模型m(x)是一个平滑函数,因此可采用吉洪诺夫正则化作为反问题的正则化约束项.对含噪声的人工合成数据进行吉洪诺夫正则化反演.在反演过程中,采用了三种不同的正则化参数选取方法,分别是本文提议的G-SURE法、L曲线法、矛盾准则法.反演结果如图 1所示.为显示不同反演结果的质量,图 1还给出了真实模型参数(如图 1中的黑线所示).从图 1中可以看出,基于G-SURE得到的反演结果与真实模型最近接.为了进一步说明G-SURE的优势,计算三种反演结果与真实模型的MSE,结果如表 1所示.可以看出,基于G-SURE得到的反演结果的MSE最小.
|
图 1 不同正则化参数选取方法反演结果 Fig. 1 Inversion results with different regularization parameter selecting methods |
|
|
表 1 不同正则化参数选取方法在不同程度噪声下的反演结果与模型1的MSE Table 1 MSEs for inversion results under different levels noise with different methods for selecting regularization parameter compared to model 1 |
为测试本文方法在不同程度随机噪声影响下的反演效果,并比较不同正则化参数选取方法MSE的总体变化趋势,对人工合成的理论数据d加入不同比例的高斯随机噪声.对含不同比例噪声的人工合成数据进行吉洪诺夫正则化反演.反演结果与真实模型的MSE如表 1所示.可以看出,总体上,无论噪声的程度如何,基于G-SURE得到的反演结果的MSE都是最小的.但是另一方面,随着噪声比例的增加,噪声对反演结果的影响越来越大,因此G-SURE同其他两种方法的MSE有接近的趋势.
此外,G-SURE法在反演求解过程中直接求取最优的正则化参数,并不需要在反演求解前进行大量的正则化参数试验(而L曲线法与矛盾准则法求取正则化参数时, 则需要进行大量的试验),因此可以推断,反演的求解效率也能够得到提高.
2.2 模型试验2模型测试2是一个地震信号稀疏脉冲反褶积实例.地震学中,检波器接收到的地震信号被认为是由地下反射系数序列与有限带宽震源子波的褶积结果(Robinson and Treitel, 1980),即

|
(51) |
其中, d是接收到的地震信号, w是有限带宽的震源子波, r是反射系数序列,即反褶积问题中的模型参数.在求解反褶积问题中,若假设地震子波已知,则问题相对要简单一点;若地震子波未知,则称为盲反褶积.由于本文主要讨论正则化参数的选取,因此在下面的模型测试中不考虑盲反褶积,采用确定性的子波进行反褶积.
通常,地震数据的处理都是以离散形式在计算机上操作的.因此,将式(51)写成离散的矩阵与矢量形式为

|
(52) |
其中,d是地震数据矢量,W是子波褶积矩阵,r是反射系数矢量.
在求解稀疏脉冲反褶积时,通常采用基于模型参数L1模极小的正则化约束方法,以得到脉冲状的地震反射系数序列(Claerbout and Muir, 1973; Li and Zhang, 2017; Zhang and Castagna, 2011; Zhang et al., 2014).由式(34)可得,稀疏脉冲反褶积的目标函数为
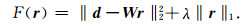
|
(53) |
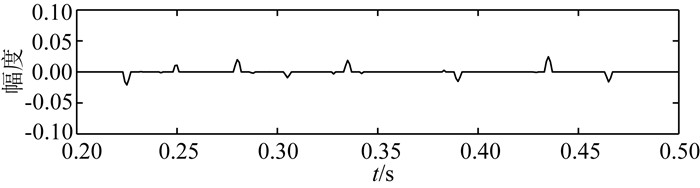
首先,设计如图 2所示的反射系数序列模型.将该模型反射系数与主频为35 Hz的雷克子波进行褶积,并对褶积结果加入10%的高斯随机噪声,结果如图 3所示.对含噪声的合成地震数据进行稀疏脉冲反褶积.在反褶积过程中,采用三种不同的正则化参数选取方法,即G-SURE法、L曲线法和矛盾准则法.反褶积结果分别如图 4、图 5和图 6所示.可以看出,三种反褶积结果都与真实模型反射系数很接近.虽然反射系数的绝对振幅没有得到完全地恢复(这是由于反问题的本质特征所决定的,即反问题的不适定性),但反射系数的位置与相对振幅大小都得到了很好的保持.为了说明G-SURE的优势,计算三种反褶积结果与真实反射系数的MSE,结果如表 2所示.可以看出,同模型测试1的结果类似,基于G-SURE得到的反褶积结果具有最小的MSE.

|
图 2 反射系数模型 Fig. 2 Reflection coefficients model |
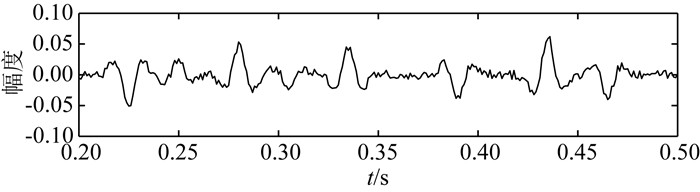
|
图 3 含噪合成地震数据 Fig. 3 Synthetic seismic data with noise |

|
图 4 G-SURE正则化参数选取的反褶积结果 Fig. 4 Deconvolution results with G-SURE regularization parameter selection |
|
图 5 L曲线正则化参数选取的反褶积结果 Fig. 5 Deconvolution results with L-curve regularization parameter selection |

|
图 6 矛盾准则正则化参数选取的反褶积结果 Fig. 6 Deconvolution results with discrepancy criterion regularization parameter selection |
|
|
表 2 不同正则化参数选取方法反褶积结果与模型2的MSE Table 2 MSEs for deconvolution results with different methods for selecting regularization parameter compared to model 2 |
为了试验G-SURE正则化参数求取在实际数据中的效果,选取中国东部某工区的实际叠后地震资料进行叠后波阻抗反演分析.
通常,叠后波阻抗反演分为两个步骤.首先对叠后地震数据进行稀疏脉冲反褶积,得到稀疏脉冲状的反射系数序列;然后由反射系数序列通过求解下式
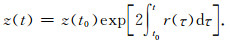
|
(54) |
可得到叠后波阻抗数据体(Dai et al., 2016; Zhang et al., 2014),其中t是时间采样点,t0是初始采样时间,z为叠后波阻抗.
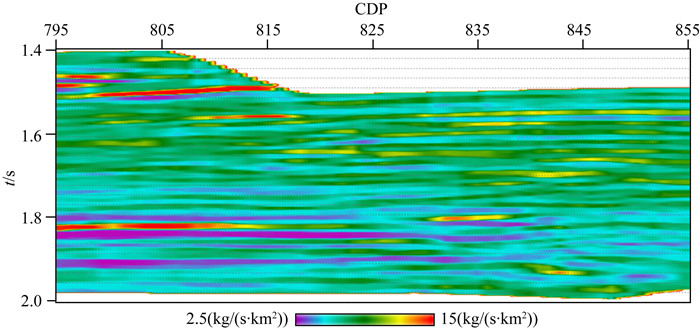
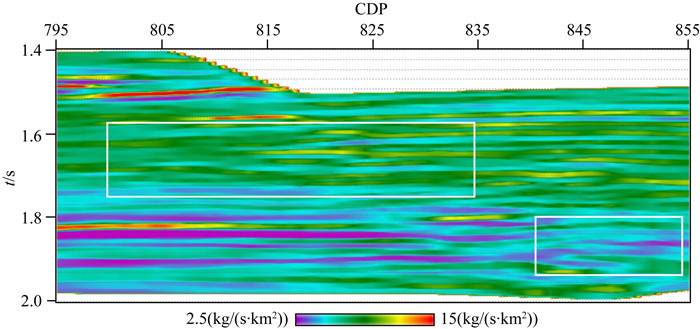
该地震工区有141条Inline线,线号范围为525到665,每条Inline线有61个CDP,CDP号范围为795到855.图 7所示为Inline600线的叠后地震剖面.可以看出,地震数据的质量非常好,同相轴连续,断层与断点位置十分清楚.对该叠后地震数据体进行叠后地震波阻抗反演,在反演过程中,采用两种不同的正则化参数选取方法,即G-SURE法和实际地震数据反演中最常用的质量控制法.图 8与图 9显示了Inline600线的反演结果.从图 8与图 9的对比可知,两种反演结果同图 7所示的叠后地震剖面在构造形态上都十分地吻合.但是图 9所示的反演结果在地层的横向展布上不如图 8所示的反演结果清晰自然,例如位于图 9中的两个白色矩形框内的地层展布形态.这是因为,质量控制法选取正则化参数的具体做法是对质控地震道试验不同的正则化参数并进行反演,然后选出最优的正则化参数,并将该正则化参数应用于整个工区.对于质控地震道来说,选取的正则化参数是最优的,但是对于远离质控地震道的地震道数据,则可能不是最优的.而G-SURE法在反演迭代过程中自动地修正正则化参数,因此对于每一道地震数据,G-SURE法求出的正则化参数都是最优的.

|
图 7 Inline600线实际地震剖面 Fig. 7 Real seismic data profile of Inline 600 |
|
图 8 Inline600线G-SURE正则化参数选取反演结果 Fig. 8 Inversion results with G-SURE regularization parameter selection of Inline 600 |
|
图 9 Inline600线质量控制法正则化参数选取反演结果 Fig. 9 Inversion results with regularization parameter selection by quality control of Inline 600 |
为了说明G-SURE在实际数据反演中的优势,计算两种反演结果的无偏估计MSE,结果如表 3所示.可以看出,G-SURE反演结果的MSE小于质量控制法反演结果的MSE.
|
|
表 3 不同正则化参数选取方法实际地震资料反演结果的无偏估计MSE Table 3 MSEs for real seismic data inversion results with different methods for selecting regularization parameter |
不同的正则化有不同的反问题目标函数,并且对于同一个目标函数,不同的求解算法所得到的模型参数估计函数的形式也是不同的.地球物理反问题的正则化约束方法与求解算法是非常多的,很多问题并不存在显式的模型参数估计函数Φ(x),或者模型参数估计函数Φ(x)的表达式十分复杂,例如全变差正则化约束.但本文提议的正则化参数求取思路仍然能够推广至这些复杂的反问题情形.在这些情况,G-SURE公式中的各项都是数值形式的,例如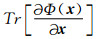
一般地,在反问题求解的迭代过程中,可利用任何有效的线性搜索数值算法对正则化参数进行寻优,例如对分法、牛顿下山法、埃特金迭代法等(Antoniou and Lu, 2007; 徐士良, 马尔妮, 2013).下面给出基于埃特金迭代法的正则化参数迭代数值解,且该迭代过程可加入到反问题的迭代求解过程中.正则化参数的具体迭代步骤为:
取初始正则化参数λ0(从理论上说,该初始正则化参数可以是大于0的任意数,不需要大量的试验),并假设反问题求解已进行到第k次迭代;计算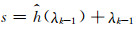
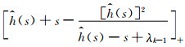
埃特金迭代法具有良好的收敛性(徐士良, 马尔妮, 2013),随着迭代的进行,最终能够收敛到最优的正则化参数.
5 结论本文提议了一种新的地球物理反问题正则化参数求取方法.该方法基于广义Stein无偏风险估计理论(G-SURE);其具体思路是通过求解模型参数均方误差(MSE)的G-SURE函数,在反问题求解过程中自动求取正则化参数.本文模型试验与实际数据试验结果表明, 相比于目前常用的正则化参数选取方法(例如L曲线法、矛盾准则法、质量控制法等),采用G-SURE法求取的正则化参数进行反演,所得到反演结果与真实模型参数之间具有最小的MSE.从这个角度来说,本文提议的基于G-SURE求得的正则化参数是最优的.
本文在G-SURE公式的基础上,推导出了在地球物理反问题中常用的吉洪诺夫正则化与L1模正则化约束下的正则化参数求取方法.为了方便阐述G-SURE法求取正则化参数的基本思路,本文采用了具有显式结构的模型参数估计函数Φ(x).本文的模型参数估计函数Φ(x)也许和现有文献中的其他模型参数估计方法不同,但G-SURE法求取正则化参数的基本思路可推广至其他类型的正则化约束方法以及其他形式的模型参数估计函数,例如柯西分布正则化约束、广义高斯分布正则化约束等等.这可作为后续进一步研究的方向.
Aki K, Richards P G. 2002. Quantitative Seismology. 2nd ed. Sausalito: University Science Books.
|
Antoniou A, Lu W S. 2007. Practical Optimization:Algorithms and Engineering Applications. New York: Springer.
|
Aster R C, Borchers B, Thurber C H. 2013. Parameter Estimation and Inverse Problems. 2nd ed. Waltham: Elsevier Academic Press.
|
Beck A, Teboulle M. 2009. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal of Imaging Sciences, 2(1): 183-202. DOI:10.1137/080716542 |
Claerbout J F, Muir F. 1973. Robust modeling with erratic data. Geophysics, 38(5): 826-844. DOI:10.1190/1.1440378 |
Craven P, Wahba G. 1979. Smoothing noisy data with spline functions:Estimating the correct degree of smoothing by the method of generalized cross-validation. Numerische Mathematik, 31(4): 377-403. |
Cui Y, Wang Y F. 2015. Tikhonov regularization and gradient descent algorithms for tomography using first-arrival seismic traveltimes. Chinese Journal of Geophysics (in Chinese), 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
Dai Q W, Jiang F B, Dong L. 2014. RBFNN inversion for electrical resistivity tomography based on Hannan-Quinn criterion. Chinese Journal of Geophysics (in Chinese), 57(4): 1335-1344. DOI:10.6038/cjg20140430 |
Dai R H, Zhang F C, Liu H Q. 2016. Seismic inversion based on proximal objective function optimization algorithm. Geophysics, 81(5): R237-R246. DOI:10.1190/geo2014-0590.1 |
Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion. Chinese Journal of Geophysics (in Chinese), 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
Donoho D L, Johnstone I M. 1995. Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
Eldar Y C. 2009. Generalized SURE for exponential families:applications to regularization. IEEE Transactions on Signal Processing, 57(2): 471-481. DOI:10.1109/TSP.2008.2008212 |
Gholami A. 2015. Nonlinear multichannel impedance inversion by total-variation regularization. Geophysics, 80(5): R217-R224. DOI:10.1190/geo2015-0004.1 |
Golub G H, Von Matt U. 1997. Generalized cross-validation for large-scale problems. Journal of Computational and Graphical Statistics, 6(1): 1-34. |
Hansen P C. 1992. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Review, 34(4): 561-580. DOI:10.1137/1034115 |
Kay S M. 1993. Fundamentals of Statistical Signal Processing, Volume Ⅰ:Estimation Theory. New Jersey: Prentice-Hall.
|
Li C, Zhang F. 2017. Amplitude-versus-angle inversion based on the L1-norm-based likelihood function and the total variation regularization constraint. Geophysics, 82(3): R173-R182. DOI:10.1190/geo2016-0182.1 |
Robinson E A, Treitel S. 1980. Geophysical Signal Analysis. Englewood Cliffs: Prentice-Hall.
|
Sacchi M D. 1997. Reweighting strategies in seismic deconvolution. Geophysical Journal International, 129(3): 651-656. DOI:10.1111/gji.1997.129.issue-3 |
Sen M K, Stoffa P L. 1991. Nonlinear one-dimensional seismic waveform inversion using simulated annealing. Geophysics, 56(10): 1624-1638. DOI:10.1190/1.1442973 |
Sen M K, Biswas R. 2015. Choice of regularization weight in basis pursuit reflectivity inversion. Journal of Geophysics and Engineering, 12(1): 70-79. DOI:10.1088/1742-2132/12/1/70 |
Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies. Geophysics, 69(1): 231-248. DOI:10.1190/1.1649391 |
Stein C M. 1981. Estimation of the mean of a multivariate normal distribution. Annals of Statistics, 9(6): 1135-1151. DOI:10.1214/aos/1176345632 |
Tarantola A. 2005. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia: Society for Industrial and Applied Mathematics.
|
Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-Posed Problems. Washington DC: Winston and Sons.
|
Wahba G. 1990. Spline Models for Observational Data. Philadelphia: Society for Applied Mathematics.
|
Wang J Y. 1998. Inverse Theory in Geophysics (in Chinese). Wuhan: China University of Geosciences Press.
|
Xu S L, Ma E N. 2013. Commonly Used Algorithm Assemblies (in Chinese). 5th ed. Beijing: Tsinghua University Press.
|
Yang W C. 1997. Theory and Methods of Geophysical Inversion (in Chinese). Beijing: Geological publishing house.
|
Yao Y. 2002. Basic Theory and Application Methods of Geophysical Inversion (in Chinese). Wuhan: China University of Geosciences Press.
|
Yilmaz O. 2001. Seismic data analysis:processing, inversion, and interpretation of seismic data. Tulsa: Society of Exploration Geophysicists.
|
Zhang F C, Dai R H, Liu H Q. 2014. Seismic inversion based on L1-norm misfit function and total variation regularization. Journal of Applied Geophysics, 109: 111-118. DOI:10.1016/j.jappgeo.2014.07.024 |
Zhang F C, Dai R H. 2016. Nonlinear inversion of pre-stack seismic data using variable metric method. Journal of Applied Geophysics, 129: 111-125. DOI:10.1016/j.jappgeo.2016.03.035 |
Zhang F X, Wu Q J, Li Y H. 2014. A traveltime tomography study by teleseismic S wave data in the Northeast China area. Chinese Journal of Geophysics (in Chinese), 57(1): 88-101. DOI:10.6038/cjg20130818 |
Zhang R, Castagna J. 2011. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition. Geophysics, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
Zhu X S, Wu R S, Chen X F. 2014. Generalized diffraction tomography. Chinese Journal of Geophysics (in Chinese), 57(1): 241-260. DOI:10.6038/cjg20140120 |
崔岩, 王彦飞. 2015. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法. 地球物理学报, 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
戴前伟, 江沸菠, 董莉. 2014. 基于汉南-奎因信息准则的电阻率层析成像径向基神经网络反演. 地球物理学报, 57(4): 1335-1344. DOI:10.6038/cjg20140430 |
董良国, 迟本鑫, 陶纪霞, 等. 2013. 声波全波形反演目标函数性态. 地球物理学报, 56(10): 3445-3460. DOI:10.6038/cjg20131020 |
王家映. 1998. 地球物理反演理论. 武汉: 中国地质大学出版社.
|
徐士良, 马尔妮. 2013. 常用算法程序集. 北京: 清华大学出版社.
|
杨文采. 1997. 地球物理反演的理论与方法. 北京: 地质出版社.
|
姚姚. 2002. 地球物理反演基本理论与应用方法. 武汉: 中国地质大学出版社.
|
张风雪, 吴庆举, 李永华. 2014. 中国东北地区远震S波走时层析成像研究. 地球物理学报, 57(1): 88-101. DOI:10.6038/cjg20130818 |
朱小三, 吴如山, 陈晓非. 2014. 广义散射层析成像反演. 地球物理学报, 57(1): 241-260. DOI:10.6038/cjg20140120 |
 2019, Vol. 62
2019, Vol. 62


