地球物理学报  2019, Vol. 62 Issue (3): 836-848   PDF    
引用本文
唐滢, 徐昕, 王元. 2019. 地形重力波举力效应对台风路径偏转的影响. 地球物理学报, 62(3): 836-848, doi: 10.6038/cjg2019L0328.  
Tang Y, Xu X, Wang Y. 2019. Influence of the mountain-wave lifting effect on the deflection of typhoon track. Chinese J. Geophys. (in Chinese), 62(3): 836-848, doi: 10.6038/cjg2019L0328.  
地形重力波举力效应对台风路径偏转的影响
唐滢1,2, 徐昕1,2, 王元1     
1. 南京大学大气科学学院, 南京 210023;
2. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
收稿日期 2018-03-11, 2019-01-09 收修定稿
基金项目: 国家基础研究发展计划项目（2015CB452801），国家自然科学基金青年基金项目（41505046）以及中国气象科学研究院基本科研业务费项目（2017Z017）共同资助
第一作者简介: 唐滢, 主要从事中尺度灾害性天气研究.E-mail:mg1628011@smail.nju.edu.cn
通讯作者: 徐昕, 主要从事中尺度地形动力学研究.E-mail:xinxu@nju.edu.cn
摘要：举力效应是指方向性切变气流经过地形激发的重力波能够使平均气流发生水平旋转.本文首先根据日本气象厅台风数据集统计了2006-2015年登陆台湾的台风个例，分析台风路径的偏转情况.然后利用二维傅里叶变换对欧洲中间尺度天气预报中心的再分析数据进行滤波，得到台风的环境大气层结和水平风场.最后根据台风环境风场以及台湾地形计算地形重力波举力，分析举力对台风路径偏转的可能贡献.结果表明，近十年共有20个台风登陆台湾，其中2006-2008年有10个.除去5个路径较为复杂的台风，本文对15个台风的地形重力波举力进行分析，发现有14个台风的路径偏转方向与举力方向一致.对于路径偏转最为明显的6个台风（偏转角度大于30°），地形重力波举力对台风路径偏转的贡献可达10%，部分解释了台风经过台湾地形时发生的路径偏转.
关键词: 台风路径偏转      地形      重力波      举力效应     
Influence of the mountain-wave lifting effect on the deflection of typhoon track
TANG Ying1,2, XU Xin1,2, WANG Yuan1     
1. School of Atmospheric Sciences, Nanjing University, Nanjing 210023, China;
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
Abstract: Mountain waves generated in directionally sheared wind are able to induce horizontal rotation of the mean flow, which is designated as the lifting effect. In this work, we first investigate the typhoons land-falling in Taiwan between 2006 and 2015 from the Japan Meteorological Agency (JMA) typhoon dataset and analyze their track deflection. Then the environmental winds and stratification of land-falling typhoons are derived from the European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis data using the two-dimensional Fourier transform. Lastly, the lift force is computed according to the environmental wind and Taiwan orography. The results show that there are 20 typhoons land-falling in Taiwan in recent 10 years, half of which occurred during 2006-2008. The effect of orographic gravity wave lift (OGWL) is examined for 15 typhoon cases except 5 typhoons with complex tracks. In 14 of these 15 typhoons, the orientation of OGWL is consistent with that of typhoon track deflection. As for the 6 typhoons with most notable track deflection (greater than 30 degrees), OGWL is found to contribute up to 10% of the track deflection, which partly explains the track deflection of typhoons passing over Taiwan.
Keywords: Typhoon track deflection    Terrain    Mountain wave    Lifting effect    
0 引言

热带气旋(在北大西洋被称作飓风, 在西北太平洋被称作台风)是世界上最具灾害性的天气现象之一(Chan, 2005).鉴于热带气旋对社会经济的重要影响, 自有热带天气预报以来, 提高热带气旋路径预报的准确性始终受到高度重视.常规的台风路径主要包括西移路径, 西北移路径, 以及转向路径(田华等, 2010).除了常规路径以外, 还有很多特殊路径, 如倒抛物线路径(段晶晶等, 2014)、回旋路径(朱智慧等, 2015)、蛇形路径、顺时针打转和逆时针打转(芮建勋和何梦梦, 2013)等.台风路径的复杂多样导致其预报难度大大增加.

台风的移动主要是由外部强迫和内部动力因子共同决定的(王斌等, 1998).外部强迫主要包括大尺度环境气流的引导, 邻近气旋或其他天气系统的影响, 下垫面摩擦以及地形和热通量的影响.内部动力因子主要包括对流的不对称性、中尺度系统、高低层涡旋的垂直耦合和流出层的动力不稳定等.Chan和Gary(1982)研究发现, 热带气旋在正压大气中的移动主要由环境气流引导决定, 但是科氏力和环境气流的水平涡度梯度会改变其移动.

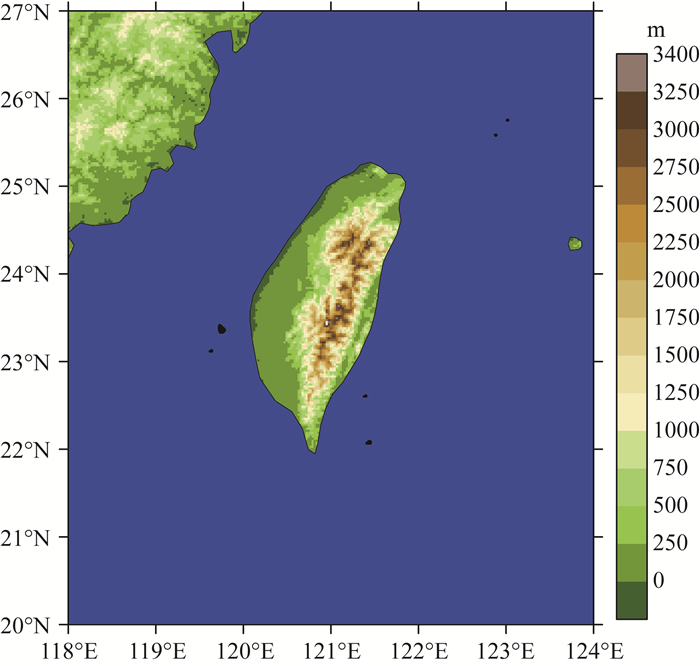
地处西北太平洋的台湾岛每年遭到3~6次台风侵袭.台湾岛地形复杂, 包括西部平原以及从北到南起伏的山脉.最显著的地形是中央山脉, 平均海拔约为2000 m, 最高峰达到4000 m左右(图 1).台湾岛地形的存在能够影响台风的路径.例如，罗哲贤和陈联寿(1995)利用β平面准地转正压模式研究了台湾岛地形对台风路径的影响.结果表明, 台湾岛地形引起台风环流的最大风速区向台风中心方向移动，造成台风环流空间尺度减小, 最终导致台风路径向右偏移.Lin等(2006)使用非静力中尺度数值模式MM5分别对登陆台湾的超强台风碧利斯和台风桃芝进行模拟.研究发现碧利斯强度更强, 具有相对更快的向前移动趋势, 其路径持续穿过中央山脉, 而较弱的台风桃芝被台湾中央山脉阻挡导致路径不连续.通过一系列敏感性数值模拟试验, Jian和Wu(2008)同样证实, 较弱和移动缓慢的热带气旋经过台湾时更容易转向, 而较强和移动较快的台风能够以持续的路径穿过台湾中央山脉.此外, Tang和Chan(2016)采用理想数值模拟探讨了台湾地形对不同大小台风的路径影响.对于较小的台风, 其路径偏转往往较迟; 而较大的台风具有更为明显的路径偏转.根据中尺度数值模式MM5, 余贞寿等(2007)研究了台风海棠登陆台湾前的异常打转路径, 指出台湾地形不仅能够直接影响台风的路径, 还可以通过影响台风的非对称结构来间接改变台风的移动.刘爱鸣等(2008)研究了台风韦帕趋岸左折的原因.当台风接近台湾岛时, 地形的摩擦导致台风气压场结构变得非对称, 从而产生与台风移动方向相反的气压梯度力增量.Huang等(2011)利用高分辨率数值模式对台风罗莎登陆台湾前的路径偏转现象进行分析, 发现台湾岛地形高度对罗莎登陆时的环形运动占主导作用, 而地表性质、地形细节以及云微物理过程对路径偏转起次要作用.

图 1 台湾岛地形 Fig. 1 Terrain of Taiwan

尽管过去的研究在一定程度上解释了台湾地形对台风路径的复杂影响, 但是具体的物理机制还不是十分清楚.除了阻挡作用, 地形对气流的影响还存在其他机制, 如地形重力波.地形重力波又称山地波, 是层结稳定流体受下垫面地形扰动产生的垂直运动, 在阿基米德净浮力作用下围绕平衡位置形成的周期性振荡(叶笃正, 1956).在地球上的山脉地区, 如青藏高原、安第斯山、落基山、阿尔卑斯山、以及南极半岛等, 经常观测到重力波活动(Klemp and Lilly, 1975; Gary, 1989; Nastrom and Fritts, 1992).地表产生的重力波能够垂直传播至地球大气的中高层, 是对流层和中层大气耦合的重要物理过程(Article et al., 2003; McLandress et al., 2012; Xu et al., 2017).当地形重力波达到饱和发生破碎时, 能够将其携带的动量传递给平均气流, 并对平均气流施加一个天气尺度的体力(synoptic-scale body force)(Bretherton, 1969; Lindzen, 1981), 即

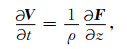
(1)

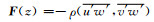
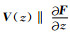
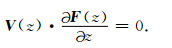
其中V (z)为平均气流，ρ=ρ(z)为大气密度, 为地形重力波动量通量(又称波应力), (u′, v′, w′)为波动速度.过去研究认为, 地形重力波破碎产生的体力与平均气流平行且反向(即), 因此平均气流将减速.这种效应通常被称为地形重力波拖曳(orographic gravity wave drag, OGWD; Article et al., 2003).然而Broad(1995)根据线性波动理论对方向性切变气流(即环境风场方向随高度变化)经过三维地形激发的重力波进行研究, 发现在这种情况下平均气流与波应力的垂直导数满足

(2)

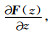
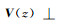
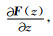
对于非零的平均气流和必有 即地形重力波对平均气流施加的作用力与其垂直.在流体力学领域, 通常将水平面上与流体运动方向垂直的力称为举力(lift force; Lott, 1999).与曳力(drag force)不同, 举力只改变流体的运动方向, 而不影响流体的速度大小.Martin和Lott (2007)根据理想数值模式对方向性切变气流经过地形时的天气尺度响应进行研究, 发现当冷锋(即风场随高度逆时针旋转)过境能够在地形上方诱发气旋性环流; 与此相反, 暖锋(即风场随高度顺时针旋转)经过时在地形上方诱发反气旋性环流.Xu等(2012, 2013)从理论和数值模拟两方面详细分析了地形重力波在方向性切变气流中的动量传输.研究结果表明, 对于随高度逆时针旋转的平均气流, 地形重力波举力与气流垂直, 指向其左侧(图 2a); 反之当平均气流随高度顺时针旋转时, 举力与气流垂直, 指向其右侧(图 2b).这一结论很好地解释了Martin和Lott(2007)的数值模拟结果, 提高了对地形重力波动量传输的认识和理解.

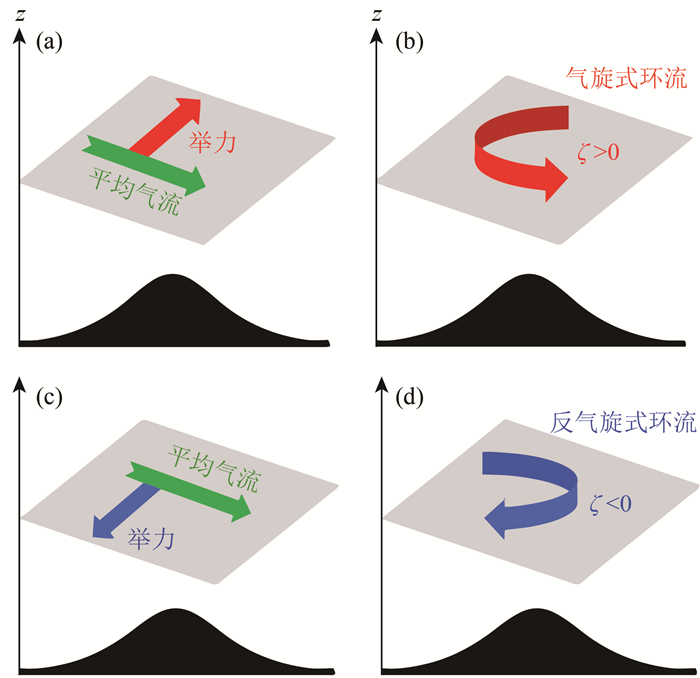
图 2 地形重力波举力概念图 (a)(b)平均气流随高度逆时针旋转时, 举力与平均气流垂直，指向其左侧, 引发气旋式环流. (c)(d)与(a)(b)类似, 但是平均气流随高度顺时针旋转. Fig. 2 Conceptual model of lifting force by mountain waves (a) and (b) In the case of mean wind turning anticlockwise with height, the lifting force points perpendicularly to the left side of the mean wind, tending to induce a cyclonic circulation. (c) and (d) are the same as (a) and (b) but the mean wind turns clockwise with height.

由于地形重力波的动量传递能够影响天气尺度的平均气流, 那么地形重力波是否可以通过其举力效应改变环境气流的方向, 进而影响台风的路径?目前国内外在这方面的研究还尚属空白.本文通过对2006—2015年登陆台湾并且路径发生偏转的台风个例进行分析, 探讨地形重力波的举力效应对台风路径偏转的可能影响.本文第1节介绍了研究使用的数据以及地形重力波举力的分析方法.第2节对近十年登陆台湾的台风个例进行介绍并分析台风的环境场特征; 第3节通过对地形重力波举力进行定量计算, 探讨了举力对台风路径偏转的可能影响.最后是总结和讨论.

1 数据和方法

本文主要根据日本气象厅提供的台风数据集对登陆台湾的台风路径进行统计分析.在西北太平洋地区, 除了日本气象厅以外, 中国上海台风所以及美国关岛台风联合预警中心也都对台风进行整理.Song等(2010)对这三个机构的台风数据集进行比较分析, 发现三者对台风路径的记录比较一致.为了研究台风的环境条件, 并对地形重力波举力进行定量计算, 本文还采用了欧洲中间尺度天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)的ERA-interim再分析资料(Dee et al., 2011), 水平分辨率为0.75°, 垂直37层, 时间分辨率6小时.具体研究过程如下.

(1) 台风个例选取.根据日本气象厅的台风数据集对近十年(2006—2015年)登陆台湾的台风进行统计, 挑选出路径发生偏转的个例.

(2) 台风环境条件分析.利用ECMWF的再分析资料, 通过对不同高度的水平风场和温度场进行二维傅里叶变换, 滤掉波长小于3000 km的波动(即台风和更小尺度的扰动场), 从而得到台风的环境风场和温度场.对台湾地区滤波后的风场和温度场进行区域平均, 得到水平均匀的风廓线和温度廓线, 并可进一步计算环境大气层结.

(3) 举力的定性分析.Xu等(2012)研究表明, 对于随高度逆时针旋转的背景风场, 举力与平均气流垂直, 指向其左侧, 反之则相反.通过对环境风场的方向性切变进行分析, 得到举力的方向, 并将其与台风路径的偏转方向进行比较.

(4) 定量计算地形重力波举力.由(1)式可知, 地形重力波对平均气流的影响取决于重力波动量通量的垂直分布.根据Xu等(2012)的研究, 地形重力波动量通量可表示为

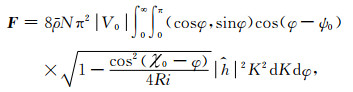
(3)

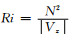
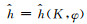
其中ρ为大气密度, N2=g∂(lnθ0)/∂z为大气层结, N为浮力频率, g为重力加速度, θ0=θ0(z)为平均位温, |V0|为地表风速, ψ0为地表风向, χ0为环境风场垂直切变方向, 为环境大气理查德森数, K =K(cosφ, sinφ)为水平波数矢量, K为波矢大小, φ为波矢方向. 为地形谱, 通过对地形数据进行二维傅里叶变换得到.实际大气中通常Ri≫1, 因此从而(3)式可简化为

(4)

(4) 式对z求偏导可得,

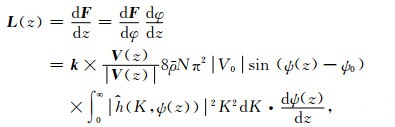
(5)

其中k为垂直方向单位矢量, ψ(z)为高度z处的风向.由(4)式可知, L (z)总是和平均气流V (z)垂直, 因此称之为举力(Lott, 1999).

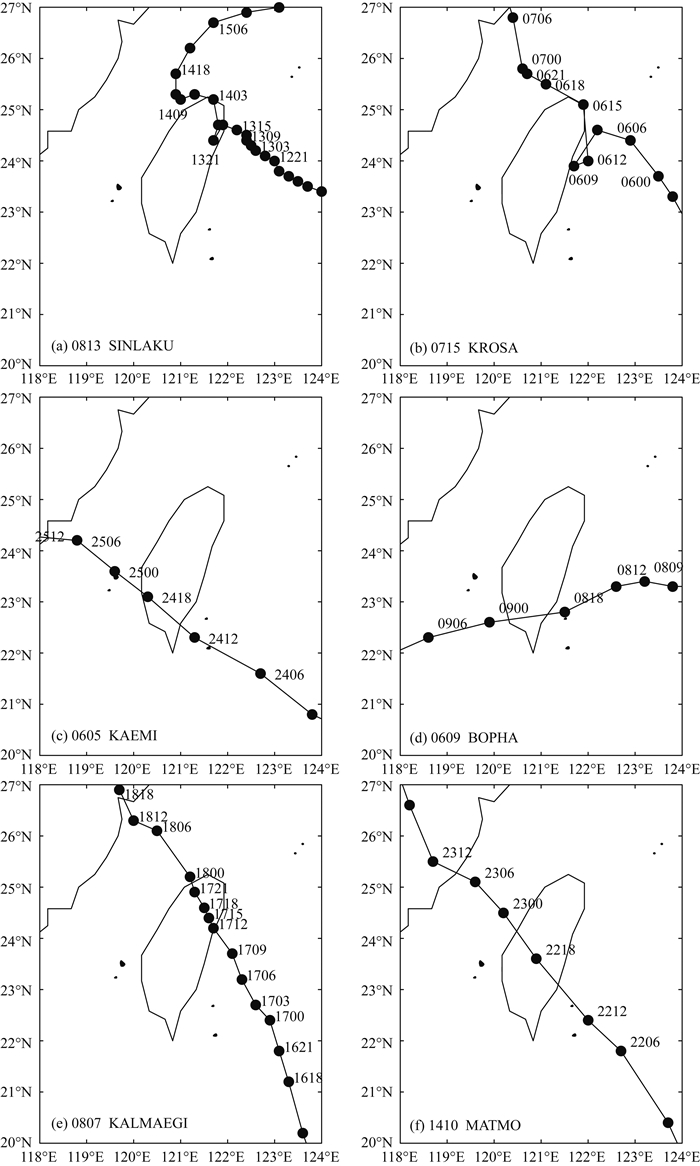
2 个例介绍与环境场分析 2.1 登陆台湾的台风个例

根据日本气象厅2006—2015年的台风数据集，近十年总共有20个台风登陆台湾, 其中2007年最多，有4个; 2006和2008年次之，各有3个; 其他年份相对较少(详见表 1).在这20个登陆台风中, 0813号以及0715号(图 3a, 图 3b)等5个台风的路径较为复杂, 本文暂不考虑; 0609号和1111号等9个台风经过台湾时路径偏转并不明显(偏转角度小于20°, 见表 1), 图 3c—图 3f给出了部分个例; 剩余的6个台风, 即0708号、0815号、0908号、1011号、1307号、1513号, 经过台湾时路径偏转较为明显(偏转角度大于30°), 下面分别对其进行介绍.

表 1 2006—2015年登陆台湾的台风 Table 1 Land-falling typhoons in Taiwan between 2006 and 2015
图 3 (a) 0813, (b) 0715, (c) 0605, (d) 0609, (e) 0807, (f) 1410号台风路径 Fig. 3 Tracks of typhoons (a) 0813, (b) 0715, (c) 0605, (d) 0609, (e) 0807 and (f) 1410

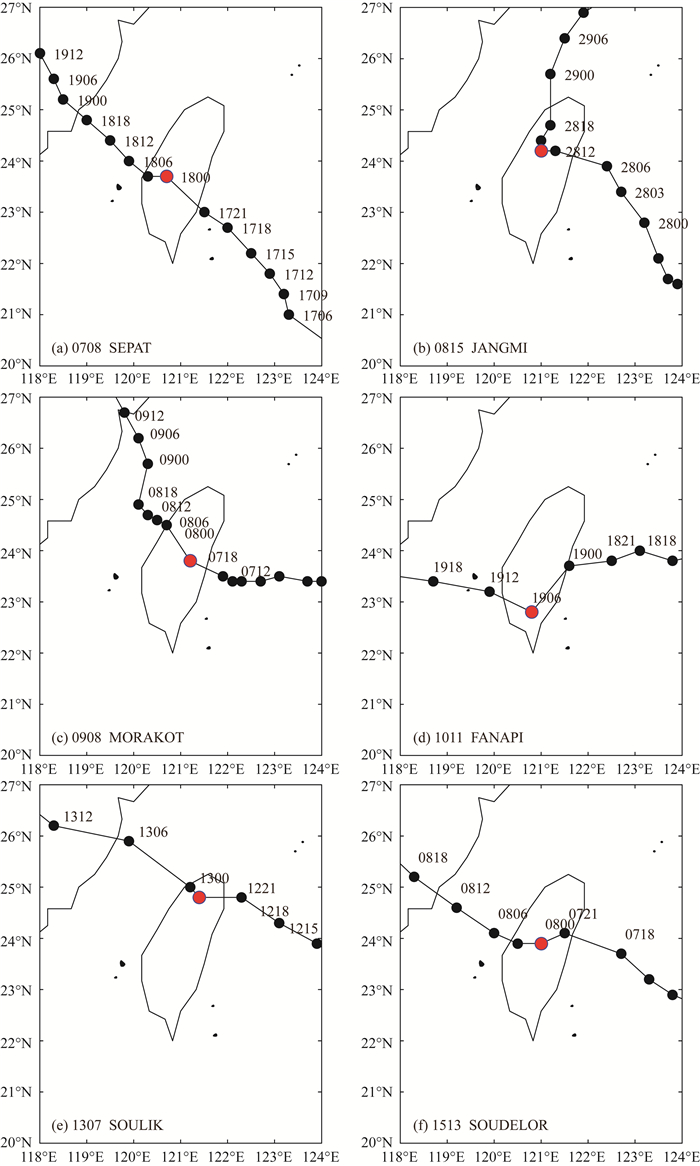
0708号台风(图 4a)于2007年8月17日2100 UTC前后登陆台湾, 在8月18日0000 UTC向左偏转大约43.47°, 随后持续前进在福建登陆.0815号台风(图 4b)于2008年9月28日0800 UTC左右登陆台湾, 在9月28日1200 UTC向右发生明显偏转, 角度97.04°, 随后北翘前进.0908号台风(图 4c)于2009年8月7日1500 UTC左右登陆台湾, 在8月7日1800 UTC向右偏转32.10°, 最后在福建登陆.1011号台风(图 4d)于2010年9月19日0000 UTC左右登陆台湾, 在9月19日0600 UTC向右偏转76.86°.1307号台风(图 4e)于2013年7月12日2100UTC左右登陆台湾, 在7月13日0000 UTC明显向右偏转89.39°, 随后持续前进在福建登陆.1513号台风(图 4f)于2015年8月7日2000 UTC左右登陆台湾, 在8月8日0000 UTC向右偏转36.18°, 随后持续前进在福建登陆.

图 4 (a) 0708, (b) 0815, (c) 0908, (d) 1011, (e) 1307, (f) 1513号台风路径 红点表示台风偏转的时间和地点. Fig. 4 Tracks of typhoons (a) 0708, (b) 0815, (c) 0908, (d) 1011, (e) 1307 and (f) 1513 The red dots indicate the time and position of typhoon track deflection.
2.2 台风环境场分析

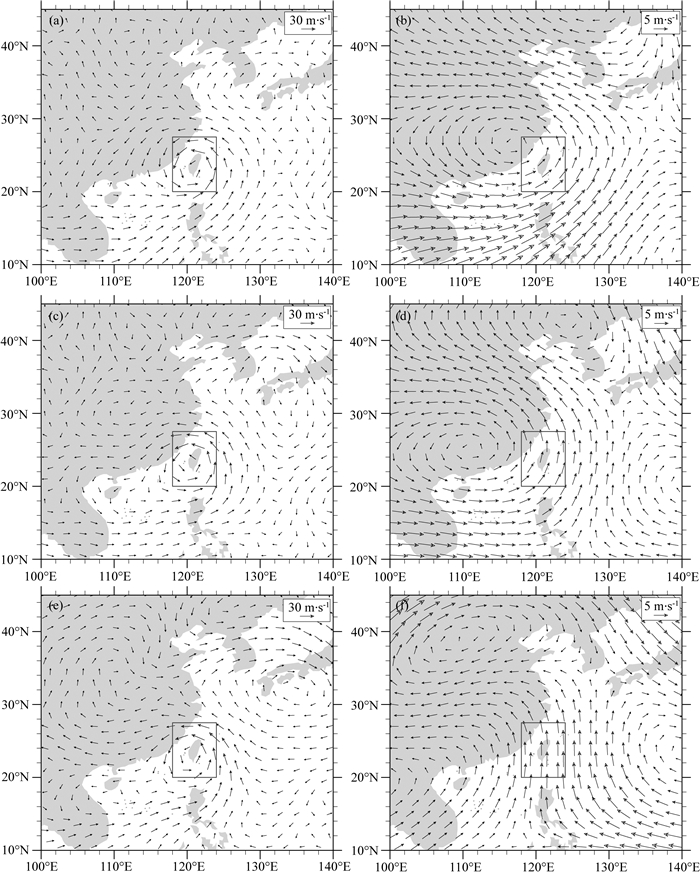
为了得到台风的环境风场, 利用二维傅里叶变换对ECMWF的ERA-Interim再分析水平风场进行滤波, 滤掉波长小于3000 km的波动(即台风流场和更小尺度的风场).以0708号台风为例, 图 5给出了8月18日0000 UTC(即台风路径偏转时刻)滤波前和滤波后的900 hPa、700 hPa和500 hPa的水平风场.滤波前低层、中层和高层的水平风场在台湾地区都呈现气旋式环流, 环流中心位于台湾岛, 即台风环流.滤波以后, 低层受西南低空气流的影响, 在台湾地区表现为西南风(图 5b), 而中高层为南风(图 5d和图 5f).以上分析表明, 本文采用的二维傅里叶变换滤波能够把台风以及更小尺度的流场滤掉, 从而得到台风的环境流场.类似地, 对其他台风的水平风场进行滤波处理, 能够得到各自的环境风场(图略).

图 5 0708号台风8月18日0000 UTC滤波前(左)和滤波后(右)的水平风场 a) (b) 900 hPa, (c) (d) 700 hPa, (e) (f) 500 hPa. Fig. 5 Horizontal winds of Typhoon 0708 at 0000 UTC 18 August before (left) and after (right) filtering

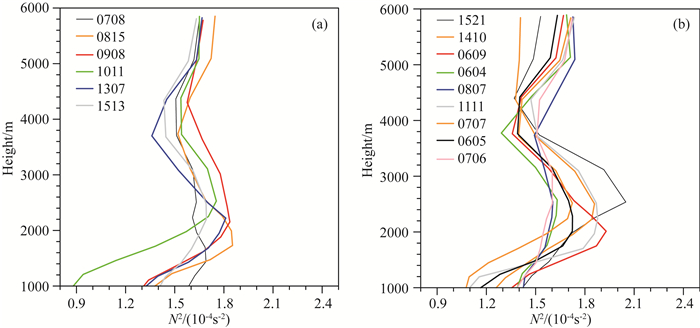
地形重力波总是在稳定层结大气中产生和传播.为了研究台风的环境大气层结, 首先对不同高度的温度场进行二维傅里叶变换滤波, 然后对台湾地区滤波后的温度场进行区域平均, 得到水平均匀的温度廓线(图略), 并进一步计算大气层结.图 6给出了台风路径发生偏转时刻(见表 1)台湾地区(图 5中方框区域)环境大气层结的垂直分布.由图可以看出, 边界层(2 km以下)的大气层结相对较弱，而边界层以上的大气层结较强.总体而言, 台风的环境大气皆为稳定层结(N2>0), 有利于地形重力波的传播.

图 6 路径偏转(a)显著和(b)不显著的台风环境大气层结廓线 Fig. 6 Profiles of environment atmospheric stratification for the land-falling typhoons (a) with and (b) without notable track deflection

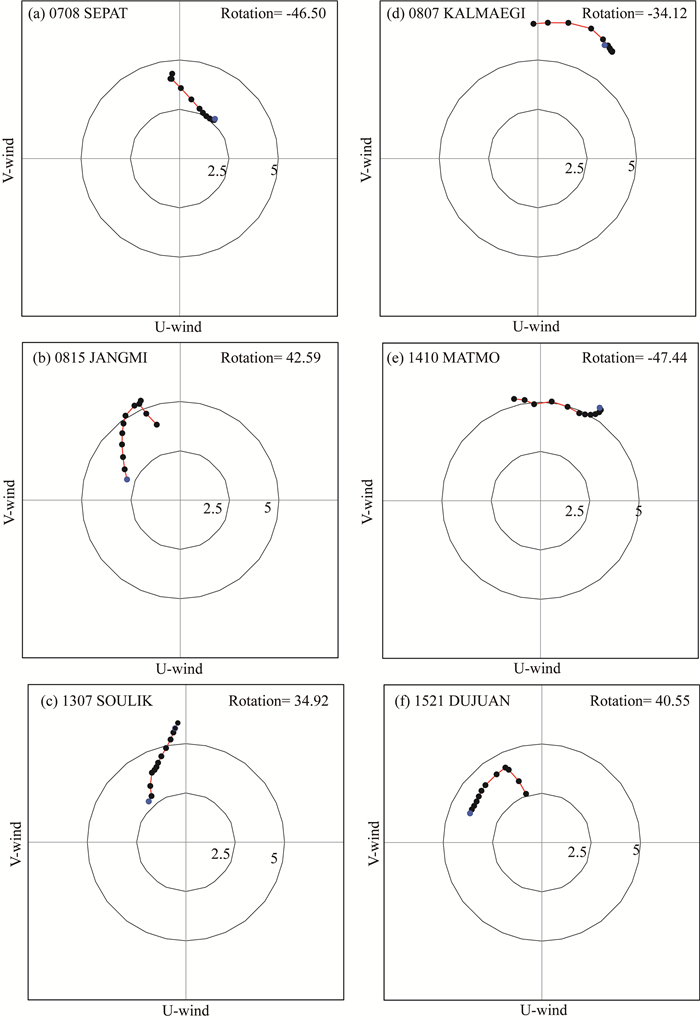
地形重力波举力与平均气流的方向性切变密切相关.因此进一步对台湾地区的环境风场进行区域平均, 可得到平均气流的矢端曲线图, 如图 7所示.首先对路径发生显著偏转的台风个例进行分析(图 7a—7c).对于0708号台风, 8月18日0000 UTC(即台风路径偏转时刻)的平均气流随高度逆时针旋转(图 7a).根据Xu等(2012)的研究, 对于随高度逆时针旋转的平均气流, 地形重力波举力指向气流的左侧, 因此有利于引导台风路径左偏.对照台风路径图, 该台风在8月18日0000 UTC的确向左发生偏转(图 4a), 两者相吻合.对于0815和1307号台风, 平均气流都随高度顺时针旋转(图 7b和图 7c).在这种情况下, 地形重力波举力指向平均气流的右侧.由图 4b和图 4e可知, 这两个台风的路径也向右偏转, 与举力的方向一致.对其他三个路径偏转明显的台风个例进行分析, 各自路径的偏转方向也都定性地与地形重力波举力的方向相同.

图 7 台风路径偏转时刻的环境风场矢端曲线图 (a) 0708; (b) 0815; (c) 1307; (d) 0807; (e) 1410; (f) 1521号台风.图中蓝色起点为900 hPa, 末端点为500 hPa, 风场等值线间隔2.5 m·s-1.风场随高度的旋转角度见图的右上, 其中正(负)的角度表示顺(逆)时针旋转. Fig. 7 Hodographs of environmental wind of typhoons (a) 0708, (b) 0815, (c) 1307, (d) 0807, (e) 1410, and (f) 1521 at their times of track deflection The hodograph starts from 900 hPa (blue point), ending at 500 hPa. The contour interval of wind speed is 2.5 m·s-1. The degree of wind turning with height is shown at the top right of each figure, with positive (negative) degrees for clockwise (anticlockwise) rotation.

类似地, 对路径偏转并不明显的台风个例也进行分析.图 7d—图 7f给出了0807、1410和1521号台风的平均气流的矢端曲线.对于0807和1521号台风, 平均气流分别随高度逆时针和顺时针旋转, 地形重力波举力指向气流的左侧和右侧.由表 1可知, 这两个台风的路径也都分别向左和向右偏转, 与举力的方向一致.然而对于1410号台风, 平均气流随高度逆时针旋转(图 7e), 举力指向气流的左侧; 但是该台风的路径向右偏转, 与地形重力波举力的方向相反.对于其他六个路径偏转并不明显的台风个例, 举力的方向与路径偏转方向也一致(图略).

3 举力分析

第2节研究了台风的环境场特征, 并定性分析地形重力波举力与台风路径偏转之间的关系.为了定量评估地形重力波举力对台风路径偏转的影响, 下面根据公式(5)对举力进行计算, 重点探讨0708等6个路径偏转明显的台风个例.由公式(5)可知, 举力与地形的谱分布密切相关, 因此首先对台湾地形进行二维傅里叶变换.(为了排除其他地形的影响, 将台湾地形以外的地形统一设置为0.)

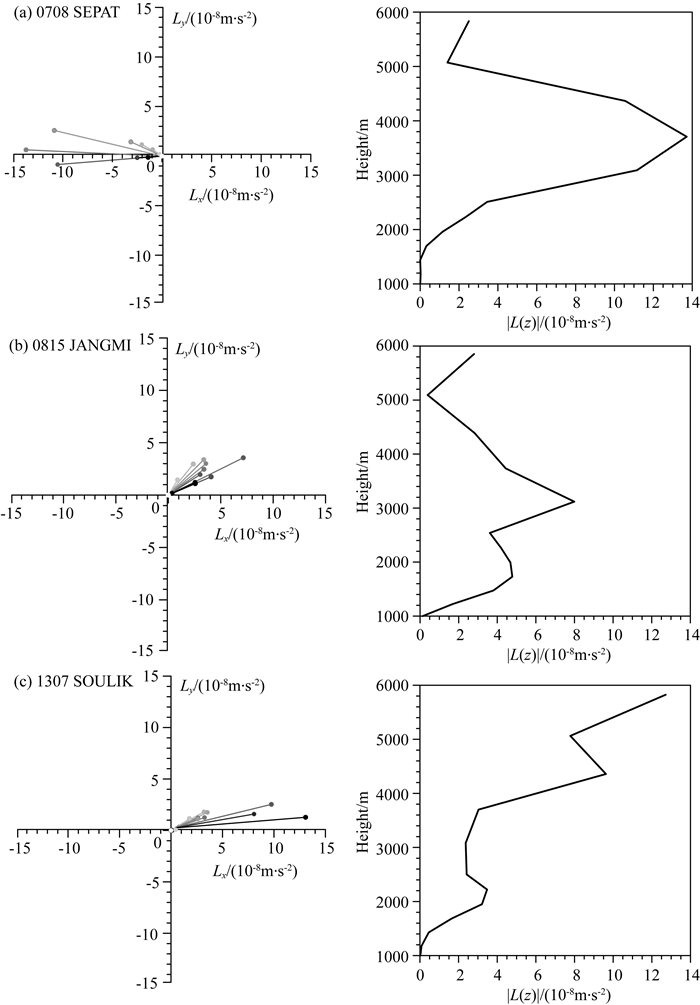
图 8给出了0708、0815以及1307等3个台风的路径偏转时刻, 地形重力波举力的垂直分布.对于0708号台风(图 8a), 地形重力波举力在低层主要指向西北方向, 随着高度的增加, 举力逐渐逆时针旋转至偏西方向.举力的大小随高度递增, 在3 km左右达到最大值, 之后随高度逐渐减小, 在5 km处再次变为零.根据计算公式(5), 平均气流方向随高度的变化, 即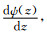对举力具有重要影响.由图 7a可以看出, 0708号台风的环境风场方向在对流层中层变化最大, 因此举力也最大.对于0815号台风(图 8b), 低层的地形重力波举力指向东北方向, 随着高度逐渐顺时针旋转至偏东方向.与0708号台风相比, 0815号台风的举力大小有所减弱，但是两者随高度的变化非常类似.对于1307号台风(图 8c), 举力的大小随高度呈增加趋势，在6 km处达到最大值; 举力方向的变化同0815号台风的举力相似, 由低层东北方向顺时针旋转至高层偏东方向.对于其他三个路径偏转明显的台风, 1513号台风的地形重力波举力类似于1307号台风，而1011和0908号台风的举力类似于0815号台风.本文不再一一赘述.

图 8 举力矢量(左)和大小(右)的垂直分布(a) 0708, (b) 0815, (c) 1307 左列图横轴表示x方向举力, 纵轴表示y方向举力.右列图横轴表示举力的大小.颜色从浅到深表示低层到高层. Fig. 8 Vertical distribution of lift force vectors (left) and amplitudes (right) for typhoons (a) 0708, (b) 0815 and (c) 1307 The horizontal (vertical) axis in the left column is the lift force in the x (y) direction, while the horizontal axis in the right column denotes the magnitude of lift force. Colors from light to dark denote low layer to high layer.

根据地形重力波举力, 可进一步计算由举力引起的台风路径偏转角度.由于举力与平均气流垂直, 因此在举力作用下气流将作圆周运动.根据向心加速度以及角速度公式

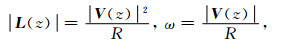
(6)

其中| L (z)|为举力大小, | V (z)|为速度大小, R为圆周运动的半径, ω为角速度.因此在Δt时间内, 由举力引起的气流偏转角度θ可表示为

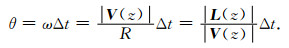
(7)

计算时Δt取6 h, 这与台风路径发生偏转的时间尺度相当(图 4).由于| L (z)|随高度变化, 这里取其最大值.需要指出的是, 对于本文所采用的0.75°低分辨率地形, 台湾平均海拔为300 m, 而实际台湾中央山脉的平均海拔约为2000 m.根据公式(5), 举力的大小与地形高度的平方成正比.因此实际举力应是计算得到举力的(2000/300)2 ≈45倍, 因此计算得到的偏转角度也需要同比扩大45倍.(地形高度的变化也会影响环境水平风速的大小及分布.降低地形高度有利于增强地形上方的水平风速, 从而导致举力增大.然而对于地形高度与水平风速之间的定量关系并不清楚, 因此本文没有考虑采用0.75°低分辨率地形对水平风速的影响.)台风路径的实际偏转角度δ可根据台风中心在各个时刻的位置计算得到.最后, 根据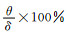即可得出地形重力波举力对台风路径偏转的贡献(表 2).

表 2 举力对台风路径偏转的贡献 Table 2 Contributions of lift force to the deflection of typhoon track

由表 2可知, 对于0708和0908号台风, 地形重力波举力对台风路径偏转的贡献较大.0708号台风路径实际偏转大约43°, 地形重力波举力导致的偏转角度约为4°, 举力的贡献约占10%.0908号台风实际偏转约32°, 举力引起的路径偏转为3°, 举力的贡献大约9%.对于其他四个台风, 地形重力波举力对台风路径偏转也有一定的贡献, 但是所占比例相对较小, 尤其是0815号台风, 地形重力波举力的贡献仅占约2%, 这与该台风较大的路径偏转角度有关.类似的还有1011和1307号台风.

本文同样对路径偏转不明显的台风个例的地形重力波举力进行分析.(由于再分析数据的时间分辨率为6 h, 因此部分台风个例缺少资料而无法计算.)由表 2可知, 地形重力波举力对0605, 0706和0707三个台风路径偏转的贡献约为4%到10%;对于其他个例, 地形重力波举力的贡献很大, 甚至超过100%.尽管如此, 考虑到这些台风路径的实际偏转角度较小, 因此对地形重力波举力的讨论并无太多实际意义.

4 总结与讨论

登陆台风受复杂下垫面地形的影响有时会发生路径偏转, 这给台风的路径预报带来挑战.台风的移动在很大程度上受到平均气流的引导.近年来Xu等(2012)研究发现, 在方向性切变气流中产生的地形重力波能够使平均气流改变方向, 即地形重力波的举力效应.针对2006—2015年登陆台湾的台风, 本文首次探讨了地形重力波举力对台风路径偏转的可能影响.

根据日本气象厅的台风数据集, 近十年共有20个台风登陆台湾, 主要集中在2006—2008年(共10个).在这20个台风中, 有5个台风的路径较为复杂, 产生打转等现象.剩余的15个台风, 有6个出现较为明显的路径偏转(偏转角度大于30°, 最大约100°).对这15个台风个例, 本文首先根据ECMWF的ERA-interim再分析数据研究了各自的环境大气层结以及环境风场的垂直变化, 然后对地形重力波举力进行定性分析和定量计算.

研究结果表明, 台风的环境大气一般处于稳定层结, 因此有利于地形重力波的传播, 有可能对台风路径产生影响.尽管对于不同的台风个例, 环境风场的垂直切变也各不相同, 但是几乎所有台风的路径偏转方向都与地形重力波举力的方向保持一致.即, 对于随高度逆时针旋转的环境风场, 举力指向平均气流的左侧, 台风也左偏; 当环境风场随高度顺时针旋转时, 举力指向平均气流的右侧, 台风路径右偏.针对路径偏转较为明显的6个台风, 定量计算了地形重力波举力, 以及举力所导致的台风路径偏转角度.通过与台风路径的实际偏转角度进行比较, 发现地形重力波举力的贡献最大可达10%, 部分解释了登陆台风的路径偏转现象.

本文研究只选取了近十年登陆台湾的台风, 研究的样本数不是很多, 还需要对更多的台风个例进行分析, 验证本文的结论.此外, 地形重力波举力的大小和方向通常随高度变化.根据公式(5), 对于给定的地形, 举力大小主要受大气密度、大气层结、以及水平风向垂直切变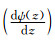的影响.一般而言, 大气密度随高度减小, 平流层比对流层大气层结更稳定, 而水平风向的垂直切变则需具体分析.本文研究仅考虑举力的最大值, 有可能造成对举力效应的高估.例如, 对于0708台风个例, 举力最大值出现在3.8 km高度.若选取2 km或5 km高度的举力, 则地形重力波对台风路径偏转的贡献降低至1%~1.35%左右.地形重力波举力对台风路径的影响, 主要通过影响台风的引导气流来实现.因此对于深厚的台风系统, 需要考虑环境引导气流的高度, 针对该高度的地形重力波举力进行分析.尽管如此, 当台风系统在不同高度受到不同(大小和方向)举力作用时, 其结构特征是否会发生改变?这种结构变化是否会进一步影响台风的路径?对于上述种种问题, 目前都不得而知.在今后研究中将选取合适的登陆台风个例, 借助数值模拟等手段对其进行更为详细的研究.

值得注意的是, 尽管本文计算得到的地形重力波举力与台风路径偏转具有较好的对应关系, 但是举力对台风路径偏转的贡献毕竟是小量, 有可能在弱环境引导气流中作用才会明显.因此台风路径偏转与举力之间的因果关系还有待商榷.

致谢  感谢日本气象厅提供的台风数据集以及欧洲中间尺度天气预报中心提供的再分析数据.作者对匿名审稿人提出的宝贵意见表示衷心感谢.
References
Article S, Kim Y J, Eckermann S D, et al. 2003. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmosphere-Ocean, 41(1): 65-98. DOI:10.3137/ao.410105
Bretherton F P. 1969. Momentum transport by gravity waves. Quarterly Journal of the Royal Meteorological Society, 95(404): 213-243. DOI:10.1002/qj.49709540402
Broad A S. 1995. Linear theory of momentum fluxes in 3-D flows with turning of the mean wind with height. Quarterly Journal of the Royal Meteorological Society, 121(528): 1891-1902. DOI:10.1002/(ISSN)1477-870X
Chan J C L, Gary W M. 1982. Tropical cyclone movement and surrounding flow relationships. Monthly Weather Review, 110(10): 1354-1373. DOI:10.1175/1520-0493(1982)110<1354:TCMASF>2.0.CO;2
Chan J C L. 2005. The physics of tropical cyclone motion. Annual Review of Fluid Mechanics, 37(1): 99-128. DOI:10.1146/annurev.fluid.37.061903.175702
Dee D P, Uppala S M, Simmons A J, et al. 2011. The ERA-Interim reanalysis:Configuration and performance of the data assimilation system. Quarterly Journal of the Royal Meteorological Society, 137(656): 553-597. DOI:10.1002/qj.828
Duan J J, Wu L G, Ni Z P. 2014. Analysis of unusual changes in Typhoon Aere (2004) and Meari (2004). Acta Meteorologica Sinica (in Chinese), 72(1): 1-11.
Gary B L. 1989. Observational results using the microwave temperature profiler during the Airborne Antarctic ozone experiment. Journal of Geophysical Research, 94(D9): 11223-11231. DOI:10.1029/JD094iD09p11223
Huang Y H, Wu C C, Wang Y Q. 2011. The influence of island topography on typhoon track deflection. Monthly Weather Review, 139(6): 1708-1727. DOI:10.1175/2011MWR3560.1
Jian G J, Wu C C. 2008. A numerical study of the track deflection of supertyphoon Haitang (2005) Prior to Its Landfall in Taiwan. Monthly Weather Review, 136(2): 598-615. DOI:10.1175/2007MWR2134.1
Klemp J B, Lilly D R. 1975. The dynamics of wave-induced downslope winds. Journal of the Atmospheric Sciences, 32: 320-339. DOI:10.1175/1520-0469(1975)032<0320:TDOWID>2.0.CO;2
Lin Y L, Witcraft N C, Kuo Y H. 2006. Dynamics of track deflection associated with the passage of tropical cyclones over a mesoscale mountain. Monthly Weather Review, 134(12): 3509-3538. DOI:10.1175/MWR3263.1
Lindzen R S. 1981. Turbulence and stress owing to gravity wave and tidal breakdown. Journal of Geophysical Research, 86(C10): 9707-9714. DOI:10.1029/JC086iC10p09707
Liu A M, Lin Y, Huang M J, et al. 2008. Analysis on the difficulties of typhoon Wipha (0713) path forecast. Meteorological Monthly (in Chinese), 34(10): 27-33.
Lott F. 1999. Alleviation of stationary biases in a GCM through a mountain drag parameterization scheme and a simple representation of mountain lift forces. Monthly Weather Review, 127: 788-801. DOI:10.1175/1520-0493(1999)127<0788:AOSBIA>2.0.CO;2
Luo Z X, Chen L S. 1995. Effect of the orography of Taiwan Island on typhoon tracks. Scientia Atmospherica Sinica (in Chinese), 19(6): 701-706. DOI:10.3878/j.issn.1006-9895.1995.06.06
Martin A, Lott F. 2007. Synoptic responses to mountain gravity waves encountering directional critical levels. Journal of the Atmospheric Sciences, 64(3): 828-848. DOI:10.1175/JAS3873.1
McLandress C, Shepherd T G, Polavaparu S, et al. 2012. Is missing orographic gravity wave drag near 60°S the cause of the stratospheric zonal wind biases in chemistry-climate models?. Journal of the Atmospheric Sciences, 69(3): 802-818. DOI:10.1175/JAS-D-11-0159.1
Nastrom G D, Fritts D C. 1992. Sources of mesoscale variability of gravity waves.Part Ⅰ:Topographic excitation. Journal of the Atmospheric Sciences, 49: 101-110. DOI:10.1175/1520-0469(1992)049<0101:SOMVOG>2.0.CO;2
Rui J X, He M M. 2013. The study of the spatio-temporal characteristics of turning typhoons in the western north Pacific. Journal of Shanghai Normal University:Natural Sciences (in Chinese), 42(3): 320-326.
Song J J, Wang Y, Wu L G. 2010. Trend discrepancies among three best track data sets of Western North Pacific tropical cyclones. Journal of Geophysical Research:Atmospheres, 115(D12): D12128. DOI:10.1029/2009JD013058
Tang C K, Chan J C L. 2016. Idealized simulations of the effect of Taiwan topography on the tracks of tropical cyclones with different sizes. Quarterly Journal of the Royal Meteorological Society, 142(695): 793-804. DOI:10.1002/qj.2681
Tian H, Li C Y, Yang H. 2010. Modulation of typhoon tracks over the Western North Pacific by the intraseasonal oscillation. Chinese Journal of Atmospheric Sciences (in Chinese), 34(3): 559-579.
Wang B, Elsberry R L, Wang Y Q, et al. 1998. Dynamics in tropical cyclone motion:A review. Scientia Atmospherica Sinica (in Chinese), 22(4): 535-547.
Xu X, Wang Y, Xue M. 2012. Momentum flux and flux divergence of gravity waves in directional shear flows over three-dimensional mountains. Journal of the Atmospheric Sciences, 69(12): 3733-3744. DOI:10.1175/JAS-D-12-044.1
Xu X, Xue M, Wang Y. 2013. Gravity wave momentum flux in directional shear flows over three-dimensional mountains:Linear and nonlinear numerical solutions as compared to linear analytical solutions. Journal of Geophysical Research:Atmospheres, 118(14): 7670-7681. DOI:10.1002/jgrd.50471
Xu X, Wang Y, Xue M, et al. 2017. Impacts of horizontal propagation of orographic gravity waves on the wave drag in the stratosphere and lower mesosphere. Journal of Geophysical Research:Atmospheres, 122(21): 11301-11312. DOI:10.1002/2017jd027528
Ye D Z. 1956. Topographical effect on the airflow. Acta Meteorologica Sinica (in Chinese), 27(3): 243-262.
Yu Z S, Hao Z Z, Xie H H, et al. 2007. A numerical study of the effect of Taiwan Island terrain on typhoon Haitang (0505) track. Journal of Tropical Meteorology (in Chinese), 23(6): 575-580.
Zhu Z H, Huang L N, Wen X M. 2015. Diagnostic analysis of interaction between binary typhoons Tembin and Bolaven. Meteorological Science and Technology (in Chinese), 43(3): 506-511.
段晶晶, 吴立广, 倪钟萍. 2014. 2004年台风"艾利"与"米雷"路径异常变化分析. 气象学报, 72(1): 1-11.
刘爱鸣, 林毅, 黄美金, 等. 2008. 0713号台风韦帕路径预报难点分析. 气象, 34(10): 27-33. DOI:10.7519/j.issn.1000-0526.2008.10.004
罗哲贤, 陈联寿. 1995. 台湾岛地形对台风移动路径的作用. 大气科学, 19(6): 701-706. DOI:10.3878/j.issn.1006-9895.1995.06.06
芮建勋, 何梦梦. 2013. 西北太平洋打转台风的时空规律. 上海师范大学学报:自然科学版, 42(3): 320-326.
田华, 李崇银, 杨辉. 2010. 大气季节内振荡对西北太平洋台风路径的影响研究. 大气科学, 34(3): 559-579. DOI:10.3878/j.issn.1006-9895.2010.03.09
王斌, Elsberry R L, 王玉清, 等. 1998. 热带气旋运动的动力学研究进展. 大气科学, 22(4): 535-547. DOI:10.3878/j.issn.1006-9895.1998.04.15
叶笃正. 1956. 小地形对于气流的影响. 气象学报, 27(3): 243-262.
余贞寿, 郝增周, 谢海华, 等. 2007. 台湾岛地形对台风"海棠"(0505)移动路径影响的数值试验研究. 热带气象学报, 23(6): 575-580. DOI:10.3969/j.issn.1004-4965.2007.06.008
朱智慧, 黄宁立, 问晓梅. 2015. 双台风"天秤"和"布拉万"相互作用诊断分析. 气象科技, 43(3): 506-511. DOI:10.3969/j.issn.1671-6345.2015.03.028