0 引言

大地电磁测深是一种天然场源的地球物理勘探方法，具有野外施工方便、探测深度大、不受高阻层屏蔽等优点(Cagniard，1953; 汤井田等, 2015; 赵国泽等, 2007)，为研究深部流体分布、板块构造和大陆动力学等科学问题，提供了重要的地球物理依据(Wei et al., 2001; 金胜等, 2010; 赵国泽等, 2008).好的数据质量是大地电磁数据反演解释的前提(Schaa et al., 2016)，而MT天然电磁场信号幅值微弱、频带宽，极易受到噪声干扰(Junge, 1996).大量实验结果表明，如矿区资源开采产生很强的相关噪声，导致测点即使偏离干扰源十几公里也无法获得较好的数据，造成重要地质构造区域深部物质电性资料的缺失(汤井田等, 2012a, 2012b; 李晋等, 2014, 2017a, 2017b).

人文电磁噪声成分非常复杂，先验信息少，各地区也有差异，加之MT信号场源也比较复杂，两者耦合在一起，很难用一种方法精确分离(Egbert, 1997; 王辉等，2014; 李晋等, 2017a, 2017b；汤井田等, 2017).大地电磁数据去噪方法的研究始于20世纪80年代，一直伴随着MT的发展，目前已经提出了很多方法，可以简单分为三类：①频率域中的方法，如最小二乘法、Robust估计、远参考；②时频域的处理方法，如小波变换和希尔伯特-黄变换(Hilbert-Huang transform，HHT)；③时域中对时间序列进行预处理：如形态滤波、信噪辨识、递归分析和聚类以及压缩感知重构算法，IARWR，基于同步时间序列依赖关系的大地电磁去噪方法以及STIN.

最小二乘法可以压制高斯随机噪声(Sims et al., 1971)，但少数“飞点”也会导致估算值偏离真值.Robust估计的本质是加权估计(Egbert and Booker, 1986; Larsen, 1989)，根据残差大小赋予数据不同的权重，从而压制“飞点”的影响.该方法要求大部分数据可靠，而且当输入端含噪声时，Robust估计反而会加重噪声的影响(Egbert, 1997; 柳建新等, 2003).远参考方法利用参考点信号与本地点信号相关的特点，压制不相关噪声(Gamble et al., 1979)，远参考的处理效果依赖于参考点与本地点信号和噪声的相关性，实际中很难选择合适的参考距离，以保证测点之间信号相关的同时尽可能地远离噪声(Shalivahan and Bhattacharya, 2002; Goubau et al., 1984).

实测MT信号往往是非平稳的(王书明和王家映, 2004)，很多学者试图用时频分析和处理非平稳信号的方法来代替傅里叶变换，以提高对噪声的分析能力，主要有小波变换和希尔伯特-黄变换.徐义贤和王家映(2000)提出了基于小波分析的大地电磁信号谱估计方法，可以有效抑制随机噪声和局部相关噪声.小波变换的处理效果还依赖于母波的选取和阈值的设定(Trad and Travassos, 2000)，对于噪声成分复杂而信号频谱丰富的MT实测数据而言，母波的选取规则至今没有得到很好的解决(Escalas et al., 2013; Tary et al., 2014).希尔伯特-黄变换是一种分析非线性非平稳信号的方法(Huang et al., 1998)，汤井田等利用HHT压制MT噪声，先对数据进行经验模态分解，判别各经验模态分量中的噪声，再对各分量进行阈值滤波，最后将滤波后的各分量数据相加，重构信号(汤井田等, 2008; Cai et al., 2009; Cai, 2014).HHT的缺点在于进行经验模态分解时，窗口首尾两端会引入误差，且运算速度较慢(Chen et al., 2012a; Neukirch and Garcia, 2014).

由于傅里叶变换是全时域到全频域的，导致时域突变噪声扩散至频域多个频带甚至全频带，对于这种噪声，可在时域中直接处理.汤井田等(2012a)将形态滤波应用到MT信噪分离中，表明该方法可以精细刻画数据的主体轮廓，滤除大尺度噪声.李晋等在形态滤波的基础上做二次信噪分离，保留低频信号(2014)，但目前对结构元素的参数选择还没有形成完善的理论体系，这是形态滤波的灵活性也是其难度所在，汤井田等近两年又提出利用信噪辨识、递归分析和聚类以及压缩感知重构算法，以对复杂大地电磁干扰进行分离并取得了较好的应用效果(李晋等, 2017a, b；汤井田等, 2017).Di et al.(2018)也提出了伪随机编码发射，时间序列实时相干解码接收，在去噪技术上有重要突破，实际深部找矿应用中效果显著.

在时域中处理MT噪声必须十分谨慎，确保微弱的信号不被滤除，否则即使得到了光滑的测深曲线，其正确性也无法保证，可能导致错误的地质解释.为了提高时间域去噪的精度，更多挖掘合成天然电磁场信号之间的内在关系，近年来学者们利用同步观测的天然电磁场在一定区域内具有相关性的特点，利用参考点数据合成本地点信号，用于替换本地点的噪声段数据，达到去噪的目的.Kappler(2012)方法通过对同步大地电磁数据进行维纳滤波，利用同步观测的参考点磁场数据，在时间域合成本地点信号，再利用方差比识别噪声，用合成信号替换噪声，达到去除突变噪声的目的，该方法可以提高低频数据质量，但对滤波后数据精确度缺乏有效验证，还会引入阶跃噪声.王辉等(2014)提出基于同步大地电磁时间序列依赖关系的去噪方法，该方法可以有效去除强噪声干扰，结合远参考方法可以抑制中高频段的近场源效应，同时保留了微弱的有效信号.Wang等(2017)提出STIN方法(Synthesis of natural electric and magnetic Time-series using Inter-station transfer functions and time-series from a Neighboring site，简称STIN)，通过对站间传递函数进行傅里叶反变换，从而得到本地点合成数据，可以实现从时间域处理噪声，但合成数据的精度依赖于站间传递函数的数据质量，对于强干扰噪声，仍难以获得较高质量的站间传递函数，其应用范围受到一定限制.以上方法的不同之处在于构建同步天然电磁之间内在关系的模型不同，其合成信号的精度也存在一定差异.

本文提出利用两个同步测点天然电磁场时间序列之间的单位脉冲响应，合成本地点电磁场数据(Synthesis natural electric and magnetic Time series of local site using an Impulse Response and a reference)，方法简称STIR，用合成数据替换本地点含噪声时段的数据，从时间域去除大地电磁噪声.

1 基本原理

大地电磁测深方法假设电磁波以均匀平面波的形式入射地表，通过在地表上观测水平电磁场，就可以获得代表地下物质电性结构的阻抗.设本地测点L和参考测点R的时间域电场和磁场分别为e_l、h_l与e_r、h_r，在频率域中分别为E_l、H_l与E_r、H_r.通常大地电磁测深方法中的阻抗是指同一测点电场与磁场之间的传递函数，对本地点来说，Z_l阻抗满足(Cagniard, 1953)：

(1)

其中，E_l=FFT(e_l)，H_l=FFT(h_l)，式中电场E和磁场H分别包括两个互相正交的分量[E_x, E_y]和[H_x, H_y]，因此Z是2×2的复数张量，Z=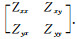

当存在两个或多个同步测点时，其中任意一个测点的电场或磁场与另一个测点磁场之间的传递函数，称之为站间传递函数(Egbert, 1997).包括拟阻抗和水平磁场传递函数，分别为：

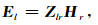
(2a)

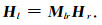
(2b)

Z_lr为本地点电场E_l与参考点磁场H_r之间的传递函数，由于H_l与H_r具有较高的相关性，当参考点与本地点距离不远时，Z_lr近似于Z_l，也称拟阻抗.M_lr为本地点磁场H_l与参考点磁场H_r之间的传递函数，称为水平磁场传递函数.

根据卷积定理，可以将公式(2a)和(2b)改写为时间域的卷积形式：

(3a)

(3b)

对于离散数据，上式可以改写为

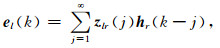
(4a)

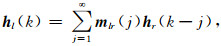
(4b)

其中z和m分别表示拟阻抗和水平磁场传递函数在时间域的离散脉冲响应(Discrete Time domain Impulse Responses, DTIR).实际情况下，考虑噪声的影响，(4)式的无穷求和可以统一写为有限长度单位脉冲响应(Finite Impulse Response，FIR)的求和形式(Ljung, 1985)：

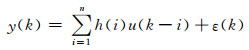
(5a)

式(5a)可以改写为矩阵形式：

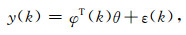
(5b)

其中：

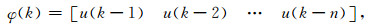
(5c)

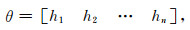
(5d)

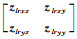
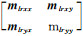
y为模型输出信号，本文中具体为本地点合成的电场[e_lx, e_ly]与磁场[h_lx, h_ly], u为模型输入信号，本文中为参考点磁场[h_rx, h_ry]，n表示单位脉冲响应函数的阶数，ε为噪声.h表示模型单位脉冲响应函数，本文中为拟阻抗z_lr和水平磁场传递函数m_lr的时间域单位脉冲响应，z_lr和m_lr也是一个2×2阶的矩阵，分别为和，若已知h，结合参考点磁场数据，可以利用式(4a)和(4b)得到本地点的电场与磁场时间序列.

h可以通过最小二乘法估算得到(Ljung, 1985)，具体如下：

目标函数设为

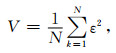
(6)

其中，

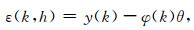
(7)

最小二乘法以均分误差最小，即要求：

(8)

上式的解为(Ljung, 1985):

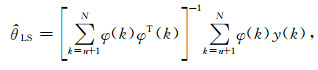
(9)

即为估算的单位脉冲响应，当噪声与信号无关，且满足高斯分布时，通过增大脉冲响应的阶数，可以获得真实的单位脉冲响应，实际数据含有噪声，通过设定阈值，当均方误差小于阈值时，即认为估算的单位脉冲响应精度满足要求(Chen et al., 2012b).

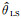
Egbert等(1992)指出大地电磁场离散时间序列之间的单位脉冲响应函数是非因果的，反映在估算的单位脉冲响应函数h中，具有小于零时刻的值.因此，式(5c)和(5d)可以写为：

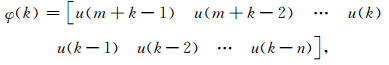
(10a)

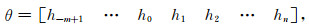
(10b)

其中n>0，m为该单位脉冲响应中非因果部分的阶数(m>0).

一般情况下，地下物质的电性结构不随时间变化，因此测点之间的站间传递函数也不随时间变化，所以可以利用某一时段站间传递函数的单位脉冲响应函数，结合参考点磁场数据，根据(4)式合成本地点任意时段的电场和磁场时间序列(参考点磁场所采集的时段内).

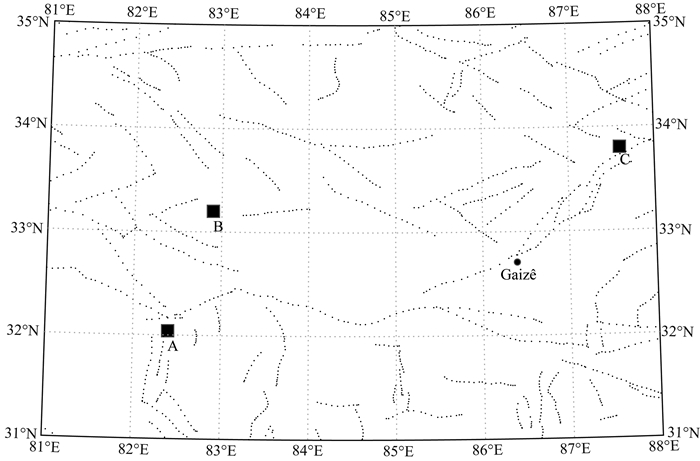
2 实测高信噪比数据的试算

为了验证本文STIR方法的可行性，选用一组高信噪比的实测大地电磁数据进行模拟试算，将合成数据与原始数据进行对比，讨论合成数据的精度，以及参考点对合成数据的影响.为此，选择西藏地区的A、B和C三个MT测点，如图 1所示，采用加拿大凤凰地球物理公司的V5系列大地电磁仪器进行采集，测点同步采集时间为11 h，测点附近没有人文噪声干扰，数据质量较好.首先以测点A为本地点，B为参考点，利用STIR方法，合成本地点A的电磁场信号.具体步骤如下：

第一步，选择模型先验数据，估算单位脉冲响应函数h.从测点A和B同步之后的时间序列中，随机选择一段2 min的离散数据(采样率15 Hz，共1800个采样点)，前1 min数据用于(9)式估算单位脉冲响应函数，后1 min数据作为验证数据，利用(4)式计算实测数据与合成数据的差值，评价所估算单位脉冲响应函数的有效性，利用拟合系数(Fit percent parameter, FITP)评价所估算单位脉冲响应函数的有效性，拟合系数的定义如下(Chen et al., 2012b)：

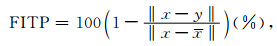
(11)

其中x为实测数据(测点A的原始数据)，y为合成数据(利用单位脉冲响应和参考点B，合成的测点A数据).‖‖表示L₂的范数，拟合系数表示合成数据与实际数据的吻合度，其范围为负无穷至100%，如果两者完全一致，拟合系数为100%，拟合系数越小，表示合成数据与实测数据差别越大，意味着估算的单位脉冲响应误差较大.

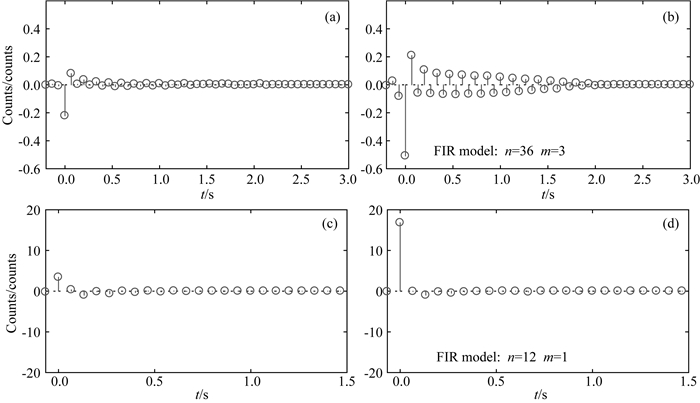
图 2是拟合系数随单位脉冲响应函数阶数n及非因果部分阶数m的变化，图中只给出了e_x与h_y的结果，e_y与h_x的结果类似，文中未给出.从图中可以看出，当模型阶数增大到一定数值时，拟合系数不再增大，对e_x来说，最佳的模型阶数与非因果部分阶数分别为n=36、m=3，此时拟合系数为85.9%，对h_y来说，最佳的模型阶数与非因果部分阶数分别为n=12、m=1，此时拟合系数为81.4%.此时对应的最佳单位脉冲响应函数如图 3所示，对Z_lr而言，XY模式的单位脉冲响应系数要大于XX模式，这表示本地点的e_x主要由参考点h_y有关，对M_lr而言，YY响应远大于YX的响应，表明本地点的h_y几乎只与参考点h_y有关，与h_x无关.

第二步，合成本地点电场与磁场数据.由上一步估算的单位脉冲响应函数h和参考点磁场数据[h_rx, h_ry]，利用式(4a)和(4b)分别合成本地点电场和磁场数据.为了定量评价合成数据的精度，采用拟合系数、相关系数(Correlated coefficient, CORC)和信噪比(Signal to noise ratio, SNR)三个参数进行比较(Wang et al., 2017)，相关系数和信噪比的定义如下：

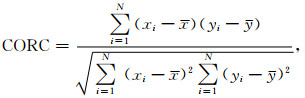
(12)

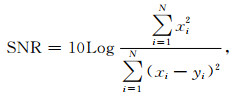
(13)

其中x表示实测数据，y表示合成数据，N表示数据长度.

相关系数表示合成数据与实测数据的相似程度，而不考虑幅值的变化，信噪比表示实测数据与残差(实测数据与合成数据之间的差值)功率的比值.理想情况下，希望合成数据与实测数据完全一致，即拟合系数接近100%，相关系数接近1，而信噪比越大越好.信噪比等于0表示实际数据与残差具有相当的功率，等于10 dB表示实际数据功率是残差功率的10倍，信噪比等于20 dB表示实际数据功率是残差功率的100倍.

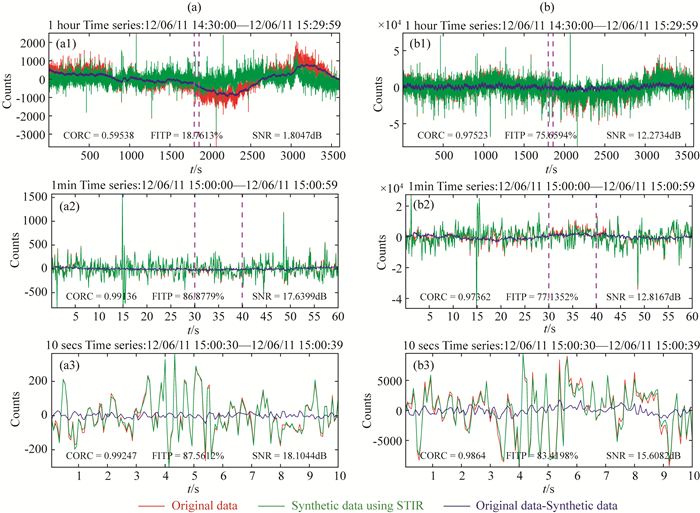
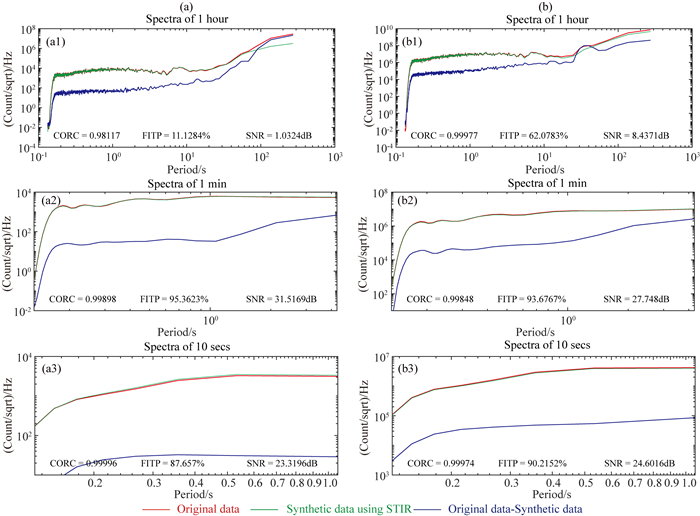
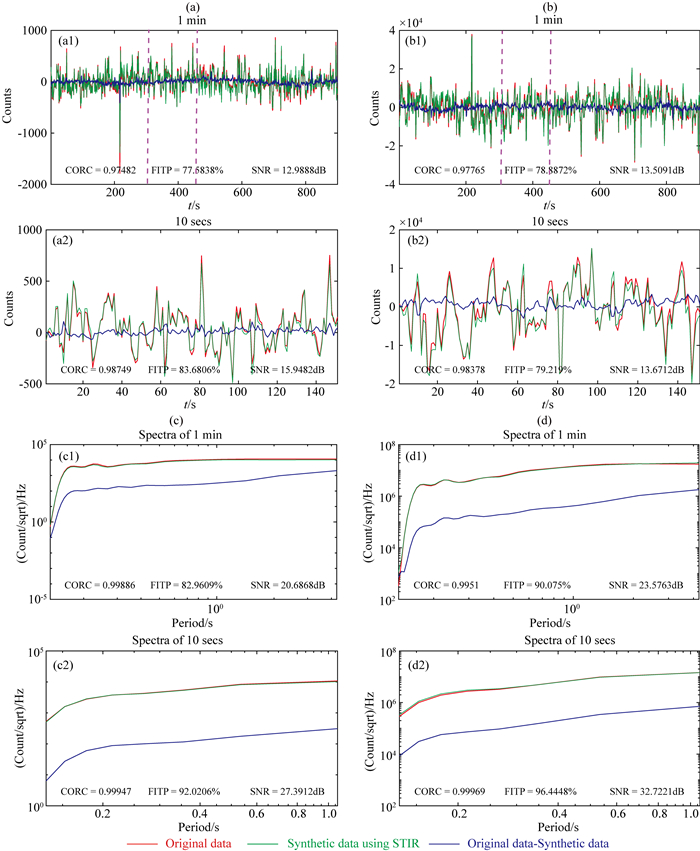
图 4为任意一段合成数据与实测数据的对比，其中图 4a1和4b1为1 h数据，图 4a2和4b2为将图 4a1和4b1虚线标出区域放大后的1 min数据，图 4a3和4b3为将图 4a2和4b2虚线标出区域放大后的10s数据.图 5为图 4对应的频谱图，从图 4与图 5中可以发现.对磁场而言，无论是高频还是低频，合成数据精度都较高，在时间域合成数据与原始数据的相关系数大于0.97，拟合系数大于75%，信噪比大于12 dB，在频率域，两者的相关系数大于0.99，拟合系数大于62%，信噪比大于8 dB.对电场而言，高频部分电场合成数据与原始数据精度较高，在时间域两者的相关系数大于0.99，拟合系数大于86%，信噪比大于17 dB(图 4a2和图 4a3)，在频率域两者相关系数大于0.99，拟合系数大于95%，信噪比大于23 dB(图 5a2和图 5a3)，但低频部分合成数据噪声较大(图 4a1和图 5a1)，这是因为天然磁场信号具有区域性，不同测点磁场低频信号的相似性仍较高，而电场与磁场之间的相关性随着频率的降低而降低(Egbert et al., 1992)，加之电场信号容易受到噪声干扰和电极极差漂移等非感应信号的影响，因此，电场难以获得高精度的低频合成信号.

为了测试不同参考点对合成数据的影响，选择距离测点A较远的测点C作为参考点，按照上述步骤，合成本地点A数据，合成数据与实测数据的对比如图 6所示，其结果与图 4与图 5类似，无论从时间域还是从频率域对比，对于高频部分数据，电场与磁场的合成数据精度都较高，说明在一定区域范围内，合成数据的精度与参考点的选取位置关系不大.

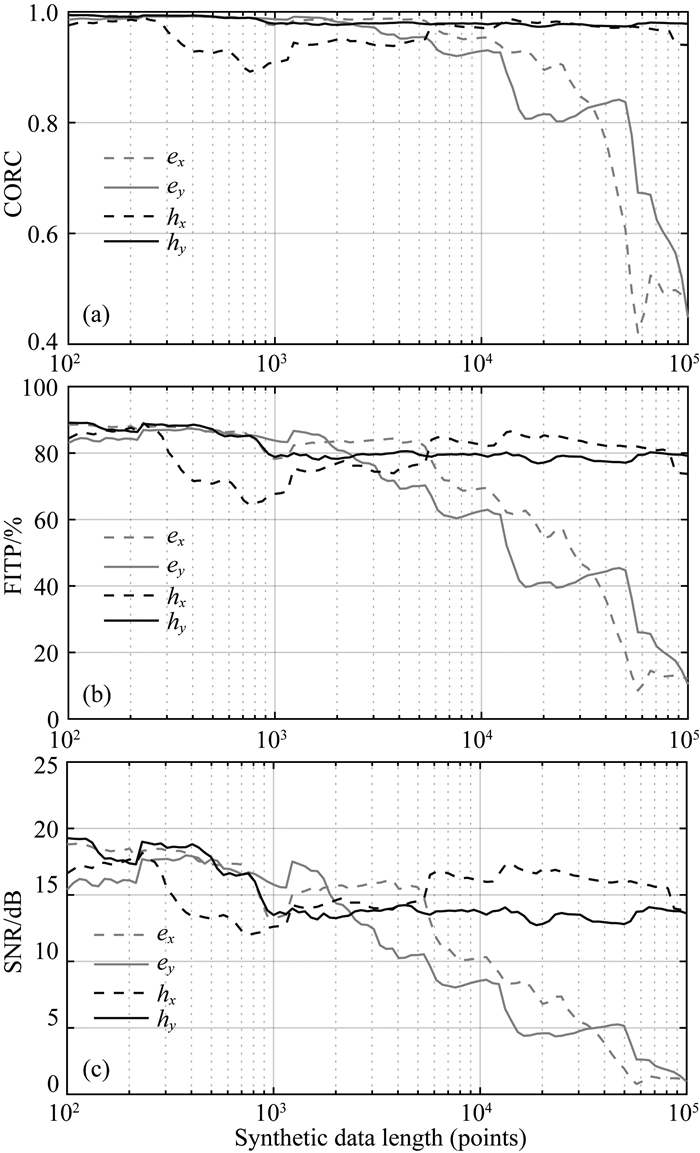
能否选择一小段高信噪比模型先验数据，获得长段高精度合成数据呢？为此，测试合成数据精度与合成数据长度的关系，模型先验数据长度固定为1800个采样点，图 7为合成数据长度与合成数据精度变化的关系，总体上电场合成数据的精度随着合成数据长度的增大而降低，磁场变化不大.从图 7可知，为了同时获得高信噪比的电场与磁场合成数据，对于本文所选择的测试数据而言，合成数据的长度不宜大于5000个采样点，此时可以同时保证合成数据的相关系数大于0.9，拟合系数大于70%，信噪比大于10 dB.

3 实测含噪数据的处理

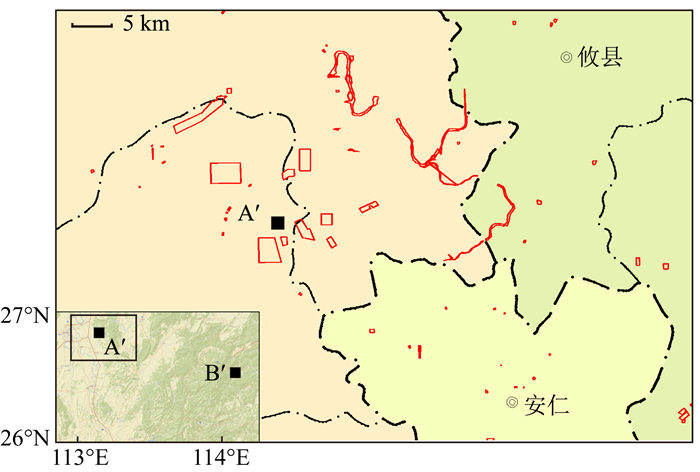
为了验证本文方法对实测数据的处理效果，选择一个受噪声干扰较为严重的A′号测点进行处理，如图 8所示，该测点位于湖南衡阳某钨矿附近，几乎被矿区包围，受矿区近场源电磁强噪声干扰(王辉等，2016)，参考点B′位于A′号测点西南方向130 km处，数据质量较好，两测点同步时长约为40.5 h.采用STIR方法对测点A′时间序列进行去噪处理：

首先利用方差比方法识别在时间域识别噪声，其基本原理是基于相同分量同步观测的电磁场在不同地区具有相关性的特点，来识别噪声，该方法可以在时间域快速有效判别噪声(Kappler, 2012; 王辉等, 2014; Wang et al., 2017)，阈值通过人为设置，大于阈值的部分被标识为噪声，其结果如图 9所示，可以发现，测点A′的电场的大部分时段受到了严重的相关噪声影响，而磁场受噪声干扰相对较小.

对于实测含人文噪声的数据而言，噪声不满足高斯分布，因此, 模型先验数据的选择至关重要，对于本例而言，首先通过图 9判断受噪声干扰较小的时段，如从不含明显人文噪声的6000~7000个窗口(窗口长度为300个采样点)中，人为选择较为干净的2 min数据作为先验数据.利用最小二乘法估算站间单位脉冲响应函数，再结合参考点磁场数据合成本地点电场与磁场数据，最后将合成数据替换含本地点含噪声窗口的数据，获得本地点去噪后的新数据，数据替换时在窗口的两端对数据进行平滑以避免引入噪声(Wang et al., 2017).测点A′去噪后的数据与原始数据的对比如图 10所示，由于磁场受噪声影响较小，图中只给出了电场的结果，可以发现，去噪后的电场时间序列消除了较为明显的人文噪声，如图 10中矩形框标出部分与图 9大于阈值部分对应.图 10a2、图 10b2分别为图 10a1、图 10b1虚线标出T₁时段1 h的时间序列，图 10a3、图 10b3分别为图 10a2、图 10b2虚线标出T₂时段1 min的时间序列，从中可以发现，去噪后的新数据去除了较为明显的人文强干扰噪声，如脉冲和方波等典型人文强噪声.

图 11是测点A′原始数据与去噪后数据的测深曲线及其误差的对比，数据采用开源的EMTF代码进行处理(Egbert and Booker, 1986)，以B′为参考点，采用远参考方法处理.对比原始数据与去噪后数据的测深曲线可以发现，原始数据视电阻率曲线与相位曲线在10 s附近存在明显的噪声干扰，同时低频数据质量也较差，导致估算误差在该频段增大，而去噪后数据对应的视电阻率曲线和相位曲线更为光滑，尤其是10 s附近和低频段数据，有了明显的改善，同时大幅降低了估算的误差，使得绝大部分频段的估算误差小于5%(图 11b中虚线所示).

4 讨论

如何提高干扰地区大地电磁数据的信噪比，已经成为制约大地电磁方法应用的一个重要因素.从时间域进行噪声去除，思路简单，难点在于如何保证合成数据或去噪后数据的精度.STIN方法和本文提出STIR的方法，其物理前提都是基于不同测点之前电磁场都满足平面波的假设条件，两者的区别在于前者利用天然电磁场在频率域线性关系(式(2))，对站间传递函数进行傅里叶逆变换，得到时间域电磁场信号，后者利用天然电磁场在时间域的卷积关系(式(3))，直接合成本地点时间域电磁场.STIN方法的合成数据精度依赖于全时段的站间传递函数和参考点数据质量，其优点在于合成数据在全频段都具有较高的质量(Wang et al., 2017)，而STIN只要求本地点数据在观测的某一时段内是不受人文噪声干扰的(STIR方法不适用于持续不断电磁干扰，如电网等)，而参考点在全时段受噪声干扰较小，至少应该保证本地点受噪声干扰时段内，参考点数据质量较好，才能保证用于替换噪声数据段的合成数据精度较高.

STIR方法合成数据的精度取决于站间单位脉冲响应函数的估算精度，以及参考道数据的信噪比.而单位脉冲响应的估算精度主要与选取的先验数据有关，因此，先验数据的选取及参考道的信噪比对合成数据的精度至关重要.实际中可以通过人为选择一段较为干净(图 9中，方差比基本不变的时段)的数据，作为先验数据，便可以得到精度较高的合成数据.诚然，合成数据必然会引入噪声，但是相对于人文强干扰，其噪声水平小了很多，采用常规Robust估计和远参考方法，便可以去除，获得较为可靠的阻抗(Kappler, 2012).反之，如果不进行去噪，原始数据中保留了这类强噪声，且是相关噪声，通过Robust估计等常规方法难以去除，最终导致测深曲线存在“飞点”或“视电阻率曲线在双对数坐标下呈45°上升，相位趋于0°的近场源干扰现象”.当然，有时合成数据引入的噪声可能比原始数据的噪声更大，这时通过方差比进行判断噪声水平，如果合成数据的方差比，比原始数据方差比还大，说明合成数据精度不够，其噪声水平比原始数据中噪声水平还高，则不进行替换，保留原始数据，从而保证不“过度去噪”.

STIR方法的去噪效果不仅与合成数据的精度有关，还与噪声识别的精度有关，即与方差比的阈值选择有关，阈值的选择不仅与测点间电磁场时间域信号的幅值比有关，还与窗口的长度有关，实际中通过对比不受干扰时段的窗口(如图 9所示，方差比基本不变的时段)，通过人为设定阈值，容易判断噪声所在的窗口.除了采用方差比，还可以参用相干度、小波系数等参数在时间域判别大地电磁信号与人文噪声(Trad and Travassos, 2000).虽然STIR方法可以获得较高精度的本地点电磁场信号，为了确保不引入过多噪声，实际去噪过程中，只针对被识别为噪声部分的数据进行去噪.

从本文的试验结果来看，实际工作中，可以将参考点布设在远离噪声干扰的区域，即使参考距离大于500 km(图 1中测点A与测点C的距离大于500 km)也不会影响合成数据的精度.对于模型先验数据的选择，可以选择方差比方法判别为不受噪声干扰的时段，还可以人为手动选择，阈值的选择，不同的参考点有所不同，建议人为选择.模型先验数据的长度也不易太长，由于实测数据不可避免含有噪声，尤其是电场数据容易受到噪声的影响(人文噪声、自然电位和电极极差漂移等)，导致估算的单位脉冲响应误差较大.从本文的实验看来，对于15 Hz的采样数据，2 min(1800个采样点)的数据足够估算精度较高的单位脉冲响应.

STIR方法适用于对间断噪声进行时间域处理，可以较为明显的提高中高频带的数据质量，同时可以避免强脉冲、方波等高频噪声扩散至整个频带，改善低频数据质量.合成数据还可以直接用于替换缺失时段的数据(如电源断电)，将数据进行拼接.理论上，还可以利用参考点的电场数据合成本地点的电磁场，实际中由于电场资料容易受到干扰，合成数据的质量比不上以磁场为参考，本文中没有给出相关结果.

5 结论

本文基于站间天然电磁场单位脉冲响应函数，结合参考点磁场数据，合成本地点电磁场时间序列，用合成数据替换本地点受噪声时段的数据，实现从时间域去除大地电磁噪声.该方法的优点在于：①即使本地点存在相关噪声的情况下，选择一小段不受噪声干扰的时间序列，便可以合成任意时刻本地点电磁场时间序列信号，且合成信号的精度较高；②用合成数据替换本地点噪声数据，可以有效去除大地电磁噪声，提高阻抗数据质量，降低阻抗估算误差，以获得地下物质真实的电性结构信息.

致谢  本文中的实测大地电磁测深数据取自于国家科技专项“深部探测技术与实验研究”(SinoProbe)下属的“大陆电磁参数标准网实验研究”(SinoProbe-01，SinoProbe-01-02)和“大地电磁测深大剖面观测实验与壳/幔三维电性研究”(SinoProbe-02-04)，在此对项目组所有成员表示感谢.感谢两位审稿人对论文的认真评审和给出的修改意见.