2. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;
3. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
2. The Key Laboratory of Metallogenic Prediction of Nonferrous Metals of Ministry of Education, Central South University, Changsha 410083, China;
3. Key Laboratory of Non-Ferrous Resources and Geological Hazard Detection, Changsha 410083, China
磁法是一种重要的地球物理勘探方法,被广泛应用于固体矿产与石油天然气勘探、地质构造填图以及深部与区域构造研究等方面(Borradaile and Henry, 1997; 管志宁, 1997; Schmidt et al., 2004; Verduzco et al., 2004).磁法正演模拟作为磁法数据解释和反演的基础,一直是国内外学者的研究热点(Okabe, 1979; Cady, 1980; Won and Bevis, 1987; 管志宁, 1997; 贾春生, 1999; 安玉林等, 2003; Lelièvre and Oldenburg, 2006; Zhang et al, 2015).
目前,磁法正演主要分为两大类:频率域和空间域(Blakely, 1996).频率域磁法正演主要采用快速傅里叶变换法(Tontini et al., 2009; Tontini, 2012)和小波变换(Li and Oldenburg, 2010),具有计算速度快的特点,但是只能采用规则的六面体单元剖分网格,不适合模拟带地形和复杂异常体模型.空间域方法可以采用四面体单元进行网格剖分,能较好的拟合复杂模型体(Ren et al., 2017b; Ren et al., 2017c).其主要可分为两种,一种为求解微分方程的方法,如有限单元法、边界单元法和有限差分法等(王书惠, 1981; 徐世浙和楼云菊, 1986; Ferguson et al., 1994; Davis et al., 2010; Dolgal et al., 2012),此类方法在求解磁位和磁场时,会导致梯度数值精度降低;另一种为积分求和的方法,该方法虽然可以保证精度,但在计算规模较大的情况下,存在耗时长,计算效率低等问题(陈召曦等, 2012),假设有M个观测点,N个四面体源单元,积分求和法的计算复杂度将达到O(MN).
为了能更好的模拟复杂磁法模型、确保高精度的解,同时又能获得更高的计算效率,本文开发了一种基于非结构化的四面体单元和自适应多层快速多极的磁法高精度、快速正演算法.相比于长方体单元(Lelièvre, 2003; 姚长利, 2003; Lelièvre et al., 2006; 陈召曦等, 2012; 樊俊昌等, 2012),四面体单元能最大程度的减小模型体与实际地质体的误差,更好的描述地下场源特性(Ren et al., 2013b; Ren et al., 2018).与此同时,本文采用的自适应多层快速多极算法能够实现磁法积分求和加速处理.快速多极算法主要被应用于计算电磁学问题和声波问题中(Liu, 2009; Schobert et al., 2012),近几年也逐渐应用到地球物理的地震、电磁法和位场计算中(Çakir 2006; Ren et al. 2013a, 2014, 2017d).该方法不仅对网格无限制,且可以大幅加快计算速度.假设一个模型有M个观测点,有N个源单元,采用自适应多层快速多极算法计算时间复杂度仅为O(MlogN).本文将四面体网格剖分与自适应快速多极算法有机结合,从而解决了大规模复杂模型的磁法正演中耗时长、精度低等问题.
1 计算理论 1.1 磁法正演对于通常的磁法问题,采用Ω表示三维地质体(如图 1).假设它的磁化强度分布为M(r′),此时,在观测点r处产生的磁位 V(r) 和磁感应场B(r) 可以表示为(Blakely, 1996):

|
图 1 磁法模型 Fig. 1 Magnetic model |
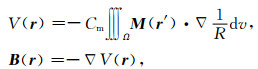
|
(1) |
其中,Cm 为磁比例常数,Cm=10-7H·m-1,R=|r-r′| 为观测点r到地质体内部积分点r′的距离,▽ 为对观测点r求梯度.
本文采用能够高精度逼近复杂模型的四面体单元进行网格剖分.对于大规模磁法正演问题,本文采用快速多极算法来加速计算公式(1)中的积分.其思想是:将计算区的四面体单元并分成两部分,即靠近观测点的区域(近区)、远离观测点的区域(远区).在近区采用精确的解析公式进行计算,在远区采用自适应多层快速多极算法求解.文中将观测点和源单元分别放置于两个独立的八叉树中.每个源四面体单元可由它的中心点代替,由此产生一组源中心点表示所有的源四面体单元.然后采用分层分布的方法将这些源中心点构建在源八叉树中.为构建源八叉树,首先需要设置一个最小的长方体,它完全包围所有的源中心点.将该长方体定义为八叉树的根细胞.从根细胞开始,每个细胞将被细分为八个子细胞,其边长为原细胞边长的1/2.如果子细胞不包含任何源中心点,则称之为空细胞,将会在源八叉树中自适应的删除.在所有的子细胞中重复执行细分操作,直到每个子细胞中的源中心点达到设定数量,或者构造的源八叉树达到预定深度.在该八叉树中,不包含子细胞的细胞被称为叶子细胞.每个叶子细胞所包含的源中心点数量小于或等于预定数量,所有叶细胞的源中心点必须与整个源中心点相同,以等效表示源四面体元素.观测点八叉树的构建与此类似.
1.2 近区、远区分离定义参数 λ=D/S 划分近区远区,其中 S 为观测点细胞和源细胞的最大长度,D 为观测点细胞和源细胞的距离.将观测点r与地质体内部积分点r′的距离小于设定距离的部分称之为近区Tnear,其他区域称之为远区Tfar.则积分区域Ω可表示为

|
(2) |
在实际处理过程中,对离散好的四面体单元,取其中心点位置,计算其与每一个观测点的距离,通过参数λ判别该点属于近区或远区,参数λ的数值大小人为设定.λ的值越大,则近区的范围越大,计算精度越高.
1.3 计算远区积分对于远区的积分,通过选取扩展点,即每个细胞的中心点,将每个观测点与所有的源四面体单元的积分转化成观测点所在细胞的中心点与源四面体所在细胞的中心点的连接,从而减少了积分计算的次数,达到了加速的目的(如图 2).

|
图 2 (a) 传统积分求和方法; (b)快速多极展开法 Fig. 2 Concentional integral summation method; (b) The fast multipole method |
为了使用快速多极展开算法,需要对积分点进行转换,即对积分核函数 1/|r-r′| 进行展开,当满足条件 |r-r′c|>|r′-r′c| 时,积分核函数可以展开为(Abramowitz and Stegun, 1964)

|
(3) |
其中,r′c 为源点r′的扩展中心(见图 3),Rnm和Snm 分别为常规的和奇异的球谐函数:

|
图 3 在源八叉树和观测点八叉树中M2M、M2L和L2L转换示意图 Fig. 3 Demonstration of M2M, M2L and L2L transformations on the observation octree and the source octree |

|
(4) |
其中,(r, θ, ϕ) 为点x的球坐标,r>0, 0≤θ≤π, 0≤ϕ≤2π.Pnm 为伴随勒让德函数:
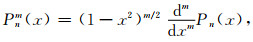
|
(5) |
其中,Pn(x)为n 阶标准勒让德函数.
从式(3)可以看出,公式(1)中积分核函数观测点r与源点r′之间的耦合关系通过球谐函数展开而消除,即通过引入扩展点r′c (远区的中心点),将积分核函数分成了两部分,一部分是关于观测点r和r′c 的函数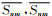
那么,磁位可以表示为
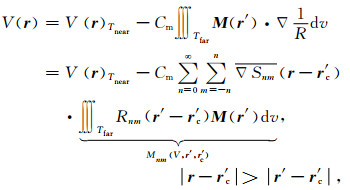
|
(6) |
其中,Mnm(V,r′,r′c) 为磁位在远区的多极矩.多极矩只与r′和r′c 有关,与观测点r无关,不随观测点的变化而变化,这就意味着,即使有很多个观测点,多极矩也只需要计算一次.一旦计算好多极矩,当计算新的观测点的远区积分时,只需要进行一些简单的代数操作,即计算依赖于观测点的基础函数
如果需要将远区积分从扩展中心r′c 转移更高一层的扩展中心r″c (见图 3),即:从源八叉树中的子细胞的中心点r′c 转移到该子细胞的母细胞的中心点r″c 处,那么,磁位在远区的计算表达式可以表示为

|
(7) |
其中,点r″c 处新的多极矩Mnm(V,r′,r″c),可以通过M2M转换(Yoshida 2001)得到:

|
(8) |
M2M实现了子细胞与母细胞之间的联系,同样Mnm(V,r′,r″c) 包含两部分,一部分为与r′c和r″c 有关的 Rn′m′(r′c-r″c),另一部分为与r′和r′c 有关的Mn-n′, m-m′(V,r′,r′c),即为子细胞的多极矩.可以看出,通过M2M转换,点r″c 处新的多极矩Mnm(V,r′,r″c) 只需要进行简单的几何运算即可求得.
类似地,如果点rc 为观测点的局部扩展中心,当满足条件 |r-rc| < |r′-rc|时,积分核函数可以展开为
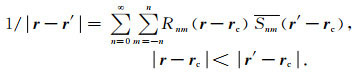
|
(9) |
那么,磁位在远区的积分可以表示为
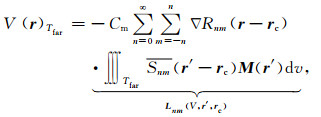
|
(10) |
其中,Rnm(r-rc) 为已知的基础函数,Lnm(V,r′,rc) 为未知的局部系数,可以通过计算远区Tfar的积分得到.而本文通过已经计算好的多极矩来计算Lnm(V,r′,rc),以达到减少计算量,加快计算速度的目的.
借助源细胞中心点r″c 的多极矩Mnm(V,r′,r″c) 计算扩展点rc (见图 3)的局部系数Lnm(V,r′,rc),通过对 Snmr′-rc 进行展开:
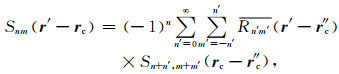
|
(11) |
这里,|rc-r″c|>|r′-r″c|. 此时,将 Snm(r′-rc) 展开成两部分,一部分为与r′和r″ 相关的

|
(12) |
如果观测点的局部展开点变为点rcc (见图 3),即一子细胞的中心点,那么,该点处的磁位远区表达式可以表示为

|
(13) |
点rcc 的局部系数可以通过该子细胞的母细胞的中心点rc 的局部系数,借助L2L转换得到,那么,需要对 Rnm(r-rcc) 进行变换,将 Rnm(r-rcc) 表示为

|
(14) |
那么,可以得到L2L转换(Yoshida 2001):
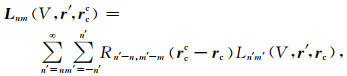
|
(15) |
其中Ln′m′(V,r′,rc) 为母细胞中心点rc 的局部系数,那么,点rcc 的局部系数可以通过简单的代数求和直接计算得到.使用上述L2L转换,可以最大程度的减少计算时间.
逐层计算,从上往下,便可以计算得到每个观测点的磁位远区积分.
1.3.3 磁场计算磁感应场B(r) 具有相同的积分核函数 1/R,因此,远场区的磁感应场也具有相同的计算方法.磁感应场的局部展开系数可以用相似的计算得到.对于磁感应场,可作如下计算:

|
(16) |
其中,局部系数与磁位局部系数相同.这就意味着,如果磁位的点rcc 处局部系数已经计算得到,那么,只需要计算磁位的点rcc 处局部系数和函数▽▽Rnm(r-rcc)的乘积,便可以计算得到磁感应场.
计算函数 ▽▽Rnm(r-rcc),需要使用坐标转换,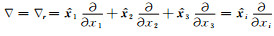


|
(17) |
▽▽Rnm(r-rcc) 可以写为
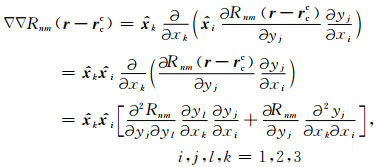
|
(18) |
其中,yi(i=1, 2, 3)表示为球坐标系下三个分量,y1=r>0,y2=θ,y3=φ,0≤θ≤π,0≤φ≤2π.xi和yi 之间的关系可以表示为
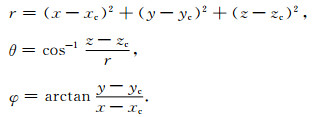
|
(19) |
近区场积分与常规磁法正演计算方法类似.本文采用基于四面体单元的不含奇异性的解析表达式进行计算求解.磁位和磁场计算如下(Blakely, 1996):

|
(20) |
其中,R=1/|r-r′|. 通过采用散度理论、梯度定理,可将体积分转化到面积分计算,在每个小四面体中磁化强度大小和方向恒定,则可得到:
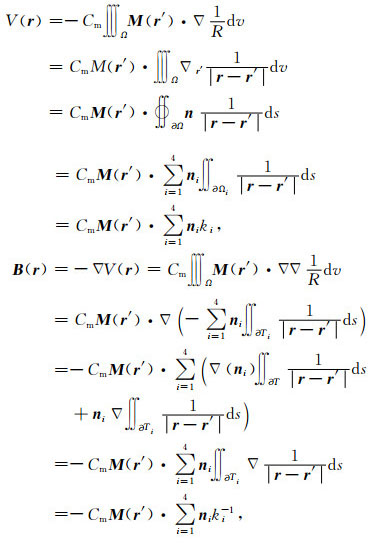
|
(21) |
其中,
经过以上过程,即对远区采用自适应多层快速多极算法加速计算,对近区采用基于四面体无奇异性解析解计算,再把计算所得到的远区和近区的积分求和,则可得到由源目标体产生的总场磁位和磁场.
2 数值算例 2.1 测试环境本文建立两个模型,分别为组合体模型(包含四个相同的正方体)和安徽怀宁地区带地形的航空数据模型.测试环境为Intel(R) Core(TM) i5-4590 CPU 3.30 GHz、4线程和8GB RAM.
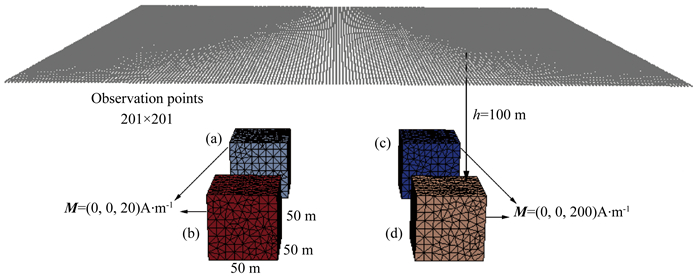
2.2 组合体模型建立组合体模型(见图 4),其中,(a)、(b)、(c)、(d)四个小正方体边长均为50 m,中心点坐标分别为(-75 m, -75 m, -25 m)、(-75 m, 75 m, -25 m)、(75 m, -75 m, -25 m)和(75 m, 75 m, -25 m).(a)、(b)两个小正方体磁化强度为M=(0, 0, 20)A·m-1,(c)、(d)两个小正方体磁化强度为M=(0, 0, 200)A·m-1.采用Tetgen对模型进行四面体单元网格剖分(Si and TetGen, 2006; Si, 2015),共剖分为11862个四面体单元.观测平面在该模型上方100 m处,40401个观测点均匀分布在x=[-200m, 200 m]、y=[-200 m, 200 m]、z=100 m的平面上.
|
图 4 组合体模型及参数 Fig. 4 Combination model and its parameters |
采用基于四面体网格的自适应多层快速多极(AMFM)算法和基于四面体的无奇异性解析解(Closed-form)分别计算了该模型的磁位和垂直方向的磁场,并计算了两种方法的相关误差(见图 5):
|
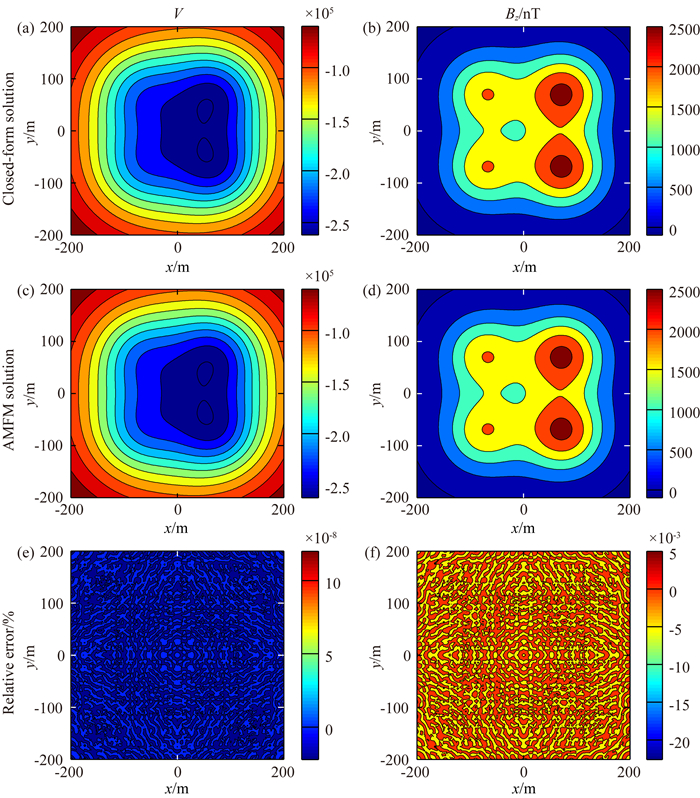
图 5 组合体模型基于四面体解析解与自适应多层快速多极算法对比 Fig. 5 Comparison between AMFM solution and tetrahedral closed-form solution of a combination model |
图 5中,(a)和(b)表示采用基于四面体解析解计算的磁位V和垂向磁场Bz;(c)和(d)表示采用自适应多层快速多极算法计算的磁位V和垂向磁场Bz;(e)和(f)分别表示磁位V和垂向磁场Bz的相对误差.由正演结果可以清晰的分辨出四个正方体的位置.与解析解相比,采用自适应多层快速多极算法计算磁位时相对误差可控制在10-7%以下,计算垂向磁场时相对误差可控制在10-2%以下.则说明了该方法具有很好的精度.
同时,本文采用了自适应多层快速多极法(AMFM)、一阶高斯积分法(G1)、二阶高斯积分法(G2)(Hwang et al., 2003; May et al., 2011)和基于四面体的无奇异性解析解(Closed-form)四种方法对磁位和垂直方向的磁场进行了对比计算,并分别统计了它们的计算时间(见表 1).
|
|
表 1 对组合体模型采用不同方法计算时间的比较结果 Table 1 Comparison of the computing time of four methods for the combination model |
由表 1可以看出,与解析解相比,采用一阶高斯积分法加速比为31.9,采用二阶高斯积分法加速比为22.1,而采用自适应多层快速多极法加速比可达到287.1.由此可见,在误差允许范围内,自适应多层快速多极法相比于一阶、二阶高斯积分法更加高效.与此同时,由于组合体模型磁化强度是变化的,可知该方法对于磁化强度任意分布的模型也会有很好的效果.
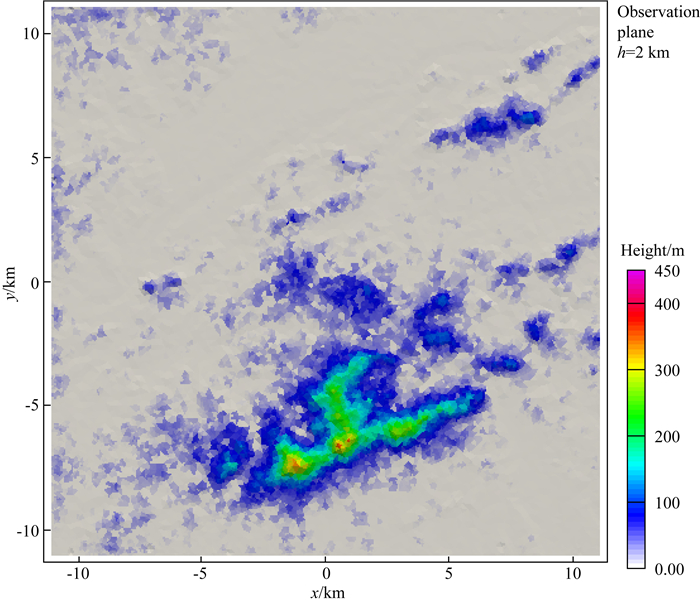
2.3 带地形的航空数据模型为了测试本文算法处理大规模带地形问题的能力,建立了安徽怀宁地区(116.3°—116.6°E、30.3°—30.5°N范围内)带地形的航空磁法模型(见图 6),该模型由安徽怀宁地区的数字高程模型(DEM)建立.当获得高精度的数字高程模型(DEM)时,首先采用三角剖分将地形面剖分成一系列的三角单元,该地形面连同地下封闭边界面可转化为体积模型,此模型沿x、y轴长度均为20.2 km,最大高度为439 m,深度为5 km.观测平面高度为2 km,观测点个数为M=160801,均匀分布在x=[-10 km, 10 km]、y=[-10 km, 10 km]、z=2 km的平面上.采用Tetgen将该模型剖分为494075个四面体单元.设置该模型的磁化强度为常量,即每一个四面体单元的磁化强度为M=(0, 0, 100)A·m-1.
|
图 6 安徽省怀宁地区的航空数据模型 Fig. 6 An airborne data model of the Huaining County, Anhui Province |
同样,采用基于四面体网格的自适应多层快速多极算法(AMFM)和基于四面体的无奇异性解析解(Closed-from)分别计算了该模型的磁位和垂直方向的磁场,并计算两种方法的相关误差(见图 7).
|
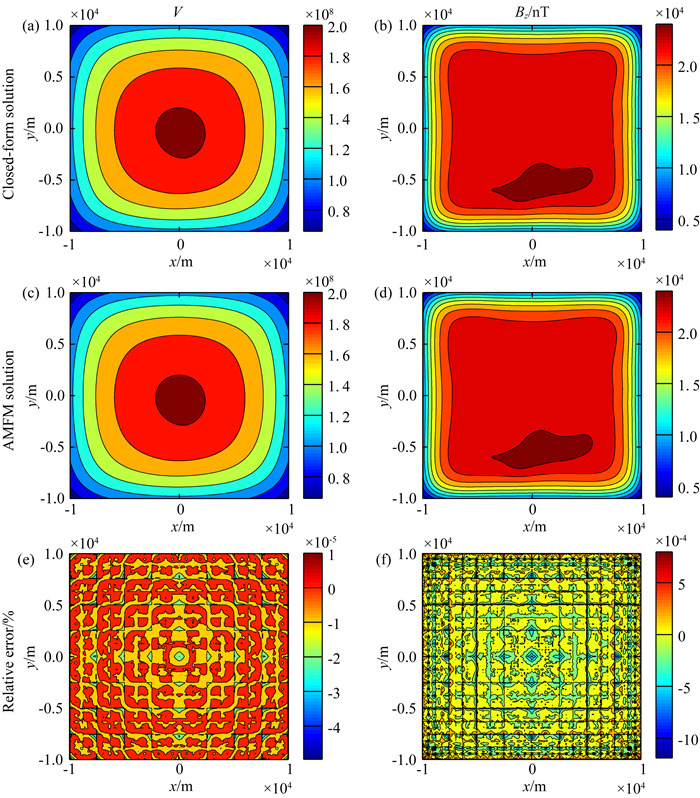
图 7 航空数据模型基于四面体解析解与自适应多层快速多极算法对比 Fig. 7 Comparison between AMFM solution and tetrahedral closed-form solution of an airborne data model |
图 7中,(a)和(b)表示采用基于四面体解析解计算的磁位V和垂向磁场Bz;(c)和(d)表示采用自适应多层快速多极算法计算的磁位V和垂向磁场Bz;(e)和(f)分别表示磁位V和垂向磁场Bz的相对误差.由图 7可以看出,对于计算大规模的带地形航空数据,与解析解相比,采用自适应多层快速多极算法计算磁位时相对误差仍可控制在10-5%以下,计算垂向磁场时相对误差仍可控制在10-3%以下,说明自适应多层快速多极算法在计算大规模复杂地形模型时依然会有良好的精度.
分别采用先前所述四种方法对磁位和垂向磁场进行对比计算,并统计计算时间(见表 2).
|
|
表 2 对航空数据模型采用不同方法计算时间的比较结果 Table 2 Comparison of the computing time of four methods for the airborne data model |
由表 2可以看出,与解析解相比,采用一阶高斯积分法加速比为25.1,采用二阶高斯积分法加速比为18.8,而采用自适应多层快速多极法加速比可达到358.2.解析解计算需要4天,而采用自适应多层快速多极展开算法只需16 min.由此可见,在误差允许范围内,自适应多层快速多极法具有更高的计算效率,非常适用于计算大规模复杂带地形模型.
3 结论本文基于非结构化四面体单元剖分技术以及多层快速多极算法实现了大规模带地形复杂模型三维磁法高精度、快速正演计算.首先,该算法弥补了传统积分求解不能够处理带地形复杂模型的缺陷,同时,数值结果进一步证明了算法的正确性以及能够处理复杂模型的能力.
本文的研究成果证明了本文的算法处理大尺度磁法正问题的能力,为磁法的大规模反演与解释等后续研究提供了基础.
Abramowitz M, Stegun I A. 1964. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. New York: Courier Corporation.
|
An Y L, Chen T D, Huang J M. 2003. Advance in theory and method for forward and inverse problem of gravity and magnetic prospecting. Earth Science Frontiers (in Chinese), 10(1): 141-149. |
Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press.
|
Borradaile G J, Henry B. 1997. Tectonic applications of magnetic susceptibility and its anisotropy. Earth-Science Reviews, 42(1-2): 49-93. DOI:10.1016/S0012-8252(96)00044-X |
Cady J W. 1980. Calculation of gravity and magnetic anomalies of finite-length right polygonal prisms. Geophysics, 45(10): 1507-1512. DOI:10.1190/1.1441045 |
Çakir Ö. 2006. The multilevel fast multipole method for forward modelling the multiply scattered seismic surface waves. Geophysical Journal International, 167(2): 663-678. |
Chen C J, Ren Z Y, Pan K J, et al. 2018. Exact solutions of the vertical gravitational anomaly for a polyhedral prism with vertical polynomial density contrast of arbitrary orders. Geophysical Journal International, 214(3): 2115-2132. DOI:10.1093/gji/ggy250 |
Chen Z X, Meng X H, Liu G F, et al. 2012. The GPU-baseds parallel calculation of gravity and magnetic anomalies for 3D arbitrary bodies. Procedia Environmental Sciences, 12: 628-633. DOI:10.1016/j.proenv.2012.01.327 |
Davis K, Li Y G. 2010. 3D joint inversion of gradient and total-field magnetic data.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1784-1788.
|
Dolgal A S, Balk P I, Demenev A G, et al. 2012. The Finite-element method application for interpretation of gravity and magnetic data. Vestn Kraunts, 1(19): 108-127. |
Fan J C, Mao X C, Zhao Y, et al. 2012. Voxel model and its magnetic forward model of stereoscopic prediction of concealed ore body. The Chinese Journal of Nonferrous Metals (in Chinese), 22(1): 239-250. |
Ferguson A S, Zhang X, Stroink G. 1994. A complete linear discretization for calculating the magnetic field using the boundary element method. IEEE Transactions on Biomedical Engineering, 41(5): 455-460. DOI:10.1109/10.293220 |
Guan Z N. 1997. Researches and progresses of magnetic prospecting in China. Acta Geophysica Sinica (in Chinese), 40(S1): 299-307. |
Hwang C, Wang C G, Hsiao Y S. 2003. Terrain correction computation using Gaussian quadrature. Computers & Geosciences, 29(10): 1259-1268. |
Jia C S. 1999. A method for estimating the magnetic anomaly of an uniformly-magnetized polyhedron. Oil Geophysical Prospecting (in Chinese), 34(4): 430-464. |
Lelièvre P G, Oldenburg D W. 2006. Magnetic forward modelling and inversion for high susceptibility. Geophysical Journal International, 166(1): 76-90. DOI:10.1111/gji.2006.166.issue-1 |
Lelièvre P G. 2003. Forward modelling and inversion of geophysical magnetic data[Master's thesis]. Vancouver: University of British Columbia.
|
Li Y G, Oldenburg D W. 2010. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophysical Journal of the Royal Astronomical Society, 152(2): 251-265. |
Liu Y J. 2009. Fast Multipole Boundary Element Method:Theory and Applications in Engineering. Cambridge: Cambridge University Press.
|
May D A, Knepley M G. 2011. Optimal, scalable forward models for computing gravity anomalies. Geophysical Journal International, 187(1): 161-177. DOI:10.1111/gji.2011.187.issue-1 |
Okabe M. 1979. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics, 44(4): 730-741. DOI:10.1190/1.1440973 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013a. Boundary element solutions for broad-band 3-D geo-electromagnetic problems accelerated by an adaptive multilevel fast multipole method. Geophysical Journal International, 192(2): 473-499. DOI:10.1093/gji/ggs043 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013b. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718. DOI:10.1093/gji/ggt154 |
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2014. A hybrid boundary element-finite element approach to modeling plane wave 3D electromagnetic induction responses in the Earth. Journal of Computational Physics, 258: 705-717. DOI:10.1016/j.jcp.2013.11.004 |
Ren Z Y, Chen C J, Tang J T, et al. 2017a. A new integral equation approach for 3D magnetotelluric modeling. Chinese Journal of Geophysics (in Chinese), 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
Ren Z Y, Chen C J, Tang J T, et al. 2017b. Closed-form formula magnetic gradient tensor for a homogeneous polyhedral magnetic target:A tetrahedral grid example. Geophysics, 82(6): WB21-WB28. DOI:10.1190/geo2016-0470.1 |
Ren Z Y, Chen C J, Pan K J, et al. 2017c. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surveys in Geophysics, 38(2): 479-502. DOI:10.1007/s10712-016-9395-x |
Ren Z Y, Tang J T, Kalscheuer T, et al. 2017d. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. Journal of Geophysical Research:Solid Earth, 122(1): 79-109. DOI:10.1002/2016JB012987 |
Ren Z Y, Zhong Y J, Chen C J, et al. 2018a. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics, 83(1): G1-G13. DOI:10.1190/geo2017-0219.1 |
Ren Z Y, Chen H, Tang J T. 2018b. Accurate volume integral solutions of direct current resistivity potentials for inhomogeneous conductivities in half space. Journal of Applied Geophysics, 151: 40-46. DOI:10.1016/j.jappgeo.2018.02.005 |
Schmidt P, Clark D, Leslie K, et al. 2004. GETMAG-A SQUID magnetic tensor gradiometer for mineral and oil exploration. Exploration Geophysics, 35(4): 297-305. DOI:10.1071/EG04297 |
Schobert D T, Eibert T F. 2012. Fast integral equation solution by multilevel Green's function interpolation combined with multilevel fast multipole method. IEEE Transactions on Antennas and Propagation, 60(9): 4458-4463. DOI:10.1109/TAP.2012.2210291 |
Si H, TetGen A. 2006. A quality tetrahedral mesh generator and three-dimensional delaunay triangulator. Berlin, Germany: Weierstrass Institute for Applied Analysis and Stochastic.
|
Si H. 2015. TetGen, a delaunay-based quality tetrahedral mesh generator. ACM Transactions on Mathematical Software, 41(2): 1-36. |
Tontini F C, Cocchi L, Carmisciano C. 2009. Rapid 3-D forward model of potential fields with application to the Palinuro Seamount magnetic anomaly (southern Tyrrhenian Sea, Italy). Journal of Geophysical Research:Solid Earth, 114(B2): B02103. DOI:10.1029/2008JB005907 |
Tontini F C. 2012. Rapid interactive modeling of 3D magnetic anomalies. Computers & Geosciences, 48: 308-315. |
Verduzco B, Fairhead J D, Green C M, et al. 2004. New insights into magnetic derivatives for structural mapping. The Leading Edge, 23(2): 116-119. DOI:10.1190/1.1651454 |
Wang S H. 1981. On the theory using the finite element method to solve direct problem of magnetic exploration. Chinese Journal of Geophysics (in Chinese), 24(2): 206-217. |
Won I J, Bevis M. 1987. Computing the gravitational and magnetic anomalies due to a polygon:algorithms and fortran subroutines. Geophysics, 52(2): 232-238. DOI:10.1190/1.1442298 |
Xu S Z, Lou Y J. 1986. A method of calculating magnetic anomaly of an arbitrary body. Computing Techniques for Geophysical & Geochemical Exploration (in Chinese), 18(4): 260-275. |
Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion. Chinese Journal of Geophysics, 46(2): 351-361. DOI:10.1002/cjg2.v46.2 |
Yao C L. 2003. High-speed computation and efficient storage in-3D gravity and magnetic inversion based on genetic algorithms. Chinese Journal of Geophysics (in Chinese), 46(2): 252-258. |
Yoshida K I. 2001. Applications of fast multipole method to boundary integral equation method[Ph. D. thesis]. Kyoto: Kyoto University. https://www.researchgate.net/publication/265936813_Applications_of_Fast_Multipole_Method_to_Boundary_Integral_Equation_Method
|
Zhang Y, Chen C, Du J, et al. 2015. Forward modeling method of gravity and magnetic fields and their gradient tensors based on 3-D delaunay discretization in cartesian and spherical coordinate systems.//American Geophysical Union, Fall Meeting 2015.
|
安玉林, 陈玉东, 黄金明. 2003. 重磁勘探正反演理论方法研究的新进展. 地学前缘, 10(1): 141-149. DOI:10.3321/j.issn:1005-2321.2003.01.016 |
陈召曦, 孟小红, 刘国峰, 等. 2012. 基于GPU的任意三维复杂形体重磁异常快速计算. 物探与化探, 36(1): 117-121. |
樊俊昌, 毛先成, 赵莹, 等. 2012. 隐伏矿体立体预测的体元模型及其磁法正演模型. 中国有色金属学报, 22(1): 239-250. |
管志宁. 1997. 我国磁法勘探的研究与进展. 地球物理学报, 40(S1): 299-307. |
贾春生. 1999. 均匀磁化多面体磁异常计算方法. 石油地球物理勘探, 34(4): 430-464. |
任政勇, 陈超健, 汤井田, 等. 2017. 一种新的三维大地电磁积分方程正演方法. 地球物理学报, 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
王书惠. 1981. 关于用有限元法作磁法勘探正演计算的理论问题. 地球物理学报, 24(1): 207-217. |
徐世浙, 楼云菊. 1986. 计算任意形体磁异常的边界元法. 物探化探计算技术, 18(4): 260-275. |
姚长利. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
 2019, Vol. 62
2019, Vol. 62


