0 引言

利用重力卫星技术监测全球质量分布的时变信息取得了显著进展，尤其是美德联合实施的GRACE(Gravity Recovery and Climate Experiment)重力卫星计划，使我们可以成功获取月际(甚至周际和日际)时间分辨率以及300km左右空间分辨率的全球和区域性地表质量变化信息(Dahle et al., 2013; Mayer-Gürr et al., 2016; Tapley et al., 2004; Wahr et al., 2004).以高精度轨道和星间距离观测相结合的模式，为利用重力卫星数据监测全球质量变化提供了基本的技术途径，已经开始实施的GRACE-FO任务也是基于这种观测模式，并采用激光干涉测量技术进一步提高星间距离的观测精度(Sheard et al., 2012).因此，充分发掘和利用重力卫星观测数据进行全球质量变化监测，需要在理论方法和数据处理技术上持续深入研究，对促进相关数据在全球环境变化监测中的广泛应用具有重要意义.

点质量模型法是基于牛顿万有引力定律直接建立卫星受摄运动与地面质量点变化之间的关系，目前已发展出了扰动位点质量模型法、径向加速度点质量模型法和三维加速度点质量模型法(Baur and Sneeuw, 2011; Baur, 2013; Han et al., 2005a, 2005b; Tangdamrongsub et al., 2012; 苏勇等, 2017)，各个方法的主要区别在于联系地面点质量变化与卫星受摄运动的中间量不一样，三者分别采用扰动位、球坐标系中的径向加速度和直角坐标系中的三维加速度构建关系式.由于直接采用卫星观测数据计算的全球质量变化会在空域出现严重的南北条带噪声，真实的质量变化信号会被噪声覆盖，无法分辨；而且利用重力卫星数据计算地表质量变化是一个向下延拓的过程，会导致利用点质量模型法计算的法矩阵呈病态，直接求解无法得到稳定解.因此，点质量模型法在求解过程中需要采用合适的正则化手段或空间约束技术进行处理(Baur and Sneeuw, 2011; Han et al., 2005a; 苏勇等, 2017).

目前，利用重力卫星数据计算全球质量变化常用的方法包括球谐函数法、Mascon法和点质量模型法(Baur and Sneeuw, 2011; Han et al., 2005a, 2005b; Luthcke et al., 2006; Rowlands et al., 2005; Ran et al., 2017; Wahr et al., 1998; 苏勇等, 2017)，各类方法在处理南北条带噪声时采用的技术手段也各不相同.球谐函数直接采用谱域的球谐位系数进行计算，针对噪声的处理，许多学者发展了一系列的滤波平滑技术，如针对位系数的相关误差发展了多项式拟合去相关法(Swenson and Wahr, 2006)，以及基于高斯滤波技术的各种谱域平滑滤波法(Duan et al., 2009; Klees et al., 2008; Wahr et al., 1998; Zhang et al., 2009)；去相关算法会对短波信号产生一定影响，会导致局部区域的正负信号发生变化，而且在赤道附近的效果不理想(詹金刚等, 2015)；高斯滤波则是以牺牲模型空间分辨率为代价换取条带噪声信号的平滑.换句话说，要保持较高的空间分辨率，则条带噪声的影响相对较强，要降低条带噪声的影响，则会降低空间分辨率，两种情况均不利于真实地球物理信号的提取.Mascon法采用时间-空间约束方程对解算结果进行约束处理，可有效提升地表质量变化的时空分辨率，显示出较好的效果(Rowlands et al., 2010; Save et al., 2016).点质量模型法在解算过程中通常采用简单的零阶Tikhonov正则化方法处理条带噪声，模拟和实测数据结果均表明该方法的有效性(Baur and Sneeuw, 2011; Chen et al., 2016; 苏勇等, 2017)，但该方法是否最优仍存疑问，需进一步发展更精细的去条带噪声方法.

本文在三维加速度点质量模型法的原理基础上，对其进一步发展和完善.针对基于卫星轨道和星间观测数据的三维加速度点质量模型法无法直接考虑地表质量变化导致的负荷形变的影响，本文推导建立了时变重力场模型的球谐位系数和地表点质量变化之间的关系，采用负荷勒夫数分离负荷形变的影响.一般而言，邻近地表点的质量变化存在空间相关性，可以采用含有空间相关信息的约束矩阵处理地表点质量变化的解算结果；本文引入等权形式、线性形式、指数形式和高斯形式的空间约束方法处理三维加速度点质量模型法解算结果的条带噪声，并将其与零阶Tikhonov正则化方法进行对比.通过模拟数据和实测GRACE时变重力场模型数据对本文的方法进行了分析，验证了各类方法的有效性，对比分析了各类空间约束方法去条带噪声的能力.

1 三维加速度点质量模型法的空间约束求解

在三维空间直角坐标系中，设地面某质量变化点M_j(x_j, y_j, z_j)的质量为δm_j，卫星在某时刻的位置为P(x, y, z)，相对于整个地表质量变化而言，可以将卫星视为单位质量体.由于卫星同时受地面所有质量变化点的引力摄动作用，因此地表质量变化引起的卫星总摄动加速度可以表示为(苏勇等, 2017)

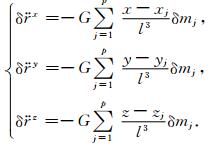
(1)

其中，表示万有引力常量，p表示地面质量变化点的总个数，式(1)即为三维加速度点质量模型法的基本关系式.设地表质量变化引起的球谐位系数的变化用δC_nm和δS_nm来表示，那么卫星受到的摄动加速度可以表示为(Ilk, 1983; Mayer-Gürr, 2006)

(2)

其中，GM表示地球引力常量，R表示地球半径，n和m分别表示球谐位系数的阶和次，C_nm^-, C_nm⁰, C_nm⁺和S_nm^-, S_nm⁰, S_nm⁺等系数的计算可以参见文献(Ilk, 1983; Mayer-Gürr, 2006).

由于固体地球并非刚体，而是一个黏弹体，因此地表质量变化会导致固体地球产生负荷形变(Wahr et al., 1998)，这部分负荷形变也会引起卫星摄动加速度的变化.重力卫星无法直接区分地表质量变化及其导致的负荷形变，设全球地表形变引起的球谐位系数的变化用ΔC_nm和ΔS_nm表示，则ΔC_nm和ΔS_nm包含了地表质量变化及其导致的负荷形变两部分，此时有(Baur and Sneeuw, 2011)

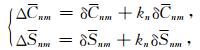
(3)

式中，k_n表示n阶负荷勒夫数(Farrell, 1972; Wahr et al., 1998)，(k_nδC_nm, k_nδS_nm)即表示了地表质量变化导致的负荷形变.将式(3)代入式(2)中可得地表质量变化引起的卫星摄动加速度为

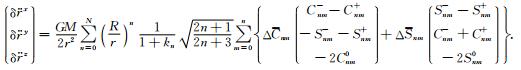
(4)

联合式(1)和式(4)即可建立完整的利用时变重力场模型求解地表质量变化的三维加速度点质量模型法.基于高斯-马尔科夫模型可以建立基于时变重力场模型求解地表质量变化的观测方程：

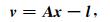
(5)

其中，A表示设计矩阵，l表示观测向量，x表示未知参数向量，v表示观测数据的改正向量.根据最小二乘的基本思想，可得未知参数的最优线性无偏估值为

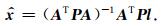
(6)

由于时变重力场模型的球谐位系数存在相关误差和南北条带噪声的影响，式(6)呈病态，直接求解无法得到未知参数的最优估值.为了获得稳定的最优估值，需要引入正则化平衡项，构造如下最小二乘准则(Kusche and Klees, 2002)：

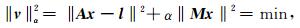
(7)

其中，α表示正则化参数，M为正则化矩阵.可得未知参数的正则化解为

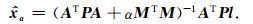
(8)

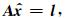
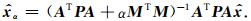
如果考虑式(5)和式(6)，未知参数的最优估值应该满足代入式(8)可得

(9)

在本文中未知参数的估值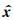表示地表点的质量变化，采用时变重力场模型求解.由于时变重力场模型中存在南北条带噪声，真实的地表质量变化信号会被噪声掩盖，常用的做法是采用合适的去相关算法或滤波平滑技术处理时变重力场模型的球谐位系数.但从式(9)可以看出，矩阵(A^TPA+αM^TM)^-1A^TPA相当于一个滤波器，可以对受条带噪声影响的地表质量变化进行滤波平滑处理.

考虑到邻近地表质量变化点之间存在空间相关性，因此可以采用空间约束方程构建正则化矩阵(Baur and Sneeuw, 2011; Han et al., 2005a; Luthcke et al., 2006; Ramillien et al., 2012; Rowlands et al., 2005; Tangdamrongsub et al., 2012).地面点的质量变化可以表示为其余点质量变化的线性组合，设对角线元素为零的p×p阶相关矩阵B满足

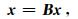
(10)

转换后可得

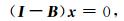
(11)

此时可令

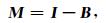
(12)

其中，I为单位矩阵，则M为对角占优的对称矩阵.设d_ij表示地面两个质量点i和j之间的球面距离，D表示地面质量点的相关距离，L表示以质量点i为中心的相关距离半径内的质量点个数，此时可以定义不同类型的空间约束矩阵，当质量点之间的球面距离不大于相关距离时(d_ij≤D)，本文采用如下相关矩阵形式(Ramillien et al., 2012)：

(1) 等权形式：

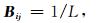
(13)

(2) 线性形式：

(14)

(3) 指数形式：

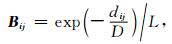
(15)

(4) 高斯形式：

(16)

当质量点之间的球面距离大于相关距离时(即d_ij>D)，B_ij=0.除此之外，相关文献常采用零阶Tikhonov正则化方法(ZOT)处理病态问题和进行空间约束处理(Baur and Sneeuw, 2011; Chen et al., 2016; 苏勇等, 2017)，本文同时对其效果进行比较，此时正则化矩阵为单位矩阵，即M=I，该矩阵与相关距离无关.采用L曲线法确定最优正则化参数(Hansen, 1992).

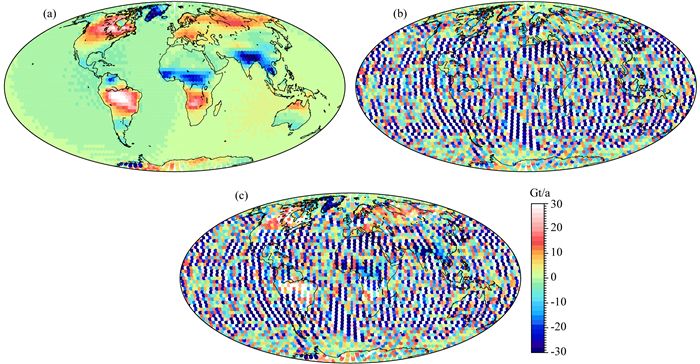
2 模拟分析

为了分析基于时变重力场模型的三维加速度点质量模型法计算地表质量变化时，各类空间约束方法的效果，本文首先采用模拟数据进行分析.首先合成空域中的全球质量变化，采用球谐分析的方法将合成的空域信号转换为谱域的球谐位系数，球谐位系数截断至60阶次(图 1a所示).同时，采用真实的GRACE月时变重力场模型减去平滑滤波后的模型模拟全球范围的南北条带噪声(图 1b所示)，将合成的全球质量变化模型与条带噪声模型相加得到含条带噪声的全球质量变化模型(图 1c所示)，具体的合成过程可参见文献(苏勇等，2017).

由于本文采用球谐位系数建立三维加速度点质量模型法的基本方程，而不是直接采用重力卫星的轨道和星间观测量求解地表质量变化，因此不需要模拟卫星的轨道和星间数据.此时，为了建立三维加速度点质量模型法的基本关系，直接采用式(4)计算空间中的摄动加速度.本文采用等面积格网作为地面质量点和空间摄动加速度点的分布类型，由于本文采用的重力场模型均截断至60阶次，其对应的地表质量变化点的空间分辨率为3°左右，为了使已知信号频谱和恢复信号的频谱一致，地面质量点采用3°等面积格网，全球范围内共有4554个格网点.空间格网的大小主要受地面格网大小的限制，从数学形式上要求满足已知数多于未知数，即空间格网点的个数不能少于地面格网点的个数；增加空间格网点的密度有助于解的稳定性，但却不能为解算的地表质量变化提供更多的有效信息，而且空间格网点越密，计算工作量越大；由于空间格网点大小的选取比较复杂，某些文献采用奇异值大小的方式进行确定(Chen et al., 2016)，但仍带有半经验分析的因素，因此，更科学地确定空间格网点的大小还需要进一步研究.综合而言，本文空间格网点采用1°等面积格网，且空间格网中每个点距离地表的距离设为500 km.

相关距离的大小会影响各类空间约束方法的相关矩阵的形式，本文直接预设系列相关距离，然后进行数值模拟分析寻找不同约束方法的最优相关距离，相关距离的取值范围为100~1600 km，以100 km为间隔.

最优正则化参数的选择已有众多文献进行了研究，常用的方法有广义交叉验证、截断 奇异值分解法、L曲线法和均方根误差最小准则等方法(Hansen, 1992; Kusche and Klees, 2002; Xu at al., 2006; Shen et al., 2012 ).本文处理模拟数据时，由于已知无南北条带噪声的全球质量变化，因此直接采用正 则化解与合成模型之差的标准差最小为准则确定最优正则化参数；但在后文处理实测 GRACE时变重力场模型时，由于不知道真实地表质量变化，无法采用标准差最小的准 则，在综合考虑计算复杂度和效率的情况下，采用L曲线法确定最优正则化参数.

由于很难找到一个公认的准则对实测时变重力场模型的滤波平滑效果进行评判，平滑滤波方法对条带噪声的处理能力和对真实信号的影响大小很多时候采用半经验的方法进行估计.因此，本文在评估各类空间约束方法的效果时，采用不同的对比分析方法，具体而言：(1)对于模拟地表质量变化，采用正则化解与合成模型之差的标准差最小为准则进行估计，此时评估各类方法的效果在统计上具有较好的合理性；(2)对于实际GRACE重力场模型而言，无法采用标准差最小的准则，根据已有的大量研究结果，本文采用300 km的高斯滤波方法和300 km的扇形滤波方法作为对比，分析各类空间约束条件下三维加速度点质量模型法求解的地表质量变化情况.

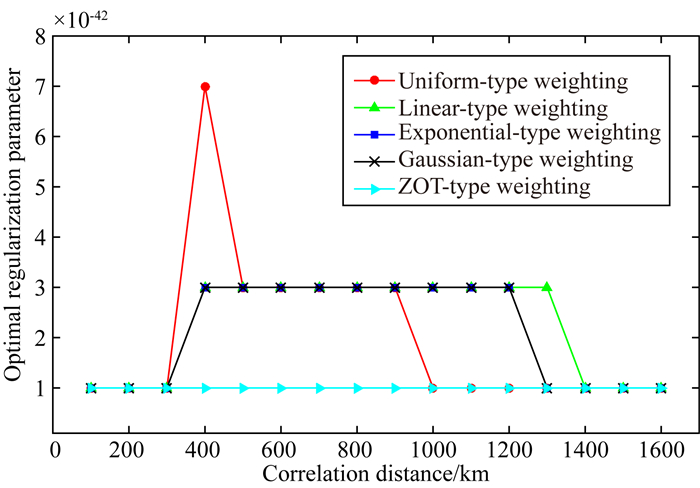
分别对等权形式、线性形式、指数形式和高斯形式的空间相关矩阵以及零阶Tikhonov正则化矩阵进行分析.图 2反映了不同约束矩阵在不同相关距离时的最优正则化参数，不同约束矩阵对应的最优正则化参数存在差异，但随着相关距离的增大，最优正则化参数趋于一致；由于零阶Tikhonov正则化矩阵与相关距离无关，因此零阶Tikhonov正则化方法对应的最优正则化参数在所有相关距离上为同一数值(α=1×10^-42).

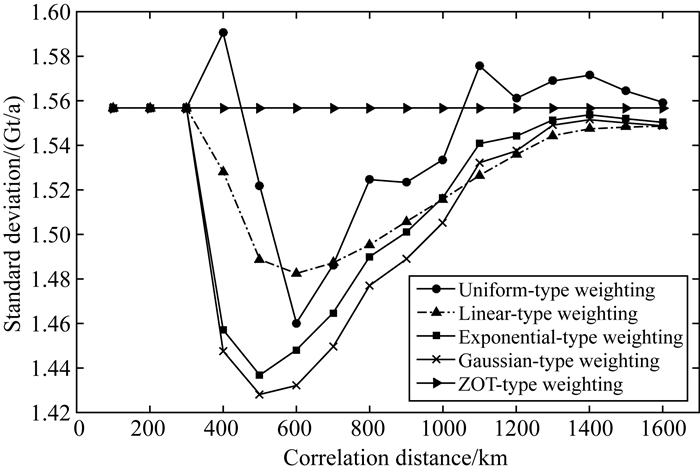
确定了各类约束形式在不同相关距离时的最优正则化参数，可进一步分析各类约束形式对应的最优相关距离.图 3表示不同空间约束形式在不同的相关距离时求解的地表质量变化与合成模型(图 1a)之差的标准差的统计比较结果.可以看出，零阶Tikhonov正则化形式与相关距离无关，标准差维持在一个稳定水平；等权形式的约束解在不同相关距离的误差波动较大，而线性形式的约束解波动较小.指数形式和高斯形式的最优相关距离为500 km，而等权形式和线性形式的最优相关距离为600 km；但随着相关距离的增大，各类约束形式的解趋近一致.综合而言，在最优正则化参数和最优相关距离时，指数形式和高斯形式的约束方法具有最优解，而零阶Tikhonov正则化形式的约束精度差于其余四种空间约束形式.

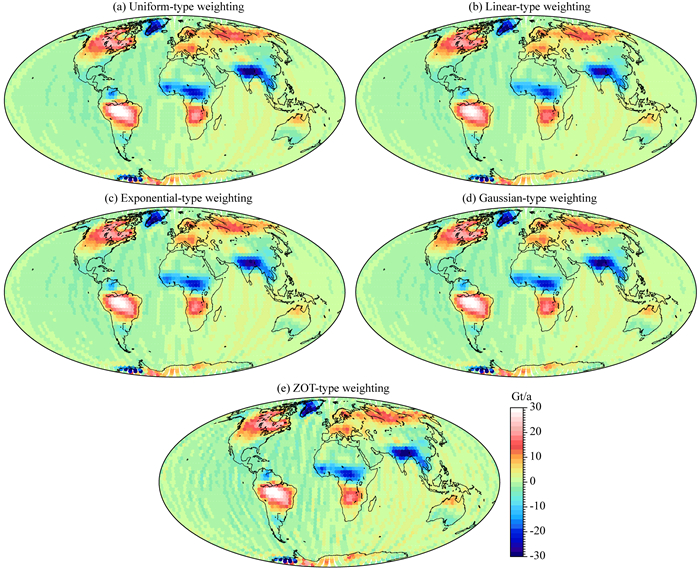
在最优正则化参数和最优相关距离时，各类约束方法求解的最优解如图 4所示.整体而言，各类约束方法均能有效处理南北条带噪声，并且各自的计算结果差别不大，这也可以从图 3看出，最优相关距离解算结果的标准差的大小差异小于0.1 Gt/a，但零阶Tikhonov正则化形式解算结果的条带噪声稍强于其余四种形式的解.局部区域的比较可以看出，在委内瑞拉附近和非洲西部利比里亚附近，各类约束解的空域信号强度存在差别.

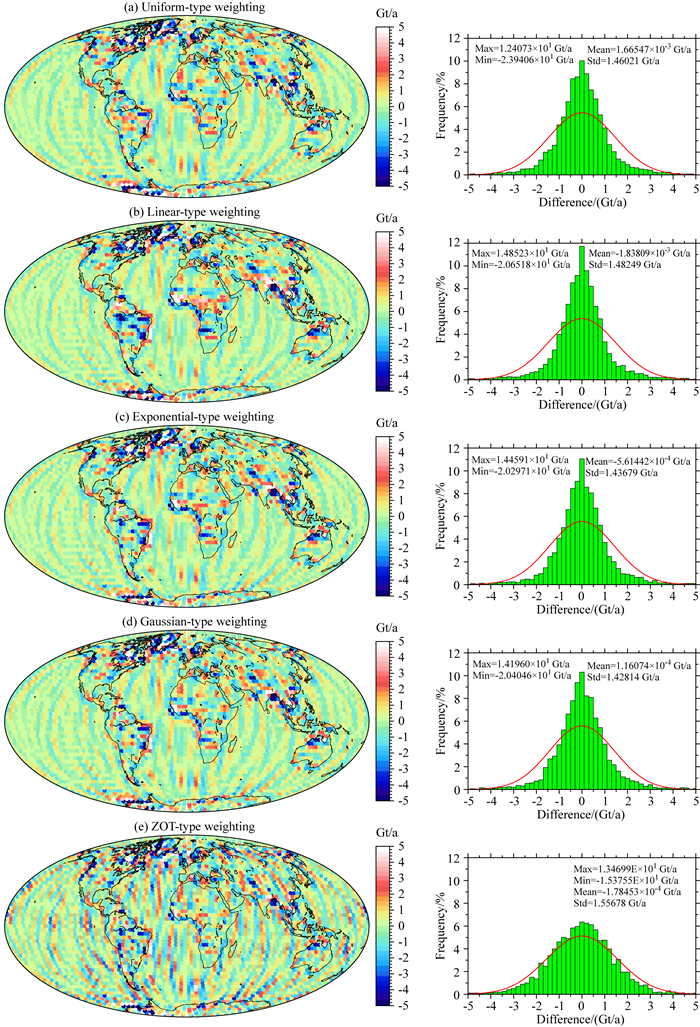
由于各类空间约束方法计算的结果差别不明显，直接分析各类约束方法的解算结果较为困难.为了较为精确的比较各类约束方法的精度，将计算结果与合成模型(图 1a)做差并进行统计分析(如图 5所示).可以看出，各类约束方法均较大程度的滤除了南北条带噪声，但仍存在残留噪声信号；各类约束方法解的残差信号的大小和符号在局部空域中的分布存在差别，而且在信号强度较大的地区残差较大，也就是说各类约束方法会对信号产生削弱现象，在滤除条带噪声的同时会滤除部分真实的地球物理信号.

等权约束形式的残差如图 5a所示，残差的最大值约为12.41 Gt/a，最小值约为-23.94 Gt/a，均值约为1.67×10^-3 Gt/a，标准差约为1.46 Gt/a；在非洲大陆的南部和南美洲亚马逊河流域存在明显的正残差信号，在格陵兰岛东西海岸存在明显的负残差信号.线性约束形式的残差如图 5b所示，残差的最大值约为14.85 Gt/a，最小值约为-20.65 Gt/a，均值约为-1.84×10^-3 Gt/a，标准差约为1.48 Gt/a；在非洲大陆的赤道附近存在明显的正残差信号.指数约束形式的残差如图 5c所示，残差的最大值约为14.46 Gt/a，最小值约为-20.30 Gt/a，均值约为-5.61×10^-4 Gt/a，标准差约为1.44 Gt/a.高斯约束形式的残差如图 5d所示，残差的最大值约为14.20 Gt/a，最小值约为-20.40 Gt/a，均值约为-1.16×10^-4 Gt/a，标准差约为1.43 Gt/a.ZOT约束形式的残差如图 5e所示，残差的最大值约为13.47 Gt/a，最小值约为-15.38 Gt/a，均值约为-1.78×10^-4 Gt/a，标准差约为1.56 Gt/a.整体而言，指数形式、高斯形式和ZOT形式的约束方法所计算结果的残差在空域中的分布存在较强的一致性，各类约束形式的残差在哈德逊湾均存在较为明显的正残差信号，在孟加拉湾沿海存在较为明显的负残差信号.

为了进一步评估各类空间约束方法的有效性，本文采用信噪比(SNR)对各类方法的效果进行对比分析，信噪比定义为

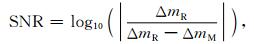
(17)

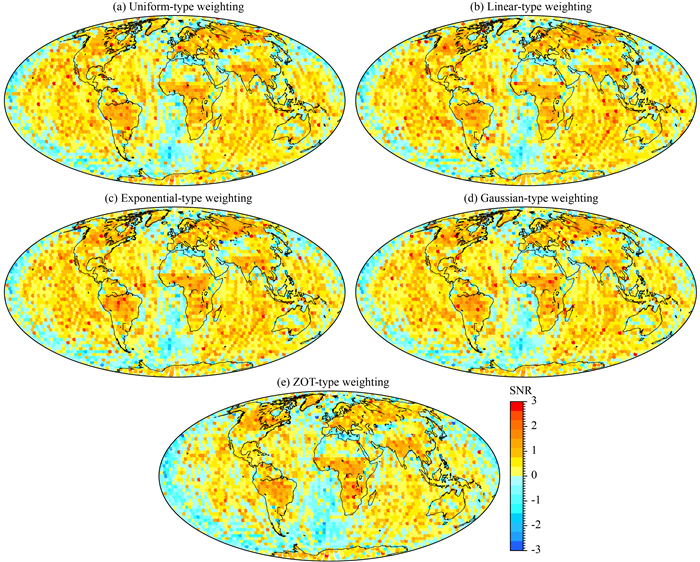
其中，Δm_R表示模拟的地表质量变化，Δm_M表示采用各类约束方法解算的地表质量变化.从定义可以看出，当SNR>0表示信号强于噪声，反之亦反.SNR值越大，结果越好.根据式(17)计算的不同空间约束形式解算的最优结果的信噪比如图 6所示，可以看出，ZOT形式的结果信噪比较差，四种空间约束方法之间的信噪比差别不大，整体优于ZOT形式的结果.更精确的比较，各约束方法最优解SNR>0(即信号强于噪声)的空域格网点的个数统计见表 1，线性形式的约束效果最好，其次为指数形式，等权形式和高斯形式的结果差别不大，ZOT形式的结果全球只有64.38%的点的信号强于噪声，而四种空间约束方法的结果SNR>0的比例均可达75%左右.

综合各类约束形式结果的残差在空域中的分布和统计直方图以及信噪比进行分析，可以看出，线性形式、等权形式、指数形式和高斯形式的约束求解效果优于ZOT形式的结果，线性形式的约束效果更好.因此，从模拟分析的结果来看，在利用三维加速度点质量模型法求解地表质量变化时建议优先采用线性形式的空间约束方法.下面将进一步采用GRACE实测时变重力场模型分析各类约束形式的空间约束效果.

3 GRACE模型分析

本节主要分析各类空间约束方法处理实测GRACE时变重力场模型的效果，随机取美国德克萨斯大学空间研究中心(CSR: Center for Space Research, University of Texas at Austin)发布的2003年12月的GRACE Level-2(Release 05)月时变重力场模型，球谐位系数截断至60阶次，同时以GGM05s模型(截断至60阶次)作为平均重力场模型.由于本文主要考虑各类空间约束方法去条带噪声的效果，不涉及定量分析该月地表质量的变化情况，因此，本文不考虑该月时变重力场模型位系数的一阶项和C₂₀项的改正问题，也不考虑冰后回弹的影响.而且由于CSR的时变重力场模型和GGM05s模型的永久潮汐系统均为零潮汐系统，不需要对它们的潮汐系统进行改正，直接将该月的时变重力场模型与GGM05s模型的前60阶球谐位系数做差，计算球谐位系数的变化量，进而计算相应的地表质量变化情况.

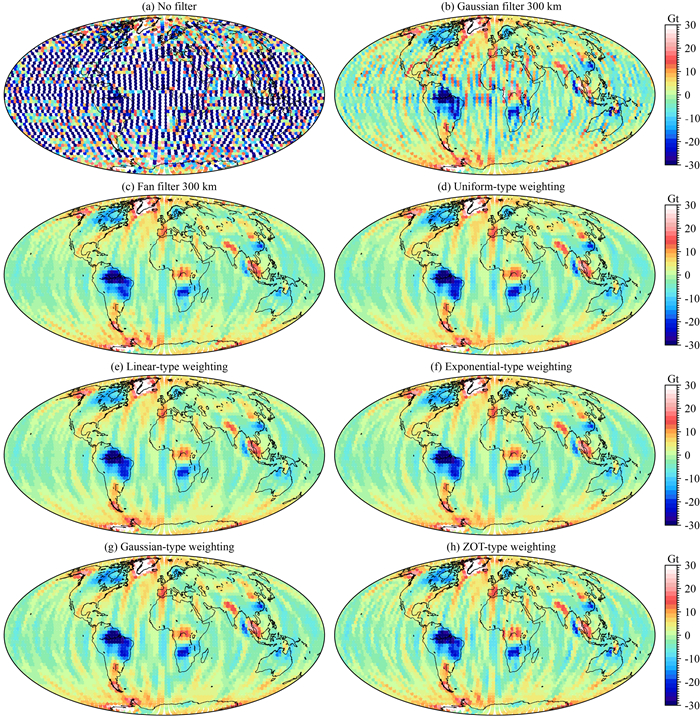
由于没有理论的地表质量变化参考值，无法采用前文模拟数据的方法对各类约束形式的效果进行评估.作为对比，本文同时采用300 km高斯滤波平滑技术和300 km扇形滤波平滑技术处理球谐位系数，比较本文的各类空间约束方法求解的三维点质量解的效果.根据模拟分析结果作为参考，三维加速度点质量模型法解算时指数和高斯形式空间约束方法的最优相关距离取500 km，等权和线性形式空间约束方法的最优相关距离取600 km，最优正则化参数采用L曲线法确定，各类方法的解算结果如图 7所示，格网大小均为3°等面格网.图 7a表示未采用任何滤波或空间约束技术解算的结果，可以看出空域信号受严重的南北条带噪声信号的影响，而采用滤波或空间约束方法均能有效处理条带噪声的影响，如图 7(b—h)所示.300 km高斯滤波的效果较差，其解算的空域信号还存在较为明显的南北条带噪声；300 km扇形滤波的效果基本与各类空间约束方法的效果相当，均能较大程度的滤除噪声的影响.但各类方法的解算结果也存在差别，如亚马逊河流域的空域信号强度存在差别，300 km扇形滤波、等权形式和ZOT形式的空间约束结果在南极威德尔海附近和北大西洋部分地区存在更强的正条带噪声的影响.综合而言，等权形式、线性形式、指数形式、高斯形式和ZOT形式的空间约束方法均能有效处理南北条带噪声的影响，优于300 km高斯滤波的效果，与300 km扇形滤波的效果基本相当或部分更优；其中等权形式、线性形式、指数形式和高斯形式四种空间约束方法的效果更好.

4 结论

本文进一步发展和完善了基于三维加速度点质量模型法和重力卫星数据解算地表质量变化的理论方法，建立了球谐位系数的变化和地表点质量变化之间的关系式，考虑了地表质量变化引起的负荷形变的影响，并引入了等权形式、线性形式、指数形式和高斯形式四种空间约束方法，将其与一般采用的零阶Tikhonov正则化方法进行对比，分析了各类空间约束方法的滤波平滑效果.

为了验证分析基于球谐位系数的三维加速度点质量模型法和各类空间约束方法的有效性，本文采用模拟和实测时变重力场模型计算全球质量变化.采用统计分析的手段对基于模拟数据的解算结果进行精确分析，比较各类约束方法的效果；将基于实测时变重力场模型数据的解算结果与采用300 km高斯滤波和300 km扇形滤波的结果进行对比分析，进一步验证和分析了方法的有效性和各类约束方法的优劣.模拟和实测数据分析表明，基于球谐系数的三维加速度点质量模型法可有效用于时变重力场模型计算地表质量变化，等权形式、线性形式、指数形式和高斯形式的空间约束方法均可有效用于对南北条带噪声的滤波平滑处理，其中线性形式的空间约束方法的效果较好.

本文发展的三维加速度点质量模型法直接基于时变重力场模型球谐位系数进行计算，通过球谐位系数和摄动加速度的扰动泛函关系，可充分考虑地表质量变化引起的负荷形变的影响，而基于卫星轨道和星间观测数据的三维加速度点质量模型法，只能采用间接的方法考虑负荷形变的影响.

目前，大量文献采用点质量模型法计算地表质量变化时，一般都采用零阶Tikhonov正则化方法处理条带噪声和信号延拓导致的法方程病态问题，取得了明显的效果.但是采用零阶Tikhonov正则化方法是否能取得最佳的效果还存在疑问，本文引入了四种新的空间约束方法进行对比分析，结果表明，四种约束方法均能达到零阶Tikhonov正则化方法的效果，而且引入的四种空间约束方法的效果整体上更优.

虽然本文引入的空间约束方法形式简单，能有效处理条带噪声的影响，但相关计算结果仍然受不同程度的噪声影响，这主要是GRACE任务本身的仪器精度和设计缺陷导致，随着下一代更高精度的重力卫星计划的实施，有望获得更好的效果.本文发展的基于球谐位系数的三维加速度点质量模型法的计算量明显小于直接采用卫星轨道和星间观测数据的计算量，但由于全球地表质量点的分布密度，未知数的个数仍然较多，对计算机的硬件条件仍有一定程度的要求.

致谢  感谢匿名审稿专家提出的宝贵意见和建议；本文部分图件由GMT(Wessel et al., 2013)生成，在此表示感谢.