2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3. 中海石油(中国)有限公司深圳分公司, 广州 510214;
4. 中国石油集团测井有限公司辽河分公司, 辽宁盘锦 124010
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao Shandong 266071, China;
3. CNOOC Ltd. Shenzhen Branch, Guangzhou 510240, China;
4. CNPC Logging Liaohe Branch, Panjin Liaoning 124010, China
地震反演方法在油气储层预测中具有重要的作用,它根据记录的地震数据、建立的正演模型和先验信息来推断地下的模型参数.确定性反演方法通常利用一些优化算法来对模型参数进行平滑估计(Aster et al., 2012;Sen and Stoffa, 2013).模型误差和噪声等因素的影响使得反演的解并不是唯一的.因此,反演结果不应该局限于单一的预测值,而应该用概率等形式来表示,同时量化模型参数的不确定性.贝叶斯方法属于概率统计的一种,被广泛地应用于地球物理反演问题中.在贝叶斯方法中,所有信息状态都用概率密度函数表示,反演的解由后验概率表示(Tarantola and Valette, 1982;Scales and Tenorio, 2001;Ulrych et al., 2001;Buland and Omre, 2003;Zong et al., 2012;杨培杰和印兴耀,2008;杨千里等,2016).如果模型参数和观测数据之间的关系可以线性表示或者线性近似表示,并且模型参数的先验分布服从高斯分布,则贝叶斯反演问题的解可以用后验概率的解析表达式来表示(Tarantola,2005);如果模型参数与观测数据之间的关系是非线性的,可以利用马尔科夫蒙特卡洛(Markov chain Monte Carlo,McMC)的方法进行求解(Mosegaard and Tarantola, 1995;Sen and Stoffa, 1996;张广智等,2011;孙瑞莹等,2015;Pan et al., 2017).
然而,模型参数服从高斯分布的假设在许多情况下并不适用,模型参数如弹性参数、孔隙度和渗透率等由于不同的岩相或地质流体而呈现多峰的非高斯的分布(Grana and Rossa, 2010;Dubreuil-Boisclair et al., 2012;Sauvageau et al., 2014;Amaliksen,2014).高斯混合模型(Gaussian Mixture Model,GMM)是不同高斯分量的线性结合,能够用于描述模型参数的多峰特性(Hasselblad,1966).Sung(2004)在多元非线性回归建模中介绍了高斯混合模型(GMM).
在高斯线性反演理论中,反演解通常以最小二乘的意义最小化模型参数响应和观测数据之间的误差,因此后验分布的均值是模型参数的一个平滑估计.为了克服这个限制,Hansen等(2006)将地质统计学中的序贯模拟方法(Deutsch and Journel, 1992)引入到高斯线性反演理论中,该方法不仅可以获得模型参数的多次实现,还可以避免计算大型矩阵的问题.序贯模拟方法在随机反演中应用较多(González et al., 2008;Connolly and Hughes, 2016;王保丽等,2015;孙瑞莹等,2016;刘兴业等,2018).Grana等(2012)将序贯模拟方法引入到高斯混合的情况中,提出了序贯高斯混合模拟算法(Sequential Gaussian Mixture Simulation, SGMixSim),并获得了离散变量和连续变量的多次实现.然而,利用单一的高斯混合模型(GMM)计算的离散变量的条件权值是不准确的,尤其是在强噪声的情况下,会导致离散变量的错误分类.主要原因是只考虑了连续变量和观测数据的约束条件,而忽略了离散变量自身的空间相关性.为了描述离散变量的空间相关性并获得序贯模拟中离散变量的条件权值,Journel和Gomez-Hernandez(1989)提出了序贯指示模拟(Sequential Indicator Simulation, SIS)算法,该算法在井位较多的条件下,能够取得较好的模拟效果,且在井附近的模拟结果较为可靠;Strébelle(2000)提出了基于单一正态方程模拟(Single Normal Equation Simulation, SNES)算法的多点统计,多点统计用训练图像代替了两点统计的变差函数,但在实际应用中存在训练图像难以获取和数据模板大小难以确定等问题;Cordua等(2016)提出了混点模拟(Mixed-point Simulation, MixSim)算法,该算法是将SNES和SIS相结合,垂向上进行多点统计,横向上进行两点统计,只适用于水平层状介质.
本文在贝叶斯线性反演的基础上,结合序贯高斯混合模拟(SGMixSim)和序贯指示模拟(SIS)来求取空间相关的离散变量的后验条件权值和连续变量的后验解析解,并利用序贯采样的方法求取整个模型参数,形成了结合序贯指示模拟的贝叶斯高斯混合线性反演方法.该方法能够对离散变量实现更加准确的分类,从而得到更好的连续变量反演结果,且具有较好的抗噪性.模型数据的试算和实际资料的应用结果表明本文提出的方法是有效的.
1 方法原理 1.1 贝叶斯理论考虑一个正演问题:
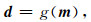
|
(1) |
式中,d表示观测数据,m表示模型参数,g是一个正演算子,表示将模型参数m映射到观测数据d.相应的反演问题可以表述为:在观测数据d、模型参数与观测数据之间的正演关系g及关于模型参数的先验信息的条件下,去推断模型参数m.为了能够量化待估模型参数的不确定性,本文使用贝叶斯的方法.在贝叶斯方法中,所有的信息状态都是用概率密度函数的形式表示,而反演问题的解就是后验概率密度函数,它是所有信息状态的一个结合,可以表示为
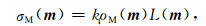
|
(2) |
式中,k是一个归一化常数,ρM(m)是模型参数的先验概率,L(m)是似然函数,描述了模型参数与观测数据的匹配程度.
1.2 高斯混合线性反演理论 1.2.1 高斯线性反演在贝叶斯的框架下,反演问题的解归结为求取后验条件概率,为了获得后验条件概率的解析解,通常假设观测数据d可以通过模型参数m的线性变换而得到,可以表示为:
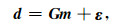
|
(3) |
式中,G代表线性算子,ε代表噪声.这里让N(μ, Σ)代表的是一个均值为μ,协方差为Σ的高斯分布.如果先验模型m~N(μm, Σm)和噪声ε~N(0, Σε),那么后验条件概率的均值和协方差矩阵的解析解可以表示为(Tarantola,2005):
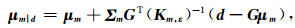
|
(4) |
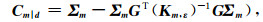
|
(5) |
式中,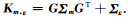
(4) 和(5)式是在高斯线性假设的基础上求取的后验概率解析解,然而模型参数通常并不符合高斯分布,模型参数由于不同离散变量的影响,往往呈现多峰特性,因此可以借助高斯混合模型(GMM)来描述模型参数的多峰分布.下面是将高斯线性反演理论拓展到高斯混合的情况中.
假设模型参数m服从高斯混合分布,即:
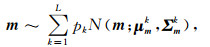
|
(6) |
式中,L代表分量的个数;pk代表分量的权值;N代表高斯分布;μmk和Σmk分别是第k个分量的先验均值和协方差矩阵,k=1, …, L.那么在给定观测数据d的条件下,模型参数m的后验条件分布也服从高斯混合分布(Grana et al., 2012),即:
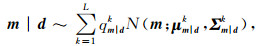
|
(7) |
式中,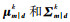
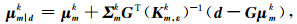
|
(8) |
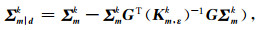
|
(9) |
式中,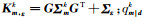
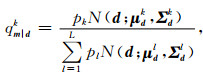
|
(10) |
式中,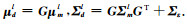
以上公式是逐点计算后验分布的,没有考虑后验建模的空间相关性,对后验分布进行采样是空间独立的,不能保持地质的连续性.因此,需要建立空间相关的后验模型.
1.3.1 连续变量空间相关的后验模型如果mi表示随机位置的待模拟点,ms表示在待模拟点的一定邻域内的已模拟的连续变量的值,那么mi在已模拟点ms和观测数据d的条件下的后验条件分布可以表示为一个高斯混合分布,即:
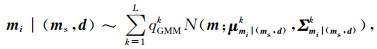
|
(11) |
式中,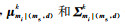
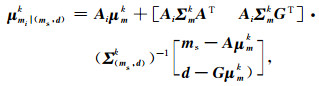
|
(12) |
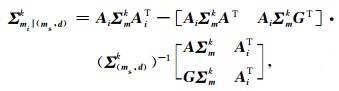
|
(13) |
式中,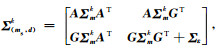
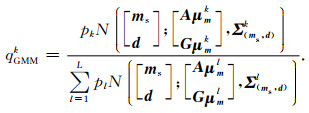
|
(14) |
基于高斯混合模型计算的离散变量的后验系数qGMMk只考虑了连续变量与观测数据的影响,而忽视了离散变量本身的空间结构变化,这会使离散变量在某些点被错误的归类,从而影响连续变量的反演结果.
在井位较多的情况下,可以利用序贯指示模拟(SIS)(Journel and Gomez-Hernandez, 1989)描述离散变量的空间相关性,同时获得离散变量的后验条件系数,且在离井较近的位置获得较为准确的后验条件系数.序贯指示模拟的主要原理是通过求解指示克里金方程组来计算条件累积分布函数,这里我们使用简单指示克里金,即:
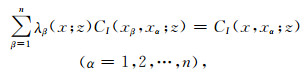
|
(15) |
式中,CI(xβ, xα; z)和CI(x, xα; z)分别是在位置xβ, xα和x, xα处截断值为z的指示协方差函数,λβ(x; z)是权值.然后通过序贯模拟的方法,就可以得到每一个分量的条件权值,将其表示为qSISk,qSISk右下角中的SIS表示该系数是通过序贯指示模拟(SIS)得到的.
为了利用序贯指示模拟的优点,建立离散变量空间相关的后验模型,本文将qGMMk和qSISk的线性组合作为最终的后验条件权值qk,即:
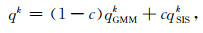
|
(16) |
式中,c=e-αd,d表示模拟点位置离所有已知井最近的横向距离,α是一个大于零的可调系数.
从c的表达式中可以看出,当模拟点离井越近c的值就越大,离井越远c的值就越小.这是考虑到序贯指示模拟以井数据作为条件数据,模拟结果在离井较近的位置较为准确,而在离井较远的位置准确度会下降,因此应该使序贯指示模拟得到的条件权值在离井较近的位置所占比重变大,在离井较远的位置比重变小.这样就可以借助序贯指示模拟改善离井较近的位置的归类效果,同时约束离井较远的位置的归类结果.最后通过后验系数qk就可以得到离散变量的归类结果和概率.
1.3.3 序贯采样然而,空间相关模型的采样需要非常大的计算代价.为了克服这个问题,我们利用序贯模拟的方法对后验模型进行采样(Hansen et al., 2006),同时可以对模型参数的随机场产生多次独立的实现.对于一个给定的空间位置,只需要确定在已知的模型参数值和观测数据条件下的该点的条件概率分布就能进行采样,具体步骤如下:
(1) 随机访问模型空间中的某一点mi.
(2) 按照(12)、(13)及(16)式分别计算后验条件均值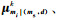
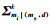
(3) 根据计算的的后验条件分布,随机的抽取一个值作为当前位置的反演结果.这一步,首先通过比较离散变量条件权值的大小确定高斯分量,然后从选择的分量中抽取一个连续变量的模拟值.
(4) 然后根据随机路径访问下一个位置,将上一次模拟的值作为已知数据,并作为该点的条件数据.
(5) 重复步骤(1)—(4)直到访问完所有的点.
所有这些采样点的集合就是这个后验随机场的一次独立实现,如果我们改变随机路径,将会得到一个不同的实现结果.如果对该方法进行多次运行,就会得到模型参数的多次实现结果.这种方法获得的每一次实现结果都忠实模型的先验分布、观测数据及模型的空间结构.
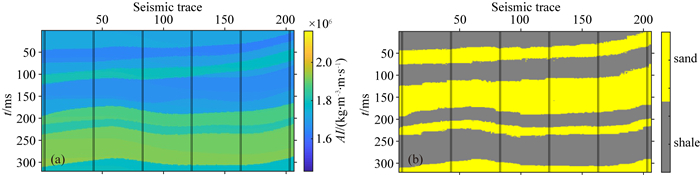
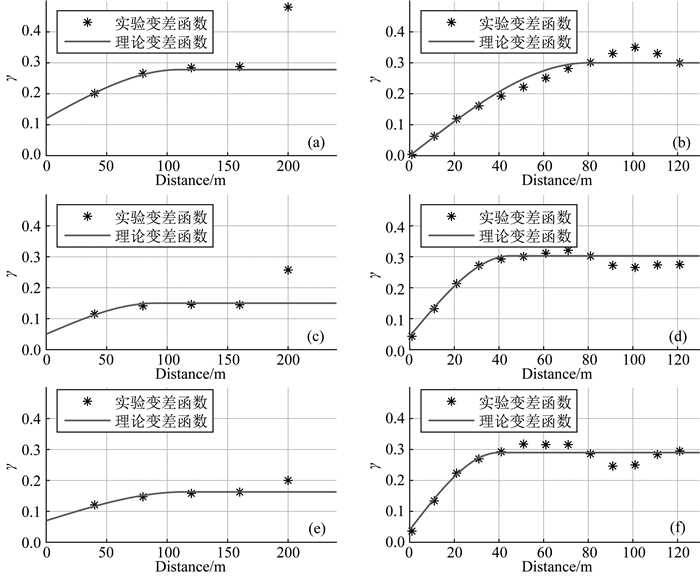
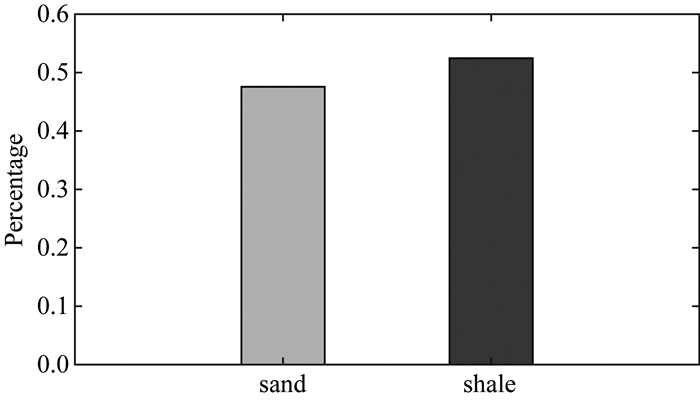
2 模型测试首先利用一个二维的模型来测试本文提出的方法的可行性.图 1中的(a)和(b)分别是声波阻抗(Acoustic Impedance,AI)模型和岩相模型,岩相模型中砂岩具有较低阻抗,泥岩具有较高阻抗,模型网格的大小为302×206,并假设每个网格的大小为1 m.在反演过程中,由于需要计算连续变量和离散变量的空间协方差矩阵,因此在图中的黑线位置处抽取6口伪井用作变差函数分析和条件数据.图 2为变差函数分析结果,声波阻抗、砂岩和泥岩所用的理论变差函数都是球状模型,从图中可以看出,声波阻抗的横向和纵向变程分别为110 m和80 m;砂岩的横向和纵向变程分别为90 m和45 m;泥岩的横向和纵向变程分别为115 m和40 m.在利用高斯混合模型和序贯指示模拟时,还需要砂泥岩的先验概率.图 3为从抽取的伪井数据中统计的砂泥岩的先验概率,得到砂岩和泥岩的先验概率分别为0.48和0.52.
|
图 1 模型数据 (a)声波阻抗模型;(b)岩相模型. Fig. 1 Model data (a) AI model; (b) Facies model. |
|
图 2 变差函数分析 (a)和(b)是声波阻抗(AI)在横向和纵向上的变差函数;(c)和(d)是砂岩在横向和纵向上的指示变差函数; (e)和(f)是泥岩在横向和纵向上的指示变差函数. Fig. 2 Analysis of variograms in the testing model (a) and (b) are variograms for AI in horizontal and vertical; (c) and (d) are indicator variograms for sand in horizontal and vertical; (e) and (f) are indicator variograms for shale in horizontal and vertical. |
|
图 3 砂泥岩的先验比例统计 Fig. 3 Statistics of prior proportion for sand and shale |
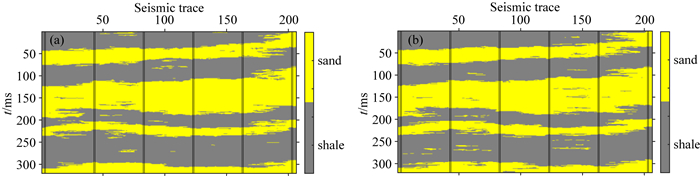
图 4为利用序贯指示模拟(SIS)得到的两次岩相模拟结果.与岩相模型对比,可以看到模拟结果在离井较远的位置存在许多岩相被错误归类的情况,因此仅依据序贯指示模拟并不能对岩相进行正确地分类.
|
图 4 利用序贯指示模拟得到的两次岩相模拟结果 Fig. 4 Two simulation results of facies using Sequential Indication Simulation |
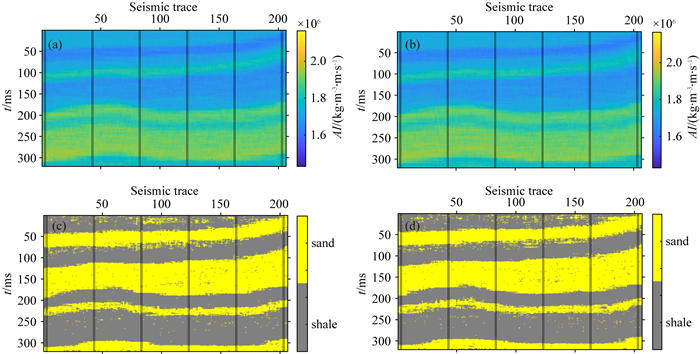
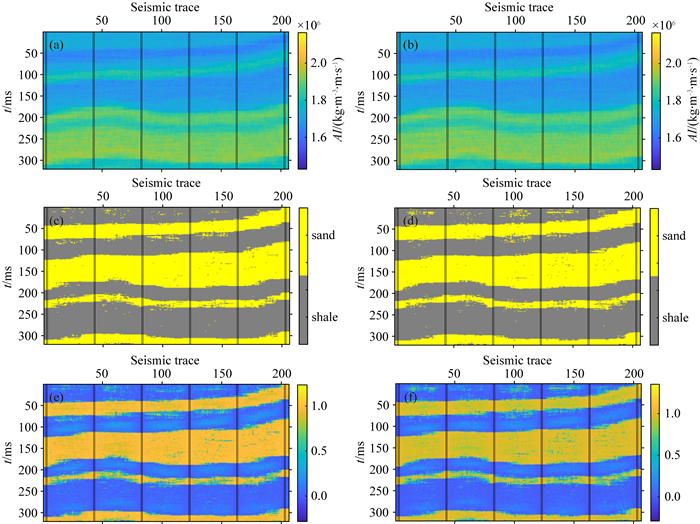
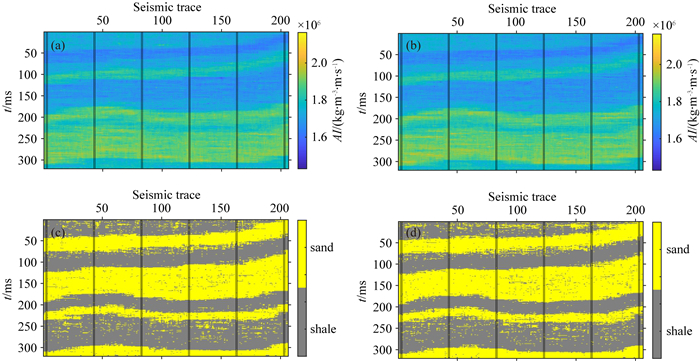
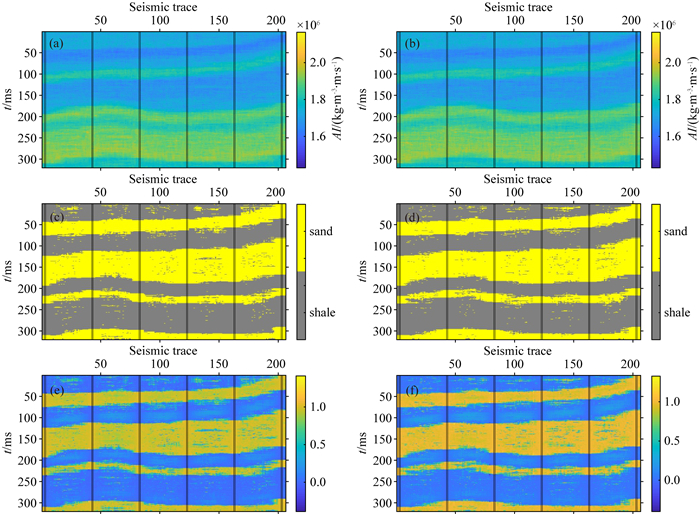
通过改变序贯模拟的路径和随机种子可以得到多次反演结果,图 5和图 6分别是序贯贝叶斯高斯混合线性反演(利用GMM)和本文提出的方法(结合GMM和SIS)在无噪声的情况下反演的两次结果.将反演结果与模型进行对比可以看出,在无噪声的情况下,两种方法反演的岩相大部分都能得到正确的归类,并且本文提出的方法岩相归类效果更好一些,而两种方法反演的声波阻抗没有太大差异.图 7和图 8分别是这两种方法在信噪比为4的情况下反演的两次结果,从图中可以看出,利用序贯贝叶斯高斯混合线性反演得到的结果中出现许多岩相被错误归类的情况,从而影响了声波阻抗的反演结果,而本文提出的方法依然能够较好的归类岩相,尤其是在井附近的位置,同时反演的声波阻抗结果也更好.主要原因是高斯混合模型在求取离散变量的后验条件权值时,它依赖于地震数据,容易受到地震数据噪声的影响,而本文提出的方法在求取离散变量的后验系数时,结合了SIS获取的后验系数,SIS考虑了离散变量本身的空间结构,而与地震噪声无关.在离井较近的位置使SIS得到的后验系数具有更大的比重,可以使井附近的位置反演效果更好,同时可以约束离井较远的位置的反演结果.因此将高斯混合判别模型和序贯指示模拟结合起来求取的离散变量的后验条件权值更加准确且具有更好地抗噪性.图 6和图 8中的(e)、(f)是使用本文提出的方法反演的砂岩概率,可以用作反演的岩相的不确性分析,在井附近的位置可以看到砂岩的概率更加稳定,而在远离井的位置,砂岩的概率出现波动性,这是SIS对井附近位置的反演结果的控制作用.通过模型测试,可以看出本文提出的方法能够更加准确地归类离散变量,从而提高反演的质量.
|
图 5 无噪声时利用GMM反演的两次结果 (a)和(b)是声波阻抗的两次反演结果;(c)和(d)是岩相的两次反演结果. Fig. 5 Two inversion results using GMM without noise (a) and (b) are two inversion results of AI; (c) and (d) are two inversion results of facies. |
|
图 6 无噪声时利用GMM和SIS反演的两次结果 (a)和(b)是声波阻抗的两次反演结果;(c)和(d)是岩相的两次反演结果;(e)和(f)是砂岩概率的两次反演结果. Fig. 6 Two inversion results using GMM and SIS without noise (a) and (b) are two inversion results of AI; (c) and (d) are two inversion results of facies; (e) and (f) are two inversion results of sand probability. |
|
图 7 信噪比为4时利用GMM反演的两次结果 (a)和(b)是声波阻抗的两次反演结果;(c)和(d)是岩相的两次反演结果. Fig. 7 Two inversion results using GMM when the SNR is 4 (a) and (b) are two inversion results of AI; (c) and (d) are two inversion results of facies. |
|
图 8 信噪比为4时利用GMM和SIS反演的两次结果 (a)和(b)是声波阻抗的两次反演结果;(c)和(d)是岩相的两次反演结果;(e)和(f)是砂岩概率的两次反演结果. Fig. 8 Two inversion results using GMM when the SNR is 4 (a) and (b) are two inversion results of AI; (c) and (d) are two inversion results of facies; (e) and (f) are two inversion results of sand probability. |
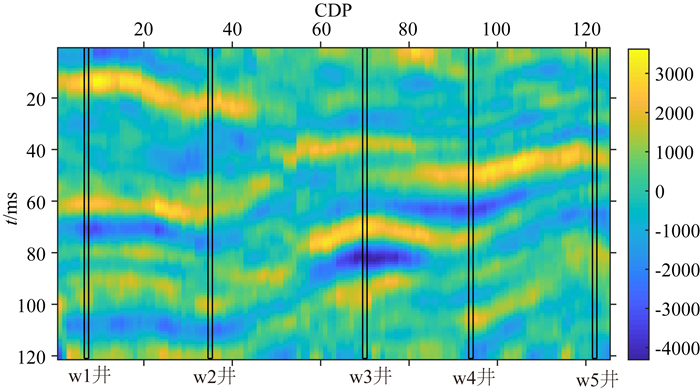
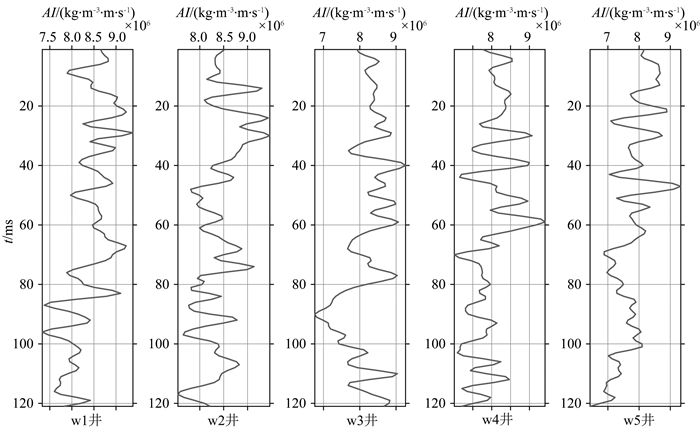
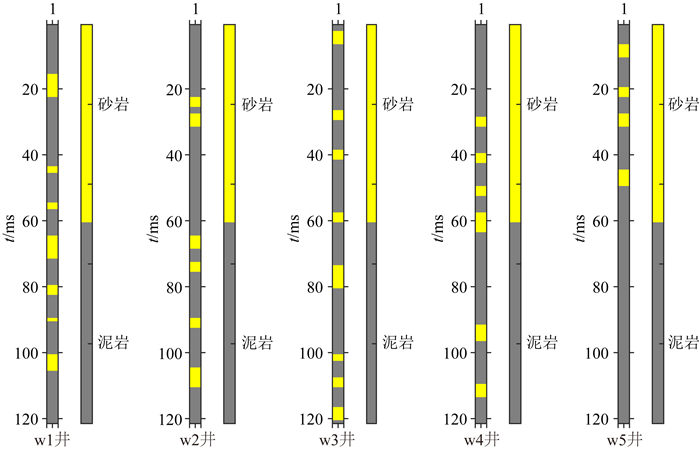
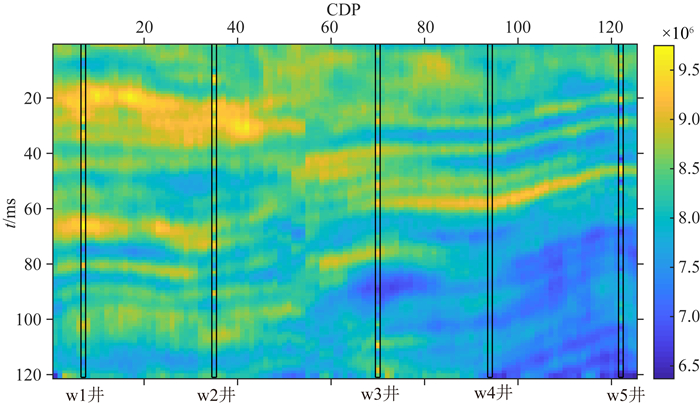
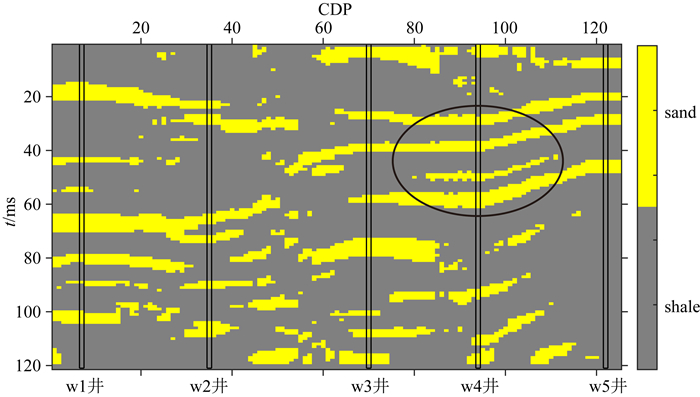
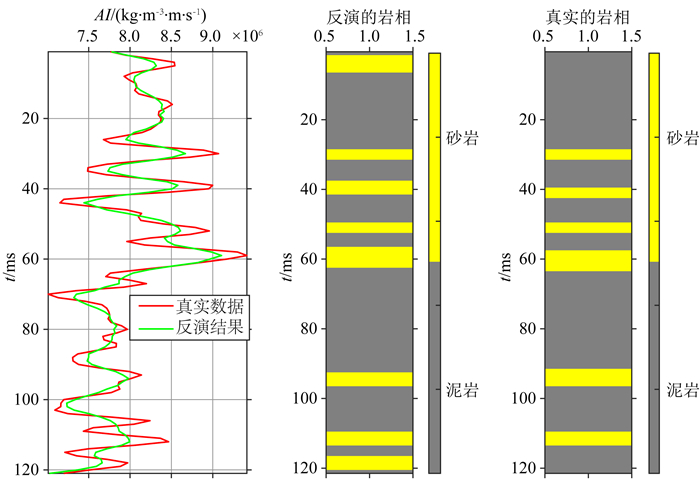
将本文提出的方法应用于国内某油田的实际工区,实际资料的研究表明目标工区主要以砂泥岩为主,且砂岩表现为高阻,泥岩表现为低阻.图 9为该工区的地震资料,共有125个CDP道集,每道121个采样点,采样率为2 ms.目标工区共有W1、W2、W3、W4和W5五口井,如图中的黑色方框所示.图 10和图 11分别为这五口井的声波阻抗(AI)曲线和岩相分类结果.结合邻近工区和这五口井的资料进行变差分析和砂泥岩的先验比例统计,W4井没有参与反演,用作验证井位,其他四口井用于反演的硬数据.从地震数据中提取一个主频为30 Hz的子波用于反演.图 12和图 13分别为反演得到的声波阻抗和岩相剖面,可以看到反演的结果具有较好的空间连续性,并在岩相剖面的黑色椭圆处有四套砂体,体现了空间相关的后验模型在保持离散相和连续变量的空间相关性的优势.图 14为反演的砂岩概率,可以用于判断各位置处砂岩的概率并预测储层的有利位置(如图中的黑色椭圆所示).为了验证本文提出的方法的可靠性,我们将W4井位置处的反演结果和W4的真实数据进行对比,如图 15所示.可以看到反演的声波阻抗与真实的数据吻合较好,反演的岩相除了少数点被错误归类外,大部分与真实的数据吻合较好,特别是在与图 14的黑色椭圆对应的位置处.实际资料的应用结果验证了本文提出的结合序贯指示模拟的贝叶斯高斯混合线性反演方法是有效可行的.
|
图 9 真实地震剖面 Fig. 9 Real seismogram |
|
图 10 五口井的声波阻抗曲线 Fig. 10 AI curves of five wells |
|
图 11 五口井的岩相 Fig. 11 Facies of five wells |
|
图 12 声波阻抗的反演结果 Fig. 12 Inversion result of AI |
|
图 13 岩相的反演结果 Fig. 13 Inversion result of facies |

|
图 14 砂岩概率的反演结果 Fig. 14 Inversion results of sand probability |
|
图 15 W4井位置的反演结果与真实井数据的对比 (a)声波阻抗AI的对比(红色代表真实数据,绿色代表反演结果);(b)岩相的对比(黄色代表砂岩,灰色代表泥岩). Fig. 15 Comparison of inversion results with real data in well W4 (a) Comparison of AI (Curves in red represent actual well data, Curves in green represent inverted data); (b) Comparison of facies (sand in yellow, shale in grey). |
基于高斯混合模型的贝叶斯线性反演方法容易受到观测数据中噪声的影响而不能实现离散变量的准确归类,从而影响了连续变量的反演结果.在此基础上,本文考虑离散变量的空间结构,利用序贯指示模拟确定离散变量自身的每一个空间位置的条件权值,再与高斯混合模型的得到条件权值进行线性结合得到最终的离散变量的后验条件权值,提出了结合序贯指示模拟的贝叶斯高斯混合线性反演方法,并对该方法进行了模型测试和实际资料的应用.研究表明:(1)离散变量和连续变量的空间相关的后验模型的建立使反演结果不易受观测数据中噪声的影响,提高了离散变量和连续变量的反演效果,并使反演结果保持较好的空间连续性;(2)考虑序贯指示模拟在井附近模拟结果较为准确的特点,从而根据模拟点的位置调整序贯指示模拟在后验条件权值的比重,使该方法在井数据较多的情况下具有较好的实用性;(3)该方法不仅可以反演连续变量,同时还可以反演离散变量及其概率,因此在储层预测中具有一定的潜力;(4)该方法还可以与岩石物理相结合,同时反演弹性参数和物性参数.
Amaliksen I. 2014. Bayesian inversion of time-lapse seismic data using bimodal prior models[Master's thesis]. Trondheim: Norwegian University of Science and Technology.
|
Aster R C, Borchers B, Thurber C H. 2012. Parameter Estimation and Inverse Problems. Amsterdam: Academic Press.
|
Buland A, Omre H. 2003. Bayesian linearized AVO inversion. Geophysics, 68(1): 185-198. DOI:10.1190/1.1543206 |
Connolly P A, Hughes M J. 2016. Stochastic inversion by matching to large numbers of pseudo-wells. Geophysics, 81(2): M7-M22. DOI:10.1190/geo2015-0348.1 |
Cordua K S, Hansen T M, Gulbrandsen M L, et al. 2016. Mixed-point geostatistical simulation:A combination of two-and multiple-point geostatistics. Geophysical Research Letters, 43(17): 9030-9037. DOI:10.1002/2016GL070348 |
Deutsch C V, Journel A G. 1992. GSLIB Geostatistical software library and user's guide. New York: Oxford University Press.
|
Dubreuil-Boisclair C, Gloaguen E, Bellefleur G, et al. 2012. Non-Gaussian gas hydrate grade simulation at the Mallik site, Mackenzie Delta, Canada. Marine and Petroleum Geology, 35(1): 20-27. DOI:10.1016/j.marpetgeo.2012.02.020 |
González E F, Mukerji T, Mavko G. 2008. Seismic inversion combining rock physics and multiple-point geostatistics. Geophysics, 73(1): R11-R21. DOI:10.1190/1.2803748 |
Grana D, Rossa E D. 2010. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion. Geophysics, 75(3): O21-O37. DOI:10.1190/1.3386676 |
Grana D, Mukerji T, Dovera L, et al. 2012. Sequential simulations of mixed discrete-continuous properties: Sequential Gaussian mixture simulation.//Abrahamsen P, Hauge R, Kolbjørnsen O eds. Geostatistics Oslo. Dordrecht: Springer, 17: 239-250.
|
Hansen T M, Journel A G, Tarantola A, et al. 2006. Linear inverse Gaussian theory and geostatistics. Geophysics, 71(6): R101-R111. DOI:10.1190/1.2345195 |
Hasselblad V. 1966. Estimation of parameters for a mixture of normal distributions. Technometrics, 8(3): 431-444. DOI:10.1080/00401706.1966.10490375 |
Journel A G, Gomez-Hernandez J J. 1989. Stochastic imaging of the Wilmington clastic sequence. SPE Formation Evaluation, 8(1): 33-40. |
Liu X Y, Li J Y, Chen X H, et al. 2018. A stochastic inversion method integrating multi-point geostatistics and sequential Gaussian simulation. Chinese Journal of Geophysics (in Chinese), 61(7): 2998-3007. DOI:10.6038/cjg2018L0543 |
Mosegaard K, Tarantola A. 1995. Monte Carlo sampling of solutions to inverse problems. Journal of Geophysical Research:Solid Earth, 100(B7): 12431-12447. DOI:10.1029/94JB03097 |
Pan X P, Zhang G Z, Chen H Z, et al. 2017. McMC-based AVAZ direct inversion for fracture weaknesses. Journal of Applied Geophysics, 138: 50-61. DOI:10.1016/j.jappgeo.2017.01.015 |
Sauvageau M, Gloaguen E, Claprood M, et al. 2014. Multimodal reservoir porosity simulation:an application to a tight oil reservoir. Journal of Applied Geophysics, 107: 71-79. DOI:10.1016/j.jappgeo.2014.05.007 |
Scales J A, Tenorio L. 2001. Prior information and uncertainty in inverse problems. Geophysics, 66(2): 389-397. DOI:10.1190/1.1444930 |
Sen M K, Stoffa P L. 1996. Bayesian inference, Gibbs' sampler and uncertainty estimation in geophysical inversion. Geophysical Prospecting, 44(2): 313-350. DOI:10.1111/j.1365-2478.1996.tb00152.x |
Sen M K, Stoffa P L. 2013. Global Optimization Methods in Geophysical Inversion. Cambridge: Cambridge University Press.
|
Strébelle S B. 2000. Sequential simulation drawing structures from training images[Ph. D. thesis]. Stanford: Stanford University.
|
Sun R Y, Yin X Y, Wang B L, et al. 2015. Stochastic inversion of elastic impedance based on Metropolis sampling algorithm. Geophysical and Geochemical Exploration (in Chinese), 39(1): 203-210. |
Sun R Y, Yin X Y, Wang B L, et al. 2016. A direct estimation method for the Russell fluid factor based on stochastic seismic inversion. Chinese Journal of Geophysics (in Chinese), 59(3): 1143-1150. DOI:10.6038/cjg20160334 |
Sung H. 2004. Gaussian mixture regression and classification[Ph. D. thesis]. Houston, Texas, USA: Rice University.
|
Tarantola A, Valette B. 1982. Inverse problems=quest for information. Journal of Geophysics, 50(3): 159-170. |
Tarantola A. 2005. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia: SIAM.
|
Ulrych T J, Sacchi M D, Woodbury A. 2001. A Bayes tour of inversion:a tutorial. Geophysics, 66(1): 55-69. DOI:10.1190/1.1444923 |
Wang B L, Yin X Y, Ding L X, et al. 2015. Study of fast stochasticinversion based on FFT-MA spectrum simulation. Chinese Journal of Geophysics (in Chinese), 58(2): 664-673. DOI:10.6038/cjg20150227 |
Yang P J, Yin X Y. 2008. Non-linear quadratic programming Bayesian prestack inversion. Chinese Journal of Geophysics (in Chinese), 51(6): 1876-1882. |
Yang Q L, Wu G C. 2016. Multi-scale seismic inversion method based on Bayesian theory. Progress in Geophysics (in Chinese), 31(3): 1246-1256. DOI:10.6038/pg20160343 |
Zhang G Z, Wang D Y, Yin X Y, et al. 2011. Study on prestack seismic inversion using Markov Chain Monte Carlo. Chinese Journal of Geophysics (in Chinese), 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
Zong Z Y, Yin X Y, Wu G C. 2012. AVO inversion and poroelasticity with P-and S-wave moduli. Geophysics, 77(6): N17-N24. DOI:10.1190/geo2011-0214.1 |
刘兴业, 李景叶, 陈小宏, 等. 2018. 联合多点地质统计学与序贯高斯模拟的随机反演方法. 地球物理学报, 61(7): 2998-3007. DOI:10.6038/cjg2018L0543 |
孙瑞莹, 印兴耀, 王保丽, 等. 2015. 基于Metropolis抽样的弹性阻抗随机反演. 物探与化探, 39(1): 203-210. |
孙瑞莹, 印兴耀, 王保丽, 等. 2016. 基于随机地震反演的Russell流体因子直接估算方法. 地球物理学报, 59(3): 1143-1150. DOI:10.6038/cjg20160334 |
王保丽, 印兴耀, 丁龙翔, 等. 2015. 基于FFT-MA谱模拟的快速随机反演方法研究. 地球物理学报, 58(2): 664-673. DOI:10.6038/cjg20150227 |
杨培杰, 印兴耀. 2008. 非线性二次规划贝叶斯叠前反演. 地球物理学报, 51(6): 1876-1882. DOI:10.3321/j.issn:0001-5733.2008.06.030 |
杨千里, 吴国忱. 2016. 基于贝叶斯理论的多尺度地震反演方法. 地球物理学进展, 31(3): 1246-1256. DOI:10.6038/pg20160343 |
张广智, 王丹阳, 印兴耀, 等. 2011. 基于MCMC的叠前地震反演方法研究. 地球物理学报, 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
 2019, Vol. 62
2019, Vol. 62


