2. 河北省地震动力学重点实验室, 河北三河 065201
2. Key Laboratory of Earthquake Dynamics in Hebei Province, Sanhe Hebei 065201, China
震源机制是分析地壳应力场的重要资料(Gephart and Forsyth, 1984; Michael, 1987; 许忠淮,1985;Angelier, 2002; Wan et al., 2016).地震震源机制的确定方法有P波初动解法(Reasenberg and Oppenheimer, 1985; 俞春泉等,2008)、P波初动和P/S振幅比结合的方法(Kisslinger et al., 1981; Snoke et al., 1984; 梁尚鸿等,1984; 吴大铭等,1989; Hardebeck and Shearer, 2003)、近震体波波形方法(倪江川等,1991;Dreger and Helmberger, 1993; 姚振兴等, 1994; Herrmann, 2013;杨宜海等,2017)、CAP方法(Zhao and Helmberger, 1994; Zhu and Helmberger, 1996;易桂喜等,2012)、面波方法(Udias, 1971; Aki and Patton, 1978; Patton, 1980; Kanamori and Given, 1981)、远震长周期地震波的矩心矩张量方法(Dziewonski et al., 1981)、W-Phase确定方法(Duputel et al., 2012)、大地测量资料确定的方法(陈运泰等,1979;巩守文等,1993)等等.这些资料确定同一地震的结果也有相当的离散度(万永革等,2001),为地震动力学分析或其他应用带来抉择的困难.这些结果都是震源错动方式的一种测量,因此可以按照测量结果给出一个中心值供以后的地震发生背景(陈章立等,2009)、地震应力触发(万永革等,2009)、地壳应力场分析(Michael, 1987; 许忠淮,1985)以及地震前应力方向改变的地震前兆研究(刁桂苓等,1994;万永革,2008).然而,震源机制描述有两个节面的走向、倾角和滑动角,又有P轴、T轴和B轴的倾向和倾伏角;对于P、T、B轴又存在相反的两个方向均表达同一结果,不能直接根据所测的多个震源机制对应参数的算术平均值求出多个震源机制的中心解.为解决此问题,必须首先定义两个震源机制结果之间的差别.在得到两个震源机制差别的表达方法之后,本研究对于几个震源机制测量结果,确定一个震源机制,使其与所有测量的震源机制的差别的平方和最小,这就是多个震源机制的中心解.本文首先分析了两个震源机制差别的最小空间旋转角的表达,然后根据最小空间旋转角平方的非线性问题将得到震源机制中心解的问题线性化,给出求解多个震源机制中心解的算法和程序.应该指出,Kagan(1991)已经给出了两个震源机制差别的计算方法,但该文的原理相当繁琐,难以理解.本文推导完全用另外一种较为简洁的思路推导,编制相应程序.刁桂苓等(1992)在对震源机制进行聚类分析时将震源机制P轴、T轴和B轴和另外一个震源机制的P轴、T轴和B轴的夹角之和作为两个震源机制的差别,但由于震源机制的三个力轴(P, T和B轴)在其相反方向表达意义完全相同,到底取哪个方向计算两个轴的夹角就陷入了难于选择的境地.万永革等(2001)曾经将震源机制节面上的滑动矢量的夹角作为两个震源机制差别,但同样面临震源机制的两个节面的选择困难.对于几个震源机制的中心解的求解则未见前人叙述.
1 两个震源机制的最小空间旋转角将两个震源机制进行比较,需要建立坐标系,将一个震源机制在坐标系中的表达通过坐标旋转转换到另一个震源机制对应坐标系的相同分量,从而进行定量比较.由于震源机制的P、T、B轴相互正交,并且仅考虑地震错动的方向,不考虑大小,可以采用P、T、B轴作为坐标轴,并且按照右手准则,P、T、B轴不能任意交换方向.只要将一个震源机制的P、T、B轴通过坐标旋转转换到另一个震源机制的P、T、B轴上,其空间旋转的角度就代表了两个震源机制的差别.因此本文选择震源机制的P、T、B轴组成的坐标系进行讨论.
假定震源机制m的P、T、B轴组成的坐标系经过旋转完全转到震源机制n的P、T、B轴组成的坐标系,其旋转矩阵为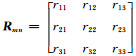
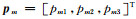
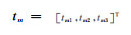
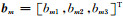
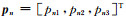
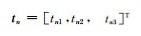
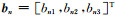
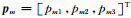
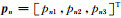
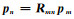

|
(1) |
同理得
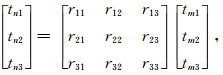
|
(2) |

|
(3) |
令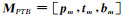
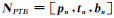
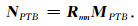
|
(4) |
在式(4)中右边同时乘以MPTBT,又考虑MPTB的列向量均为单位向量,并且正交,必有MPTBTMPTB=E,即MPTB为正交阵,有MPTB-1=MPTBT.这样可以得到
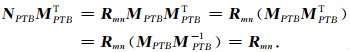
|
(5) |
所以

|
(6) |
Rmn的迹tr(Rmn),即主对角线上元素之和为
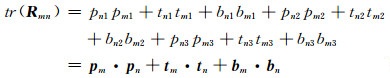
|
(7) |
现在考虑震源机制m的PTB坐标系经过绕着某个空间轴(假定为z轴)旋转θmn就完全转换到震源机制n的PTB坐标系下,则旋转矢量在xoy平面上,x轴和y轴绕着z轴的一次旋转就实现将震源机制m的PTB坐标系转换到震源机制n的PTB坐标系.而震源机制m的PTB坐标系三个矢量在xyz坐标系下表示为Mxyz,震源机制n的PTB坐标系三个单位矢量在xyz坐标系下表示为Nxyz,则有
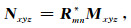
|
(8) |
其中
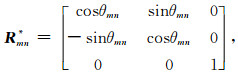
|
(9) |
式(4)和(8)的两种变换分别是以PTB轴为基和以xyz轴为基进行的变换,它们对应于同一种变换在不同基矢量中的表示,PTB轴坐标系和xyz轴坐标系一定存在着可逆的线性变换关系.设这种变换关系为可逆矩阵P,则
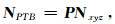
|
(10) |
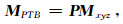
|
(11) |
则有

|
(12) |
(12) 式左乘P-1可得:
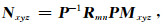
|
(13) |
比较(13)和(8)式可以得到

|
(14) |
根据线性代数中的相似矩阵定义可知,Rmn和Rmn*是相似矩阵.由于相似矩阵具有相同迹(《数学手册》编写组,1979),有tr(Rmn*)=tr(Rmn).
显然tr(Rmn*)=1+2cosθmn,这样有
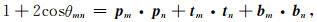
|
(15) |
即

|
(16) |
由于θnm1是一次空间旋转就将震源机制m的PTB坐标系转到震源机制n的PTB坐标系下,可以用该旋转角定义两个震源机制m和n的差别.由于这里定义的z轴旋转可能沿空间的任意方向,本文称之为空间旋转角.
在震源机制解中,PTB每个轴都有两个相反方向可作为坐标轴方向.假定m震源机制坐标系的P轴不变,T轴和B轴均改为反方向作为坐标轴,即tm和bm应改变符号为-tm和-bm,此时坐标轴仍然满足右手法则.则(16)式可变为
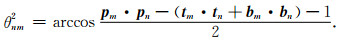
|
(17) |
同理假定m震源机制坐标系的T轴不变,B轴和P轴分别取相反方向,按照相同道理可以得到旋转角为
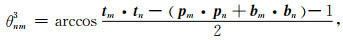
|
(18) |
假定m震源机制坐标系的B轴不变,T轴和P轴分别取相反方向,则可以得到旋转角为
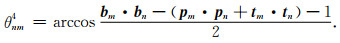
|
(19) |
因此按照震源机制P、T、B轴的两个方向的二义性,上面的四种考虑[(16)—(19)式]包括了旋转角的所有可能解,这四个旋转角都是从m震源机制坐标系到n震源机制坐标系的转换,表达这两个震源机制的差别可以采用它们中的最小值代替,本文称之为最小空间旋转角.有

|
(20) |
其中,α, β, γ分别是pm·pn,tm·tn和bm·bn,参看式(16—18).由于arccos是减函数,所以,α+(β+γ)的值越大,得到的(θmn)min越小.如果震源机制m和震源机制n的PTB轴完全重合,则α+(β+γ)=3,可以得到最小旋转角为0.这是很容易理解的,相当于不用任何旋转即可由震源机制m的PTB坐标系到震源机制n的PTB坐标系.反之如果α+(β+γ)为零,则可以得到(θmn)min最大,值为120°,这与Kagan(1991)的分析是一致的.
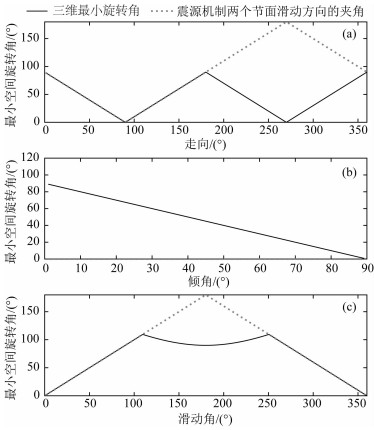
为验证上述分析结果的正确性,这里选择一个走向90°,倾角90°,滑动角为0°的震源机制为基准震源机制,(1)使其走向自0°到360°变化,倾角和滑动角不变,(2)倾角自0°到90°变化,走向和倾角不变,(3)滑动角自0°到360°变化,而走向和倾角不变,比较变化的震源机制和基准震源机制的空间旋转角(图 1).之所以这样选择,是因为震源机制的走向、倾角和滑动角是描述震源机制数据的三个独立变量,如果选择P, T轴的走向和倾伏角,则必定有一个输入参数不是独立的.采用走向、倾角和滑动角的数值可以转换为P, T轴的走向和倾伏角(万永革,2016).本文将参数变化后的震源机制和基准震源机制的最小空间旋转角以及两者之间的滑动方向夹角的变化绘成图 1.由图 1a可知,随着走向角的变化,最小空间旋转角分段呈线性变化.由于走向为90°和270°与规定的标准震源机制一致,因此最小空间旋转角为零;在走向为0°,180°和360°时,震源机制与标准震源机制差别最大,最小空间旋转角为90°;其余均随走向呈线性变化.这些定量计算的震源机制差别与通常的认识是一致的.本文也给出了变化的震源机制(所给定节面)与标准震源机制滑动方向(所给定节面)的滑动方向夹角的变化.可以看到,对于本例,在0°~180°范围内,两者表达是一致的.但在180°~360°范围内,两个震源机制的差别表达是不一致的.因为在180°~360°范围内,需要与变化震源机制另一个节面的滑动方向进行比较了.图 1b为走向和滑动角不变,改变倾角的情况,由于倾角为90°与规定的标准震源机制一致,因此在倾角为90°的最小空间旋转角为零,而倾角为0°时的震源机制与规定的标准震源机制差别最大,其最小空间旋转角为90°,在其余中间段两者为线性变化,这与通常的震源机制变化的认识一致.对于本例,最小空间旋转角与两个震源机制滑动方向夹角是一致的.图 1c为走向和倾角不变,改变滑动角的情况,这里滑动角为0°和360°与规定的标准震源机制一致,因此这时的最小空间旋转角为零.滑动角自0°变化至110°,震源机制与标准震源机制的最小空间旋转角自0°线性变化至109.2°,而后随着滑动角的增加,最小空间旋转角又逐渐减小,到滑动角为180°时达到一个低值(90°);滑动角自180°到360°是与0°到180°的最小空间旋转角是对称的.可见最小空间旋转角随着滑动角的变化是较为复杂的.本文也给出了变化的震源机制(所给定节面)与标准震源机制滑动方向(所给定节面)的滑动方向夹角的变化.可以看到,对于本例,在滑动角的110°~250°范围内,两者表达不一致的.在其他范围内基本一致.这说明采用两个震源机制滑动方向夹角所面临的问题:其一是震源机制存在2个节面,到底选择震源机制的哪个节面是不能提前给出的;其二是两个滑动方向的夹角最大为180°,而本文定义的最小空间旋转角最大为120°.但总的来说,采用最小空间旋转角表达震源机制之间的差别最为科学.
|
图 1 走向(a)、倾角(b)和滑动角(c)分别变化震源机制与基准震源机制的最小空间旋转角及滑动矢量夹角 Fig. 1 The minimum 3-D rotation angles and angles of slip vectors of focal mechanisms with variation of strike (a), dip (b) and rake (c) and the standard focal mechanism |
上节已经描述了两个震源机制差别的最小空间旋转角,本节叙述已知采用多种资料或多种方法得到的一个地震的多个震源机制,找到一个中心解,中心解与所有测量震源机制的最小空间旋转角的平方和最小,这就是本问题的目标函数.目标函数可以表述为
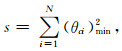
|
(21) |
其中(θci)min为中心震源机制与测量震源机制的最小空间旋转角.从上节分析来看,最小空间旋转角随震源机制参数的变化是非线性的,各个测量震源机制与中心震源机制的差别的平方也是非线性的.要采用线性方法求解,必须将其转换为线性问题.
对问题进行迭代求解必须选定一个接近“真实解”的初始解,在这个解的基础上采用Levenberg-Marquardt方法(Levenberg, 1944; Marquardt, 1963)进行迭代求解.由于初始解接近于估计的解,估计解可以表达为初始解邻域的泰勒展开,忽略2阶及以上导数项,得到

|
(22) |
其中,vi为所求震源机制中心解和第i个震源机制的最小空间旋转角平方和,i遍历所有已经得到的震源机制,从1到得到的震源机制总数N.将该式写成矩阵形式为

|
(23) |
(23) 式左边的第一个矩阵为雅克比矩阵,设为J,第二个矩阵为参数在初始解基础上的改变量,设为x,右边矩阵设为d,则改变量x可以采用
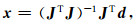
|
(24) |
求解,得到改变量x(即Δφ,Δδ,Δλ).然后令
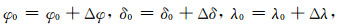
|
(25) |
将(25)式代入(23)式,重复上面的过程,直至达到最大迭代次数,或者解的改变量非常小,迭代终止,此时得到的解即为对非线性问题求解得到的最优解.
为防止雅克比矩阵奇异,又使求解过程快速收敛,Levenberg-Marquardt在前述算法的基础上加了一个可变的阻尼项(Marquardt, 1963),即将(24)式改为

|
(26) |
其中,I为单位矩阵,κ为执行过程中可变的数.在操作过程中,初始给定0.01, 如果采用阻尼项得到的参数修正使目标函数减少,则将κ降低10倍,使得步长增大,使解尽快逼近最优解;反之,如果采用阻尼项得到的参数修正使目标函数增大,说明步长取得太大,使参数超出了使目标函数减小的范围,此时将κ增加10倍,使得步长减少.这样反复迭代直至达到最大迭代次数,或对解的改善非常小,迭代终止.
将中心震源机制与测量的各个震源机制的最小空间旋转角的标准差作为其误差范围,标准差表述为

|
(27) |
其中s为式(21)所描述的反演问题目标函数值.类似于万永革(2015)的表述应力场误差的方法,将位于标准差S内的断层面解、P、T、B轴的范围求出,并展示在海滩球上,即可显示出中心震源机制的误差范围.
为避免选择初始解的不同对所得结果的影响,本研究分别将输入的各个机构的震源机制作为初始解,比较每次反演得到的目标函数,将目标函数最小的解作为最终解给出各个机构得到震源机制的中心解.
3 应用举例为验证上面方法的可行性,本研究首先搜集了对我国影响较大的2008年汶川地震的各个研究人员和机构给出的震源机制(表 1第2列),并得到了以各机构震源机制为“初始解”得到的中心震源机制(表 1第4列)及(27)式给出的标准差(表 1第5列).可以看到:不管以哪个机构或作者得到的震源机制为初始震源机制,采用本方法得到的中心震源机制解之间的差别很小,并且标准差精确到小数点后3位,表明本文解法对于不同的初始解是稳定的.尽管如此,本研究在程序设计中将各个机构测定的震源机制分别作为初始解,比较得到残差最小的解作为最终结果.对于汶川地震震源机制,发现将张勇等(2008)的震源机制作为初始解得到的中心震源机制的标准差最小.本研究以此结果(走向220.14°,倾角32.54°,滑动角116.35°)作为最终结果,压轴走向111.20°,倾伏角14.79°, 不确定范围分别为92.10°~129.60°和-2.66°~32.25°; 张轴的走向246.26°,倾伏角69.54°,不确定范围分别为227.16°~264.66°和59.89°~77.98°; 中间轴的走向17.48°,倾伏角13.81°,不确定范围分别为-1.12°~35.88°和4.16°~22.25°.得到的中心震源机制和各个机构测定震源机制的最小空间旋转角见表 1第6列,可以看到所得到的汶川地震震源机制中与中心解的最小空间旋转角的最大值为35.2°,最小值为1.8°,最小三维空间旋转角的标准差为19.3°.这里需要指出的是,选择张勇等(2008)的震源机制作为初始解得到的中心解的标准差最小,但并不意味着张勇等(2008)的震源机制解距中心解的距离最近,本例距中心解最近的震源机制为刘超等(2008)提供的.如前所述,寻找中心解的问题是一个非线性问题,采用雅克比矩阵求解各个参数的偏量有可能略微超过或者未到最优解.但应该偏离最优解很近,表 1第4列就说明了这个问题.这也是本文采用所有测得的震源机制作为初始解逐个进行反演选择标准差最小的解作为最优解的原因.所得到的中心震源机制及其不确定性绘于图 2.由图 2中的各个机构得到震源机制的P, T, B轴的位置,发现本研究得到中心解的不确定范围与其不完全符合.看上去似乎T轴分布比其不确定范围更大,而P轴和B轴分布比其不确定范围略小.这是由于我们按照两个震源机制P, T, B所组成的正交坐标系的最小空间旋转角,必须保证这三个轴是相互垂直的.这也说明我们不能用统计各个轴的方法得到各个轴的不确定范围.
|
|
表 1 不同作者给出的汶川地震震源机制解及得到的中心震源机制解及标准差 Table 1 Focal mechanisms given by different authors and central focal mechanism and its residuals |
|
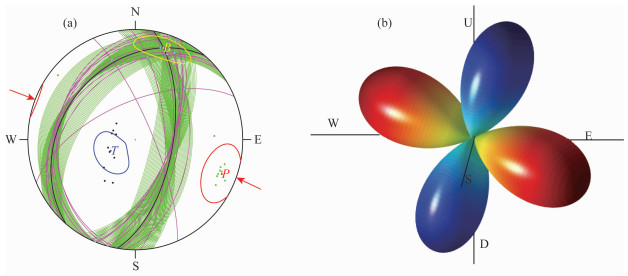
图 2 2008年汶川地震的中心震源机制解(a)及空间三维辐射花样(b) (a)中的黑色弧线表示中心震源机制的两个节面,绿色弧线覆盖区域为其不确定范围;红色、蓝色和黄色的点表示中心震源机制解的P轴、T轴和B轴,其周围对应颜色的封闭曲线表示其不确定性范围,绿色、黑色和蓝绿色的点表示各个机构得到的震源机制解P轴、T轴和B轴;紫色弧线表示各个机构和作者得到的震源机制节面.(b)中的压缩区域和膨胀区域分别用蓝色和红色表示. Fig. 2 Central focal mechanism of the 2008 Wenchuan earthquake (a), and its 3-D radiation pattern (b) In (a), black curves stand for nodal planes of central focal mechanism, and area of covered by green curves stands for its uncertainty. The red, blue and yellow dots show P, T and B axes, respectively, and the corresponding colored closed curves show their uncertainties. The green, black and cyan dots show P, T and B axes given by different authors or organizations, respectively. Magenta curves stand for focal mechanisms derived by different authors or organizations. In (b), the red and blue color stands for extensive and compressive areas, respectively. |
应该指出,虽然采用不同的资料(P波初动、P/S振幅比,体波,面波,CAP方法,大地测量资料等等)得到的震源机制有不同的含义:P波初动和体波资料表明了初始破裂的机制,而面波和大地测量资料得到的震源机制表达了地震破裂的整体机制,但震源机制都表达了同一种物理参数.虽然对于地震震级较大的汶川地震的北川—映秀断裂在西南部具有逆冲性质,而东北部具有走滑性质(Wan et al., 2017),但各种资料反演的震源机制具有可比性,采用本研究给出的中心震源机制解法仍然具有参考意义.下面给出一个可以看做一次破裂的较小地震的中心震源机制求解的例子.
2018年10月16日新疆精河5.4级地震发生后,地震监测人(https://mp.weixin.qq.com/s/uDFm91fjHKjW3uym1-8Bdw)发布了中国地震台网中心、中国地震局地球物理所、地震预测所等采用不同方法和资料得到的该地震的多个震源机制解.各个研究机构和作者所给出的该地震应急震源机制列成表 2.分别以各个震源机制为初始解得到的中心震源机制给出的标准差(表 2第5列)大体一致(在小数点四位后有一定涨落),表明采用这种方法得到的解是稳定的.尽管如此,本研究将各个机构和作者测定的震源机制分别作为初始解,比较得到标准差最小的解作为最终结果,发现采用赵博等震源机制结果作为初始解得到的震源机制的标准差最小.本研究以此(第一个节面走向109.00°,倾角, 51.81°,滑动角109.28°,第二个节面走向259.50°,倾角42.11°,滑动角67.23°)作为最终结果,P轴走向185.45°,倾伏角5.01°, 不确定范围分别为170.00°~201.00°和-10.00°~20.12°; T轴的走向77.50°,倾伏角74.11°, 不确定范围分别为62.05°~93.05°和62.08°~85.74°; B轴的走向276.80°,倾伏角15.04°, 不确定范围分别为261.35°~292.35°和3.01°~26.68°.得到的中心震源机制和各个机构和作者测定震源机制的最小空间旋转角见表 2第6列,中心震源机制及其不确定性绘于图 3.从图中可以看出,该地震震源机制测定的T轴的误差范围略小,P轴和B轴的误差范围略大一些.该例也成功给出了2018年新疆精河地震的中心震源机制解.
|
|
表 2 不同作者给出的新疆精河地震震源机制解及得到的中心震源机制解及标准差 Table 2 Focal mechanisms of the Jinghe, Xinjiang earthquake, given by different authors and central focal mechanism and its residuals |
|
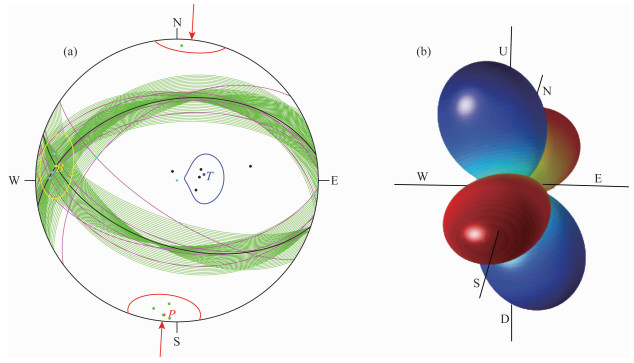
图 3 2018年新疆精河地震的中心震源机制解(a)及空间三维辐射花样(b) 图中符号表示意义见图 2图注. Fig. 3 Central focal mechanism of the Jinghe, Xinjiang, earthquake occurred in 2018 (a), and its 3-D radiation pattern (b) The symbolic meaning in the figure is the same as Fig. 2. |
本文推导了两个震源机制最小空间旋转角表示震源机制差别的方法,并采用分别改变一个震源机制的走向、倾角和滑动角验证了所推导的公式.然后构建了求解多个震源机制中心解的非线性求解方法,以近年来影响较大的2008年汶川地震和最近发生的2018年新疆精河地震为例求得了其中心震源机制解及其节面、P、T、B轴的误差范围,通过展示震源机制中心解与各个作者和机构给出的震源机制的空间关系表明所得到的中心解代表了所得的震源机制解的特征,为以后自同一地震的多个震源机制解中确定一个更为合理的解提供了方法.
按照最小空间旋转角的方法寻找中心震源机制的问题是一个非线性问题,本研究采用在初始解邻域中进行泰勒展开,仅取一阶项的方法将其转换为线性问题,并且迭代求解,得到中心震源机制解参数,这是求解非线性问题常用的方法.但其初始解的选择是一个关键问题,如果初始解离“真实解”太远,则在初始解邻域内进行泰勒展开只取一阶项则会产生较大误差.本研究采用两个措施来解决这个问题:(1)采用迭代求解,逐步逼近真实解.这样每步在前面初始解附近泰勒展开,相应减小了所求解与初始解的距离.(2)将所有观测的震源机制解逐个作为初始解比较所得解的标准差,选择标准差最小的解作为最优解.这样就避免了陷入局部极值问题.
对于最优化问题,为加快寻优速度,本研究采用Levenberg-Marquardt方法进行迭代求解.其实其他方法,如划界法、二分法、弦截法、牛顿-拉普森法等(Press et al., 1992),也可以得到问题的解.但这种寻优过程是类似的,得到的结果应该大体一致.
对于同一地震的多种方法或多种资料得到的震源机制,可以采用这种方法得到中心震源机制,可供以后进行应力触发(如万永革等,2007)、应力场反演(Michael, 1987)等地震动力学分析之用,也可以采用中心解和各个震源机制的最小旋转角判断各个震源机制的优劣.这种方法也可以在采用某种资料得到震源机制后,比较所得到震源机制与前人得到同一地震震源机制结果的差别,以检验自己所得到的震源机制与前人所得震源机制解的总体偏差,从而判断方法和资料的优劣.
本研究研发的求解两个震源机制最小空间旋转角以及求解几个震源机制中心解的程序可向感兴趣的读者提供.
致谢 审者提出了建设性修改意见,绘图采用MATLAB软件绘制而成,特此致谢.
Aki K, Patton H. 1978. Determination of seismic moment tensor using surface waves. Tectonophysics, 49(3-4): 213-222. DOI:10.1016/0040-1951(78)90180-4 |
Chen Y T, Lin B H, Wang X H, et al. 1979. A dislocation model of the Tangshan earthquake of 1976 from the inversion of geodesic data. Chinese Journal of Geophysics (in Chinese), 22(3): 201-217. |
Chen Z L, Zhao C P, Wang Q C, et al. 2009. A study on the occurrence background and process of Wenchuan MS8.0 earthquake. Chinese Journal of Geophysics (in Chinese), 52(2): 455-463. |
Compile Group of Mathematical Handbook. 1979. Mathematical Handbook (in Chinese). Beijing: People's Education press: 1398.
|
Cui X F, Hu X P, Yu C Q, et al. 2011. Research on focal mechanism solutions of Wenchuan earthquake sequence. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese), 47(6): 1063-1072. |
Diao G L, Yu L M, Li Q Z. 1992. Hierarchical clustering analysis of the focal mechanism solution-taking the Haicheng earthquake sequences for example. Earthquake Research in China (in Chinese), 8(3): 86-92. |
Diao G L, Yu L M, Li Q Z. 1994. Variation of stress field in the source region around a strong shock:an example. Acta Seismologica Sinica (in Chinese), 16(1): 64-69. DOI:10.1007/BF02651912 |
Dreger D S, Helmberger D V. 1993. Determination of source parameters at regional distances with three-component sparse network data. Journal of Geophysical Research:Solid Earth, 98(B5): 8107-8125. DOI:10.1029/93JB00023 |
Duputel Z, Rivera L, Kanamori H, et al. 2012. W phase source inversion for moderate to large earthquakes (1990-2010). Geophysical Journal International, 189(2): 1125-1147. DOI:10.1111/j.1365-246X.2012.05419.x |
Dziewonski A M, Chou T A, Woodhouse J H. 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. Journal of Geophysical Research:Solid Earth, 86(B4): 2825-2852. DOI:10.1029/JB086iB04p02825 |
Gephart J W, Forsyth D W. 1984. An improved method for determining the regional stress tensor using earthquake focal mechanism data:application to the San Fernando earthquake sequence. Journal of Geophysical Research:Solid Earth, 89(B11): 9305-9320. DOI:10.1029/JB089iB11p09305 |
Gong S W, Wang Q L, Lin J H. 1993. Study on dislocation model of the vertical deformation field of the Gonghe M6.9 earthquake and its evolution characteristics. Acta Seismologica Sinica (in Chinese), 15(3): 289-295. DOI:10.1007/BF02650403 |
Guo X Y, Chen X Z, Li Y E. 2010. Focal mechanism solutions for the 2008 MS8.0 Wenchuan earthquake and part of its aftershocks. Earthquake (in Chinese), 30(1): 50-60. |
Hardebeck J L, Shearer P M. 2003. Using S/P amplitude ratios to constrain the focal mechanisms of small earthquakes. Bulletin of the Seismological Society of America, 93(6): 2434-2444. DOI:10.1785/0120020236 |
Herrmann R B. 2013. Computer programs in seismology:An evolving tool for instruction and research. Seismological Research Letters, 84(6): 1981-1088. DOI:10.1785/0220110096 |
Hu X P, Yu C Q, Tao K, et al. 2008. Focal mechanism solutions of Wenchuan earthquake and its strong aftershocks obtained from initial P wave polarity analysis. Chinese Journal of Geophysics (in Chinese), 51(6): 1711-1718. |
Hu X P. 2010. Focal mechanism solutions of Wenchuan earthquake sequence and its dynamic explanation.[Master's thesis] (in Chinese). Beijing: The Institute of Crustal Dynamics.
|
Angelier J. 2002. Inversion of earthquake focal mechanisms to obtain the seismotectonic stress Ⅳ-a new method free of choice among nodal planes. Geophysical Journal International, 150(3): 588-609. DOI:10.1046/j.1365-246X.2002.01713.x |
Kagan Y Y. 1991. 3-D rotation of double-couple earthquake sources. Geophysical Journal International, 106(3): 709-716. DOI:10.1111/j.1365-246X.1991.tb06343.x |
Kanamori H, Given J W. 1981. Use of long-period surface waves for rapid determination of earthquake-source parameter. Physics of the Earth and Planetary Interiors, 27(1): 8-31. DOI:10.1016/0031-9201(81)90083-2 |
Kisslinger C, Bowman J R, Koch K. 1981. Procedures for computing focal mechanisms from local (SV/P) z data. Bulletin of the Seismological Society of America, 87(6): 1719-1729. |
Levenberg K. 1944. A method for the solution of certain non-linear problems in least squares. Quarterly of Applied Mathematics, 2(2): 164-168. DOI:10.1090/qam/10666 |
Liang S H, Li Y M, Su P Y, et al. 1984. On the determining of source parameters of small earthquakes by using amplitude ratios of P and S from regional network observations. Chinese Journal of Geophysics (in Chinese), 27(3): 249-257. |
Liu C, Zhang Y, Xu L S, et al. 2008. A new technique for moment tensor inversion with applications to the 2008 Wenchuan MS8.0 earthquake sequence. Acta Seismologica Sinica (in Chinese), 30(4): 329-339. DOI:10.1007/s11589-008-0333-y |
Marquardt D W. 1963. An algorithm for least-squares estimation of nonlinear parameters. Journal of the Society for Industrial and Applied Mathematics, 11(2): 431-441. DOI:10.1137/0111030 |
Michael A J. 1987. Use of focal mechanisms to determine stress:A control study. Journal of Geophysical Research Solid Earth:Solid Earth, 92(B1): 357-368. DOI:10.1029/JB092iB01p00357 |
Ni J C, Chen Y T, Wang M, et al. 1991. Moment tensor inversion of some aftershocks of the April 18, 1985, Luquan, Yunnan, China, earthquake. Acta Seismologica Sinica (in Chinese), 13(4): 412-419. |
Patton H. 1980. Reference point equalization method for determining the source and path effects of surface waves. Journal of Geophysical Research:Solid Earth, 85(B2): 821-848. DOI:10.1029/JB085iB02p00821 |
Press W H, Teukolsky S A, Vetterling B P. 1992. Numerical Recipes in Fortran 77:The Art of Scientific Computing. 2nd ed. Cambridge: Cambridge University Press: 1574.
|
Reasenberg P A, Oppenheimer D H. 1985. FPFIT, FPPLOT and FPPAGE:Fortran computer programs for calculating and displaying earthquake fault-plane solutions. U. S. Geol. Surv. Open-File Rept, No. 85-739. Menlo Park, California: U.S. Geological Survey.
|
Snoke J A, Munsey J W, Teague A G, et al. 1984. A program for focal mechanism determination by combined use of polarity and SV-P amplitude ratio data. Earthquake Notes, 55(3): 15. |
Udias A. 1971. Source parameters of earthquakes from spectra of Rayleigh waves. Geophysical Journal of the Royal Astronomical Society, 22(4): 353-376. DOI:10.1111/j.1365-246X.1971.tb03606.x |
Wan Y G, Zhou G W, Wu Z L, et al. 2001. China seismic mechanisms comparison for different determination. Seismological and Geomagnetic Observation and Research (in Chinese), 22(5): 1-15. |
Wan Y G, Shen Z K, Zeng Y H, et al. 2007. Evolution of cumulative Coulomb failure stress in northeastern Qinghai-Xizang (Tibetan) Plateau and its effect on large earthquake occurrence. Acta Seismologica Sinica (in Chinese), 29(2): 115-129. |
Wan Y G. 2008. Study on consistency of focal mechanism of mainshock and that of preshocks in Landers and Hector Mine Earthquake in United States. Earthquake Research in China (in Chinese), 24(3): 216-225. |
Wan Y G, Shen Z K, Sheng S Z, et al. 2009. The influence of 2008 Wenchuan earthquake on surrounding faults. Acta Seismologica Sinica (in Chinese), 31(2): 128-139. |
Wan Y G. 2015. A grid search method for determination of tectonic stress tensor using qualitative and quantitative data of active faults and its application to the Urumqi area. Chinese Journal of Geophysics (in Chinese), 58(9): 3144-3156. DOI:10.6038/cjg20150911 |
Wan Y G, Sheng S Z, Huang J C, et al. 2016. The grid search algorithm of tectonic stress tensor based on focal mechanism data and its application in the boundary zone of China, Vietnam and Laos. Journal of Earth Science, 27(5): 777-785. DOI:10.1007/s12583-015-0649-1 |
Wan Y G. 2016. Introduction to Seismology (in Chinese). Beijing: Science Press: 469.
|
Wan Y G, Shen Z K, Bürgmann R, et al. 2017. Fault geometry and slip distribution of the 2008 MW7.9 Wenchuan, China earthquake, inferred from GPS and InSAR measurements. Geophysical Journal International, 208(2): 748-766. DOI:10.1093/gji/ggw421 |
Wang W M, Zhao L F, Li J, et al. 2008. Rupture process of the MS8.0 Wenchuan earthquake of Sichuan, China. Chinese Journal of Geophysics (in Chinese), 51(5): 1403-1410. |
Wu F T, Wang P D, Chen Y T. 1989. Determination of focal mechanism using SH to P amplitude ratio. Acta Seismologica Sinica (in Chinese), 11(3): 275-278. |
Xu Z H. 1985. Mean stress field in Tangshan aftershock area obtained from focal mechanism data by fitting slip direction. Acta Seismologica Sinica (in Chinese), 7(4): 349-362. |
Yang Y H, Fan J, Hua Q, et al. 2017. Inversion for the focal mechanisms of the 2017 Jiuzhaigou M7.0 earthquake sequence using near-field full waveforms. Chinese Journal of Geophysics (in Chinese), 60(10): 4098-4104. DOI:10.6038/cjg20171034 |
Yao Z X, Zheng T Y, Wen L X. 1994. Moment tensor inversion method for determining the earthquake process by the use of P-wave form data. Acta Geophysica Sinica (in Chinese), 37(1): 36-44. |
Yi G X, Long F, Zhang Z W. 2012. Spatial and temporal variation of focal mechanisms for aftershocks of the 2008 MS8.0 Wenchuan earthquake. Chinese Journal of Geophysics (in Chinese), 55(4): 1213-1227. DOI:10.6038/j.issn.0001-5733.2012.04.017 |
Yu C Q, Tao K, Cui X F, et al. 2009. P-wave first-motion focal mechanism solutions and their quality evaluation. Chinese Journal of Geophysics (in Chinese), 52(5): 1402-1411. DOI:10.3969/j.issn.0001-5733.2009.05.030 |
Zhang Y, Feng W P, Xu L S, et al. 2008. Spatio-temporal rupture process of the 2008 great Wenchuan earthquake. Science in China Series D:Earth Sciences, 52(2): 145-154. |
Zhao L S, Helmberger D V. 1994. Source estimation from broadband regional seismograms. Bulletin of the Seismological Society of America, 84(1): 91-104. |
Zhu L P, Helmberger D V. 1996. Advancement in source estimation techniques using broadband regional seismograms. Bulletin of the Seismological Society of America, 86(5): 1634-1641. |
陈运泰, 林邦慧, 王新华, 等. 1979. 用大地测量资料反演的1976年唐山地震的位错模式. 地球物理学报, 22(3): 201-217. DOI:10.3321/j.issn:0001-5733.1979.03.001 |
陈章立, 赵翠萍, 王勤彩, 等. 2009. 汶川MS8.0级地震发生背景与过程的研究. 地球物理学报, 52(2): 455-463. |
崔效锋, 胡幸平, 俞春泉, 等. 2011. 汶川地震序列震源机制解研究. 北京大学学报(自然科学版), 47(6): 1063-1072. |
刁桂苓, 于利民, 李钦祖. 1992. 震源机制解的系统聚类分析-以海城地震序列为例. 中国地震, 8(3): 86-92. |
刁桂苓, 于利民, 李钦祖. 1994. 强震前后震源区应力场变化一例. 地震学报, 16(1): 64-69. |
巩守文, 王庆良, 林继华. 1993. 共和6.9级地震垂直形变场位错模式及其演化特征的研究. 地震学报, 15(3): 289-295. |
郭祥云, 陈学忠, 李艳娥. 2010. 2008年5月12日四川汶川8.0级地震与部分余震的震源机制解. 地震, 30(1): 50-60. |
胡幸平, 俞春泉, 陶开, 等. 2008. 利用P波初动资料求解汶川地震及其强余震震源机制解. 地球物理学报, 51(6): 1711-1718. DOI:10.3321/j.issn:0001-5733.2008.06.011 |
胡幸平. 2010.汶川地震序列震源机制及其动力学解释[硕士论文].北京: 中国地震局地壳应力研究所.
|
梁尚鸿, 李幼铭, 束沛镒, 等. 1984. 利用区域地震台网P、S振幅比资料测定小震震源参数. 地球物理学报, 27(3): 249-257. DOI:10.3321/j.issn:0001-5733.1984.03.005 |
刘超, 张勇, 许力生, 等. 2008. 一种矩张量反演新方法及其对2008年汶川MS8.0地震序列的应用. 地震学报, 30(4): 329-339. DOI:10.3321/j.issn:0253-3782.2008.04.001 |
倪江川, 陈运泰, 王鸣, 等. 1991. 云南禄劝地震部分余震的矩张量反演. 地震学报, 13(4): 412-419. |
《数学手册》编写组. 1979. 数学手册. 北京: 人民教育出版社, 1398: 1398.
|
万永革, 周公威, 吴忠良, 等. 2001. 中国地震震源机制测定结果的比较. 地震地磁观测与研究, 22(5): 1-15. DOI:10.3969/j.issn.1003-3246.2001.05.001 |
万永革, 沈正康, 曾跃华, 等. 2007. 青藏高原东北部的库仑应力积累演化对大地震发生的影响. 地震学报, 29(2): 115-129. DOI:10.3321/j.issn:0253-3782.2007.02.001 |
万永革. 2008. 美国Landers地震和Hector Mine地震前震源机制与主震机制一致现象的研究. 中国地震, 24(3): 216-225. DOI:10.3969/j.issn.1001-4683.2008.03.003 |
万永革, 沈正康, 盛书中, 等. 2009. 2008年汶川大地震对周围断层的影响. 地震学报, 31(2): 128-139. DOI:10.3321/j.issn:0253-3782.2009.02.002 |
万永革. 2015. 联合采用定性和定量断层资料的应力张量反演方法及在乌鲁木齐地区的应用. 地球物理学报, 58(9): 3144-3156. DOI:10.6038/cjg20150911 |
万永革. 2016. 地震学导论. 北京: 科学出版社: 469.
|
王卫民, 赵连锋, 李娟, 等. 2008. 四川汶川MS8.0级地震震源过程. 地球物理学报, 51(5): 1403-1410. DOI:10.3321/j.issn:0001-5733.2008.05.013 |
吴大铭, 王培德, 陈运泰. 1989. 用SH波和P波振幅比确定震源机制解. 地震学报, 11(3): 275-278. |
许忠淮. 1985. 用滑动方向拟合法反演唐山余震区的平均应力场. 地震学报, 7(4): 349-362. |
杨宜海, 范军, 花茜, 等. 2017. 近震全波形反演2017年九寨沟M7.0地震序列震源机制解. 地球物理学报, 60(10): 4098-4104. DOI:10.6038/cjg20171034 |
姚振兴, 郑天愉, 温联星. 1994. 用P波波形资料反演中强地震地震矩张量的方法. 地球物理学报, 37(1): 36-44. DOI:10.3321/j.issn:0001-5733.1994.01.005 |
易桂喜, 龙锋, 张致伟. 2012. 汶川MS8.0地震余震震源机制时空分布特征. 地球物理学报, 55(4): 1213-1227. DOI:10.6038/j.issn.0001-5733.2012.04.017 |
俞春泉, 陶开, 崔效锋, 等. 2009. 用格点尝试法求解P波初动震源机制解及解的质量评价. 地球物理学报, 52(5): 1402-1411. DOI:10.3969/j.issn.0001-5733.2009.05.030 |
张勇, 冯万鹏, 许力生, 等. 2008. 2008年汶川大地震的时空破裂过程. 中国科学D辑:地球科学, 38(10): 1186-1194. |
 2019, Vol. 62
2019, Vol. 62

