2. 国防科技大学气象海洋学院, 南京 211101;
3. 国家海洋局第二海洋研究所卫星海洋环境动力学国家重点实验室, 杭州 310012
2. College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China;
3. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China
随着数值模式能力以及计算机水平的不断提高,数值天气预报对人类生活的指导作用也日益加强.在这种大趋势下,GPS掩星探测技术应运而生,这是一种新兴的探测地球环境参数的方法,具有全天候、低费用、无系统长期漂移等优点,其不受天气状况影响的特点在天气预报及气候的应用中具有独特的优势.其基本原理是,由于大气的不均匀性,电磁波传播时会发生信号延迟(相对于真空环境),而这种延迟与大气状态参数有关,因此,通过对信号延迟的观测,就可以反演出大气环境参数.与其他卫星资料相比,GPS掩星观测资料能提供高精度、高分辨率、全球准均匀覆盖的地球电离层和中性层大气参数剖面(Melbourne et al., 1994;严豪健等,2007;Jin et al., 2011).
在掩星探测数据处理流程中,Abel反演是一个重要的环节,它把弯角转化成折射指数,由给定的折射指数数据n=n(r)(r为半径)通过下面的公式(称为Abel积分,其中a为影响参数,x=n(r))来计算电磁波传播的弯角序列:
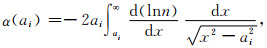
|
(1) |
其逆变换称为Abel变换,即通过给定的弯角序列α(a)来计算折射指数n:
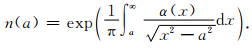
|
(2) |
Abel积分方程属于第一类Volterra型积分方程,最早是由Abel在19世纪末20世纪初在研究质点力学问题时提出的,后来在力学、光谱学、地震学、等离子物理及散射理论等许多领域中都得到了广泛的应用(刘克玲,1982;Gorenflo and Vessella, 1991;Groetsch,1993;Bukhgeim,1999;林剑等,2009;周义炎,2012)).众所周知,第一类Volterra型积分方程是不适定的(黄思训和伍荣生,2011),尤其其不稳定性为实际应用带来了很大的困难,在实际问题中常常利用Tikhonov正则化进行处理(Vauhkonen et al., 1998;Zhao et al., 2011;Yang and Fu, 2013;崔岩和王彦飞,2015);同时,无论是Abel积分方程还是Abel变换,在实际应用中都面临着如何进行高精度离散的问题.正因为如此,Abel积分方程(包括Abel变换)引发了许多学者的兴趣(Minerbo and Levy, 1969;Wing,1992;普小云等,1996;Steiner et al., 1999;Avazzadeh et al., 2011;吕涛和黄晋,2013).
从数学物理反问题的角度来看,在弯角α(a)已知的情况下,反演折射指数n(r)有两条途径:①利用Abel变换(2)直接计算;②把Abel积分方程(1)作为反问题求解.由于弯角α(a)是通过观测计算得到的,不可避免地含有误差,这部分误差在积分计算过程中很可能会被放大.因此,如果直接利用Abel变换(2)进行计算,所得到的结果是有问题的(肖庭延和宋金来,2000).如果利用Abel积分方程,首先需要将积分方程离散化,变成线性方程组再进行求解.这里有两个问题需要解决:一是被积函数具有弱奇性,同时,观测数据是离散的,导致了ln(n)可能不够光滑,因此,不能进行简单离散,需要找到合适的方法来定义导数dln(n)/dx以获得积分的高精度数值离散结果; 二是由于Abel积分方程(1)的不适定性,导致离散化后得到的线性方程组即线性反问题仍然具有不适定性,为解决该问题,常用的是正则化技术,其中以Tikhonov正则化技术(Tikhonov and Arsenin, 1977)的应用最为广泛.该技术通过添加正则化项η‖x‖2来实现,但当解具有不连续点时,该方法反演得到的近似解将会与真解产生较大偏差.在实际观测中,由于电离层及水汽作用的影响,弯角数据可能存在高频成分,从而导致剧烈的梯度变化,另外,电离层的影响可能导致解间断,此时,采用Tikhonov正则化方法会产生较大误差.作为处理这类问题有效的方法,Bayes算法被提了出来.
本文利用Bayes算法,基于Abel积分方程来反演折射指数.首先利用EGOPS软件仿真出150 km以下的弯角、碰撞参数及折射率等数据信息,并将60 km以下的折射率数据作为真实值; 然后采用Tikhonov正则化(通过L-曲线来确定最优的正则化参数η)来反演折射指数,并将该技术与Bayes算法的反演结果进行对比,依此来探究当原始数据具有误差时,Bayes算法是否可以得到优于Tikhonov正则化的反演结果.
1 Bayes算法的实施Bayes估计是将Bayes理论应用于参数估计的结果,是Bayes统计的主要部分.其基本思想是:通过“归纳推理”的统计方法,利用研究对象的先验信息形成先验分布,并结合观测得到的样本信息利用Bayes公式得到未知量的后验概率,再根据后验概率大小进行决策分类.

|
在求解第一类积分方程的过程中,相比于Tikhonov正则化以及全变差方法,Bayes算法具有很明显的优势,即无论待定的函数是连续的还是具有间断点,均能得到比较令人满意的反演结果(陆璐,2008).
我们将Abel积分方程(1)中的α(ai)记为αi,i=1, …, m,积分上限记为a1,根据大气折射指数与折射率的关系式
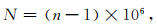
|
(3) |
利用等价无穷小代换,将lnn近似为10-6·N,并记为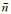
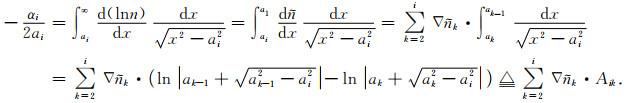
|
(4) |
经过一系列处理,我们将方程(1)离散化为

|
(5) |
其中,矩阵A的分量为Aik,
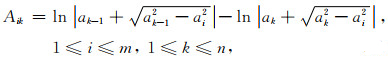
|
(6) |
向量e表示观测误差矩阵,满足Gauss型分布:
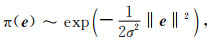
|
(7) |
其中,σ表示该分布的标准差,可以是一个数,也可以是一个矩阵.
定义一个向量ξ,其分量为
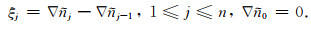
|
(8) |
ξ与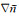

|
(9) |
此时,方程(5)化为
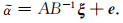
|
(10) |
我们把对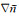
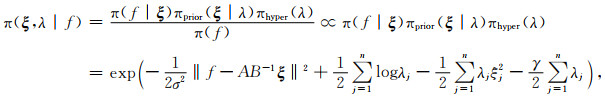
|
(11) |
其中,πprior表示先验密度.
在实际计算中,令k从1开始,给λ赋初值λ1,然后按如下步骤进行迭代,寻找ξ和λ的最大后验估计值.
第一步:从上式解得ξk,使其最大化π(ξ|λk, y),
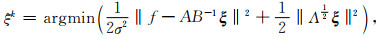
|
(12) |
即

|
(13) |
其中,Λ=diag(λk).
第二步:解λk+1,使其最大化π(λ|ξk, y),
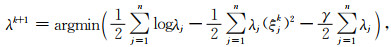
|
(14) |
即
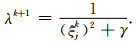
|
(15) |
第三步:计算ξk+1以及它与上次迭代结果的差|ξk+1-ξk|.如果小于事先设定的误差水平δ,则输出ξk+1和λk+1;否则,回到第二步.
整个Bayes算法过程如图 1所示.

|
图 1 Bayes算法及Tikhonov正则化算法流程图 Fig. 1 Flow chart of Bayesian algorithm and Tikhonov regularization |
为了探讨不同算法在利用弯角反演折射指数时的效果,我们利用EGOPS软件进行数据仿真.将Abel积分方程(1)中的积分上限截断到150 km处,利用该软件仿真出该高度以下的弯角、碰撞参数以及折射率等数据信息,由于电离层、水汽等的影响, 以及原始弯角数据的数量级变化,我们在弯角数据中加入误差水平为8%的相对误差,以及10-6与10-4的绝对误差,然后分别利用Bayes算法以及Tikhonov正则化技术进行反演,将反演结果分别与EGOPS给出的60 km以下的折射率廓线进行比较,并通过50次数值试验,给出了两种方法反演结果的平均误差随高度变化的廓线图.
2.2 反演结果首先,我们直接利用EGOPS仿真出的弯角数据进行反演,即认为此时的观测是没有误差的,结果如图 2所示.

|
图 2 Bayes算法与Tikhonov正则化方法反演的折射指数廓线对比图 Fig. 2 The refractive index profiles inversed by Bayesian algorithm and Tikhonov regularization |
图 2表示直接利用EGOPS仿真的弯角数据进行反演时,Bayes算法与Tikhonov正则化反演的折射指数的对比图,其中,蓝色实线代表的是EGOPS软件给出的根据其仿真出的弯角数据计算得到的60 km以下的折射指数廓线(我们在这里认为是真实值),红色的虚线代表Bayes算法的反演结果,绿色的虚线代表Tikhonov正则化的反演结果.上图表明,Bayes算法与Tikhonov正则化方法的反演结果一致,二者的均方根误差均为2.5470×10-8.
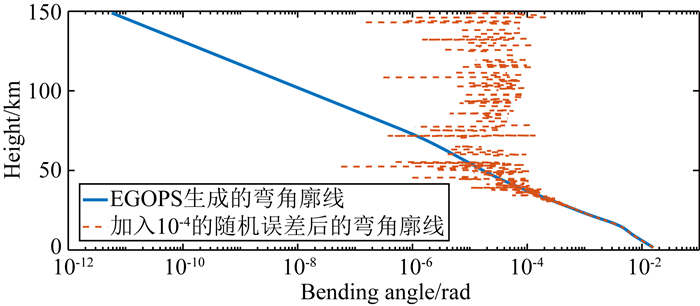
下面我们给出EGOPS仿真出的用于反演计算的弯角数据以及分别加入了8%、10-6以及10-4的随机误差的弯角数据示意图,如图 3、图 4、图 5所示.是否能利用该弯角数据较好地反演出折射指数,是我们对Bayes算法以及Tikhonov正则化技术的一个考察方面.

|
图 3 EGOPS仿真的弯角廓线及加入8%的相对误差后的弯角廓线 Fig. 3 Bending angle profiles of EGOPS simulation and with 8% relative error |

|
图 4 EGOPS仿真的弯角廓线及加入了10-6的绝对误差后的弯角廓线 Fig. 4 Bending angle profiles of EGOPS simulation and with 10-6 absolute error |
|
图 5 EGOPS仿真的弯角廓线及加入了10-4的随机误差后的弯角廓线 Fig. 5 Bending angle profiles of EGOPS simulation and with 10-4 absolute error |
将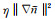

|
图 6 正则化参数对应的L-曲线 Fig. 6 The L-curve of regularized parameter |
利用EGOPS软件模拟的数据,针对所加入的8%的相对误差以及两组绝对误差(10-6与10-4),我们分别给出了Bayes算法及Tikhonov正则化反演的折射指数廓线,如图 7、8、9所示.

|
图 7 Bayes算法与Tikhonov正则化方法反演出的折射指数廓线(对应于8%的相对误差) Fig. 7 The refractive index profiles inversed by Bayesian algorithm and Tikhonov regularization (corresponding to 8% relative error) |

|
图 8 Bayes算法与Tikhonov正则化方法反演出的折射指数廓线(对应于10-6的绝对误差) Fig. 8 The refractive index profiles inversed by Bayesian algorithm and Tikhonov regularization (corresponding to 10-6 absolute error) |

|
图 9 Bayes算法与Tikhonov正则化方法反演出的折射指数廓线(对应于10-4的绝对误差) Fig. 9 The refractive index profiles inversed by Bayesian algorithm and Tikhonov regularization (corresponding to 10-4 absolute error) |
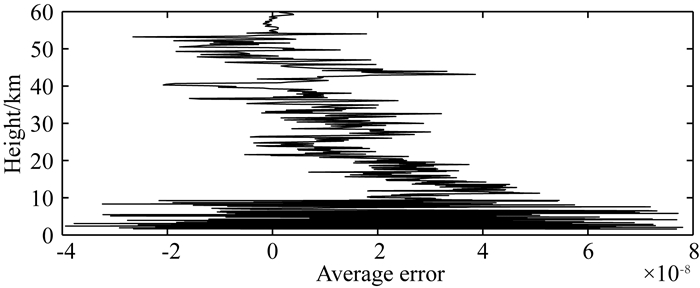
图 7、8、9表示在EGOPS仿真的弯角数据中加入随机误差后,Bayes算法与Tikhonov正则化反演出的折射指数廓线对比图,其中图 7对应的是8%的相对误差,图 8、9分别对应的是10-6与10-4的绝对误差,可以看出,Bayes算法反演得到的折射指数廓线更接近真实廓线.对于反演结果的评估,我们进行了50次数值试验,给出了在EGOPS仿真的弯角数据中加入8%的相对误差后,Bayes算法与Tikhonov正则化方法反演的折射指数的平均误差随高度变化的廓线,如图 10、11、12所示.
|
图 10 Bayes算法反演结果的平均误差廓线图 Fig. 10 Average error profile of Bayesian algorithm inversion results |

|
图 11 Tikhonov正则化方法反演结果的平均误差廓线图 Fig. 11 Average error profile of Tikhonov regularization inversion results |
|
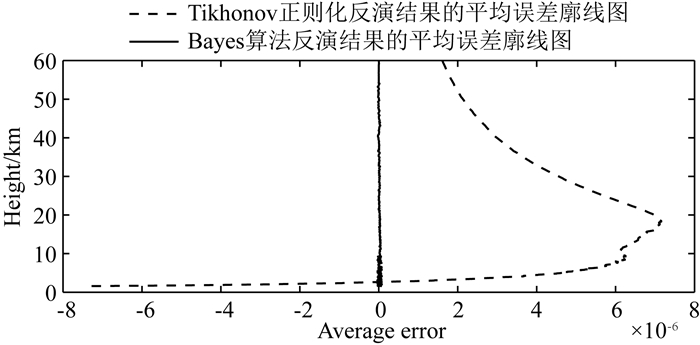
图 12 Bayes算法以及Tikhonov正则化方法反演结果的平均误差对比廓线图 Fig. 12 Average error profiles of Bayesian algorithm and Tikhonov regularization inversion results |
图 10、11分别代表利用Bayes算法以及Tikhonov正则化方法进行反演时,所得结果的平均误差随高度的变化廓线,为了对比的方便,我们绘制了图 12,其中实线代表Bayes算法对应的平均误差,虚线代表Tikhonov正则化技术对应的平均误差,通过这几张廓线图,我们有理由相信,在处理梯度变化很大、甚至有间断情况的数据时,Bayes算法比Tikhonov正则化技术更具优势.
3 总结对于折射指数的计算,无论是将其作为正问题,直接利用Abel变换(2)直接求解,还是作为反问题,利用Abel积分(1)进行求解,都面临积分方程的不适定问题.文本将Bayes算法应用到Abel积分方程(1)中,利用EGOPS软件仿真出的150 km以下的弯角数据进行反演计算,并将60 km以下的折射指数廓线作为真实廓线.当弯角数据中不含误差时,Bayes算法与Tikhonov正则化技术的反演结果具有很好的一致性,两种方法的均方根误差均为2.5470×10-8;当在弯角数据中分别加入8%的相对误差以及10-6与10-4的绝对误差后,相比于Tikhonov正则化技术,Bayes算法可以反演出更加接近真实廓线的折射指数,反演结果精度也更高.我们知道,在实际情况下,由于各方面客观因素的影响,由观测得到的数据信息往往不可避免地含有误差,因此,可以考虑利用Bayes算法,得到更加令人满意的反演结果.
致谢 感谢两位审稿人提出的宝贵意见.
Avazzadeh Z, Shafiee B, Loghmani G B. 2011. Fractional calculus for solving Abel′s integral equations using Chebyshev polynomials. Applied Mathematical Sciences, 5(45-48): 2207-2216. |
Bukhgeim A L. 1999. Volterra Equations and Inverse Problems. Netherlands: Novosibirsk, Izdatel'stvo Nauka.
|
Calvetti D, Somersalo E. 2007. A Gaussian hypermodel to recover blocky objects. Inverse Problems, 23(2): 733-754. DOI:10.1088/0266-5611/23/2/016 |
Cui Y, Wang Y F. 2015. Tikhonov regularization and gradient descent algorithms for tomography using first-arrival seismic traveltimes. Chinese Journal of Geophysics (in Chinese), 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
Gorenflo R, Vessella S. 1991. Abel Integral Equation: Analysis and Application. Berlin: Spring. DOI:10.1007/BFb0084665
|
Groetsch C W. 1993. Inverse Problems in the Mathematical Sciences. Wiesbaden: Vieweg+Teubner Verlag. DOI:10.1007/978-3-322-99202-4
|
Huang S X, Wu R S. 2011. Mathematical Physics Problems in Atmospheric Science (in Chinese). Beijing: China Meteorological Press.
|
Jin S G, Feng G P, Gleason S. 2011. Remote sensing using GNSS signals: current status and future directions. Advances in Space Research, 47(10): 1645-1653. DOI:10.1016/j.asr.2011.01.036 |
Lin J, Wu Y, Liu J N. 2009. Research on ionospheric inversion of GPS occultation. Chinese Journal of Geophysics (in Chinese), 52(8): 1947-1953. DOI:10.3969/j.issn.0001-5733.2009.08.001 |
Liu K L. 1982. Several kinds of Abel transform methods of measuring the physical parameters of axisymmetric plasma radiation source. Spectroscopy and Spectral Analysis (in Chinese), 2(1-2): 7-13. |
Lu L. 2008. Bayesian algorithm and its application for solving integral equation of the first kind [Master′s thesis] (in Chinese). Shanghai: Fudan University, 6-23.
|
Lv T, Huang J. 2013. High Precision Arithmetic of Integral Equation (in Chinese). Beijing: Science Press.
|
Melbourne W G, Davis E S, Duncan C B, et al. 1994. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring. California: JPL Publication.
|
Minerbo G N, Levy M E. 1969. Inversion of Abel′s integral equation by means of orthogonal polynomials. SIAM Journal on Numerical Analysis, 6(4): 598-616. DOI:10.1137/0706055 |
Pu X Y, Xiong Y, Lin L Z, et al. 1996. Calculation of Abel inverse transformation cofficients in any equidistant discretization. Chinese Journal of Computational Physics (in Chinese), 13(2): 181-189. |
Steiner A K, Kirchengast G, Ladreiter H P. 1999. Inversion, error analysis, and validation of GPS/MET occultation data. Annales Geophysicae, 17(1): 122-138. DOI:10.1007/s00585-999-0122-5 |
Tikhonov A N, Arsenin V Y. 1977. Solutions of ill-posed problems. Mathematics of Computation, 32(144): 1320-1322. DOI:10.2307/2006360 |
Vauhkonen M, Vadasz D, Karjalainen P A, et al. 1998. Tikhonov regularization and prior information in electrical impedance tomography. IEEE Transactions on Medical Imaging, 17(2): 285-293. DOI:10.1109/42.700740 |
Wing G M. 1992. A Primer on Integral Equations of the First Kind-the Problem of Deconvolution and Unfolding. Philadelphia: Society for Industrial and Applied Mathematics.
|
Xiao T Y, Song J L. 2000. A discrete regularization method for the numerical inversion of Abel transform. Chinese Journal of Computational Physics (in Chinese), 17(6): 602-610. |
Yan H J, Fu Y, Hong Z J, et al. 2007. Space-Based GPS Meteorology and Inversion Technology (in Chinese). Beijing: China Science and Technology Press.
|
Yang F, Fu C L. 2013. The revised generalized Tikhonov regularization for the inverse time-dependent heat source problem. Journal of Applied Mathematics and Computing, 41(1-2): 81-98. DOI:10.1007/s12190-012-0596-2 |
Zhao X F, Huang S X, Du H D. 2011. Theoretical analysis and numerical experiments of variational adjoint approach for refractivity estimation. Radio Science, 46(1): RS1006. DOI:10.1029/2010RS004417 |
Zhou Y Y, Shen W B, Wu Y, et al. 2012. Ground-based GPS VTEC constrained inversion method for ionospheric occultation. Chinese Journal of Geophysics (in Chinese), 55(4): 1088-1094. DOI:10.6038/j.issn.0001-5733.2012.04.003 |
崔岩, 王彦飞. 2015. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法. 地球物理学报, 58(4): 1367-1377. DOI:10.6038/cjg20150423 |
黄思训, 伍荣生. 2011. 大气科学中的数学物理问题. 北京: 气象出版社.
|
林剑, 吴云, 刘经南. 2009. 电离层GPS掩星反演技术研究. 地球物理学报, 52(8): 1947-1953. DOI:10.3969/j.issn.0001-5733.2009.08.001 |
刘克玲. 1982. 测量轴对称等离子体辐射源物理参数时所用的几种Abel变换法. 光谱学与光谱分析, 2(1-2): 7-13. |
陆璐. 2008.求解第一类积分方程的Bayes算法及其应用[硕士论文].上海: 复旦大学, 6-23.
|
吕涛, 黄晋. 2013. 积分方程的高精度算法. 北京: 科学出版社.
|
普小云, 熊烨, 林理忠, 等. 1996. 任意等分Abel反演变换系数计标. 计算物理, 13(2): 181-189. |
肖庭延, 宋金来. 2000. Abel变换数值反演的离散正则化方法. 计算物理, 17(6): 602-610. DOI:10.3969/j.issn.1001-246X.2000.06.002 |
严豪健, 符养, 洪振杰, 等. 2007. 天基GPS气象学与反演技术. 北京: 中国科学技术出版社.
|
周义炎, 申文斌, 吴云, 等. 2012. 地基GPS VTEC约束的电离层掩星反演方法. 地球物理学报, 55(4): 1088-1094. DOI:10.6038/j.issn.0001-5733.2012.04.003 |
 2019, Vol. 62
2019, Vol. 62


