在常规地震数据采集中,被动源地震信号往往由于其能量弱、不易提取等原因而被忽视.近年来,对被动源地震勘探方法的深入研究发现其具有一系列常规主动源地震勘探不具有的优点.为了更精确地刻画地下介质的细节和深部构造信息,必须充分利用地表接收到的多震源多分量波场信息.本文主要研究主动源和被动源弹性波多分量地震数据的联合应用对于提高速度模型构建精度的作用.
主动源地震采集是指采用人工激发的震源产生地震波,在地表或地下一定深度布设检波器接收记录.被动源地震采集是指在地表或地下一定深度布设检波器,接收由非人工震源激发产生的地震波.近年来,对被动源地震勘探方法的研究使得被动源地震数据的重要性越来越受到重视.被动源地震勘探至少有以下优点:(1)受地表环境影响较小,可在城市、自然保护区等不适合进行主动源勘探的地区展开(许卓,2012);(2)携带真实的地下介质信息,用于缺失信息补偿时,比纯数学方法更具物理依据(张盼等,2015);(3)可进行灵活重构,且重构后虚拟震源位置确定已知(Wapenaar and Fokkema, 2006;Draganov et al., 2006);(4)对深部照明更充分,来自目标层附近的震源信号携带有丰富的构造参数信息(Vesnaver et al., 2010;Zhang P et al., 2016);(5)频带宽,可用于补偿常规主动源缺失的频带信息(Zhang et al., 2015;Alali et al., 2016;张盼,2018).尽管被动源地震勘探存在如上所述的优点,但是其能量弱、信噪比低等缺点也限制了其应用效果.针对此,本文提出了主动源和被动源弹性波地震数据的多分量混合采集和联合应用.利用被动源地震数据辅助和补偿主动源地震数据,从而提高弹性波全波形反演的效果.
对主动源和被动源地震数据的重构以及联合成像已有一些研究.Berkhout和Verschuur(2009, 2011)提出了一种主动源和被动源联合成像的理论框架.Vesnaver等(2010)模拟了CO2注入区的三维主动源和被动源地震数据混合采集,并进行了层析成像研究,发现被动源可以作为新的照明震源,并且能提高薄气储层的成像效果.Forgues等(2011)在一个注蒸汽重油开采区同时采集了主动源和被动源地震数据,并成功监测到蒸汽注入期间储层的时移变换.张盼等(2015)提出了主动源和被动源地震数据的插值重构方法,并将联合地震数据应用于叠前偏移成像,验证了主被动源地震数据在成像中的互补作用.Zhang等(2015)利用被动源的低频信息成功重构了主动源地震数据的缺失低频信息,并发现利用低频重构后的地震数据能提高深部成像效果.Alali等(2016)采用多维反褶积方法对主动源和被动源地震数据进行了融合,成功达到了数据拓频的目的.另外,一些针对浅层面波勘探的主被动源地震数据联合应用研究也已展开(Park et al., 2005;Xu et al., 2013).Baradello等(2015)利用被动源面波地震数据补偿主动源面波地震数据,成功得到了浅部介质的纵横波速度比.李欣欣(2017)研究了主动源与被动源瑞利波联合成像方法,使瑞利波成像的精度和深度均得到了提高.Hayashi(2017)将主动源和被动源联合面波勘探方法应用于实际数据,成功反演了地下横波速度结构.
本文采用的速度模型构建方法为全波形反演方法,其能充分利用地震数据的走时、振幅和相位等信息,是目前精度最高的地震速度反演建模方法.地震波在地下介质中传播时,不仅有纵波,还有横波和各种转换波.因此,弹性介质比声波介质更接近实际复杂的地下介质情况.弹性波全波形反演理论和方法最初由Tarantola(1986, 1988)和Mora(1987, 1988)提出和发展.Crase等(1990)最早将弹性波全波形反演方法应用于实际数据.近年来,随着计算能力的提升,弹性波全波形反演的方法研究和实际应用得到了快速的发展.Prieux等(2013)通过立体层析成像构建初始模型,对一套宽角数据进行了频域弹性波全波形反演计算.Vigh等(2014)对墨西哥湾的一套海底电缆四分量地震数据进行了三维弹性波全波形反演计算.孙宏宇等(2015)针对金属矿速度建模问题,提出了基于可视性分析与能量补偿的弹性波全波形反演方法.王毓伟等(2016)提出了综合利用包络目标函数和多尺度等策略的弹性波全波形反演分步反演策略.Zhang Q C等(2016)通过对时间域褶积型不依赖子波的目标函数进行加窗,提出了一种稳健的不依赖子波的弹性波全波形反演方法.张盼等(2018)将各向异性全变分约束引入到弹性波全波形反演中,用以压制多震源同时反演时的串扰噪声.
本文主要研究主动源和被动源弹性波多分量地震数据的联合对于速度模型构建的作用,主要利用了被动源地震数据的照明优势和低频优势来辅助和补充主动源地震数据.首先,针对主动源和瞬态被动源数据的反演,提出了基于被动源照明补偿的弹性波全波形反演策略,并利用动态随机组合策略压制震源点附近的异常更新量.然后,针对主动源和噪声被动源数据的反演,提出了基于地震干涉和不依赖子波算法的弹性波全波形反演策略,能同时克服被动源位置不确定和子波未知的问题.最后,通过两组算例验证了本文提出方法的有效性.
1 方法原理 1.1 弹性波全波形反演方法原理二维介质中,弹性波多分量地震数据全波形反演的目标函数可以写为
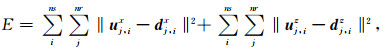
|
(1) |
其中,E为目标函数值,ns和nr分别表示震源数量和检波器数量,i和j分别表示震源索引和检波器索引,ux和uz分别表示合成数据的x和z分量,dx和dz分别表示观测数据的x和z分量.目标函数E关于拉梅常数λ和μ的导数可以分别表示为
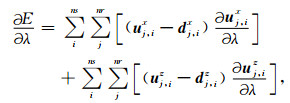
|
(2) |
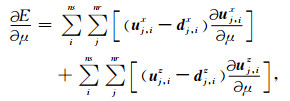
|
(3) |
根据伴随状态法(Mora,1987;Plessix,2006),梯度公式(2)和(3)可以写为:
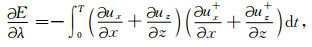
|
(4) |

|
(5) |
其中,ux和uz分别表示正传波场的x和z分量,ux+和uz+分别表示伴随波场的x和z分量.从公式(4)和(5)可知,λ的更新量主要由波场的散度决定,μ的更新量由波场的散度和旋度共同决定.对于公式(4)和(5),x分量的伴随源为(uj, ix-dj, ix),z分量的伴随源为(uj, iz-dj, iz).本文的优化算法采用介于最速下降法和牛顿法之间的共轭梯度法(Mora,1987;Sheng et al., 2006;Zhang et al., 2017),它利用当前梯度和上一次下降方向加权求得当前下降方向,具有超线性收敛速度,而且计算和存储量较牛顿类算法小.
1.2 基于动态随机组合的弹性波被动源照明补偿反演策略首先研究主动源地震数据与瞬态被动源地震数据的联合反演策略.本文中,瞬态被动源数据指震源子波有明显的主能量且延续时间较短,在记录上有明显的同相轴的被动源地震数据.本文采用不同能量的雷克子波作为瞬态被动源子波.对于该类型的被动源,定位和子波估计是较为关键的处理,并已有一些研究(Kamei and Lumley, 2014;Zhang P et al., 2016).本文重点研究反演和异常压制策略,因此,这里假设被动源位置和子波均已知,利用被动源地震数据在反演后期提高深部反演效果.
在被动源弹性波全波形反演中,由于震源点附近会产生局部的极值,导致正常的迭代方法很难收敛,且会在震源点附近产生错误的局部极小解.针对此,本文提出了动态随机组合反演策略.
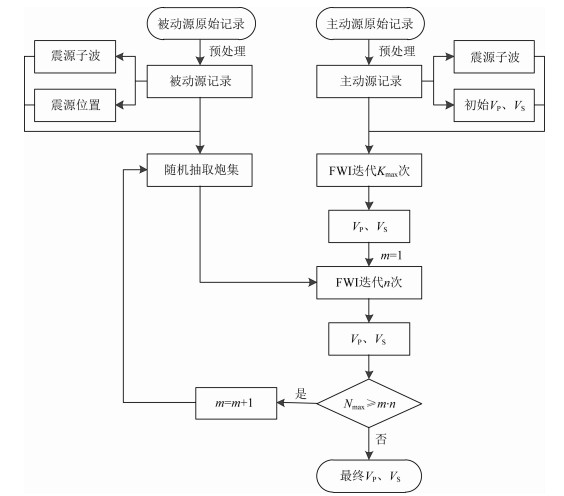
动态随机组合方法借鉴于主动源全波形反演中的动态随机编码策略(Boonyasiriwat and Schuster, 2010;Hu et al., 2016;Zhang et al., 2017; 张盼等, 2018),是在被动源反演时,每次随机抽取少量被动震源进行反演,并且在每组被动源反演迭代一定次数后,再换下一组随机抽取的被动源进行反演.在具体实施时,需要将每一炮被动源数据与相应的震源子波参数一一对应.抽取到某一炮被动源数据时,需要利用相应的震源子波参数进行正反演.前一组被动源反演时产生的震源异常值,会在接下来的动态反演中被更新校正.另外,在每组动态反演中,本文采取对震源附近的梯度值进行异常剔除和平滑的策略,进一步保证对震源点附近极值的压制.本文提出的基于动态随机组合的弹性波被动源照明补偿反演流程如图 1所示.
|
图 1 基于动态随机组合的弹性波被动源照明补偿反演策略流程图 Fig. 1 The flow diagram of elastic passive source illumination compensation FWI strategy based on dynamic random combination |
本节主要针对主动源和噪声型被动源地震数据的联合应用.本文中,噪声型被动源数据是指震源子波呈现随机噪声形态且延续时间较长,记录杂乱无章的被动源数据.本文采用随机噪声序列作为震源子波模拟该类被动源地震记录.噪声型被动源存在子波估计困难和震源定位困难等问题.针对此,本文提出了基于地震干涉与不依赖子波算法的联合反演策略.
假设地下弹性介质中随机分布有n个噪声源,地表xi和xj位置布设有两个检波器.则弹性介质噪声源干涉重构方程为(Wapenaar and Fokkema, 2006;Draganov et al., 2006)
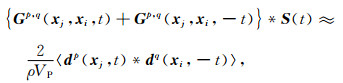
|
(6) |
其中,上角标p和q代表数据的不同分量,对于二维情况,均可以代表x分量或z分量.Gp, q(xj, xi, t)代表在xi位置的q分量震源激发,在xj位置接收的p分量格林函数,t代表时间.*表示褶积运算,S(t)表示虚拟震源子波,ρ代表密度,VP表示纵波速度,dp(xj, t)表示在xj接收的p分量地震记录,dq(xi, -t)表示在xi接收的q分量地震记录,〈·〉表示空间整体平均.为简便起见,将公式(6)简写为
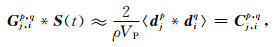
|
(7) |
其中,Cj, ip, q代表重构的虚拟炮记录,i和j分别表示虚拟震源和虚拟检波器的位置,q和p分别表示震源和检波器的分量.
由公式(6)和(7)可知,在地表分别接收x和z分量的被动源地震记录,可以得到四种不同类型的虚拟炮记录,分别是Cj, ix, z,Cj, ix, x,Cj, iz, z和Cj, iz, x.不同的虚拟炮记录对于不同速度模型构建的贡献是不同的.考虑到充分利用不同虚拟炮组合的优势,本文采用Cj, ix, z和Cj, iz, z反演纵波速度模型,采用Cj, ix, x和Cj, iz, x反演横波速度模型.
要利用公式(7)中的虚拟炮记录进行全波形反演,需要知道虚拟炮记录的震源位置和震源子波.经过地震干涉之后,震源位置是确定已知的,为地表作为虚拟震源的检波器位置.但是,虚拟震源子波S(t)是较难估计的.首先,理论上S(t)是地下噪声震源子波的自相关的平均,但是,由于被动震源子波未知,无法计算S(t).其次,重构记录中除了含有观测噪声和相干噪声外,还会产生由于不满足干涉假设而导致的假象,因此,用子波估计方法对S(t)进行估计也是较为困难的(Zhang et al., 2017).即使是构建速度模型的长波长成分,震源子波的误差也会对反演结果产生不可忽略的影响(Zhang et al., 2018).
借鉴于Choi和Alkhalifah(2011)提出的声波介质不依赖子波的反演算法,下面构建不依赖子波的弹性波多分量数据的目标函数,来消除虚拟子波对反演过程的影响.构建目标函数如下:
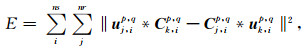
|
(8) |
其中,u表示合成地震记录,上角标p和q分别表示检波器分量和震源分量.合成记录的检波器分量和震源分量与所反演的虚拟炮记录保持一致.k表示参考道索引.本文中,对于炮点位置在xs的单炮记录,选取的参考道位置为(xs+2).将公式(8)中地震记录展开为格林函数与子波褶积的形式,得到

|
(9) |
其中,g表示合成记录对应的格林函数,ssyn表示合成记录对应的子波.将公式(9)进一步整理得到
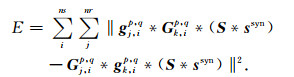
|
(10) |
可见,公式(10)所示的目标函数中,第一项和第二项含有公共子波项(S*ssyn).无论采用什么样的合成子波ssyn,也无论虚拟子波S的具体形态如何,采用公式(10)所示的目标函数后,子波对反演过程的影响几乎被消除.
该目标函数的另一个优点是无论接收的波场是位移还是速度,均可以用速度或位移方程来反演.假如接收到的波场为速度分量dv,其转化为位移分量du的频域积分公式可以写为

|
(11) |
其中,du表示位移观测数据,dv表示速度观测数据,ω表示频率,Gv表示速度观测数据对应的格林函数,S表示震源子波,S′为S的积分.可见,对速度数据dv转化为位移数据du,仅相当于更换了另一个积分子波,而格林函数项不变.采用公式(10)的目标函数进行反演时,新子波S′的影响将被消除.
公式(8)所示的目标函数对模型参数m的导数为
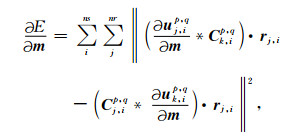
|
(12) |
其中,rj, ip, q=uj, ip, q*Ck, ip, q-Cj, ip, q*uk, ip, q.
对公式(12)应用伴随状态法的推导类似于Choi和Alkhalifah(2011)的推导,这里不再给出细节,直接给出伴随源的形式如下:
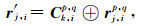
|
(13) |
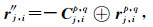
|
(14) |
其中,⊕表示互相关运算.r′j, i为除参考道之外,其他检波器位置处的伴随源.r″j, i为参考道位置的伴随源.伴随源的反传得到伴随波场,结合公式(4)和公式(5)可以得到梯度
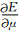
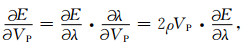
|
(15) |
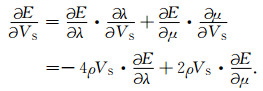
|
(16) |
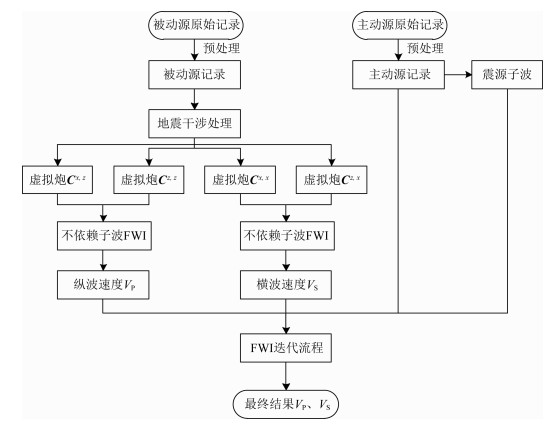
本文提出的基于地震干涉与不依赖子波算法的弹性波主被动源串联反演方法流程如图 2所示.
|
图 2 基于地震干涉法的弹性波主被动源串联反演策略流程图 Fig. 2 The flow diagram of elastic active and passive source successive inversion strategy based on seismic interferometry |
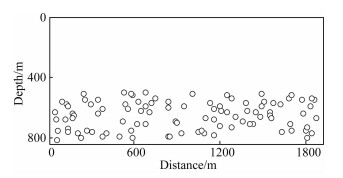
本节用模型数据测试基于动态随机组合的弹性波被动源照明补偿反演策略.采用的真实VP(纵波速度)模型如图 3a所示,采用的真实VS(横波速度)模型如图 3b所示.主动源采集时,震源在地表放炮,震源数量为24,左侧第一个震源位于x=50 m位置处,炮间距为80 m.检波器布设在地表 0~1910 m范围内,总共192个检波器,检波器间距为10 m.被动源采集时,100个被动震源随机分布于地下,震源位置如图 4所示.检波器布设与主动源采集时相同.

|
图 3 真实速度模型 (a)真实VP模型;(b)真实VS模型. Fig. 3 The true velocity model (a) The true VP model; (b) The true VS model. |
|
图 4 被动震源分布图 Fig. 4 The distribution of passive sources |
采用20 Hz主频的雷克子波,在x=930 m炮点位置模拟主动源记录.采样间隔为0.001 s,记录时长为1.44 s,得到的z分量和x分量弹性波主动源记录分别如图 5a和图 5b所示.可见,在记录时间内,可以清晰的看出直达波与地下反射信息.在震源位置为x=890 m,z=690 m处模拟被动源记录,采用同样的采样间隔和记录时间,得到的z分量和x分量弹性波被动源记录分别如图 5c和图 5d所示.可见,被动源地震数据的直达波与主动源数据的直达波有明显的区别,其能量较强,是识别瞬态被动源事件的主要依据.地震记录中直达波下方存在丰富的反射信息.

|
图 5 弹性波多分量地震记录 (a)主动源地震记录z分量;(b)主动源地震记录x分量;(c)被动源地震记录z分量;(d)被动源地震记录x分量. Fig. 5 Elastic multi-component seismic records (a) z-component of active seismic records; (b) x-component of active seismic records; (c) z-component of passive seismic records; (d) x-component of passive seismic records. |
采用如图 6a和图 6b的模型分别作为VP和VS的初始模型.首先进行主动源的多尺度全波形反演,迭代200次,VP和VS的反演结果分别如图 7a和图 7b所示.可见,主动源多尺度反演后,模型的整体构造较为清晰,中部和浅部细节构造恢复的比较好,但是,深部储层位置和其他构造均不够清晰.以图 7a和图 7b的结果作为初始模型,进行被动源照明补偿反演.从图 4所示的震源中,选取24个震源进行反演,反演过程震源位置固定不动,即不进行动态反演策略.迭代50次,VP和VS的反演结果分别如图 7c和7d所示.可见,如果震源位置固定不动,将在震源位置处产生大的更新极值,并且导致更多的位置陷入错误的局部极小解.采用本文提出的动态随机组合策略,每组包含10个震源,每迭代4次更换一组震源.以图 7a和图 7b所示的主动源多尺度反演结果为初始模型,总共迭代200次,VP和VS的反演结果分别如图 7e和图 7f所示.与图 7a和图 7b对比可见,经过被动源照明补偿反演后,VP和VS模型的储层位置信息和深部构造细节较常规主动源结果有明显的提升.与图 7c和图 7d对比可知,本文提出的动态随机组合策略能够有效压制震源点附近的极值异常.将图 7a,7b,7e,7f的反演结果与真实纵横波速度模型进行局部对比,如图 8所示.可见,虽然两种反演结果在浅部相近,但是深部复杂构造区的反演效果有较为明显的差异.动态随机组合策略的反演结果比常规主动源多尺度反演结果能够得到更加准确的细节构造,前者对复杂构造区的刻画更加清晰.对图 7所示的反演结果进行局部抽道对比,VP和VS的抽道结果分别如图 9a和图 9b所示.可见,常规主动源多尺度反演能够得到较为准确的深部构造变化趋势,而被动源照明补偿反演能够得到更加准确的速度信息.

|
图 6 初始速度模型 (a)初始VP模型;(b)初始VS模型. Fig. 6 Initial velocity model (a) Initial VP model; (b) Initial VS model. |

|
图 7 弹性波被动源照明补偿策略反演结果 (a)主动源多尺度反演VP结果;(b)主动源多尺度反演VS结果;(c)非动态被动源照明补偿VP反演结果;(d)非动态被动源照明补偿VS反演结果;(e)动态随机组合被动源照明补偿VP反演结果;(f)动态随机组合被动源照明补偿VS反演结果. Fig. 7 Inversion results using elastic passive source illumination compensation strategy (a) VP result using active source multiscale inversion; (b) VS result using active source multiscale inversion; (c) VP result using passive source illumination compensation inversion without dynamic; (d) VS result using passive source illumination compensation inversion without dynamic; (e) VP result using passive source illumination compensation inversion with dynamic random combination; (f) VS result using passive source illumination compensation inversion with dynamic random combination. |
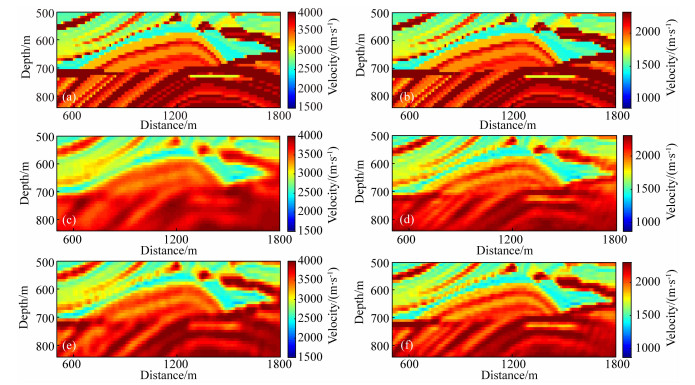
|
图 8 图 7反演结果局部对比图 (a)真实VP局部模型;(b)真实VS局部模型;(c)图 7a局部结果;(d)图 7b局部结果;(e)图 7e局部结果;(f)图 7f局部结果. Fig. 8 Local comparisons of inversion results in Fig. 7 (a) Local true VP model; (b) Local true VS model; (c) Local result of Fig. 7a; (d) Local result of Fig. 7b; (e) Local result of Fig. 7e; (f) Local result of Fig. 7f. |

|
图 9 反演结果抽道对比 (a) VP结果抽道对比;(b) VS结果抽道对比. True:真实模型;Initial:初始模型;FWI:常规主动源多尺度反演结果;PSFWI:本文提出的被动源照明补偿反演结果. Fig. 9 Single trace comparisons (a) Single trace comparisons of VP result; (b) Single trace comparisons of VS result. True: True velocity model; Initial: Initial velocity model; FWI: Conventional active source multiscale FWI result; PSFWI: The proposed passive source illumination compensation FWI result. |
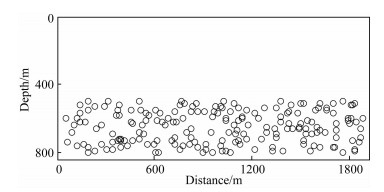
本节用模型数据测试基于地震干涉与不依赖子波算法的弹性波主被动源串联反演策略.本节重点测试如何利用噪声型被动源的低频信息构建速度模型的长波长分量.采用的真实VP(纵波速度)模型如图 3a所示,采用的真实VS(横波速度)模型如图 3b所示.主动源采集时,震源在地表放炮,震源数量为24,左侧第一个震源位于x=50 m位置处,炮间距为80 m.检波器布设在地表 0~1910 m范围内,总共192个检波器,检波器间距为10 m.主动源子波采用缺失低频的雷克子波,如图 10所示.图 10a为20 Hz主频的雷克子波去除9 Hz以下低频成分后的子波.图 10b为震源子波的频谱分析,可见,9 Hz以下的频率成分几乎为零.被动源采集时,200个被动震源随机分布于地下,震源位置如图 11所示.震源子波采用频带范围为0~15 Hz的随机噪声序列.检波器布设与主动源采集时相同.

|
图 10 缺失低频地震子波 (a)子波波形;(b)子波频谱. Fig. 10 Source wavelet without low-frequency information (a) Source wavelet waveform; (b) Source wavelet spectrum. |
|
图 11 被动震源分布图 Fig. 11 The distribution of passive sources |
首先模拟弹性波被动源地震数据.200个噪声震源随机激发地震信号,采样间隔为1 ms,记录总时长为1200 s.得到被动源原始记录后,进行基于互相关的被动源地震干涉重构,得到重构的虚拟炮记录.其中,虚拟炮点位置在x=850 m的x分量激发,z分量接收的一个虚拟炮记录如图 12a所示.虚拟炮点位置在x=850 m的z分量激发,x分量接收的一个虚拟炮记录如图 12b所示.为对比方便,采用10 Hz主频的雷克子波模拟了相同炮点位置和相同激发接收分量的弹性波主动源多分量记录,分别如图 12c和图 12d所示.由于被动源重构记录的直达波信息是不准确的,因此,主动源参考记录均为去除了直达波之后的结果.对比被动源重构记录和主动源参考记录可知,虽然被动源地震记录中含有较多的干扰,但是仍可见许多的有效反射信息.另外,可以发现,被动源重构记录和主动源参考记录之间存在一定的时移,这是由虚拟子波与模拟子波的不同导致的.这种子波引起的时移误差可以通过本文的不依赖子波算法消除掉.
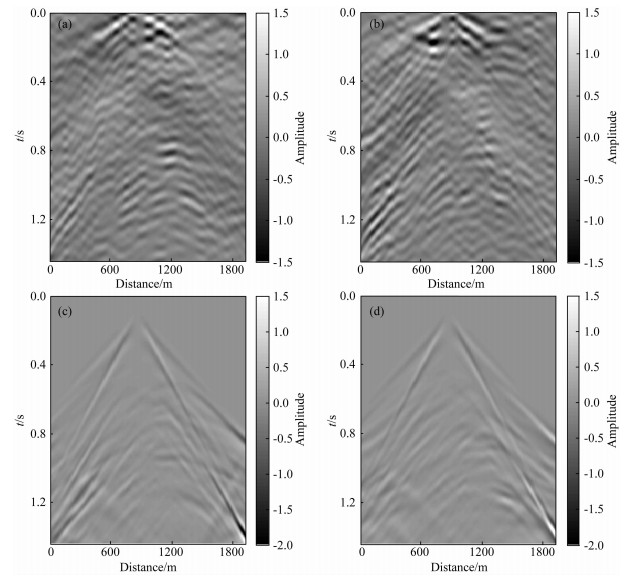
|
图 12 弹性波被动源干涉重构记录 (a)重构记录z分量;(b)重构记录x分量;(c)主动源参考记录z分量;(d)主动源参考记录x分量. Fig. 12 Reconstructed elastic records based on passive seismic interferometry (a) z-component of reconstructed records; (b) x-component of reconstructed records; (c) z-component of active seismic reference records; (d) x-component of active seismic reference records. |
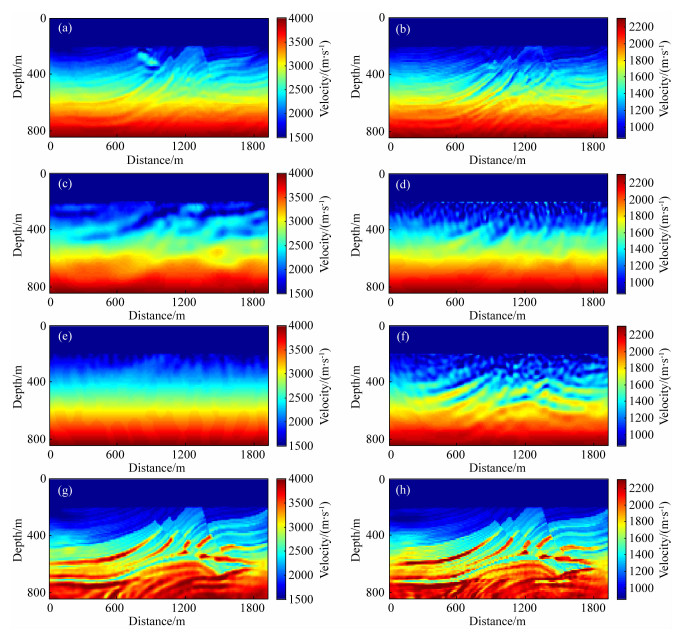
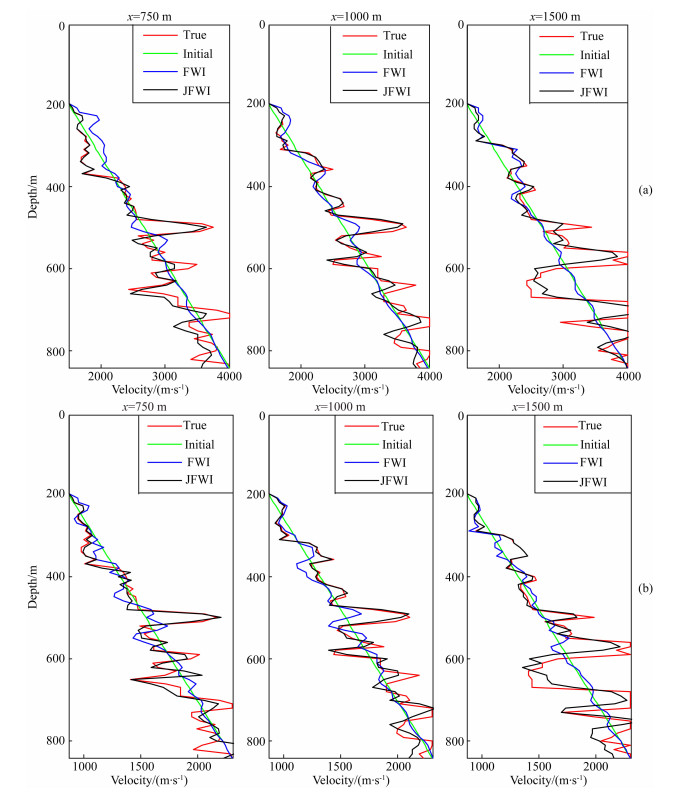
下面进行弹性波全波形反演测试.采用图 10a所示的缺失低频子波,直接进行常规的主动源弹性波全波形反演.采用如图 6所示的模型作为初始模型,迭代100次的VP和VS结果分别如图 13a和图 13b所示.可见,由于子波主频较高且缺失低频,结果的浅部有明显的局部极小值,且深部反演效果较差.采用不依赖子波的算法对被动源重构数据进行反演.由公式(10)可知,反演可以采用任意的模拟子波.为有效提取被动源数据的低频成分用于反演,这里采用的模拟子波为8 Hz主频的雷克子波.首先,对z分量激发的被动源多分量虚拟炮记录进行反演,迭代100次的VP和VS结果分别如图 13c和图 13d所示.可见,VP结果体现了较好的宏观背景速度构造信息,模型深部的构造轮廓也被反演出来.VS结果中含有一些干扰信息,但是基本上也体现了VS模型的大尺度构造信息.然后,对x分量激发的被动源多分量虚拟炮记录进行反演,迭代100次的VP和VS结果分别如图 13e和图 13f所示.可见,VP结果构造信息十分不明显,仅在浅层有微弱的构造显示.VS结果体现了大量的大尺度构造信息,且结果的分辨率比VP的结果高.对比两组被动源反演结果可知:虚拟子波的影响在反演中被成功的消除;z分量激发的被动源虚拟炮记录反演得到的VP结果较好,x分量激发的被动源虚拟炮记录反演得到的VS结果较好.因此,本文提出了将两组结构进行交叉组合,采用图 13c和图 13f分别作为下一步反演的VP和VS的初始模型.以图 13c和图 13f为初始模型,采用图 10a所示的缺失低频子波进行常规主动源弹性波全波形反演.迭代200次的VP和VS结果分别如图 13g和图 13h所示.与图 13a和图 13b所示的常规反演结果对比可知,浅部的跳周现象被克服,最终结果的浅部并未出现明显的局部极小解.模型的主体构造清晰,断层部分的分辨率较高,细节构造较清晰.模型的深部构造也得到了较好的恢复,尤其是在VP和VS模型中,储层位置得到了较明显的体现.对图 13所示的反演结果进行抽道对比,VP和VS的抽道结果分别如图 14a和图 14b所示.可见,常规全波形反演对模型的浅部信息有一定的恢复,但是没能得到深部的速度结构信息.本文提出的主被动源串联全波形反演方法不仅能得到较为准确的浅部速度构造,还能得到较好的深部速度结构信息.
|
图 13 基于地震干涉法的弹性波主被动源串联反演结果 (a)常规主动源VP反演结果;(b)常规主动源VS反演结果;(c) z分量虚源被动源VP反演结果;(d) z分量虚源被动源VS反演结果;(e) x分量虚源被动源VP反演结果;(f) x分量虚源被动源VS反演结果;(g)主被动源串联VP反演结果;(h)主被动源串联VS反演结果. Fig. 13 Inversion results of elastic active and passive source successive inversion strategy based on seismic interferometry (a) VP result using conventional active source inversion; (b) VS result using conventional active source inversion; (c) Inversion result of VP using passive seismic data due to z-component virtual sources; (d) Inversion result of VS using passive seismic data due to z-component virtual sources; (e) Inversion result of VP using passive seismic data due to x-component virtual sources; (f) Inversion result of VS using passive seismic data due to x-component virtual sources; (g) VP result using active and passive source successive inversion; (h) VS result using active and passive source successive inversion. |
|
图 14 反演结果抽道对比 (a) VP结果抽道对比;(b) VS结果抽道对比. True:真实模型;Initial:初始模型;FWI:常规主动源反演结果;JFWI:本文提出的主被动源串联反演结果. Fig. 14 Single trace comparisons (a) Single trace comparisons of VP result; (b) Single trace comparisons of VS result. True: True velocity model; Initial: Initial velocity model; FWI: Conventional active source FWI result; JFWI: The proposed active and passive source successive FWI result. |
本文提出了两种针对弹性波主被动源多分量混采地震数据的全波形反演策略,并分别进行了数值算例的测试.第一种策略适用于弹性波主动源和瞬态被动源地震数据的全波形反演.在主动源全波形反演的后期,加入被动源地震数据用作照明补偿,可以得到更加准确的深部细节构造信息.动态随机组合反演策略能有效压制被动震源位置附近的局部异常值.但是,该方法在对被动源数据进行反演时,要求已知被动震源的位置和震源子波.如果被动源定位存在较大误差,则会由于震源位置不准导致模拟数据与观测数据的差异,从而引起反演的跳周现象.同样,震源子波不准也会降低反演的效果.在实际应用中可以考虑在反演过程中不断更新被动源的位置和震源子波.
第二种策略适用于弹性波主动源和噪声型被动源地震数据的全波形反演.提出了基于地震干涉和不依赖子波的联合反演算法,能够克服被动源记录重构后虚拟震源子波对反演结果的影响.利用被动源的低频信号可以得到纵、横波速度模型的大尺度宏观构造信息,用作常规缺失低频主动源全波形反演的初始模型,可以很大程度上缓解反演的跳周问题.与第一种策略不同,该策略无需进行被动震源定位与震源子波估计,该方法的关键是被动源地震数据的质量.由于本方法采用地震干涉法重构被动源地震数据,因此,影响被动源地震干涉法的因素也会最终影响被动源数据的反演效果,如被动源地震数据的记录时长、被动源的分布区域等都是影响重构效果的重要因素.
Alali A, Van Der Neut J, Draganov D. 2016. Merging active and passive seismic reflection data with interferometry by multidimensional deconvolution.//86th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 5182-5186.
|
Baradello L, Accaino F, Bohm G, et al. 2015. Elastic tomographic inversion of the near surface by active and passive seismic.//Near-Surface Asia Pacific Conference, Expanded Abstracts, 280-283.
|
Berkhout A J, Verschuur D J. 2009. Integrated imaging with active and passive seismic data.//Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1592-1596.
|
Berkhout A J, Verschuur D J. 2011. A scientific framework for active and passive seismic imaging, with applications to blended data and micro-earthquake responses. Geophysical Journal International, 184(2): 777-792. DOI:10.1111/j.1365-246X.2010.04855.x |
Boonyasiriwat C, Schuster G T. 2010.3D multisource full-waveform inversion using dynamic random phase encoding.//80th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1044-1049.
|
Choi Y, Alkhalifah T. 2011. Source-independent time-domain waveform inversion using convolved wavefields:Application to the encoded multisource waveform inversion. Geophysics, 76(5): R125-R134. DOI:10.1190/geo2010-0210.1 |
Crase E, Pica A, Noble M, et al. 1990. Robust elastic nonlinear waveform inversion:Application to real data. Geophysics, 55(5): 527-538. DOI:10.1190/1.1442864 |
Draganov D, Wapenaar K, Thorbecke J. 2006. Seismic interferometry:reconstructing the earth's reflection response. Geophysics, 71(4): SI61-SI70. DOI:10.1190/1.2209947 |
Forgues E, Schisselé-Rebel E, Cotton J. 2011. Simultaneous active/passive seismic monitoring of steam assisted heavy oil production.//81th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4082-4086.
|
Hayashi K. 2017. Application of active and passive surface-wave methods to shallow to deep S-wave velocity estimation.//87th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 5202-5206.
|
Hu Y, Han L G, Zhang P, et al. 2016. Multistep full-waveform inversion based on waveform-mode decomposition.//86th SEG Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1501-1505.
|
Kamei R, Lumley D. 2014. Passive seismic imaging and velocity inversion using full wavefield methods.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2273-2277.
|
Li X X. 2017. Study on the joint tomographic method for active and passive source Rayleigh wave data[Ph. D thesis] (in Chinese). Xi'an: Chang'an University.
|
Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data. Geophysics, 52(9): 1211-1228. DOI:10.1190/1.1442384 |
Mora P. 1988. Elastic wave-field inversion of reflection and transmission data. Geophysics, 53(6): 750-759. DOI:10.1190/1.1442510 |
Park C B, Miller R D, Ryden N, et al. 2005. Combined use of active and passive surface waves. Journal of Environmental and Engineering Geophysics, 10(3): 323-334. DOI:10.2113/JEEG10.3.323 |
Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophysical Journal International, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
Prieux V, Lambaré G, Operto S, et al. 2013. Building starting models for full waveform inversion from wide-aperture data by stereotomography. Geophysical Prospecting, 61(S1): 109-137. |
Sheng J M, Leeds A, Buddensiek M, et al. 2006. Early arrival waveform tomography on near-surface refraction data. Geophysics, 71(4): U47-U57. DOI:10.1190/1.2210969 |
Sun H Y, Han L G, Han M, et al. 2015. Elastic full waveform inversion based on visibility analysis and energy compensation for metallic deposit exploration. Chinese Journal of Geophysics (in Chinese), 58(12): 4605-4616. DOI:10.6038/cjg20151222 |
Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
Tarantola A. 1988. Theoretical background for the inversion of seismic waveforms including elasticity and attenuation. Pure and Applied Geophysics, 128(1-2): 365-399. DOI:10.1007/BF01772605 |
Vesnaver A, Lovisa L, Böhm G. 2010. Joint 3D processing of active and passive seismic data. Geophysical Prospecting, 58(5): 831-844. DOI:10.1111/j.1365-2478.2010.00868.x |
Vigh D, Jiao K, Watts D, et al. 2014. Elastic full-waveform inversion application using multicomponent measurements of seismic data collection. Geophysics, 79(2): R63-R77. DOI:10.1190/geo2013-0055.1 |
Wang Y W, Dong L G, Huang C, et al. 2016. A multi-step strategy for mitigating severe nonlinearity in elastic full-waveform inversion. Oil Geophysical Prospecting (in Chinese), 51(2): 288-294. |
Wapenaar K, Fokkema J. 2006. Green's function representations for seismic interferometry. Geophysics, 71(4): SI33-SI46. DOI:10.1190/1.2213955 |
Xu Y X, Zhang B L, Luo Y H, et al. 2013. Surface-wave observation after integrating active and passive source data. The Leading Edge, 32(6): 634-637. DOI:10.1190/tle32060634.1 |
Xu Z. 2012. A study of imaging technique and application based on seismic interferometry method[Ph. D. thesis] (in Chinese). Changchun: Jilin University.
|
Zhang P, Han L G, Liu Q, et al. 2015. Interpolation of seismic data from active and passive sources and their joint migration imaging. Chinese Journal of Geophysics (in Chinese), 58(5): 1754-1766. DOI:10.6038/cjg20150525 |
Zhang P, Han L G, Zhou Y, et al. 2015. Passive-source multitaper-spectral method based low-frequency data reconstruction for active seismic sources. Applied Geophysics, 12(4): 585-597. DOI:10.1007/s11770-015-0520-2 |
Zhang P, Han L G, Jin Z Y, et al. 2016. Passive source illumination compensation based full waveform inversion.//78th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts.
|
Zhang P, Han L G, Xu Z, et al. 2017. Sparse blind deconvolution based low-frequency seismic data reconstruction for multiscale full waveform inversion. Journal of Applied Geophysics, 139: 91-108. DOI:10.1016/j.jappgeo.2017.02.021 |
Zhang P. 2018. The study on full waveform inversion based on low-frequency seismic wavefield reconstruction[Ph. D. thesis] (in Chinese). Changchun: Jilin University.
|
Zhang P, Han L G, Gong X B, et al. 2018. Multi-source elastic full waveform inversion based on the anisotropic total variation constraint. Chinese Journal of Geophysics (in Chinese), 61(2): 716-732. DOI:10.6038/cjg2018L0122 |
Zhang P, Wu R S, Han L G. 2018. Source-independent seismic envelope inversion based on the direct envelope Fréchet derivative. Geophysics, 83(6): R581-R595. DOI:10.1190/geo2017-0360.1 |
Zhang Q C, Zhou H, Li Q Q, et al. 2016. Robust source-independent elastic full-waveform inversion in the time domain. Geophysics, 81(2): R13-R28. DOI:10.1190/geo2015-0258.1 |
李欣欣. 2017.主动源与被动源瑞利波联合成像方法研究[博士论文].西安: 长安大学.
|
孙宏宇, 韩立国, 韩淼, 等. 2015. 基于可视性分析与能量补偿的金属矿弹性波全波形反演. 地球物理学报, 58(12): 4605-4616. DOI:10.6038/cjg20151222 |
王毓玮, 董良国, 黄超, 等. 2016. 降低弹性波全波形反演强烈非线性的分步反演策略. 石油地球物理勘探, 51(2): 288-294. |
许卓. 2012.基于地震干涉法的波场成像技术及应用研究[博士论文].长春: 吉林大学.
|
张盼, 韩立国, 刘强, 等. 2015. 主动源与被动源地震数据插值及联合数据成像. 地球物理学报, 58(5): 1754-1766. DOI:10.6038/cjg20150525 |
张盼. 2018.基于低频地震波场重构的全波形反演研究[博士论文].长春: 吉林大学.
|
张盼, 韩立国, 巩向博, 等. 2018. 基于各向异性全变分约束的多震源弹性波全波形反演. 地球物理学报, 61(2): 716-732. DOI:10.6038/cjg2018L0122 |
 2019, Vol. 62
2019, Vol. 62

